Comprehensive Design Example for Prestressed Concrete (PSC) Girder Superstructure Bridge
Design Step 5 Design of Superstructure
Design Step 5.1 Live Load Distribution Factors (S4.6.2.2)
The AASHTO-LRFD Specifications allow the use of advanced methods of analysis to determine the live load distribution factors. However, for typical bridges, the specifications list equations to calculate the distribution factors for different types of bridge superstructures. The types of superstructures covered by these equations are described in Table S4.6.2.2.1-1. From this table, bridges with concrete decks supported on precast concrete I or bulb-tee girders are designated as cross-section "K". Other tables in S4.6.2.2.2 list the distribution factors for interior and exterior girders including cross-section "K". The distribution factor equations are largely based on work conducted in the NCHRP Project 12-26 and have been verified to give accurate results compared to 3-dimensional bridge analysis and field measurements. The multiple presence factors are already included in the distribution factor equations except when the tables call for the use of the lever rule. In these cases, the computations need to account for the multiple presence factors. Notice that the distribution factor tables include a column with the heading "range of applicability". The ranges of applicability listed for each equation are based on the range for each parameter used in the study leading to the development of the equation. When the girder spacing exceeds the listed value in the "range of applicability" column, the specifications require the use of the lever rule (S4.6.2.2.1). One or more of the other parameters may be outside the listed range of applicability. In this case, the equation could still remain valid, particularly when the value(s) is(are) only slightly out of the range of applicability. However, if one or more of the parameters greatly exceed the range of applicability, engineering judgment needs to be exercised.
Article S4.6.2.2.2d of the specifications states: "In beam-slab bridge cross-sections with diaphragms or cross-frames, the distribution factor for the exterior beam shall not be taken less than that which would be obtained by assuming that the cross-section deflects and rotates as a rigid cross-section". This provision was added to the specifications because the original study that developed the distribution factor equations did not consider intermediate diaphragms. Application of this provision requires the presence of a sufficient number of intermediate diaphragms whose stiffness is adequate to force the cross section to act as a rigid section. For prestressed girders, different jurisdictions use different types and numbers of intermediate diaphragms. Depending on the number and stiffness of the intermediate diaphragms, the provisions of S4.6.2.2.2d may not be applicable. For this example, one deep reinforced concrete diaphragm is located at the midspan of each span. The stiffness of the diaphragm was deemed sufficient to force the cross-section to act as a rigid section, therefore, the provisions of S4.6.2.2.2d apply.
Notice that the AASHTO Standard Specifications express the distribution factors as a fraction of wheel lines, whereas the AASHTO-LRFD Specifications express them as a fraction of full lanes.
For this example, the distribution factors listed in S4.6.2.2.2 will be used.
Notice that fatigue in the prestressing steel need not be checked for conventional prestressed girders (S5.5.3) when maximum stress in the concrete at Service III limit state is taken according to Table S5.9.4.2.2-1. This statement is valid for this example. The fatigue distribution factors are calculated in the following sections to provide the user with a complete reference for the application of the LRFD distribution factors.
Required information:
AASHTO Type I-Beam (28/72)
| Noncomposite beam area, Ag | = 1,085 in2 |
| Noncomposite beam moment of inertia, Ig | = 733,320 in4 |
| Deck slab thickness, ts | = 8 in. |
| Span length, L | = 110 ft. |
| Girder spacing, S | = 9 ft. - 8 in. |
| Modulus of elasticity of the beam, EB | = 4,696 ksi (S5.4.2.4) |
| Modulus of elasticity of the deck, ED | = 3,834 ksi (S5.4.2.4) |
| C.G. to top of the basic beam | = 35.62 in. |
| C.G. to bottom of the basic beam | = 36.38 in. |
Design Step 5.1.1
Calculate n, the modular ratio between the beam and the deck.
| n | = EB/ED = 4,696/3,834 = 1.225 |
(S4.6.2.2.1-2) |
Design Step 5.1.2
Calculate eg, the distance between the center of gravity of the noncomposite beam and the deck. Ignore the thickness of the haunch in determining eg. It is also possible to ignore the integral wearing surface, i.e., use ts = 7.5 in. However the difference in the distribution factor will be minimal.
| eg | = NAYT + ts/2 = 35.62 + 8/2 = 39.62 in. |
Design Step 5.1.3
Calculate Kg, the longitudinal stiffness parameter.
| Kg | = n(I + Aeg2) = 1.225[733,320 + 1,085(39.62)2] = 2,984,704 in4 |
(S4.6.2.2.1-1) |
Design Step 5.1.4 - Interior girder
Calculate the moment distribution factor for an interior beam with two or more design lanes loaded using Table S4.6.2.2.2b-1.
| DM | = 0.075 + (S/9.5)0.6 (S/L)0.2 (Kg/12.0Lts3)0.1 = 0.075 + (9.667/9.5)0.6 (9.667/110)0.2 [2,984,704/[12(110)(8)3]]0.1 = 0.796 lane (1) |
Design Step 5.1.5
According to S4.6.2.2.2e, a skew correction factor for moment may be applied for bridge skews greater than 30 degrees. The bridge in this example is skewed 20 degrees, and, therefore, no skew correction factor for moment is allowed.
Calculate the moment distribution factor for an interior beam with one design lane loaded using Table S4.6.2.2.2b-1.
| DM | = 0.06 + (S/14)0.4 (S/L)0.3 (Kg/12.0Lts3)0.1 = 0.06 + (9.667/14)0.4 (9.667/110)0.3 [2,984,704/[12(110)(8)3]]0.1 = 0.542 lane (2) |
Notice that the distribution factor calculated above for a single lane loaded already includes the 1.2 multiple presence factor for a single lane, therefore, this value may be used for the service and strength limit states. However, multiple presence factors should not be used for the fatigue limit state. Therefore, the multiple presence factor of 1.2 for the single lane is required to be removed from the value calculated above to determine the factor used for the fatigue limit state.
For single-lane loading to be used for fatigue design, remove the multiple presence factor of 1.2.
| DM | = 0.542/1.2 = 0.452 lane (3) |
Design Step 5.1.6 - Skew correction factor for shear
According to S4.6.2.2.3c, a skew correction factor for support shear at the obtuse corner must be applied to the distribution factor of all skewed bridges. The value of the correction factor is calculated using Table S4.6.2.2.3c-1
| SC | = 1.0 + 0.20(12.0Lts3/Kg)0.3 tan θ = 1.0 + 0.20[[12.0(110)(8)3]/2,984,704]0.3 tan 20 = 1.047 |
Design Step 5.1.7
Calculate the shear distribution factor for an interior beam with two or more design lanes loaded using Table S4.6.2.2.3a-1.
| DV | = 0.2 + (S/12) - (S/35)2 = 0.2 + (9.667/12) - (9.667/35)2 = 0.929 lane |
Apply the skew correction factor:
| DV | = 1.047(0.929) = 0.973 lane (4) |
Design Step 5.1.8
Calculate the shear distribution factor for an interior beam with one design lane loaded using Table S4.6.2.2.3a-1.
| DV | = 0.36 + (S/25.0) = 0.36 + (9.667/25.0) = 0.747 lane |
Apply the skew correction factor:
| DV | = 1.047(0.747) = 0.782 lane (5) |
For single-lane loading to be used for fatigue design, remove the multiple presence factor of 1.2.
| DV | = 0.782/1.2 = 0.652 lane (6) |
Design Step 5.1.9
From (1) and (2), the service and strength limit state moment distribution factor for the interior girder is equal to the larger of 0.796 and 0.542 lane. Therefore, the moment distribution factor is 0.796 lane.
From (3):
The fatigue limit state moment distribution factor is 0.452 lane
From (4) and (5), the service and strength limit state shear distribution factor for the interior girder is equal to the larger of 0.973 and 0.782 lane. Therefore, the shear distribution factor is 0.973 lane.
From (6):
The fatigue limit state shear distribution factor is 0.652 lane
Design Step 5.1.10 - Exterior girder
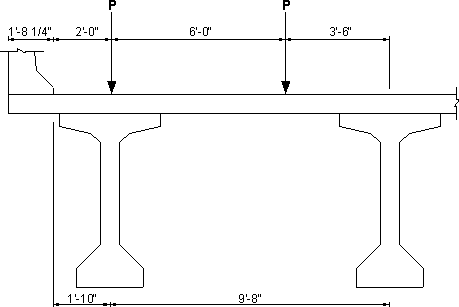
Figure 5.1-1 - Lever Rule
Design Step 5.1.11
Calculate the moment distribution factor for an exterior beam with two or more design lanes using Table S4.6.2.2.2d-1.
| DM | = eDMInterior
e = 0.77 + de/9.1 where de is the distance from the centerline of the exterior girder to the inside face of the curb or barrier. e = 0.77 + 1.83/9.1 = 0.97 |
| DM | = 0.97(0.796) = 0.772 lane (7) |
Design Step 5.1.12
Calculate the moment distribution factor for an exterior beam with one design lane using the lever rule as per Table S4.6.2.2.2d-1.
| DM | = [(3.5 + 6) + 3.5]/9.667 = 1.344 wheels/2 = 0.672 lane (8) (Fatigue) |
Notice that this value does not include the multiple presence factor, therefore, it is adequate for use with the fatigue limit state. For service and strength limit states, the multiple presence factor for a single lane loaded needs to be included.
| DM | = 0.672(1.2) = 0.806 lane (9) (Strength and Service) |
Design Step 5.1.13
Calculate the shear distribution factor for an exterior beam with two or more design lanes loaded using Table S4.6.2.2.3b-1.
| DV | = eDVinterior |
where:
| e | = 0.6 + de/10 = 0.6 + 1.83/10 = 0.783 |
| DV | = 0.783(0.973) = 0.762 lane (10) |
Design Step 5.1.14
Calculate the shear distribution factor for an exterior beam with one design lane loaded using the lever rule as per Table S4.6.2.2.3b-1. This value will be the same as the moment distribution factor with the skew correction factor applied.
| DV | = 1.047(0.672) = 0.704 lane (11) (Fatigue) |
| DV | = 1.047(0.806) = 0.845 lane (12) (Strength and Service) |
Notice that S4.6.2.2.2d includes additional requirements for the calculation of the distribution factors for exterior girders when the girders are connected with relatively stiff cross-frames that force the cross-section to act as a rigid section. As indicated in Design Step 5.1, these provisions are applied to this example; the calculations are shown below.
Design Step 5.1.15 - Additional check for rigidly connected girders (S4.6.2.2.2d)
The multiple presence factor, m, is applied to the reaction of the exterior beam (Table S3.6.1.1.2-1)
| m1 | = 1.20 |
| m2 | = 1.00 |
| m3 | = 0.85 |
| R | = NL/Nb + Xext(Σe)/Σx2 (SC4.6.2.2.2d-1) |
where:R = reaction on exterior beam in terms of lanes
NL = number of loaded lanes under consideration
e = eccentricity of a design truck or a design land load from the center of gravity of the pattern of girders (ft.)
x = horizontal distance from the center of gravity of the pattern of girders to each girder (ft.)
Xext = horizontal distance from the center of gravity of the pattern to the exterior girder (ft.)
See Figure 5.1-1 for dimensions.
One lane loaded (only the leftmost lane applied):
| R | = 1/6 + 24.167(21)/[2(24.1672 + 14.52 + 4.8332)] = 0.1667 + 0.310 = 0.477 (Fatigue) |
Add the multiple presence factor of 1.2 for a single lane:
| R | = 1.2(0.477) = 0.572 (Strength) |
Two lanes loaded:
| R | = 2/6 + 24.167(21 + 9)/[2(24.1672 + 14.52 + 4.8332)] = 0.333 + 0.443 = 0.776 |
Add the multiple presence factor of 1.0 for two lanes loaded:
| R | = 1.0(0.776) = 0.776 (Strength) |
Three lanes loaded:
| R | = 3/6 + 24.167(21 + 9 - 3)/[2(24.1672 + 14.52 + 4.8332)] = 0.5 + 0.399 = 0.899 |
Add the multiple presence factor of 0.85 for three or more lanes loaded:
| R | = 0.85(0.899) = 0.764 (Strength) |
These values do not control over the distribution factors summarized in Design Step 5.1.16.
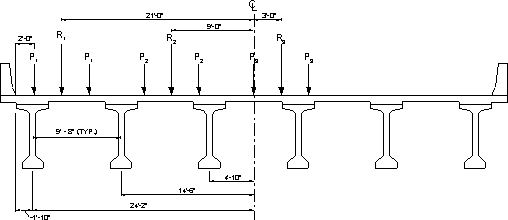
Figure 5.1-2 - General Dimensions
Design Step 5.1.16
From (7) and (9), the service and strength limit state moment distribution factor for the exterior girder is equal to the larger of 0.772 and 0.806 lane. Therefore, the moment distribution factor is 0.806 lane.
From (8):
The fatigue limit state moment distribution factor is 0.672 lane
From (10) and (12), the service and strength limit state shear distribution factor for the exterior girder is equal to the larger of 0.762 and 0.845 lane. Therefore, the shear distribution factor is 0.845 lane.
From (11):
The fatigue limit state shear distribution factor is 0.704 lane
Table 5.1-1 - Summary of Service and Strength Limit State Distribution Factors
| Load Case | Moment interior beams | Moment exterior beams | Shear interior beams | Shear exterior beams | |
|---|---|---|---|---|---|
| Distribution factors from Tables in S4.6.2.2.2 | Multiple lanes loaded | 0.796 | 0.772 | 0.973 | 0.762 |
| Single lane loaded | 0.542 | 0.806 | 0.782 | 0.845 | |
| Additional check for rigidly connected girders | Multiple lanes loaded | NA | 0.776 | NA | 0.776 |
| Single lane loaded | NA | 0.572 | NA | 0.572 | |
| Design value | 0.796 | 0.806 | 0.973 | 0.845 |
Table 5.1-2 - Summary of Fatigue Limit State Distribution Factors
| Load Case | Moment interior beams | Moment exterior beams | Shear interior beams | Shear exterior beams | |
|---|---|---|---|---|---|
| Distribution factors from Tables in S4.6.2.2.2 | Multiple lanes loaded | NA | NA | NA | NA |
| Single lane loaded | 0.452 | 0.672 | 0.652 | 0.704 | |
| Additional check for rigidly connected girders | Multiple lanes loaded | NA | NA | NA | NA |
| Single lane loaded | NA | 0.477 | NA | 0.477 | |
| Design value | 0.452 | 0.672 | 0.652 | 0.704 |

