LRFD Steel Girder SuperStructure Design Example
Design Step 1 - General Information/Introduction
Table of Contents
Introduction
Design Step 1.1 - Obtain Design Criteria
Design Step 1.2 - Obtain Geometry Requirements
Design Step 1.3 - Perform Span Arrangement Study
Design Step 1.4 - Obtain Geotechnical Recommendations
Design Step 1.5 - Perform Type, Size and Location Study
Design Step 1.6 - Plan for Bridge Aesthetics
Introduction
Design Step 1 is the first of several steps that illustrate the design procedures used for a steel girder bridge. This design step serves as an introduction to this design example and it provides general information about the bridge design.
Purpose
The purpose of this project is to provide a basic design example for a steel girder bridge as an informational tool for the practicing bridge engineer. The example is also aimed at assisting the bridge engineer with the transition from Load Factor Design (LFD) to Load and Resistance Factor Design (LRFD).
AASHTO References
For uniformity and simplicity, this design example is based on the AASHTO LRFD Bridge Design Specifications (Second Edition, 1998, including interims for 1999 through 2002). References to the AASHTO LRFD Bridge Design Specifications are included throughout the design example. AASHTO references are presented in a dedicated column in the right margin of each page, immediately adjacent to the corresponding design procedure. The following abbreviations are used in the AASHTO references:
S designates specifications
STable designates a table within the specifications
SFigure designates a figure within the specifications
SEquation designates an equation within the specifications
SAppendix designates an appendix within the specifications
C designates commentary
CTable designates a table within the commentary
CFigure designates a figure within the commentary
CEquation designates an equation within the commentary
State-specific specifications are generally not used in this design example. Any exceptions are clearly noted.
Design Methodology
This design example is based on Load and Resistance Factor Design (LRFD), as presented in the AASHTO LRFD Bridge Design Specifications. The following is a general comparison between the primary design methodologies:
Service Load Design (SLD) or Allowable Stress Design (ASD) generally treats each load on the structure as equal from the viewpoint of statistical variability. The safety margin is primarily built into the capacity or resistance of a member rather than the loads.
Load Factor Design (LFD) recognizes that certain design loads, such as live load, are more highly variable than other loads, such as dead load. Therefore, different multipliers are used for each load type. The resistance, based primarily on the estimated peak resistance of a member, must exceed the combined load.
Load and Resistance Factor Design (LRFD) takes into account both the statistical mean resistance and the statistical mean loads. The fundamental LRFD equation includes a load modifier (η), load factors (γ), force effects (Q), a resistance factor (Φ), a nominal resistance (Rn), and a factored resistance (Rr = ΦRn). LRFD provides a more uniform level of safety throughout the entire bridge, in which the measure of safety is a function of the variability of the loads and the resistance.
S1.3
Detailed Outline and Flowcharts
Each step in this design example is based on a detailed outline and a series of flowcharts that were developed for this project.
The detailed outline and the flowcharts are intended to be comprehensive. They include the primary design steps that would be required for the design of various steel girder bridges.
This design example includes the major steps shown in the detailed outline and flowcharts, but it does not include all design steps. For example, longitudinal stiffener design, girder camber computations, and development of special provisions are included in the detailed outline and the flowcharts. However, their inclusion in the design example is beyond the scope of this project.
Software
An analysis of the superstructure was performed using AASHTO Opis® software. The design moments, shears, and reactions used in the design example are taken from the Opis output, but their computation is not shown in the design example.
Organization of Design Example
To make this reference user-friendly, the numbers and titles of the design steps are consistent between the detailed outline, the flowcharts, and the design example.
In addition to design computations, the design example also includes many tables and figures to illustrate the various design procedures and many AASHTO references. It also includes commentary to explain the design logic in a user-friendly way. A figure is generally provided at the end of each design step, summarizing the design results for that particular bridge element.
 |
Tip BoxesTip boxes are used throughout the design example computations to present useful information, common practices, and rules of thumb for the bridge designer. Tip boxes are shaded and include a tip icon, just like this. Tips do not explain what must be done based on the design specifications; rather, they present suggested alternatives for the designer to consider. |
Design Parameters
The following is a list of parameters upon which this design example is based:
- Two span, square, continuous structure configuration
- Bridge width 44 feet curb to curb (two 12-foot lanes and two 10-foot shoulders)
- Reinforced concrete deck with overhangs
- F-shape barriers (standard design)
- Grade 50 steel throughout
- Opis superstructure design software to be used to generate superstructure loads
- Nominally stiffened web with no web tapers
- Maximum of two flange transitions top and bottom, symmetric about pier centerline
- Composite deck throughout, with one shear connector design/check
- Constructibility checks based on a single deck pour
- Girder to be designed with appropriate fatigue categories (to be identified on sketches)
- No detailed cross-frame design (general process description provided)
- One bearing stiffener design
- Transverse stiffeners designed as required
- One field splice design (commentary provided on economical locations)
- One elastomeric bearing design
- Reinforced concrete cantilever abutments on piles (only one will be designed, including pile computations)
- One cantilever type wingwall will be designed (all four wingwalls are similar in height and configuration)
- Reinforced concrete hammerhead pier configuration with pile foundation
Summary of Design Steps
The following is a summary of the major design steps included in this project:
Design Step 1 - General Information
Design Step 2 - Concrete Deck Design
Design Step 3 - Steel Girder Design
Design Step 4 - Bolted Field Splice Design
Design Step 5 - Miscellaneous Steel Design (i.e., shear connectors, bearing stiffeners, and cross frames)
Design Step 6 - Bearing Design
Design Step 7 - Abutment and Wingwall Design
Design Step 8 - Pier Design
Design Step 9 - Miscellaneous Design (i.e., approach slabs, deck drainage, and bridge lighting)
Design Step 10 - Special Provisions and Cost Estimate
Design Step P - Pile Foundation Design (part of Design Steps 7 & 8)
To provide a comprehensive summary for general steel bridge design, all of the above design steps are included in the detailed outline and in the flowcharts. However, this design example includes only those steps that are within the scope of this project. Therefore, Design Steps 1 through 8 are included in the design example, but Design Steps 9 and 10 are not.
The following units are defined for use in this design example:
![]()
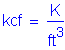
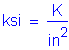
Design Step 1.1 - Obtain Design Criteria
The first step for any bridge design is to establish the design criteria. For this design example, the following is a summary of the primary design criteria:
Design Criteria
| Governing specifications: | AASHTO LRFD Bridge Design Specifications (Second Edition, 1998, including interims for 1999 through 2002) | |
| Design methodology: | Load and Resistance Factor Design (LRFD) | |
| Live load requirements: | HL-93 | S3.6 |
| Deck width: | ||
| Roadway width: | ||
| Bridge length: | ||
| Skew angle: | ||
| Structural steel yield strength: | STable 6.4.1-1 | |
| Structural steel tensile strength: | STable 6.4.1-1 | |
| Concrete 28-day compressive strength: | S5.4.2.1 | |
| Reinforcement strength: | S5.4.3 & S6.10.3.7 | |
| Steel density: | STable 3.5.1-1 | |
| Concrete density: | STable 3.5.1-1 | |
| Parapet weight (each): | ||
| Future wearing surface: | STable 3.5.1-1 | |
| Future wearing surface thickness: |
Design Factors from AASHTO LRFD Bridge Design Specifications
S1.3.2.1The first set of design factors applies to all force effects and is represented by the Greek letter η (eta) in the Specifications. These factors are related to the ductility, redundancy, and operational importance of the structure. A single, combined eta is required for every structure. When a maximum load factor from STable 3.4.1-2 is used, the factored load is multiplied by eta, and when a minimum load factor is used, the factored load is divided by eta. All other loads, factored in accordance with STable 3.4.1-1, are multiplied by eta if a maximum force effect is desired and are divided by eta if a minimum force effect is desired. In this design example, it is assumed that all eta factors are equal to 1.0.
For loads for which the maximum value of γi is appropriate:
| SEquation 1.3.2.1-2 |
For loads for which the minimum value of γi is appropriate:
| SEquation 1.3.2.1-3 |
Therefore for this design example, use:
The following is a summary of other design factors from the AASHTO LRFD Bridge Design Specifications. Additional information is provided in the Specifications, and specific section references are provided in the right margin of the design example.
Load factors:
STable 3.4.1-1 & STable 3.4.1-2
| Limit State | Load Factor | |||||||
|---|---|---|---|---|---|---|---|---|
| DC Max |
DC Min |
DW Max |
DW Min |
LL | IM | WS | WL | |
| Strength I | 1.25 | 0.90 | 1.50 | 0.65 | 1.75 | 1.75 | - | - |
| Strength III | 1.25 | 0.90 | 1.50 | 0.65 | - | - | 1.40 | - |
| Strength V | 1.25 | 0.90 | 1.50 | 0.65 | 1.35 | 1.35 | 0.40 | 1.00 |
| Service I | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.30 | 1.00 |
| Service II | 1.00 | 1.00 | 1.00 | 1.00 | 1.30 | 1.30 | - | - |
| Fatigue | - | - | - | - | 0.75 | 0.75 | - | - |
Table 1-1 Load Combinations and Load Factors
The abbreviations used in Table 1-1 are as defined in S3.3.2.
The extreme event limit state (including earthquake load) is not considered in this design example.
Resistance factors:
S5.5.4.2 & S6.5.4.2
| Material | Type of Resistance | Resistance Factor Φ |
|---|---|---|
| Structural Steel | For flexure | Φf = 1.00 |
| For shear | Φv = 1.00 | |
| for axial compression | Φc = 0.90 | |
| for bearing | Φb = 1.00 | |
| Reinforced Concrete | for flexure and tension | Φf = 0.90 |
| for shear and tension | Φv = 0/90 | |
| for axial compression | Φa = 0.75 | |
| for compression with flexure |
Φ = 0.75 to 0.90 (linear interpolation) |
Table 1-2 Resistance Factors
Multiple presence factors:
STable 3.6.1.1.2-1
| Number of lanes Loaded | Multiple Presence Factor, m |
|---|---|
| 1 | 1.20 |
| 2 | 1.00 |
| 3 | 0.85 |
| >3 | 0.65 |
Table 1-3 Multiple Presence Factors
Dynamic load allowance:
STable 3.6.2.1-1
| Limit State | Dynamic Load Allowance, IM |
|---|---|
| Fatigue and Fracture Limit State | 15% |
| All Other limit States | 33% |
Table 1-4 Dynamic Load Allowance
Design Step 1.2 - Obtain Geometry Requirements
Geometry requirements for the bridge components are defined by the bridge site and by the highway geometry. Highway geometry constraints include horizontal alignment and vertical alignment.
Horizontal alignment can be tangent, curved, spiral, or a combination of these three geometries.
Vertical alignment can be straight sloped, crest, sag, or a combination of these three geometries.
For this design example, it is assumed that the horizontal alignment geometry is tangent and the vertical alignment geometry is straight sloped.
Design Step 1.3 - Perform Span Arrangement Study
Some clients require a Span Arrangement Study. The Span Arrangement Study includes selecting the bridge type, determining the span arrangement, determining substructure locations, computing span lengths, and checking horizontal clearance for the purpose of approval.
Although a Span Arrangement Study may not be required by the client, these determinations must still be made by the engineer before proceeding to the next design step.
For this design example, the span arrangement is presented in Figure 1-1. This span arrangement was selected to illustrate various design criteria and the established geometry constraints identified for this example.
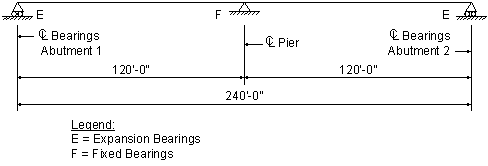
Figure 1-1 Span Arrangement
Design Step 1.4 - Obtain Geotechnical Recommendations
The subsurface conditions must be determined to develop geotechnical recommendations.
Subsurface conditions are commonly determined by taking core borings at the bridge site. The borings provide a wealth of information about the subsurface conditions, all of which is recorded in the boring logs.
It is important to note that the boring log reveals the subsurface conditions for a finite location and not necessarily for the entire bridge site. Therefore, several borings are usually taken at each proposed substructure location. This improves their reliability as a reflection of subsurface conditions at the bridge site, and it allows the engineer to compensate for significant variations in the subsurface profile.
After the subsurface conditions have been explored and documented, a geotechnical engineer must develop foundation type recommendations for all substructures. Foundations can be spread footings, pile foundations, or drilled shafts. Geotechnical recommendations typically include allowable bearing pressure, allowable settlement, and allowable pile resistances (axial and lateral), as well as required safety factors for overturning and sliding.
For this design example, pile foundations are used for all substructure units.
Design Step 1.5 - Perform Type, Size and Location Study
Some clients require a Type, Size and Location study for the purpose of approval. The Type, Size and Location study includes preliminary configurations for the superstructure and substructure components relative to highway geometry constraints and site conditions. Details of this study for the superstructure include selecting the girder types, determining the girder spacing, computing the approximate required girder span and depth, and checking vertical clearance.
Although a Type, Size and Location study may not be required by the client, these determinations must still be made by the engineer before proceeding to the next design step.
For this design example, the superstructure cross section is presented in Figure 1-2. This superstructure cross section was selected to illustrate selected design criteria and the established geometry constraints. When selecting the girder spacing, consideration was given to half-width deck replacement.
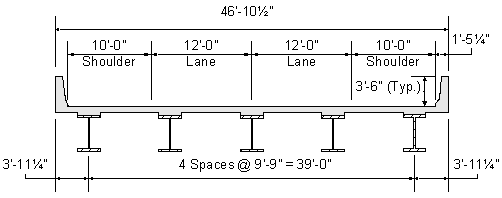
Figure 1-2 Superstructure Cross Section
Design Step 1.6 - Plan for Bridge Aesthetics
Finally, the bridge engineer must consider bridge aesthetics throughout the design process. Special attention to aesthetics should be made during the preliminary stages of the bridge design, before the bridge layout and appearance has been fully determined.
To plan an aesthetic bridge design, the engineer must consider the following parameters:
- Function: Aesthetics is generally enhanced when form follows function.
- Proportion: Provide balanced proportions for members and span lengths.
- Harmony: The parts of the bridge must usually complement each other, and the bridge must usually complement its surroundings.
- Order and rhythm: All members must be tied together in an orderly manner.
- Contrast and texture: Use textured surfaces to reduce visual mass.
- Light and shadow: Careful use of shadow can give the bridge a more slender appearance.

