Composite Behavior of Geosynthetic Reinforced Soil Mass

CHAPTER 1.  INTRODUCTION

1.1 PROBLEM STATEMENT

Over the past two decades, geosynthetic reinforced soil (GRS) structures, including retaining walls, slopes, embankments, roadways, and load-bearing foundations, have gained increasing popularity in the United States and abroad. In construction, GRS structures have demonstrated several distinct advantages over their conventional counterparts. Generally, GRS structures require less over-excavation and are more ductile, more flexible (hence more tolerant to differential settlement and to seismic loading), more adaptable to low-permeability backfill, easier to construct, and more economical than conventional Earth structures.^(2–4)

Among the various types of GRS structures, GRS walls have seen far more applications than other types of reinforced soil structures. A GRS wall comprises two major components: a facing element and a GRS mass. Figure 1 shows a schematic diagram of a typical GRS wall with a modular block facing.

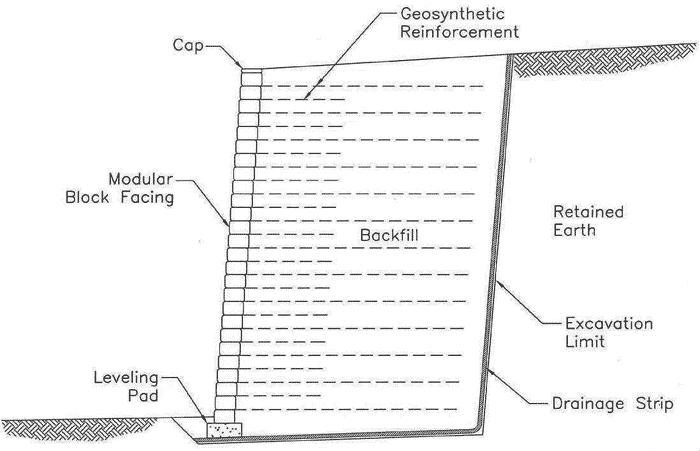
Figure 1. Illustration. Typical cross section of a GRS wall with modular block facing

The GRS wall facing may be of various shapes and sizes. It may also be made of different materials. However, the other component of a GRS wall, the GRS mass, is always a compacted soil mass reinforced by layers of geosynthetic reinforcement.

Soil is weak in tension and relatively strong in compression and shear. In a reinforced soil, the soil mass is reinforced by incorporating an inclusion (or reinforcement) that is strong in tensile resistance. Through soil reinforcement interface bonding, the reinforcement restrains lateral deformation of the surrounding soil, increases its confinement, reduces its tendency for dilation, and, consequently increases the stiffness and strength of the soil mass.

Many studies have been conducted on the behavior of GRS structures; however, the interactive behavior between soil and reinforcement in a GRS mass has not been fully elucidated. This has resulted in design methods that are fundamentally deficient.⁽⁵⁾ Perhaps the most serious deficiency is that the current methods ignore the composite nature of the GRS mass and consider the reinforcement as tiebacks added to the soil mass. The reinforcement strength is determined by requiring that the reinforcement be sufficiently strong to resist Rankine, Coulomb, or at-rest pressure that is assumed not to be affected by the configuration of the reinforcement. Specifically, the design strength of the reinforcement, T_required, has been determined by multiplying an assumed lateral Earth pressure at a given depth, σ_h, by the value of reinforcement spacing, S_v, and a safety factor, F_s, as shown by the equation in figure 2.

Figure 2. Equation. Design strength

Figure 2 implies that as long as the reinforcement strength is kept linearly proportional to the reinforcement spacing, all walls with the same σ_h (walls of a given height with the same backfill compacted to the same density) will behave the same. In other words, a GRS wall with reinforcement strength T at spacing S_v will behave the same as one with twice the reinforcement strength (2 × T) at twice the spacing (2 × S_v). Figure 2 has important practical significance in that it has encouraged designers to use stronger reinforcement at larger spacing because the use of larger spacing will generally reduce construction time and effort.

Some engineers, however, have learned that figure 2 cannot be true. In actual construction, reinforcement spacing appears to play a much greater role than reinforcement strength in the performance of a GRS wall. Researchers at the Turner-Fairbank Highway Research Center (TFHRC) conducted a series of full-scale experiments in which a weak reinforcement at a small spacing and a strong reinforcement (with several times the strength of the weak reinforcement) at twice the spacing were load-tested.^(6,7) The former was found to be much stronger than the latter. An indepth study on the relationship between reinforcement spacing and reinforcement stiffness/strength in regards to their effects on the behavior of a GRS mass is of critical importance to the design of GRS structures.

The effects of compaction-induced stress (CIS) in unreinforced soil masses and Earth structures have been the subject of many studies. (See references 8–14.) These studies indicated that CIS would significantly increase the lateral stresses in soil (also known as the locked-in lateral stresses or residual lateral stresses) provided that there is sufficient constraint to lateral movement of the soil during compaction. The increase in lateral stresses will increase the stiffness and strength of the compacted soil mass.

The effect of CIS is likely to be more significant in a soil mass reinforced with layers of geosynthetics than in an unreinforced soil mass. This is because the interface bonding between the soil and reinforcement will increase the degree of restraint to lateral movement of the soil mass during fill compaction. With greater restraint to lateral movement, the resulting locked-in lateral stresses are likely to become larger.

In most studies, the effects of CIS in numerical analysis of Earth structures have been either overly simplified or ignored. (See references 15–18.) In the case of GRS walls, failure to account for CIS may have led to the erroneous conclusion by many numerical studies that the equation in figure 2 is completely or approximately valid. Evaluation of CIS is an important issue in the study of GRS structures.

In addition, GRS walls with modular block facing are rather flexible. Thus, the design of these structures should consider not only the stresses in the GRS mass but also the deformation. The Jewell-Milligan method is recognized as the best available method for estimating lateral movement of GRS walls.⁽¹⁹⁾ However, it only applies to walls with little or no facing rigidity. With the increasing popularity of GRS walls with modular block facing where facing rigidity should not be ignored, an improvement over the Jewell-Milligan method for calculating lateral wall movement is needed.

1.2 RESEARCH OBJECTIVES

The objectives of this study were fourfold. The first objective was to investigate the composite behavior of GRS masses with different reinforcing configurations. The second objective was to examine the relationship between reinforcement strength and reinforcement spacing with regard to their effects on the behavior of a GRS mass. The third objective was to develop an analytical model for evaluating CIS in a GRS mass. The fourth objective was to develop an analytical model for predicting lateral movement of a GRS wall with a modular block facing.

1.3 RESEARCH TASKS

To achieve the research objectives, the following tasks were carried out in this study:

1. Reviewed previous studies on the composite behavior of a GRS mass, CIS in a soil mass, and the reinforcing mechanism of GRS structures. Previous studies on composite behavior of a GRS mass were reviewed. The review included theoretical analyses as well as experimental tests. Studies on CIS in an unreinforced soil mass were also reviewed, including simulation models for fill compaction. In addition, a literature study on reinforcing mechanisms of GRS structures was conducted.
   
   
2. Developed a hand computation analytical model for estimation of CIS in a GRS mass. An analytical model for simulation of CIS in a GRS mass was developed. The compaction model was developed by modifying an existing fill compaction simulation model for unreinforced soil. The model allows CIS in a GRS mass to be estimated by hand computations.
   
   
3. Developed an analytical model for the relationship between reinforcement strength and reinforcement spacing and derived an equation for calculating composite strength properties. An analytical model for describing the relationship between reinforcement strength and reinforcement spacing was developed. Based on the model and the average stress concept for a GRS mass, an equation for calculating the composite strength properties of a GRS mass was derived.(20) The model represents a major improvement over the existing current design methods used and more precisely reflects the role of reinforcement spacing versus reinforcement strength on the performance of a GRS mass. The equation allows the strength properties of a GRS mass to be evaluated by a simple hand computation method.
   
   
4. Designed and conducted laboratory experiments on a generic soil geosynthetic composite (GSGC) to investigate the performance of GRS masses with different reinforcing conditions. A GSGC plane-strain test was designed by considering several factors culled from previous studies. A series of finite element (FE) analyses were performed to determine the dimensions of the test specimen that would yield stress-strain and volume change behavior representative of a very large GSGC mass. Five GSGC tests with different reinforcement strengths, reinforcement spacing, and confining pressures were conducted. These tests allowed direct observation of the composite behavior of a GRS mass in various reinforcing conditions. They also provided measured data for verification of analytical and numerical models for investigating the behavior of a GRS mass (including the models developed in tasks 2 and 3).
   
   
5. Performed FE analyses to simulate the GSGC tests and analyze the behavior of the GRS mass. FE analyses were performed to simulate the GSGC tests conducted in task 4. The analyses allowed the stresses in the soil and forces in the reinforcement to be determined. They also allowed an investigation of the behavior of GRS composites under conditions different from those employed in the GSGC tests of task 4.
   
   
6. Verified the analytical models developed in tasks 2 and 3 by using the measured data from the GSGC tests and relevant test data in the literature. The compaction model developed in task 2 was employed to determine the CIS for the GSGC tests. The results were incorporated into an FE analysis to calculate the global stress-strain relationship and then compared to the measured results. The measured data from the GSGC tests, relevant test data available in the literature, and results from FE analyses were also used to verify the analytical models developed in task 3 for calculating composite strength properties of a GRS mass and for calculating required tensile strength of reinforcement based on the forces induced in the reinforcement.
   
   
7. Developed an analytical model for predicting lateral movement of GRS walls with modular block facing. An analytical model was developed for predicting the lateral movement of GRS walls with a modular block facing. The model was based on an existing model for reinforced soil walls without a modular block facing.⁽¹⁹⁾ The results obtained from the model were compared with measured data from a full-scale experiment of a GRS wall with modular block facing. The analytical model can also be used in design for determining the required design strength of reinforcement under a prescribed value of maximum allowable lateral wall movement.