Composite Behavior of Geosynthetic Reinforced Soil Mass

CHAPTER 5. ANALYTICAL MODELS FOR EVALUATING CIS, COMPOSITE STRENGTH PROPERTIES, AND REQUIRED REINFORCEMENT STRENGTH

This chapter describes analytical models for evaluating CIS in a GRS mass, strength properties of a GRS mass, and required tensile strength of reinforcement in the design of GRS structures.

The first analytical model is a simple compaction model that is capable of estimating CIS, or the increase of the horizontal stresses, in a GRS mass due to fill compaction. The model was developed by combining a compaction model developed by Seed, the companion hand-calculation procedure for an unreinforced soil mass by Duncan and Seed, and the theory of GRS composite behavior proposed by Ketchart and Wu.^(11,12,20)

The second analytical model is for the determination of the strength properties of a GRS composite mass. With the analytical model, a new relationship between reinforcement strength and reinforcement spacing is introduced to reflect an observation made in actual construction and in controlled experiments regarding the relative effects of reinforcement spacing and reinforcement strength on the performance of GRS structures.

The third analytical model is for the determination of reinforcement strength in design. This model was also developed based on the relationship between reinforcement strength and reinforcement spacing.

5.1 EVALUATING CIS IN A GRS MASS

5.1.1 Conceptual Model for Simulation of Fill Compaction of a GRS Mass

Based on previous studies regarding CIS for unreinforced soil masses and very limited studies for reinforced soil masses, a conceptual stress path for loading-unloading-reloading of a GRS mass is shown in figure 202.

 
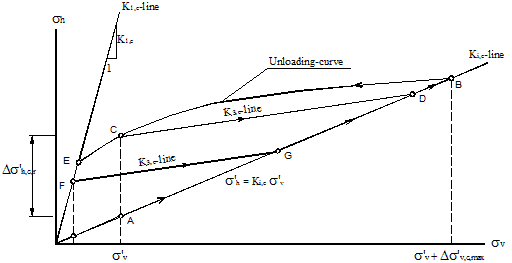
Figure 202. Illustration. Conceptual stress path for compaction of a GRS mass.

 

Elements in figure 202 are as follows:

• A GRS mass is loaded (due to application of compaction loads) from an initial state (point A) following the K_i,c line (with horizontal stress, σ'_h = K_i,c σ'_v, where K_i,c is the coefficient of lateral Earth pressure of the GRS mass for initial loading) up to point B. At point B, the GRS mass reaches a maximum stress state with the vertical stress of σ'_{v, max} = σ'_v + Δσ'_{v, c, max} ( σ'_v is the vertical stress at the initial stress and Δσ'_{v, c, max} is the maximum increase in vertical stress due to compaction loading).
  
  
• Upon unloading (i.e., removal of the compaction loads), the stresses in the soil are reduced by following a nonlinear path from point B to point C.
  
  
• In cases of significant unloading in which the unloading path reaches the limiting line (K_1,c) at point E, further unloading stress path will follow line EF (with σ'_h = K_{1, c} σ'_v ).
  
  
• Upon reloading due to the next cycle of compaction-load application, the stress follows a K_{3, c} line (with σ'_h = K_{3, c} σ'_v ) from either point C or point F until it meets the initial loading path (line AB).
  
  
• The subsequent cycles of unloading and reloading will not deviate much from the K_{3, c} line, as suggested by Broms, Seed, and Ehrlich and Mitchell.^(9,11,46) Therefore, the same K₃ line can be used for all subsequent cycles of reloading and unloading.

5.1.2 Simplified Model to Simulate Fill Compaction of a GRS Mass

A simplified compaction simulation model is proposed for simulation of fill compaction of a GRS mass, as depicted in figure 203. By using the proposed model, the increase of the horizontal stresses in a GRS mass due to compaction can be estimated. These stresses, namely CIS, are represented by the horizontal residual stresses, Δσ_{h, c, r}, in figure 203. The proposed model is based on the bilinear compaction model for an unreinforced soil mass suggested by Seed and the companion hand-calculation procedure suggested by Duncan and Seed.^(11,12) The proposed model considers the presence of geosynthetic inclusions.

 
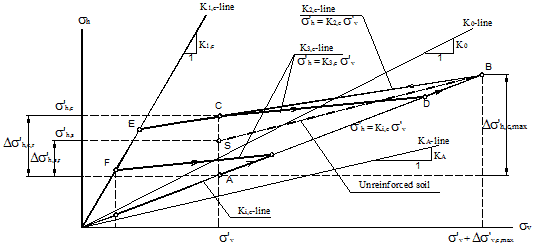
Figure 203. Illustration. Stress path of the proposed simplified model for fill compaction of a GRS mass.

The stress path for fill compaction of a GRS mass in the proposed model can be considered as a simplified form of the conceptual model described in section 5.1. The differences between the simplified model and the conceptual model are as follows:

• Upon removal of the compaction loads, the stresses in the soil are reduced by following the K_{2, c} line from point B to point C, of which the vertical stress, σ'_v, is equal to that of point A. The horizontal residual stress due to the compaction loading is Δσ'_{h, c, r}.
  
  
• In the case of an unreinforced soil mass (or where the reinforcement stiffness is negligible), the stress in the soil in response to the removal of compaction loads will reduce to point S (instead of point C). The horizontal residual stress due to compaction loading will be Δσ'_{h, s, r} with Δσ'_{h, s, r} ≤ Δσ'_{h, c, r}.
  
  
• Upon application of the next cycle of compaction loads or placement of new fill layers, the reloading path will follow the K_{3, c} line (with σ'_h = K_{3 ,c} σ'_v, and K_{3, c} ≤ K_{2, c} ). The stress path follows the K_{3, c} line from point C or point F until it meets the initial loading path. It then follows the K_{i, c} line to a new stress state.

5.1.3 Model Parameters of the Proposed Compaction Simulation Model

Four model parameters are needed for the proposed compaction simulation model: K_{i, c}, K_{1, c}, K_{2, c}, and K_{3, c}. These parameters can be estimated from soil and reinforcement properties using correlations shown in table 19. The empirical coefficients (e.g., α and F ) are calibrated by the measured data from the GSGC tests described in chapter 4. Recommended values of the empirical coefficients are given for routine applications. Alternatively, the model parameters can be obtained directly from the results of GSGC tests. Note that the term for the estimation of K_{2, c} is to account for the presence of reinforcement.For hand calculations, the maximum increase of vertical stress due to compaction, Δσ'_{v, c, max}, can be estimated simply by using Westergaard's solution as shown in figure 203.⁽⁷⁸⁾

Table 19. Model parameters for the proposed compaction simulation model.

Parameter	Name	Range of the Parameter Values	Preliminary Estimation Based on Soil and Reinforcement Properties
Ki, c	Coefficient of lateral Earth pressure of a GRS mass for initial loading	K A ≤ Ki, c ≤ K 0	Ki, c ≅ β K A 1.0 ≤ β ≤ 1.5 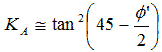K0 ≅ 1 - sin Φ'
K1, c	Limiting coefficient of lateral Earth pressure for unloading	K1, c ≅ K P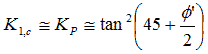
K2, c	Coefficient of lateral Earth pressure for unloading	0 ≤ K2, c ≤ K 0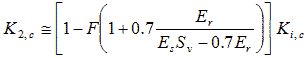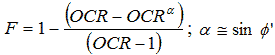
K3, c	Coefficient of lateral Earth pressure for reloading	0 ≤ K3, c ≤ K 0	K3, c ≅ K2, c
Ko = Coefficient of at-rest lateral Earth pressure. KA = Coefficient of active lateral Earth pressure. KP = Coefficient of passive lateral Earth pressure. OCR = Over-consolidation ratio. Es = Soil stiffness (kPa). Er = Reinforcement stiffness (kN/m). Sv = Reinforcement spacing (m).

 

5.1.4 Simulation of Fill Compaction Operation

Fill compaction is a complex operation in terms of change in stresses. This section describes the maximum increase of vertical stress at depth z along a given section in a soil mass due to typical compaction operation. Consider the change of vertical stress at depth z in section I-I due to moving compaction loads, as shown in figure 204 through figure 207. The directions of the moving compaction plant may either be coming toward section I-I or moving away from section I-I. The compaction loads are simulated by loading and unloading at different locations (locations 1, 2, and i), as shown in figure 204 and figure 206. Figure 205 and figure 207 show the stress path of the stresses at depth z along section I-I.

 
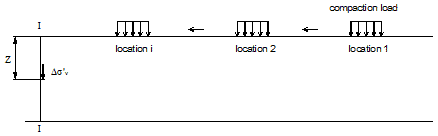
Figure 204. Illustration. Locations of compaction loads moving toward section I-I.

 

 
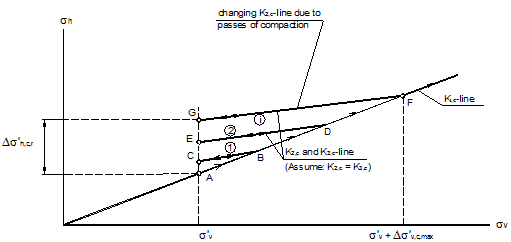
Figure 205. Illustration. Stress paths during compaction at depth z as compaction loads move toward section I-I.

 

 
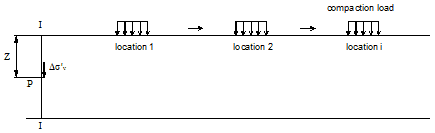
Figure 206. Illustration. Locations of compaction loads moving away from section I-I.

 

 
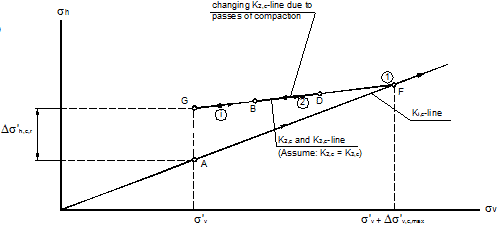
Figure 207. Illustration. Stress paths during compaction at depth z as compaction loads move away from section I-I.

Elements in figure 205 are as follows:

• The initial stress condition at depth z along section I-I is denoted by point A, with the initial vertical stress being σ_v.
  
  
• With the compaction loads at location 1, the stresses will increase by following the K_i,c line to point B.
  
  
• As the compaction loads are removed from location 1, the stresses will reduce from point B to point C by following the K_2,c line.
  
  
• When compaction loads move to a new location (location 2), the stresses will increase from point C through point B to point D.
  
  
• As the compaction loads are removed from location 2, the stresses will reduce from point D to point E by again following the K_2,c line.
  
  
• The previous steps are repeated for all subsequent new locations as the compaction plant moves toward section I-I. As the compaction plant moves closer to section I-I, the vertical stress at depth z will become larger.
  
  
• The maximum vertical stress condition will be reached when the compaction plant is directly above section I-I. The corresponding stress condition is represented by point F. Upon removal of the compaction loads, the stress path will follow the K₂ line to point G.

In figure 206 and figure 207, the compaction plant moves away from section I-I. Initially, the compaction is located directly above section I-I, which causes the stresses to increase from point A to point F due to the compaction loads. As the compaction loads are removed from section I-I, the stresses are reduced from point F to point G, following the K_2,c line. As the compaction plant moves away from section I-I, the stress conditions will move to points D and B along line FG. As the compaction plant is finally removed, the stress condition will be at point G.

As shown in figure 204 through figure 207, the residual stresses, denoted by the vertical distance AG, are the same for the two cases. This indicates that to determine the CIS at a certain section due to a moving compaction plant, only the residual lateral stresses need to be determined as the compaction loads are directly above the section under consideration.

Figure 208 shows the conceptual stress path on the effect of the number of compaction passes. For the first pass, the residual stress at point A is represented by point G. With the subsequent pass of the compaction plant, the slope of the K2line increases, and point G becomes point G'. As the number of compaction pass increases, the final residual stresses will move from G' to G'' to G'''.

 
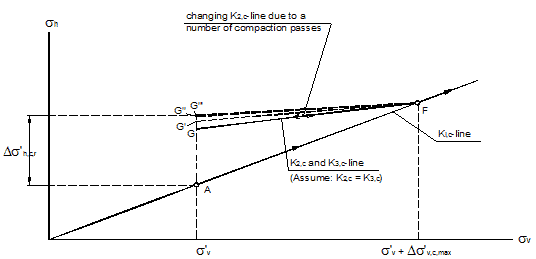
Figure 208. Illustration. Stress path at depth z when subject to multiple compaction passes.

 

5.1.5 Estimation of K_{2, c}

This section presents the estimation of K_{2, c} in the proposed model for determining CIS in a GRS mass. Two stress reduction factors, F and A, are introduced (see figure 209). Factor F represents CIS for unreinforced soil in Seed’s model, and factor A is considered the presence of the reinforcement in the GRS mass.⁽¹¹⁾

 
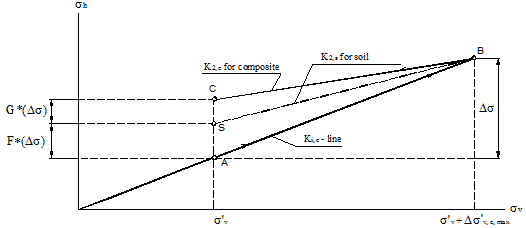
Figure 209. Illustration. Stress path of the proposed model for fill compaction of a GRS mass.

 

5.1.5.1 Compacted Soil

For an unreinforced soil fill, the coefficient of lateral Earth pressure for unloading in figure 203 can be estimated by using the expression in figure 210, as suggested by Seed.⁽¹¹⁾

 
Figure 210. Equation. Coefficient of later Earth pressure.

 

Where:

α ≅ sin Φ'
OCR ≅ 5 for typical compacted sand.⁽¹¹⁾

5.1.5.2 GRS Composite

For a GRS mass, total residual strain in the soil can be determined as shown in figure 211.

 
Figure 211. Equation. Total residual strain.

 

Where:
 F and G = Stress reduction factors shown in figure 209.
Δσ = Increase in horizontal stress due to compaction.
E_s = Soil stiffness.

From figure 211, the reinforcement force, T, due to residual strain in the soil can be determined as shown in figure 212.

 
Figure 212. Equation. Reinforcement force.

 

Where E_r is the reinforcement stiffness.

The average residual stress in the soil due to compaction, G * ( Δσ ), is calculated as shown in figure 213 and figure 214.

 
Figure 213. Equation. Average residual stress in the soil due to compaction.

 

 
Figure 214. Equation. Second equation for average residual stress in the soil due to compaction.

 

Figure 215 is a result of the previous two equations.

 
Figure 215. Equation. Result of figure 213 and figure 214.

 

Substituting figure 215 into figure 216 results in figure 217.

 
Figure 216. Equation. First equation for estimation of K_{2, c}.

 

 
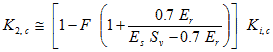
Figure 217. Equation. Second equation for estimation of K_{2, c}.

 

The factor 0.7 in figure 213 is explained in section 5.2.1. The increased horizontal stress in a GRS mass due to compaction can be estimated using figure 218.

 
Figure 218. Equation. Increased horizontal stress in a GRS mass due to compaction.

 

Substituting figure 217 into figure 218 results in figure 219 and figure 220.

 
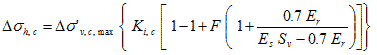
Figure 219. Equation. Second equation of increased horizontal stress in a GRS mass due to compaction.

 

 
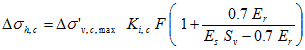
Figure 220. Equation. Residual lateral stress in a GRS mass due to compaction and the effect of CIS in a GRS mass.

 

Figure 220 shows the calculation of the residual lateral stress in a GRS mass due to compaction as well as the effect of CIS in a GRS mass.

Using figure 220, the increase in lateral stress in a GRS mass can be estimated, and the increase in soil stiffness can be evaluated. For example, the stiffness of a soil can be evaluated using figure 221.

 
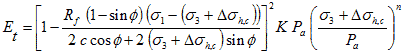
Figure 221. Equation. Stiffness of a soil.

 

Where:
E_t = Tangent modulus.
R_f = Ratio of ultimate deviator stress to the failure deviator stress.
c = Cohesive strength.
Φ = Angle of friction.
P_a = Atmospheric pressure.
K and n = Material parameters.

5.2 STRENGTH PROPERTIES OF GRS COMPOSITE

Schlosser and Long proposed the concepts of increase of apparent confining pressure and apparent cohesion of a GRS composite.⁽²⁵⁾ The Mohr circles of an unreinforced cohesive soil and a reinforced cohesive soil at failure are shown in figure 222.

 
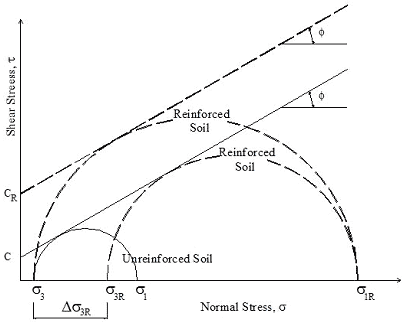
Figure 222. Illustration. Concept of apparent confining pressure and apparent cohesion of a GRS composite.

 

The apparent cohesion of a GRS composite can be determined as shown in figure 223.

 
Figure 223. Equation. Apparent cohesion of a GRS composite.

 

Where:
c_R= Apparent cohesion of a GRS composite.
c = Cohesion of soil.
K_p = Coefficient of passive Earth pressure.
Δσ_{3 R}= Increase of confining pressure due to reinforcement.

Schlosser and Long also proposed figure 224 to calculate increased confining pressure.⁽²⁵⁾

 
Figure 224. Equation. Increased confining pressure.

 

This expression implies that an increase in reinforcement strength, T_f, has the same effect as a proportional decrease in reinforcement spacing, S_v. Many experimental test results have shown that figure 224 is not correct. Reinforcement spacing plays a more important role than reinforcement strength. (See references 6, 7, 30, 31, and 35.) This point is also supported by the experiments conducted as a part of this study and presented in chapter 4.

5.2.1 Increased Confining Pressure

A new method to estimate the increased confining pressure in soil due to the presence of reinforcement is expressed in figure 225.

 
Figure 225. Equation. New method to estimate the increased confining pressure in soil due to the presence of reinforcement.

 

Where the factor, W, can be estimated as shown in figure 226.

 
Figure 226. Equation. Estimation of the factor W.

 

Where:
T_f = Extensile strength of reinforcement.
r = Dimensionless factor.
S_v = Vertical spacing of reinforcement.
S_ref = Reference spacing.

To estimate the factor r in figure 226, the concept of average stresses proposed by Ketchart and Wu was employed.⁽²⁰⁾ However, instead of using average stresses, average reinforcement forces were used.

5.2.1.1 Average Stress in GRS Mass by Ketchart and Wu⁽²⁰⁾

Ketchart and Wu developed a concept of average stress to determine the behavior of a GRS composite based on a load transfer analysis.⁽²⁰⁾ From a simplified preloading-reloading (SPR) model for GRS mass, the equations to calculate stresses and displacements of a GRS mass were developed using the idealized geometry of a plane-strain GRS mass and differential elements of soil and reinforcement for equilibrium equations, as shown in figure 227.

 
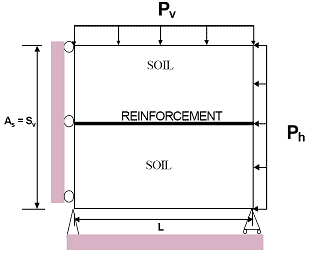
Figure 227. Illustration. Idealized plane-strain GRS mass for the SPR model.

 

Based on the equilibrium equations and several assumptions, the stresses in soil and the force in the reinforcement can be calculated using the following equations.

The force in the reinforcement is calculated with figure 228.

 
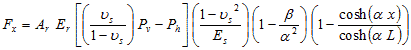
Figure 228. Equation. Force in the reinforcement.

 

The horizontal stress in the soil is calculated with figure 229.

 
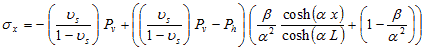
Figure 229. Equation. Horizontal stress in the soil.

 

Based on a load-transfer analysis, the average stresses were determined.

The average vertical stress,_v, is assumed to be equal to the boundary vertical pressure, as shown in figure 230.

 
Figure 230. Equation. Average vertical stress.

 

The average horizontal stress, _h, is as shown in figure 231 and figure 232.

 
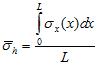
Figure 231. Equation. First equation of average horizontal stress.

 

 
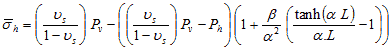
Figure 232. Equation. Second equation of average horizontal stress.

 

5.2.1.2. Average Reinforcement Forces in a GRS Mass

The equations of the forces in the reinforcement and the maximum force in the reinforcement are expressed as shown in figure 233 and figure 234.

 
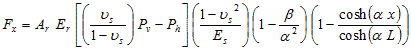
Figure 233. Equation. Forces in the reinforcement.

 

 
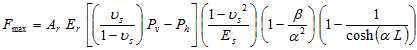
Figure 234. Equation. maximum force in the reinforcement.

 

The average force in the reinforcement is calculated as shown in figure 235.

 
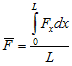
Figure 235. Equation. Average force in the reinforcement.

 

Substituting figure 233 into figure 235 results in figure 236 and figure 237, which is simplified to figure 238.

 
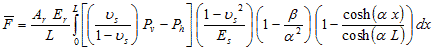
Figure 236. Equation. Second equation of average force in the reinforcement.

 

 
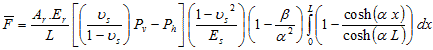
Figure 237. Equation. Third equation of average fore in the reinforcement.

 

 
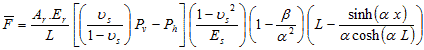
Figure 238. Equation. Fourth equation of average force in the reinforcement.

 

Introducing a factor  and using figure 234 and figure 238, r can be determined using figure 239.

 
Figure 239. Equation. Estimation of factor r.

Table 20 shows the values of factor r for different applied pressures and reinforcement lengths using the data from the calculation example in the SPR model.⁽²⁰⁾

Table 20. Values of factor r under different applied pressure and reinforcement lengths.

Increment of Vertical Pressure (Pv) kPa)	Reinforcement Length, L (m)	α
9.0	0.127	13.875	0.698
18.0	0.127	14.616	0.701
9.0	0.225	6.851	0.691
18.0	0.225	6.966	0.692
1 kPa = 0.145 psi 1 m = 3.28 ft

 

Table 20 shows that the average reinforcement forces are about 70 percent of the maximum reinforcement force. The highest value of the maximum reinforcement force, F_max, cannot exceed the tensile strength of reinforcement, T_f, as shown in figure 240.

 
Figure 240. Equation. Maximum reinforcement force.

 

The average reinforcement force is as shown in figure 241.

 
Figure 241. Equation. Average reinforcement force.

 

Figure 226 becomes figure 242.

 
Figure 242. Equation. Second estimation of the factor W.

 

5.2.2 Apparent Cohesion and Ultimate Pressure Carrying Capacity of a GRS Mass

Substituting figure 242 into figure 225, the increased confining pressure in a GRS mass is calculated in figure 243.

 
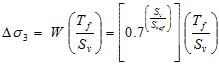
Figure 243. Equation. Increased confining pressure in a GRS mass.

 

Therefore, the apparent cohesion, c_R, of a GRS composite can be evaluated using figure 244.

 
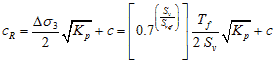
Figure 244. Equation. Apparent cohesion.

 

Where:
c = Cohesion of soil.
K_p = Coefficient of passive Earth pressure.
T_f = Extension strength of reinforcement.
S_v = Vertical spacing of reinforcement.
S_ref = Reference spacing, which can be calculated using figure 245.

 
Figure 245. Equation. Reference spacing.

 

Where:
d_max = Maximum particle/grain size of soil.

Therefore, the ultimate pressure carrying capacity, σ_1R, of a soil-geosynthetic composite mass is calculated using figure 246.

 
Figure 246. Equation. Pressure carrying capacity.

 

Where σ₃ is the confining pressure.

5.3 VERIFICATION OF THE ANALYTICAL MODEL WITH MEASUREMENT DATA

Verification of the proposed analytical model for GRS composite strength properties was made by comparing the model calculation results with the measured data from GSGC tests presented in chapter 4 and with the measured data by Elton and Patawaran.⁽³¹⁾

5.3.1 Comparison Between the Analytical Model and GSGC Test Results

The dimensions of the GSGC tests were 6.6 ft (2 m) high and 4.6 ft (1.4 m) wide in a plane-strain condition. The soil mass in the tests was reinforced with Geotex^® 4×4 geotextile at 0.7- and 1.3-ft (0.2- and 0.4-m) spacing. For the diabase soil used in GSGC tests, the maximum particle size was about 1.3 inches (66 mm). Therefore, S_ref = 6 d_max = 7.8 inches (0.2 m). Comparisons of the results between the analytical model and the GSGC tests are presented in table 21. The deviatoric stresses at failure calculated from the analytical model are in good agreement with those of the GSGC tests, with differences of less than 10 percent.

Table 21 . Comparison of the results of the analytical model and the GSGC tests.

Parameter	Test 2 (T, S)	Test 3 (2T, 2S)	Test 4 (T, 2S)
Tf (kN/m)	70	140	70
Sv (m)	0.2	0.4	0.4
Δσ3 (kN/m2) by the analytical model	245	172	86
cR (kN/m2) by the analytical model	407	305	188
(σ1R - σ3) (kN/m2) from measured data	2,700	1,750	1,300
(σ1R - σ3) (kN/m2) by the analytical model	2,460	1,900	1,250
Difference between analytical model and measured data	-9 percent	+8 percent	-4 percent
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kN/m2 = 0.021 kip/ft2 Note: Internal friction angle of soil = 50 degrees and cohesion of soil = 10.15 psi (70 kPa).

For reference purposes, comparisons of the results between Schlosser and Long’s method and the GSGC tests are presented in table 22. The deviatoric stresses at failure calculated from Schlosser and Long’s method are about 20 to 86 percent larger than the measured values.

Table 22. Comparison of the results of Schlosser and Long’s method and the GSGC tests.

Parameter	Test 2 (T, S)	Test 3 (2T, 2S)	Test 4 (T, 2S)
Tf (kN/m)	70	140	70
Sv (m)	0.2	0.4	0.4
Δσ3 (kN/m2) by Schlosser and Long’s method	350	350	175
cR (kN/m2) by Schlosser and Long’s method	550	550	310
(σ1R - σ3) (kN/m2) from measured data	2,700	1,750	1,300
(σ1R - σ3) (kN/m2) by Schlosser and Long’s method	3,250	3,250	1,930
Difference between Schlosser and Long’s method and measured data	+20 percent	+86 percent	-48 percent
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kN/m2 = 0.021 kip/ft2 Note: Internal friction angle of soil = 50 degrees and cohesion of soil = 10.15 psi (70 kPa).

 

5.3.2 Comparison Between the Analytical Model and Elton and Patawaran’s Test Results

Elton and Patawaran conducted seven large-size triaxial tests for reinforced soil 5 ft (1.5 m) in height and 2.5 ft (0.76 m) in diameter.⁽³¹⁾ All the tests were conducted under an unconfined condition. The properties of the tests were as follows:

• Backfill:The soil used in the test was a poorly graded sand with the gradation test results shown in figure 247. The maximum dry unit weight, γ_dry, was 121 pcf (1,900 kg/m³), the optimum moisture content, w_opt, was 9.3 percent, the internal friction, Φ, was 40 percent, and the cohesion, c, was 4 psi (27 kPa).
  
  
• Reinforcement:Six types of reinforcement (TG500, TG600, TG700, TG800, TG1000, and TG028) were used for the tests with reinforcement spacing of 6 and 12 inches (150 and 300 mm).

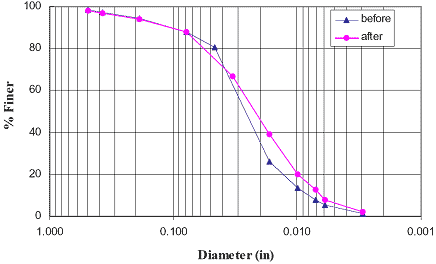
1 mm = 0.039 inches
Figure 247. Graph. Backfill grain size distribution before and after large-size triaxial tests.

 

The maximum particle size of the backfill in the large-size triaxial tests was d_max = 0.5 inches (12.7 mm). Therefore, S_ref = 6 d_max = 3 inches (0.08 m). The measured results are shown in figure 248. The comparisons of Elton and Patawaran’s tests results with the analytical model and with Schlosser and Long’s method are presented in table 23 and table 24, respectively.

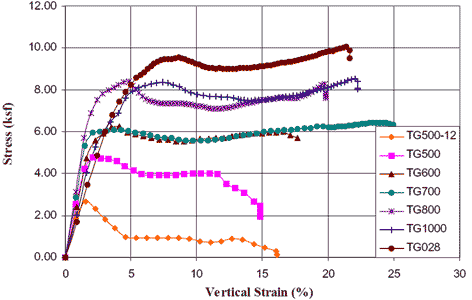
1 ksf = 47.88 kPa
Figure 248. Graph. Large-size triaxial test results.

 

Table 23. Comparison of the results of the analytical model and Elton and Patawaran’s tests.⁽³¹⁾

Parameter	TG 500	TG 500	TG 600	TG 700	TG 800	TG 1000	TG 028
Tf (kN/m)	9	9	14	15	19	20	25
Sv (m)	0.15	0.30	0.15	0.15	0.15	0.15	0.15
Δσ3 (kN/m2) by the analytical model	30	8	47	48	62	67	83
cR (kN/m2) by the analytical model	60	36	78	79	94	99	116
(σ1R - σ3) (kN/m2) from measured data	230	129	306	292	402	397	459
(σ1R - σ3) (kN/m2) by the analytical model	256	153	333	341	402	426	498
Difference between the analytical model and measured data (percent)	11	18	9	17	0	7	8
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kN/m2 = 0.021 kip/ft2 Note: Internal friction angle of soil = 40 degrees and cohesion of soil = 4.0 psi (27.6 kPa).

 

Table 24. Comparison of the results of Schlosser and Long’s method and Elton and Patawaran’s tests.⁽³¹⁾

Parameter	TG 500	TG 500	TG 600	TG 700	TG 800	TG 1000	TG 028
Tf (kN/m)	9	9	14	15	19	20	25
Sv (m)	0.15	0.30	0.15	0.15	0.15	0.15	0.15
Δσ3 (kN/m2) by Schlosser and Long’s method	59	30	92	122	122	132	163
cR (kN/m2) by Schlosser and Long’s method	91	59	126	158	158	169	202
(σ1R - σ3) (kN/m2) from measured data	230	129	306	402	402	397	459
(σ1R - σ3) (kN/m2) by Schlosser and Long’s method	390	254	541	678	678	726	868
Difference between Schlosser and Long’s method and measured data (percent)	70	97	77	69	69	83	89
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kN/m2 = 0.021 kip/ft2 Note: Internal friction angle of soil = 40 degrees and cohesion of soil = 4.0 psi (27.6 kPa).

 

The differences in the deviatoric stresses at failure calculated from the analytical model and Elton and Patawaran’s measured data are less than 18 percent. The results calculated from Schlosser and Long’s method are 69 to 97 percent larger than the measured values.

5.3.3 Comparison Between the Analytical Model and FE Results

FE analyses were conducted to provide additional data for verifying the analytical model. The test conditions and material properties used for the FE analyses were the same as those used in GSGC test 2 but with confining pressures of 4.9, 10, 15, and 29 psi (34, 70, 100, and 200 kPa). The confining pressure used in GSGC test 2 was 4.9 psi (34 kPa). The comparison shown in table 25 indicates that the results of the analytical model are in good agreement with those obtained from the FE analyses at the different confining pressures. The largest difference in terms of the deviatoric stress at failure is 9 percent.

Table 25. Comparison of the results of analytical model and GSGC test 2 with different confining pressures from FE analyses.

Parameter	σ3 = 34 kPa	σ3 = 70 kPa	σ3 = 100 kPa	σ3 = 200 kPa
Δσ3 (kN/m2) by the analytical model	245	245	245	245
cR (kN/m2) by the analytical model	407	407	407	407
(σ1R - σ3) (kN/m2) from FE analysis	2,700	2,970	3,190	3,860
(σ1R - σ3) (kN/m2) by the analytical model	2,490	2,760	2,990	3,740
Difference between the analytical model and FE analyses	-8 percent	-7 percent	-6 percent	-3 percent
1 kN/m = 0.145 kip/ft 1 kN/m2 = 0.021 kip/ft2 Note: Internal friction angle of soil = 50 degrees, cohesion of soil = 10.15 psi (70 kPa), reinforcement strength = 4.83 kip/ft (70 kN/m), and reinforcement spacing = 0.65 ft (0.2 m).

 

5.4 REQUIRED REINFORCEMENT STRENGTH IN DESIGN

In this section, an analytical model for determining required tensile strength in reinforcement is developed, the analytical model is compared with the current design equation, and verification of the analytical model is presented.

5.4.1 Proposed Model for Determining Reinforcement Force

In current design methods, figure 249 is used to determine the required reinforcement strength for the design of GRS structures.

 
Figure 249. Equation. Required strength for reinforcement.

 

Where:
T_required = Required strength for reinforcement at depth z.
σ_h = Horizontal stress in a GRS mass at depth z.
F_s = Safety factor.

Assuming F_s = 1, then T_required = T_f , the ultimate strength of reinforcement, and figure 249 becomes figure 250.

 
Figure 250. Equation. T_f divided by S_v

 

Note that when the horizontal stress, σ_h, is a constant, the ratio T_f /S_v becomes a constant (i.e., T_f is linearly proportional to S_v). Using figure 225, a new expression for the increase of confining pressure due to tensile inclusion, a modified equation for determination of required reinforcement strength can be obtained. The horizontal stress, σ_h, in a GRS structure at depth z is calculated using figure 251 or figure 252.

 
Figure 251. Equation. First equation for horizontal stress in a GRS structure.

 

 
Figure 252. Equation. Second equation for horizontal stress in a GRS structure.

 

Substituting figure 225 into figure 250 leads to figure 253 and figure 254.

 
Figure 253. Equation. Third equation for horizontal stress in a GRS structure.

 

 
Figure 254. Equation. Second equation for T_f divided by S_v.

 

Substituting figure 241 into figure 254 results in figure 255.

 
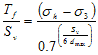
Figure 255. Equation. Third equation for T_f divided by S_v.

 

For a GRS wall with modular block facing, the lateral constraint pressure, σ₃, at depth z, can be estimated as shown in figure 256.

 
Figure 256. Equation. Lateral constraint pressure.

 

Where:
γ_b = Unit weight of facing block.
b = Width of facing block.
δ = Friction angle between modular block facing elements ( δ can be the friction angle between facing blocks if there is no reinforcement between the blocks or it can be the friction angle between facing block and geosynthetic if there is reinforcement sandwiched between blocks).
d_max = Maximum grain size of the backfill.

The required tensile strength of the reinforcement in design is shown in figure 257.

 
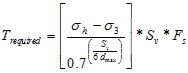
Figure 257. Equation. Required tensile strength of the reinforcement in design.

 

Where σ_h is the maximum lateral stress in a GRS mass and can be evaluated as the Rankin active Earth pressure. Note that T_required is always equal or greater than zero. For a GRS mass without lateral constraint (e.g., a wrapped wall), σ₃ equals 0, and figure 257 becomes figure 258.

 
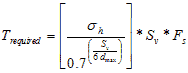
Figure 258. Equation. Second equation for required tensile strength of the reinforcement in design.

 

5.4.2 Comparison of Reinforcement Strength Between the Analytical Model and Current Design Equation

A comparison of reinforcement forces was made between the proposed model (figure 257) and the current design equation (figure 249). The reinforcement forces in a 20-ft (6.0-m)-high GRS wall, as determined by the two equations, are shown in table 26. Note that the facing stiffness is ignored in the current design method, while the facing rigidity, as denoted by the lateral constraint pressure, σ₃, can be accounted for in the proposed model.

Table 26. Comparison of reinforcement forces in proposed model and current design equation for a GRS wall.

z (m)	Trequired (kN/m) for Fs = 1
	Current Design Equation	Proposed Model
		No Facing	Modular Block Facing with δ b-b = 35 degrees	Modular Block Facing with δ b-b = 54 degrees
0.4	0.3	0.4	0.0	0.0
0.8	0.6	0.9	0.0	0.0
1.2	1.0	1.3	0.0	0.0
1.6	1.3	1.8	0.3	0.0
2.0	1.6	2.2	0.8	0.0
2.4	1.9	2.7	1.2	0.0
2.8	2.3	3.1	1.7	0.3
3.2	2.6	3.5	2.1	0.7
3.6	2.9	4.0	2.5	1.2
4.0	3.2	4.4	3.0	1.6
4.4	3.6	4.9	3.4	2.0
4.8	3.9	5.3	3.9	2.5
5.2	4.2	5.8	4.3	2.9
5.6	4.5	6.2	4.8	3.4
6.0	4.9	6.6	5.2	3.8
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft δ b-b = Friction angle between facing blocks. Note: Internal friction angle of soil = 38 degrees, cohesion of soil = 0, reinforcement spacing = 0.65 ft (0.2 m), maximum grain size of soil = 1.48 inches (38 mm), unit weight of soil = 0.11 kip/ft3) (17 kN/m3), unit weight of facing block = 0.16 kip/ft3 (25 kN/m3), and width of blocks = 0.98 ft (0.3 m).

 

5.4.3 Verification of the Analytical Model for Determining Reinforcement Strength

Verification of the analytical model for determination of reinforcement strength was made by comparing the forces in reinforcement at failure from the GSGC tests with the data measured by Elton and Patawaran and with a typical GRS wall.⁽³¹⁾

Table 27 shows a comparison of the results from the proposed model and measured data from the GSGC tests. Note that cohesion, c, was included in model calculations. The largest difference in reinforcement forces between the two is 16 percent, whereas there is 47 percent difference between the current design methods and the test data.

Table 27. Comparison of reinforcement forces in the proposed model and the GSGC tests.

Parameter	Test 2 (T, S)	Test 3 (2T, 2S)	Test 4 (T, 2S)	Test 5 (T, S)
Reinforcement force at failure, Tf (kN/m)	70	140	70	70
Reinforcement spacing, Sv (m)	0.2	0.4	0.4	0.2
Measured failure pressure (kPa)	2,700	1,750	1,300	1,900
Lateral constraint pressure σ3 (kPa)	34	34	34	0
Maximum reinforcement force from current design equation (kN/m)	62.4	74.4	50.5	41.2
Difference between current design equation and Tf (percent)	-11	-47	-28	-41
Maximum reinforcement force from proposed model (kN/m)	79.4	124.1	75.4	58.8
Difference between proposed model and Tf (percent)	+13	-11	+8	-16
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kPa = 0.145 psi Note: Internal friction angle of soil = 50 degrees, cohesion of soil = 10.15 psi (70 kPa), unit weight of soil = 0.15 kip/ft3 (24 kN/m3), and maximum grain size of soil = 1.29 inches (33 mm).

 

A comparison of the reinforcement forces between the proposed model and the measured data from Elton and Patawaran’s tests is shown in table 28.⁽³¹⁾ The largest difference in reinforcement forces between the two is 13 percent, whereas it was as high as 74 percent between the current design method and the test results. The proposed model clearly gives a much improved value for estimating reinforcement strength compared to the current design methods.

Table 28. Comparison of reinforcement forces between proposed model and test data from Elton and Patawaran.⁽³¹⁾

Parameter	TG 500	TG 500	TG 600	TG 700	TG 800	TG 1000	TG 028
Reinforcement force at failure, Tf (kN/m)	9	9	14	15	19	20	25
Reinforcement spacing, Sv (m)	0.15	0.30	0.15	0.15	0.15	0.15	0.15
Measured failure pressure (kPa)	230	129	306	292	402	397	459
Maximum reinforcement force from current design equation (kN/m)	4.47	2.35	6.95	6.49	10.08	9.91	11.94
Difference between current design equation and Tf (percent)	-50	-74	-50	-57	-47	-50	-52
Maximum reinforcement force from proposed model (kN/m)	9.02	9.56	14.02	13.10	20.34	20.01	24.09
Difference between proposed model and Tf (percent)	0	+6	0	-13	+7	0	-4
1 kN/m = 0.069 kip/ft 1 m = 3.28 ft 1 kPa = 0.145 psi Note: Internal friction angle of soil = 40 degrees, cohesion of soil = 4.0 psi (27.6 kPa), unit weight of soil = 0.12 kip/ft3 (18.8 kN/m3), lateral constraint pressure = 0 psi (0 kPa), and maximum grain size of soil = 0.49 inches (12.7 mm).