U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

Report
This report is an archived publication and may contain dated technical, contact, and link information
Publication Number: FHWA-RD-02-078
Date: November 2003

Bottomless Culvert Scour Study: Phase I Laboratory Report

4. RESULTS

SCOUR RESULTS

Extensive analysis was performed using various combinations of equations for resultant velocity and critical velocity. Figure 22 shows how the experimental data was processed and the different evaluation methods used to derive the adjustment coefficients. This section presents the results using the Maryland DOT (Chang) and GKY methods for representative velocity and critical velocity, and the combination that yielded the best results.

Figure 22. Post-processing: data analysis flowchart. Diagram. This flowchart begins with a picture of a model culvert, which feeds into a box that lists D subscript 50, Y subscript S, Q, V, and Y subscript 0. This box feeds into a box with the masthead, "National Instruments Lab View," as do three other boxes: V subscript R from Chang, GKY; V subscript C from Niells, SMB; and the Ishbash method. An arrow points from the National Instruments box to a box that reads, "K subscript ADJ, K subscript RIP.

Figure 22. Post-processing: data analysis flow chart.

The regression analysis was performed for two sets of data: data for the vertical face and data for the wingwall entrances. Separate equations were derived for the two data sets; however, we determined that the two equations could be combined into one general equation by incorporating an entrance coefficient (KWW) to account for the streamlining effects of the wingwalls. Equation 34 is the general expression for the maximum depth to be expected at the upstream corners of a bottomless culvert with no upstream sediment being transported into the scour hole.

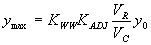Equation 34. Y subscript max equals K subscript WW, which is the wingwall entrance coefficient, times K subscript ADJ, which is the empirical adjustment factor to account for turbulence and vorticity at the upstream corner of the culvert derived from regression analysis, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (34)

where:

KWW= wingwall entrance coefficient
KADJ= empirical adjustment factor to account for turbulence and vorticity at the upstream corner of the culvert derived from regression analysis

We used R2 and MSE to indicate which combinations of representative velocity, critical velocity, and independent regression variables worked best for this data.

Maryland DOT (Chang) Method for Representative Velocity and Critical Velocity

Four different independent regression variables were tested for the Maryland DOT method. One of these, the Froude number (NF) (originally the Chang method), was compared to KADJ using three different regression methods: linear, second order, and quadratic. The linear regression gave R2 values of 0.22 for the vertical face data and 0.10 for the wingwall data (figures 23 and 24, respectively).

Figure 23. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation and local scour ratio as a function of the Froude number, using a linear regression. Graph. On this graph, the Froude number (N subscript F) is charted on the horizontal axis from 0 to 0.35, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1.8697 minus 1.3630 N subscript F, RSQ equals 0.2150, MSE equals 0.0237" and "K subscript ADJ equals 1.6145 minus 0.7884 N subscript F, RSQ equals 0.1031, MSE equals 0.0273." The trend for all four data sets is downward; K subscript ADJ decreases as N subscript F increases.

Figure 23. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation and local scour ratio as a function of the Froude number, using a linear regression.

Figure 24. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.9630, MSE equals 0.0154; wingwall shape factor equals 0.890 (RSQ equals 0.7969, MSE equals 0.0403); and wingwall (RSQ equals 0.8972, MSE equals 0.0205). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 24. Measured and computed data with and without wingwalls, based on figure 23 regression.

Incorporating the adjustment function from figure 23 leads to the general equation:

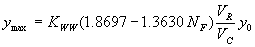Equation 35. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.8697 minus 1.3630 N subscript F, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (35)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

The Froude number (NF) with a second order regression gave R2 values of 0.35 for the vertical face data and 0.28 for the wingwall data (figures 25 and 26, respectively).

Figure 25. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation for critical velocity and local scour ratio as a function of the Froude number, using a second order regression. Graph. On this graph, the Froude number (N subscript F) is charted on the horizontal axis from 0 to 0.35, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 2.0011 minus 3.1682 N subscript F plus 5.3345 N subscript F squared, RSQ equals 0.2295, MSE equals 0.0232" and "K subscript ADJ equals 2.0237 minus 6.6820 N subscript F plus 17.2493 N subscript F squared, RSQ equals 0.2895, MSE equals 0.0217." The trend for all four data sets is downward with a slight leveling out as N subscript F approaches 0.2. The without wingwall and its corresponding regression generally have higher K subscript ADJ values at the same N subscript F values. The wingwall and wingwall regression begins to rise after these coordinates, and the wingwall regression crosses over the without wingwall regression at coordinates 0.29, 1.55.

Figure 25. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation for critical velocity and local scour ratio as a function of the Froude number, using a second order regression.

Figure 26. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.9658, MSE equals 0.0159; wingwall shape factor equals 0.890 (RSQ equals 0.7910, MSE equals 0.0415); and wingwall (RSQ equals 0.9118, MSE equals 0.0178). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 26. Measured and computed data with and without wingwalls, based on figure 25 regression.

Incorporating the adjustment function from figure 25 leads to the general equation:

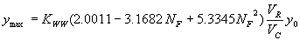Equation 36. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 2.0011 minus 3.1682 N subscript F squared, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (36)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

The Froude number (NF) with a quadratic regression gave R2 values of 0.15 for the vertical face data and 0.06 for the wingwall data (figures 27 and 28, respectively).

Figure 27. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation for critical velocity and local scour ratio as a function of the Froude number, using a linear regression. Graph. On this graph, the Froude number (N subscript F) is charted on the horizontal axis from 0 to 0.35, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1.7617 minus 3.1682 N subscript F squared, RSQ equals 0.1865, MSE equals 0.9561" and "K subscript ADJ equals 1.5428 minus 1.6944 N subscript F squared, RSQ equals 0.0574, MSE equals 0.4309." The trend for all four data sets is downward with an increase in slope beginning as N subscript F approaches 0.2. The without wingwall and its corresponding regression generally have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, however, the data begin to converge as the N subscript F values rise.

Figure 27. Maryland DOT's (Chang's) resultant velocity with Chang's approximation for critical velocity and local scour ratio as a function of the Froude number, using a linear regression.

Figure 28. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.9594, MSE equals 0.0156; wingwall shape factor equals 0.890 (RSQ equals 0.7996, MSE equals 0.0398); and wingwall (RSQ equals 0.8913, MSE equals 0.0217). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 28. Measured and computed data with and without wingwalls, based on figure 27 regression.

Incorporating the adjustment function from figure 27 leads to the general equation:

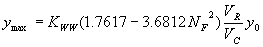Equation 37. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.7617 minus 3.1682 N subscript F squared, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (37)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

Using the approach flow area that is blocked by the embankments on one side of the channel over the squared flow depth as the independent regression variable yielded R2 values of 0.004 for the vertical face data and 0.08 for the wingwall data (figures 29 and 30, respectively).

Figure 29. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation for critical velocity and local scour ratio as a function of the blocked area over the squared flow depth. Graph. On this graph, the blocked area over the squared flow depth (A subscript B over Y subscript 0 squared) is charted on the horizontal axis from 2 to 16, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals negative 0.002 times (A subscript B over Y subscript 0) plus 1.833, RSQ equals 0.00453, MSE equals 0.0182" and "K subscript ADJ equals negative 0.013 times (A subscript B over Y subscript 0) plus 1.603, RSQ equals 0.0835, MSE equals 0.0182." The without wingwall regression remains relatively flat, while the trend for the wingwall regression is a gentle slope downward. The without wingwall and wingwall data are scattered along the ends of their respective regressions. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression.

Figure 29. Maryland DOT's (Chang's) resultant velocity with Chang's approximation for critical velocity and local scour ratio as a function of the blocked area over the squared flow depth.

Figure 30. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.94910, MSE equals 0.0125; wingwall shape factor equals 0.88 (RSQ equals 0.88072, MSE equals 0.0237); and wingwall (RSQ equals 0.88719, MSE equals 0.0236). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 30. Measured and computed data with and without wingwalls, based on figure 29 regression.

Incorporating the adjustment function from figure 29 leads to the general equation:

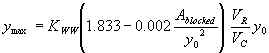Equation 38. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.833 minus 0.002 times the quotient of A subscript blocked divided by Y subscript 0, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (38)

where:

KWW= 1.0 for vertical face entrances
= 0.88 for wingwall entrances

The third independent regression variable tested was the approach flow area that is blocked by the embankments on one side of the channel over the squared computed equilibrium depth, resulting in R2 values of 0.29 for the vertical face data and 0.11 for the wingwall data (figures 31 and 32, respectively).

Figure 31. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation for critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth. Graph. On this graph, the blocked area over the squared computed equilibrium depth (A subscript B over Y subscript 2 squared) is charted on the horizontal axis from 0 to 20, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.5967 times (A subscript B over Y subscript 2 squared), RSQ equals 0.28907, MSE equals 0.02712" and "K subscript ADJ equals 1 plus 0.3484 times (A subscript B over Y subscript 2 squared) to the 0.25075 power, RSQ equals 0.1101, MSE equals 0.02712." The trend for all data points is a gentle slope upward. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, and the latter data points end at an A subscript B over Y subscript 2 squared of 9.5.

Figure 31. Maryland DOT's (Chang's) resultant velocity with Chang's approximation for critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth.

Figure 32. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.96473, MSE equals 0.00801; wingwall shape factor equals 0.91 (RSQ equals 0.90507, MSE equals 0.0188); and wingwall (RSQ equals 0.91380, MSE equals 0.01902). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 32. Measured and computed data with and without wingwalls, based on figure 31 regression.

Incorporating the adjustment function from figure 31 leads to the general equation:

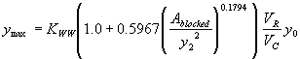Equation 39. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.91 for wingwall entrances, times the result of 1.0 plus 0.5967 times the quotient, raised to the power of 0.1794, of A subscript blocked divided by Y subscript 2 squared, times the quotient of V subscript R divided by V subscript C, times Y subscript 0.     (39)

where:

KWW= 1.0 for vertical face entrances
= 0.91 for wingwall entrances

The fourth independent regression variable tested was the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth. The R2 values were 0.07 for the vertical face data and 0.002 for the wingwall data (figures 33 and 34, respectively).

Figure 33. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation and local scour ratio as a function of the blocked discharge normalized by the acceleration of gravity (G) and the computed equilibrium depth. Graph. On this graph the blocked discharge normalized by the acceleration of gravity and the computed equilibrium depth (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) is charted on the horizontal axis from 0 to 2.5, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two additional datapoints are graphed; submerged without wingwalls and submerged with wingwalls. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.854 times (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) raised to the 0.103 power, RSQ equals 0.0639, MSE equals 0.0206" and "K subscript ADJ equals 1 plus 0.627 times (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) raised to the 0.251 power, RSQ equals 0.0613, MSE equals 0.0234." The trend for all data points is a gentle slope upward. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, and the latter data points end at a blocked discharged point of 1.1. There are two submerged with wingwalls data points along the without wingwalls regression line, at coordinates 0.8, 1.9 and 1.1, 1.9. There are two submerged without wingwalls data points near the top of the graph at coordinates 0.8, 2.1 and 0.9, 2.3.

Figure 33. Maryland DOT's (Chang's) resultant velocity with Chang's approximation equation and local scour ratio as a function of the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth.

Figure 34. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.94272, MSE equals 0.01221; wingwall shape factor equals 0.90 (RSQ equals 0.87024, MSE equals 0.0187); and wingwall (RSQ equals 0.88351, MSE equals 0.02265). Two additional datapoints are graphed; submerged without wingwalls and submerged with wingwalls. All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5. There are two datapoints each for the submerged without and with wingwalls, and they fall between coordinates 0.9, 0.8 and coordinates 1.4, 1.25.

Figure 34. Measured and computed data with and without wingwalls, based on figure 33 regression.

Using the adjustment function from figure 33 gives the general equation:

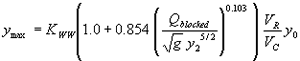Equation 40. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.0 plus 0.854 times the quotient, raised to the power of 0.103, of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power, all times V subscript R divided by V subscript C, times Y subscript 0.     (40)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

Table 1 below gives an overview for the tested independent regression variables and R2 values using the Maryland DOT (Chang) method for representative velocity and critical velocity.

Table 1. Independent regression variables and R2 values using the Maryland DOT (Chang) method.

Maryland DOT (Chang) Method for VR and VC R2 Regression R2 Meas. vs. Comp Equation No.
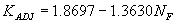Equation 41. K subscript ADJ equals 1.8697 minus 1.3630 N subscript F.0.21500.9630(41)
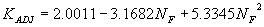Equation 42. K subscript ADJ equals 2.001 minus 3.1682 N subscript F plus 5.3345 N subscript F squared.0.22950.9658(42)
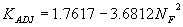Equation 43. K subscript ADJ equals 1.7617 minus 3.1682 N subscript F squared.0.18650.9594(43)
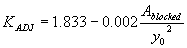Equation 44. K subscript ADJ equals 1.833 minus 0.002 times the quotient A subscript blocked divided by Y subscript 0 squared.0.00450.9491(44)
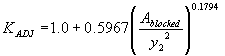Equation 45. K subscript ADJ equals 1.0 plus 0.5967 times the quotient, raised to the 0.1794 power, of A subscript blocked divided by Y subscript 2 squared.0.28910.9647(45)
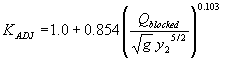Equation 46. K subscript ADJ equals 1.0 plus 0.854 times the quotient, raised to the 0.103 power, of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power.0.06390.9427(46)

GKY Method for Representative Velocity and Maryland DOT (Chang) Method for Critical Velocity

Two different independent regression variables were examined for this combination. Again, the approach flow area that is blocked by the embankments on one side of the channel over the squared flow depth was used as the independent regression variable, which gave R2 values of 0.00002 for the vertical face data and 0.05 for the wingwall data (figures 35 and 36, respectively).

Figure 35. GKY's resultant velocity with Chang's approximation equation for the critical velocity and local scour ratio as a function of the blocked area over the squared flow depth. Graph. On this graph, the blocked area over the squared flow depth (A subscript B over Y subscript 0 squared) is charted on the horizontal axis from 2 to 16, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.812 times (A subscript B over Y subscript 0 squared), RSQ equals 0.00002, MSE equals 0.0156" and "K subscript ADJ equals 1 plus 0.709 times (A subscript B over Y subscript 0 squared) to the negative 0.156 power, RSQ equals 0.0548, MSE equals 0.0241." The without wingwall regression remains relatively flat, while the trend for the wingwall regression is a gentle slope downward. The without wingwall and wingwall data are scattered along the ends of their respective regressions. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression.

Figure 35. GKY's resultant velocity with Chang's approximation equation for the critical velocity and local scour ratio as a function of the blocked area over the squared flow depth.

Figure 36. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.95967, MSE equals 0.01004; wingwall shape factor equals 0.89 (RSQ equals 0.90125, MSE equals 0.01960); and wingwall (RSQ equals 0.90395, MSE equals 0.01975). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 36. Measured and computed data with and without wingwalls, based on figure 37 regression.

The general equation can be formulated by inserting KADJ from figure 35:

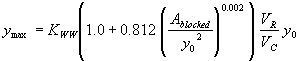Equation 47. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.0 plus 0.812 times the quotient, raised to the power of 0.002, of A subscript blocked divided by Y subscript 0 squared, all times V subscript R divided by V subscript C, times Y subscript 0.     (47)

where:

KWW = 1.0 for vertical face entrances
= 0.89 for wingwall entrances

The second independent regression variable tested for this combination was the blocked area over the squared computed equilibrium depth. The R2 values were 0.30 for the vertical face data and 0.06 for the wingwall data (figures 37 and 38, respectively).

Figure 37. GKY's resultant velocity with Chang's approximation equation for the critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth. Graph. On this graph, the blocked area over the squared computed equilibrium depth (A subscript B over Y subscript 2 squared) is charted on the horizontal axis from 1 to 21, and K subscript ADJ is charted on the vertical axis from 1 to 2.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.634 times (A subscript B over Y subscript 2 squared) raised to the 0.163 power, RSQ equals 0.2987, MSE equals 0.0109" and "K subscript ADJ equals 1 plus 0.408 times (A subscript B over Y subscript 2 squared) to the 0.171 power, RSQ equals 0.0645, MSE equals 0.0239." The trend for all data points is a gentle slope upward. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, and the latter data points end at an A subscript B over Y subscript 2 squared of 9.5.

Figure 37. GKY's resultant velocity with Chang's approximation equation for the critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth.

Figure 38. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.97148, MSE equals 0.00633; wingwall shape factor equals 0.92 (RSQ equals 0.92869, MSE equals 0.01415); and wingwall (RSQ equals 0.92088, MSE equals 0.01668). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 38. Measured and computed data with and without wingwalls, based on figure 37 regression.

Incorporating the adjustment function from figure 37 leads to the general equation:

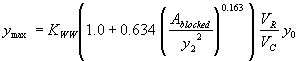Equation 48. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.92 for wingwall entrances, times the result of 1.0 plus 0.634 times the quotient, raised to the power of 0.163, of A subscript blocked divided by Y subscript 2 squared, all times V subscript R divided by V subscript C, times Y subscript 0.     (48)

where:

KWW= 1.0 for vertical face entrances
= 0.92 for wingwall entrances

Table 2 gives an overview for the tested independent regression variables and R2 values using the GKY method for representative velocity and the Maryland DOT (Chang) method for critical velocity.

Table 2. Independent regression variables and R2 values using the GKY and Maryland DOT (Chang) methods.

GKY Method for VR, Maryland DOT (Chang) Method for VC R2 Regression R2 Meas. vs. Comp. Equation No.
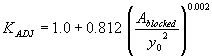Equation 49. K subscript ADJ equals 1.0 plus 0.812 times the quotient, raised to the 0.002 power, of A subscript blocked divided by Y subscript 0 squared.0.000020.9596(49)
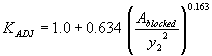Equation 50. K subscript ADJ equals 1.0 plus 0.634 times the quotient, raised to the 0.163 power, of A subscript blocked divided by Y subscript 2 squared.0.29870.9715(50)

GKY Method for Representative Velocity and Critical Velocity

Three independent regression variables were tried using the GKY method for representative velocity and the GKY method for critical velocity, which is a combination of the SMB equations. Starting again with the approach flow area that is blocked by the embankments on one side of the channel over the squared flow depth as the independent regression variable results in R2 values of 0.50 for the vertical face data and 0.41 for the wingwall data (figures 39 and 40, respectively).

Figure 39. GKY's resultant velocity with the SMB equation for the critical velocity and local scour ratio as a function of the blocked area over the squared flow depth. Graph. On this graph, the blocked area over the squared flow depth (A subscript B over Y subscript 0 squared) is charted on the horizontal axis from 2 to 16, and K subscript ADJ is charted on the vertical axis from 0.6 to 3. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.3953 times (A subscript B over Y subscript 0 squared) raised to the 0.4490 power, RSQ equals 0.2883, MSE equals 0.01849" and "K subscript ADJ equals 1 plus 0.1513 times (A subscript B over Y subscript 0 squared) to the 0.4740 power, RSQ equals 0.1849, MSE equals 0.0861." Both regression lines gently slope upward, although the without wingwall line has a steeper slope than the wingwall line. The without wingwall and wingwall data are scattered along the ends of their respective regressions. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression.

Figure 39. GKY's resultant velocity with the SMB equation for critical velocity and local scour ratio as a function of the blocked area over the squared flow depth.

Figure 40. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3. Three sets of data are plotted: without wingwall (RSQ equals 0.8806, MSE equals 0.0721; wingwall shape factor equals 0.84 (RSQ equals 0.8596, MSE equals 0.0479); and wingwall (RSQ equals 0.8521, MSE equals 0.0294). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 40. Measured and computed data with and without wingwalls, based on figure 39 regression.

Incorporating the adjustment function from figure 39 leads to the general equation:

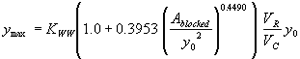Equation 51. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.87 for wingwall entrances, times the result of 1.0 plus 0.3953 times the quotient, raised to the power of 0.4490, of A subscript blocked divided by Y subscript 0 squared, all times V subscript R divided by V subscript C, times Y subscript 0.     (51)

where:

KWW= 1.0 for vertical face entrances
= 0.87 for wingwall entrances

The blocked area over the squared computed equilibrium depth was used as the second independent regression variable. The R2 values were 0.78 for the vertical face data and 0.38 for the wingwall data (figures 41 and 42, respectively).

Figure 41. GKY's resultant velocity with the SMB equation for critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth. Graph. On this graph, the blocked area over the squared computed equilibrium depth (A subscript B over Y subscript 2 squared) is charted on the horizontal axis from 0 to 45, and K subscript ADJ is charted on the vertical axis from 0.6 to 3.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 0.4205 times (A subscript B over Y subscript 2 squared) raised to the 0.4263 power, RSQ equals 0.8782, MSE equals 0.0148" and "K subscript ADJ equals 1 plus 0.1978 times (A subscript B over Y subscript 2 squared) to the 0.5308 power, RSQ equals 0.5819, MSE equals 0.0189." The trend for all data points is a gentle slope upward. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, and the latter data points end at an A subscript B over Y subscript 2 squared of 13.

Figure 41. GKY's resultant velocity with the SMB equation for critical velocity and local scour ratio as a function of the blocked area over the squared computed equilibrium depth.

Figure 42. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3.5. Three sets of data are plotted: without wingwall (RSQ equals 0.9690, MSE equals 0.0091; wingwall shape factor equals 0.89 (RSQ equals 0.9097, MSE equals 0.0179); and wingwall (RSQ equals 0.9145, MSE equals 0.0221). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 42. Measured and computed data with and without wingwalls, based on figure 41 regression.

Incorporating the adjustment function from figure 41 leads to the general equation:

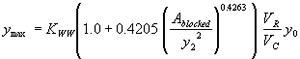Equation 52. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.0 plus 0.4205 times the quotient, raised to the power of 0.4263, of A subscript blocked divided by Y subscript 2 squared, all times V subscript R divided by V subscript C, times Y subscript 0.     (52)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

Testing the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth as the independent regression variable yielded the best results. The R2 values were 0.84 for the vertical face data and 0.47 for the wingwall data (figures 43 and 44, respectively).

Figure 43. GKY's resultant velocity with the SMB equation for the critical velocity and local scour ratio as a function of the blocked discharge normalized by the acceleration of gravity (G) and the computed equilibrium depth. Graph. On this graph, the blocked discharge normalized by the acceleration of gravity and the computed equilibrium depth (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) is charted on the horizontal axis from 0 to 7, and K subscript ADJ is charted on the vertical axis from 0.6 to 3.4. Four sets of data are plotted: without wingwall and the corresponding regression; and wingwall and its corresponding regression. Two text boxes on the graph read, "K subscript ADJ equals 1 plus 1.0056 times (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) raised to the 0.3710 power, RSQ equals 0.862, MSE equals 0.0168" and "K subscript ADJ equals 1 plus 0.6235 times (Q subscript B over the square root of G times Y subscript 2 to the five-seconds power) raised to the 0.4803 power, RSQ equals 0.522, MSE equals 0.0216." The trend for all data points is a gentle slope upward. The without wingwall and its corresponding regression have higher K subscript ADJ values at the same N subscript F values than the wingwall and wingwall regression, and the latter data points end at a blocked discharged point of 1.5.

Figure 43. GKY's resultant velocity with the SMB equation for critical velocity and local scour ratio as a function of the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth.

Figure 44. Measured and computed data with and without wingwalls. Graph. Y subscript max, measured, is presented on the horizontal axis from 0 to 3, and Y subscript max, computed, is presented on the vertical axis from 0 to 3.5. Three sets of data are plotted: without wingwall (RSQ equals 0.9558, MSE equals 0.0114; wingwall shape factor equals 0.89 (RSQ equals 0.8946, MSE equals 0.0252); and wingwall (RSQ equals 0.9044, MSE equals 0.0190). All three sets of data trend upward at a relatively constant rate, beginning at coordinates 0.5, 0.5, and ending at coordinates 2.5, 2.5.

Figure 44. Measured and computed data with and without wingwalls, based on figure 43 regression.

Incorporating the adjustment function from figure 43 leads to the general equation:

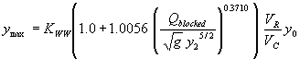Equation 53. Y subscript max equals K subscript WW, which equals 1.0 for vertical face entrances and 0.89 for wingwall entrances, times the result of 1.0 plus 1.0056 times the quotient, raised to the power of 0.3710, of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power, all times V subscript R divided by V subscript C, times Y subscript 0.     (53)

where:

KWW= 1.0 for vertical face entrances
= 0.89 for wingwall entrances

Table 3 below summarizes the results for the tested independent regression variables and R2 values using the GKY method for representative velocity and the SMB equation for critical velocity.

Table 3. Independent regression variables and R2 values using the GKY method for representative velocity and critical velocity.

GKY Method forVR, SMB Equations for VC R2 Regression R2 Meas. vs. Comp. Equation No.
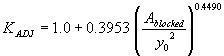Equation 54. K subscript ADJ equals 1.0 plus 0.3953 times the quotient, raised to the 0.4490 power, of A subscript blocked divided by Y subscript 0 squared.0.28830.8806(54)
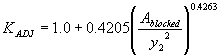Equation 55. K subscript ADJ equals 1.0 plus 0.4205 times the quotient, raised to the 0.4263 power, of A subscript blocked divided by Y subscript 2 squared.0.87820.9690(55)
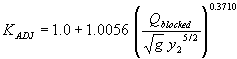Equation 56. K subscript ADJ equals 1.0 plus 1.0056 times the quotient, raised to the 0.3710 power, of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power.0.86210.9558(56)

RIPRAP RESULTS

For the riprap analysis, the Maryland DOT (Chang) and GKY methods for computing representative velocity were used to calculate the effective velocity that accounts for turbulence and vorticity in the mixing zone at the upstream corner of a culvert. Two independent regression variables were used for the blocked area over the squared flow depth and the blocked discharge normalized by the acceleration of gravity (g) and the flow depth to compute the adjustment coefficient KRIP.

Maryland DOT (Chang) Method for Representative Velocity

Using Chang's approximation equation for representative velocity and the approach flow area that is blocked by the embankments on one side of the channel over the squared flow depth to regress the effective velocity gives an R2 value of 0.39 (figures 45 and 46).

Figure 45. Maryland DOT's (Chang's) resultant velocity and stable riprap size from the Ishbash equation with the blocked area over the squared flow depth as the independent regression variable. Graph. N subscript F is graphed on the horizontal axis from 0.06 to 0.2, and K subscript RIP is graphed on the vertical axis from 0.8 to 1.3. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "K subscript RIP equals 1.33257 minus 1.82111 N subscript F, RSQ equals 0.22166, MSE equals 0.01271." The regression line follows a straight, downward-sloping path, from coordinates 0.08, 1.19 to 0.19, 0.99. The riprap data points are scattered on both sides of the regression line.

Figure 45. Maryland DOT's (Chang's) resultant velocity and stable riprap size from the Ishbash equation with the blocked area over the squared flow depth as the independent regression variable.

Figure 46. Measured and computed data. Graph. D subscript 50, measured, is graphed on the horizontal axis from 0.03 to 0.09, and D subscript 50, computed, is graphed on the vertical axis from 0.02 to 0.11. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "riprap data (rsq equals 0.73568, mse equals 0.00015)." The regression line follows a straight, upward-sloping path, from coordinates 0.03, 0.03 to 0.084, 0.084. Four sets of three vertically spaced riprap data fall along the regression line, at D subscript 50 measurements of 0.03, 0.041, 0.068, and 0.084.

Figure 46. Measured and computed data, based on figure 45 regression.

The expression for sizing riprap at the upstream corners to protect bottomless culvert footings from scour is:

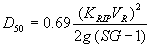Equation 57. D subscript 50 equals 0.69 times the quotient of the product, squared, of K subscript RIP times V subscript R, divided by the product of 2G times the result of SG minus 1.     (57)

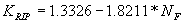Equation 58. K subscript RIP equals 1.3326 minus 1.8211 times N subscript F.     (58)

from figure 45.

Testing the blocked discharge normalized by the acceleration of gravity (g) and the flow depth as the independent regression variable leads to a regression coefficient, R2, value of 0.036 (figures 47 and 48).

Figure 47. Maryland DOT's (Chang's) resultant velocity and stable riprap size from the Ishbash equation with the blocked discharge normalized by the acceleration of gravity (G) and the flow depth as independent regression variable. Graph. Q subscript B over the square root of G times Y subscript 0 to the five-seconds power is graphed on the horizontal axis from 0.3 to 1.3, and K subscript RIP is graphed on the vertical axis from 0.8 to 1.3. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "K subscript RIP equals 1.01544 plus 0.07351 times (Q subscript B over the square root of G times Y subscript 0 to the five-seconds power), RSQ equals 0.03635, MSE equals 0.01574." The regression line follows a straight, upward-sloping path, from coordinates 0.35, 1.04 to 1.35, 1.12. The riprap data points are scattered on both sides of the regression line.

Figure 47. Maryland DOT's (Chang's) resultant velocity and stable riprap size from the Ishbash equation with the blocked discharge normalized by the acceleration of gravity (g) and the flow depth as the independent regression variable.

Figure 48. Measured and computed data. Graph. D subscript 50, measured, is graphed on the horizontal axis from 0 to 0.12, and D subscript 50, computed, is graphed on the vertical axis from 0 to 0.12. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "Riprap data (RSQ equals 0.83676, MSE equals 0.00025)." The regression line diagonally bisects the graph, following a straight, upward-sloping path. Four sets of two to three vertically spaced riprap data fall along the regression line, at D subscript 50 measurements of 0.03, 0.04, 0.065, and 0.082.

Figure 48. Measured and computed data, based on figure 47 regression.

According to figure 47, the adjustment function for KRIP is:

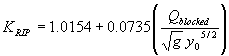Equation 59. K subscript RIP equals 1.0154 plus 0.0735 times the quotient of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power.     (59)

Equation 59 can be substituted into equation 57 for the expression for sizing riprap.

Table 4 gives an overview of the tested independent regression variables and R2 values using Maryland DOT's (Chang's) representative velocity equations.

Table 4. Independent regression variables and R2 values using the Maryland DOT (Chang) method for representative velocity.

Maryland DOT (Chang)Method for VR R2 Regression R2 Meas. vs. Comp. Equation No.
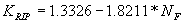Equation 58. K subscript RIP equals 1.3326 minus 1.8211 times N subscript F.0.22170.7357(58)
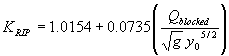Equation 59. K subscript RIP equals 1.0154 plus 0.0735 times the quotient of Q subscript blocked divided by the product of the square root of G times Y subscript 2 raised to the five-seconds power.0.03630.8367(59)

GKY Method for Representative Velocity

Computing the GKY method for representative velocity and the approach flow area that is blocked by the embankments on one side of the channel over the squared flow depth to determine the effective velocity gives an R2 value of 0.39 (figures 49 and 50).

Figure 49. GKY's resultant velocity and stable riprap size from the Ishbash equation with the blocked area over the squared flow depth as the independent regression variable. Graph. A subscript B over Y subscript 0 squared is graphed on the horizontal axis from 4 to 8.5, and K subscript RIP is graphed on the vertical axis from 0.8 to 1.4. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "K subscript RIP equals 0.828 plus 0.05 times (A subscript B over Y subscript 0 squared), RSQ equals 0.3946, MSE equals 0.01032." The regression line follows a straight, upward-sloping path, from coordinates 4.1, 1.04 to 8.05, 1.25. The riprap data points are scattered on both sides of the regression line, but are concentrated on both ends of the line.

Figure 49. GKY's resultant velocity and stable riprap size from the Ishbash equation with the blocked area over the squared flow depth as the independent regression variable.

Figure 50. Measured and computed data. Graph. D subscript 50, measured, is graphed on the horizontal axis from 0.03 to 0.09, and D subscript 50, computed, is graphed on the vertical axis from 0.02 to 0.11. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "riprap data (rsq equals 0.9009, mse equals 0.00013)." The regression line follows a straight, upward-sloping path, beginning at coordinates 0.03, 0.03, and ending at coordinates 0.084, 0.084. Four sets of two to three vertically spaced riprap data fall along the regression line, at D subscript 50 measurements of 0.03, 0.042, 0.067, and 0.083.

Figure 50. Measured and computed data, based on figure 49 regression.

As indicated in figure 49, the regression analysis leads to:

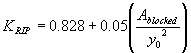Equation 60. K subscript RIP equals 0.828 plus 0.05 times the quotient of A subscript blocked divided by Y subscript 0 squared.     (60)

Inserting equation 60 into equation 57 yields the expression for sizing riprap.

Finally, the blocked discharge normalized by the acceleration of gravity (g) and the flow depth as the independent regression variable was tested, resulting in a regression coefficient, R2, value of 0.04 (figures 51 and 52).

Figure 51. GKY's resultant velocity and stable riprap size from Ishbash equation with the blocked discharge normalized by the acceleration of gravity (G) and the flow depth as the independent regression variable. Graph. Q subscript B over the square root of G times Y subscript 0 to the five-seconds power is graphed on the horizontal axis from 0.3 to 1.35, and K subscript RIP is graphed on the vertical axis from 0.8 to 1.4. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "K subscript RIP equals 1.0488 plus 0.0792 times (Q subscript B over the square root of G times Y subscript 0 to the five-seconds power), RSQ equals 0.04043, MSE equals 0.01636." The regression line follows a straight, upward-sloping path, from coordinates 0.35, 1.08 to 1.33, 1.16. The riprap data points are scattered on both sides of the regression line.

Figure 51. GKY's resultant velocity and stable riprap size from the Ishbash equation with the blocked discharge normalized by the acceleration of gravity (g) and the flow depth as the independent regression variable.

Figure 52. Measured and computed data. Graph. D subscript 50, measured, is graphed on the horizontal axis from 0 to 0.12, and D subscript 50, computed, is graphed on the vertical axis from 0 to 0.12. Riprap data and a regression line are plotted on the graph. A text box on the graph reads, "Riprap data (RSQ equals 0.83485, MSE equals 0.00024)." The regression line diagonally bisects the graph, following a straight, upward-sloping path. Four sets of two to three vertically spaced riprap data fall along the regression line, at D subscript 50 measurements of 0.032, 0.042, 0.067, and 0.082.

Figure 52. Measured and computed data, based on figure 51 regression.

As shown in figure 51, the regression coefficient function is:

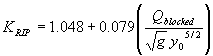Equation 61. K subscript RIP equals 1.048 plus 0.079 times the quotient of Q subscript blocked divided by the product of the square root of G times Y subscript 0 raised to the five-seconds power.     (61)

To gain the expression for sizing riprap, equation 61 may be substituted into equation 57. Table 5 is an overview of the computed independent regression variables and their R2 values when using GKY's representative velocity to account for turbulence and vorticity in the mixing zone at the upstream corner of a culvert.

Table 5. Independent regression variables and R2 values using the GKY method for representative velocity.

GKY Method for VR R2 Regression R2 Meas. vs. Comp. Equation No.
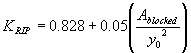Equation 62. V subscript R equals the square root of the sum of V subscript X, which is the velocity in the flow direction in feet per second, squared, plus V subscript Y, which is the velocity orthogonal to the flow direction, in feet per second, squared.0.39460.9009(60)
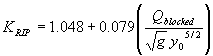Equation 61. K subscript RIP equals 1.048 plus 0.079 times the quotient of Q subscript blocked divided by the product of the square root of G times Y subscript 0 raised to the five-seconds power.0.04040.8348(61)

Previous | Table of Contents | Next

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse
U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101