U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-03-083 Date: June 2003 |
Pier scour has been extensively studied in the past for uniform and graded sediment mixtures. In general, pier scour equations account for the variation in sediment properties by either including a correction factor for sediment gradation or by using median size and the gradation coefficient in developing the experimental regression equations. In this study, a new governing sediment parameter was brought to attention. This parameter, which describes the characteristics of the coarse fraction available in mixtures, accounts for the wide variation in scour depth for mixtures with the same median size and size gradation factor. Along with a dimensionless flow intensity parameter, a new pier scour equation was developed to account for the sediment properties in clear-water scour range. This equation was shown to be applicable to a wide range of sediment sizes ranging all the way from 0.1 mm to 40 mm. Pier scour experiments conducted in noncohesive materials in this study were aimed at identifying the effects of sediment properties on the resulting scour. For this purpose 10 sets of experiments were designed to vary sediment size, gradation, and other size distribution properties. Pier scour experiments for each sediment mixture were conducted by varying the approach flow conditions. Since the primary goal of the study was to define effects of gradation and coarse material fraction on pier scour, other flow variables such as depth, flow angle of attack, pier shape, etc., were kept constant.
This section presents experimental flumes, sediment mixtures used as bed materials, piers, experimental procedures, as well as the individual measurements employed in quantifying effects of gradation and coarse material fraction on pier scour.
Laboratory Flumes
Three laboratory flumes, designated as the hydrodynamics flume, sedimentation flume, and the river mechanics flume, were simultaneously utilized for conducting the pier scour experiments in noncohesive sediment mixtures. The first two flumes are sediment recirculating facilities, while the latter does not recirculate sediment. All flumes are housed at the Hydraulics Laboratory of the Engineering Research Center at CSU. The water supply to these flumes is from the nearby Horsetooth Reservoir. The temperature of the water in the laboratory is controlled through a heating pipe system.
Hydrodynamics Flume
The hydrodynamics flume is a tilting, water and sediment recirculating laboratory facility. The flume is 0.6-m wide, 0.75-m deep, and 18-m long and is made of a steel bottom and Plexiglas side walls to facilitate visual observations. The facility is rigidly supported on U-shaped steel frames located every 1.2 m and is equipped with angled upper and lower flange stiffeners. The bottom flanges are supported on two I-beams spanning the full length of the flume and ground supported at the far upstream, the middle, and far downstream. Two carefully leveled guide rails are mounted on the top flanges to provide an escorting track for the measuring carriage. The flume can be tilted around its middle lateral axis through the synchronized operation of two mechanical jacks located at the upstream and downstream ends. Flow is supplied to the flume from a ground sump via a 0.3-m diameter steel pipe line, equipped with a 0.15-m diameter bypass for fine tuning of the flow, and a 20-horsepower (HP) centrifugal pump. The flow is first introduced to an upstream head box equipped with a multi-layer screen containing gravel at its outlet to serve as a flow guide to provide uniform velocities and turbulence characteristics at the entrance of the flume. A wave suppressor is then introduced to ensure accomplishment of the previous concerns. The flow depth is controlled by a downstream rotating gate hinged across the bottom of the flume, spanning the full width, and operated by a system of pulleys. Because of the tail gate control and the nature of the flume, a back water effect is sometimes noticed, causing the water depth to increase as the gate is approached. A uniform sediment layer 23 centimeters (cm) thick is prepared from the tested mixture and is spread along the full length of the flume with provisions made for a downstream 1.8-m long sediment trap and an upstream 1.8-m long transition zone. The upstream transition zone is composed of coarser sediments, with a sloping profile carefully designed to provide excess friction to ensure the existence of fully developed turbulent flow, with a boundary layer hitting the free surface, far upstream of the study reaches for all flow conditions.
Sedimentation Flume
The sedimentation flume is an elevated sediment transport testing facility that provides for both longitudinal tilting and sediment recirculation. The flume is 60-m long, 2.4-m wide, 1.2-m deep, and allows for slope adjustments up to 3 percent through a system of hydraulic jacks. The flume is constructed from steel plates at the bottom and sides, with provisions for Plexiglas windows along specific locations at its side. The structure's skeleton is composed of U-shaped lateral steel frames supported on box-sectioned longitudinal girders. A walkway is cantilevered from the lateral frames on each side of the structure. The upper flanges house guide rails for an electrically motorized measuring carriage that can virtually move to any point in the flume. Three different pumps (125, 150, and 250 HP), with a maximum combined capacity of 3 cubic meters per second (m3/s), can be simultaneously operated to supply water to the flume from a reservoir sump via three separate steel pipe lines. The flow is first introduced to the upstream head box, which contains several guide vanes and flow straighteners followed by a honeycomb mesh. It then passes through a gravel-filled screen succeeded by a wave suppressor. Rapid development of the fully turbulent boundary layer is achieved through an upstream concrete ramp and/or artificial roughening of the entrance zone. The flow depth is regulated through a manually operated downstream adjustable tail gate. The sediment bed is built to a thickness of about 0.4 m, with provisions made for a downstream sediment trap that extends for 6 m. To facilitate drainage of the flume after the experiments, a perforated 10-cm diameter poly vinyl chloride (PVC) pipe was embedded in the bed material and spanned the full length of the study reach. A motorized instrument carriage runs longitudinally on rails mounted on the side walls of the flume.
River Mechanics Flume
The river mechanics flume is a fixed-slope facility. The flume is 6-m wide, 0.9-m deep, and around 30-m long. The test section, however, was 24-m long, 5.1-m wide, and 0.9-m deep, providing for two Plexiglass viewing sections along one side of the flume and a large upstream reservoir to create uniform entrance conditions. I-beam rails are mounted on the side walls to provide a track for the measuring carriage. A 75-HP axial pump of maximum capacity around 0.6 m3/s supplies water to the flume through a 0.6-m diameter pipeline. The upstream main ends in a similar size diffuser located orthogonal to the main flow direction to distribute the flow uniformly across the flume width. The flow then passes through a gravel-filled screen followed by an artificially coarsened concrete ramp that joins the main sediment bed. The setup also provides for a downstream sediment trap and a downstream sill for depth regulation.
Piers
For the pier scour experiments conducted in the sedimentation flume, three identical 1.22-m high clear Plexiglas cylindrical piers with an outside diameter of 0.18 m were utilized. Circular piers were used because of their symmetry and the abundance of data available for comparative purposes. All three piers were placed at the center line of the flume for each run. In the longitudinal direction, the leading pier was 13.7 m from the head box of the flume, the second one was 24.4 m from the head of the flume, and the third one was 36.6 m from the head of the flume. To keep side-wall effects insignificant, the maximum pier size (for use in the 2.4-m wide flume) was kept at 0.18 m resulting in a flume width-to-pier ratio of 13.7. The depth measurements for pier scour with time were achieved utilizing visual techniques. For this purpose, the piers were constructed of transparent Plexiglas material, and three measuring scales were glued to the front, side, and back of each pier, in addition to a mirror with handle angled at 45o placed at the base of the pier. The base of the scour hole and the deepest point of the scour hole at any time could be easily identified and recorded by sliding the mirror within the Plexiglas pier and reading the corresponding measurement on the scale. In this way, scour depth with elapsed time could be obtained up to an accuracy of ±0.0015 m. A bright light located above the water surface was used to improve the visibility of the scour region under clear water-scour conditions. For the hydrodynamics flume experiments, three Plexiglas piers with outside diameters of 0.051 m, 0.051 m, and 0.07 m were installed in the flume, equidistant from the walls. Pier scour experiments in the river mechanics flume investigated the effects of pier width on the resulting scour. For this purpose six additional pier diameters including 0.019 m, 0.032 m, 0.057 m, 0.089 m, 0.165 m, and 0.216 m were tested.
Sediment Mixtures
Previous researchers have indicated that there is a very strong tendency for alluvial sediments to follow the log-normal size distribution. Such size distribution can be represented by a straight line on plots using logarithmic-normal probability scales. In this case the median sediment size D50
is also the geometric mean diameter, Dg of the sediment mixture, where D50 is the sediment diameter for which 50 percent of the sediment material is finer by weight. The geometric standard deviation ![]() gis given by:
gis given by:
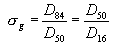 |
(1)
|
or
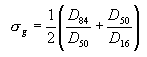 |
(2)
|
or
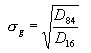 |
(3)
|
where: D16
, D50 , and D84 are the sediment diameters for which 16, 50, and 84 percent of the sediment material is finer by weight, respectively. The log-normal distribution function is a two-parameter distribution and is completely defined by D50 and 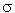 g. However, most natural sediments show an approximate log-normal distribution only through the mid part of the distribution, say D50 ±
g. However, most natural sediments show an approximate log-normal distribution only through the mid part of the distribution, say D50 ± 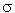 g, but they usually have long tails in both the coarse and fine fractions. Thus, equations 1 through 3 are for gradation coefficients that measure the spread of the distribution only between D84 and D16 in most natural sediments. The presence of coarse material in sediment mixtures is better defined by sizes of different quantities, such as D98, D95, D90, etc. For the work here, D50 and sgwere held constant and sizes of D90, D95, D98, etc., were changed since armoring in the scour hole involves mostly the coarser fractions of the mixture.
g, but they usually have long tails in both the coarse and fine fractions. Thus, equations 1 through 3 are for gradation coefficients that measure the spread of the distribution only between D84 and D16 in most natural sediments. The presence of coarse material in sediment mixtures is better defined by sizes of different quantities, such as D98, D95, D90, etc. For the work here, D50 and sgwere held constant and sizes of D90, D95, D98, etc., were changed since armoring in the scour hole involves mostly the coarser fractions of the mixture.
There is a specific requirement that needs to be met in determining the gradation of the initial grain size distribution for the sediment mixtures. This requirement is to keep the median size diameter constant throughout the study. In the sedimentation flume sand-scour experiments, the median diameter was chosen to be 0.75 mm, with gradation coefficients varying between 1.3 and 4.0. In the hydrodynamics flume sand-scour experiments, the median diameter was chosen to be 1.8 mm, with gradation coefficients varying between 1.1 and 4. Additional runs using 0.75-mm diameter uniform sand were conducted to study scaling effects. In the river mechanics flume sand-scour experiments, 0.45-mm diameter sand with a gradation coefficient of 2.3 was used. Finally, in the gravel-scour experiments conducted in the sedimentation flume, the median diameter was chosen to be 18 mm, with gradation coefficients varying between 1.4 and 2.3.
The properties of the sediment mixtures used in the pier-scour experiments are given in table 1.
Measurements
A series of measurements is needed to define the relationship between local pier scour and the various hydraulic, geometric, and sediment parameters. These measurements are presented below.
Flow Discharge
The water discharge in all three test flumes was measured through a system of orifice-meter and a differential manometer. For the hydrodynamics flume, two orifice plates were available: one mounted on the 0.3-m diameter main, and the other attached to the 0.15-m diameter bypass line. Both orifice plates are connected to a dual water-mercury manometer for detecting the pressure drop across the ends of the plate. The flow discharge was then computed from the calibration curves for the orifices. The pressure tapping across the orifice plate is connected to the manometer through hard vinyl tubing provided with bleeding valves for drainage and for ensuring an air-free environment. The sedimentation flume is equipped with three similar setups for measuring the discharge, each attached to a different pump. Extreme care was taken to ensure the release of air bubbles entrapped in all manometer lines. Flow discharges were also estimated by integrating the vertical velocity profiles over the entire cross section of the flume at several locations. The error in measuring the discharge in the hydrodynamics flume is around 3 percent, in the sedimentation flume around 4 percent, and in the river mechanics flume around 5 percent. These error estimates are due to the calibration errors of orifice plates, unsteadiness in the pump discharge, and fluctuations in manometer readings.
Flow Velocity
In the hydrodynamics flume, velocities were measured utilizing a two-dimensional electromagnetic Marsh McBirney, Model 523 velocity meter attached to a point gauge to measure velocity components in two orthogonal directions in a plane parallel to the bottom of the flume. The meter consists of a spherical electromagnetic probe with cable and signal processor powered by 6-volts direct current (V DC) externally charged with 110-volts alternating current (V AC). The probe has a diameter of 12 mm and is mounted on a 6-mm diameter vertical standing rod. The analog signals corresponding to the two orthogonal velocities sensed by the probe are intercepted by a multichannel data acquisition board connected to a personal computer. The sampling duration was 30 s, with a frequency of 50 Hertz (Hz). Overall accuracy of the latter setup is around 3.5 percent.
In the river mechanics and sedimentation flumes, velocities were measured with a one‑dimensional Marsh McBirney, Model 2000 electromagnetic flow meter with a 2.54-cm elliptic probe and a digital display conversion voltmeter. The accuracy of the flow meter is reported to be ±2 percent by the manufacturer, and its operating range is from -0.015 m/s to +6.1 m/s within temperature extremes of 0 oC to 71 oC. Overall accuracy of the velocity measuring setup is estimated to be 5 percent.
Flow Depth and Hydraulic Grade Line
In the case of nonuniform material, bed irregularities affect the accuracy of bed elevation measurements. Theoretically, during experiments the bed surface is not known and the bed elevation measurement at any section depends on the position of the tip of the point gauge relative to the larger grains on the bed. To reduce such errors, during the sedimentation flume experiments three different point gauge readings utilizing a flat tip were taken across each of the test sections. The bed elevation was accepted as the average of these three values. Using a pointed point-gauge tip, the corresponding water surface elevations were also measured. At specified test sections the depth of flow was then calculated as the average difference between the water surface and the bed surface elevations. For all experimental runs a uniform flow depth over the entire flume length was maintained at 0.3 m ±0.03 m by regulating the tail gate at the flume exit. However, the local flow depth varied along the flume length during runs No. MA-12, MA-19, and MA-27, in response to the presence of bed features.
Slope in laboratory flumes is one of the most difficult quantities to measure. Special attention was devoted to reduce the error in slope measurements as much as possible. For this reason bed levels were measured using the point gauge, then corrected through conversion factors obtained from a careful leveling of the carriage along the entire flume using a surveyor's level and rod. The bed slope was then computed as the slope of the line of best fit based on least square-criteria. The water surface slope was calculated in a similar manner.
In the hydrodynamics flume, the water surface elevations were measured using point gauges with a resolution of ±0.3 mm. Water surface elevation measurements were conducted at a minimum of three approach cross sections per pier and at a minimum of four locations across the flume width at each cross section. At every location in the cross section, the water level was considered to be the average of detected values, to account for any residual fluctuations in the supply discharge and any surface waves induced by the setup. This tedious procedure assumes an accuracy of 2 percent in the computed water depth. The hydraulic grade line is identified through regressing the measured water surface values after being adjusted with the level correction factors. The regression results in high correlation coefficients (R2 = 0.95). The velocity head was then added to the hydraulic grade line to define the total energy line.
Free Stream Bed and Scour Hole Topographies
The bed topographies for the scour holes and the free stream approaches are measured using point gauges. In all flumes, the standard topography measurement procedure started with the leveling of instrumentation carriages at each measurement location along and across the flume to account for the potential unevenness of tracks. Choosing an arbitrary fixed level, every location in the flume, as identified by its Cartesian coordinates, was assigned a correction factor reflecting its elevation relative to the fixed level. In the hydrodynamics flume, point gauges with flat/pointed tips were utilized for measuring purposes depending on the location and accuracy desired. The bed topographies at four different approach sections were measured for each pier model to define the upstream bed elevation. At each cross section, the bed level was considered to be the average of 10 measurements evenly distributed across the flume's width. To define bed topography in the vicinity of local scour requires more intensive measurements. An intensive measuring grid was adopted to describe the scour hole region for each pier. A similar procedure was followed for the other two flumes, with provisions made for measuring the initial as well as the final levels. The raw measurements are adjusted with the leveling correction factors for each location and then regressed together to yield the value of the bed slope. Approximately 300 topography measurements were performed for each pier model per experiment. Due to the large sampling size, the error in bed elevation measurements is considered to be equal to 0.25 of the D90 grain size. The maximum scour depth value for each run was calculated as the difference between the mean initial bed elevation and the lowest measured point of scour around each pier.
Scour versus Time Measurements
The measurement of the scour hole development for piers utilized visual techniques. As mentioned earlier, piers were made out of transparent Plexiglas. Measuring grid tapes were pasted on the interior wall at the front, side, and back of each pier. Using a simple periscope manufactured by an inclined-mirror, the development of scour with time was recorded without interference with the flow. A series of lights was used to facilitate the observation of the scour hole development. The depth of scour was recorded at regular intervals as the scour hole formed. The frequency of scour depth measurements decreased as the rate of scouring decreased. The experiments were stopped when no change occurred to the maximum depth of the scour hole over a minimum period of 4 hours.
Sampling of the Armor Layer
At the end of each experiment, the particle size distribution of the armor layers formed around each pier in the scour hole, approach bed to each pier, and downstream of the pier were measured from samples obtained by the flour paste technique described by Abdou(7). Sieve analysis was then performed on the samples using U.S. standard sieves and the available shaker in the Sediment Laboratory of the Engineering Research Center, CSU.
To determine the grain size distribution of the armor layer, it was required to collect all grains in the top layer only. The most common method used by previous researchers for such a purpose is the wax method. Gessler(8) used molten resin at 200 oC, Little and Mayer(9) used purified bee's wax at 65 oC to 68 oC, Davies(10) used molten petroleum wax at 76 oC to 78 oC, and Proffitt(11) used paraffin wax at 55 oC to 57 oC. In previous work, the measured grain size distribution of the armor layers was found to be highly affected by the temperature at which the wax was poured onto the bed. If the temperature is outside the narrow ranges specified above, the wax either permeates down before solidifying or solidifies before all grains in the top layer adhere to it.
Day(12) used the paint method to identify grains in the top layer but still used the wax method to lift it up. This method predicted a coarser grain size distribution of the armor layer than the wax method. Day explained this to be caused by the penetration of the wax below the armor layer.
In the present study, the flour paste technique developed by Abdou(7) was used. The procedure proved to be much easier than the wax method in terms of preparation, use, time elapsed, and separation of the grains adhering to the paste. The paste was sticky enough for all grain sizes to adhere easily and thickly enough so that it did not penetrate further than the surface layer.
After the bed was allowed to dry, the paste was placed on the surface of the bed. A gentle uniform pressure was applied downward on the paste to pick up all the grain sizes on the surface layer. The paste was then lifted up bringing with it the grains that had been the surface layer. Washing the surface of the paste with warm water and then gently brushing by hand achieved the separation of grains from the paste. A visual observation of the paste surface clearly indicated that all grains, even the finest, were separated from the paste. The material was then dried, weighed, sieved, and the grain size distribution of the armor layer at a specific area for a given flow condition was obtained.
Grain Size Distribution
Mechanical (or sieve) analysis was used to determine the particle sizes and their relative distribution for particles greater than 0.074 mm. The smallest sieve size used in this analysis was the U.S. No. 200. The sieve number corresponds to the number of openings per linear inch; for example, the U.S. Bureau of Standards No. 8 sieve has eight openings per inch.
To accomplish the mechanical analysis, sieves were stacked one on top of the other in the shape of a nest of sieves, in which the largest screen opening (smallest sieve number) was on top, progressing to the sieve with the smallest screen openings (largest sieve number) on the bottom of the nest. A lid was placed on top of the nest and a pan was placed below the bottom sieve to catch any sediment that passed through the smallest opening. A 10-minute shaking period was used in this procedure. A larger sample required a longer shaking period. Similarly, a sample composed primarily of fine-grained material requires a longer shaking period than a coarse-grained sample of equal weight.
Experimental Procedure
Preparation for the scour test was initiated by leveling the bed. Prior to each run, the sediment bed was leveled with the aid of a flat plate that was of the same width as the flume and was connected vertically to the instrument carriage by clamps. By employing the point gauge mounted on the carriage, initial bed elevations were taken to check the leveling of the flume and calculate the average initial bed elevation around each pier.
The gate was kept closed until the flume was filled with water. Then the gate was adjusted to get the desired depth, and the valves of the pump were adjusted to get the desired discharge, which was determined with an orifice inserted in the recirculating pipeline. Flow depth in the sedimentation flume experiments was maintained around 0.3 m; water surface and bed slopes were almost parallel. For the hydrodynamics flume experiments flow depth was kept around 0.08 m.
Once the requested flow conditions were verified, the carriage and the point gauge were moved along the flume in such a way that any point in the study area could be reached with the measuring devices. Water surface profile was measured along the length of the flume to calculate the water surface slope. Vertical velocity profiles and development of scour with time were recorded during each experiment. In the sedimentation flume experiments, the duration of runs was selected to be 16 hours (h) to allow maximum scour to be reached and the final scour hole geometry to be established. This period was long enough to maintain the maximum scour depth constant for at least 3 to 4 h. For the hydrodynamics flume experiments longer experiment durations were tested. Test runs up to 56 h showed that, for the ranges of sediment sizes and gradation used in the experiments, the longer experiment durations did not alter maximum scour. For a given discharge, once the surface armor layer was formed, bed profiles remained virtually constant. At the end of each run, the tail gate was slowly closed and the pump stopped to drain the flume without any disturbance. Then the flume was slowly drained with the aid of an efficient drainage system on the floor of the flume with its end open toward the tail gate.
The bed was then allowed to dry over a 24-h period, photos of scour holes around each pier were taken, and measurements of the final bed elevations were recorded to determine the maximum scour depth around each pier and the final bed slope. The bed was allowed to dry another 24 h, and then the armored layers around each pier and different areas in the approach and downstream of the piers were sampled using the flour paste technique described by Abdou(7). Sieve analysis was then performed on the samples using U.S. standard sieves (the sieving of the sediment samples was completed by using a series of sieves at intervals 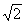 times sieve diameter).
times sieve diameter).
This procedure was repeated for each run. In the sedimentation flume experiments, the area around each pier within 6.1 m had to be refilled with the proper mixtures, leveled, and saturated with water. Flow conditions were verified, and velocity was measured at the approach of each pier in addition to the water surface profile measurements and scour depth with time. After the scour depth became constant with time for at least 3.0 to 4.0 h, the flow was stopped to let the bed dry, then the final bed elevations were taken. Finally, the surface layer around each pier as well as the approach and downstream of each pier was sampled to determine the size distribution of the armored layers.
A comprehensive experimental program was designed to investigate the different aspects of gradation and coarse material fraction effects on local pier scour. These experiments are categorized into 10 different sets of runs labeled 1 through 10. The experimental program was carried out concurrently in three different laboratory facilities. Sets 1 through 3, 9, and 10 were conducted in the sedimentation flume; sets 4 through 7 were performed in the hydrodynamics flume; and set 8 experiments were carried out in the mechanics flume. Thirteen different sediment mixtures and 10 different pier models were subjected to a range of flow conditions, resulting in a total of 188 different pier scour case studies.
Set 1 experiments were conducted by subjecting three identical piers to specified flow conditions. The purpose of this set of runs was to check the repeatability of results for scour depth at the three piers subjected to the same flow conditions. This first set (runs MA-1 through MA-12) was performed using a graded sand mixture with a geometric standard deviation, ![]() g of 2.43, and D50
of 0.75 mm. Set 2 experiments (runs MA-13 through MA-19) were conducted using the same sand with
g of 2.43, and D50
of 0.75 mm. Set 2 experiments (runs MA-13 through MA-19) were conducted using the same sand with ![]() g
of 2.43 and D50 of 0.75 mm as the bed material around pier 1. Around piers 2 and 3 the size of coarse material fraction in the original sediment mixture corresponding to 10 percent (around pier 2) and to 5 percent (around pier 3) was increased. The gradation coefficient,
g
of 2.43 and D50 of 0.75 mm as the bed material around pier 1. Around piers 2 and 3 the size of coarse material fraction in the original sediment mixture corresponding to 10 percent (around pier 2) and to 5 percent (around pier 3) was increased. The gradation coefficient, ![]() g, and D50 were kept constant at 2.43 and 0.75 mm, respectively. The purpose of this second set of runs was to examine the behavior of the scour depth with increasing the sizes of sediments for the fraction above D90 and D95
in the original sediment mixture without changing the gradation coefficient. Set 3 experiments (runs MA-20 through MA-27) used a sediment mixture with
g, and D50 were kept constant at 2.43 and 0.75 mm, respectively. The purpose of this second set of runs was to examine the behavior of the scour depth with increasing the sizes of sediments for the fraction above D90 and D95
in the original sediment mixture without changing the gradation coefficient. Set 3 experiments (runs MA-20 through MA-27) used a sediment mixture with ![]() g of 3.4 and D50
of 0.75 mm as the bed material around pier 2 and increasing the coarse fraction above D90 in the same sediment mixture as the bed material around pier 1. For pier 3, a uniform sand with
g of 3.4 and D50
of 0.75 mm as the bed material around pier 2 and increasing the coarse fraction above D90 in the same sediment mixture as the bed material around pier 1. For pier 3, a uniform sand with ![]() g
of 1.38 and D50 of 0.75 mm was used. The purpose of set 2 and 3 experiments was to investigate the effect of increasing coarse material fraction and gradation of bed materials on local pier scour depth.
g
of 1.38 and D50 of 0.75 mm was used. The purpose of set 2 and 3 experiments was to investigate the effect of increasing coarse material fraction and gradation of bed materials on local pier scour depth.
Sets 4 through 7 were conducted in a smaller flume with scaled down (1:4) flume width, flow depth, and pier width. In sets 4 through 6, a coarse sand mixture with the same median diameter, D50, of 1.8 mm, but different gradation coefficients were subjected to a range of approach flow conditions. In set 4, a uniform mixture with ![]() g
of 1.15 was used; whereas in sets 5 and 6,
g
of 1.15 was used; whereas in sets 5 and 6, ![]() g
was 2.43 and 3.4, respectively. Finally, in set 7 the same sediment used in set 1 (with D50 of 0.75 mm and
g
was 2.43 and 3.4, respectively. Finally, in set 7 the same sediment used in set 1 (with D50 of 0.75 mm and ![]() g
of 2.43) was used to study scaling effects.
g
of 2.43) was used to study scaling effects.
Set 8 experiments were conducted in the 5.18-m wide river mechanics flume to examine and verify pier size effects. For this purpose, a series of circular piers with varying diameters was subjected to the same oncoming flows. The sediment used for these experiments was medium sand with a median diameter of 0.55 mm and gradation coefficient of 2.43. The results of these experiments were used to establish scaling parameters for pier widths. In general terms, it is found that pier scour is a function of b2/3.
Sets 9 and 10 were conducted in the sedimentation flume and examined the effects of coarse fraction on gravel scour. The two sediment mixtures used in these experiments had both a median diameter of 18 mm and gradation coefficient of 1.45. However, the gravel mixture used in set 9 experiments contained larger coarse fractions. The D90 for the mixtures used in sets 9 and 10 was 40 mm and 22 mm, respectively. The purpose of these experiments was to investigate the range of applicability of the theory developed from the study.
A summary table of the sediment characteristics associated with the different mixtures utilized in the study is given in table 1. Tables 2 through 7 present these cases. In the pier scour experiments presented in this section, the effects of the following parameters were investigated:
The following sections present results of experiments. References to related summary tables are given whenever applicable.
Table 1. Properties of sediment mixtures used in pier scour experiments.
| Mixture No. (1) |
Mixture ID (2) |
sg |
Dm (mm) (4) |
D16 (mm) (5) |
D35 (mm) (6) |
D50 (mm) (7) |
D65 (mm) (8) |
D84.6 (mm) (9) |
D85 (mm) (10) |
D90 (mm) (11) |
D95 (mm) (12) |
D99 (mm) (13) |
Dcfm (mm) (14) |
Dcfm/D5 (mm) (15) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 |
MA-1A | 2.43 | 0.75 | 0.31 | 0.50 | 0.75 | 1.11 | 1.83 | 1.83 | 2.10 | 2.36 | 4.80 | 2.59 | 3.46 |
2 |
MA-1B | 2.43 | 0.75 | 0.31 | 0.50 | 0.75 | 1.11 | 1.83 | 1.83 | 2.80 | 5.00 | 8.00 | 4.24 | 5.65 |
3 |
MA-1C | 2.43 | 0.75 | 0.31 | 0.50 | 0.75 | 1.11 | 1.83 | 1.83 | 2.00 | 2.36 | 8.00 | 3.09 | 4.12 |
4 |
MA-2E | 3.40 | 0.75 | 0.23 | 0.45 | 0.75 | 1.31 | 2.65 | 2.65 | 4.76 | 6.40 | 8.00 | 5.50 | 7.33 |
5 |
MA-2D | 3.40 | 0.75 | 0.23 | 0.45 | 0.75 | 1.31 | 2.65 | 2.65 | 3.20 | 4.20 | 8.00 | 4.24 | 5.66 |
6 |
MA-3 | 1.38 | 0.75 | 0.55 | 0.65 | 0.75 | 0.87 | 1.05 | 1.05 | 1.18 | 1.22 | 1.30 | 1.19 | 1.59 |
7 |
HN-1 | 3.70 | 1.87 | 0.40 | 1.02 | 1.87 | 3.00 | 5.47 | 5.47 | 6.30 | 8.04 | 10.00 | 7.36 | 3.93 |
8 |
HN-2 | 1.15 | 1.87 | 1.56 | 1.74 | 1.87 | 2.01 | 2.21 | 2.21 | 2.26 | 2.32 | 2.38 | 2.29 | 1.23 |
9 |
HN-3 | 2.17 | 1.80 | 1.10 | 1.29 | 1.80 | 2.53 | 3.89 | 3.89 | 4.39 | 4.93 | 5.60 | 4.69 | 2.61 |
10 |
HN-4 | 1.28 | 0.76 | 0.63 | 0.66 | 0.76 | 0.87 | 1.03 | 1.03 | 1.08 | 1.14 | 1.19 | 1.11 | 1.46 |
11 |
MH-1 | 2.24 | 0.55 | 0.22 | 0.40 | 0.55 | 0.75 | 1.10 | 1.10 | 1.30 | 1.60 | 2.30 | 1.53 | 3.40 |
12 |
MH-2 | 1.28 | 16.90 | 11.50 | 16.10 | 16.90 | 17.84 | 19.10 | 38.10 | 40.00 | 42.40 | 45.00 | 41.30 | 2.44 |
13 |
MH-3 | 1.30 | 16.70 | 13.00 | 15.20 | 16.70 | 18.16 | 20.20 | 20.20 | 20.90 | 21.70 | 22.40 | 21.30 | 1.28 |
Table 2. Summary of sand-scour experiments in sedimentation flume for set 1 (runs 1 through 12).
| Run ID |
Mixture ID |
Median Diameter D50 (mm) |
Gradation Coefficient 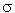 g g |
Flow Discharge Q (l/s) |
Approach Depth Y(m) |
Approach Velocity V (m/s) |
Energy Slope Se |
Froude Number Fr |
Scour |
Flow |
|---|---|---|---|---|---|---|---|---|---|---|
| MA- 1-1 | MA-1 | 0.75 | 2.43 | 206.43 | 0.384 | 0.213 | 0.00020 | 0.11 | 0.037 |
8 |
| MA- 1-2 | MA-1 | 0.75 | 2.43 | 206.43 | 0.396 | 0.204 | 0.00020 | 0.10 | 0.037 |
8 |
| MA- 1-3 | MA-1 | 0.75 | 2.43 | 206.43 | 0.399 | 0.201 | 0.00020 | 0.10 | 0.034 |
8 |
| MA- 2-1 | MA-1 | 0.75 | 2.43 | 246.07 | 0.287 | 0.347 | 0.00040 | 0.21 | 0.076 |
8 |
| MA- 2-2 | MA-1 | 0.75 | 2.43 | 246.07 | 0.293 | 0.341 | 0.00040 | 0.20 | 0.067 |
8 |
| MA- 2-3 | MA-1 | 0.75 | 2.43 | 246.07 | 0.293 | 0.338 | 0.00040 | 0.20 | 0.067 |
8 |
| MA- 3-1 | MA-1 | 0.75 | 2.43 | 300.16 | 0.287 | 0.421 | 0.00060 | 0.25 | 0.168 |
19 |
| MA- 3-2 | MA-1 | 0.75 | 2.43 | 300.16 | 0.290 | 0.405 | 0.00060 | 0.24 | 0.143 |
19 |
| MA- 3-3 | MA-1 | 0.75 | 2.43 | 300.16 | 0.293 | 0.405 | 0.00060 | 0.24 | 0.143 |
19 |
| MA- 4-1 | MA-1 | 0.75 | 2.43 | 300.16 | 0.381 | 0.302 | 0.00040 | 0.16 | 0.049 |
12 |
| MA- 4-2 | MA-1 | 0.75 | 2.43 | 300.16 | 0.375 | 0.302 | 0.00040 | 0.16 | 0.049 |
12 |
| MA- 4-3 | MA-1 | 0.75 | 2.43 | 300.16 | 0.378 | 0.290 | 0.00040 | 0.15 | 0.046 |
12 |
| MA- 5-1 | MA-1 | 0.75 | 2.43 | 263.63 | 0.354 | 0.296 | 0.00042 | 0.16 | 0.046 |
8 |
| MA- 5-2 | MA-1 | 0.75 | 2.43 | 263.63 | 0.344 | 0.293 | 0.00042 | 0.16 | 0.046 |
8 |
| MA- 5-3 | MA-1 | 0.75 | 2.43 | 263.63 | 0.341 | 0.296 | 0.00042 | 0.16 | 0.040 |
8 |
| MA- 6-1 | MA-1 | 0.75 | 2.43 | 280.34 | 0.335 | 0.332 | 0.00045 | 0.18 | 0.088 |
12 |
| MA- 6-2 | MA-1 | 0.75 | 2.43 | 280.34 | 0.335 | 0.332 | 0.00045 | 0.18 | 0.082 |
12 |
| MA- 6-3 | MA-1 | 0.75 | 2.43 | 280.34 | 0.335 | 0.329 | 0.00045 | 0.18 | 0.079 |
12 |
| MA- 7-1 | MA-1 | 0.75 | 2.43 | 323.10 | 0.323 | 0.396 | 0.00060 | 0.22 | 0.146 |
16 |
| MA- 7-2 | MA-1 | 0.75 | 2.43 | 323.10 | 0.326 | 0.390 | 0.00060 | 0.22 | 0.134 |
16 |
| MA- 7-3 | MA-1 | 0.75 | 2.43 | 323.10 | 0.326 | 0.387 | 0.00060 | 0.22 | 0.134 |
16 |
| MA- 8-1 | MA-1 | 0.75 | 2.43 | 360.76 | 0.320 | 0.442 | 0.00065 | 0.25 | 0.186 |
12 |
| MA- 8-2 | MA-1 | 0.75 | 2.43 | 360.76 | 0.326 | 0.411 | 0.00065 | 0.23 | 0.183 |
12 |
| MA- 8-3 | MA-1 | 0.75 | 2.43 | 360.76 | 0.323 | 0.421 | 0.00065 | 0.24 | 0.183 |
12 |
| MA- 9-1 | MA-1 | 0.75 | 2.43 | 267.03 | 0.320 | 0.335 | 0.00043 | 0.19 | 0.091 |
16 |
| MA- 9-2 | MA-1 | 0.75 | 2.43 | 267.03 | 0.311 | 0.335 | 0.00043 | 0.19 | 0.079 |
16 |
| MA- 9-3 | MA-1 | 0.75 | 2.43 | 267.03 | 0.305 | 0.341 | 0.00043 | 0.20 | 0.079 |
16 |
| MA- 10-1 | MA-1 | 0.75 | 2.43 | 390.49 | 0.332 | 0.469 | 0.00070 | 0.26 | 0.195 |
10 |
| MA- 10-2 | MA-1 | 0.75 | 2.43 | 390.49 | 0.326 | 0.457 | 0.00070 | 0.26 | 0.186 |
10 |
| MA- 10-3 | MA-1 | 0.75 | 2.43 | 390.49 | 0.317 | 0.460 | 0.00070 | 0.26 | 0.183 |
10 |
| MA- 11-1 | MA-1 | 0.75 | 2.43 | 429.00 | 0.335 | 0.491 | 0.00073 | 0.27 | 0.207 |
14 |
| MA- 11-2 | MA-1 | 0.75 | 2.43 | 429.00 | 0.329 | 0.479 | 0.00073 | 0.27 | 0.198 |
14 |
| MA- 11-3 | MA-1 | 0.75 | 2.43 | 429.00 | 0.320 | 0.494 | 0.00073 | 0.28 | 0.207 |
14 |
| MA- 12-1 | MA-1 | 0.75 | 2.43 | 473.74 | 0.363 | 0.503 | 0.00085 | 0.27 | 0.198 |
16 |
| MA- 12-2 | MA-1 | 0.75 | 2.43 | 473.74 | 0.363 | 0.524 | 0.00085 | 0.28 | 0.195 |
16 |
| MA- 12-3 | MA-1 | 0.75 | 2.43 | 473.74 | 0.384 | 0.482 | 0.00085 | 0.25 | 0.201 |
16 |
Table 3. Summary of sand-scour experiments in sedimentation flume for set 2 (runs 13 through 19).
| RunID | MixtureID | Median Diameter D50 (mm) |
Gradation Coefficient 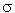 g g |
Flow Discharge Q (l/s) |
Approach Depth Y (m) |
Approach Velocity V (m/s) |
Energy Slope Se |
Froude Number Fr |
Scour Depth Ds (m) |
Flow Duration t (h) |
|---|---|---|---|---|---|---|---|---|---|---|
| MA-13-1 | MA-1A | 0.75 | 2.43 | 314.32 | 0.323 | 0.390 | 0.00055 | 0.22 | 0.155 | 16 |
| MA-13-2 | MA-1B | 0.75 | 2.43 | 314.32 | 0.323 | 0.366 | 0.00055 | 0.19 | 0.049 | 16 |
| MA-13-3 | MA-1C | 0.75 | 2.43 | 314.32 | 0.323 | 0.372 | 0.00055 | 0.21 | 0.067 | 16 |
| MA-14-1 | MA-1A | 0.75 | 2.43 | 206.43 | 0.311 | 0.256 | 0.00029 | 0.15 | 0.049 | 16 |
| MA-14-2 | MA-1B | 0.75 | 2.43 | 206.43 | 0.314 | 0.250 | 0.00029 | 0.14 | 0.012 | 16 |
| MA-4-3 | MA-1C | 0.75 | 2.43 | 206.43 | 0.314 | 0.250 | 0.00029 | 0.14 | 0.027 | 16 |
| MA15-1 | MA-1A | 0.75 | 2.43 | 146.11 | 0.305 | 0.250 | 0.00022 | 0.11 | 0.009 | 16 |
| MA-5-2 | MA-1B | 0.75 | 2.43 | 146.11 | 0.308 | 0.183 | 0.00022 | 0.11 | 0.003 | 16 |
| MA-5-3 | MA-1C | 0.75 | 2.43 | 146.11 | 0.305 | 0.186 | 0.00022 | 0.11 | 0.006 | 16 |
| MA-6-1 | MA-1A | 0.75 | 2.43 | 236.73 | 0.329 | 0.280 | 0.00045 | 0.16 | 0.082 | 16 |
| MA-6-2 | MA-1B | 0.75 | 2.43 | 236.73 | 0.335 | 0.265 | 0.00045 | 0.15 | 0.027 | 16 |
| MA-16-3 | MA-1C | 0.75 | 2.43 | 236.73 | 0.338 | 0.259 | 0.00045 | 0.14 | 0.046 | 16 |
| MA-17-1 | MA-1A | 0.75 | 2.43 | 259.38 | 0.329 | 0.302 | 0.00050 | 0.17 | 0.091 | 16 |
| MA-17-2 | MA-1B | 0.75 | 2.43 | 259.38 | 0.332 | 0.293 | 0.00050 | 0.16 | 0.030 | 16 |
| MA-17-3 | MA-1C | 0.75 | 2.43 | 259.38 | 0.332 | 0.290 | 0.00050 | 0.16 | 0.049 | 16 |
| MA-18-1 | MA-1A | 0.75 | 2.43 | 380.30 | 0.329 | 0.451 | 0.00062 | 0.25 | 0.213 | 16 |
| MA-18-2 | MA-1B | 0.75 | 2.43 | 380.30 | 0.329 | 0.427 | 0.00062 | 0.24 | 0.085 | 16 |
| MA-18-3 | MA-1C | 0.75 | 2.43 | 380.30 | 0.335 | 0.433 | 0.00062 | 0.24 | 0.128 | 16 |
| MA-19-1 | MA-1A | 0.75 | 2.43 | 477.14 | 0.335 | 0.549 | 0.00098 | 0.30 | 0.226 | 16 |
| MA-19-2 | MA-1B | 0.75 | 2.43 | 477.14 | 0.335 | 0.558 | 0.00098 | 0.31 | 0.180 | 16 |
| MA-19-3 | MA-1C | 0.75 | 2.43 | 477.14 | 0.305 | 0.646 | 0.00098 | 0.37 | 0.201 | 16 |
Table 4. Summary of sand-scour experiments in sedimentation flume for set 3 (runs 20 through 27).
| RunID | MixtureID | Median Diameter D50 (mm) |
Gradation Coefficient 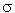 g g |
Flow Discharge Q (l/s) |
Approach Depth Y (m) |
Approach Velocity V (m/s) |
Energy Slope Se |
Froude Number Fr |
Scour Depth Ds (m) |
Flow Duration t (h) |
|---|---|---|---|---|---|---|---|---|---|---|
| MA-20-1 | MA-2E | 0.75 | 3.40 | 147.25 | 0.305 | 0.195 | 0.00047 | 0.11 | 0.003 | 16 |
| MA-20-2 | MA-2D | 0.75 | 3.40 | 147.25 | 0.308 | 0.189 | 0.00047 | 0.11 | 0.003 | 16 |
| MA-20-3 | MA-3 | 0.75 | 1.38 | 147.25 | 0.308 | 0.186 | 0.00047 | 0.11 | 0.009 | 16 |
| MA-21-1 | MA-2E | 0.75 | 3.40 | 184.06 | 0.341 | 0.207 | 0.00050 | 0.11 | 0.009 | 16 |
| MA-21-2 | MA-2D | 0.75 | 3.40 | 184.06 | 0.338 | 0.210 | 0.00050 | 0.12 | 0.012 | 16 |
| MA-21-3 | MA-3 | 0.75 | 1.38 | 184.06 | 0.338 | 0.213 | 0.00050 | 0.12 | 0.040 | 16 |
| MA-22-1 | MA-2E | 0.75 | 3.40 | 206.71 | 0.323 | 0.250 | 0.00054 | 0.14 | 0.012 | 16 |
| MA-22-2 | MA-2D | 0.75 | 3.40 | 206.71 | 0.329 | 0.241 | 0.00054 | 0.13 | 0.015 | 16 |
| MA-22-3 | MA-3 | 0.75 | 1.38 | 206.71 | 0.332 | 0.238 | 0.00054 | 0.13 | 0.064 | 16 |
| MA-23-1 | MA-2E | 0.75 | 3.40 | 259.38 | 0.335 | 0.305 | 0.00062 | 0.17 | 0.018 | 16 |
| MA-23-2 | MA-2D | 0.75 | 3.40 | 259.38 | 0.335 | 0.299 | 0.00062 | 0.16 | 0.021 | 16 |
| MA-23-3 | MA-3 | 0.75 | 1.38 | 259.38 | 0.338 | 0.293 | 0.00062 | 0.16 | 0.128 | 16 |
| MA-24-1 | MA-2E | 0.75 | 3.40 | 314.32 | 0.326 | 0.387 | 0.00070 | 0.22 | 0.030 | 16 |
| MA-24-2 | MA-2D | 0.75 | 3.40 | 314.32 | 0.329 | 0.378 | 0.00070 | 0.21 | 0.052 | 16 |
| MA-24-3 | MA-3 | 0.75 | 1.38 | 314.32 | 0.326 | 0.381 | 0.00070 | 0.21 | 0.213 | 16 |
| MA-25-1 | MA-2E | 0.75 | 3.40 | 379.45 | 0.332 | 0.451 | 0.00090 | 0.25 | 0.070 | 16 |
| MA-25-2 | MA-2D | 0.75 | 3.40 | 379.45 | 0.332 | 0.436 | 0.00090 | 0.24 | 0.085 | 16 |
| MA-25-3 | MA-3 | 0.75 | 1.38 | 379.45 | 0.335 | 0.430 | 0.00090 | 0.24 | 0.250 | 16 |
| MA-26-1 | MA-2E | 0.75 | 3.40 | 478.55 | 0.317 | 0.591 | 0.00150 | 0.34 | 0.189 | 16 |
| MA-26-2 | MA-2D | 0.75 | 3.40 | 478.55 | 0.317 | 0.582 | 0.00150 | 0.33 | 0.189 | 16 |
| MA-27-1 | MA-2E | 0.75 | 3.40 | 518.20 | 0.299 | 0.674 | 0.00200 | 0.39 | 0.219 | 16 |
| MA-27-2 | MA-2D | 0.75 | 3.40 | 518.20 | 0.299 | 0.652 | 0.00200 | 0.38 | 0.201 | 16 |
Table 5. Summary of sand-scour experiments in hydrodynamics flume for sets 4 through 7.
| RunID | MixtureID | Median Diameter D50 (mm) |
Gradation Coefficient 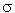 g g |
Pier Diameter b (m) |
Flow Discharge Q (l/s) |
Approach Depth Y (m) |
Approach Velocity V (m/s) |
Froude Number Fr |
Bed Slope So |
Scour Depth Ds (m) |
Flow Duration t (h) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HN-01-1 | HN-1 | 1.87 | 3.70 | 0.051 | 6.91 | 0.040 | 0.207 | 0.33 | 0.00418 | 0.010 | 8 |
| HN-01-2 | HN-1 | 1.87 | 3.70 | 0.051 | 6.91 | 0.050 | 0.165 | 0.23 | 0.00418 | 0.003 | 8 |
| HN-01-3 | HN-1 | 1.87 | 3.70 | 0.070 | 6.91 | 0.056 | 0.143 | 0.19 | 0.00418 | 0.004 | 8 |
| HN-02-1 | HN-1 | 1.87 | 3.70 | 0.051 | 13.79 | 0.065 | 0.436 | 0.54 | 0.00418 | 0.025 | 8 |
| HN-02-2 | HN-1 | 1.87 | 3.70 | 0.051 | 13.79 | 0.073 | 0.351 | 0.41 | 0.00418 | 0.009 | 8 |
| HN-02-3 | HN-1 | 1.87 | 3.70 | 0.070 | 13.79 | 0.080 | 0.314 | 0.35 | 0.00418 | 0.013 | 8 |
| HN-03-1 | HN-1 | 1.87 | 3.70 | 0.051 | 10.90 | 0.061 | 0.354 | 0.46 | 0.00363 | 0.015 | 8 |
| HN-03-2 | HN-1 | 1.87 | 3.70 | 0.051 | 10.90 | 0.071 | 0.271 | 0.32 | 0.00363 | 0.008 | 8 |
| HN-03-3 | HN-1 | 1.87 | 3.70 | 0.070 | 10.90 | 0.074 | 0.235 | 0.28 | 0.00363 | 0.008 | 8 |
| HN-04-1 | HN-1 | 1.87 | 3.70 | 0.051 | 17.58 | 0.075 | 0.488 | 0.57 | 0.00336 | 0.028 | 10 |
| HN-04-2 | HN-1 | 1.87 | 3.70 | 0.051 | 17.58 | 0.079 | 0.399 | 0.45 | 0.00336 | 0.012 | 10 |
| HN-04-3 | HN-1 | 1.87 | 3.70 | 0.070 | 17.58 | 0.081 | 0.354 | 0.40 | 0.00336 | 0.014 | 10 |
| HN-05-1 | HN-1 | 1.87 | 3.70 | 0.051 | 20.67 | 0.075 | 0.521 | 0.61 | 0.00368 | 0.032 | 10 |
| HN-05-2 | HN-1 | 1.87 | 3.70 | 0.051 | 20.67 | 0.078 | 0.451 | 0.52 | 0.00368 | 0.027 | 10 |
| HN-05-3 | HN-1 | 1.87 | 3.70 | 0.070 | 20.67 | 0.078 | 0.421 | 0.48 | 0.00368 | 0.036 | 10 |
| HN-10-1 | HN-2 | 1.87 | 1.15 | 0.051 | 6.91 | 0.075 | 0.162 | 0.19 | 0.00375 | 0.002 | 11 |
| HN-10-2 | HN-2 | 1.87 | 1.15 | 0.051 | 6.91 | 0.088 | 0.128 | 0.14 | 0.00375 | 0.000 | 11 |
| HN-10-3 | HN-2 | 1.87 | 1.15 | 0.070 | 6.91 | 0.101 | 0.110 | 0.11 | 0.00375 | 0.000 | 11 |
| HN-11-1 | HN-2 | 1.87 | 1.15 | 0.051 | 9.00 | 0.077 | 0.216 | 0.25 | 0.00375 | 0.007 | 9 |
| HN-11-2 | HN-2 | 1.87 | 1.15 | 0.051 | 9.00 | 0.087 | 0.158 | 0.17 | 0.00375 | 0.000 | 9 |
| HN-11-3 | HN-2 | 1.87 | 1.15 | 0.070 | 9.00 | 0.101 | 0.140 | 0.14 | 0.00375 | 0.000 | 9 |
| HN-12-1 | HN-2 | 1.87 | 1.15 | 0.051 | 10.90 | 0.075 | 0.256 | 0.30 | 0.00391 | 0.048 | 14 |
| HN-12-2 | HN-2 | 1.87 | 1.15 | 0.051 | 10.90 | 0.085 | 0.189 | 0.21 | 0.00391 | 0.009 | 14 |
| HN-12-3 | HN-2 | 1.87 | 1.15 | 0.070 | 10.90 | 0.098 | 0.158 | 0.16 | 0.00391 | 0.014 | 14 |
| HN-13-1 | HN-2 | 1.87 | 1.15 | 0.051 | 12.35 | 0.078 | 0.274 | 0.31 | 0.00418 | 0.058 | 21 |
| HN-13-2 | HN-2 | 1.87 | 1.15 | 0.051 | 12.35 | 0.088 | 0.204 | 0.22 | 0.00418 | 0.012 | 21 |
| HN-13-3 | HN-2 | 1.87 | 1.15 | 0.070 | 12.35 | 0.101 | 0.180 | 0.18 | 0.00418 | 0.017 | 21 |
| HN-14-1 | HN-2 | 1.87 | 1.15 | 0.051 | 13.79 | 0.077 | 0.387 | 0.44 | 0.00417 | 0.077 | 19 |
| HN-14-2 | HN-2 | 1.87 | 1.15 | 0.051 | 13.79 | 0.088 | 0.296 | 0.32 | 0.00417 | 0.042 | 19 |
| HN-14-3 | HN-2 | 1.87 | 1.15 | 0.070 | 13.79 | 0.100 | 0.247 | 0.25 | 0.00417 | 0.018 | 19 |
| HN-20-1 | HN-2 | 1.87 | 1.15 | 0.051 | 16.88 | 0.073 | 0.445 | 0.53 | 0.00417 | 0.078 | 30 |
| HN-20-2 | HN-2 | 1.87 | 1.15 | 0.051 | 16.88 | 0.089 | 0.344 | 0.37 | 0.00417 | 0.066 | 30 |
| HN-20-3 | HN-2 | 1.87 | 1.15 | 0.070 | 16.88 | 0.097 | 0.290 | 0.30 | 0.00417 | 0.061 | 30 |
| HN-21-1 | HN-3 | 1.8 | 2.17 | 0.051 | 10.90 | 0.085 | 0.212 | 0.23 | 0.00341 | 0.012 | 17 |
| HN-21-2 | HN-3 | 1.8 | 2.17 | 0.051 | 10.90 | 0.091 | 0.189 | 0.20 | 0.00341 | 0.003 | 17 |
| HN-21-3 | HN-3 | 1.8 | 2.17 | 0.070 | 10.90 | 0.097 | 0.149 | 0.15 | 0.00341 | 0.007 | 17 |
| HN-22-1 | HN-3 | 1.8 | 2.17 | 0.051 | 13.79 | 0.087 | 0.273 | 0.30 | 0.00341 | 0.014 | 22 |
| HN-22-2 | HN-3 | 1.8 | 2.17 | 0.051 | 13.79 | 0.094 | 0.244 | 0.25 | 0.00341 | 0.012 | 22 |
| HN-22-3 | HN-3 | 1.8 | 2.17 | 0.070 | 13.79 | 0.097 | 0.213 | 0.22 | 0.00341 | 0.012 | 22 |
| HN-23-1 | HN-3 | 1.8 | 2.17 | 0.051 | 16.88 | 0.088 | 0.342 | 0.37 | 0.00341 | 0.031 | 25 |
| HN-23-3 | HN-3 | 1.80 | 2.17 | 0.070 | 16.88 | 0.095 | 0.258 | 0.27 | 0.00341 | 0.020 | 25 |
| HN-24-1 | HN-3 | 1.80 | 2.17 | 0.051 | 20.70 | 0.088 | 0.410 | 0.44 | 0.00323 | 0.048 | 24 |
| HN-24-2 | HN-3 | 1.80 | 2.17 | 0.051 | 20.70 | 0.087 | 0.377 | 0.41 | 0.00323 | 0.042 | 24 |
| HN-29-3 | HN-4 | 0.76 | 1.28 | 0.070 | 7.56 | 0.098 | 0.122 | 0.12 | 0.00000 | 0.002 | 8 |
| HN-30-1 | HN-4 | 0.76 | 1.28 | 0.051 | 9.74 | 0.076 | 0.232 | 0.27 | 0.00000 | 0.062 | 20 |
| HN-30-2 | HN-4 | 0.76 | 1.28 | 0.051 | 9.74 | 0.086 | 0.170 | 0.19 | 0.00000 | 0.024 | 20 |
| HN-30-3 | HN-4 | 0.76 | 1.28 | 0.070 | 9.74 | 0.096 | 0.152 | 0.16 | 0.00000 | 0.017 | 20 |
| HN-31-1 | HN-4 | 0.76 | 1.28 | 0.051 | 11.95 | 0.079 | 0.261 | 0.30 | 0.00000 | 0.081 | 21 |
| HN-31-2 | HN-4 | 0.76 | 1.28 | 0.051 | 11.95 | 0.091 | 0.191 | 0.20 | 0.00000 | 0.058 | 21 |
| HN-31-3 | HN-4 | 0.76 | 1.28 | 0.070 | 11.95 | 0.101 | 0.174 | 0.18 | 0.00000 | 0.047 | 21 |
| HN-32-1 | HN-4 | 0.76 | 1.28 | 0.051 | 13.79 | 0.079 | 0.298 | 0.34 | 0.00000 | 0.085 | 23 |
| HN-32-2 | HN-4 | 0.76 | 1.28 | 0.051 | 13.79 | 0.091 | 0.255 | 0.27 | 0.00000 | 0.066 | 23 |
| HN-32-3 | HN-4 | 0.76 | 1.28 | 0.070 | 13.79 | 0.101 | 0.205 | 0.21 | 0.00000 | 0.083 | 23 |
Table 6. Summary of river mechanics flume experiments to study pier width effects for set 8.
| RunID | Mixture ID |
Median Diameter D50 (mm) |
Gradation Coeficient 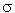 g g |
Pier Diameter b (m) |
Approach Depth Y (m) |
Approach Velocity V (m/s) |
Bed Slope So (m/m) |
Froude Number Fr |
Scour Depth Ds (m) |
Flow Duration t (h) |
|---|---|---|---|---|---|---|---|---|---|---|
| MH-11-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.238 | 0.244 | 0.001 | 0.160 | 0.045 | 16 |
| MH-10-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.157 | 0.448 | 0.001 | 0.361 | 0.196 | 16 |
| MH-9-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.198 | 0.371 | 0.001 | 0.266 | 0.153 | 16 |
| MH-8-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.212 | 0.255 | 0.001 | 0.177 | 0.060 | 16 |
| MH-7-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.255 | 0.272 | 0.001 | 0.172 | 0.079 | 16 |
| MH-6-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.239 | 0.257 | 0.001 | 0.168 | 0.072 | 16 |
| MH-5-1 | MH-1 | 0.55 | 2.24 | 0.216 | 0.246 | 0.290 | 0.001 | 0.187 | 0.120 | 16 |
| MH-12-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.237 | 0.280 | 0.001 | 0.184 | 0.088 | 16 |
| MH-13-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.210 | 0.253 | 0.001 | 0.176 | 0.069 | 16 |
| MH-14-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.224 | 0.274 | 0.001 | 0.185 | 0.089 | 16 |
| MH-15-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.244 | 0.316 | 0.001 | 0.205 | 0.116 | 16 |
| MH-16-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.214 | 0.282 | 0.001 | 0.195 | 0.081 | 16 |
| MH-17-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.290 | 0.517 | 0.001 | 0.307 | 0.248 | 16 |
| MH-18-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.247 | 0.361 | 0.001 | 0.232 | 0.191 | 16 |
| MH-19-1 | MH-1 | 0.55 | 2.24 | 0.152 | 0.224 | 0.307 | 0.001 | 0.207 | 0.111 | 16 |
| MH-11-3 | MH-1 | 0.55 | 2.24 | 0.165 | 0.219 | 0.246 | 0.001 | 0.168 | 0.049 | 16 |
| MH-10-3 | MH-1 | 0.55 | 2.24 | 0.165 | 0.138 | 0.465 | 0.001 | 0.400 | 0.143 | 16 |
| MH-9-3 | MH-1 | 0.55 | 2.24 | 0.165 | 0.182 | 0.408 | 0.001 | 0.305 | 0.158 | 16 |
| MH-8-3 | MH-1 | 0.55 | 2.24 | 0.165 | 0.194 | 0.265 | 0.001 | 0.192 | 0.065 | 16 |
| MH-7-3 | MH-1 | 0.55 | 2.24 | 0.165 | 0.237 | 0.307 | 0.001 | 0.201 | 0.088 | 16 |
| MH-11-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.238 | 0.240 | 0.001 | 0.157 | 0.037 | 16 |
| MH-10-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.157 | 0.479 | 0.001 | 0.385 | 0.117 | 16 |
| MH-9-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.198 | 0.349 | 0.001 | 0.250 | 0.111 | 16 |
| MH-8-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.212 | 0.238 | 0.001 | 0.165 | 0.066 | 16 |
| MH-7-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.255 | 0.270 | 0.001 | 0.171 | 0.077 | 16 |
| MH-6-2 | MH-1 | 0.55 | 2.24 | 0.089 | 0.239 | 0.276 | 0.001 | 0.180 | 0.073 | 16 |
| MH-11-4 | MH-1 | 0.55 | 2.24 | 0.057 | 0.219 | 0.235 | 0.001 | 0.160 | 0.035 | 16 |
| MH-10-4 | MH-1 | 0.55 | 2.24 | 0.057 | 0.138 | 0.436 | 0.001 | 0.374 | 0.057 | 16 |
| MH-9-4 | MH-1 | 0.55 | 2.24 | 0.057 | 0.182 | 0.378 | 0.001 | 0.283 | 0.068 | 16 |
| MH-8-4 | MH-1 | 0.55 | 2.24 | 0.057 | 0.194 | 0.250 | 0.001 | 0.181 | 0.036 | 16 |
| MH-7-4 | MH-1 | 0.55 | 2.24 | 0.057 | 0.237 | 0.276 | 0.001 | 0.181 | 0.032 | 16 |
| MH-10-5 | MH-1 | 0.55 | 2.24 | 0.032 | 0.138 | 0.463 | 0.001 | 0.398 | 0.029 | 16 |
| MH-9-5 | MH-1 | 0.55 | 2.24 | 0.032 | 0.182 | 0.413 | 0.001 | 0.309 | 0.037 | 16 |
| MH-8-5 | MH-1 | 0.55 | 2.24 | 0.032 | 0.194 | 0.266 | 0.001 | 0.193 | 0.022 | 16 |
| MH-7-5 | MH-1 | 0.55 | 2.24 | 0.032 | 0.237 | 0.305 | 0.001 | 0.200 | 0.038 | 16 |
| MH-10-6 | MH-1 | 0.55 | 2.24 | 0.019 | 0.157 | 0.437 | 0.001 | 0.352 | 0.014 | 16 |
| MH-9-6 | MH-1 | 0.55 | 2.24 | 0.019 | 0.198 | 0.339 | 0.001 | 0.243 | 0.034 | 16 |
|
MH-8-6 |
MH-1 |
0.55 |
2.24 |
0.019 |
0.212 |
0.219 |
0.001 |
0.152 |
0.018 |
16 |
Table 7. Summary of gravel-scour experiments in sedimentation flume for sets 9 and 10.
| RunID | Mixture ID |
Median Diameter D50 (mm) |
Gradation Coefficient 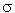 g g |
Pier Diameter b (m) |
Approach Depth Y (m) |
Approach Velocity V (m/s) |
Bed Slope So (m/m) |
Froude Number Fr |
Scour Depth Ds (m) |
Flow Duration t (h) |
|---|---|---|---|---|---|---|---|---|---|---|
| MHG1-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.296 | 0.850 | 0.0007 | 0.499 | 0.049 | 16 |
| MHG2-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.320 | 1.073 | 0.0007 | 0.605 | 0.073 | 16 |
| MHG3-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.338 | 1.192 | 0.0007 | 0.654 | 0.110 | 16 |
| MHG4-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.354 | 1.228 | 0.0007 | 0.659 | 0.113 | 16 |
| MHG5-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.372 | 1.384 | 0.0007 | 0.724 | 0.113 | 16 |
| MHG6-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.290 | 1.859 | 0.0007 | 1.103 | 0.110 | 16 |
| MHG7-1 | MH-2 | 16.90 | 1.28 | 0.178 | 0.238 | 2.286 | 0.0007 | 1.497 | 0.271 | 16 |
| MHG1-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.335 | 0.771 | 0.0007 | 0.425 | 0.073 | 16 |
| MHG2-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.357 | 0.969 | 0.0007 | 0.518 | 0.085 | 16 |
| MHG3-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.381 | 1.079 | 0.0007 | 0.558 | 0.119 | 16 |
| MHG4-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.357 | 1.186 | 0.0007 | 0.634 | 0.152 | 16 |
| MHG5-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.375 | 1.320 | 0.0007 | 0.688 | 0.183 | 16 |
| MHG6-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.250 | 2.018 | 0.0007 | 1.288 | 0.235 | 16 |
| MHG7-2 | MH-3 | 16.70 | 1.30 | 0.178 | 0.219 | 2.478 | 0.0007 | 1.688 | 0.305 | 16 |
This section presents the parameters affecting the pier scour in nonuniform mixtures and derives relationships to quantify their effects on the resulting scour depths. The equations derived from this analysis are then tested with the data from the experimental study and with data from earlier studies.
Governing Parameters
Experiments conducted for sets 1 through 3 varied the size gradation and coarse material fraction of six sand mixtures while keeping their median diameter constant. In these experiments, the flow depth was kept relatively constant, and the pier diameter remained 0.18 m while the discharge into the flume was incremented. Since the channel width and flow depth remained constant, this discharge variation in the experiments corresponded to varying velocity while keeping all other flow parameters constant. Figure 1 shows the variation of dimensionless scour depth in sets 1 through 3 experiments with approach velocity. By keeping all other variables constant, these experiments isolate the effects of gradation and coarse material fraction on pier scour. As shown in figure 1, the initiation of pier scour takes place independent of the size of coarse material fractions for approach velocities of about 0.18 m/s. This velocity is termed as the scour initiation velocity, Vi, and marks the threshold condition for clear-water scour. For approach velocities greater than Vi , the largest scour depth in figure 1 takes place in uniform sediment mixtures (gradation coefficient , ![]() g
= 1.38). As the size gradation coefficient increases from 1.38 to 2.43 to 3.4, the depth of scour decreases. This finding is in agreement with previous research. However, the reduction of scour is not a constant factor as suggested by earlier studies, but is a function of flow intensity. While the largest scour reduction takes place for an intermediate velocity value, for velocities slightly greater than 0.18 m/s and for velocities greater than 0.6 m/s, the scour reduction remains small. Figure 1 also shows two mixtures with the same median sediment sizes and gradation coefficients but with enlarged coarse fractions. In mixtures identified as 2.38A and 2.38B, while D50
and
g
= 1.38). As the size gradation coefficient increases from 1.38 to 2.43 to 3.4, the depth of scour decreases. This finding is in agreement with previous research. However, the reduction of scour is not a constant factor as suggested by earlier studies, but is a function of flow intensity. While the largest scour reduction takes place for an intermediate velocity value, for velocities slightly greater than 0.18 m/s and for velocities greater than 0.6 m/s, the scour reduction remains small. Figure 1 also shows two mixtures with the same median sediment sizes and gradation coefficients but with enlarged coarse fractions. In mixtures identified as 2.38A and 2.38B, while D50
and ![]() g
were kept at 0.75 mm and 2.43, respectively, the coarsest 5-percent and 10-percent fractions were enlarged by replacing these size groups with coarser sediments. As a result, as shown in figure 1, the scour depths corresponding to these mixtures are smaller. In fact, the scour observed for the mixture with enlarged coarsest 10-percent fraction (mixture 2.43 A) is the same as the scour observed in mixture 3.4A with a gradation coefficient of 3.4. Similarly, introducing larger coarse fractions to mixture 3.4A results in further reduction in scour depth.
g
were kept at 0.75 mm and 2.43, respectively, the coarsest 5-percent and 10-percent fractions were enlarged by replacing these size groups with coarser sediments. As a result, as shown in figure 1, the scour depths corresponding to these mixtures are smaller. In fact, the scour observed for the mixture with enlarged coarsest 10-percent fraction (mixture 2.43 A) is the same as the scour observed in mixture 3.4A with a gradation coefficient of 3.4. Similarly, introducing larger coarse fractions to mixture 3.4A results in further reduction in scour depth.
Figure 2 compares the results of sets 1 through 3 experiments with the computed scour values from the CSU equation given in Federal Highway Administration's (FHWA) HEC-18(13). In figure 2 several observations can be made: 1) As the intensity of flow increases (indicated by larger scour depth) the computed scour depths approach the measured values; 2) For larger gradation factors and for mixtures with larger coarse fractions, the convergence of computed and measured values takes place at higher flow intensities; and 3) At low flow intensities the computed values are in the order of 8 to 10 times the measured values. In figure 3, the ratio of measured to computed scour depth is plotted against the flow velocity for sets 1 through 3 experiments. For these data, this ratio approaches 1 (perfect agreement) as the flow velocity (or intensity) increases. For a given flow velocity, the ratio is closer to 1 for uniform mixtures (illustrated in the figure by the 1.38 gradation coefficient above the plot points) than for mixtures with large size variations (illustrated by the 3.40 gradation coefficient above the plot points). A general conclusion from figures 2 and 3 is that the discrepancy between measured and computed scour depths, using the current CSU equation, becomes worse as the gradation coefficient increases and as the velocity (or flow intensity) decreases.
Figure 4 shows results from set 4 through 7 experiments conducted using coarser sediment mixtures and compares these results with the finer uniform sand mixture used in sets 1 through 3. In these experiments smaller depths and pier diameters were used; without applying proper modeling scale ratios for flow depth and pier diameter the results cannot be superimposed on the previous results. However, the pattern of scour depth variation with flow intensity remains identical. Both in figures 1 and 4 the relationship between velocity and Ds /b shows that for uniform material, the variation of scour with velocity is almost linear. For graded material, and material with larger coarse fractions, this relationship assumes the characteristics of 2nd or 3rd degree polynomial (concave). At high flow velocities, both figures show that scour values tend to converge to an "ultimate" value. The velocity at which maximum clear-water scour takes place is a function of the size of coarsest size fractions present in mixtures. This velocity is identified as the critical velocity, Vc, at which the entire bed is mobilized (live-bed conditions).
It is possible to define a dimensionless excess velocity, 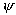 , which is a relative velocity with respect to the critical velocity that fully mobilizes the bed given by:
, which is a relative velocity with respect to the critical velocity that fully mobilizes the bed given by:
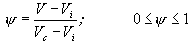 |
(4)
|
The value of varies between 0 and 1; the 0 corresponding to initiation of scour and 1 corresponding to the condition of fully mobilized bed. The values of Vi and Vc can be determined by relating these velocities to critical flow conditions corresponding to initiation of motion. Using Shields' relationship for critical shear
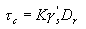 |
(5)
|
or
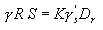 |
(6) |
where tc = critical shear; K
= experimental constant (![]() 0.047);
0.047); ![]() = submerged specific weight of sediment (
= submerged specific weight of sediment (![]() 1.65
1.65![]() ); R
= hydraulic radius; S = slope of the energy grade line; and Dr = characteristic sediment size. For critical conditions, using Manning-Strickler equation to express the slope of the energy line in terms of approach velocity ( S = Vc2 n2 / R2/3
, where Vc and R are in metric units) and using a relationship expressing the roughness coefficient, n, in terms of the characteristic sediment size (n = Dr1/6 /26.1, where Dr is in meters) it is possible to obtain:
); R
= hydraulic radius; S = slope of the energy grade line; and Dr = characteristic sediment size. For critical conditions, using Manning-Strickler equation to express the slope of the energy line in terms of approach velocity ( S = Vc2 n2 / R2/3
, where Vc and R are in metric units) and using a relationship expressing the roughness coefficient, n, in terms of the characteristic sediment size (n = Dr1/6 /26.1, where Dr is in meters) it is possible to obtain:
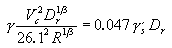 |
(7)
|
or
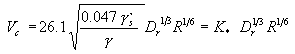 |
(8)
|
where Vc , R, and Dr are in SI units. Replacing 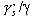 with 1.65 and after simplifications, equation 8 reduces to
Vc(m/s)≈
with 1.65 and after simplifications, equation 8 reduces to
Vc(m/s)≈![]() 7.27Dr(m)1/3Y(m)1/6. In English units, the critical velocity expression becomes Vr (ft/sec)
7.27Dr(m)1/3Y(m)1/6. In English units, the critical velocity expression becomes Vr (ft/sec) ![]() 13.16 Dr (ft)1/3 Y (ft)1/6. For the purposes of this study, however, the constant K* in equation 8 is left to be an experimentally determined value. Using results of pier scour experiments, K* was found to be 6.625 for SI units (using Dr
in meters) and 12 for English units (using Dr in feet). To reflect the characteristics of the coarse material fractions, the representative sediment size, Dr, is defined by the median size of the coarse material fraction, Dcfm, given by:
13.16 Dr (ft)1/3 Y (ft)1/6. For the purposes of this study, however, the constant K* in equation 8 is left to be an experimentally determined value. Using results of pier scour experiments, K* was found to be 6.625 for SI units (using Dr
in meters) and 12 for English units (using Dr in feet). To reflect the characteristics of the coarse material fractions, the representative sediment size, Dr, is defined by the median size of the coarse material fraction, Dcfm, given by:
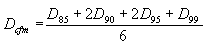 |
(9)
|
The parameter Dcfm is a representative size (in meters for SI units and in feet for English units) for the coarse fractions present in sediment mixtures. Experimental evidence in figures 1 and 4 indicate that fully mobilized bed cannot be achieved without mobilizing coarser sizes. In the absence of extensive size information, or in cases where there are no discontinuities in the size gradation curves, it is possible to utilize D90 to represent coarse fractions.
Velocities in the vicinity of piers are amplified. From potential flow theory, this amplification is in the order of 1.7 times the approach velocity. The scour initiation takes place when the accelerated flows past the pier are capable of removing the bed material from the pier region. Experimental evidence indicates that these velocities are dependent on the finer size fractions that are significantly available in the bed. For this study, the representative size for initiation of motion was determined to be D35. This size was used in the sedimentation literature by Einstein and Chien(14), Ackers and White(15) to account for the gradation effects in the transport of bed material. The expression for the initiation of pier scour can be derived from the critical velocity relationship and can be expressed as:
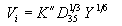 |
(10)
|
where Ki is an experimental coefficient. From the pier scour experiments, the value of Kiwas found to be 2.65 for SI units using D35 in meters (4.8 for English units using D35 in feet).
Using the dimensionless velocity factor ![]() , the data presented earlier in figure 1 are expressed in figure 5. Figure 5 shows that while maximum scour depth is reached at
, the data presented earlier in figure 1 are expressed in figure 5. Figure 5 shows that while maximum scour depth is reached at ![]() = 0.6 for the uniform mixture, for graded sediments higher flow intensities may be needed. This figure also shows that for mixtures with coarse fractions, low relative flow intensities produce significantly smaller scour depths. For these mixtures, ultimate scour is produced sharply beyond a threshold intensity. Figure 5 indicates that even though the ultimate scour might be the same, for intermediate flows, different mixtures exhibit different scour patterns. The information in figure 5 is reproduced in figure 6 in nondimensional form.
= 0.6 for the uniform mixture, for graded sediments higher flow intensities may be needed. This figure also shows that for mixtures with coarse fractions, low relative flow intensities produce significantly smaller scour depths. For these mixtures, ultimate scour is produced sharply beyond a threshold intensity. Figure 5 indicates that even though the ultimate scour might be the same, for intermediate flows, different mixtures exhibit different scour patterns. The information in figure 5 is reproduced in figure 6 in nondimensional form.
Figures 7 and 8 present dimensionless velocity versus depth of scour for sets 4 through 7, 8, and 9. In these figures the parameter Dcfm is used to differentiate between mixtures with the same median size and gradation coefficient. As shown, the representative coarse fraction size, Dcfm, can reliably identify mixtures and therefore can be used in relationships to quantify the associated scour depths. In general, for the same dimensionless velocity factor, smaller Dcfm values are associated with larger scour depths. However, a more reliable factor in differentiating sediment properties of mixtures is the Dcfm /D50
ratio used in figure 9. This dimensionless parameter can be used to normalize different sediment sizes for their expected scour potential. In figure 9, Dcfm
/D50 values of 1.23 and 1.46 represent two uniform mixtures with median sizes of 1.80 mm and 0.75 mm, respectively. For a given dimensionless velocity factor, the mixture with the larger sediment size but with smaller Dcfm
/D50 ratio produces larger scour holes. This experimental observation can be used to formulate an expression by relating scour to flow intensity (as represented by dimensionless flow velocity factor, ![]() ) and the relative coarse fraction size, Dcfm /D50.
) and the relative coarse fraction size, Dcfm /D50.
To achieve this goal, scour taking place in uniform material must first be evaluated. Then, ratios of scour values observed in mixtures with varying amounts of coarse material to scour in uniform material must be evaluated. This ratio, which is termed as the "Coarse Fraction Reduction Factor," and denoted by K4 , must then be related to flow intensity and Dcfm /D50. Figure 10 shows the results of this procedure for set 1 through 3 experiments. Several conclusions can be drawn from figure 10:
Scour reduction due to presence of coarse material cannot be expressed with a single value.
Scour reduction is a function of the coarse sediment fraction ratio Dcfm /D50. The higher the ratio, the lower the minimum value of K4.
For low flow intensities, and therefore ![]() values near zero, the K4 value must be unity since at low flow intensities there could be no effects due to coarse fractions or gradation.
values near zero, the K4 value must be unity since at low flow intensities there could be no effects due to coarse fractions or gradation.
For high flow intensities, and therefore ![]() values near or greater than unity, the K4 value must also approach unity. At high flow intensities with fully mobilized bed, effects due to the presence of coarse fractions must be minimal.
values near or greater than unity, the K4 value must also approach unity. At high flow intensities with fully mobilized bed, effects due to the presence of coarse fractions must be minimal.
There exists a certain flow intensity ![]() at which the scour reduction is minimum for a given sediment mixture. The location and magnitude of the minimum depend on the distribution and modality of sediment mixtures.
at which the scour reduction is minimum for a given sediment mixture. The location and magnitude of the minimum depend on the distribution and modality of sediment mixtures.
Derivation of K4 Relationship
Two steps are needed in order to derive a functional relationship for K4: 1) develop an expression for pier scour in uniform mixtures; and 2) separate the effects due to coarse fractions and develop an appropriate function.
Set 8 experiments given in table 6 were used to define the variation of local scour with pier diameter. Figures 11 and 12 show the variation of dimensionless scour depth with approach velocity for the six pier diameters used in the study. Since the flow depth was kept relatively constant for these experiments, and since the investigation of these effects was beyond the scope of the experimental study, the commonly accepted depth dependency of Y 1/6 was assumed for this study in normalizing the results. The best-fit line for describing the variation of scour with pier width in the pier width effect experiments utilizing 0.55-mm graded sand and the corresponding correlation coefficient are given by:
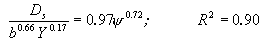 |
(11)
|
where Ds, b, and Y are in meters and R2 is the correlation coefficient. This relationship demonstrates that scour is related to pier diameter according to Ds~ b0.66. The goodness of fit of this relationship is shown in figure 13.
Next, utilizing Ds /(b0.66Y0.17) and as variables, an expression for pier scour in uniform mixtures was developed. For this purpose, the present experiments with median sediment sizes ranging from 0.75 mm to 1.80 mm and to 17 mm were utilized. The resulting expression in International System (SI) units is:
|
|
(12)
|
in which Ds, b, and Y are in meters. For preferred English units, the coefficient 0.99 becomes 1.21; Ds, b, and Y are in feet.
In using equation 12, a limiting value of 1 must be imposed on![]() to reflect maximum clear-water scour conditions. Figures 14 and 15 show the goodness of fit of the data to this equation. In figure 15 additional data (126 points) from Chabert and Engeldinger(16) and Shen, Schneider, Karaki(17, 18) that were used in the development of FHWA's CSU equation are included. This demonstrates the agreement of the new equation with other data sources. For comparison purposes, figure 16 presents the same uniform material data with the CSU equation. As expected, for coarse material and gravel, the CSU equation does not perform well.
to reflect maximum clear-water scour conditions. Figures 14 and 15 show the goodness of fit of the data to this equation. In figure 15 additional data (126 points) from Chabert and Engeldinger(16) and Shen, Schneider, Karaki(17, 18) that were used in the development of FHWA's CSU equation are included. This demonstrates the agreement of the new equation with other data sources. For comparison purposes, figure 16 presents the same uniform material data with the CSU equation. As expected, for coarse material and gravel, the CSU equation does not perform well.
The last stage in the development was the derivation of an expression to separate the effects due to coarse material fractions. This expression was derived through an extensive search for a function that could describe the physical phenomenon explained earlier in figure 10. These conditions are:
The resulting expression is:
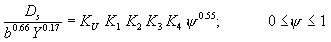 |
(13)
|
where KU = 0.99 for SI units, in which Ds, b, and Y are in meters (=1.21 for preferred English units, in which Ds, b, and Y are in feet); K1, K2, and K3 are as defined in HEC-18(13); and K4 is the Coarse Fraction Factordefined by:
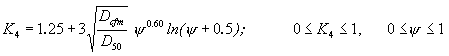 |
(14)
|
where ![]() is the dimensionless excess velocity from equation 4.
is the dimensionless excess velocity from equation 4.
Figure 17 shows the data from set 1 through 3 experiments along with predictions from FHWA's CSU equation(13) and the new K4 relationship. The goodness of fit is demonstrated in figure 18. In these figures, at low flow intensities and in the presence of coarse material, the performance of the CSU equation was poor. However, at high flow intensities, the CSU predictions converged with the new method and the measurements.
Figures 19 and 20 show the new equations with all available data from this study and with the data from earlier studies that were used in the development of the earlier CSU equation (a total of 310 data values). The performance of the CSU equation with the same data set is illustrated in figure 21.
Figure 22 compares the present HEC-18(13) correction for coarse material size with the new approach. As shown, the modifications proposed in HEC-18 cannot fully accommodate size corrections since this factor does not involve any sizes and provides maximum correction at ![]() = 0 (no scour condition).
= 0 (no scour condition).
From the analysis of all data, it is concluded that two adjustments are needed for FHWA's CSU equation: 1) implementation of initiation of scour for uniform mixtures with larger sediment diameters than those used in the derivation of the model; and 2) implementation of gradation and coarse fraction size correction for nonuniform sediment mixtures.
Since the equation was originally developed for fine sands, the initiation of motion took place at very low velocities, and therefore the need for such correction was not obvious. For coarser sediments at low flow intensities, the present analysis amplifies this deficiency. The initiation of scour may be implemented into the CSU equation by the inclusion of a scour initiation factor, Ki. This factor was found to be:
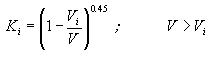 |
(15)
|
For values of, the value of the initiation of scour factor, Ki , is 0.
Figure 23 compares the adjusted scour computations with the presently used K4 adjustment. The results are almost identical. The reason for this is due to the fact that the current K4 is merely a correction for the initiation of motion since the expression used for K4 in HEC-18 is independent of relative sizes.
The second adjustment to the CSU equation to implement gradation and coarse fraction size correction for nonuniform sediment mixtures may be accomplished through the K4 factor defined earlier:
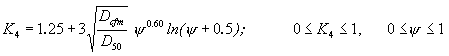 |
(14)
|
The final form of the CSU equation is:
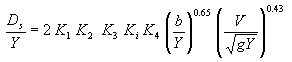 |
(16)
|
where the definition of terms K1, K2, and K3 are as defined in HEC-18. Figures 24 and 25 show the results of pier scour depth computations using both Ki and K4 and compares the results with the results from this study. As seen, major improvement takes place in the predictions. The final results are comparable to those obtained from the study with slight overestimations.
A new pier scour equation describing effects of gradation and coarse material fraction on pier scour was developed. This equation is given as:
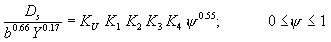 |
(13)
|
where KU = 0.99 for SI units, in which Ds, b, and Y are in meters (= 1.21 for preferred English units, in which Ds, b, and Y
are in feet); K1, K2, and K3 are as defined in HEC-18; and 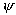 = the dimensionless excess velocity factor given by
= the dimensionless excess velocity factor given by
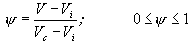 |
(4)
|
The definitions of the critical and scour initiating velocities, Vc and Vi , respectively are:
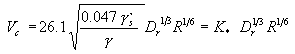 |
(8)
|
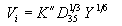 |
(10)
|
where Kc = 6.625 for SI units (= 12.0 for preferred English units); K i = 2.65 for SI units (= 4.8 for preferred English units); and Dcfm is the median size of the coarse material fractions (in meters for SI units and in feet for English units) computed from
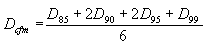 |
(9)
|
The coarse fraction reduction factor K4 is given by:
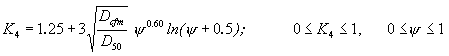 |
(14)
|
By definition, both K4 and 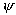 cannot be greater than 1. The new equation has the following characteristics:
cannot be greater than 1. The new equation has the following characteristics:
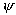 of 1 (live-bed conditions).
of 1 (live-bed conditions).The work on the existing FHWA CSU equation also provided very promising results. The adjustments needed for the FHWA equation were: 1) implementation of initiation of scour for uniform mixtures with larger sediment diameters than those used in the derivation of the model; and 2) implementation of gradation and coarse fraction size correction for nonuniform sediment mixtures.
The initiation of scour is implemented into the CSU equation by the inclusion of Ki factor. This factor was found to be:
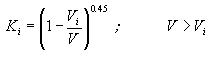 |
(15)
|
For values of V ![]() Vi, the value of the initiation of scour factor, Ki , is 0.
Vi, the value of the initiation of scour factor, Ki , is 0.
Gradation and coarse fraction size correction for nonuniform sediment mixtures is implemented into the CSU equation through the K4 factor defined earlier as:
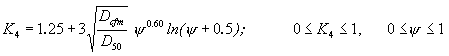 |
(14)
|
The final form of the CSU equation is:
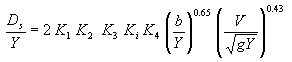 |
(16)
|
where the definition of terms K1, K2, and K3 are as defined in HEC-18.
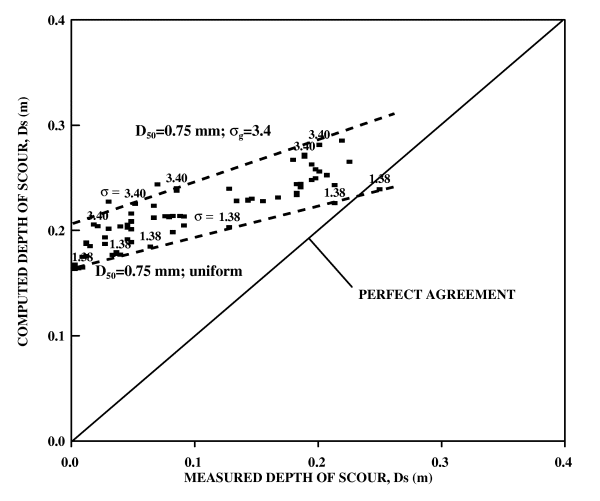
Figure 2. Comparison of FHWA's CSU equation with measured scour from sets 1 through 3.
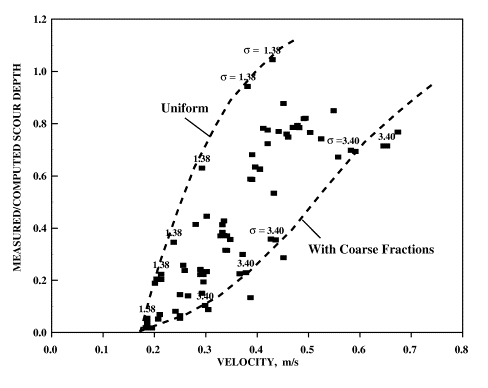
Figure 3. Velocity versus discrepancy ratio for sets 1 through 3 experiments.
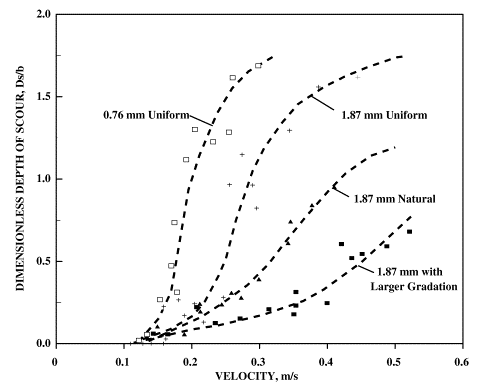
Figure 4. Flow velocity versus dimensionless scour for sets 4 through 7 experiments.
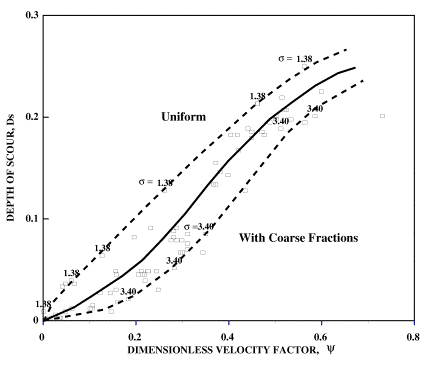
Figure 5. Dimensionless excess velocity factor, ![]() , versus depth of scour for sets 1 through 3.
, versus depth of scour for sets 1 through 3.
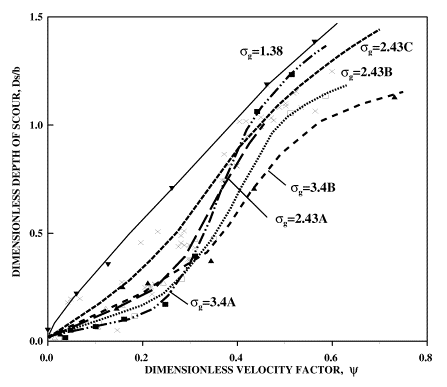
Figure 6. Variation of dimensionless scour with excess velocity factor for various mixtures.
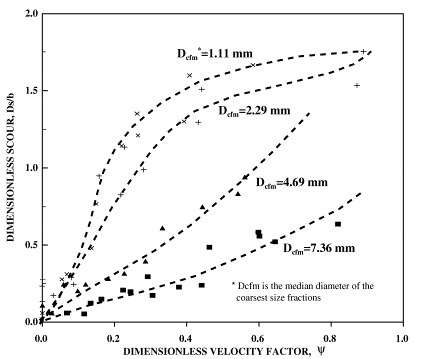
Figure 7. Variation of dimensionless scour with excess
velocity factor, ![]() for different coarse fraction sizes used in sets 4 through 7 experiments.
for different coarse fraction sizes used in sets 4 through 7 experiments.
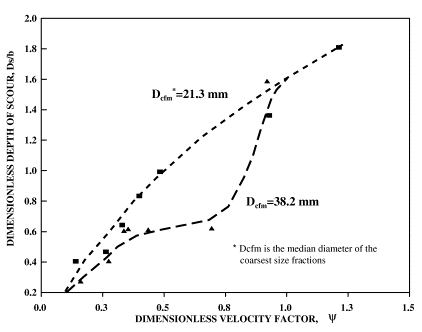
Figure 8. Variation of dimensionless scour with excess velocity factor, ![]() for different coarse fraction sizes used in sets 8 and 9.
for different coarse fraction sizes used in sets 8 and 9.
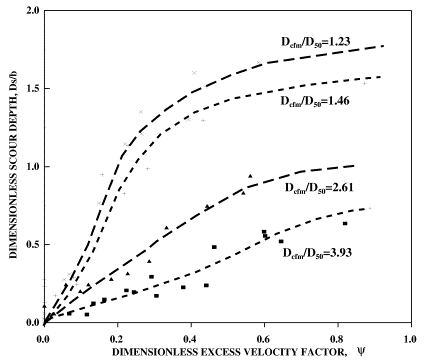
Figure 9. Variation of scour depth with excess velocity factor, ![]() for different coarse fraction size ratios used in sets 4 through 7 experiments.
for different coarse fraction size ratios used in sets 4 through 7 experiments.
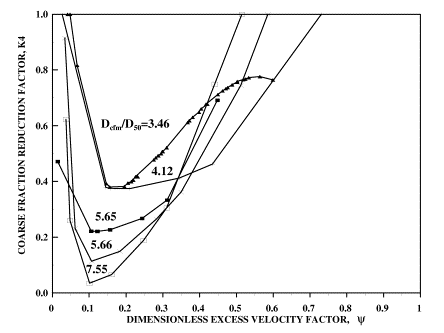
Figure 10. Variation of measured coarse fraction reduction factor, K4, with excess velocity factor, ![]() for sets 1 through 3 experiments.
for sets 1 through 3 experiments.
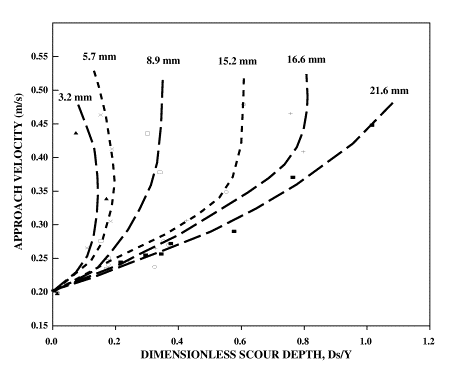
Figure 11. Variation of scour depth with pier size for the set 8 experiments.
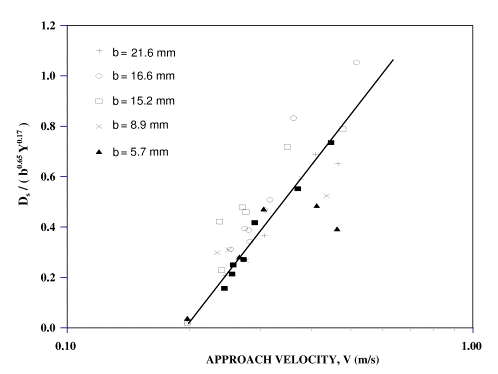
Figure 12. Relationship describing variation of pier scour with diameter.
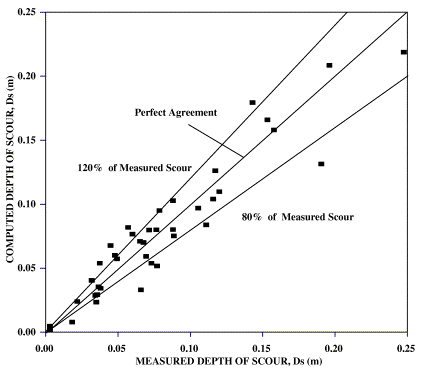
Figure 13. Computed and measured scour depths for the set 8 experiments.
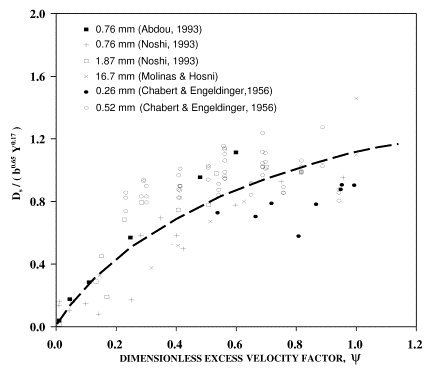
Figure 14. Variation of scour depth with excess velocity factor, ![]() for uniform sand and gravel.
for uniform sand and gravel.
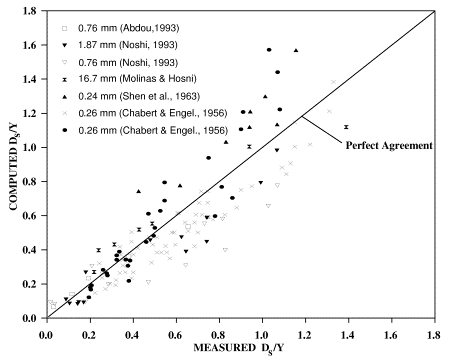
Figure 15. Measured and computed depth of scour for uniform sands and gravel using equation 12.
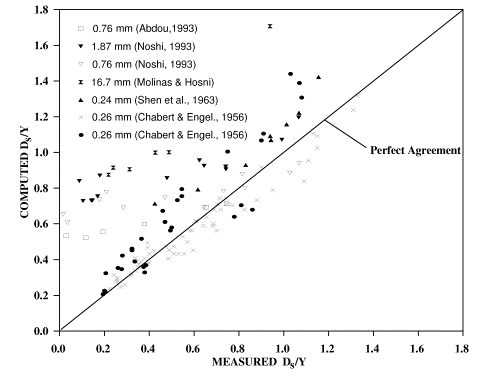
Figure 16. Measured and computed scour for uniform sediment using FHWA's CSU equation.
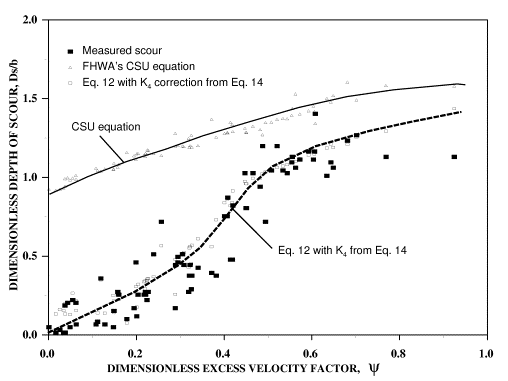
Figure 17. Computed scour for sets 1 through 3 experiments using equation 12 with K4 from equation 14.
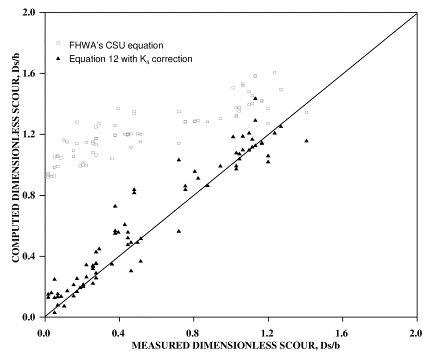
Figure 18. Measured and computed scour for nonuniform-sand experiments in sets 1 through 3.
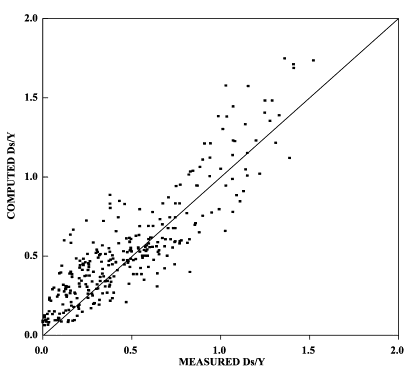
Figure 19. Computed and measured scour for all data using equation 12 (uniform-mixture equation).
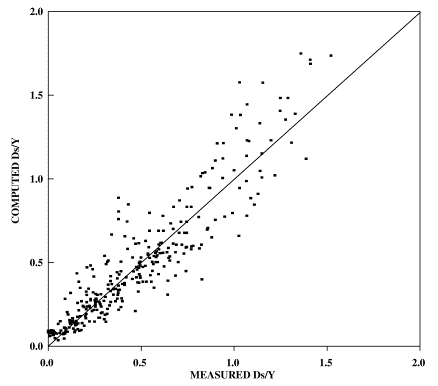
Figure 20. Computed and measured scour for all data using equation 12 with K4 correction from equation 14.
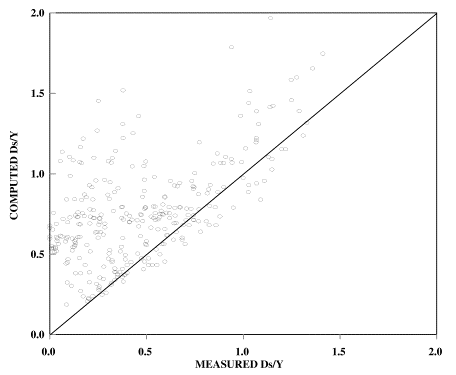
Figure 21. Computed scour using FHWA's CSU equation for uniform and nonuniform mixtures.
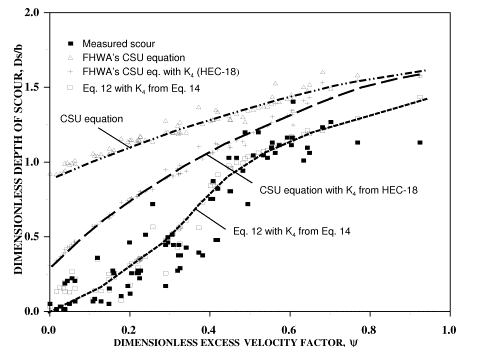
Figure 22. Computed scour by using FHWA's CSU equation with and without K4 correction from HEC 18, and by using the newly developed equation 12 with K4 correction from equation 14.
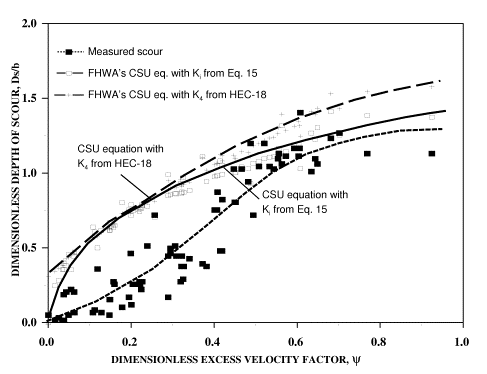
Figure 23. Comparison of FHWA's CSU equation with K4 correction (according to HEC 18) and the initiation of motion correction, Ki (according to equation 15).
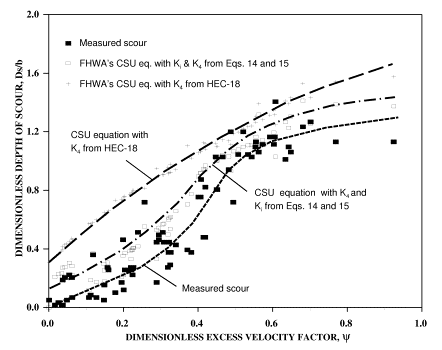
Figure 24. FHWA's CSU equation adjusted with Ki and K4 and with the HEC 18 correction for K4.
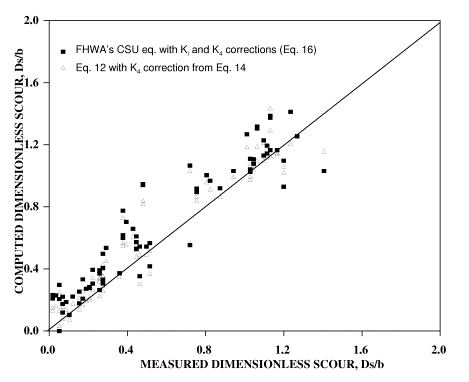
Figure 25. Comparison between computed and measured scour using Ki and K4 corrections to the FHWA's CSU equation (equation 16) and by using equation 12 with K4 correction from equation 14.