Effects of Inlet Geometry on Hydraulic Performance of Box Culverts
CHAPTER 3. THEORY AND DESIGN CALCULATIONS FOR INLET AND OUTLET CONTROL
The theory outlined in HDS-5, as described in this chapter, is the basis for analyzing data from this study.
INLET CONTROL HYDRAULICS OF CULVERTS
Empirical regression coefficients developed by fitting experimental data to semitheoretical equations are listed in HDS-5 for each inlet shape to relate headwater to discharge intensity for a range of flows.
Analysis of inlet-control data depends upon whether or not the inlet is submerged. If the inlet is not submerged, headwater can be expressed as a simple energy balance between the critical section and the upstream section, which are almost adjacent to one another. Alternatively, headwater can be analyzed as flow over a weir. In the latter instance, discharge is determined in part by the headwater raised to a power, M, which typically has a factor of two-thirds, or 0.667. If the inlet is submerged, flow through the inlet is conceptually like flow through an orifice, albeit an irregular shaped orifice. Orifice flow depends in part on the effective area of the orifice flow and the change in pressure. Since headwater depths are usually measured from the invert of a culvert, a more general expression for the orifice flow includes the distance from the invert.
Figure 12 illustrates an unsubmerged inlet control condition. Experimental data from this type of condition have been analyzed two ways. First, a simple energy balance can be made between sections 1 and 2 illustrated in figure 12. The critical specific energy Hc can be computed for any culvert shape, although it is tedious computation for some shapes. Data is regressed to determine regression coefficients K and M for computing the entrance loss, He. HDS-5 describes this analysis as the form 1 analysis for unsubmerged inlet control flow (figure 13). Most of the circular culvert inlets listed in HDS-5 are based on the form 1 analysis. The other way to analyze this type of data is to treat it as flow over a weir as illustrated in the form 2 equation (figure 14). Then the regression coefficients essentially absorb the critical specific energy control. All of the rectangular box culverts in HDS-5 are based on the form 2 equation, and in all cases, the exponent M was 0.667. Circular culverts and elliptical culverts with tapered throats are also based on the form 2 equation, but the exponent M varies a little for these inlets.
Figure 12. Diagram. Typical inlet control flow condition.
Figure 13. Equation. Unsubmerged form 1, inlet control.
Figure 14. Equation. Unsubmerged form 2, inlet control.
For inlet control under submerged conditions, regression constants c and Y are determined using the equation in figure 15.
Figure 15. Equation. Submerged form, inlet control.
| Where for figures 13, 14, and 15: |
| | |
| HWi | is headwater depth above inlet control section invert. |
| D | is interior height of culvert barrel. |
| Hc | is specific head at critical depth (dc + Vc2/2g). |
| Q | is discharge. |
| A | is full cross-sectional area of culvert barrel. |
| S | is culvert barrel slope. |
| K, M, c, Y | are regression constants. |
| Ku | is 1.811 for SI and 1.0 for English units. |
OUTLET CONTROL HYDRAULICS OF CULVERTS
Outlet control is the general case that covers everything except the special case of free surface flow passing through critical flow near the inlet. Outlet control flow occurs anytime the barrel flows full throughout, as illustrated in figure 16, regardless of the slope of the culvert.
Figure 16. Diagram. Outlet control for full flow condition.
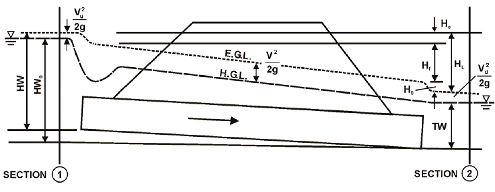 If the culvert is installed on a mild slope (0.7 percent), outlet control will occur for both a submerged or unsubmerged inlet and a submerged or unsubmerged outlet. If the culvert is installed on a steep slope (3 percent), outlet control will occur if the tailwater is sufficiently high to submerge the critical depth at the upstream end of the culvert or to cause full barrel flow throughout. If a culvert is installed on a steep slope and only a portion of the barrel is submerged, a hydraulic jump will occur in the barrel but the headwater will still be inlet controlled. The controlling relationship for outlet control is an energy balance between sections 1 and 2, as illustrated in figure16, but now the two sections are separated by all the losses and elevation changes that occur between the tailwater channel and the approach channel. The outlet control head-discharge relationship, in which head relates to the total energy, is shown in the equation in figure 17.
Figure 17. Equation. Head-discharge relationship, outlet control.
| Where: |
| | |
| HWo | is headwater depth above the outlet invert. |
| TW | is tailwater depth above the outlet invert. |
| Vu | is approach velocity. |
| Vd | is downstream velocity. |
| HL | is total energy loss. |
The total energy losses include the entrance, friction, and exit losses, as shown in figure 18.
Figure 18. Equation. Total energy losses.
| Where: |
| | |
| HLe | is entrance loss. |
| HLf | is friction loss. |
| HLo | is exit loss. |
The entrance and exit losses are commonly expressed as a fraction of the barrel velocity head, as shown in figures 19 and 20.
Figure 19. Equation. Entrance loss.
Figure 20. Equation. Exit loss.
| Where: |
| | |
| Ke | is an entrance loss coefficient. |
| Ko | is an exit loss coefficient, usually assumed to be 1.0 for design purposes. |
| V2/2g | is velocity head inside the culvert barrel. |
| Vd2/2g | is velocity head in the downstream channel near the outlet, often neglected in design. |
Since this study was focused on the effects of inlet geometry, the primary emphasis was on the entrance loss coefficient for outlet control, but exit losses were measured to determine if multiple barrels or skewed inlets affected the exit loss coefficient. It would be reasonable to express the entrance loss in terms of a difference in velocity heads, especially for wide culverts with low contraction ratios, but in this study the data were not analyzed that manner.
Previous | Contents | Next
| 