This report is an archived publication and may contain dated technical, contact, and link information

Federal Highway Administration >
Publications >
Research Publications >
03060 >
Appb.Cfm
Concrete Mixture Optimization Using Statistical Methods

Publication Number: FHWA-RD-03-060

Concrete Mixture Optimization Using Statistical Methods

APPENDIX B. Experiment Design and Data Analysis for Factorial Experiment

B.1 Experiment Design and Response Data

Table B-1. Factorial experiment: design by volume fraction of factors

Std Order	Run Order	Point	Factor Aw/c	Factor B Fine Agg	Factor C Coarse Agg	Factor DHRWRA	Factor E Silica Fume
17	1	Center	0.39525	0.2712	0.4212	0.0060	0.0200
11	2	Fact	0.3576	0.2853	0.4071	0.0069	0.0247
7	3	Fact	0.3576	0.2853	0.4353	0.0051	0.0247
10	4	Fact	0.4329	0.2571	0.4071	0.0069	0.0247
4	5	Fact	0.4329	0.2853	0.4071	0.0051	0.0247
12	6	Fact	0.4329	0.2853	0.4071	0.0069	0.0153
2	7	Fact	0.4329	0.2571	0.4071	0.0051	0.0153
1	8	Fact	0.3576	0.2571	0.4071	0.0051	0.0247
18	9	Center	0.39525	0.2712	0.4212	0.0060	0.0200
8	10	Fact	0.4329	0.2853	0.4353	0.0051	0.0153
9	11	Fact	0.3576	0.2571	0.4071	0.0069	0.0153
6	12	Fact	0.4329	0.2571	0.4353	0.0051	0.0247
3	13	Fact	0.3576	0.2853	0.4071	0.0051	0.0153
14	14	Fact	0.4329	0.2571	0.4353	0.0069	0.0153
15	15	Fact	0.3576	0.2853	0.4353	0.0069	0.0153
13	16	Fact	0.3576	0.2571	0.4353	0.0069	0.0247
19	17	Center	0.39525	0.2712	0.4212	0.0060	0.0200
5	18	Fact	0.3576	0.2571	0.4353	0.0051	0.0153
16	19	Fact	0.4329	0.2853	0.4353	0.0069	0.0247
25	20	Axial	0.39525	0.2712	0.4494	0.0060	0.0200
21	21	Axial	0.47055	0.2712	0.4212	0.0060	0.0200
23	22	Axial	0.39525	0.2994	0.4212	0.0060	0.0200
27	23	Axial	0.39525	0.2712	0.4212	0.0078	0.0200
20	24	Axial	0.31995	0.2712	0.4212	0.0060	0.0200
31	25	Center	0.39525	0.2712	0.4212	0.0060	0.0200
26	26	Axial	0.39525	0.2712	0.4212	0.0042	0.0200
28	27	Axial	0.39525	0.2712	0.4212	0.0060	0.0106
24	28	Axial	0.39525	0.2712	0.3930	0.0060	0.0200
29	29	Axial	0.39525	0.2712	0.4212	0.0060	0.0294
22	30	Axial	0.39525	0.243	0.4212	0.0060	0.0200
30	31	Center	0.39525	0.2712	0.4212	0.0060	0.0200

Table B-2. Factorial experiment: slump and 1-day strength data

Run	Point	Slump (mm)		1-Day Strength (MPa)
1	Center	76	70	16.6	16.0	16.2
2	Fact	44	44	22.2	22.5	23.0
3	Fact	13	13	22.5	17.9	22.0
4	Fact	102	102	15.8	16.7	16.8
5	Fact	57	57	16.4	16.7	16.1
6	Fact	140	146	13.4	14.2	13.2
7	Fact	70	64	13.9	11.1	13.7
8	Fact	13	13	17.7	22.8	20.5
9	Center	89	83	17.9	18.6	18.7
10	Fact	102	102	15.2	15.2	15.2
11	Fact	140	140	20.9	20.7	20.4
12	Fact	32	32	13.8	18.8	18.9
13	Fact	13	13	24.5	23.3	24.7
14	Fact	76	76	17.3	17.2	17.2
15	Fact	13	13	22.7	19.5	21.8
16	Fact	13	13	20.8	20.6	21.4
17	Center	51	64	19.4	18.9	18.1
18	Fact	32	25	21.4	22.2	22.1
19	Fact	38	32	16.0	16.1	16.3
20	Axial	38	38	18.7	19.3	18.9
21	Axial	121	114	14.5	14.9	14.0
22	Axial	70	64	18.0	17.8	17.5
23	Axial	64	64	19.3	20.0	20.4
24	Axial	19	13	26.0	25.4	27.7
25	Center	83	76	20.2	17.3	19.6
26	Axial	64	64	18.9	19.5	18.9
27	Axial	152	152	16.4	17.0	16.9
28	Axial	95	95	20.1	20.8	19.7
29	Axial	38	32	17.2	20.1	18.0
30	Axial	102	102	17.7	17.0	17.7
31	Center	76	76	16.8	19.6	18.8

Table B-3. Factorial experiment: 28-day strength and RCT charge passed data

Run	Point	28-Day Strength (MPa)				RCT Charge Passed (coulombs)
1	Center	54.0	63.0	-	-	263	296	300
2	Fact	59.4	60.2	-	-	186	472	268
3	Fact	53.5	52.8	51.7	-	151	151	178
4	Fact	62.7	60.8	55.1	62.9	280	329	279
5	Fact	52.6	56.6	55.8	-	273	236	262
6	Fact	60.4	52.1	60.6	61.3	553	585	485
7	Fact	50.1	49.4	51.5	-	468	550	490
8	Fact	51.0	56.3	47.2	55.2	253	240	208
9	Center	63.5	62.5	-	-	247	315	305
10	Fact	53.8	54.2	56.3	-	460	437	439
11	Fact	61.6	64.5	60.8	-	415	427	393
12	Fact	56.5	55.3	56.8	-	258	258	240
13	Fact	58.1	50.2	54.4	-	343	362	317
14	Fact	52.3	46.6	52.1	-	596	527	481
15	Fact	60.3	58.7	58.6	-	218	288	330
16	Fact	60.2	58.5	62.9	-	208	194	216
17	Center	59.9	54.5	55.5	-	299	327	318
18	Fact	58.4	60.1	56.3	-	360	364	340
19	Fact	65.0	59.9	63.9	-	242	243	206
20	Axial	56.7	57.0	62.1	-	168	242	224
21	Axial	53.9	51.1	56.7	-	463	461	449
22	Axial	60.7	62.9	63.6	-	319	305	257
23	Axial	68.4	66.8	67.1	-	272	280	251
24	Axial	62.1	59.4	54.0	-	190	184	192
25	Center	58.2	55.8	56.8	-	239	246	287
26	Axial	52.9	48.2	51.6	-	258	281	280
27	Axial	51.3	55.2	56.8	-	704	766	644
28	Axial	50.0	55.2	54.8	-	268	302	351
29	Axial	55.5	53.8	56.2	-	163	170	153
30	Axial	50.4	49.0	51.6	-	340	304	351
31	Center	55.8	53.3	56.5	-	262	294	274

B.2 Data Analysis and Model Fitting

B.2.1 Slump

Table B-4. Factorial experiment: sequential model sum of squares for slump

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Mean	130296.6	1	130296.6	-	-
Linear	31972.38	5	6394.48	9.10	< 0.0001
2FI	10539.29	10	1053.93	2.25	0.0755
Quadratic	2598.70	5	519.74	1.18	0.3856
Cubic (aliased)	2316.86	5	463.37	1.10	0.4593
Residual	2104.40	5	420.88	-	-
Total	179828.3	31	5800.91	-	-

Table B-5. Factorial experiment: lack-of-fit test for slump

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Linear	17103.61	21	814.46	7.15	0.0345
2FI	6564.32	11	596.76	5.24	0.0618
Quadratic	3965.62	6	660.94	5.80	0.0553
Cubic (aliased)	1648.75	1	1648.75	14.47	0.0190
Pure error	455.64	4	113.91	-	-

Table B-6. Factorial experiment: ANOVA for slump model

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Model	40109.97	7	5730.00	13.99	< 0.0001
A	12138.75	1	12138.75	29.63	< 0.0001
B	606.52	1	606.52	1.48	0.2360
C	6048.38	1	6048.38	14.77	0.0008
D	2426.07	1	2426.07	5.92	0.0231
E	10752.67	1	10752.67	26.25	< 0.0001
AB	1837.19	1	1837.19	4.48	0.0452
CD	6300.39	1	6300.39	15.38	0.0007
Residual	9421.67	23	409.64	-	-
Lack of fit	8966.03	19	471.90	4.14	0.0887
Pure error	455.64	4	113.91	-	-
Cor total	49531.64	30	-	-	-

Table B-7. Factorial experiment: summary statistics for slump model

Std. Dev.	20.24	R-Squared	0.8098
Mean	64.83	Adj R-Squared	0.7519
C.V.	31.22	Pred R-Squared	0.6275
PRESS	18452.19	Adeq Precision	15.6200

Table B-8. Factorial experiment: coefficient estimates for slump model

Factor	Coefficient Estimate	DF	Standard Error	95% CI Low	95% CI High
Intercept	64.83	1	3.64	57.31	72.35
A (w/c)	22.49	1	4.13	13.94	31.04
B (fine agg)	-5.03	1	4.13	-13.57	3.52
C (coarse agg)	-15.87	1	4.13	-24.42	-7.33
D (HRWRA)	10.05	1	4.13	1.51	18.60
E (silica fume)	-21.17	1	4.13	-29.71	-12.62
AB	10.72	1	5.06	0.25	21.18
CD	-19.84	1	5.06	-30.31	-9.38

Model equation for slump in terms of coded factors:

Slump = 64.83 + 22.49*A - 5.03*B - 15.87*C + 10.05*D - 21.17*E + 10.72*A*B - 19.84*C*D

Model equation for slump in terms of actual factors:

Slump =	-1365.5 - 4876.9w/c - 8334.7fine agg + 8256.5*coarse agg
	+ 6.6982 x 10⁵HRWRA - 4503.6silica fume + 20185w/cfine agg
	- 1.564 x 10⁶coarse aggHRWRA

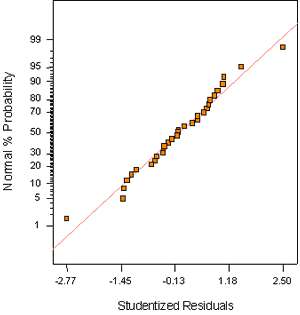
This figure shows a normal probability plot of residuals for slump from the factorial experiment. The normal percent probability is plotted on the Y-axis against the studentized residuals on the X-axis. In this case, most of the points fall on a straight line, indicating that the normality assumption is reasonable.

Figure B-1. Factorial experiment: normal probability plot for slump

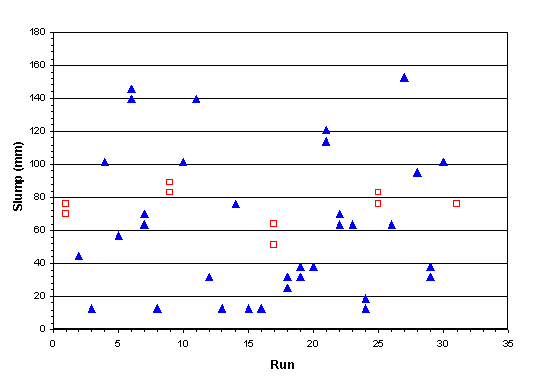
This figure shows a raw data plot for slump. The slump (in millimeters) is plotted on the Y-axis against corresponding runs on the X-axis. Two data points are shown for each run. The data points for control runs are shown as hollow squares, while the other data points are shown as filled triangles. The plot indicates that the control mixes showed little variation, and there were no obvious trends in the data with time.

Figure B-2. Factorial experiment: raw data plot for slump (hollow squares indicate control runs)

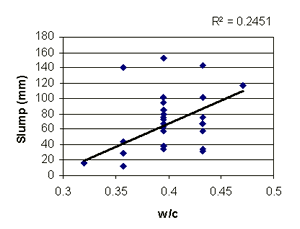
This figure shows a scatterplot of slump (Y-axis) versus water-cement ratio (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of water-cement ratio, as defined by the experiment design. There is wide scatter in the data with a slight upward trend. A best-fit line indicates the upward trend.

Figure B-3. Factorial experiment: scatterplot of slump vs. w/c

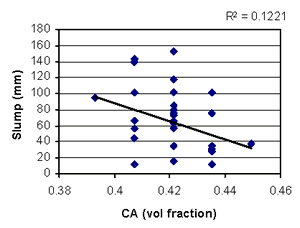
$This figure shows a scatterplot of slump (Y-axis) versus coarse aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of coarse aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a slight downward trend. A best-fit line indicates the downward trend.$

Figure B-4. Factorial experiment: scatterplot of slump vs. coarse aggregate

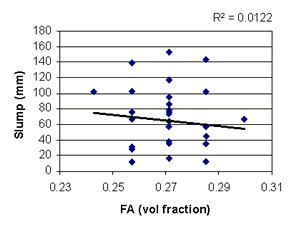
$This figure shows a scatterplot of slump (Y-axis) versus fine aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of fine aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a very slight downward trend. A best-fit line indicates the trend.$

Figure B-5. Factorial experiment: scatterplot of slump vs. fine aggregate

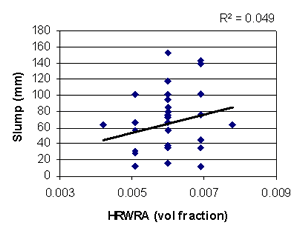
$This figure shows a scatterplot of slump (Y-axis) versus HRWRA volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of HRWRA, as defined by the experiment design. There is wide scatter in the data with a slight upward trend. A best-fit line indicates the upward trend.$

Figure B-6. Factorial experiment: scatterplot of slump vs. HRWRA

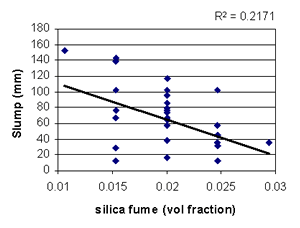
$This figure shows a scatterplot of slump (Y-axis) versus water-cement ratio (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of silica fume volume fraction, as defined by the experiment design. There is wide scatter in the data with a downward trend. A best-fit line indicates the upward trend.$

Figure B-7. Factorial experiment: scatterplot of slump vs. silica fume

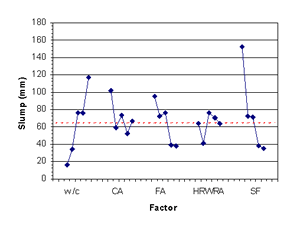
This figure shows a set of means plots for slump. In the graph, slump is on the Y-axis, and the five variables (factors) in the experiment are shown on the X-axis. From left to right, the factors are water-cement ratio, coarse aggregate, fine aggregate, HRWRA, and silica fume. For each factor, there are five data points shown, indicating the mean values for slump at each of the five settings of the factor. The data points are plotted from lowest setting (coded value negative 2) on the left to highest setting (coded value positive 2) on the right. The data points are connected by a line. The lines show the following general trends: slump increases with increasing water-cement ratio, slump is relatively unaffected by coarse aggregate, fine aggregate, and HRWRA, and slump decreases with increasing silica fume content.

Figure B-8. Factorial experiment: means plots for slump

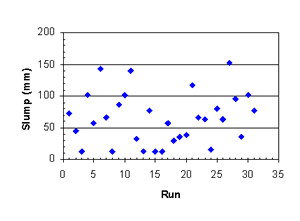
This figure shows a plot of slump (Y-axis) versus run sequence (X-axis). This plot is similar to figure B-2, the raw data plot for slump. In this plot, the mean values of slump for each run are shown. The plot is used to assess any trends in slump with time. This plot shows a random distribution of slump with run, indicating no significant trends with time.

Figure B-9. Factorial experiment: slump vs. run sequence

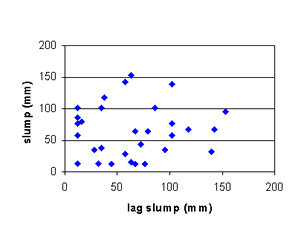
Chart. This figure shows a lag plot for slump. In the lag plot, slump for a given run is plotted on the Y-axis, and the slump for the previous run is plotted on the X-axis. The X-axis value is referred to as the "lag slump." The purpose of plot is to identify whether any two consecutive runs appear be more alike than those taken farther apart. For random data, plots should show no structure or pattern. If significant exists in plot, assumption randomness may violated. There apparent this indicating that assumptions are valid.

Figure B-10. Factorial experiment: lag plot for slump

Table B-9. Factorial experiment: sequential model sum of squares for 1-day strength

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Mean	10780.54	1	10780.54	-	-
Linear	215.97	5	43.19	22.15	< 0.0001
2FI	27.35	10	2.73	1.92	0.1236
Quadratic	13.60	5	2.72	3.48	0.0441
Cubic (aliased)	1.86	5	0.37	0.31	0.8865
Residual	5.95	5	1.19	-	-
Total	11045.26	31	356.30	-	-

Table B-10. Factorial experiment: lack-of-fit test for 1-day strength

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Linear	43.98	21	2.09	1.75	0.3129
2FI	16.63	11	1.51	1.27	0.4444
Quadratic	3.03	6	0.51	0.42	0.8339
Cubic (aliased)	1.18	1	1.18	0.98	0.3772
Pure error	4.78	4	1.19	-	-

Table B-11. Factorial experiment: ANOVA for 1-day strength model

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Model	240.87	8	30.11	27.76	< 0.0001
A	213.26	1	213.26	196.66	< 0.0001
B	0.48	1	0.48	0.45	0.5113
C	0.043	1	0.043	0.040	0.8433
E	2.06	1	2.06	1.90	0.1819
A²	6.20	1	6.20	5.72	0.0257
AC	5.15	1	5.15	4.75	0.0404
AE	7.16	1	7.16	6.60	0.0175
BC	6.51	1	6.51	6.00	0.0227
Residual	23.86	22	1.08	-	-
Lack of fit	19.08	18	1.06	0.89	0.6248
Pure error	4.78	4	1.19	-	-
Cor total	264.72	30	-	-	-

Table B-12. Factorial experiment: summary statistics for 1-day strength model

Std. Dev.	1.04	R-Squared	0.9099
Mean	18.65	Adj R-Squared	0.8771
C.V.	5.58	Pred R-Squared	0.8294
PRESS	45.16	Adeq Precision	22.583

Table B-13. Factorial experiment: coefficient estimates for 1-day strength model

Factor	Coefficient Estimate	DF	Standard Error	95% CI Low	95% CI High
Intercept	18.29	1	0.24	17.80	18.79
A (w/c)	-2.98	1	0.21	-3.42	-2.54
B (fine agg)	0.14	1	0.21	-0.30	0.58
C (coarse agg)	0.043	1	0.21	-0.40	0.48
E (silica fume)	0.29	1	0.21	-0.15	0.73
A²	0.46	1	0.19	0.061	0.86
AC	0.57	1	0.26	0.027	1.11
AE	0.67	1	0.26	0.13	1.21
BC	-0.64	1	0.26	-1.18	-0.098

Model equation for 1-day strength in terms of coded factors:

1-day strength = 18.29 - 2.98*A + 0.14*B + 0.043*C + 0.29*E + 0.46*A² + 0.57*A*C + 0.67*A*E - 0.64*B*C

Model equation for 1-day strength in terms of actual factors:

1-day strength =	-63.8 - 860.8w/c + 1361.3fine agg + 450.8coarse agg - 1431.5silica fume
	+ 323.9(w/c)² + 1068w/ccoarse agg + 3780w/c*silica fume
	- 3208fine aggcoarse agg

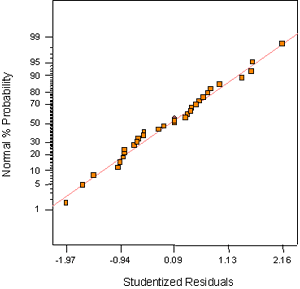
This figure shows a normal probability plot of residuals for 1-day strength from the factorial experiment. The normal percent probability is plotted on the Y-axis against the studentized residuals on the X-axis. In this case, most of the points fall on a straight line, indicating that the normality assumption is reasonable.

Figure B-11. Factorial experiment: normal probability plot for 1-day strength

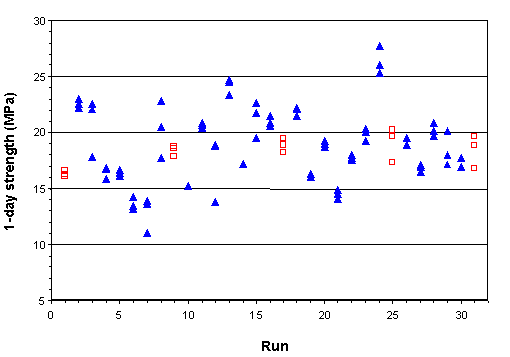
This figure shows a raw data plot for 1-day strength. The strength (in megapascals) is plotted on the Y-axis against corresponding run on the X-axis. Three data points are shown for each run (each data point representing an individual cylinder break). The data points for control runs are shown as hollow squares, while the other data points are shown as filled triangles. The plot indicates that the control mixes showed little variation, and there were no obvious trends in the data with time.

Figure B-12. Factorial experiment: raw data plot for 1-day strength (hollow squares indicate control runs)

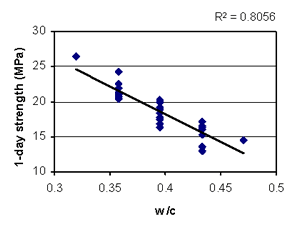
This figure shows a scatterplot of 1-day strength (Y-axis) versus water-cement ratio (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of water-cement ratio, as defined by the experiment design. The data show a definite downward trend. A best-fit line indicates the downward trend.

Figure B-13. Factorial experiment: scatterplot of 1-day strength vs. w/c

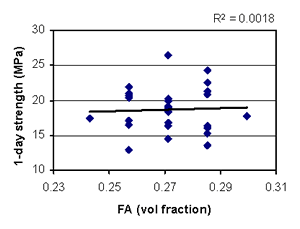
$This figure shows a scatterplot of 1-day strength (Y-axis) versus fine aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of fine aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with virtually no trend. A nearly horizontal best-fit line indicates the lack of any trend.$

Figure B-14. Factorial experiment: scatterplot of 1-day strength vs. fine aggregate

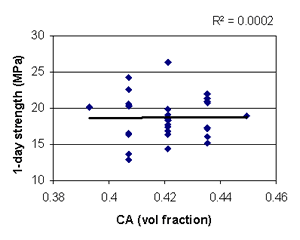
$This figure shows a scatterplot of 1-day strength (Y-axis) versus coarse aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of coarse aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with no trend, as indicated by the horizontal best-fit line.$

Figure B-15. Factorial experiment: scatterplot of 1-day strength vs. coarse aggregate

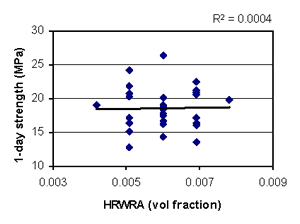
$This figure shows a scatterplot of 1-day strength (Y-axis) versus HRWRA volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of HRWRA, as defined by the experiment design. There is wide scatter in the data with no significant trend, as indicated by a horizontal best-fit line.$

Figure B-16. Factorial experiment: scatterplot of 1-day strength vs. HRWRA

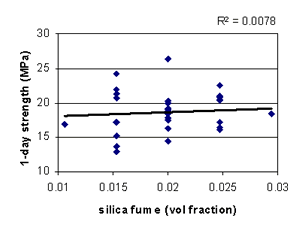
$This figure shows a scatterplot of 1-day strength (Y-axis) versus silica fume volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of silica fume volume fraction, as defined by the experiment design. There is wide scatter in the data with virtually no trend, as indicated by the nearly horizontal best-fit line.$

Figure B-17. Factorial experiment: scatterplot of 1-day strength vs. silica fume

This figure shows a set of means plots for 1-day strength. In the graph, 1-day strength is on the Y-axis and the five variables (factors) in the experiment are shown on the X-axis. From left to right, the factors are water-cement ratio, coarse aggregate, fine aggregate, HRWRA, and silica fume. For each factor, there are five data points shown, indicating the mean values for 1-day strength at each of the five settings of the factor. The data points are plotted from lowest setting (coded value negative 2) on the left to highest setting (coded value positive 2) on the right. For each factor, the data points are connected by a line. The lines show the following general trends: 1-day strength decreases with increasing water-cement ratio, 1-day strength is relatively unaffected by coarse aggregate, fine aggregate, HRWRA, and silica fume.

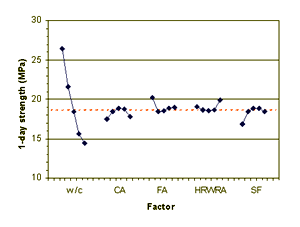
Figure B-18. Factorial experiment: means plot for 1-day strength

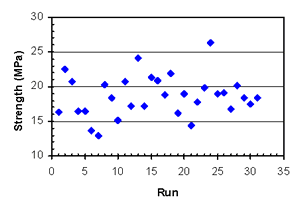
This figure shows a plot of 1-day strength (Y-axis) versus run sequence (X-axis). In this plot, the mean values of 1-day strength for each run are plotted. The plot is used to assess any trends in 1-day strength with time. This plot shows a random distribution of 1-day strength with run, indicating no significant trends with time.

Figure B-19. Factorial experiment: 1-day strength vs. run sequence

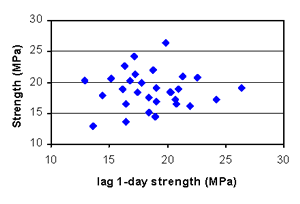
This figure shows a lag plot for 1-day strength. In the lag plot, the 1-day strength for a given run is plotted on the Y-axis, and the 1-day strength for the previous run is plotted on the X-axis. The X-axis value is referred to as the "lag 1-day strength." The purpose of plot is to identify whether any two consecutive runs appear be more alike than those taken farther apart. For random data, plots should show no structure or pattern. If significant exists in plot, assumption randomness may violated. There apparent this indicating that assumptions are valid.

Figure B-20. Factorial experiment: lag plot for 1-day strength

B.2.3. 28-Day Strength

Table B-14. Factorial experiment: sequential model sum of squares for 28-day strength

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Mean	100300.0	1	100300.0	-	-
Linear	292.28	5	58.46	5.71	0.0012
2FI	129.24	10	12.92	1.53	0.2208
Quadratic	27.53	5	5.51	0.56	0.7318
Cubic (aliased)	61.25	5	12.25	1.62	0.3050
Residual	37.84	5	7.57	-	-
Total	100848.1	31	3253.17	-	-

Table B-15. Factorial experiment: lack-of-fit test for 28-day strength

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Linear	219.79	21	10.47	1.16	0.4972
2FI	90.55	11	8.23	0.91	0.5942
Quadratic	63.02	6	10.50	1.16	0.4620
Cubic (aliased)	1.76	1	1.76	0.20	0.6813
Pure error	36.08	4	9.02	-	-

Table B-16. Factorial experiment: ANOVA for 28-day strength model

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Model	300.21	4	75.05	7.87	0.0003
A	16.57	1	16.57	1.74	0.1990
D	223.41	1	223.41	23.43	< 0.0001
E	7.47	1	7.47	0.78	0.3842
AE	52.76	1	52.76	5.53	0.0265
Residual	247.94	26	9.54	-	-
Lack of fit	211.86	22	9.63	1.07	0.5389
Pure error	36.08	4	9.02	-	-
Cor total	548.15	30	-	-	-

Table B-17. Factorial experiment: summary statistics for 28-day strength model

Std. Dev.	3.09	R-Squared	0.5477
Mean	56.88	Adj R-Squared	0.4781
C.V.	5.43	Pred R-Squared	0.3997
PRESS	329.05	Adeq Precision	9.964

Table B-18. Factorial experiment: coefficient estimates for 28-day strength model

Factor	Coefficient Estimate	DF	Standard Error	95% CI Low	95% CI High
Intercept	56.88	1	0.55	55.74	58.02
A (w/c)	-0.83	1	0.63	-2.13	0.46
D (HRWRA)	3.05	1	0.63	1.76	4.35
E (silica fume)	0.56	1	0.63	-0.74	1.85
AE	1.82	1	0.77	0.23	3.40

Model equation for 28-day strength in terms of coded factors:

28-day strength = 56.88 - 0.83*A + 3.05*D + 0.56*E + 1.82*A*E

Model equation for 28-day strength in terms of actual factors:

28-day strength = 124.0 - 227.3*w/c + 3390*HRWRA - 3937.5*silica fume + 10262*w/c*silica fume

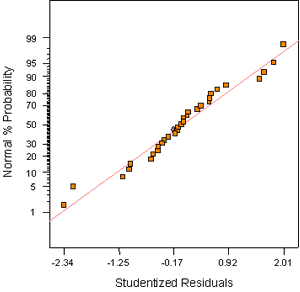
This figure shows a normal probability plot of residuals for 28-day strength from the factorial experiment. The normal percent probability is plotted on the Y-axis against the studentized residuals on the X-axis. In this case, most of the points fall on a straight line, indicating that the normality assumption is reasonable.

Figure B-21. Factorial experiment: normal probability plot for 28-day strength

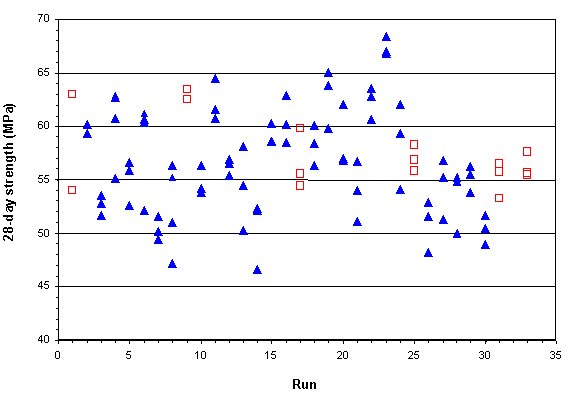
This figure shows a raw data plot for 28-day strength. The strength (in megapascals) is plotted on the Y-axis against corresponding runs on the X-axis. Three data points are shown for each run (each data point representing an individual cylinder break). The data points for control runs are shown as hollow squares, while the other data points are shown as filled triangles. The plot indicates that the control mixes showed little variation, and there were no obvious trends in the data with time.

Figure B-22. Factorial experiment: raw data plot for 28-day strength (hollow squares indicate control runs)

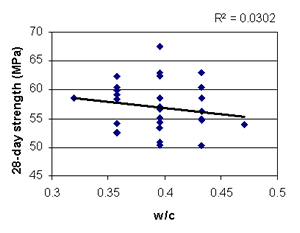
This figure shows a scatterplot of 28-day strength (Y-axis) versus water-cement ratio (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of water-cement ratio, as defined by the experiment design. The data show a very slight downward trend. A best-fit line indicates the trend.

Figure B-23. Factorial experiment: scatterplot of 28-day strength vs. w/c

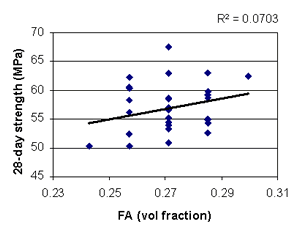
$This figure shows a scatterplot of 28-day strength (Y-axis) versus fine aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of fine aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a very slight upward trend. A best-fit line indicates the trend.$

Figure B-24. Factorial experiment: scatterplot of 28-day strength vs. fine aggregate

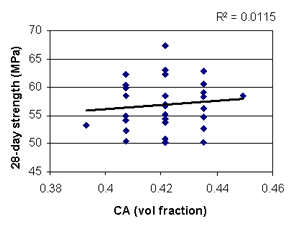
$This figure shows a scatterplot of 28-day strength (Y-axis) versus coarse aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of coarse aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a very slight upward trend, indicated by the nearly horizontal best-fit line.$

Figure B-25. Factorial experiment: scatterplot of 28-day strength vs. coarse aggregate

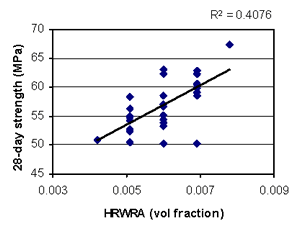
$This figure shows a scatterplot of 28-day strength (Y-axis) versus HRWRA volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of HRWRA, as defined by the experiment design. There is wide scatter in the data with a definite upward trend, indicated by a best-fit line.$

Figure B-26. Factorial experiment: scatterplot of 28-day strength vs. HRWRA

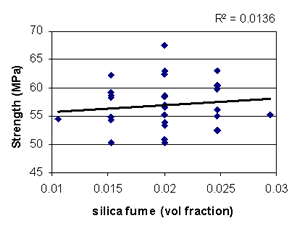
$This figure shows a scatterplot of 28-day strength (Y-axis) versus silica fume volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of silica fume volume fraction, as defined by the experiment design. There is wide scatter in the data with a very slight upward trend, as indicated by the nearly horizontal best-fit line.$

Figure B-27. Factorial experiment: scatterplot of 28-day strength vs. silica fume

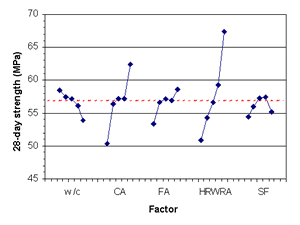
This figure shows a set of means plots for 28-day strength. In the graph, 28-day strength is on the Y-axis and the five variables (factors) in the experiment are shown on the X-axis. From left to right, the factors are water-cement ratio, coarse aggregate, fine aggregate, HRWRA, and silica fume. For each factor, there are five data points shown, indicating the mean values for 28-day strength at each of the five settings of the factor. The data points are plotted from lowest setting (coded value negative 2) on the left to highest setting (coded value positive 2) on the right. For each factor, the data points are connected by a line. The lines show the following general trends: 28-day strength is slightly affected by water-cement ratio; relatively unaffected by coarse aggregate, fine aggregate, and silica fume; and significantly affected by HRWRA.

FIgure B-28. Factorial experiment: means plot for 28-day strength

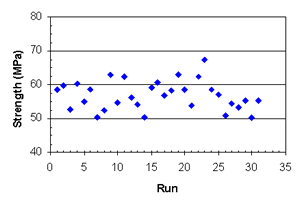
This figure shows a plot of 28-day strength (Y-axis) versus run sequence (X-axis). In this plot, the mean values of 28-day strength for each run are plotted. The plot is used to assess any trends in 28-day strength with time. This plot shows a random distribution of 28-day strength with run, indicating no significant trends with time.

Figure B-29. Factorial experiment: 28-day strength vs. run sequence

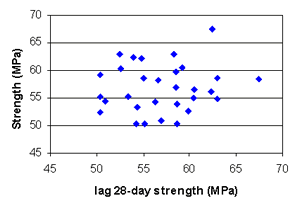
This figure shows a lag plot for 28-day strength. In the lag plot, the 28-day strength for a given run is plotted on the Y-axis, and the 28-day strength for the previous run is plotted on the X-axis. The X-axis value is referred to as the "lag 28-day strength." The purpose of plot is to identify whether any two consecutive runs appear be more alike than those taken farther apart. For random data, plots should show no structure or pattern. If significant exists in plot, assumption randomness may violated. There apparent this indicating that assumptions are valid.

Figure B-30. Factorial experiment: lag plot for 28-day strength

Table B-19. Factorial experiment: sequential model sum of squares for RCT charge passed

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Mean	3155867	1	3155867	-	-
Linear	393517.2	5	78703.43	27.43	< 0.0001
2FI	15156.50	10	1515.65	0.40	0.9252
Quadratic	44410.76	5	8882.15	7.31	0.0040
Cubic (aliased)	10046.83	5	2009.37	4.77	0.0557
Residual	2104.61	5	420.92	-	-
Total	3621103	31	116809.8	-	-

Table B-20. Factorial experiment: lack-of-fit test for RCT charge passed

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Linear	69614.70	21	3314.99	6.30	0.0432
2FI	54458.20	11	4950.75	9.41	0.0221
Quadratic	10047.44	6	1674.57	3.18	0.1410
Cubic (aliased)	0.61	1	0.61	.001	0.9745
Pure error	2104.00	4	526.00	-	-

Table B-21. Factorial experiment: ANOVA for RCT charge passed model

Source	Sum of Squares	DF	Mean Square	F Value	Prob > F
Model	441455.3	6	73575.89	74.25	< 0.0001
A	81666.67	1	81666.67	82.42	< 0.0001
B	6868.17	1	6868.17	6.93	0.0146
C	11440.67	1	11440.67	11.55	0.0024
E	292604.2	1	292604.2	295.30	< 0.0001
E²	38369.41	1	38369.41	38.72	< 0.0001
AE	10506.25	1	10506.25	10.60	0.0034
Residual	23780.54	24	990.86	-	-
Lack of fit	21676.54	20	1083.83	2.06	0.2537
Pure error	2104.00	4	526.00	-	-
Cor total	465235.9	30	-	-	-

Table B-22. Factorial experiment: summary statistics for RCT charge passed model

Std. Dev.	31.48	R-Squared	0.9489
Mean	319.06	Adj R-Squared	0.9361
C.V.	9.87	Pred R-Squared	0.8784
PRESS	56577.00	Adeq Precision	34.166

Table B-23. Factorial experiment: coefficient estimates for RCT charge passed model

Factor	Coefficient Estimate	DF	Standard Error	95% CI Low	95% CI High
Intercept	291.11	1	7.22	276.20	306.01
A (w/c)	58.33	1	6.43	45.07	71.59
B (fine agg)	-16.92	1	6.43	-30.18	-3.66
C (coarse agg)	-21.83	1	6.43	-35.09	-8.57
E (silica fume)	-110.42	1	6.43	-123.68	-97.16
E²	36.11	1	5.80	24.14	48.09
AE	-25.63	1	7.87	-41.87	-9.38

Model equation for RCT charge passed in terms of coded factors:

RCT charge passed = 291.11 + 58.33*A - 16.92*B - 21.83*C - 110.42*E + 36.11*E² - 25.63*A*E

Model equation for RCT charge passed in terms of actual factors:

RCT charge passed = 635.4 + 4445.6*w/c - 1199.8*fine agg - 1548.5*coarse agg - 31651*silica fume + 1.635 x 10⁶*(silica fume)² - 1.448 x 10⁵*w/c*silica fume

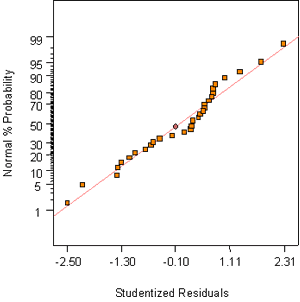
This figure shows a normal probability plot of residuals for RCT from the factorial experiment. The normal percent probability is plotted on the Y-axis against the studentized residuals on the X-axis. In this case, most of the points fall on a straight line, indicating that the normality assumption is reasonable.

Figure B-31. Factorial experiment: normal probability plot for RCT charge passed

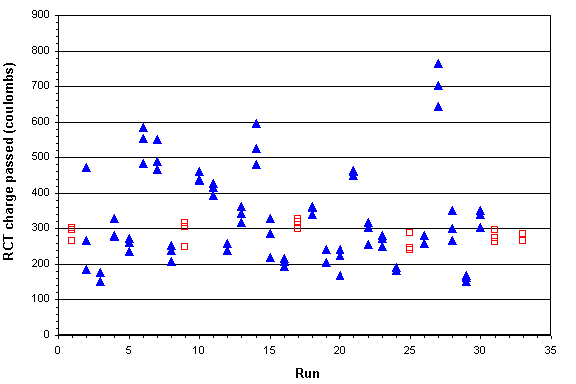
This figure shows a raw data plot for RCT. The charge passed (in coulombs) is plotted on the Y-axis against corresponding run on the X-axis. Three data points are shown for each run (each data point representing an individual test run). The data points for control runs are shown as hollow squares, while the other data points are shown as filled triangles. The plot indicates that the control mixes showed little variation, and there were no obvious trends in the data with time. However, run 27 has a significantly higher charge passed than the others and could be an outlier.

Figure B-32. Factorial experiment: raw data plot for RCT charge passed (hollow squares indicate control runs)

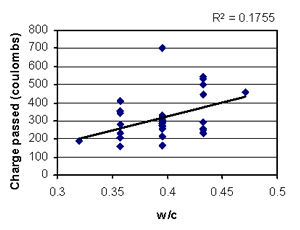
This figure shows a scatterplot of RCT (Y-axis) versus water-cement ratio (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of water-cement ratio, as defined by the experiment design. The data show an upward trend, as indicated by a best-fit line.

Figure B-33. Factorial experiment: scatterplot of RCT charge passed vs. w/c

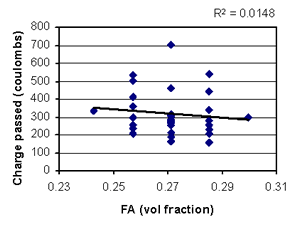
$This figure shows a scatterplot of RCT (Y-axis) versus fine aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of fine aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a slight downward trend, shown by a nearly horizontal best-fit line.$

Figure B-34. Factorial experiment: scatterplot of RCT charge passed vs. fine aggregate

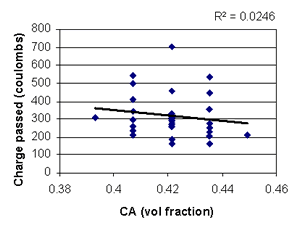
$This figure shows a scatterplot of RCT (Y-axis) versus coarse aggregate volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of coarse aggregate volume fraction, as defined by the experiment design. There is wide scatter in the data with a slight downward trend, as indicated by the nearly horizontal best-fit line.$

Figure B-35. Factorial experiment: scatterplot of RCT charge passed vs. coarse aggregate

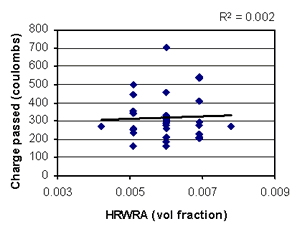
$This figure shows a scatterplot of RCT (Y-axis) versus HRWRA volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of HRWRA, as defined by the experiment design. There is wide scatter in the data with no significant trend, as indicated by a horizontal best-fit line.$

Figure B-36. Factorial experiment: scatterplot of RCT charge passed vs. HRWRA

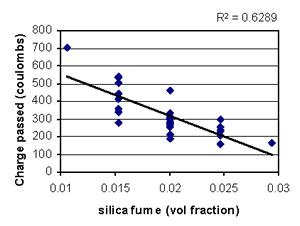
$This figure shows a scatterplot of RCT (Y-axis) versus silica fume volume fraction (X-axis). Each data point represents an experimental run. The data are plotted at five distinct settings of silica fume volume fraction, as defined by the experiment design. The data show a definite downward trend, which is clearly indicated by a best-fit line.$

Figure B-37. Factorial experiment: scatterplot of RCT charge passed vs. silica fume

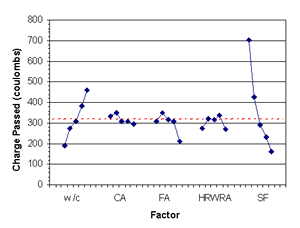
This figure shows a set of means plots for RCT. In the graph, RCT is on the Y-axis and the five variables (factors) in the experiment are shown on the X-axis. From left to right, the factors are water-cement ratio, coarse aggregate, fine aggregate, HRWRA, and silica fume. For each factor, there are five data points shown, indicating the mean values for slump at each of the five settings of the factor. The data points are plotted from lowest setting (coded value negative 2) on the left to highest setting (coded value positive 2) on the right. For each factor, the data points are connected by a line. The lines show the following general trends: RCT increases with increasing water-cement ratio, RCT is relatively unaffected by coarse aggregate, fine aggregate, and HRWRA; and RCT decreases with increasing silica fume.

Figure B-38. Factorial experiment: means plot for RCT charge passed

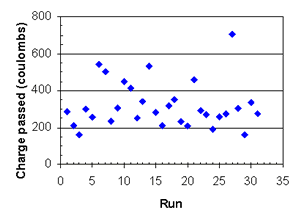
This figure shows a plot of RCT (Y-axis) versus run sequence (X-axis). In this plot, the mean values of RCT for each run are plotted. The plot is used to assess any trends in RCT with time. This plot shows a random distribution of RCT with run, indicating no significant trends with time.

Figure B-39. Factorial experiment: RCT charge passed vs. run sequence

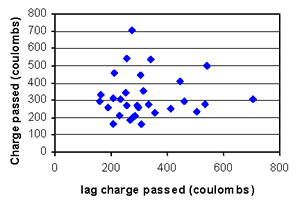
This figure shows a lag plot for RCT. In the lag plot, the RCT for a given run is plotted on the Y-axis, and the RCT for the previous run is plotted on the X-axis. The X-axis value is referred to as the "lag RCT." The purpose of the lag plot is to identify whether any two consecutive runs appear to be more alike than those taken farther apart. For random data, lag plots should show no structure or pattern. If significant structure exists in the lag plot, the assumption of randomness may be violated. There is no apparent structure in this lag plot, indicating that randomness assumptions are valid.

Figure B-40. Factorial experiment: lag plot for RCT charge passed

Previous | Table of Contents | Next

Page Owner: Office of Research, Development, and Technology, Office of Infrastructure, RDT

Topics: research, infrastructure, pavements and materials
Keywords: research, infrastructure, pavements and materials, High Performance Concrete Pavement; HIPERPAV; Jointed; Continuously Reinforced; Early-Age Behavior; Long-Term Performance; Mechanistic-Empirical Models; Temperature; Hydration; Shrinkage; Relaxation; Creep; Thermal Expansion; Slab Base Restraint; Curling; Warping; Plastic Shrinkage; Cracking; JPCP; CRCP
TRT Terms: research, facilities, transportation, highway facilities, roads, parts of roads, pavements
Scheduled Update: Archive - No Update needed

This page last modified on 03/08/2016

Slump =	-1365.5 - 4876.9w/c - 8334.7fine agg + 8256.5*coarse agg
	+ 6.6982 x 10⁵HRWRA - 4503.6silica fume + 20185w/cfine agg
	- 1.564 x 10⁶coarse aggHRWRA

1-day strength =	-63.8 - 860.8w/c + 1361.3fine agg + 450.8coarse agg - 1431.5silica fume
	+ 323.9(w/c)² + 1068w/ccoarse agg + 3780w/c*silica fume
	- 3208fine aggcoarse agg