U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-05-062
Date: May 2007 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Users Manual for LS-DYNA Concrete Material Model 159PDF Version (1.49 KB)
PDF files can be viewed with the Acrobat® Reader® Chapter 3. Users ManualThis chapter is intended to be a brief Users Manual for those who want to run the model with a cursory, rather than indepth, understanding of the underlying theory and equations. This chapter begins with a description of the LS-DYNA concrete model input, followed by a brief theoretical description of the model theory. All information in this chapter is included in the LS-DYNA Keyword Users Manual.(6) LS-DYNA Input*MAT_CSCM {OPTION} This is material type 159. This is a smooth or continuous surface cap model and is available for solid elements in LS-DYNA. The user has the option of inputting his or her own material properties (<BLANK> option), or requesting default material properties for normal strength concrete (CONCRETE). Options include: <BLANK> CONCRETE In selecting an option the keyword cards appear: *MAT_CSCM *MAT_CSCM _CONCRETE Define the following card for all options. Card Format
Define the following card for the CONCRETE option. Do not define for the <BLANK> option.
Define the following cards for the <BLANK> option. Do not define for CONCRETE.
Define for all options.
Define for CONCRETE option.
Remarks: Default concrete input parameters are for normal strength concrete with unconfined compression strengths between about 20 and 58 MPa (2,901 and 8,412 psi). Define for <BLANK> option only.
Model Formulation and Input ParametersThis is a cap model with a smooth intersection between the shear yield surface and hardening cap, as shown in Figure 84. The initial damage surface coincides with the yield surface. Rate effects are modeled with viscoplasticity.
Figure 84. Illustration. General shape of the concrete model yield surface in two dimensions. Stress Invariants. The yield surface is formulated in terms of three stress invariants: J1, the first invariant of the stress tensor; J¢2, the second invariant of the deviatoric stress tensor; and J¢3, the third invariant of the deviatoric stress tensor. The invariants are defined in terms of the deviatoric stress tensor, Sij and pressure, P, as shown in Figure 85:
Figure 85. Equation. Three stress invariants, J1, J′2, J′3. Plasticity Surface. The three invariant yield function is based on these three invariants, and the cap hardening parameter, κ, as shown in Figure 86:
Figure 86. Equation. Plasticity yield function f. Here Ff is the shear failure surface, Fc is the hardening cap, and ℜ is the Rubin three-invariant reduction factor. The cap hardening parameter κ is the value of the pressure invariant at the intersection of the cap and shear surfaces. Trial elastic stress invariants are temporarily updated via the trial elastic stress tensor, σT. These are denoted J1T, J¢2T, and J¢3T. Elastic stress states are modeled when f (J1T, J¢2T, J¢3T, κT ) < 0. Elastic-plastic stress states are modeled when f (J1T, J¢2T, J¢3T, κT ) > 0. In this case, the plasticity algorithm returns the stress state to the yield surface in a manner that f (J1P, J¢2P, J¢3P, κP) = 0. Shear Failure Surface. The strength of concrete is modeled by the shear surface in the tensile and low confining pressure regimes (see Figure 87):
Figure 87. Equation. Shear surface function Ff. Here the values of Rubin Scaling Function. Concrete fails at lower values of J¢2(principal stress difference) for TXE and TOR tests than it does for TXC tests conducted at the same pressure. The Rubin scaling function ℜ determines the strength of concrete for any state of stress relative to the strength for TXE, via ℜFf. Strength in TOR is modeled as Q1Ff . Strength in TXE is modeled as Q2Ff, in Figure 88, where:
Figure 88. Equation. Most general form for scaling functions Q1, Q2. Cap Hardening Surface. The strength of concrete is modeled by a combination of the cap and shear surfaces in the low to high confining pressure regimes. The cap is used to model plastic volume change related to pore collapse (although the pores are not explicitly modeled). The isotropic hardening cap is a two-part function that is either unity or an ellipse, as shown in Figure 89:
Figure 89. Equation. Cap surface function, Fc. where L(κ) is defined in Figure 90:
Figure 90. Equation. Definition of L of kappa. The equation for Fc is equal to unity for J1 £ L(κ). It describes the ellipse for J1 > L(κ). The intersection of the shear surface and the cap is at J1 = κ. κ0 is the value of J1 at the initial intersection of the cap and shear surfaces before hardening is engaged (before the cap moves). The equation for L(κ) restrains the cap from retracting past its initial location at κ0. The intersection of the cap with the J1 axis is at J1 = X(κ). This intersection depends on the cap ellipticity ratio R, where R is the ratio of its major to minor axes (see Figure 91):
Figure 91. Equation. Pressure invariant X as a function of kappa. The cap moves to simulate plastic volume change. The cap expands (X(κ) and κincrease) to simulate plastic volume compaction. The cap contracts (X(κ) and κ decrease) to simulate plastic volume expansion, called dilation. The motion (expansion and contraction) of the cap is based on the hardening rule, as shown in Figure 92:
Figure 92. Equation. Plastic volume strain hardening rule, ε pv. Here ε ρv is the plastic volume strain, W is the maximum plastic volume strain, and D1 and D2 are model input parameters. X0 is the initial location of the cap when κ= κ0. The five input parameters (X0, W, D1, D2, and R) are obtained from fits to the pressure-volumetric strain curves in isotropic compression and uniaxial strain. X0 determines the pressure at which compaction initiates in isotropic compression. R, combined with X0, determines the pressure at which compaction initiates in uniaxial strain. D1 and D2 determine the shape of the pressure-volumetric strain curves. W determines the maximum plastic volume compaction. Shear Hardening Surface. In unconfined compression, the stress-strain behavior of concrete exhibits nonlinearity and dilation before the peak. This type of behavior is modeled with an initial shear yield surface, NHFf, which hardens until it coincides with the ultimate shear yield surface, Ff. Two input parameters are required. One parameter, NH, initiates hardening by setting the location of the initial yield surface. A second parameter, CH, determines the rate of hardening (amount of nonlinearity). Damage. Concrete exhibits softening in the tensile and low to moderate compressive regimes (see Figure 93):
Figure 93. Equation. Transformation of viscoplastic stress to damaged stress, σdij. A scalar damage parameter, d, transforms the viscoplastic stress tensor without damage, denoted s vp, into the stress tensor with damage, denoted s d. Damage accumulation is based on two distinct formulations, which are called brittle damage and ductile damage. The initial damage threshold is coincident with the shear plasticity surface; thus, the user does not have to specify the threshold. Ductile Damage. Ductile damage accumulates when the pressure (P) is compressive and an energy-type term, τd, exceeds the damage threshold, r0d. Ductile damage accumulation depends on the total strain components, εij, as shown in Figure 94:
Figure 94. Equation. Ductile damage accumulation, τ d. The stress components sij are the elasto-plastic stresses (with kinematic hardening) calculated before application of damage and rate effects. Brittle Damage. Brittle damage accumulates when the pressure is tensile and an energy-type term, τb, exceeds the damage threshold, r0b. Brittle damage accumulation depends on the maximum principal strain, εmax, as shown in Figure 95:
Figure 95. Equation. Brittle damage accumulation, τb. Softening Function. As damage accumulates, the damage parameter d increases from an initial value of zero, towards a maximum value of 1, via Figures 96 and 97:
Figure 96. Equation. Brittle damage, d of tb.
Figure 97 Equation. Ductile damage, d of τd. The damage parameter applied to the six stresses is equal to the current maximum of the brittle or ductile damage parameter. The parameters A and B or C and D set the shape of the softening curve plotted as stress-displacement or stress-strain. The parameter dmax is the maximum damage level that can be attained. It is calculated internally and is less than 1 at moderate confining pressures. The compressive softening parameter, A, may also be reduced with confinement, using the input parameter pmod, as shown in Figure 98:
Figure 98. Equation. Reduction of A with confinement. Regulating Mesh Size Sensitivity. The concrete model maintains constant fracture energy, regardless of element size. The fracture energy is defined here as the area under the stress-displacement curve from peak strength to zero strength. Constant fracture energy is achieved by internally formulating the softening parameters A and C in terms of the element length, L (cube root of the element volume), the fracture energy, Gf, the initial damage threshold, τ0t or τ0c , and the softening shape parameters, D or B. The fracture energy is calculated from up to five user-specified input parameters (Gfc, Gft, Gfs, pwrc, pwrc). The user specifies three distinct fracture energy values. These are the fracture energy in uniaxial tensile stress, Gft, pure shear stress, Gfs, and uniaxial compressive stress, Gfc. The model internally selects the fracture energy from equations, which interpolate between the three fracture energy values as a function of the stress state (expressed via two stress invariants). The interpolation equations depend on the user-specified input powers pwrc and pwrt, as shown in Figure 99:
Figure 99. Equation. Brittle and ductile damage thresholds, Gf. The internal parameter trans is limited to range between 0 and 1. Element Erosion. An element loses all strength and stiffness as d®1. To prevent computational difficulties with very low stiffness, element erosion is available as a user option. An element erodes when d > 0.99 and the maximum principal strain is greater than a user-supplied input value, 1-ERODE. Viscoplastic Rate Effects. At each time step, the viscoplastic algorithm interpolates between the elastic trial stress,
Figure 100. Equation. Viscoplastic stress, σvpij. This interpolation depends on the effective fluidity coefficient, η, and the time step, Δt. The effective fluidity coefficient is internally calculated from five user-supplied input parameters and interpolation equations shown in Figure 101:
Figure 101. Equation. Variation of the fluidity parameter η in tension and compression. The input parameters are η0t and Nt for fitting uniaxial tensile stress data, η0c and Nc for fitting the uniaxial compressive stress data, and Srate for fitting shear stress data. The effective strain rate is shown in Figure 102: Figure 102. Definition of effective strain rate. This viscoplastic model may predict substantial rate effects at high strain rates (
Figure 103. Equation. Overstress limit of η. where over = overt when the pressure is tensile, and over = overc when the pressure is compressive. The user has the option of increasing the fracture energy as a function of effective strain rate via the repow input parameter, as shown in Figure 104: 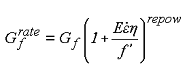 Figure 104. Equation. Fracture energy with rate effects, . Here |