U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: N/A Date: N/A |
Paper prepared for presentation at the 81st TRB Annual Meeting and for subsequent publication in the Transportation Research Record: Journal of the Transportation Research Board
Aroon
Shenoy
Senior Research Fellow
Turner -Fairbank Highway Research Center
6300 Georgetown Pike
McLean, VA 22101
Tel: 202 -493 -3105; Fax: 202 -493 -3161; e -mail: aroon.shenoy@fhwa.dot.gov
and
Pedro
Romero
Assistant Professor
Department of Civil and Environmental Engineering
The University of Utah
Salt Lake City, UT 84112
Tel: 801 -587 -7725; Fax: 801 -585 -5477; e -mail: romero@eng.utah.edu
Word
Count: Text = 4509
8 Tables = 2000
5 Figures = 1250
- - - - - - - - - - - - - - - - - - - - - -
Total = 7759
The present work provides a standardized procedure by which various asphalt concrete mixtures can be compared and their expected performance can be assessed in a uniform manner using the simple performance test suggested under the National Co -operative Highway Research Program NCHRP 9 -19 – Superpave Support and Performance Models Management program.
The frequency sweep data generated from the test are available in terms of dynamic modulus |E*| versus frequency at the measurement temperature under different levels of confining stress (0, 20, 30 psi or 0, 2.9, 4.35 mPa). The moduli versus frequency data at different temperatures are unified to form a single curve for each mixture through a normalizing parameter. The temperature at which the normalizing parameter becomes equal to one is designated the specification parameter TS (°C) for assessing mixture performance.
Each unified curve is fitted with a constitutive equation from which model parameters are evaluated. The slope B1 in the low frequency region of the unified curve, when normalized with the term (T/ TS), results in a parameter that is related to asphalt pavement distress at high temperature T. It is shown that B1/ TS is related to rut depths measured at different WesTrack, a full -scale test track, sections and the correlation improves with increasing confining stress. There is a good possibility that the slope B2 in the high frequency region of the unified curve may relate to distresses in the intermediate temperature range, such as fatigue cracking. A preliminary check shows that this might be true, but data is too limited to draw firm conclusions.
A Simple Performance Test to estimate intermediate and high temperature distresses of asphalt mixtures is being evaluated under the Superpave Models Management Contract Task C – Simple Performance Study (1). The triaxial complex modulus test used in this study involves the application of a sinusoidal strain with a certain peak amplitude under different levels of confining stress (0, 20, 30 psi or 0, 2.9, 4.35 mPa) at a fixed temperature of interest at each of the following frequencies: 25, 10, 5, 2, 1, 0.5, and 0.1 Hz. The response of the material at these frequencies to the applied strain is analyzed in terms of the complex modulus (E*) and the phase angle (f). The aim of the study was (1) to measure the stiffness characteristics of ten mixtures from WesTrack, a full -scale test track (2 -4) and (2) to relate the absolute value of the complex modulus, termed the dynamic modulus |E*|, obtained from servo -hydraulic testing to the distresses in the pavement at intermediate and high temperatures.
The relationship is established under the hypothesis that the stiffness of the asphalt mixture can be used to predict distresses at intermediate and high temperatures. Stiffness using the dynamic modulus test is the parameter of choice for the National Co -operative Highway Research Program NCHRP 9 -19 – Superpave Support and Models contract as well as the American Association of State Highway and Transportation Officials AASHTO 2002 design guide (5). The stiffer the mixture at high temperatures, the more rut resistant the mixture is expected to be in the field. At intermediate temperatures, the stiffer mixture is more resistant to fatigue cracking for thicker pavements while the softer mixture is more resistant to fatigue cracking for thinner pavements.
Using properties measured on laboratory -prepared mixtures and from field performance data on ten sections of the WesTrack, a full -scale test track (2 -4) test site, the measured stiffness of the mixtures is compared to the equivalent measured rut depth and cracking (1). For rutting, the analysis (1) was conducted for two combinations of temperature [100°F (37.8°C), 130°F (54.4°C)] and one time of loading [5 Hz]. For fatigue cracking, the analysis (1) was conducted for different two combinations of temperature [40°F (4.4°C), 70°F (21.1°C)] and a different time of loading [10 Hz].
The choice of their combinations of temperatures and loading time for each of the distresses is, undoubtedly, appropriate because rutting is expected to occur at higher temperatures and lower loading times while fatigue cracking is expected to occur in the lower range of temperatures and higher loading times. However, neither the temperatures nor the times of loading are selected on any standardized basis. Hence, different researchers could choose different values of temperatures and loading times as per their own convenience or preference so long as they relate the higher temperatures and lower loading times to rutting behavior, and the lower temperatures and higher loading times to fatigue behavior. This could result in different researchers coming up with different conclusions when comparing the same set of mixtures if their temperature and loading time choices are different. Such a practice will eventually lead to the availability of lots of mixture data that, however, cannot be compared on a common platform. Thus, the information from the simple performance test will be under -utilized and restricted to only specific systems under the limited sets of chosen test conditions.
The present paper establishes a standardized procedure to analyze and interpret data generated from the triaxial test proposed in the NCHRP 9 -19 program (1). This is done by reanalysis of data already generated under the NCHRP 9 -19 program (1). The set up procedure is general in nature. There are no restrictions on the choice of the temperatures of measurement. Any temperatures within the range of low temperature [e.g. 15.8°F ( -9°C)] and high temperature [e.g. 130°F (54.4°C)] may be chosen in order to generate a specification temperature TS. Using a normalizing parameter, a unified curve is generated within a temperature range, which again is insensitive to the actual choice of the temperatures. So long as three temperatures are selected between the intermediate temperature [e.g. 40°F (4.4°C)] and high temperature [e.g. 100°F (40°C)], the unified curve generated by the suggested procedure will be the same for the same mixture.
The unified curve is then fitted with a rheological model, and the values of the model parameters are determined. The slopes B1 and B2 in the low frequency and high frequency portions of the unified curve are used for determining the controlling terms CR and CF for ranking the aggregate -asphalt mixtures by their expected performance to resist distresses in high and intermediate temperature ranges. The assessment parameters (TS, CR, and CF) introduced in the present work could be used as identification tags to grade mixtures and rank their expected field performance. This would then establish uniformity among different researchers and data sharing between various practitioners would occur on a common platform. It would also be useful for developing mixtures targeted towards particular specifications when designing pavements for specific regions.
The mixtures analyzed in the present work are those described in detail in the NCHRP report (1). The specimens were fabricated in the laboratory to duplicate the measured material compositions for each of the ten WesTrack test sections utilized in the study, namely, sections 2, 4, 7, 15, 23 and 24 for rutting and sections 2, 5, 6 and 24 for cracking. Table 1 gives the binder and air void content as well as gradations for the mixtures, and Table 2 gives the measured rut depths and fatigue cracking as percent area.
All mixtures were designed using the SHRP level 1 (Volumetric) mix design method with one conventional PG64 -22 binder. The mixing and compaction temperatures were determined using the protocol followed earlier by the NCHRP 9 -19 research team (6).
All mixtures were short -term oven aged for 4 hours at 135°C according to the AASHTO test method (7) before compaction. The specimens were compacted with a ‘Servo Pac Gyratory Compactor’ into a 150 -mm diameter gyratory mold to approximately 160 -mm height. Test samples of 100 -mm diameter were cored from the center of the gyratory compacted specimen. Approximately 5 mm were sawed from each sample end in accordance with the NCHRP 9 -19 research team’s protocol (6).
Specification Temperature TS (°C)
The procedure to obtain a specification temperature follows along the lines introduced earlier (8, 9) during the analysis of the frequency sweep at constant height (FSCH) data generated from the Superpave Shear Tester (SST).
The triaxial complex modulus testing data is available in the form of the variation of the dynamic modulus |E*| with frequency w at five different temperatures, namely, 15.8°F ( -9°C), 40°F (4.4°C), 70°F (21.1°C), 100°F (37.8°C) and 130°F (54.4°C). A normalizing frequency parameter w0 is first determined corresponding to a particular reference dynamic modulus value. The choice of the reference dynamic modulus is arbitrary as has been explained in previous publications (8, 9). In the present case, the reference dynamic modulus |E0*| value is chosen to be equal to 4,000,000 Pa, and this value is recommended for future data analyses. The value of w0 corresponding to the reference dynamic modulus |E0*| = 4,000,000 Pa is estimated using the following equation:
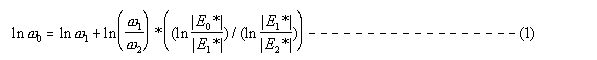
where the normalizing frequency parameter w0 corresponds to the reference dynamic modulus |E0*| =4,000,000 Pa. |E1*|, w1 and |E2*|, w2 are two sets of data corresponding to (a) one value of |E*| > 4,000,000 Pa and (b) another value of |E*| < 4,000,000 Pa. In cases where data does not include the range covering the value of |E0*| = 4,000,000 Pa, Equation (1) is used for extrapolation. The values of w0 for various mixtures are given in Table 3.
The variation of the normalizing frequency parameter with temperature is expressed through a semi -logarithmic plot of w0 versus 1/T (where T is the temperature in degrees Kelvin) (8, 9). The data points are fitted with the best line (R2 @ 0.93 -0.97) using an equation of the following form (8, 9):
![]()
The values of A0 and T0 for all sets of data as determined from Equation (2) are given in Table 4. The specification temperature is determined as TS (°C) = T0 (K) - 273. This is in essence the temperature at which the mixture has a stiffness of 4,000,000 Pa at a loading frequency of 1 Hz.
Using the appropriate value of w0 corresponding to each temperature, the original data of |E*| versus w as shown in Figure 1 (for one mixture sample) are replotted as |E*| versus w / w0 in Figure 2 combining data for the different temperatures, basically using the principles of time -temperature superposition. It can be seen that a unified curve is obtained through the use of this normalization. Only three temperatures [40°F (4.4°C), 70°F (21.1°C), 100°F (37.8°C)] are utilized in the unification for the following reasons. First, the lowest temperature of 15.8°F ( -9°C) and the highest temperature of 130°F (54.4°C) include data wherein the values of w0 were obtained by gross extrapolation and, hence, would not give reliable unification. Second, the three temperatures [40°F (4.4°C), 70°F (21.1°C), 100°F (37.8°C)] suffice to cover the temperature range from intermediate to high that is relevant to the distresses of fatigue cracking and rutting, because the unification automatically extends the range beyond the values of 40°F (4.4°C) and 100°F (37.8°C) based on the superposition principle. Unified curves similar to the one shown in Figure 2 were obtained for all mixture data sets in Table 3.
The best -fit curves through the data points in Figure 2 and other similar unified curves (not shown here) are obtained using the following equation having a form similar to the one used in the earlier work for fitting unified curves for (a) mixtures from the SST data [8, 9] and (b) asphalt binders from dynamic shear rheometer (DSR) data [10]:
![]()
where the values of A1, B1, A2 and B2 for the unified curve for each mixture are given in Table 5.
The development of the unified curves in the manner described herein has a number of distinct advantages. The unified curve helps to extend the range of data and can be used for predicting the dynamic mechanical behavior of the mixture at temperatures outside the measured values. For example, though the temperatures used for the unification are 40°F (4.4°C), 70°F (21.1°C) and 100°F (37.8°C), the values of w 0 at temperatures outside this range can be predicted using Equation (2) and values of A0 and T0 from Table 4. These values of w 0, in turn, when used in Equation (3) with values of coefficients A1, A2 and exponents B1, B2 from Table 5 help to give the variation of |E*| versus w at any other temperature of interest. This fact becomes useful, especially, when there is a need to know the dynamic mechanical behavior of the mixture at a temperature where the sample stiffness, particularly of a low performance grade binder, makes the measurement fall outside the sensitive range of the equipment.
The model described by Equation (3) that is used for fitting the data points on the unified curve is a combination of the following two equations – one for the lower frequency region and the other for the higher frequency region (8 -10):
![]() for 0.00001 < w/w0
< 1 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(4a)
for 0.00001 < w/w0
< 1 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(4a)
![]() for 1 < w/w0 <
100000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(4b)
for 1 < w/w0 <
100000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(4b)
This automatically marks the two portions of the unified curve that are of significance. The portion of the unified curve in the low frequency region describes the dynamic mechanical behavior of the mixture at higher temperatures applicable to rutting, while the other portion of the unified curve in the higher frequency region describes the dynamic mechanical behavior at lower temperatures applicable to the intermediate temperature distress of fatigue cracking. This is because the unification automatically aligns data at higher temperatures so as to lie in the lower region of the normalized frequency while aligning data at intermediate temperatures to fall within the higher region of normalized frequency.
Thus, an indicator of mixture resistance to permanent deformation at high temperatures should, in principle, be linked to the portion of the unified curve in the lower frequency region given by Equation (4a). The stiffness of the mixture at the temperature of interest could be obtained from this equation at any desired frequency or frequencies. If a single frequency value is used, then the dynamic mechanical behavior is expressed at one specific condition only. The coefficient A1 is actually the value of stiffness at w /w 0 = 1 and is again an expression of the dynamic mechanical behavior under one specific condition. On the other hand, the exponent B1, being the slope of |E*| versus w /w 0 on a log -log plot, captures the behavioral pattern through a range of temperatures and frequencies applicable to rutting. Hence, B1 is recommended for use in order to establish the relationship between the dynamic mechanical data and rutting.
The lower the exponent B1, the greater is the resistance of the mixture to rutting. Similarly, the higher the value of TS, the greater is the resistance of the mixture to rutting. This implies that the permanent deformation DT at temperature T would essentially be a function of T, TS and B1. The form (T/ TS)* B1 would give an adequate description of this function and could be considered as the rutting control term, CR, for giving a measure of the rutting resistance. The lower the value of CR, the better is the rutting resistance. The rutting control term CR is given by the following equation:
![]() - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(5)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -(5)
If the temperature of interest T were equal to the specification temperature TS, then the rutting control term CR would simply be equal to B1. Thus, in such circumstances, if one were to compare the behavior of two mixtures at their respective specification temperatures, then it would be sufficient to compare their respective B1 values to ascertain that the one with the lower value would be expected to exhibit less rutting under the same loading and environmental conditions.
On the other hand, if the temperature of interest were a particular average pavement temperature T, then to understand how two mixtures would perform under identical temperature conditions, it would be enough to compare their (B1/ TS) ratio. As a matter of fact, it would be this ratio that could be used for ranking mixtures.
Table 6 gives the values of the (B1/ TS) ratio for the mixtures analyzed in this work. The lab -predicted permanent deformation based on the (B1/ TS) ratio when compared with the field rut depth shows the correlation for the WesTrack sections in Figures 3 -5 for different confining stresses of 0, 20, 30 psi (0, 2.9, 4.35 mPa), respectively. The correlation coefficient R2 is 0.42 when data is acquired from tests performed under unconfined conditions. The correlation coefficient R2 improves to 0.60 when confining stress of 20 psi (2.9 mPa) is used during data acquisition. It is known that confined creep testing in triaxial measurements has a better correlation to permanent deformation than unconfined testing [11]. Thus, when a higher confining stress of 30 psi (4.35 mPa) is used in the measurements, the correlation coefficient R2 rises to 0.89, indicating that these conditions favor a good correlation between the laboratory test and field performance. The confining stress in the WesTrack pavements based on truck loadings is not known. However, the present work indicates that the suggested method of using the slope of the unified curve obtained from data when confining stress equals 30 psi (4.35 mPa) is effective in predicting mixture rutting performance. It is therefore recommended for future use with an understanding that this is not the optimum value, and a value greater than 30 psi (4.35 mPa), perhaps 40 psi (5.8 mPa), may be an optimum and should be used if such a value is determined through future experiments.
The portion of the unified curve in the higher frequency region describes the dynamic mechanical behavior at lower temperatures applicable to the other distress mode, namely, fatigue cracking. The exponent representing the behavior in that portion of the curve is B2. The structural design of the pavement would dictate whether a higher stiffness material or a lower stiffness material would mitigate this distress at intermediate temperatures. As an example, a pavement structure wherein a material with lower stiffness would provide better resistance to fatigue cracking could be considered. In such a circumstance, the resistance of the mixture to the distress at intermediate temperatures would be greater when the exponent B2 is lower and the value of TS is lower. This implies that the resistance to intermediate temperature distress at temperature T would adequately be described by the functional form (TS /T)* B2 and this could be considered as the control term CF, giving a measure of the resistance of a mixture to the intermediate temperature distress of fatigue cracking. The lower the value of CF, the better would be the resistance.
The control term CF would simply be equal to B2 in case the temperature of interest were equal to the specification temperature. Thus, in such circumstances, if one were to compare the behavior of two mixtures at their respective specification temperatures, then it would be sufficient to compare their respective B2 values to ascertain that the one with the lower value would be expected to exhibit less fatigue cracking at intermediate temperatures.
On the other hand, if the temperature of interest were a particular average pavement temperature T, then it would be enough to compare their (TS *B2) product in order to evaluate how two mixtures would perform under identical temperature conditions, and in fact, this product could be used for ranking mixtures.
Table 7 gives the values of the (TS *B2) product for the mixtures analyzed in this work. A comparison with field performance cannot be done in an effective manner because the field information on cracking is available for only three sites. When plots of TS *B2 were made against the cracking length for the three sections, the correlation coefficient R2 = 0.8 was obtained for a confining stress of 30 psi (4.35 mPa). However, much emphasis should not be placed on this result as it was obtained with only three data points, and the findings from this part of the analysis should be reconfirmed when more data becomes available.
The present work introduces certain assessment parameters (TS, CR, and CF) that could be used as identification tags to grade mixtures and rank their expected field performance. This method of performance -related specification would help in streamlining the data analysis procedure from triaxial modulus testing. It would provide a uniform platform to compare data from different practitioners and project the expected performance of the mixtures. It would also be useful for developing mixtures targeted towards particular specifications when designing pavements for specific regions.
The suggested method is simple and straightforward. It involves the determination of a specification temperature TS (°C) from the dynamic modulus versus frequency data. This is done by determining the normalizing parameter w0 corresponding to the value of |E0*| = 4,000,000 Pa using Equation (1). The values of w0 at two different temperatures are sufficient to determine the value of T0 (K) from Equation (2), from which TS (°C) is immediately obtained. In case w0 is available at more than two temperatures (as was the case in the present work), then a semi -logarithmic plot of w0 versus 1/T (K) is to be used to determine the value of T0 (K) and, subsequently, TS (°C).
The dynamic modulus |E*| versus frequency w data at different temperatures for each aggregate -asphalt mixture is unified by normalizing the frequency using corresponding values of w0. The unified data is then fitted with the rheological model given by Equation (3), and the values of the model parameters are determined. The slopes B1 and B2 of the two portions of the unified curve are used for determining the controlling terms CR and CF for ranking the aggregate -asphalt mixtures by their expected performance to resist distresses in high and intermediate temperature ranges.
The reliability of the information generated from the slopes B1 and B2 is dependent on the quality of the generated data and the resultant unification. The experimental data must be generated within the sensitive range of the equipment capabilities. In order to ensure that this is always the case, it is prudent to generate dynamic modulus versus frequency data in the triaxial modulus test for different binders not at some predetermined fixed temperatures but rather at temperatures where the stiffness of the material is within the measurement sensitivity of the equipment. For example, it would be better to take data at lower temperatures from 5°C to 30°C for low stiffness binders while at higher temperatures from 15°C to 40°C for high stiffness binders. This would result in data that will unify without scatter over the entire frequency range.
By generating data within different temperatures but similar stiffness ranges, the other advantage is that the normalizing parameter will not need gross extrapolation. Using unextrapolated values of w 0 would result in better unification of data. It is difficult to guess the stiffness of the aggregate -asphalt system before any triaxial modulus measurements are performed. Hence, it may not always be easy to choose the temperature range for the measurement such that the stiffness of the system lies within the sensitivity range of the equipment.
Based on the present work, a rough guideline is suggested that should help in making a reasonable choice of the measurement temperatures. It is recommended that the first measurement temperature should be chosen to be half the value of the high performance grade temperature of the binder used. The subsequent temperatures are selected such that each is lower by 6°C. Table 8 shows an example of how the temperatures could be chosen.
It should be noted that the methodology described herein only addresses load -related distresses. In addition, the case of thick pavements where stiff mixtures are desired for resistance to fatigue cracking was not considered in the analysis. The controlling term for this case can be easily deduced because the functional form must be the same as that for the rutting control term, except for the fact that B1 needs to be replaced by B2. A higher value of B2 and a lower value of TS would indicate better resistance of thick pavements to fatigue cracking. Thus, for the case of thick pavements, the control term for fatigue cracking CF = (T/ TS)* B2, and higher the CF value the better would be the resistance of such pavements to fatigue cracking.
The concepts used in this work are general in nature and applicable to mixtures as well as binders [8 -10]. The developed methodology in principle should be applicable to any pavement. Thus, it is recommended that this analysis procedure be checked with data from other test sites and with other unmodified and modified binders in order to validate the findings of this work.
Disclaimer
The opinions, findings, and conclusions expressed in this document are those of the authors only and not necessarily of the Federal Highway Administration or the University of Utah.
The authors would like to express their gratitude to Dr. Ernest J. Bastian, Jr. for his comments.
References
TABLE
1 – WesTrack Mixture Compositions (1)
TABLE 2 – WesTrack Performance Data (1)
TABLE 3 – Values of the normalizing frequency parameter, w0 (Hz) using |E*0|=4,000,000(Pa)
TABLE 4 – Values of A0, T0(K)
and TS(°C) from Equation (2)
TABLE 5 – Values of the coefficients and exponents in
Equation (3)
TABLE 6 – Performance ranking for resistance to distress
at high temperatures
TABLE 7 – Performance ranking for resistance to distress
at intermediate temperatures
TABLE 8 – Examples of proper choice of temperatures for
triaxial modulus testing
Figure 1: Dynamic modulus |E*| with frequency w at three different temperatures of 40°F (4.4°C), 70°F (21.1°C), and 100°F (37.8°C) for WST_WC2 laboratory -prepared samples
Figure 2: Unified curve of the dynamic modulus |E*| with modified frequency w / w0 covering a range of 40°F (4.4°C) - 100°F (37.8°C) for WST_WC2 laboratory -prepared samples
Figure 3: Variation of the term (B1/TS) obtained from the triaxial modulus unconfined (confining stress=0psi or 0mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance
Figure 4: Variation of the term (B1/TS) obtained from the triaxial modulus (confining stress=20psi or 2.9mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance
Figure 5: Variation of the term (B1/TS) obtained from the triaxial modulus (confining stress=30psi or 4.35mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance
TABLE 1 –WesTrack Mixture Compositions (1) (a) Volumetric Properties |
||||||
| Section | Aggregate Nominal Size (mm) | Binder Type | AC% | Va% | Gmm | Distress: C=Cracking R=Rutting |
| 2 | 12.5 Fine -B | PG 64 -22 | 4.76 | 9.3 | 2.466 | C |
| 24 | 12.5 Coarse -B | PG 64 -22 | 5.78 | 7.5 | 2.431 | C |
| 5 | 12.5 Fine -B | PG 64 -22 | 5.61 | 7.0 | 2.437 | C |
| 6 | 12.5 Fine -B | PG 64 -22 | 5.89 | 11.3 | 2.427 | C |
| 15 | 12.5 Fine -T | PG 64 -22 | 5.55 | 8.7 | 2.438 | R |
| 2 | 12.5 Fine -T | PG 64 -22 | 5.02 | 10.4 | 2.457 | R |
| 23 | 12.5 Coarse -T | PG 64 -22 | 5.78 | 4.9 | 2.430 | R |
| 24 | 12.5 Coarse -T | PG 64 -22 | 5.91 | 7.2 | 2.425 | R |
| 4 | 12.5 Fine -T | PG 64 -22 | 5.24 | 6.6 | 2.449 | R |
| 7 | 12.5 Coarse -T | PG 64 -22 | 6.28 | 6.9 | 2.412 | R |
| B=Bottom layer; T=Top layer | ||||||
(b)
Gradations |
||||
Fine |
Coarse |
|||
| Sieve mm | Top % Passing | Bottom % Passing | Top % Passing | Bottom % Passing |
| 19.0 | 100 | 100 | 100 | 100 |
| 12.5 | 88.2 | 88.3 | 79.2 | 81.7 |
| 9.50 | 76.6 | 75.9 | 65.0 | 66.2 |
| 4.75 | 51.1 | 48.6 | 41.8 | 42.0 |
| 2.36 | 39.8 | 36.7 | 28.6 | 27.7 |
| 1.18 | 35.2 | 32.3 | 21.0 | 19.9 |
| 0.60 | 28.6 | 26.4 | 16.1 | 14.9 |
| 0.30 | 16.1 | 15.1 | 12.2 | 11.0 |
| 0.15 | 8.1 | 7.4 | 9.0 | 7.9 |
| 0.075 | 5.0 | 4.4 | 6.6 | 5.5 |
TABLE
2 – WesTrack Performance Data (1) |
|||
| Section | Gradation | % Cracking =100*crack length/section length | Rut Depth millimeters |
| (a) Cracking Sections measured on 5/27/1997 at 2.8M ESALs | |||
| 2 | Fine | 7 | 6 |
| 24 | Coarse | 0 | 22 |
| 5 | Fine | 51 | - |
| 6 | Fine | 100 | 21 |
| (b) Rutting Sections measured on 11/11/1997 at 1.5M ESALs | |||
| 15 | Fine | 0 | 8 |
| 2 | Fine | 7 | 6 |
| 23 | Coarse | - | 13 |
| 24 | Coarse | 0 | 22 |
| 4 | Fine | - | 7 |
| 7 | Coarse | - | 36 |
TABLE
3 - - Values of the normalizing frequency parameter, w0 (Hz) using |E*0|=4,000,000(Pa) |
|||||
| Mixture | @15.8°F ( -9°C) |
@40°F (4.4°C) |
@70°F (21.1°C) |
@100°F (37.8°C) |
@130°F (54.4°C) |
| Confining stress s
|
|||||
| WST_WC2 | 1.76E -05 | 0.0427 | 8.5806 | 1729.3 | 12579 |
| WST_WC24 | 8.89E -08 | 0.0025 | 3.9575 | 117.43 | 19188 |
| WST_WC5 | 2.07E -10 | 0.0003 | 0.1336 | 209.27 | 1251.2 |
| WST_WC6 | 1.72E -07 | 0.0070 | 3.4828 | 280.25 | 21145 |
| WST_WR15 | 5.71E -10 | 0.0005 | 0.6300 | 57.648 | 1836.2 |
| WST_WR2 | 2.37E -06 | 0.0190 | 11.631 | 349.07 | 5741.6 |
| WST_WR23 | 1.20E -09 | 0.0001 | 0.4386 | 38.019 | 2837.5 |
| WST_WR24 | 1.48E -07 | 0.0613 | 4.9453 | 238.81 | 18750 |
| WST_WR4 | 1.57E -12 | 5.3E -5 | 0.2375 | 26.939 | 1167.8 |
| WST_WR7 | 5.36E -08 | 0.0013 | 2.3512 | 117.07 | 3822.5 |
| Confining stress s0= 20 psi (2.9 mPa) | |||||
| WST_WC2 | 2.39E -09 | 0.0034 | 0.3307 | 119.72 | 801.81 |
| WST_WC24 | 1.80E -08 | 0.0003 | 0.4466 | 14.671 | 8E+07 |
| WST_WC5 | 2.79E -07 | 0.0002 | 0.1338 | 9.0021 | 3E+06 |
| WST_WC6 | 2.76E -07 | 0.0043 | 0.4632 | 44.035 | 2E+06 |
| WST_WR15 | 2.06E -09 | 0.0008 | 0.1756 | 4.1226 | 4621.1 |
| WST_WR2 | 3.78E -06 | 0.0036 | 0.2660 | 25.202 | 2717.5 |
| WST_WR23 | 1.91E -10 | 0.0003 | 0.2117 | 15.254 | 25094 |
| WST_WR24 | 5.51E -08 | 0.0008 | 0.1950 | 43.557 | 21057 |
| WST_WR4 | 3.02E -08 | 0.0003 | 0.1361 | 2.5590 | 472.90 |
| WST_WR7 | 2.91E -10 | 0.0004 | 0.2338 | 13.305 | 75017 |
| Confining stress s0= 30 psi (4.35 mPa) | |||||
| WST_WC2 | 5.17E -08 | 0.0010 | 0.2613 | 43.637 | 1115.3 |
| WST_WC24 | 3.91E -04 | 0.0019 | 1.4699 | 80.789 | 61954 |
| WST_WC5 | 6.69E -09 | 0.0047 | 1.3149 | 87.459 | 2E+05 |
| WST_WC6 | 4.89E -05 | 0.0650 | 9.0402 | 872.61 | 16633 |
| WST_WR15 | 4.31E -10 | 0.0026 | 0.8467 | 93.292 | 4981.9 |
| WST_WR2 | 9.35E -08 | 0.0026 | 1.0168 | 86.354 | 2909.9 |
| WST_WR23 | 5.27E -09 | 0.0002 | 0.4796 | 54.305 | 2837.5 |
| WST_WR24 | 2.51E -09 | 0.0010 | 0.6501 | 126.33 | 6E+06 |
| WST_WR4 | 1.25E -12 | 3.0E -5 | 0.1680 | 27.825 | 971.01 |
| WST_WR7 | 4.30E -10 | 0.0021 | 0.4797 | 117.59 | 2E+06 |
| Note: WST_WC (WesTrack Cracking Section); WST_WR (WesTrack Rutting Section) | |||||
TABLE
4 - - Values of A0, T0(K) and TS(°C)
from Equation (2) |
|||
| Mixture | A0 | T0(K) | TS(°C) |
| Confining stress s0= 0 psi (0 mPa) | |||
| WST_WC2 | 95.94 | 289.98 | 16.98 |
| WST_WC24 | 114.97 | 296.18 | 23.18 |
| WST_WC5 | 129.74 | 302.01 | 29.01 |
| WST_WC6 | 113.05 | 294.92 | 21.92 |
| WST_WR15 | 124.58 | 301.38 | 28.38 |
| WST_WR2 | 98.10 | 292.97 | 19.97 |
| WST_WR23 | 124.65 | 301.76 | 28.76 |
| WST_WR24 | 109.20 | 293.86 | 20.86 |
| WST_WR4 | 145.41 | 304.33 | 31.33 |
| WST_WR7 | 111.66 | 298.02 | 25.02 |
| Confining stress s0= 20 psi (2.9 mPa) | |||
| WST_WC2 | 114.44 | 300.77 | 27.77 |
| WST_WC24 | 150.22 | 295.23 | 22.23 |
| WST_WC5 | 128.68 | 296.82 | 23.82 |
| WST_WC6 | 124.31 | 294.47 | 21.47 |
| WST_WR15 | 116.70 | 302.58 | 29.58 |
| WST_WR2 | 89.62 | 298.43 | 25.43 |
| WST_WR23 | 135.90 | 301.29 | 28.29 |
| WST_WR24 | 115.79 | 298.94 | 25.94 |
| WST_WR4 | 99.41 | 305.07 | 32.07 |
| WST_WR7 | 137.85 | 300.44 | 27.44 |
| Confining stress s0= 30 psi (4.35 mPa) | |||
| WST_WC2 | 104.65 | 300.95 | 27.95 |
| WST_WC24 | 89.17 | 291.88 | 18.88 |
| WST_WC5 | 130.77 | 296.24 | 23.24 |
| WST_WC6 | 91.23 | 289.13 | 16.13 |
| WST_WR15 | 127.53 | 299.72 | 26.72 |
| WST_WR2 | 106.49 | 298.32 | 25.32 |
| WST_WR23 | 152.64 | 295.81 | 22.81 |
| WST_WR24 | 150.26 | 295.63 | 22.63 |
| WST_WR4 | 146.47 | 304.77 | 31.77 |
| WST_WR7 | 150.17 | 296.63 | 23.63 |
| Note: WST_WC (WesTrack Cracking Section); WST_WR (WesTrack Rutting Section) | |||
TABLE
5 - - Values of the coefficients and exponents in Equation (3) |
||||
Mixture |
A1 |
B1 |
A2 |
B2 |
| Confining stress s0= 0 psi (0 mPa) | ||||
| WST_WC2 | 4885789 | 0.2717 | 4020677 | 0.1240 |
| WST_WC24 | 4201185 | 0.3824 | 4476110 | 0.1272 |
| WST_WC5 | 4317307 | 0.2901 | 6539619 | 0.1071 |
| WST_WC6 | 4690443 | 0.3757 | 4357089 | 0.1404 |
| WST_WR15 | 3720400 | 0.3445 | 5320671 | 0.1362 |
| WST_WR2 | 4432267 | 0.2866 | 4246827 | 0.1060 |
| WST_WR23 | 3876511 | 0.3667 | 5179212 | 0.1242 |
| WST_WR24 | 4407584 | 0.3402 | 4186176 | 0.1037 |
| WST_WR4 | 3916019 | 0.3260 | 5697063 | 0.0922 |
| WST_WR7 | 4010997 | 0.3613 | 4808233 | 0.1204 |
| Confining stress s0= 20 psi (2.9 mPa) | ||||
| WST_WC2 | 4368704 | 0.1638 | 4924440 | 0.0970 |
| WST_WC24 | 3886442 | 0.2071 | 4746965 | 0.1299 |
| WST_WC5 | 3810473 | 0.2248 | 5530017 | 0.1419 |
| WST_WC6 | 3898491 | 0.2101 | 4797932 | 0.1406 |
| WST_WR15 | 3839755 | 0.2258 | 4948604 | 0.1167 |
| WST_WR2 | 4051580 | 0.2142 | 4854067 | 0.1256 |
| WST_WR23 | 3859662 | 0.2696 | 5733998 | 0.1311 |
| WST_WR24 | 3732573 | 0.2446 | 6307348 | 0.1315 |
| WST_WR4 | 3923409 | 0.2527 | 5335953 | 0.0954 |
| WST_WR7 | 3702444 | 0.2165 | 5657348 | 0.1409 |
| stress s0= 30 psi (4.35 mPa) | ||||
| WST_WC2 | 3991865 | 0.2105 | 4700157 | 0.1436 |
| WST_WC24 | 4015736 | 0.2602 | 4886535 | 0.1142 |
| WST_WC5 | 3823842 | 0.2544 | 4794059 | 0.1161 |
| WST_WC6 | 3802345 | 0.1939 | 4069616 | 0.1570 |
| WST_WR15 | 3876539 | 0.2183 | 4544094 | 0.1531 |
| WST_WR2 | 3910521 | 0.2114 | 4532523 | 0.1221 |
| WST_WR23 | 3645308 | 0.2593 | 4844419 | 0.1321 |
| WST_WR24 | 3902006 | 0.2696 | 5018301 | 0.1194 |
| WST_WR4 | 3872405 | 0.2380 | 5515970 | 0.1149 |
| WST_WR7 | 3297151 | 0.2246 | 4878915 | 0.1406 |
| Note: WST_WC (WesTrack Cracking Section); WST_WR (WesTrack Rutting Section) | ||||
TABLE
6 – Performance ranking for resistance to distress at high temperatures |
||||
Predicted
from Laboratory Measurements |
Field -Performance | |||
| Binder | Ts | B1 | B1 / Ts | Rut Depth (mm) |
| Confining stress s0= 0 psi (0 mPa) | ||||
| WST_WC2 | 16.98 | 0.2717 | 0.0160 | 6 |
| WST_WC24 | 23.18 | 0.3824 | 0.0165 | 22 |
| WST_WC5 | 29.01 | 0.2901 | 0.0099 | - |
| WST_WC6 | 21.92 | 0.3757 | 0.0171 | 21 |
| WST_WR15 | 28.38 | 0.3445 | 0.0121 | 8 |
| WST_WR2 | 19.97 | 0.2866 | 0.0144 | 6 |
| WST_WR23 | 28.76 | 0.3667 | 0.0128 | 13 |
| WST_WR24 | 20.86 | 0.3402 | 0.0163 | 22 |
| WST_WR4 | 31.33 | 0.3260 | 0.0104 | 7 |
| WST_WR7 | 25.02 | 0.3613 | 0.0144 | 36 |
| Confining stress s0= 20 psi (2.9 mPa) | ||||
| WST_WC2 | 27.77 | 0.1638 | 0.0059 | 6 |
| WST_WC24 | 22.24 | 0.2071 | 0.0093 | 22 |
| WST_WC5 | 23.82 | 0.2248 | 0.0094 | - |
| WST_WC6 | 21.47 | 0.2101 | 0.0098 | 21 |
| WST_WR15 | 29.58 | 0.2258 | 0.0076 | 8 |
| WST_WR2 | 25.43 | 0.2142 | 0.0084 | 6 |
| WST_WR23 | 28.29 | 0.2696 | 0.0095 | 13 |
| WST_WR24 | 25.94 | 0.2446 | 0.0094 | 22 |
| WST_WR4 | 32.07 | 0.2527 | 0.0079 | 7 |
| WST_WR7 | 27.44 | 0.2165 | 0.0079 | 36 |
| Confining stress s0= 30 psi (4.35 mPa) | ||||
| WST_WC2 | 27.95 | 0.2105 | 0.0075 | 6 |
| WST_WC24 | 18.88 | 0.2602 | 0.0138 | 22 |
| WST_WC5 | 23.24 | 0.2544 | 0.0109 | - |
| WST_WC6 | 16.13 | 0.1939 | 0.0120 | 21 |
| WST_WR15 | 26.72 | 0.2183 | 0.0082 | 8 |
| WST_WR2 | 25.32 | 0.2114 | 0.0083 | 6 |
| WST_WR23 | 22.81 | 0.2593 | 0.0114 | 13 |
| WST_WR24 | 22.63 | 0.2696 | 0.0119 | 22 |
| WST_WR4 | 31.77 | 0.2380 | 0.0075 | 7 |
| WST_WR7 | 23.63 | 0.2246 | 0.0095 | 36 |
| Note: WST_WC (WesTrack Cracking Section); WST_WR (WesTrack Rutting Section) | ||||
TABLE
7– Performance ranking for resistance to distress at intermediate temperatures |
||||
| Predicted from Laboratory Measurements | Field -Performance % Cracking | |||
| Binder | Ts | B1 | B2*Ts | |
| Confining stress s0= 0 psi (0 mPa) | ||||
| WST_WC2 | 16.98 | 0.1240 | 2.1053 | 7 |
| WST_WC24 | 23.18 | 0.1272 | 2.9476 | - |
| WST_WC5 | 29.01 | 0.1071 | 3.1065 | 51 |
| WST_WC6 | 21.92 | 0.1404 | 3.0761 | 100 |
| WST_WR15 | 28.38 | 0.1362 | 3.8670 | - |
| WST_WR2 | 19.97 | 0.1060 | 2.1170 | - |
| WST_WR23 | 28.76 | 0.1242 | 3.5723 | - |
| WST_WR24 | 20.86 | 0.1037 | 2.1627 | - |
| WST_WR4 | 31.33 | 0.0922 | 2.8890 | - |
| WST_WR7 | 25.02 | 0.1204 | 3.0118 | - |
| Confining stress s0= 20 psi (2.9 mPa) | ||||
| WST_WC2 | 27.77 | 0.0970 | 2.6943 | 7 |
| WST_WC24 | 22.24 | 0.1299 | 2.8886 | - |
| WST_WC5 | 23.82 | 0.1419 | 3.3784 | 51 |
| WST_WC6 | 21.47 | 0.1406 | 3.0191 | 100 |
| WST_WR15 | 29.58 | 0.1167 | 3.4521 | - |
| WST_WR2 | 25.43 | 0.1256 | 3.1926 | - |
| WST_WR23 | 28.29 | 0.1312 | 3.7101 | - |
| WST_WR24 | 25.94 | 0.1315 | 3.4114 | - |
| WST_WR4 | 32.07 | 0.0954 | 3.0584 | - |
| WST_WR7 | 27.44 | 0.1409 | 3.8669 | - |
| Confining stress s0= 30 psi (4.35 mPa) | ||||
| WST_WC2 | 27.95 | 0.1436 | 4.0120 | 7 |
| WST_WC24 | 18.88 | 0.1142 | 2.1552 | - |
| WST_WC5 | 23.24 | 0.1161 | 2.6983 | 51 |
| WST_WC6 | 16.13 | 0.1570 | 2.5321 | 100 |
| WST_WR15 | 26.72 | 0.1531 | 4.0898 | - |
| WST_WR2 | 25.32 | 0.1221 | 3.0917 | - |
| WST_WR23 | 22.81 | 0.1321 | 3.0132 | - |
| WST_WR24 | 22.63 | 0.1194 | 2.7014 | - |
| WST_WR4 | 31.77 | 0.1149 | 3.6498 | - |
| WST_WR7 | 23.63 | 0.1406 | 3.3218 | - |
| Note: WST_WC (WesTrack Cracking Section); WST_WR (WesTrack Rutting Section) | ||||
TABLE
8 – Examples of proper choice of temperatures for triaxial modulus testing |
||||||
| Binder | High
PG Temperature |
Choice
of Five Measurement Temperatures |
||||
| PGxx -xx | TPG(°C) |
(TPG/2=) T1 (°C) |
(T1 -6=) T2 (°C) |
(T2 -6=) T3 (°C) |
(T3 -6=) T4 (°C) |
(T4 -6=) T5 (°C) |
| PG58 -34 | 58 |
(58/2=) 29 |
(29 -6=) 23 |
(23 -6=) 17 |
(17 -6=) 11 |
(11 -6=) 5 |
| PG64 -22 | 64 |
(64/2=) 32 |
(32 -6=) 26 |
(26 -6=) 20 |
(20 -6=) 14 |
(14 -6=) 8 |
| PG70 -28 | 70 |
(70/2=) 35 |
(35 -6=) 29 |
(29 -6=) 23 |
(23 -6=) 17 |
(17 -6=) 11 |
| PG82 -22 | 82 |
(82/2=) 41 |
(41 -6=) 35 |
(35 -6=) 29 |
(29 -6=) 23 |
(23 -6=) 17 |
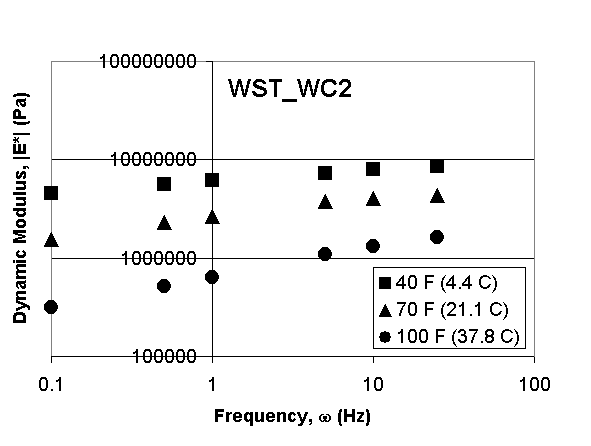
Figure 1: Dynamic modulus |E*| with frequency w at three different temperatures of 40°F (4.4°C), 70°F (21.1°C), and 100°F (37.8°C) for WST_WC2 laboratory -prepared samples
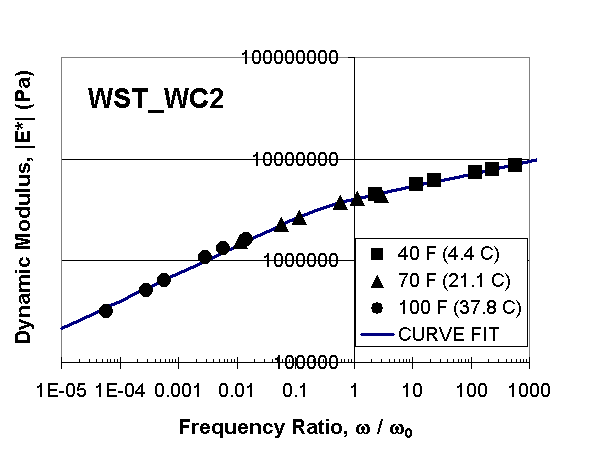
Figure 2: Unified curve of the dynamic modulus |E*| with modified frequency w / w0 covering a range of 40°F (4.4°C) - 100°F (37.8°C) for WST_WC2 laboratory -prepared samples
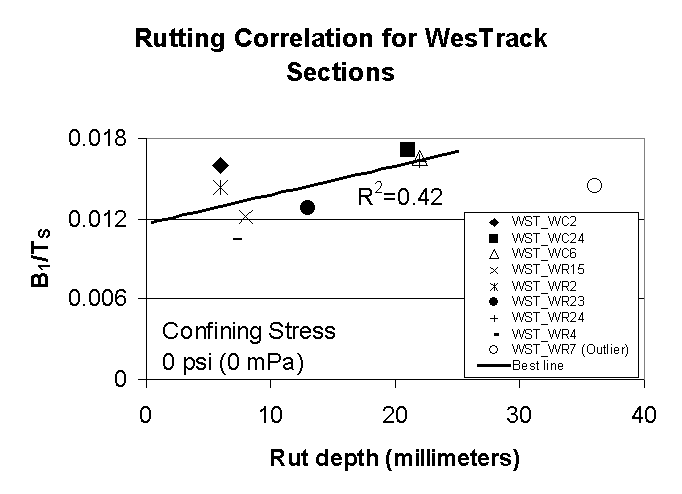
Figure 3: Variation of the term (B1/TS) obtained from the triaxial modulus unconfined (confining stress=0psi or 0mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance
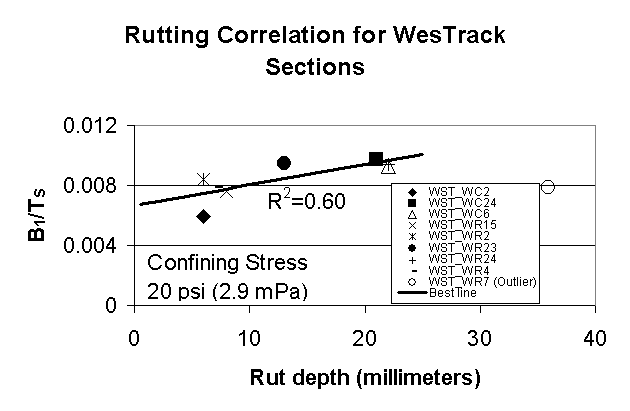
Figure 4: Variation of the term (B1/TS) obtained from the triaxial modulus (confining stress=20psi or 2.9mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance
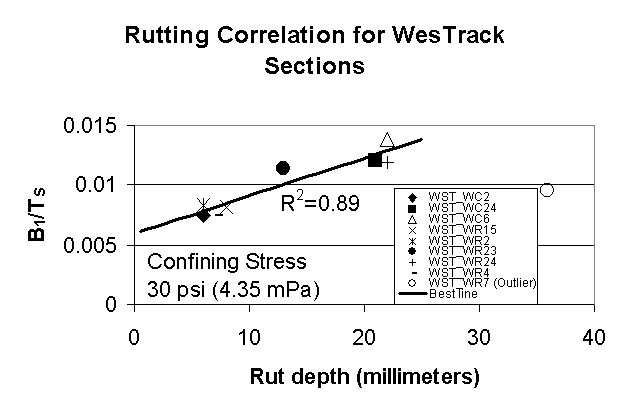
Figure 5: Variation of the term (B1/TS) obtained from the triaxial modulus (confining stress=30psi or 4.35mPa) testing of laboratory -prepared samples with rut depth measurements (in millimeters) from field performance