Seasonal Variations in The Moduli of Unbound
Pavement LayersChapter 7: Conclusions and Recommendations
This research represents the first application of the data
collected via the LTPP Seasonal Monitoring Program to the
development of improved methods for estimating seasonal variations
in backcalculated moduli for unbound pavement layers exclusive of
frost effects. The approach taken was to build upon the foundation
of the EICM by: (1) evaluating the moisture predictive capabilities
of that model; (2) developing predictive equations for
backcalculated pavement layer moduli; and (3) demonstrating how the
resulting relationships might be applied in practice.
This investigation provided the impetus for developing EICM
Version 2.6 by demonstrating the practical inadequacies of EICM
Versions 2.0 and 2.1 when applied to the prediction of in situ
moisture content, and then demonstrated that substantial
improvement in the moisture predictive capability of the EICM had
been achieved in Version 2.6. Second, the research identified
fundamental discrepancies between the stress states used in
laboratory resilient modulus testing and those computed using
linear layered-elastic theory.
Detailed implications of these findings and other conclusions of
lesser importance are presented below. The conclusions are followed
by recommendations to address needs identified or reaffirmed
through this study and to improve upon the results obtained.
CONCLUSIONS
The Enhanced Integrated Climatic Model
In the short term, the most important findings from this study
are those related to the moisture prediction accuracy of the EICM,
by virtue of their contribution to the development of the 2002
Guide for Design of New and Rehabilitated Pavement Structures
currently ongoing through NCHRP Project 1-37A. Key conclusions
related to the EICM moisture prediction capabilities are as
follows:
- Application of EICM Version 2.0 with data commonly available to
pavement engineers and assumed or model default values for key
input parameters (e.g., the Gardener coefficients) yielded
predicted moisture content profiles that were markedly different
from the monitored data for two LTPP Seasonal Monitoring Program
sites, one in Connecticut, the other in Minnesota. Volumetric
moisture content differences of 20 percentage points or more were
observed for some monitoring depths in the limited evaluation that
was conducted. The EICM model revisions embodied in Version 2.1
were the direct result of this finding.
- Application of EICM Version 2.1 with data commonly available to
pavement engineers may yield poor predictions of in situ moisture
contents. For the test sections and data sets considered in the
evaluation of EICM Version 2.1, the R2 values for the
relationship between monitored and predicted moisture contents for
base and subgrade layers were only 0.01 and 0.30, respectively.
Numerical differences between monitored and predicted volumetric
moisture contents again exceeded 20 percentage points in some
cases. The model revisions embodied in EICM Version 2.6 were the
direct result of this finding.
- Enhancements in EICM Version 2.6 have substantially improved
the practical applicability of the model. When applied with data
commonly available to pavement engineers, EICM Version 2.6 yielded
predicted volumetric moisture contents that were within the
estimated 95 percent confidence intervals for the monitored
moisture data in most instances. The R2 values for the
relationship between monitored and predicted subgrade moisture
contents for the base and subgrade layers for applications of EICM
Version 2.6 were 0.71 and 0.51, respectively, a substantial
improvement in predictive accuracy. Thus, application of EICM
Version 2.6 with input data commonly available to pavement
engineers can provide reasonable predictions of in situ moisture
contents for unbound pavement layers.
- Between-user differences in the application of the EICM may
yield significant differences in the model output. In the limited
evaluation of between-user differences, the observed mean
difference in predicted volumetric moisture content for individual
pavement layers (reported in Table 31) varied in the range of 0.1
to 11.1 percentage points, depending on the pavement section under
consideration and the nature and extent of the between-user
differences. The observed differences for 84 percent of the
pavement layers considered were statistically significant at the 5
percent level of significance. Thus improved user guidance and
other measures to ensure consistent and correct application of the
EICM are needed.
Models for Prediction of Backcalculated Pavement Layer
Moduli
- Predictive models that are rational when evaluated in the
context of laboratory resilient modulus test experience cannot be
derived using layer moduli backcalculated using linear layered
elastic theory and computed stress states. Factors that contribute
to the observed inconsistencies include:
- The use of stress states computed for a single "representative"
point for the entire layer when the location of a truly
representative point is difficult to define. A single
representative point is required in linear layered-elastic theory
because each layer is assumed to be homogeneous, when the reality
for a nonlinear unbound layer is that stresses, and thus stiffness,
vary both vertically and horizontally through the layer.
- The fact that the computed radial stresses may increase or
decrease as the applied FWD load increases, depending on the
location of the point for which the stresses are computed.
- The fact that the assumptions on which linear layered-elastic
theory is based may yield negative (tensile) radial load
stresses.
The net effect of these factors is that both the
sign and the relative importance of the bulk and octahedral stress
terms in the constitutive model
E/Pa=k1?/Pak2(t/Pa+1)k3
often contradict those observed in the laboratory.
- The preceding conclusion has several important implications for
considering stress dependency in pavement modeling. First,
application of laboratory-derived constitutive model coefficients
in combination with stress parameters computed using linear
layered-elastic theory may yield inaccurate stress-dependent
modulus values by virtue of the discrepancies between the
laboratory stress states and those computed using linear
layered-elastic theory. Second, meaningful advances in the state of
the art for backcalculation of pavement layer moduli cannot be
achieved without addressing the limitations inherent in the use of
linear layered-elastic theory to model structures composed of
materials that are stress-dependent. Models that allow more
realistic consideration of the stress-dependent nature of these
materials are needed.
- In many instances, variations in moisture content are not the
most important driver of seasonal variations in backcalculated
layer moduli for unbound, nonfrozen pavement layers. Evidence for
this may be found in:
- The fact that the backcalculated layer moduli for all base
layers, 82 percent of the subbase/upper subgrade (layer 3) layers,
and 80 percent of the subgrade/lower subgrade (layer 4) layers were
less strongly correlated with moisture than they were with one or
more of the stress parameters considered.
- For some pavement layers (base and subgrade for section 481077
(Texas), base for section 131005 (Georgia), and base and subgrade
for section 091803 (Connecticut) the observed correlation between
mean layer moisture and backcalculated modulus is close to zero,
indicating that there is little or no linear relationship between
modulus and moisture for the unbound pavement layers represented.
In contrast, relatively strong relationships between modulus and
moisture are observed for other layers, such as the subgrade at
section 131005 (Georgia), where the R2 values varied in
the range of 0.30 to 0.78, depending on layer (upper or lower
subgrade) and FWD load level.
- The high degree of variability in the ratio ?E/?Vw,
as summarized in Table 37 (Chapter 3), suggests that other factors
such as stress state and random errors in the backcalculated moduli
confound the modulus-moisture relationship.
-
Given the current state of the art, the combined effects of
stress and moisture on backcalculated pavement layer moduli may be
modeled for practical purposes using the constitutive model form
previously presented as Equation 31:
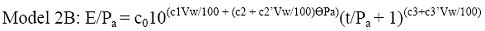 (43) (43)
This conclusion applies only to moduli backcalculated using
linear layered-elastic theory. Model coefficients derived using
backcalculated layer moduli are not applicable to laboratory
resilient modulus data. The applicability of the constitutive model
form to laboratory resilient modulus test data has not been
established. Soil class models based on Model 2B are presented in
Table 43 (Chapter 5).
Variations in Backcalculated Moduli for Unbound
Pavement Layers
Information about the extent of variation in backcalculated
moduli exclusive of frost effects was presented in Table 21 through
Table 26 of Chapter 3. Summary conclusions derived from this
information are as follows.
- The single point, within-day coefficient of variation for
backcalculated moduli for unbound pavement layers may approach 40
percent, with values in the range of 5 to 20 percent being typical.
Furthermore, the "conventional wisdom" that backcalculated moduli
for deeper layers are less variable than those for the upper layers
is supported by these findings. The pooled single-point within-day
coefficient of variation for the base layers was 19 percent, while
that for the subgrade layers was 11 percent.
- The amplitude of seasonal variations in backcalculated layer
moduli, exclusive of frost effects, ranges from less than 10
percent (typically for deeper subgrade layers) to more than 200
percent (typically for base layers). The amplitude of the
variations (whether expressed on a percentage basis or absolute
magnitude) is typically greatest for the base layers and least for
the deepest layers.
Application of Research Results To Predict Moduli
Backcalculated for Unbound Pavement Layers Using Linear
Layered-Elastic Theory
In light of the low overall rate of success in predicting
backcalculated layer moduli in the trial applications discussed in
Chapter 6, particularly when using either limited data set or soil
class models, the only well-founded conclusion that can be drawn is
that further research is needed to develop: (1) procedures for
backcalculation that rely on more accurate models of the pavement
structure and material response; (2) better, broadly applicable
predictive models; and (3) improved procedures for their
application. Specific recommendations in this regard are provided
in the next section.
RECOMMENDATIONS
This study has shed light on a number of issues warranting
further investigation. While many are in no sense new, the findings
presented earlier reinforce the need for further work. Specific
recommendations are as follows.
The Enhanced Integrated Climatic Model
- As noted in Chapter 4, the evaluation of the EICM conducted for
this study was imperfect because the available data set did not
include complete, section-specific values for all input parameters
required by the EICM. Another limitation of the evaluation was the
consideration of only one test section representing an arid
climate. Further evaluation of the EICM moisture predictive
capabilities is needed to: (1) more fully establish the sensitivity
of the model to the input parameters; (2) confirm or refute the
hypothesis that the poor results achieved for section 041024
(Arizona, see Figure 17) are attributable to incompatibility
between the theory on which the EICM is based and the true
mechanisms of soil moisture movement in arid climates. If possible,
this work should be pursued using data sets that include all
required input parameters for the test sections under
consideration
- Further enhancement to the EICM user interface is recommended
to improve ease of use and reduce the potential for error arising
from the need for manual manipulation of data to create input data
sets. Automated entry (and interpolation) of initial temperature
profiles would be particularly helpful.
- The development of improved user documentation (relative to
that available to the author when this work was initiated) is
recommended. It is imperative that very specific guidance for the
application of the model be provided to minimize the potential for
incorrect application of the model and between-user differences.
Issues that must be clearly addressed include the ramifications of
using or not using input data that are recommended but not
required, the selection of the initial conditions used in the
moisture prediction (such as the need to avoid simulation starting
dates that reflect frozen pavement conditions), and information on
the required precision of the input parameters–e.g., how accurate
does the depth to ground water need to be, and how does the answer
vary with climatic conditions?
The State of the Art of Backcalculation of Pavement
Layer Moduli
The stress-sensitive nature and lack of tensile strength in
unbound pavement materials has long been recognized. The findings
of this study reaffirm the importance of considering the stress
sensitivity of unbound materials when analyzing pavement
structures. It is therefore recommended that improved methods of
backcalculation be developed that provide for more correct
consideration of stress sensitivity of pavement layer
materials.
Consideration of Stress Dependency in Pavement
Modeling
Despite its inadequacies, it is likely that practicing pavement
engineers will continue to use linear layered elastic theory in
pavement analysis for some time to come. For this reason, the
applicability of laboratory-derived resilient modulus nonlinear
constitutive model coefficients to pavement analysis based on
linear layered-elastic theory should be studied further to fully
assess the magnitude and implications of the observed discrepancies
between the computed stress states and those used in current
laboratory test protocols (see Figure 39 through Figure 41 in
Chapter 5).
LTPP Data Used in This Investigation
- Supplementary data collection at all LTPP seasonal monitoring
test sections should be undertaken to provide an expanded data set
for verification of the TDR-based moisture data and to meet other
data needs. (This work is in progress via NCHRP 9-23.) The
collected data should be incorporated into the LTPP database.
- A comprehensive review of all LTPP backcalculation results
should be undertaken to: (1) identify those data sets for which the
backcalculation conducted to date needs to be revisited, such that
the data stored in and disseminated from the LTPP database are of
the highest possible quality; and (2) provide the basis to advance
the state of the art relative to the evaluation of backcalculation
results in general. Use of Model 3 (E/Pa =
k110k2?/Pa(t/Pa+1)k3))as
the basis for additional objective evaluation criteria should be
considered.
|
