U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-06-121 Date: November 2006 |
This appendix provides details on the prediction models for each of the performance measures evaluated in the study. In addition, the use of each model is illustrated through examples. Following is a list of the performance measures:
| IRI = Pavement roughness (m/km (ft/mi))—flexible and rigid. |
| RUT = Rut depth (mm (inch))—flexible. |
| FWPC = Fatigue and wheelpath cracking (deduct value)—flexible. |
| fwpc = Fatigue and wheelpath cracking (percentage of wheelpath area)—flexible. |
| TC = Transverse cracking (deduct value)—flexible. |
| TC = Transverse cracking (percentage of total section area)—rigid. |
| LC = Longitudinal cracking (percentage of total section area)—rigid. |
| FLT = Transverse joint faulting (mm (inch))—rigid. |
Following is a list of the explanatory variables input into the equations:
| ACTHICK = Thickness of AC layer (mm (inch)). |
| ADJ_AGE = Pavement age after distress initiation (years). |
| AGE = Pavement age (years). |
| BASE = Base type (DGAB, ATB, PATB, LCB, NONBIT, NONE). |
| CI = Cooling index (degree-Celsius days). |
| DEPTH = Thickness of PCC layer (mm (inch)). |
| FC = Functional classification of roadway. |
| FI = Freezing index (degree-Celsius days). |
| FTC = Annual number of freeze-thaw cycles (each). |
| LESN = Logarithm of annual ESAL divided by structural number. |
| LEDT = Logarithm of annual ESAL divided by PCC layer thickness. |
| MIRI = Initial IRI (m/km (ft/mi)). |
| MIRI_AGE = Pavement age when MIRI was recorded (years). |
| Pavement Structure = AC nonoverlay with unbound base, AC nonoverlay with bound base, AC overlay (either bound or unbound base), JPCC. |
| PRECIP = Annual precipitation (mm (inch)). |
| SG = Subgrade classification (FINE, COARSE, ROCK/STONE, OTHER). |
Equation 12 shows the IRI regression equation (R-squared = 0.78, total observations = 4,544) and equation 13 defines the delta equation.
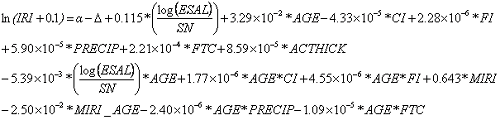 | (12) |
Where:
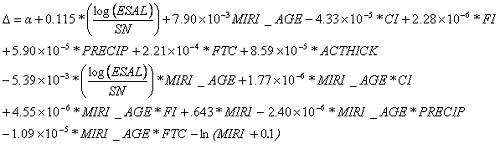 | (13) |
Table 37 shows the coefficients for a flexible IRI model.
| a Values for FINE SUBGRADE | |||
|---|---|---|---|
| BASE | Nonoverlay,Unbound Base | Nonoverlay,Bound Base | Overlay, Bound or Unbound Base |
| ATB | NA | -0.714 | -0.759 |
| DGAB | -0.713 | NA | -0.753 |
| LCB | NA | -0.658 | -0.702 |
| NONBIT | NA | -0.674 | -0.718 |
| NONE | -0.658 | NA | -0.698 |
| PATB | NA | -0.734 | -0.779 |
| a Values for COARSE SUBGRADE | |||
| ATB | NA | -0.77 | -0.815 |
| DGAB | -0.769 | NA | -0.810 |
| LCB | NA | -0.714 | -0.759 |
| NONBIT | NA | -0.730 | -0.774 |
| NONE | -0.714 | NA | -0.755 |
| PATB | NA | -0.790 | -0.835 |
| a Values for ROCK/STONE SUBGRADE | |||
| ATB | NA | -0.671 | -0.716 |
| DGAB | -0.670 | NA | -0.711 |
| LCB | NA | -0.615 | -0.660 |
| NONBIT | NA | -0.631 | -0.676 |
| NONE | -0.615 | NA | -0.656 |
| PATB | NA | -0.691 | -0.736 |
As discussed in the main body of the report, the flexible IRI prediction model incorporates a delta factor that shifts the model to correspond with the measured initial IRI value (MIRI). The first step in predicting IRI for flexible pavements is to calculate that delta factor. With this factor determined, the IRI can be estimated from the regression equation. A pseudopavement section was fabricated with the explanatory conditions in table 38 for use as an example.
| Input | Value |
|---|---|
| Pavement Structure | Nonoverlay, Unbound Base |
| BASE | DGAB |
| SG | FINE |
| ESAL | 126,000 |
| SN | 5.0 |
| ACTHICK | 6.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| Age | 2 |
Substituting the inputs from table 38 into the delta equation and extracting the alpha value from table 37 based on pavement structure, base type, and subgrade type appears in equation 14.
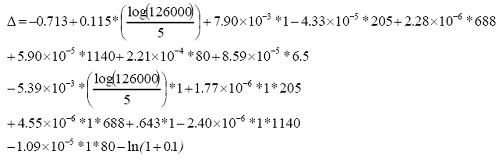 | (14) |
Therefore, the result is equation 15.
| (15) |
Using this delta and the regression equation, the result is equation 16.
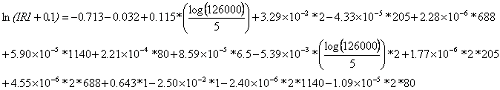 | (16) |
Therefore, the results appear in equations 17 and 18.
| (17) |
| (18) |
Equation 19 shows the IRI regression equation (R-squared=0.78, total observations=2,652) for rigid pavements.
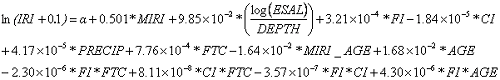 | (19) |
Table 39 lists the coefficients for a rigid IRI model.
| a Values for FINE SUBGRADE | |||||
|---|---|---|---|---|---|
| ATB Base | DGAB Base | LCB Base | NONBIT Base | PATB Base | |
| FC 1 | -0.478 | -0.499 | -0.497 | -0.413 | -0.539 |
| FC 2 | -0.488 | -0.510 | -0.507 | -0.423 | -0.550 |
| FC 6 | -0.529 | -0.551 | -0.548 | -0.464 | -0.591 |
| FC 7 | -0.492 | -0.514 | -0.511 | -0.427 | -0.554 |
| FC 9 | -0.402 | -0.424 | -0.421 | -0.337 | -0.464 |
| FC 11 | -0.455 | -0.476 | -0.473 | -0.389 | -0.516 |
| FC 12 | -0.469 | -0.491 | -0.488 | -0.404 | -0.531 |
| FC 14 | -0.526 | -0.547 | -0.544 | -0.460 | -0.587 |
| FC 17 | -0.408 | -0.430 | -0.427 | -0.343 | -0.470 |
| a Values for COARSE SUBGRADE | |||||
| FC 1 | -0.475 | -0.497 | -0.494 | -0.410 | -0.537 |
| FC 2 | -0.486 | -0.507 | -0.505 | -0.420 | -0.547 |
| FC 6 | -0.527 | -0.548 | -0.545 | -0.461 | -0.588 |
| FC 7 | -0.489 | -0.511 | -0.508 | -0.424 | -0.551 |
| FC 9 | -0.400 | -0.421 | -0.419 | -0.334 | -0.461 |
| FC 11 | -0.452 | -0.473 | -0.471 | -0.387 | -0.513 |
| FC 12 | -0.467 | -0.488 | -0.485 | -0.401 | -0.528 |
| FC 14 | -0.523 | -0.544 | -0.542 | -0.458 | -0.584 |
| FC 17 | -0.406 | -0.427 | -0.424 | -0.340 | -0.467 |
| a Values for ROCK/STONE SUBGRADE | |||||
| FC 1 | -0.540 | -0.562 | -0.559 | -0.475 | -0.602 |
| FC 2 | -0.551 | -0.573 | -0.570 | -0.486 | -0.612 |
| FC 6 | -0.592 | -0.614 | -0.611 | -0.527 | -0.653 |
| FC 7 | -0.555 | -0.576 | -0.574 | -0.490 | -0.616 |
| FC 9 | -0.465 | -0.487 | -0.484 | -0.400 | -0.526 |
| FC 11 | -0.517 | -0.539 | -0.536 | -0.452 | -0.579 |
| FC 12 | -0.532 | -0.553 | -0.551 | -0.467 | -0.593 |
| FC 14 | -0.588 | -0.610 | -0.607 | -0.523 | -0.650 |
| FC 17 | -0.471 | -0.493 | -0.490 | -0.406 | -0.532 |
| a Values for OTHER SUBGRADE | |||||
| FC 1 | -0.482 | -0.504 | -0.501 | -0.417 | -0.544 |
| FC 2 | -0.493 | -0.514 | -0.512 | -0.428 | -0.554 |
| FC 6 | -0.534 | -0.555 | -0.553 | -0.468 | -0.595 |
| FC 7 | -0.497 | -0.518 | -0.515 | -0.431 | -0.558 |
| FC 9 | -0.407 | -0.428 | -0.426 | -0.341 | -0.468 |
| FC 11 | -0.459 | -0.481 | -0.478 | -0.394 | -0.520 |
| FC 12 | -0.474 | -0.495 | -0.492 | -0.408 | -0.535 |
| FC 14 | -0.530 | -0.551 | -0.549 | -0.465 | -0.591 |
| FC 17 | -0.413 | -0.434 | -0.431 | -0.347 | -0.474 |
The rigid IRI model does not incorporate a delta factor; therefore, the regression equation can be used directly. The pavement structure shown in table 40 illustrates the use of the regression model.
| Input | Value |
|---|---|
| Pavement Structure | JPCC |
| BASE | DGAB |
| SG | FINE |
| ESAL | 410,000 |
| FC | 2 |
| D | 9.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 2 |
Substituting the inputs from table 40 into the regression equation and extracting the alpha value from the table 39 based on pavement structure, base type, and subgrade type leads to equation 20.
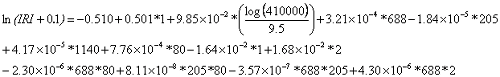 | (20) |
Equations 21 and 22 show the results.
| (21) |
| (22) |
Equation 23 shows the logistic FWPC prediction model for flexible pavements (total observations = 1977).
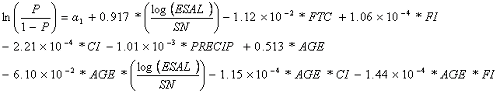 | (23) |
Table 41 lists the coefficients for the flexible FWPA logistic model.
| a1 Values | |
|---|---|
| Nonoverlay, Unbound Base | -1.06 |
| Nonoverlay, Bound Base | -0.635 |
| Overlay, Bound or Unbound Base | 0.101 |
Where crack initiation age is determined as the AGE at which P, cutoff probability, equals 0.7 (percent correct = 72.6). If the crack initiation age is determined to be less than zero from the logistic model, a value of zero is used.
Equation 24 shows the regression equation (R-squared = 0.63, total observations = 1,486).
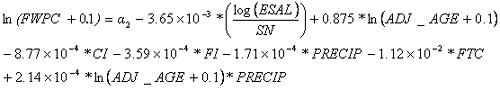 | (24) |
Table 42 lists the coefficients for the flexible FWPC regression model.
| a2 Values for FINE SUBGRADE | |||
|---|---|---|---|
| BASE | Nonoverlay, | Nonoverlay, | Overlay, Bound |
| ATB | NA | 3.13 | 2.88 |
| DGAB | 3.25 | NA | 2.94 |
| LCB | NA | 2.79 | 2.54 |
| NONBIT | NA | 2.76 | 2.51 |
| NONE | 2.91 | NA | 2.60 |
| PATB | NA | 3.06 | 2.81 |
| a2Values for COARSE SUBGRADE | |||
| ATB | NA | 2.88 | 2.63 |
| DGAB | 3.00 | NA | 2.68 |
| LCB | NA | 2.54 | 2.29 |
| NONBIT | NA | 2.51 | 2.25 |
| NONE | 2.65 | NA | 2.34 |
| PATB | NA | 2.81 | 2.56 |
| a2 Values for ROCK/STONE SUBGRADE | |||
| ATB | NA | 3.17 | 2.91 |
| DGAB | 3.28 | NA | 2.97 |
| LCB | NA | 2.82 | 2.57 |
| NONBIT | NA | 2.79 | 2.54 |
| NONE | 2.94 | NA | 2.63 |
| PATB | NA | 3.09 | 2.84 |
Where ADJ_AGE equals pavement age minus crack initiation age. If the pavement age is less than or equal to the crack initiation age, the predicted FWPC equals zero.
Equation 25 gives the logistic model (total observations = 1977).
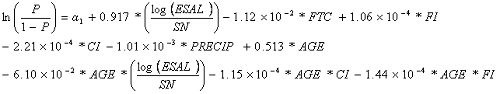 | (25) |
Table 43 lists the coefficients for the flexible FWPC logistic model.
| a1 Values | |
|---|---|
| Nonoverlay, Unbound Base | -1.06 |
| Nonoverlay, Bound Base | -0.635 |
| Overlay, Bound or Unbound Base | 0.101 |
Where the crack initiation age is determined as the AGE at which P, cutoff probability, equals 0.7 (percent correct = 72.6). If the crack initiation age is determined to be less than zero from the logistic model, a value of zero is used.
Equation 26 shows the regression equation (R-squared = 0.63, total observations = 1486).
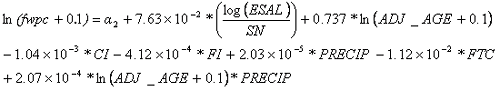 | (26) |
Table 44 lists the coefficients for the flexible FWPC regression model.
| a2 Values for FINE SUBGRADE | |||
|---|---|---|---|
| BASE | Nonoverlay, Unbound Base | Nonoverlay, Bound Base | Overlay, Bound, or Unbound Base |
| ATB | NA | 2.43 | 1.97 |
| DGAB | 2.51 | NA | 2.14 |
| LCB | NA | 2.80 | 2.33 |
| NONBIT | NA | 1.97 | 1.51 |
| NONE | 2.15 | NA | 1.78 |
| PATB | NA | 2.45 | 1.98 |
| a2Values for COARSE SUBGRADE | |||
| ATB | NA | 2.06 | 1.59 |
| DGAB | 2.14 | NA | 1.77 |
| LCB | NA | 2.43 | 1.96 |
| NONBIT | NA | 1.60 | 1.13 |
| NONE | 1.77 | NA | 1.40 |
| PATB | NA | 2.08 | 1.61 |
| a2Values for ROCK/STONE SUBGRADE | |||
| ATB | NA | 2.11 | 1.64 |
| DGAB | 2.19 | NA | 1.81 |
| LCB | NA | 2.47 | 2.01 |
| NONBIT | NA | 1.65 | 1.18 |
| NONE | 1.82 | NA | 1.45 |
| PATB | NA | 2.12 | 1.66 |
Where ADJ_AGE = pavement Age—crack initiation age. If the pavement age is less than or equal to the crack initiation age, the predicted FWPC equals zero.
The prediction model for FWPC involves a two-step process. In the first step, the logistic equation in equation 25 is used to estimate the age of crack initiation. This is done solving for the AGE variable so that P is equivalent to the cutoff value (0.7 for this model). This AGE is denoted as the crack initiation age. In some cases, the resulting crack initiation age may be less than zero. A value of zero is used in place of the estimated negative crack initiation age.
If the FWPC estimate is for a pavement age less than or equal to the crack initiation age, the predicted FWPC value is equal to zero. If the FWPC estimate is for a pavement age greater than the crack initiation age, the ADJ_AGE is calculated as the pavement age of interest less the crack initiation age. Table 45 lists information for an example pavement section.
| Input | Value |
|---|---|
| Pavement Structure | Nonoverlay, Unbound Base |
| BASE | DGAB |
| SG | FINE |
| ESAL | 126,000 |
| SN | 5.0 |
| ACTHICK | 6.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 12 |
Equation 27 substitutes information from table 45 as well as a P value of 0.7 into the logistic equation and extracting the a1 value from the appropriate table.
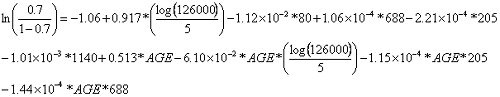 | (27) |
Equation 28 is solving for AGE through an iterative process.
| (28) |
FWPC prediction of interest occurs at a pavement age of 12. Therefore, ADJ_AGE = 12-9.13 = 2.87. Equation 29 substitutes this age and the information from table 45 into the regression equation.
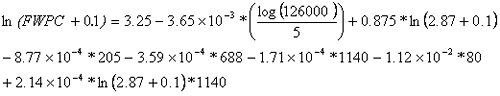 | (29) |
Therefore, the results are shown in equations 30 and 31.
| (30) |
| (31) |
Equation 32 shows the logistic model (observations = 1,920).
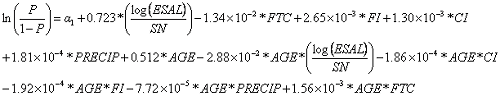 | (32) |
Table 46 lists the coefficients for the flexible TC logistic model.
| a1 Values | |
|---|---|
| Nonoverlay, Unbound Base | -3.75 |
| Nonoverlay, Bound Base | -3.29 |
| Overlay, Bound or Unbound Base | -1.97 |
Where the crack initiation age is determined as the AGE at which P, cutoff probability, equals 0.7 (percent correct = 78.4). If the crack initiation age is determined to be less than zero from the logistic model, a value of zero is used.
Equation 33 is the regression equation (R-squared = 0.71, total observations = 1,077).
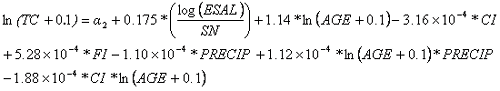 | (33) |
Table 47 lists the coefficients for the flexible TC regression model.
| a2 Values for FINE SUBGRADE | |||
|---|---|---|---|
| BASE | Nonoverlay, Unbound Base | Nonoverlay, Bound Base | Overlay, Bound or Unbound Base |
| ATB | NA | 1.48 | 1.10 |
| DGAB | 1.03 | NA | 0.996 |
| LCB | NA | 1.58 | 1.20 |
| NONBIT | NA | 1.55 | 1.17 |
| NONE | 1.41 | NA | 1.37 |
| PATB | NA | 1.82 | 1.44 |
| a2 Values for COARSE SUBGRADE | |||
| ATB | NA | 1.17 | 0.792 |
| DGAB | 0.72 | NA | 0.687 |
| LCB | NA | 1.27 | 0.891 |
| NONBIT | NA | 1.24 | 0.859 |
| NONE | 1.10 | NA | 1.06 |
| PATB | NA | 1.51 | 1.13 |
| a2 Values for ROCK/STONE SUBGRADE | |||
| ATB | NA | 0.976 | 0.599 |
| DGAB | 0.527 | NA | 0.494 |
| LCB | NA | 1.08 | 0.698 |
| NONBIT | NA | 1.04 | 0.666 |
| NONE | 0.905 | NA | 0.871 |
| PATB | NA | 1.32 | 0.939 |
Where ADJ_AGE equals pavement age less the crack initiation age. If the pavement age is less than or equal to the crack initiation age, the predicted TC equals zero.
The prediction model for TC involves a two-step process. In the first step, the logistic model in equation 32 is used to estimate the age of crack initiation. This is done by solving for the AGE variable so that P is equivalent to the cutoff value (0.7 for this model). This AGE is denoted as the crack initiation age. In some cases, the resulting crack initiation age may be less than zero. A value of zero is used in place of the estimated negative crack initiation age.
If the TC estimate is for a pavement age less than or equal to the crack initiation age, the predicted TC value is equal to zero. If the TC estimate is for a pavement age greater than the crack initiation age, the ADJ_AGE is calculated as the pavement age of interest less the crack initiation age. Table 48 lists information for an example pavement section.
| Input | Value |
|---|---|
| Pavement Structure | Nonoverlay, Unbound Base |
| BASE | DGAB |
| SG | FINE |
| ESAL | 126,000 |
| SN | 5.0 |
| ACTHICK | 6.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 12 |
Equation 34 substitutes information from table 48 as well as a P value of 0.7 into the logistic equation and extracts the alpha 1 value from the appropriate table.
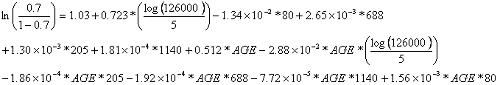 | (34) |
Solving for AGE through an iterative process results in equation 35.
| (35) |
TC prediction of interest occurs at a pavement age of 12. Therefore, ADJ_AGE = 12-7.54 = 4.46. Equation 36 substitutes this age and the information in table 48 into the regression equation.
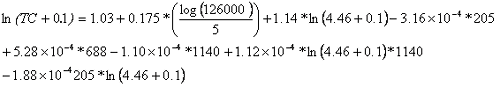 | (36) |
Therefore, the results are shown in equations 37 and 38.
| (37) |
| (38) |
Equation 39 shows the logistic model (total observations = 400).
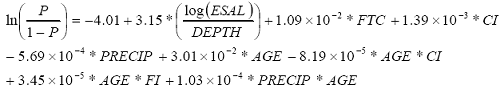 | (39) |
Where the crack initiation age is determined as the AGE at which P, cutoff probability, equals 0.55 (percent correct = 63.5). If the crack initiation age is determined to be less than zero from the logistic model, a value of zero is used.
Equation 40 is the regression equation (R-squared = 0.38, total observations = 240).
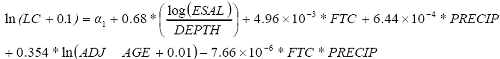 | (40) |
| BASE | a1 |
|---|---|
| ATB | -1.36 |
| DGAB | -1.89 |
| LCB | -1.03 |
| NONBIT | -0.84 |
| PATB | -2.14 |
Where ADJ_AGE equals pavement age less the crack initiation age. If the pavement age is less than or equal to the crack initiation age, the predicted LC equals zero. If the predicted LC is less than zero for pavement age is greater than crack initiation age, the predicted LC was set to zero.
The prediction model for LC involves a two-step process. In the first step, logistic equation 39 is used to estimate the age of crack initiation. This is done solving for the AGE variable so that P is equivalent to the cutoff value (0.55 for this model). This AGE is denoted as the crack initiation age. In some cases, the resulting crack initiation age may be less than zero. A value of zero is used in place of the estimated negative crack initiation age.
If the LC estimate is for a pavement age less than or equal to the crack initiation age, the predicted TC value is equal to zero. If the LC estimate is for a pavement age greater than the crack initiation age, the ADJ_AGE is calculated as the pavement age of interest less the crack initiation age.
Table 50 gives the information for an example pavement section.
| Input | Value |
|---|---|
| Pavement Structure | JPCC |
| BASE | DGAB |
| SG | FINE |
| ESAL | 410,000 |
| FC | 2 |
| D | 9.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 14 |
Equation 41 substitutes information from the table 50 as well as a P value of 0.55 into the logistic equation and extracts the alpha 1 value from the appropriate table.
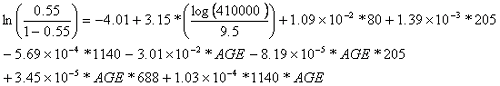 | (41) |
Equation 42 is solving for AGE through an iterative process.
| (42) |
LC prediction of interest occurs at a pavement age of 14. Therefore, ADJ_AGE = 14-11.86 = 2.14. Substituting this age and the information in table 50 into the regression equation results in equation 43.
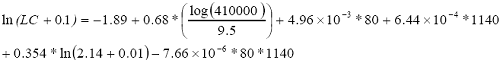 | (43) |
Therefore, the results are shown in equations 44 and 45.
| (44) |
| (45) |
Equation 46 shows the logistic model (total observations = 414).
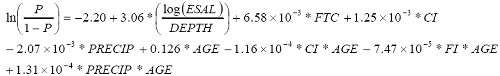 | (46) |
Where The crack initiation age is determined as the AGE at which P, cutoff probability, equals 0.6 (percent correct = 63.5). If the crack initiation age is determined to be less than zero from the logistic model, a value of zero is used.
Equation 47 shows the regression equation (R-squared = 0.54, total observations = 228).
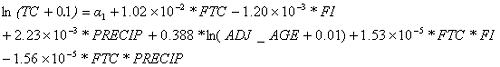 | (47) |
Table 51 lists the coefficients for the rigid TC regression model.
| BASE | a2 |
|---|---|
| ATB | -3.05 |
| DGAB | -2.28 |
| LCB | -1.76 |
| NONBIT | -2.65 |
| PATB | -2.55 |
Where ADJ_AGE equals pavement age less the crack initiation age. If the pavement age is less than or equal to the crack initiation age, the predicted TC equals zero
The prediction model for TC involves a two-step process. In the first step, the logistic model in equation 46 is used to estimate the age of crack initiation. This is done by solving for the AGE variable so that P is equivalent to the cutoff value (0.6 for this model). This AGE is denoted as the crack initiation age. In some cases, the resulting crack initiation age may be less than zero. A value of zero is used in place of the estimated negative crack initiation age.
If the TC estimate is for a pavement age less than or equal to the crack initiation age, the predicted TC value is equal to zero. If the TC estimate is for a pavement age greater than the crack initiation age, the ADJ_AGE is calculated as the pavement age of interest less the crack initiation age.
Table 52 lists information for an example pavement section.
| Input | Value |
|---|---|
| Pavement Structure | JPCC |
| BASE | DGAB |
| SG | FINE |
| ESAL | 410,000 |
| FC | 2 |
| D | 9.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 18 |
Equation 48 substitutes information from table 52 as well as a P value of 0.6 into the logistic equation and extracts the alpha 1 value from the appropriate table.
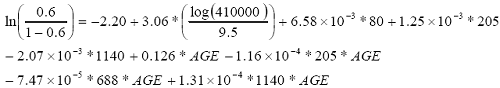 | (48) |
Equation 49 is solving for AGE through an iterative process.
| (49) |
The TC prediction of interest occurs at a pavement age of 18. Therefore, ADJ_AGE = 18-11.86 = 6.14. Equation 50 substitutes this age and the information in table 52 into the regression equation shown in equation 50.
| (50) |
Therefore, the results are as shown in equations 51 and 52.
| (51) |
| (52) |
Equation 53 shows the regression equation (R-squared = 0.45, total observations = 1,966).
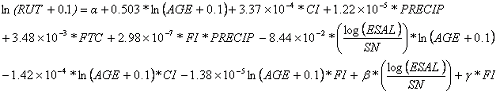 | (53) |
Table 53 lists the coefficients for the flexible RUT model.
| a Values for FINE SUBGRADE | |||
|---|---|---|---|
| BASE | Nonoverlay, Unbound Base | Nonoverlay, Bound Base | Overlay, Bound or Unbound Base |
| ATB | NA | 0.136 | 0.124 |
| DGAB | 0.367 | NA | 0.31 |
| LCB | NA | 0.624 | 0.612 |
| NONBIT | NA | 0.436 | 0.425 |
| NONE | -0.539 | NA | -0.597 |
| PATB | NA | -0.309 | -0.321 |
| a Values for COARSE SUBGRADE | |||
| ATB | NA | 0.0958 | 0.084 |
| DGAB | 0.327 | NA | 0.269 |
| LCB | NA | 0.583 | 0.572 |
| NONBIT | NA | 0.396 | 0.384 |
| NONE | -0.580 | NA | -0.637 |
| PATB | NA | -0.350 | -0.361 |
| a Values for ROCK/STONE SUBGRADE | |||
| ATB | NA | -0.0199 | -0.0317 |
| DGAB | 0.211 | NA | 0.154 |
| LCB | NA | 0.468 | 0.456 |
| NONBIT | NA | 0.280 | 0.269 |
| NONE | -0.695 | NA | -0.753 |
| PATB | NA | -0.465 | -0.477 |
| ß and ? values | |||
| BASE | ß | ? | |
| ATB | 0.331 | -.000228 | |
| DGAB | 0.225 | -.000266 | |
| LCB | 0.0236 | -.00507 | |
| NONBIT | 0.108 | .00120 | |
| NONE | 1.13 | .000283 | |
| PATB | 0.769 | .000150 | |
The prediction model for rut depth on flexible pavement uses one regression equation.
Table 54 lists information for the example pavement structure to illustrate the model.
| Input | Value |
|---|---|
| Pavement Structure | Nonoverlay, Unbound Base |
| BASE | DGAB |
| SG | FINE |
| ESAL | 126,000 |
| SN | 5.0 |
| ACTHICK | 6.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1,140 |
| MIRI_AGE | 1 |
| MIRI | 1 |
| AGE | 2 |
Equation 54 substitutes the information from table 54 into the delta equation and extracts the alpha value from table 53 based on pavement structure, base type, and subgrade type.
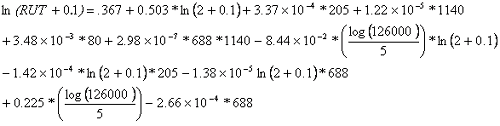 | (54) |
Therefore, the results are shown in equations 55 and 56.
| (55) |
| (56) |
Equation 57 shows the regression equation (R-squared = 0.47, total observations = 1,384).
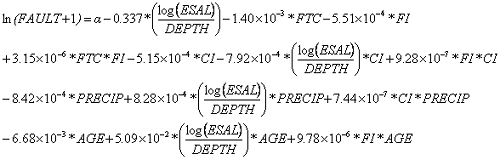 | (57) |
Table 55 lists the coefficients for the rigid FLT model.
| a Values | ||||
|---|---|---|---|---|
| BASE | Fine Subgrade | Coarse Subgrade | Other Subgrade | Rock/Stone Subgrade |
| ATB | 0.755 | 0.810 | 1.20 | 0.515 |
| DGAB | 0.732 | 0.786 | 1.18 | 0.492 |
| LCB | 0.665 | 0.720 | 1.11 | 0.425 |
| NONBIT | 0.834 | 0.889 | 1.28 | 0.595 |
| PATB | 0.693 | 0.748 | 1.14 | 0.453 |
The prediction model for faulting on rigid pavement uses one regression equation. Table 56 lists information for an example pavement structure to illustrate the use of the model.
| Input | Value |
|---|---|
| Pavement Structure | JPCC |
| BASE | DGAB |
| SG | FINE |
| ESAL | 410,000 |
| FC | 2 |
| D | 9.5 |
| FTC | 80 |
| FI | 688 |
| CI | 205 |
| PRECIP | 1140 |
| AGE | 15 |
Equation 58 substitutes the information from table 56 into the delta equation and extracts the alpha value from table 55 based on base type and subgrade type.
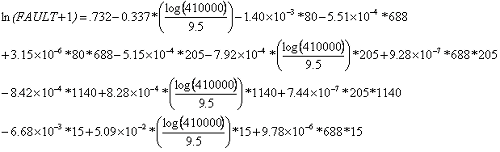 | (58) |
Therefore, equations 59 and 60 show the results.
| (59) |
| (60) |