U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-08-035 Date: March 2008 |
Relative to the least squares error associated with linear regression, assuming that y1 = ax1 + b, then the error (ri) and the variance (ri2) at a point can be expressed as:
![]() (99)
(99)
![]() (100)
(100)
![]() (101)
(101)
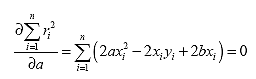 (102)
(102)
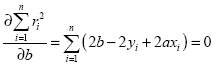 (103)
(103)
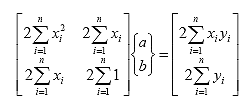 (104)
(104)
![]() (105)
(105)
The total variance over all points n is:
Setting the derivatives of the variance with respect to the coefficients a and b to zero gives:
and yields two equations in the two unknown coefficients a and b:
Which expresses the definition of linear regression. In matrix form, where there are a number (i) independent variables xi associated with observations yj (dependent variable) that form a matrix of independent variables, xi,j can be expressed as:
Where:
| = vector of j observations | |
| X | = matrix of xi,j |
| = vector of unknown coefficients | |
| = vector of regression errors |
Solving for ![]() :
:
![]() (106)
(106)
![]() (107)
(107)
![]() (108)
(108)
![]() (109)
(109)
![]() (110)
(110)
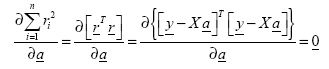 (111)
(111)
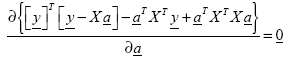 (112)
(112)
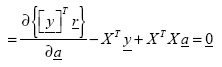 (113)
(113)
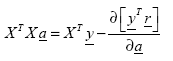 (114)
(114)
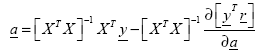 (115)
(115)
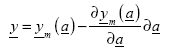 (116)
(116)
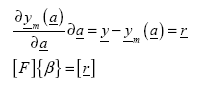 (117)
(117)
Where the second part of the above expression represents the residual regression error. Formulating this on the basis of partial derivatives:
Differentiating with respect to the vector of unknown coefficients ![]() and setting to zero:
and setting to zero:
Rearranging and solving for ![]() :
:
Where again the second part of the above expression represents the residual regression error. Drawing the analogy to the system identification method (SID):
Where ![]() (
(![]() ) is the matrix of model predictions. Rearranging:
) is the matrix of model predictions. Rearranging:
Where:
| [F] | = 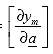 which is a rectangular sensitivity matrix (k x n); k = number of coefficients a which is a rectangular sensitivity matrix (k x n); k = number of coefficients a |
| {ß} | = |
| = the matrix of change in the model prediction or the residual error (k x 1) |
Therefore:
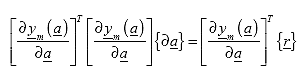 (118)
(118)
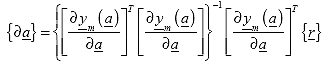 (119)
(119)
This yields a solution for the changes in the model coefficients based on the residual error in the model prediction.
| < Previous | Contents | Next >> |