U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-08-035 Date: March 2008 |
Environmental factors such as moisture content, temperature gradient, and depth of frost penetration have a significant effect on pavement performance. Understanding the effect of these factors on performance is crucial to the optimal design of pavement structures and involves consideration of not only seasonal variations but also changes throughout the day.
To provide a means for studying the contribution of environmental factors on pavement structures, SMP was initiated within LTPP. This program was designed to provide (1) the means to link pavement response data obtained at random points in time relative to critical design conditions, (2) the means to validate models for relationships between environmental conditions and in situ structural properties of pavement materials, and (3) expanded knowledge of the magnitude and impact of the changes involved. To accomplish this, SMP sites were instrumented with the equipment in table 1.
| Instruments | Measurement |
|---|---|
| TDR (time domain reflectometry) | Moisture content of subsurface |
| Thermistor sensors | Pavement temperature gradients and air temperature |
| Electrical resistivity probes | Depth of frost/thaw |
| Piezometer | Depth of ground water table |
| Tipping-bucket rain gauge | Precipitation |
The design of SMP was a two-tiered approach including the core experiment and supplemental studies. The core experiment included 64 LTPP test sections selected by the categories listed in table 2. An additional six test sections were included as supplemental studies to the original SMP experimental design. To capture seasonal and diurnal changes, pavement response data were collected more frequently than routine LTPP monitoring. The supplemental studies were carried out in response to highway agencies' desire to collect data on LTPP test sections not included in the core sites.
| Pavement type | - Flexible-thin asphalt concrete (AC) surface (<127 mm (5 inches)) - Flexible-thick AC surface (>127 mm (5 inches)) - Rigid-jointed plain concrete - Rigid-jointed reinforced concrete |
| Subgrade soil | - Fine grained - Coarse grained |
| Environment | - Wet-freeze - Wet-no freeze - Dry-freeze - Dry-no freeze |
The collection of TDR waveforms from subsurface materials is of particular interest in this study. Although the importance of in situ moisture content of subsurface layers in pavement structures has been well recognized, moisture measurement has sometimes been difficult because of the limitations of existing measurement and computational methods.
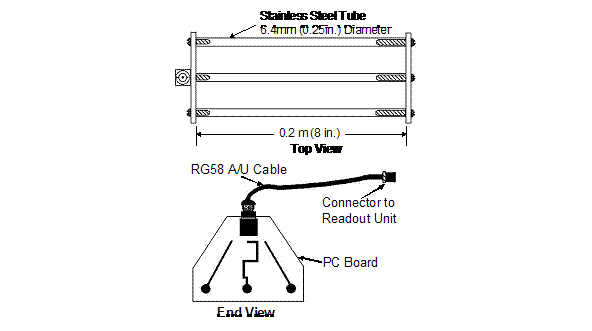
Figure 1. Diagram. TDR probe for SMP. (3)
The TDR method was selected for use in the SMP core experiment. TDR equipment was originally developed for measuring electromagnetic wave travel times to detect breaks or shorts in electrical conductors and subsequently was adapted to collect sufficient data to allow for soil moisture to be estimated. The TDR system records an electromagnetic waveform that can be analyzed as it is transmitted and reflected to characterize the nature of objects that reflect the waves. The waveform pulse is transmitted along a coaxial metallic cable shielded by a waveguide at a velocity that is influenced by the dielectric constant (e) of material surrounding the conductors. This dielectric constant is a dimensionless ratio of a material's dielectric permittivity to the permittivity of free space. Changes in the dielectric constant of the surrounding material occur as its moisture content or conductivity (the reciprocal of resistance) changes. Signal reflectivity also varies (from 1 to -1) as a function of the degree of open to short circuitry, respectively, and exists in the wave reflections as evidenced by slope changes in the return wave pulse recorded by the TDR readout unit. A full short circuit eliminates any additional return signals, while varying degrees of an open circuit results in a variety of return signals.(3)
The Federal Highway Administration (FHWA) TDR moisture probe is shown in figure 1. The coaxial lead cable (signal lead) is connected to the center of the three stainless steel rods, which are inserted horizontally into the soil at the point of monitoring. The cable's outer shield is connected to the outer rods, which serve as the waveguide. The recorded TDR signal rises to a peak (initial inflection point), as the electromagnetic wave enters the probe rods, followed by a fall in the return signal to a second inflection point as the wave hits the end of the probes as illustrated in figure 2. The distance between the first inflection point (point Dl) and final inflection point (point D2) is known as the "apparent" length of the probe, La. (3)
Ten TDR probes were used to measure in situ moisture content of pavement sublayers at SMP test sections that were placed in one hole located in the outer wheel path. ([4]) At most sites, the TDR installation hole was located at approximately 0.76 m (2.5 ft) from the outside edge of the white stripe and at least 1.2 m (4 ft) away from joints and/or cracks to avoid unrepresentative surface moisture infiltration. Figure 3 provides a schematic of the instrumentation.
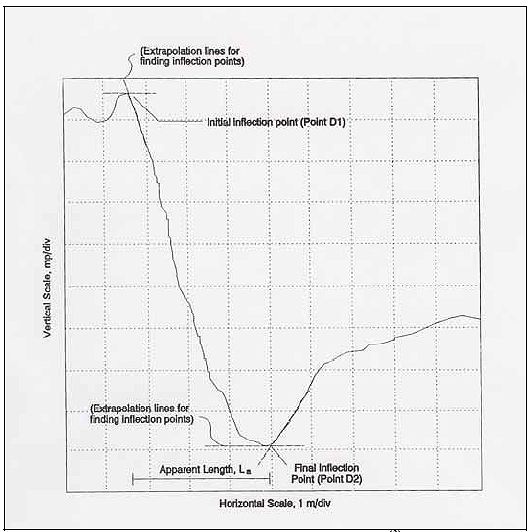
Figure 2. Graph. Typical TDR signal.(3)
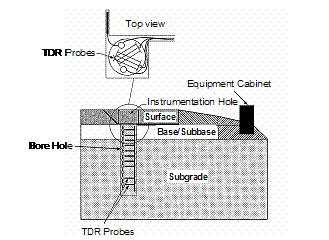
Figure 3. Diagram. Illustration of instrumentation installation.
The TDR probes were placed at specified depths as the type of sublayer and its thickness varied. If the top granular base (or subbase) layer was greater than 305 mm (12 in), the first TDR probe was placed 152 mm (6 in) below the surface layer and/or bottom of the lowest stabilized layer; otherwise, the probe was placed at mid depth of the top granular base (or subbase) layer. The next seven TDR probes were placed at 152 mm (6 in) intervals and the last two probes were placed at 305 mm (12 in) intervals. (3)
The waveform obtained from the TDR sensor must be analyzed to determine in situ soil parameters. Existing procedures for the interpretation of TDR data have included determining the apparent length (La ) so as to compute the dielectric constant and the VMC for the material surrounding the TDR probe.
The initial inflection point (D1) is located where the signal enters the probe rods while the final inflection point (D2) occurs at the end of the probes. Both are displayed in the TDR readout device. The distance between Point D1 and D2 is the La value used to determine the dielectric constant of surrounding material. The La value can be determined using a variety of methods. Klemunes studied ways to find the most accurate methodology to determine the La value of the TDR signal response.([5]) The study investigated and compared five methods: (1) Method of Tangents, (2) Method of Peaks, (3) Method of Diverging Lines, (4) Alternate Method of Tangents, and (5) the Campbell Scientific Method.
Differences among the methods are centered on the procedure of locating the initial and final inflection points of the TDR trace. From the study, the method of tangents was found to be the most accurate while the least accurate methods are the alternate method of tangents and the method of diverging lines.
The method of tangents employs the tangent lines at the local values of the TDR traces to isolate the inflection points. D1 is located at the intersection of the horizontal and negatively sloped tangents (i.e., local maximum) of the TDR trace, and D2 is located at the intersection of the horizontal and positively sloped tangents (i.e., local minimum) as shown in figure 4(a). However, the method cannot be applied to very dry or partially frozen soils, so the method of peaks is used for those soil type situations.([6]) In the Method of Peaks, D1 is determined by locating the intersection of the tangents drawn on both sides of the initial inflection point, and D2 is at the intersection of the tangents drawn of both sides of the final inflection point, as shown in figure 4(b).
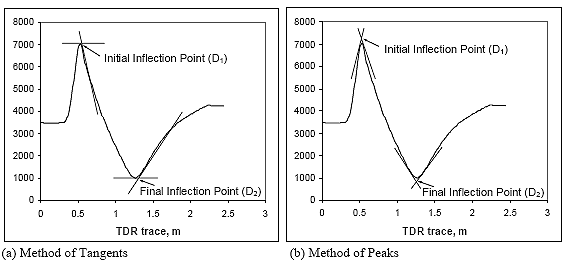
Figure 4. Graph. Illustration of trace interpretation methods. (5, 6)
An electromagnetic signal is transmitted along the TDR probe. When the signal reaches the end of the probe, it is reflected back to the data acquisition unit and the reflected signal is recorded. The velocity of this reflected electromagnetic wave in the probe depends on the dielectric constant and magnetic permeability of the surrounding material (relative to the speed of light in a vacuum) and is given in equation 1 as: ([7])
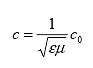 (1)
(1)
Where:
| c | = velocity of electromagnetic wave, |
| e | = dielectric constant, (approximately 1.0 for air, 80 for water, and 3-5 for dry soil) |
| m | = relative magnetic permeability of the soil |
| C0 | = speed of light in vacuum |
Assuming the effects of ferromagnetic components in soils are not significant, the magnetic permeability of soil can be set to unity (m = 1). (8) By substituting the velocity of electromagnetic wave with the travel time and the length of probe (c = 2L/Dt), the dielectric constant is:
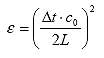 (2)
(2)
Where:
| Dt | = the travel time of the TDR signal |
| L | = actual length of TDR probe |
The travel time of the signal is also dependent on the dielectric constant, which includes signal propagation in the soil-moisture mixture; hence, the apparent probe length can be determined by the travel time of the signal if it were propagating at the speed of light:
![]() (3)
(3)
Therefore, the dielectric constant of soil can be expressed as the ratio of apparent length to actual length of TDR probe from equations 2 and 3:
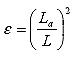 (4)
(4)
Where:
| La | = apparent length of probe, m |
The dielectric constant can be determined with the phase velocity considering the propagation as follows: (5)
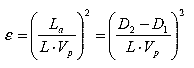 (5)
(5)
Where:
| L | = actual length of TDR probe, 0.203 m (8 inches) for FHWA probes |
| Vp | = phase velocity setting on TDR cable tester (usually 0.99); this is the ratio of the actual propagation velocity to the speed of light. |
In short, the dielectric constant is derived from the relationship between the speed of light and the wave velocity (delayed due to wave propagation caused by the dielectric properties of the soil surrounding the TDR probe).
The methods currently used to determine soil VMC from dielectric constants are mainly based on empirical approaches:
(1) Topp's equation
(2) Klemunes' model
(3) Third-order polynomial Ka - soil gradation model
Topp's equation employs empirical regression functions to relate the dielectric constant to the VMC.([8]) The third-order polynomial function developed by Topp is widely used for calculating moisture content of soil materials. Topp's equation can be applied to all types of soils but is inaccurate for certain scenarios: (1,8)
![]() (6)
(6)
Where:
| ? | = volumetric moisture content (%) |
Klemunes developed calibrated mixing models for soil samples obtained from 28 LTPP sites. (5, 6) TDR traces were obtained from the soil samples prepared at various combinations of moisture content and compaction levels. The moisture content and dry density of each combination was determined by laboratory testing after the TDR trace was obtained. A total of 415 data points were obtained; however, outliers and TDR traces that were impossible to interpret were removed from the dataset. Consequently, 397 data points were available and used to develop Klemunes' moisture models, which employ a hierarchal methodology (i.e., level 1 to level 4) relative to the level of information available and the desired accuracy.
At level 1, the moisture content would be determined without any information about the properties of the soil, such as coarse-/fine-grained or American Association of State Highway and Transportation Officials (AASHTO) classification. Therefore, level 1 has the lowest explained variance and the highest standard error. At level 2, moisture content is determined on the basis of the soil being identified as either coarse- or fine-grained. The accuracy of this level is better than that of level 1. At level 3, the VMC is based on the AASHTO soil classification, accounting for the soil's gradation and the characteristics of fraction passing No. 40.
The most accurate level of Klemunes' model is level 4 since this involves testing the soil at various moisture and density levels in the laboratory and correlating the results with the TDR recordings. Accordingly, a calibration curve is developed for a range of VMC expected in the field. The following equation is used to predict the VMC for each of the four levels. Table 3 provides the specific regression coefficients for each level.
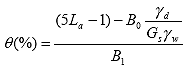 (7)
(7)
Where:
| ?d ,?w | = unit weight of the soil and water |
| Gs | = specific gravity of the soil |
| B0, B1 | = regression coefficients |
| Level | Soil Type | B0 | B1 |
|---|---|---|---|
| Level 1 | All-type | 1.41 | 7.98 |
| Level 2 | Coarse | 1.06 | 9.30 |
| Fine | 1.50 | 7.56 | |
| Level 3 | A-1-b | 1.43 | 7.69 |
| A-2-4 | 1.00 | 9.57 | |
| A-3 | 1.11 | 9.02 | |
| A-4 | 1.77 | 6.25 | |
| A-6 | -1.56 | 12.26 | |
| A-7-5 | 1.04 | 8.49 | |
| A-7-6 | 1.02 | 10.31 | |
| Level 4 | Determined based on a site-specific calibration | ||
As part of the third-order polynomial Ka -soil gradation approach, four models were developed for the VMC computation. The first three models take the third-order polynomial Ka model based on soil type while the fourth model applies to only fine-gradation soils and incorporates the contribution of the gradation into the model. (1) A computer program entitled MOISTER incorporates all four of the third-order polynomial Ka models to determine the VMC of soil, the method of tangents, and the method of peaks to determine the apparent length (and dielectric constant) of the TDR trace.
The third-order polynomial Ka models were developed based on the regression of dielectric constants and VMC from the dataset obtained in Klemunes' study. The coarse-grained soil has a different trend compared with fine- grained soil, but both of them show a third-order polynomial functional form. Hence, in order to provide a more accurate model, data for coarse-grained soil and fine-grained soil were modeled separately. The models are valid only within the dielectric constant range or the inference space that was used to develop the model. (1) The three empirical regression equations developed using the dielectric constant as the sole independent variable are given below with the regression coefficients shown in table 4.
![]() (8)
(8)
Where:
| e | = dielectric constant |
| a0, a1, a2, a3 | = regression coefficients |
| Model type | a0 | a1 | a2 | a3 |
|---|---|---|---|---|
| Coarse-Ka model | -5.7875 | 3.41763 | -0.13117 | 0.00231 |
| Fine-Ka model | 0.4756 | 2.75634 | -0.061667 | 0.000476 |
| All soil-Ka model | -0.8120 | 2.38682 | -0.04427 | 0.000292 |
To refine the regression model and to increase the R2 for fine-grained soil, another model was developed using gradation, plastic limit, and liquid limit as independent variables. Equation 9 provides the VMC model for fine-grained soil with variables: (1)
![]() (9)
(9)
Where:
| ? | = volumetric moisture content |
| e | = dielectric constant |
| a0, a1,¼, a 10 | = regression coefficients (see table 5) |
This model was used for computing the VMC for the fine-grained soils where gradation and other parameters were available and within the inference region of the model. Table 5 shows the descriptions, values, and inference ranges of these variables.
| Variable | Description | Coef. | Value | Inference Range |
|---|---|---|---|---|
| Intercept | ao | 1761.78 | ||
| Ka | Dielectic constant | a1 | 2.9145 | 3 - 58.4 |
| Ka2 | a2 | -0.07674 | ||
| Ka3 | a3 | 0.000722 | ||
| G11_2 | %passing 1 ½-sieve | a4 | -19.6649 | 99 - 100 |
| G1_2 | %passing ½-sieve | a5 | 4.3667 | 97 - 100 |
| No4 | %passing No.4 sieve | a6 | -5.1516 | 90 - 100 |
| No10 | %passing No.10 sieve | a7 | 2.7737 | 84 - 100 |
| No200 | %passing No.200 sieve | a8 | 0.06057 | 12.6 - 94.6 |
| PL | Plastic limit | a9 | -0.2057 | 0 - 45 |
| LL | Liquid limit | a10 | 0.10231 | 0 - 69 |
The four models are selected based on the dielectric constant and properties of soil to calculate moisture content. The flow chart of the model selection scheme is shown in figure 5.
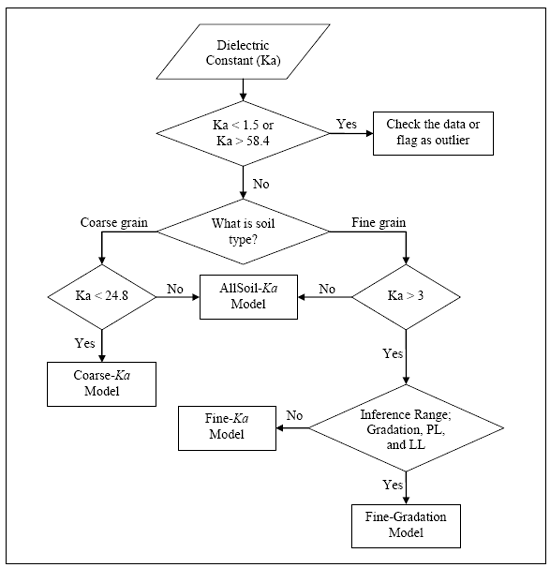
Figure 5. Flowchart. Volumetric moisture model selection process. ([9])
VMC can be converted to a gravimetric basis using volume and weight relationships. The volume relationships used for soil solid-moisture-air mixture are degree of saturation, void ratio, and porosity as shown below: ([10])
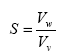 (10)
(10)
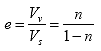 (11)
(11)
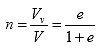 (12)
(12)
Where:
| S | = degree of saturation |
| e | = void ratio |
| n | = porosity |
| Vs | = volume of soil solids (cm3) |
| Vw | = volume of water (cm3) |
| Vv | = volume of void (cm3) |
| V | = total volume of mixture (cm3) |
The weight relationship can be represented by moisture content and unit weight:
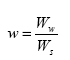 (13)
(13)
![]() (14)
(14)
Where:
w = gravimetric moisture content (%)
? = unit weight (g/cm3)
Ww = weight of water (g)
Ws = weight of solids (g)
W = total weight of mixture (g)
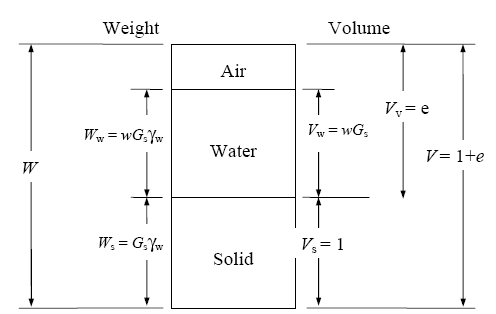
To calculate gravimetric moisture content, a relationship among moisture content and unit weight can be derived from a volume of soil mixture in which the volume of the soil solids is set to 1 as shown in figure 6. The volume of water can be defined as:
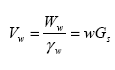 (15)
(15)
Where:
| ?w | = unit weight of water (g/cm3) |
| Gs | = specific gravity of solids |
The dry density of soil can be written as:
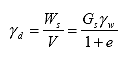 (16)
(16)
Where:
| ?d | = dry unit weight of soil (or soil dry density, g/cm3) |
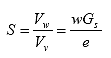 (17)
(17)
![]()
Figure 6. Diagram. Soil mixture with volume of soil solids equal to 1.
Thus, the gravimetric moisture content can be expressed in terms of the unit weight of water, unit weight of solids, and VMC by combining equations 16 and 17:
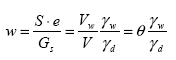 (18)
(18)
Where:
| ? | = volumetric moisture content (%) |
Equation 18 is used to convert soil moisture from a volume to a weight basis as needed in pavement engineering applications. Reasonably accurate in situ dry density estimates of material surrounding the TDR sensors must be made for moisture conversion. During installation, field moisture measurements were performed on the material placed around TDR probes with additional material samples retained for laboratory analyses. (3)
| < Previous | Contents | Next >> |