U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-10-035 Date: September 2011 |
Publication Number: FHWA-HRT-10-035 Date: September 2011 |
Several alternative predictive relationships have been developed to estimate |E*| from simpler material properties and volumetrics. These predictive relationships can be used to populate the LTPP database with estimated |E*| values. Table 1 lists the predictive relationships identified by the research team. These relationships are described briefly in the following subsections.
| Model Number | Model |
|---|---|
| 1 | Original Witczak equation (NCHRP 1-37A)(2,11) |
| 2 | Modified Witczak |G*| equation (NCHRP 1-40D)(5) |
| 3 | Hirsch model(6) |
| 4 | Law of mixtures parallel model(7) |
| 5 | ANN model |
| 6 | MR-|E*| model |
Andrei et al. revised the original Witczak |E*| predictive equation based on data from 205 mixtures with 2,750 data points.(11) The revised equation is as follows:
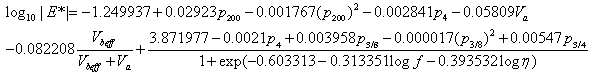 |
(1) |
Where:
| p200 | = | Percentage of aggregate passing #200 sieve. |
|---|---|---|
| p4 | = | Percentage of aggregate retained in #4 sieve. |
| p3/8 | = | Percentage of aggregate retained in 3/8-inch –(9.56-mm) sieve. |
| p¾ | = | Percentage of aggregate retained in ¾-inch (19.01-mm) sieve. |
| Va | = | Percentage of air voids (by volume of mix). |
| Vbeff | = | Percentage of effective asphalt content (by volume of mix). |
| f | = | Loading frequency (hertz). |
| η | = | Binder viscosity at temperature of interest (106 P (105 Pas). |
Witczak's equation is based on a nonlinear regression analysis using the generalized reduced gradient optimization approach in Microsoft® Excel's Solver. This model incorporates mixture volumetrics and aggregate gradation and is currently one of two options for level 3 analysis using the NCHRP 1-37A MEPDG program.(2) For the viscosity term in equation 1, the program converts all level 2 and 3 inputs into regression intercept-regression slope of viscosity temperature susceptibility (A-VTS) values for the formulation of the |E*| mastercurve. Furthermore, Witczak's model has an equation (not listed) to convert A-VTS coefficients from virgin or tank binders to RTFO- and PAV-aged binder values.
The limitations of Witczak's equation, acknowledged by Bari, include relying on other models to translate the currently used |G*| measurement into binder viscosity.(5) Because the original Witzcak predictive equation is based on regression analysis, extrapolation beyond the calibration database should be restricted. Bari also mentions that there is limited volumetric influence (precision) when the model is compared to the Shell Oil model.(5) Other researchers have also noted the need for improved sensitivity to volumetrics, such as the percentage of voids in mineral aggregate (VMA), the percentage of voids filled with asphalt (VFA), asphalt concrete percentage (AC), and Va.(12)
To include binder |G*| in the predictive model, Witczak reformulated the model to include the binder variable directly. The updated model is as follows:
 |
(2) |
Where:
| G*|b | = | Dynamic shear modulus of asphalt binder (pounds per square inch). |
|---|---|---|
| δb | = | Binder phase angle associated with |G*|b (degrees). |
As with the NCHRP 1-37A model, equation 2 is based on a nonlinear regression analysis using 346 mixtures with 7,400 data points. The measured results of the unmodified binders have a better correlation with the model (R2 = 0.87) compared to those of the modified binders (R2 = 0.79) in arithmetic scale. In logarithmic scale, both binder types have R2 = 0.99. The binder phase angle is predicted using an empirical equation (R2 = 0.83). This equation is one of two options for level 3 analysis in the most current MEPDG program.
Because some of the mixtures in this database do not contain |G*|b data, the Cox-Mertz rule, using correction factors for the non-Newtonian behaviors (see equations 3–5), is used to calculate |G*|–b from A-VTS values as follows:
| (3) |
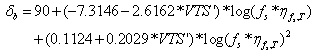 |
(4) |
| (5) |
Where:
| fs | = | Dynamic shear frequency. |
|---|---|---|
| δb | = | Binder phase angle predicted from equation 4 (degrees). |
| ηfs,T | = | Viscosity of asphalt binder at a particular loading frequency (fs) and temperature (T) determined from equation 5 (centipoise). |
| TR | = | Temperature in Rankine scale. |
Christensen et al. examined four different models based on the law of mixtures parallel model and chose the model that incorporates the binder modulus, VMA, and VFA because it provides accurate results in the simplest form.(6,7) The other more complicated forms attempt to incorporate the modulus of the mastic or the film thickness, which are difficult parameters to measure. The suggested model for |E*| estimation is provided in equations 6–8 as follows:
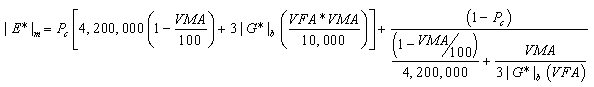 |
(6) |
| (7) |
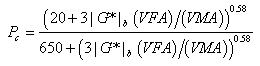 |
(8) |
Where:
| |E*|m | = | Dynamic modulus of HMA (pounds per square inch). |
|---|---|---|
| Pc | = | Aggregate contact volume. |
| ø | = | Phase angle of HMA. |
A strength of this model is the empirical phase angle equation, which is important for the interconversion of |E*| to the relaxation modulus or creep compliance. Weaknesses of the model include a lack of a strong dependence on volumetric parameters, particularly at low Va and VFA conditions. Also, questions arise regarding the ability of the |G*|b parameter to account for the possible beneficial effects of modifiers.(7) It must be noted that only 206 data points were used to determine the coefficients in the Hirsch model compared to 2,750 data points for the original Witczak model and 7,400 data points for the modified Witczak model.
Based on their findings from the Hirsch model, Al-Khateeb et al. suggest the following model:(7)
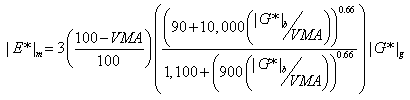 |
(9) |
Where:
| |G*|g | = | Dynamic shear modulus of asphalt binder at the glassy state (assumed to be 145,000 psi (999,050 kPa). |
|---|
Like the Hirsch model, this formulation is based on the law of mixtures for composite materials. In this model, the different material phases (aggregate, asphalt binder, and air) are considered to exist in parallel. Therefore, this model is a simpler interpretation of the Hirsch model. The researchers note that their model addresses one of the primary shortcomings of the Hirsch model (i.e., the Hirsch model's inability to accurately predict |E*| of the mixture at low frequencies and high temperatures).
Strengths of this model include the improved prediction of high-temperature and low-frequency |E*| data for mixtures used in the FHWA accelerated loading facility (ALF) test strips. Weaknesses include a lack of model verification and the fact that the researchers who developed this model did so based on |E*| values obtained from tests at higher than recommended strain amplitudes (200 µε versus the recommended maximum of 75–150 µε).
The NCSU research team employed the ANN technique to develop new |E*| predictive models. The primary advantage of this approach over statistical regression is that the functional form of the relationship is not needed a priori. Considering that so many variables affect |E*| values and their interactions, the ANN technique captures complicated nonlinear relationships between |E*| and other mixture variables better than regression analysis.
The ANN technique was used in this research to develop several different models. The first model is the ANN model that predicts |E*| values using the input variables employed in the modified Witczak equation (i.e., binder dynamic modulus and phase angle, aggregate gradation, and volumetrics of the HMA mixture). The effort to develop this ANN model is described later in this report. The ANN technique was also applied to backcalculate |E*| values from MR. During the FHWA DTFH61-05-RA-00108 project, the NCSU research team developed a mechanistic approach to compute MR from |E*| of HMA.(13,14) This approach was verified successfully using measured data from mixtures with varying gradations and binder characteristics. The verified solutions were then applied to an available |E*| database to estimate the MR values corresponding to the |E*| values. This database was used to develop an inverse algorithm based on the ANN technique that can predict |E*| from MR. The development and verification of MR-|E*| ANN are presented later in this report. Finally, the ANN technique was used to develop an |E*| predictive model based on binder viscosity information. This ANN model is also described in this report.
Table 2 presents the necessary input variables for each predictive relationship discussed previously. For models that utilize |G*|b, predictions are only possible at the temperatures and frequencies where |G*|b values are available. Having |G*|b only at the conditions used in Superpave™ testing is not sufficient for generating |E*| values over the range of conditions typically needed for mechanistic analysis (14–129.2 °F (-10–54 °C)). For example, if the user has |G*|b at only 147.2 °F (64 °C) and 10 radians per second (rad/s), then it is possible to predict the |E*| value only at 147.2 °F (64 °C) and 10 rad/s. To predict |E*| at 77 °F (25 °C) and 25 rad/s, the user must measure |G*|b at 77 °F (25 °C) and 25 rad/s.
| Variable Description | Model Number | LTPP Data Availability | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | Specific Pavement Study (SPS)1 | General Pavement Study (GPS)1 | |
| Mixture MR | X | Yes | Yes | |||||
| |G*|b | X | X | X | X | Yes2 | No | ||
| σb | X | X | Yes | No | ||||
| VMA (percent) | X | X | Yes | Yes4 | ||||
| VFA (percent) | X | Yes | Yes4 | |||||
| Aggregate passing #200 sieve (percent) | X | X | X | Yes | Yes | |||
| Aggregate passing #4 sieve (percent) | X | X | X | Yes | Yes | |||
| Aggregate passing 3/8-inch sieve (percent) | X | X | X | Yes | Yes | |||
| Aggregate passing ¾-inch sieve (percent) | X | X | X | Yes | Yes | |||
| Va (by volume of the mix (Vmix)) (percent) | X | X | X | Yes | Yes | |||
| Effective asphalt content (by total volume of the mixture) (percent) | X | X | X | Yes | Yes4 | |||
| Loading frequency (Hz) | X | Yes | No | |||||
| A-VTS | X | Yes3 | Yes5 | |||||
| 1 inch = 25.4 mm |
||||||||
A preliminary review of available information in the LTPP materials database revealed that measured |G*|b data are only available for most of the SPS-9 projects and only at 10 rad/s at multiple temperatures. Even the available |G*|b data are measured from binders aged at different levels (i.e., RTFO-aged versus PAV-aged binders). The lack of complete |G*|b data at multiple temperatures and multiple frequencies is a serious problem because all of the models except the original Witczak equation require this information. (Note that the MR-|E*| ANN model needs the binder t-T shift factor as well.) During the course of this project, the NCSU research team developed empirical models that allow the estimation of the RTFO-aged |G*|b values at multiple temperatures and frequencies from the |G*|b values obtained at a single frequency and multiple temperatures and aging levels.