U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-12-023 Date: December 2012 |
Publication Number: FHWA-HRT-12-023 Date: December 2012 |
Deflection data analysis provides qualitative and quantitative assessment of the structural integrity and bearing capacity of a pavement. Pavements with poor structural quality are more likely to develop distresses prematurely. It is commonly expected that the rate of deterioration increases as the structural condition worsens. Identifying pavements in poor structural condition is important to prevent early and rapid development of load-related distresses. This is the main motivation for the approach presented in this chapter.
Based on these premises, a probabilistic approach was developed to determine the likelihood of premature failure using load deflection techniques. Premature failure is defined by the presence of excessive distress (i.e., levels of distress higher than design threshold) occurring prior to the end of the design life of the pavement section.
Deflection data are commonly used at project-level analysis, mostly through back-calculation of layer moduli for overlay design purposes. Limited use has been observed at network-level analysis, in part due to difficulties in establishing thresholds to guide the structural evaluation. On such occasions, deflection data are used to create a rating system which yields a qualitative assessment of the structural condition. This assessment is used to determine prospective M&R treatments or remaining service life of the pavement. The rating criteria are often based on experience and common trends observed in the network.
The probabilistic approach proposed in this research can be used to establish thresholds for deflection data based on performance measures and assist with the creation of the network-level structural decision matrix. The following list includes benefits of using a deflection-based probabilistic model sensitive to structural pavement performance:
It provides a direct link to pavement performance by estimating the likelihood of the development of load-related distresses in early stages of the pavement's service life. The intent is not to have a regression predictive model based on deflection data, but rather a simplified procedure to identify critical sections with a high likelihood of developing structural distresses prematurely.
Rating criteria can be created in the same manner equivalent to the functional decision matrix. Different tiers of structural quality can be defined based on deflection thresholds and the likelihood of acceptable performance. The structural decision matrix can then follow rating criteria similar to the functional decision matrix which facilitates the implementation in existing PMS algorithms.
The probabilistic models can be locally calibrated to meet the network characteristics (e.g., typical surface distresses observed, interval between M&R projects, and the threshold of acceptable limits for distresses).
Logistic regression is useful to predict the outcome of an event based on a set of predictor variables. Logistic models are best used when the dependent variable is dichotomous (i.e., variables that assume binary values, such as acceptable and not acceptable). It is a powerful analysis tool to model complex problems where the number of variables affecting the outcome is large.(24)
Formulation and Calibration
The logistic regression model general equation is provided in figure 21. In this case, P is the probability that an event will occur, and b is the exponent parameter in logistic distribution, which is a linear function of the predictor variables, as given in general form by the equation in figure 22. The event is defined as the performance of the pavement section, "acceptable" for sections outlasting the design life and " acceptable" for sections exhibiting premature failure. The predictor variables, also known as explanatory variables, are selected to best explain the behavior of the event. In this research, the predictor variables were load deflections and site characteristics, such as climate, traffic, and pavement structure. A typical logistic model probability function of a predictor variable X is shown in figure 23.
![]()
Figure 21. Equation. General formulation of the logistic model.
![]()
Figure 22. Equation. General linear formulation for the exponent term of the logistic model.
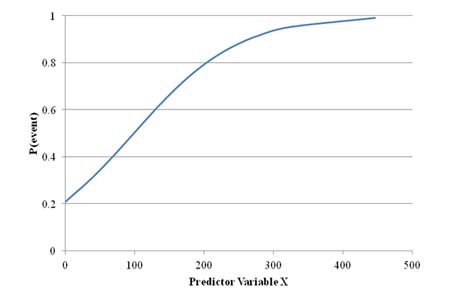
Figure 23. Graph. Typical logistic model probability function of a predictor variable X.
Predictor variables can be continuous (e.g., traffic volume) or discrete (e.g., pavement subgrade type assigned to coarse- or fine-grained soil). The dichotomous event is modeled as binary numbers - 1 for acceptable and 0 for not acceptable. The model coefficients are computed using optimization algorithms. The most widely used is the maximum likelihood estimate. In this algorithm, the coefficients of the predictor variables are obtained to maximize the probability of the event occurring. The maximum likelihood estimate is well suited for problems in which the event occurs in the majority of the cases. This is the case in pavement performance where the majority of the pavements are expected to perform well.
There is no limitation to the number of predictor variables used. In fact, it is part of the process to eliminate variables with no significant relevance to the probabilistic function. This characteristic greatly helps the analysis - there is no need to refine the selection of variables, and all possible candidates can be considered. The selection of significant variables is achieved through a stepwise regression. At first, all predictor variable candidates are used in the calibration process. The predictor coefficients are calculated using the optimization algorithm, and the significance of each predictor to the probability function is computed. One by one according to step, the predictors with the least significance to the problem are eliminated.(25) The process is concluded when all remaining variables have significance levels higher than 95 or the maximum number of iterations is reached. This approach is called "backward elimination."
Conventional statistics cannot be used to measure the goodness-of-fit of binary logistic models. Instead, the receiver operating characteristics (ROC) curve is used to evaluate the accuracy of the model. ROC curves have been used in signal detection theory to depict the tradeoff between hit rates and false alarm rates of classifiers, and they are also used in medical decisionmaking.(26) Recently, ROC curves have also been used in data mining research. One important characteristic is that ROC analysis allows the selection of possibly optimal models and allows researchers to discard suboptimal ones independently from the class distribution of the predictor.
ROC curves are useful for organizing predictors and visualizing their performance. The ROC curve is drawn using the true positive rate (TPR) and false positive rate (FPR). TPR is determined by the number of true positive predictions normalized by total number of positive observed values. Conversely, FPR defines how many incorrect positive results occur among all negative samples available during the test.
The ROC space is defined by FPR and TPR as the x- and y-axes, respectively, which depict the relative trade-offs between true positive and false positive. TPR is often described as the sensitivity of the model, while (1 - FPR) is often seen as the true negative rate (TNR) or specificity. Therefore, the ROC curve is also referred to as the sensitivity versus (1 - specificity) curve.
Each case consisting of a prediction and observed values represents one point in the ROC space. Given the discrete nature of the problem (i.e., the predicted probability is associated with a discrete definition of pavement performance, acceptable or not), algorithms are used to create the ROC curve. (26)
An example of an ROC curve is shown in figure 24. Several points in the ROC curve are important to note. The best possible prediction would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100 percent sensitivity (no false negatives) and 100 percent specificity (no false positives). The (0,1) point is also called a perfect classification. A completely random guess would give a point along a diagonal line, also referred to as line of no discrimination, which consists of points (0,0) and (1,1). Points above the diagonal line indicate good classification results. In comparative terms, one point in ROC space is better than another if it is to the northwest (TPR is higher, FPR is lower, or both) of the first.
Figure 24. Graph. Example of an ROC curve.
The area under the ROC curve defines the goodness-of-fit of the predictions. In an analogy with measures of linear optimization techniques, the area under the ROC curve can be viewed as the R2 value. By definition, the area under the ROC curve cannot be lower than 0.5, which corresponds to the reference line in figure 24. The highest value is determined by the boundary of the graph, which represents the perfect classification when the area under the ROC curve equals 1.
In addition to the goodness-of-fit, the ROC curve is used to define the cutoff value of the model. This is an important parameter that defines how the results from the probability density function can be interpreted in a binary system (i.e., the threshold used to separate probabilities that are referred to as acceptable and not acceptable). The cutoff is defined as the probability value that corresponds to the point in the ROC curve closest to the perfect classification point (0,1). When the cutoff is used to convert the predicted probabilities into binary outcomes, the model yields the highest level of accuracy (i.e., highest TPR and TNR).
Stochastic Approach to Evaluate Load Deflection Techniques to Network-Level Applications
The objective of a pavement design is to provide a structure that will exhibit adequate performance throughout its design life. In this case, performance is defined as the level of distresses that can affect the ride quality of the pavement or its structural adequacy. Therefore, a pavement has acceptable performance if distress levels do not exceed the threshold during a period of time (e.g., fatigue cracking does not exceed 25 percent of the total area in 15 years of service). Since the logistic model describes the likelihood of an event being acceptable or not as a function of a predictor variable, it can be used to model probability of acceptable performance with measurements of deflections or parameters (techniques) computed from them.
The goal of the stochastic approach proposed is to use the probability density function to obtain information about the pavement structural condition required to achieve the desired performance during a period of time. This new knowledge can then be used to define strategic treatments (maintenance or rehabilitation) to be used in the PMS optimization process.
A typical logistic model probability function is shown in figure 25. It describes the likelihood of the pavement section to exhibit acceptable performance in a particular distress as a function of a given deflection parameter, named "predictor variable X." In this example, the cutoff value was determined from the ROC curve and plotted in the figure.
In the proposed stochastic approach, the probability density function is used to determine the thresholds that define the structural condition. By definition, the cutoff value in a logistic model determines how to convert the continuous probability prediction as a dichotomous outcome (i.e., predicted probabilities above the threshold are defined as acceptable while others are defined as not acceptable). In addition to the cutoff threshold, other values can be used to further detail the structural condition. As an example, figure 25 describes a second threshold created at the 0.4 probability level and used to define sections with fair structural condition from poor ones. (Note that this definition is arbitrary and can be adjusted to better fit an agency's rehabilitation practices or network characteristics.)
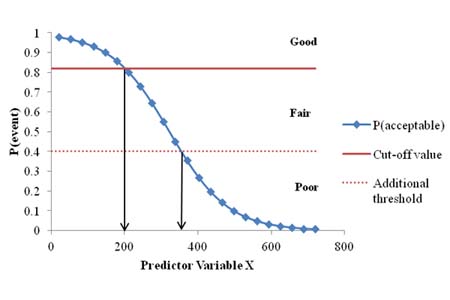
Figure 25. Graph. Example of logistic model probability function of a predictor variable X used to create a structural decision matrix.
Once thresholds and their respective deflection parameters are identified, a structural decision matrix (also referred to as a structural rehabilitation matrix) can be generated. Table 7 shows an example of a structural decision matrix obtained from the probability density function in figure 25.
Table 7. Example of structural decision matrix.
| Structural Condition | Deflection Parameter |
|---|---|
| Good | < 200 |
| Fair | 200 - 350 |
| Poor | > 350 |
The advantages of the stochastic process to evaluate the structural condition of the pavement for network-level analysis are as follows:
The evaluation of applicable deflection techniques was based on the quality and accuracy of the corresponding logistic model developed. A selection process was established to evaluate each model within each distress group and pavement type (e.g., roughness in flexible pavements). The evaluation criteria considered the accuracy of the logistic model, the consistency with engineering principles, and errors in the predictions (error types I and II). The entire analysis process can be summarized in the following steps:
Evaluation of selected techniques based on observed performance:
Verification of deflection techniques:
Validation analysis:
Selection of deflection technique:
The following sections describe the steps in the analysis process in greater detail. An example is provided in each step to illustrate the process.
The data selected for this study were prepared following the steps and processes described in chapter 3 of this report. The data type and respective LTPP table sources were described in table 3. Basic statistics on the final data set used are presented in table 8 and table 9 for flexible pavements and table 10 and table 11 for rigid pavements.
Microsoft Excel® spreadsheets were used to compute all of the deflection parameters identified in the literature review as potential candidates for evaluating the structural condition of pavements (see table 1). In the case of closed-form mechanistic parameters (i.e., subgrade Hogg and Elmod moduli), macros were used to solve the equations.
The dichotomous performance variable was determined based on expected service life of flexible and rigid pavements—arbitrarily defined as 15 years for flexible pavements and 20 years for rigid pavements. The average year in service when the first deflection measurement was taken was 2 years for both pavement types. The LTPP sections compiled for this study exhibited an average service life of 11.3 years (flexible) and 13.8 years (rigid) at the last performance measurement. As a requirement of the logistic model assumption for acceptable performance, all pavement sections had to be evaluated at the end of the chosen expected service life. Therefore, extrapolations of the performance curves were computed to achieve this requirement—3.7 years for flexible pavements and 6.2 years for rigid pavements. Typical load-related distresses in flexible and rigid pavements are given in table 12.
Table 8. Input continuous data summary for flexible pavement sections.
| Input Data | Average | Standard Deviation | Minimum | Maximum | Median |
|---|---|---|---|---|---|
Service life used |
1.5 |
1.4 |
0.0 |
10.5 |
1.0 |
Annual precipitation (mm) |
843.9 |
442.2 |
73.2 |
2,153.3 |
876.9 |
Annual minimum temperature (°C) |
6.4 |
5.9 |
-7.0 |
20.8 |
6.7 |
Annual maximum temperature (°C) |
19.6 |
6.2 |
3.8 |
31.3 |
20.3 |
Annual mean temperature (°C) |
13.0 |
6.0 |
-1.6 |
25.6 |
13.3 |
AADTT |
723.8 |
728.7 |
7.3 |
3,955.0 |
454.7 |
Total thickness (inches) |
22.1 |
9.4 |
6.3 |
85.5 |
20.3 |
AC thickness (inches) |
7.3 |
3.5 |
0.9 |
23.2 |
7.1 |
Class 5 (volume) |
146.8 |
141.7 |
2 |
1,770.0 |
106.3 |
Class 9 (volume) |
401.7 |
554.6 |
1 |
2,838.0 |
175.9 |
| 1 inch = 25.4 mm 1 °F = 1.8(°C) + 32 |
|||||
Table 9. Input discrete data summary for flexible pavement sections
| Input Data | Possible Attributes and Corresponding Binary Values | Percentage of Sections in the Database |
|---|---|---|
Subgrade type |
Fine-grained soil (1) |
32.6 percent |
Coarse-grained soil (0) |
67.4 percent |
|
Pavement type |
Bound base layer (1) |
42.3 percent |
Unbound base layer (0) |
57.7 percent |
Table 10. Input continuous data summary for rigid pavement sections.
| Input Data | Average | Standard Deviation | Minimum | Maximum | Median |
|---|---|---|---|---|---|
Service life used | 2.2 |
1.5 |
0.0 |
9.7 |
2.2 |
Annual precipitation (mm) | 848.0 |
372.1 |
128.9 |
1,856.4 |
894.7 |
Annual minimum temperature (°C) | 5.9 |
4.8 |
-2.2 |
21.0 |
5.1 |
Annual maximum temperature (°C) | 18.7 |
5.1 |
9.9 |
30.9 |
17.8 |
Annual mean temperature (°C) | 12.3 |
4.8 |
3.8 |
25.8 |
10.9 |
AADTT | 1267.2 |
1039.5 |
99.3 |
5,157.0 |
891.6 |
Total thickness (inches) | 19.6 |
9.1 |
9.2 |
61.3 |
16.4 |
AC thickness (inches) | 10.0 |
2.5 |
6.4 |
20.4 |
9.4 |
Class 5 (volume) | 238.0 |
232.2 |
14 |
998 |
178.3 |
Class 9 (volume) | 705.3 |
752.6 |
13 |
866 |
415.3 |
| 1 inch = 25.4 mm 1 &F = 1.8(°C) + 32 | |||||
Table 11. Input discrete data summary for rigid pavement sections.
| Input Data | Possible Attributes and Corresponding Binary Values | Percentage of Sections in the Database |
|---|---|---|
Subgrade type |
Fine grain soil (1) |
42.1 percent |
Coarse grain soil (0) |
57.9 percent |
|
Pavement type |
Bound base layer (1) |
55.3 percent |
Unbound base layer (0) |
44.7 percent |
Table 12. Structural distresses in flexible and rigid pavements.
| Flexible Pavements | Rigid Pavements |
|---|---|
|
|
Extrapolations were computed on a section-by-section basis by fitting nonlinear regression models to the historical data. Figure 26 provides an example of nonlinear extrapolation used to adjust the performance data.
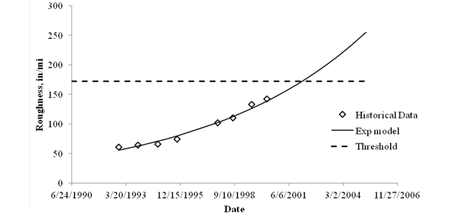
1 inch = 25.4 mm
1 mi = 1.61 km
Figure 26. Graph. Example of performance extrapolation based on historical data.
The threshold for an acceptable performance was defined based on the Mechanistic-Empirical Pavement Design Guide (MEPDG) limit values for an acceptable design and are described in table 13. (27) The acceptable level for each distress could also be defined based on the network characteristics and the agency's practice for defining rehabilitation and maintenance timing, which would provide the agency with greater flexibility to adjust the technique based on its network characteristics and preferred M&R timing.
Table 13. Distress threshold for flexible and rigid pavments.
| Flexible Pavements | Rigid Pavements | ||
|---|---|---|---|
| Distress | Threshold | Distress | Threshold |
Roughness |
172 |
Roughness |
172 |
Rutting (inches) |
0.5 |
Joint faulting (inches) |
0.12 |
Fatigue cracking (percent of total area) |
25 |
Transverse cracking (percent of slabs) |
15 |
One section would be classified as exhibiting acceptable performance for a given distress if the deterioration was lower than or equal to the threshold at 15 years for flexible pavements and 20 years for rigid pavements.
The final step in data preparation was the selection of a subset of data for model validation. The selection was based on a stratified sampling technique. The technique consisted of selecting 12 percent of the original dataset in a random process designed to pick sections distributed in a variety of site characteristics that would result in a representation equivalent to the original dataset. Climate conditions, traffic volume, pavement type (in terms of base layer type), and subgrade type were used.
The climate condition was defined based on the freeze index and average rainfall for each site. Sites with an average annual rainfall greater than 39 inches (1,000 mm) were classified as wet, otherwise dry. Sites with a freeze index greater than 140 °F (60 °C) were classified as freeze; sites with a freeze index less than 140 °F (60 °C) were classified as no freeze. This classification is part of the LTPP experiment definition. The classification of traffic was defined based on two characteristics: volume and commercial vehicle distribution. These characteristics are easy to evaluate and are most influential on pavement performance predictions estimated with the MEPDG. The combination of criteria generated two groups of sites, one identified as low traffic and the other as high traffic. Table 14 describes the characteristics of both groups used in this study.
Table 14. Traffic characteristics used for sampling.
| AADTT | Low Traffic | High Traffic |
|---|---|---|
340-950 |
75-2,750 |
|
Vehicle class 5 (percent in volume) |
25-75 |
5-20 |
Vehicle class 9 (percent in volume) |
10-50 |
40-85 |
In total, 51 deflection parameters were computed based on the literature review findings. The first deflection survey available after construction/rehabilitation was used to compute these parameters. The latest performance measurement available was used. This process was repeated for all load-related distresses in both pavement types evaluated.
The evaluation of selected deflection techniques was based on the logistic model approach and the notion that the best deflection techniques yield the most accurate models. Since there were many deflection parameters to be evaluated, a first screening was conducted to eliminate poor correlations. A simple linear Pearson regression was used to test the level of correlation between measured performance and the deflection parameter. Although this correlation is not expected to be good, Pearson's R2 and the significance level were used to identify good candidates for the full binary logistic analysis. The screenings were conducted for both flexible and rigid pavements and all load-related distress types. Tables with the results from the screening process are presented in appendix B.
As a general rule, the deflection techniques that resulted in high Pearson's R2 values and a significance level inferior to 0.05 were selected. In this case, the significance level is the probability that the null hypothesis is accepted, meaning that no correlation exists between the deflection parameters and the performance measure. Some deflection techniques were computed based on maximum deflection adjusted for temperature using the process described by Lukanen et al.(6).
After the screening was completed, the selected deflection parameters were used one at a time to develop logistic models for each load-related distress described in table 12. The statistical package IBM SPSS Statistics® was used to develop the logistic models. The process of developing the model follows a backward elimination approach. All variables described in table 8 through table 11 for flexible and rigid pavements, respectively, were used in the first step, along with the deflection parameter and the independent performance variable (acceptable or not acceptable).
The model's exponent, b, (see figure 21) was calibrated to minimize the false positives and false negatives in the probability analysis. The significance of each variable was computed, and the less significant variable was removed from the calculation in the next step, eliminating the variable with the least relationship with performance. This process continued until all remaining variables had significance levels higher than 95 percent or the maximum number of iterations was achieved. With each step, the number of variables decreased and the overall level of significance decreased, indicating an improvement in the model's capability of predicting the likelihood of acceptable performance.
The significance terminology may seem confusing, but the significance level represents the probability of the null hypothesis, which is defined as the nonexistence of any relationship between the variable in question and the predicted likelihood of acceptable performance. Therefore, high values of significance mean a high probability that the variable has a weak or no relationship as a performance predictor.
This process was repeated for all deflection variables, resulting in one model for each variable. After this first step was completed, each model was evaluated to eliminate confounding variables and unreasonable trends. Confounding variables are dependent variables that are related to each other to some extent. Volume of class 5 and 9 trucks, which according to typical vehicle class distributions are inversely proportional to each other, are a good example of confounding variables. The various site-specific temperature values selected as part of the inputs are also related to each other. During the review of each model, only one variable of each group was allowed to remain in the model. The one with the highest significance level was chosen.
Variables that resulted in unreasonable trends were also eliminated. An example of this situation was a model in which pavement thickness had an inverse trend with performance - thicker pavements would yield lower probability of acceptable performance, which is a contradiction to expected behavior. After confounding variables and variables resulting in unreasonable trends were eliminated, the model with the best accuracy was selected.
Table 15 provides the results for the logistic model based on roughness performance of flexible pavements. The primary model evaluation consists of best deflection models after the first screening was conducted and detailed analysis of each model's variables was completed to remove confounding variables and unreasonable trends.
Table 15. Statistics of calibrated models based on roughness performance of flexible pavements.
| Deflection Parameter | Primary Model Evaluation | |||||
|---|---|---|---|---|---|---|
| I2 | CI4 | CI5 | D2 | D3 | Hogg | |
Area ROC |
0.733 |
0.720 |
0.731 |
0.720 |
0.727 |
0.694 |
Hosmer-Lemeshow |
0.397 |
0.137 |
0.339 |
0.351 |
0.592 |
0.198 |
Calibration - |
68.4 |
62.8 |
67.9 |
64.6 |
67.3 |
63.9 |
Validation - |
74.2 |
61.3 |
69.4 |
66.1 |
71.0 |
74.2 |
Error type I |
6.6 |
4.7 |
5.7 |
5.9 |
6.5 |
7.0 |
Error type II |
25.0 |
32.5 |
26.4 |
29.4 |
26.2 |
29.1 |
TPR |
69.3 |
60.0 |
67.5 |
63.8 |
67.8 |
64.2 |
TNR (not acceptable) (percent) |
64.4 |
75.0 |
69.2 |
68.3 |
65.4 |
62.5 |
The following observations can be made when analyzing table 15:
Sensitivity of Model to Deflection Parameter
In addition to evaluating basic statistics of each model, it was necessary to evaluate the sensitivity of models' outcome to the deflection parameter. The main objective of this evaluation was to observe if there was any bias in the models' predictions towards acceptable or not acceptable performance.
Figure 27 shows the sensitivity curve of the I2 model based on roughness performance. In this case, the cutoff is set at 0.812, which corresponds to I2 equal to 0.1092 1/mil (0.0043 1/µm ) (or D2 equals to 9.13 mil (232 µm )), which is a reasonable value for a well designed pavement structure. (Recall that the deflection for D2 measured at 8 inches (203.2 mm) from the center of the load.) Therefore, figure 27 indicates that flexible pavements with D2 deflections below 9.13 mil (232 µm) have a higher than 80 percent chance of exhibiting acceptable roughness performance for the next 12 years and can therefore be classified as good structural condition.
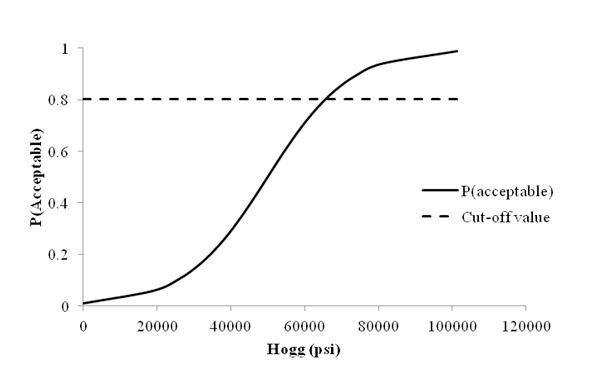
In contrast, figure 28 shows the sensitivity curve of the Hogg model based on roughness. The cutoff value of 0.802 yields a Hogg value of 65,000 psi (447,850 kPa), which is high and unreasonable for subgrade moduli. In this case, the Hogg model is biased toward probabilities under the cutoff value and, consequently, toward low probabilities of acceptable performance.
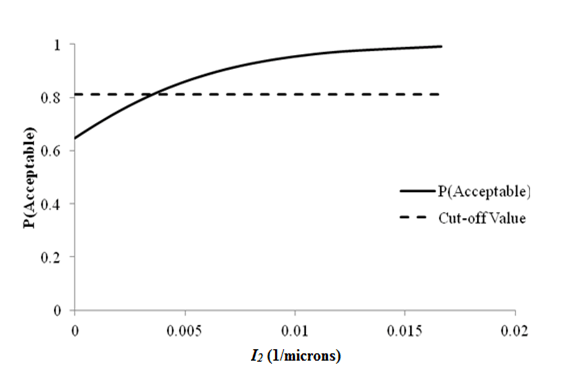
11/µm = 25.4 1/mil
Figure 27. Graph. Sensitivity of roughness acceptable probability to deflection parameter I2 for flexible pavements
1 psi=6.89 kPa
Figure 28. Graph. Sensitivity of roughness acceptable probability to deflection parameter Hogg for flexible pavements.
This type of sensitivity analysis was performed to all models developed and proved to be essential to rule out models that provided very good statistics at first but were biased. The sensitivity analyzes of other logistic models are provide in appendix C.
The validation analysis was performed on a subset of the database that was set aside prior to model calibration. In total, 12 percent of the sections available for calibration were removed from the database. Since the LTPP database covers a wide range of pavement sections, traffic levels, and environmental conditions, a stratified random sampling technique was employed to retrieve the sections. The following characteristics were used in the stratified sampling approach:
The stratified random sampling technique consists of grouping all sections in all possible combinations of the characteristics defined for the selection. After the groups are formed, the target percentage of samples is randomly selected proportionally to the size of each group and its participation in the entire dataset. For example, if one group consisting of sections with WF, low traffic, unbound base type, and fine subgrade has 43 sections, the sampling of this group would yield 5 sections randomly selected. There were 32 possible combinations of all characteristics mentioned. An algorithm was written to group the sections with equal characteristics and randomly select the target number of sections.
The validation was performed in all steps of the model evaluation. Table 14 provides the results for the structural logistic model based on roughness for flexible pavements. In this case, the validation dataset consisted of 61 sections, which is a proportional representation of all sections available in the database for model calibration. The results indicate that good accuracy was also observed in the validation dataset, which suggests that the final model is capable of identifying the structural condition of the pavement based on expected roughness performance. The validation results for all models developed in this study are provided in appendix B along with the statistics of the calibrated equation.
Deflection Parameter |
Primary Model Evaluation |
Final Model |
|||||
|---|---|---|---|---|---|---|---|
| I2 | CI4 | CI5 | D2 | D3 | Hogg | I2 | |
Validation - |
74.2 |
61.3 |
69.4 |
66.1 |
71.0 |
74.2 |
69.4 |
Selection of Deflection Technique
The logistic model based on deflection parameter I2 had the best accuracy. Table 17 shows the final model variables with respective p-values (i.e., significance of the variable to the performance variable) and the corresponding cutoff value that resulted in the highest accuracy.
Table 17. Variables in the I2 final model (based on roughness).
| Variables (bi) | ai | p-Value |
|---|---|---|
I2 |
239.849 |
0.000005706 |
Current life |
-0.189 |
0.01174 |
Class 9 volume |
-0.0006781 |
0.0001037 |
Constant |
0.8375 |
0.01071 |
Cutoff |
0.812 |
|
| Note: Variables bi and ai are defined in the equation in figure 22 | ||
Figure 29 provides the equation used to compute the deflection parameter.
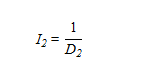
Figure 29. Equation. Calculation of I2.
Deflections are normally used to back-calculate the elastic moduli of the pavement layers. In an inverse process, the mechanistic validation consisted of simulating different pavement structures and material properties using simple multilayer elastic theory. Computed responses (deflections, stresses, and strains) were used to compute the deflection parameters and estimate damage and performance through mechanistic-empirical models. The structural logistic models were used with the computed deflection parameters as inputs. The probabilities of good structural condition were then compared with the estimated performance.
The software KENPAVE, developed by Huang, was used to model typical flexible and rigid pavement structures. (28) The mechanistic responses were then used to predict performance using the MEPDG.(27) This section describes the theoretical validation and provides examples of each step in the process. The complete validation for flexible and rigid pavement models is provided in greater detail in appendix D.
Mechanistic-Empirical Analysis
Flexible Pavements
Several pavement structures were simulated using the KENLAYER computer program that is part of the KENPAVE software. The intention was to evaluate different asphalt concrete and base layer thicknesses at different stiffnesses and different subgrade moduli. A factorial study was designed and is presented in table 18.
Table 18. Summary of the mechanistic analysis inputs for flexible pavements.
| HMA Thickness (inches) | HMA Modulus (psi) |
Base Thickness(inches) | Base Modulus(psi) | Subgrade Modulus(psi) |
|---|---|---|---|---|
3, 7, 11 |
250,000, 500,000,750,000, 1,000,000, 1,250,000, 1,500,000, 1,750,000, 2,000,000, 2,250,000, 2,500,000, 2,750,000, 3,000,000 |
8, 12, 16 |
10,000, 20,000, 30,000,40,000 |
5,000, 10,000, 20,000 |
|
1 inch = 25.4 mm 1 psi = 6.89 kPa |
||||
The combination of all parameters in the factorial experiment resulted in 1,296 sections. It was necessary to find a common variable for comparing the mechanistic responses among different combinations of the input parameters. The choice was the SN used in the 1993 AASHTO Guide for Design of Pavement Structures.(8) The equations for computing SN are provided in appendix D.
The deflection parameters of the best logistic models developed were computed for the structures simulated in the factorial experiment. Figure 30 shows the trends between deflection parameter I2 and SN. For simplicity, the data were grouped by subgrade modulus. I2 was chosen for the final structural logistic model based on roughness performance. Plots for deflection parameters used in the structural logistic models based on rutting and fatigue cracking are provided in appendix D.
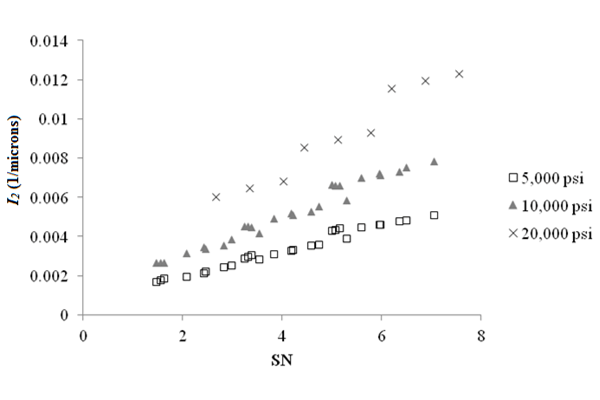
11/µm = 25.4 1/mil
1 psi = 6.89 kPa
Figure 30. Graph. Deflection parameter I2 as a function of SN for a flexible pavement with HMA modulus of 500,000 psi (3,445,000 kPa).
Rigid Pavements
Several pavement structures were simulated using KENSLAB, which is part of the KENPAVE software. (28) The intention was to evaluate different JPCP slab thicknesses and subgrade moduli and the consequences to the outcome of the structural logistic models. The pavement structure was simulated as an elastic slab on a dense liquid foundation. A factorial study was designed and is presented in table 19.
Table 19. Summary of the mechanistic analysis inputs for rigid pavements
| PCC Thickness (inches) | PCC Modulus (psi) | Subgrade Modulus (psi) |
|---|---|---|
8, 9, 10, 11, 12 |
4,000,000 |
5,000, 10,000, 20,000 |
| 1 inch = 25.4 mm 1 psi = 6.89 kPa | ||
The deflection parameters of the best logistic models developed were computed for the structures simulated in the factorial experiment. Only the FWD test at the center of the slab was evaluated. The objective was to verify if trends would agree with expected outcomes from the models. At first, the deflection parameters were plotted against the slab thickness (i.e., considered as reference for the strength of the pavement section).
Figure 31 shows the trends between deflection parameter I1 and slab thickness for three subgrade moduli. I1 was chosen for the final structural logistic model based on roughness performance. The results indicate that I1 increases as slab thickness increases, as expected. Plots for deflection parameters used in the structural logistic models based on faulting and slab cracking are provided in appendix D.
|
|
| 11/µm = 25.4 1/mil 1 inch = 25.4 mm 1 psi = 6.89 kPa |
Figure 31. Graph. Sensitivity of deflection parameter I1 to slab thickness.
Comparison with MEPDG Predicted Performance
The MEPDG performance prediction models were used to compare predicted distress performance at the end of the design life with the estimated structural condition obtained from the logistic structural model. This task was accomplished by applying the MEPDG models using the mechanistic responses calculated by KENPAVE.
Flexible Pavements
Two models were considered for flexible pavements - rutting and fatigue cracking. At first, the roughness model was also included in the scope. However, this particular model requires additional site factors that often dominate the analysis. Therefore, a comparison between the outcome of the structural logistic model based on roughness and predicted roughness performance was not included in this exercise. The calculations were performed in Microsoft Excel® and not within the MEPDG software due to computational time required to run all scenarios. Since the objective is the comparison and trend evaluation, this assumption had no impact on the outcome or conclusions. Figure 32 shows an example of the sensitivity of I1 structural logistic model probability based on fatigue cracking to MEPDG predicted fatigue cracking performance for flexible pavements. It can be seen that the trends agree with expectations; high probabilities of good structural condition are associated with low levels of fatigue cracking. As the probability decreases, the predicted area of fatigue cracking increases.
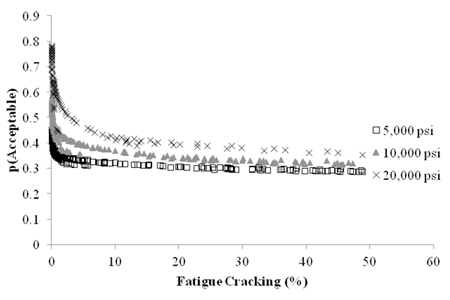
|
| 1 psi= 6.89 kPa |
Figure 32. Graph. Sensitivity of I1 structural logistic model probability based on fatigue cracking performance to MEPDG predicted fatigue cracking for flexible pavements.
The complete comparison between the outcome of the structural logistic models and MEPDG predicted performance are described in appendix D, which also includes the predictive model equations for fatigue cracking that were implemented in Microsoft Excel®.
Rigid Pavements
In the case of rigid pavements, the MEPDG was used to generate the performance predictions. There were 15 scenarios to run, and the rigid pavement analysis was performed much faster in the MEPDG than the flexible pavement analysis. Figure 33 shows the sensitivity of the I1 structural logistic model probability based on roughness to MEPDG predicted roughness performance for rigid pavements. The trends agree with expectations - high probabilities of good structural condition are associated with low values of IRI. As the probability decreases, the predicted IRI increases. This plot confirms that the structural logistic model is capable of providing an assessment of structural condition that is tied to an expectation of performance. The complete comparison between the outcome of the structural logistic models and MEPDG predicted performance is described in appendix D.
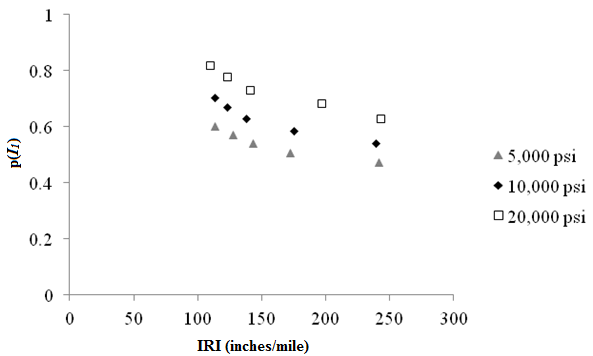
|
|
1 inch = 25.4 mm 1 mi = 1.61 km 1 psi = 6.89 kPa |
Figure 33. Graph. Sensitivity of I1 structural logistic model probability based on fatigue cracking performance to MEPDG predicted fatigue cracking for flexible pavements.
The models developed in this research were calibrated using data from several States and different local conditions. It is expected that the accuracy of the models can be improved by local calibration, which is hypothesized to minimize variability and to reduce sources of errors. Local calibration is achieved by selecting a sample dataset from the local network in which the models are to be applied and perform a local calibration of the logistic model.
Since data from a local network with comprehensive performance data for calibrating the models were not available, the LTPP database was used for this purpose. It was assumed that the models would improve accuracy if calibrated for an individual State (i.e., data from one State would have less variability and could be considered as part of a local network). Four States were used in this exercise - Texas, Minnesota, California, and Alabama. They were chosen based on the availability of data - the more data available, the higher the likelihood of a meaningful calibration.
This exercise was performed only for flexible pavements. States with a large number of rigid pavement sections were searched, but no State was found to have enough sections for this purpose. The structural logistic model based on fatigue cracking was chosen because it was the model with the least accuracy of all three models developed for flexible pavements.
The calibration process followed the same steps described in earlier sections of this chapter. Table 20 shows the statistics of the locally calibrated model for each of the four States. The statistics for the model calibrated with the entire dataset are also provided under the name of national calibration. It can be seen from the results that local calibration can significantly improve the accuracy of the model.
Table 20. Benefits of local calibration.
| Statistics | National | Texas | Minnesota | California | Alabama |
|---|---|---|---|---|---|
Number of sections |
467 |
57 |
21 |
33 |
17 |
Accuracy |
0.72 |
0.73 |
0.76 |
0.92 |
0.90 |
Correct cases (percent) |
63 |
70 |
76 |
85 |
88 |
Error type I (percent) |
15.5 |
5.3 |
4.8 |
9.1 |
5.9 |
TPR (percent) |
63 |
58 |
78 |
83 |
92 |
TNR (percent) |
63 |
67 |
67 |
86 |
80 |
The national calibration resulted in a logistic fatigue cracking model with an equivalent R2 of 0.66. The simulation of local calibration yielded models with R2 values ranging from 0.73 to 0.92. The improvement in correct predictions increased from 63 to 88 percent, which was a good improvement considering the nature of the problem. Another indication of the benefits of local calibration was the improvement in TPR. As seen in table 18, TPR values increased from 63 to 92 percent. These improvements are most likely attributed to the uniformity of the dataset in terms of site characteristics (materials, traffic, and climate) and similar design procedures.
The four examples of local calibration presented in this section show the potential improvements in accuracy and predictability that can be obtained if local data are used to calibrate the probabilistic models. Although these cases are just simple exercises retrieved from the LTPP database, it is clear that local calibration ultimately enhances the accuracy and quality of predictions, which significantly benefits analyses using PMS, especially for creation and allocation of M&R resources.
The logistic model notation is described in figure 21 and figure 22. The general form of the probabilistic logistic model is given in the equation shown in figure 21, in which the exponent term is given by the general linear equation provided in figure 22. All logistic models developed in this study follow this notation.
During the course of this research, several models were developed and evaluated according to the principles and approach described in earlier sections in this chapter. Different structural logistic models were developed based on different distress performance measures using the national LTPP database. Detailed statistics of all models evaluated are provided in appendix B. The final models are presented in this section.
Model Based on Roughness Performance
The model variables are described in table 21. The deflection parameter used is in figure 29, where D2 is the deflection 8 inches (203.2 mm) from the center of the load. The accuracy, measured by the area under the ROC curve, is 0.72, and the cutoff value is 0.812. Additional detailed statistics are provided in appendix B.
Table 21. Variables in the I2 final model for flexible pavements based on roughness performance.
| Variables (bi) | ai | p-value |
|---|---|---|
I2 |
239.849 |
0.000005706 |
Current life |
-0.189 |
0.01174 |
Class 9 volume |
-0.0006781 |
0.0001037 |
Constant |
0.8375 |
0.01071 |
Cutoff |
0.812 |
|
Roughness performance depends on the strength of the entire pavement structure. For example, it is expected that one robust pavement section tends to be smoother for longer periods of time than one weak section, assuming both have the same climate, traffic conditions, and subgrade. Therefore, the predominance of the deflection variable in the model is justified. Current life and traffic play a significant role in estimating the likelihood of premature failure due to roughness performance.
Model Based on Rutting Performance
The model variables are described in table 22, and the deflection parameter is in figure 34. The accuracy, measured by the area under the ROC curve, is 0.66, and the cutoff value is 0.792. Additional detailed statistics are provided in appendix B.
Table 22. Variables in the CI3 final model for flexible pavements based on rutting.
| Variables (bi) | ai | p-value |
|---|---|---|
CI3 |
-0.01146 |
0.00001594 |
Precipitation (mm) |
-0.0005259 |
0.04018 |
Class 9 volume |
-0.0007688 |
0.00005421 |
Constant |
2.6586 |
1.0136*10∧(-13) |
Cutoff |
0.792 |
|
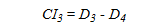
Figure 34. Equation. Calculation of CI3.
Where D3 is the deflection 12 inches (304.8 mm) from the center of the load and D4 is the deflection 18 inches (457.2 mm) from the center of the load.
The rutting model is based on deflections located at the middle of the measured deflection basin. The influence of the base and subbase is mostly noted on the deflection measured at this location. The strength of the underlying layers is critical in the development of rutting in the asphalt concrete layer and the sublayers, as well. One important aspect of the rutting phenomenon is the influence of the subgrade. It is understood that the subgrade contributes to the overall magnitude of rutting and the rate of development over time. The influence of the subgrade is not completely captured by the deflections used in this model. During the model development the type of subgrade (fine or coarse) was included as a variable, but it was excluded by the calibration process. However, the influence of precipitation was observed, which directly affects the subgrade strength more than any other granular layer in the pavement structure. Further improvements to this model at local calibration level should include the subgrade type and subgrade modulus if possible.
Model Based on Fatigue Cracking Performance
The model variables are described in table 23, and the deflection parameter is in figure 35. The accuracy, measured by the area under the ROC curve, is 0.72, and the cutoff value is 0.605. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
I1 |
154.764 |
0.0006015 |
AADTT |
-0.0005073 |
0.0007847 |
Pavement type |
0.3774 |
0.07598 |
Constant |
-0.2202 |
0.4422 |
Cutoff |
0.605 |
|
![]()
Figure 35. Equation. Calculation of I1 .
Where D1 is the deflection at the center of the load.
Fatigue cracking performance is influenced by the stiffness of the asphalt concrete layer, the number of load repetitions, and the type/strength of underlying layers. Stiff asphalt concrete layers are more susceptible to cracking because the binder hardens and becomes brittle, which reduces its flexural strength. The overall stiffness of the pavement can be captured in part by the maximum deflection, represented in this model as I1. The mechanism for crack initiation and propagation, regardless of the location where it starts (bottom or surface), depends on the growing damage due to load repetitions. The truck volume in the model addresses this issue to some extent. Finally, the type of pavement (unbound or bound base layer) is related to the stiffness of the underlying layers. Pavements with a bound base layer are less likely to develop fatigue cracking than pavements with an unbound base layer.
Two sets of models were developed for rigid pavements: one based on FWD testing at a 9,000-lb (4,086-kg) load and one at a 12,000-lb (5,448-kg) load. These tests are identified in the LTPP database as drops 2 and 3, respectively.
Model Based on Roughness Performance (9,000 lb (4,086 kg))
The model variables are described in table 24. The deflection parameter is shown in figure 36. The accuracy, measured by the area under the ROC curve, is 0.65, and the cutoff value is 0.665. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
CI5 |
-0.078 |
0.00406 |
Class 9 volume |
-0.0003877 |
0.115 |
Constant |
2.057 |
0.00002168 |
Cutoff |
0.665 |
|
![]()
Figure 36. Equation. Calculation of C15
Where D5 is the deflection 24 inches (609.6 mm) from the center of the load and D6 is the deflection 36 inches (914.4 mm) from the center of the load. Both deflections are obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated (i.e., tests at joint approach, corner edge, and mid-edge). Since they are unusual locations for typical FWD surveys conducted by State transportation departments (with the exception of the joint test), they are provided only in appendix B.
Roughness in rigid pavements is mainly related to faulting. Faulting is a distress that is directly related to the stiffness of the support layer and the quality of the dowel bars. The deflection parameter CI5 captures the influence of the underlying layer stiffness. The traffic load repetition is represented by the volume of class 9 trucks, which are the most damaging commercial vehicles to the pavement performance.
Model Based on Roughness Performance (12,000 lb (5,448 kg))
The model variables are described in table 25. The deflection parameter is shown in figure 37. The accuracy, measured by the area under the ROC curve, is 0.66, and the cutoff value is 0.695. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
CI4 |
-0.117 |
0.007378 |
Class 9 volume |
-0.0004607 |
0.06459 |
Constant |
2.148 |
0.0000447 |
Cutoff |
0.695 |
|
![]()
Figure 37. Equation. Calculation of CI4.
Where D4 is the deflection 18 inches (457.2 mm) from the center of the load and D5 is the deflection 24 inches (609.6 mm) from the center of the load. Both deflections are obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated and are provided in appendix B. This model is similar to the one developed based on the 9,000-lb (4,086-kg) FWD load. The deflection parameter is D5 in this case, which is also related to the stiffness of the underlying layers.
Model Based on Faulting at Joints Performance (9,000 lb (4,086 kg))
The model variables are described in table 26. The accuracy, measured by the area under the ROC curve, is 0.64, and the cutoff value is 0.635. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
D6 | -0.009225 |
0.138 |
Subgrade type | -0.495 |
0.2003 |
Constant | 1.499 |
0.005818 |
Cutoff |
0.635 |
|
Where D6 is the deflection 36 inches (914.4 mm) from the center of the load. The deflection is obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated and are provided in appendix B.
Faulting is a distress that is directly affected by the condition of the subgrade or the underlying base layer. The variables that were selected during the calibration process reflect the importance of the subgrade on the faulting performance of the pavement. The further the measured deflection is from the center of the applied load, the greater the contribution of the underlying layers to its magnitude. The deflection parameter D6 can be related to the instant stiffness of the supporting layers. In addition, the subgrade type (fine or coarse) was also selected as one of the variables, which confirms the importance of the subgrade on faulting performance.
Model Based on Faulting at Joints Performance (12,000 lb (5,448 kg))
The model variables are described in table 27. The accuracy, measured by the area under the ROC curve, is 0.63, and the cutoff value is 0.651. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
D6 |
-0.008789 |
0.06896 |
Subgrade type |
-0.579 |
0.139 |
Constant |
1.734 |
0.002499 |
Cutoff |
0.651 |
|
Where D6 is the deflection 36 inches (914.4 mm) from the center of the load. The deflection is obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated and are provided in appendix B.
Model Based on Transverse Slab Cracking Performance (9,000 lb (4,086 kg))
The model variables are described in table 28. The deflection parameter used is shown in figure 37. The accuracy, measured by the area under the ROC curve, is 0.77, and the cutoff value is 0.7. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
CI4 |
-0.254 |
0.0003759 |
Class 9 volume |
-0.001012 |
0.001084 |
Constant |
3.630 |
0.0000003134 |
Cutoff |
0.7 |
|
For this model, D4 is the deflection 18 inches (457.2 mm) from the center of the load, and D5 is the deflection 24 inches (609.6 mm) from the center of the load. Both deflections are obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated and are provided in appendix B.
Slab cracking develops when the slab support is no longer adequate or loading is too excessive for the designed concrete slab. As any crack mechanism, it also develops over traffic load repetition. The final model developed based on transverse slab cracking incorporates both characteristics. The deflection parameter is obtained from the midsection of the deflection basin which can be associated with the instant stiffness of the underlying support layers of the concrete slab. The load repetition is characterized by the volume of class 9 trucks.
Model Based on Transverse Slab Cracking Performance (12,000 lb (5,448 kg))
The model variables are described in table 29. The deflection parameter is shown in figure 37. The accuracy, measured by the area under the ROC curve, is 0.66, and the cutoff value is 0.695. Additional detailed statistics are provided in appendix B.
| Variables (bi) | ai | p-value |
|---|---|---|
CI4 |
-0.231 |
0.00007858 |
Class 9 volume |
-0.001029 |
0.001282 |
Constant |
3.9796 |
0.0000001201 |
Cutoff |
0.71 |
|
In this model, D4 is the deflection 18 inches (457.2 mm) from the center of the load,and D5 is the deflection 24 inches (609.6 mm) from the center of the load. Both deflections are obtained from tests at the center of the slab. Additional models based on FWD tests at different locations in the slab were investigated and are provided in appendix B.
The process for selecting the best-fitting technique is simple. A complete example is described in the previous sections of this chapter. A summary of the steps is provided as guidelines for selecting the best-fitting deflection techniques. The process for selecting the best model is as follows:
The process for selecting the best model is as follows:
Data availability is important. Logistic regression models are obtained from the statistical analysis of several independent variables that may potentially have an impact on pavement performance. At first, no variable should be eliminated without it properly being assessed. Typical groups of variables include deflection, structure, traffic, climate, and performance. It is important that any available variable in these categories is used, but dependent variables that are related to each other to some extent should be avoided.
Deflections obtained from FWD testing are used to compute deflection parameters to be used as independent variables in the logistic models. A detailed literature review of most used and more successful applications was done as part of this research.
In this study, thickness and material type were used as structure variables. In addition, two dichotomous variables based on the structure characteristics were used - one related to the subgrade type (coarse- or fine-grained) and other related to the base type (bound or unbound). Traffic was limited to the total volume of trucks and the volume of the two most predominant classes in the FHWA truck classification, classes 5 and 9. Two main variables for climate were used - precipitation and temperature. For simplification, annual averages were used for both.
The main characteristic of a logistic model is the prediction of a probability of an event occurring given a set of independent variables. The assumption is that the rate of deterioration increases as the structural condition worsens, and the probability of a pavement failing prematurely can be calculated based on a combination of a deflection parameter and site characteristics. Therefore, performance must be transformed in a dichotomous variable representing the occurrence of this event (acceptable performance after a number of years in service). The service life can be chosen to reflect the expected performance in the network.
The calibration and evaluation of selected deflection techniques is based on the logistic model approach and the notion that the best deflection techniques yield the most accurate models. Each deflection parameter available can be used to develop a logistic model for each performance measure in the dataset. A statistical package can be used to expedite the process, although a spreadsheet can be used to program the optimization algorithm. In this study, PASW Statistics™ (formerly known as SPSS) was used to develop the logistic models with an approach called backward elimination. The general formulation of the logistic model is shown in figure 21 and figure 22.
The model's exponent, b, is calibrated to minimize the false positives and false negatives in the probability analysis. The significance of each variable is computed, and the least significant variable is removed from the calculation. This process continues until no improvements in accuracy can be made or the maximum number of iterations is achieved.
Logistic model accuracy is best evaluated through the analysis of the ROC curve. An ROC analysis allows researchers to select possible optimal models and discard suboptimal ones independently from the class distribution of the predictor.
The ROC curve is drawn using only the TPR and FPR. TPR is determined by the number of true positive predictions, normalized by total number of positive observed values. Conversely, FPR defines how many incorrect positive results occur among all negative samples available during the test.
The ROC space is defined by FPR and TPR as x- and y-axes, respectively, which depicts the relative tradeoffs between true positive and false positive. TPR is often described as the sensitivity of the model, while (1 - FPR) is often seen as TNR or specificity. Therefore, the ROC curve is also referred to as the sensitivity versus (1 - specificity) curve. Each case consisting of a prediction and observed values represents one point in the ROC space. Details about the ROC curve were provided earlier in this chapter and are shown in figure 24.
The area under the ROC curve defines the goodness-of-fit of the predictions. In an analogy with measures of linear optimization techniques, the area under the ROC curve can be viewed as the R2 value. In addition to the goodness-of-fit, the ROC curve is used to define the cutoff value of the model. This is an important parameter that defines how the results from the probability density function can be interpreted in a binary system (i.e., the threshold used to separate probabilities that are referred to acceptable and not acceptable). The cutoff is defined as the probability value that corresponds to the point in the ROC curve closest to the perfect classification point (0,1). When the cutoff is used to convert the predicted probabilities into binary outcomes, the model yields the highest level of accuracy (i.e., highest TPR and TNR).
The last step in the analysis process is the sensitivity of the logistic models to its variables. It is important that the model produces as accurate results as possible, as well as reasonable probabilities with reasonable values of the deflection parameter. Plots of predicted probability versus the deflection parameter can provide valuable information about the reasonableness of the model for a given set of site characteristic variables (e.g., high truck volume, unbound base, and cold climate). If results from the sensitivity plots are unreasonable, a new model must be calibrated to eliminate unrealistic outcomes.