Estimation of Key PCC, Base, Subbase, and Pavement Engineering Properties From Routine Tests and Physical Characteristics

PDF Version (4.44 MB)

PDF files can be viewed with the Acrobat® Reader®

CHAPTER 5. MODEL DEVELOPMENT (17)

JPCP deltaT Gradient Model Development

It was observed that the data generated for the dependent variable, deltaT, correlated well with the material, design, and climate parameters when transformed from deltaT temperature differential to deltaT temperature gradient. This involved dividing the deltaT temperature differential by the slab thickness. A step-wise regression analysis and C_p analyses were performed to select the variables that are correlated to the dependent variable and to select the best combination of variables to develop the model. After an iterative process to optimize the model, the equation developed to estimate the deltaT gradient variable is as follows:

Figure 214. Equation. Prediction model 15 for deltaT/inch.

Where:

deltaT/inch = Predicted average gradient through JPCP slab, °F/inch.

TR = Difference between maximum and minimum temperature for the month of construction, °F.

SW= Slab width, ft.

PCCTHK=JPCP slab thickness, inch.

uw = Unit weight of PCC used in JPCP slab, lb/ft³.

w/c = w/c ratio.

latitude = Latitude of the project location, degrees.

The model considers climate (TR, latitude), design (SW, PCCTHK), and material (uw, w/c) parameters. The model statistics are presented in table 53. The model was developed with 147 data points and has an R² value of 0.4967 percent and an RMSE value of 0.3199 psi. Table 54 provides details of the range of data used to develop the model. Figure 215 shows the predicted versus measured for the proposed JPCP deltaT gradient model, while figure 216 shows the residual errors. Note that the measured data here refer to the deltaT gradient determined by matching MEPDG prediction to field performance. Figure 217 shows the predicted versus measured deltaT for the model.

Table 53. Regression statistics for JPCP deltaT model.

The model statistics for table 54 are as follows:

• RMSE = 0.3199 psi.
• R² = 0.4967 percent.
• N = 147.

Table 54. Range of data used for JPCP deltaT model.

Figure 215. Graph. Predicted versus measured for JPCP deltaT gradient model.

Figure 216. Graph. Residual errors for JPCP deltaT gradient model.

Figure 217. Graph. Predicted versus measured deltaT based on the JPCP deltaT gradient model.

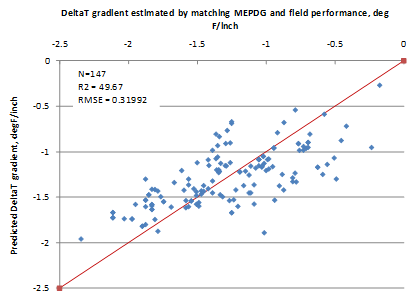
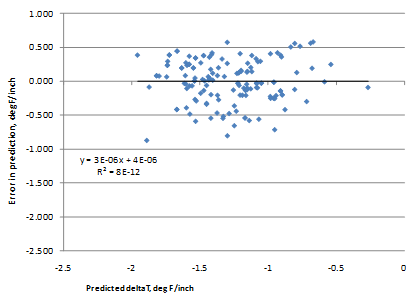
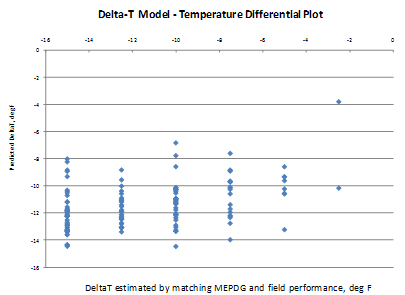
Figure 218 through figure 224 present the sensitivity analysis performed to examine the impact of varying the model parameters on its prediction. The parameters included are temperature range, slab width, slab thickness, unit weight, w/c ratio, and latitude. For each sensitivity analysis, the variable of interest was varied while holding all other variables constant at their typical values. Typical values used in this analysis were 24 °F, 12-ft slab width, 10-inch slab thickness, 145 lb/ft³ PCC unit weight, 0.40 w/c ratio, and 40 degrees latitude.

Figure 218. Graph. Sensitivity of predicted deltaT to temperature range during month of construction.

Figure 219. Graph. Sensitivity of predicted deltaT to slab width.

Figure 220. Graph. Sensitivity of predicted deltaT to slab thickness.

Figure 221. Graph. Sensitivity of predicted deltaT to PCC slab unit weight.

Figure 222. Graph. Sensitivity of predicted deltaT to PCC w/c ratio.

Figure 223. Graph. Sensitivity of predicted deltaT to latitude of the project location.

Figure 224. Graph. Predicted deltaT for different locations in the United States.

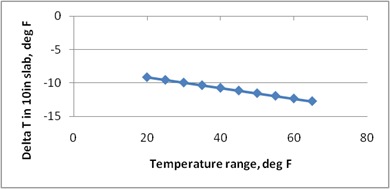
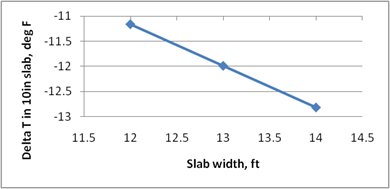
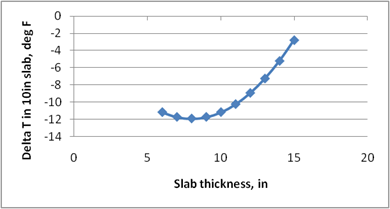
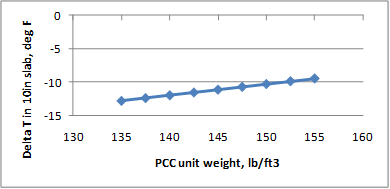
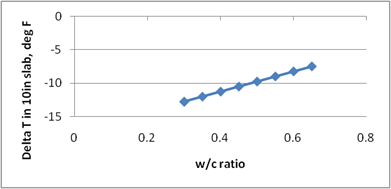
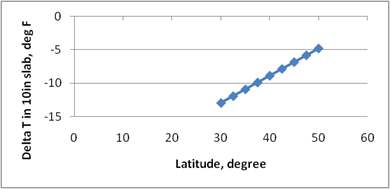
The following list contains brief observations from these sensitivity analyses:

• For the typical values used for each of these variables, the deltaT gradients estimated are in a reasonable range.
• An increase in local climate temperature range increases the temperature gradient (see figure 218). The local climate temperature range is indicative of the level of temperature drop the project location can experience. The larger the difference in the temperature between day and night (assuming paving is performed in the daytime), the larger the negative temperature gradient locked into the slab as the slab hardens within a 24-h period.
• Wider slabs produce a larger built-in gradient (see figure 219), as has been validated in several field studies. The total thermal expansion is larger for a longer/wider slab and, therefore, the resulting curvature of the slab induces a greater lift-up at the slab corners. The data did not show a significant effect of the slab length or joint spacing parameter.
• Thicker slabs reduce the deltaT gradient, as shown in figure 220. This is the expected trend, as thicker slabs, due to a greater weight, tend to restrain the corners from curling up as the concrete hardens. This figure also shows that for very thin slabs (< 8 inches), the effect is reversed. The physical significance of this cannot be fully explained or supported with data. It is therefore necessary to evaluate the sensitivity to each parameter while selecting a deltaT for each project.
• The larger unit weight of the PCC material used in the JPCP slab also reduces the magnitude of built-in gradient, primarily because of the restraint provided by the heavier slab during hardening (see figure 221).
• Lower w/c ratios have a higher rate of hydration, and, therefore, the PCC slab remains plastic for a shorter duration of time. Strength gain offers the slab the rigidity necessary to bear against the base and does not allow the slab corners to curl up. Therefore, lower w/c ratios tend to have higher built-in gradients, as seen in figure 222. Furthermore, at low w/c ratios, the PCC mix undergoes autogeneous shrinkage, which increases the potential for higher gradients in the slab.
• Figure 223 and figure 224 show the effect of latitude on predicted deltaT gradients. The United States lies between 30 and 50 degrees latitude in the Northern Hemisphere. The full range of latitudes is covered in figure 223. While this plot might appear to show deltaT’s high degree of sensitivity to the latitude parameter, for routine predictions using this model, the temperature range is a critical input. In other words, a given maximum temperature in the southern United States could have a much different temperature range relative to a location in the northern United States with the same maximum temperature. Therefore, the latitude parameter has to be evaluated combined with the temperature range parameter, as shown in figure 224. The predicted deltaT for several locations in the United States are presented.