U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-12-030 Date: August 2012 |
Publication Number: FHWA-HRT-12-030 Date: August 2012 |
PDF Version (4.44 MB)
PDF files can be viewed with the Acrobat® Reader®
Material characterization has gained increasing importance in pavement engineering, mainly due to the development of analyses and design procedures that are capable of considering material properties to predict pavement performance. This becomes crucial not only in the initial design phase, but also in QA practices and in pavement management throughout the pavement service life. Materials behave differently depending on the material type (PCC materials, unbound fine-grained materials, unbound coarse-grained materials, etc.), the type of loading (loading under compression, under flexure, under thermal differentials, etc.), and the testing conditions (rate of loading, level of loading, etc). Therefore, materials are characterized by different properties to capture the behavior of the material under different conditions. Procedures like the MEPDG use various material property inputs to model pavement response and to predict pavement performance.
Consequently, there is a need for more information about material properties, which is addressed only to a limited extent in currently available resources. Reliable correlations between material parameters and index properties offer a cost-effective alternative and are equivalent to the level 2 MEPDG inputs. The LTPP database, which contains material property test results as well as material index properties, offers an opportunity to develop such correlations for PCC materials, stabilized materials, and unbound materials.(5) Furthermore, because these data come from real-world materials, workmanship, and construction practices instead of from controlled laboratory experiments, correlations developed from LTPP data can be considered suitable for use in pavement-related applications.
The MEPDG also requires certain design-related inputs, commonly called design feature inputs, which are influenced by material properties as well as climate and construction-related parameters. The deltaT values for JPCP and CRCP design are prime examples of design feature inputs. These inputs are not directly available from simple test results. In combination with the data available from the MEPDG calibration models, the LTPP database offers the potential to provide the much-needed guidance to estimate these inputs.
This study involved developing predictive models to estimate material and design parameters. The main objectives of this study were as follows:
A thorough review of the literature was performed to identify material properties for which predictive models would be required and to identify the index properties that have a significant impact on each material property of interest. This was followed by an evaluation of the data available in the LTPP database to assess the availability of data essential for developing these correlations. Based on the review of the database, the following material categories and material properties were selected for developing predictive relationships:
The LTPP database has an extensive record of material test results. Also, test data are available for SPS and GPS sections, which have distinctly different levels of detail for material index properties and cover different pavement age ranges. Therefore, multiple models were developed for each material property if suitable data were available. The data required to develop models under the rigid pavement design features category were obtained partly from the LTPP database and partly by conducting multiple analysis runs of the LTPP sections used in the calibration of the MEPDG distress models. All models were developed under rigorous statistical analysis procedures, and a uniform set of criteria was used across all models. The statistical significance was discussed in detail throughout the report.
The following is a summary of the models developed under this study, grouped by material type and material property.
![]()
Where:
fc,28d = 28-day compressive strength, psi.
w/c = Water to cement ratio.
CMC = Cementitious materials content, lb/yd3.
![]()
Where:
fc,t = Compressive strength at age t years, psi.
CMC = Cementitious materials content, lb/yd3.
w/c = Water to cement ratio.
uw = Unit weight, lb/ft3.
t = Short-term age, years.
![]()
Where:
fc,t = Compressive strength at age t years, psi.
CMC = Cementitious materials content, lb/yd3.
uw = Unit weight, lb/ft3.
MAS = Maximum aggregate size, inch.
w/c = Water to cement ratio.
FM = Fineness modulus of fine aggregate.
t = Short-term age, years.
Where:
fc,t = Compressive strength at age t years, psi.
w/c = Water to cement ratio.
CMC = Cementitious materials content, lb/yd3.
uw = Unit weight, lb/ft3.
t= Short-term age, years.
Where:
fc, LT = Long-term compressive strength, psi.
CMC = Cementitious materials content, lb/yd3.
uw = Unit weight, lb/ft3.
Where:
MR = Flexural strength, psi.
f'c,= Compressive strength determined at the same age, psi.
Where:
MRt = Flexural strength at age t years, psi.
w/c = water to cement ratio.
uw = Unit weight, lb/ft3.
t = Pavement age, years.
Where:
MRt = Flexural strength at age t years, psi.
CMC = Cementitious materials content, lb/yd3.
uw = Unit weight, lb/ft3.
t = Pavement age, years.
Where:
Ec = PCC elastic modulus, psi.
uw = Unit weight, lb/ft3.
f'c = Compressive strength at same age, psi.
Dagg = Regressed constant depending on aggregate type as follows:
![]()
Where:
Ec,t = Elastic modulus at age t years f'ct = Compressive strength at age t years. t = Age at which modulus is determined, years.
![]()
Where:
Ec,t = Elastic modulus at age t years.
F'c28-day = 28-day compressive strength.
t = Age at which modulus is determined, years.
![]()
Where:
ft = Indirect tensile strength of the PCC material. f'c= Compressive strength of the mix determined at the same age.
|
Aggregate Type |
Average From Data Used in Level 2 Model |
|
Basalt |
4.86 |
|
Chert |
6.90 |
|
Diabase |
5.13 |
|
Dolomite |
5.79 |
|
Gabbro |
5.28 |
|
Granite |
5.71 |
|
Limestone |
5.25 |
|
Quartzite |
6.18 |
|
Andesite |
5.33 |
|
Sandstone |
6.33 |
![]()
Where:
CTEPCC = CTE of the PCC material, x10-6 inch/inch/°F.
VCA = Volumetric proportion of the coarse aggregate (value between zero and 0.6).
CTECA = Constant determined for each aggregate type as follows:
![]()
Where:
deltaT/inch = Predicted gradient in JPCP slab, °F/inch.
TR = Difference between maximum and minimum temperature for the month of construction, °F.
SW = Slab width, ft.
PCCTHK = JPCP slab thickness, inch.
uw= Unit weight of PCC used in JPCP slab, lb/ft3.
w/c= Water to cement ratio.
latitude = Latitude of the project location, degrees.
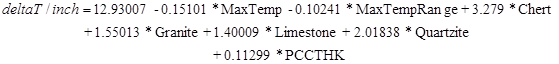
Where:
deltaT/inch = Predicted gradient in CRCP slab, °F/inch.
MaxTemp = Maximum temperature for the month of construction, °F.
MaxTempRange = Maximum temperature range for the month of construction, °F.
PCCTHK = JPCP slab thickness, inch.
Chert =1 if PCC mix coarse aggregate is chert, or 0 if otherwise.
Granite = 1 if PCC mix coarse aggregate is granite, or 0 if otherwise.
Limestone = 1 if PCC mix coarse aggregate is limestone, or 0 if otherwise.
Quartzite = 1 if PCC mix coarse aggregate is quartzite, or 0 if otherwise.
There were no modifications to the existing MEPDG erosion model.
No model was developed for this parameter.
Where:
ELCB = Elastic modulus of the LCB layer.
f'c, 28d = 28-day compressive strength of the LCB material.
Resilient modulus will be determined using the following constitutive model:
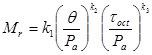
The constitutive model parameters are defined as follows:
Where:
PCTHALF = Percent passing 1/2-inch sieve.
LL = Liquid limit, percent.
OPTMOIST = Optimum moisture content, percent.
PCTNO80 = Percent passing No. 80 sieve.
PCTGRVL = Percent gravel fraction (0.078- to 2.36-inch size).
D10 = Maximum particle size of the smallest 10 percent of soil sample.
The models presented in this report, for most part, were developed from LTPP materials tables that are comprehensive and have been cleared through rigorous data screening and reviews (level E). The CTE values in the database are a relatively recent addition. Over the past year, some issues were identified with the accuracy of these data, and FHWA has made other efforts to correct the CTE test data. The CTE models developed in this study, therefore, need to be updated to reflect the recent changes.
Additionally, the deltaT models for JPCP and CRCP design are based on the calibration in the MEPDG version 1.0 software. The MEPDG rigid pavement models are being updated to account for changes in CTE values and to address software bugs identified since the release of version 1.0 in 2006. This version was completed in 2011. Therefore, the deltaT models presented here will not be applicable in the new version. These models will require updating. The procedures followed to develop these models are valid and can be used in a framework for future revisions.