U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-98-085 |
The Delta Basin Shape Factors are perhaps the oldest and simplest of the basin shape factors. Simply put, a Delta factor is the difference between the center deflection (defl0) and the deflection measured at some distance away from the center (deflx). The general equation is:
Deltax = defl0 - deflx
Where:
x = Offset from the center of the load plate, in.defl0 = Deflection measured at an offset of 0 in., µm
deflx = Deflection measured at and offset of x in., µm
Following industry practice at the expense of using mixed units, the sensor offsets used in the Delta factors presented here are in US customary units. Correction factors for Delta8, Delta12 (sometimes called the Surface Curvature Index), Delta18, Delta24, Delta48 and Delta60 are presented here.
The Deltax factor is primarily dependent on the HMA thickness and stiffness, however as "x" increases, so does the influence of the base and subgrade layers. The influence of the lower layers is dependent on many things, such the ratio of "x" to the thickness of the HMA layer and the stiffness of the HMA layer relative to the stiffness of the lower layers, so care should be exercised in the use of the Delta factors to characterize properties of the HMA layer.
As the Delta factors are strongly influenced by the stiffness of the HMA layer, they are therefore temperature dependent. This dependence is shown in Figures 22-24 using the Delta12 factor. Similar figures for the other Delta factors are available here.
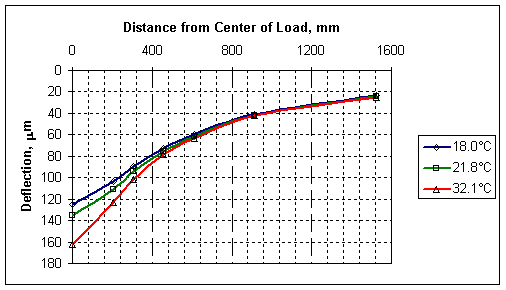
Figure 22. Sample Deflection Basins Measured at the Same Point
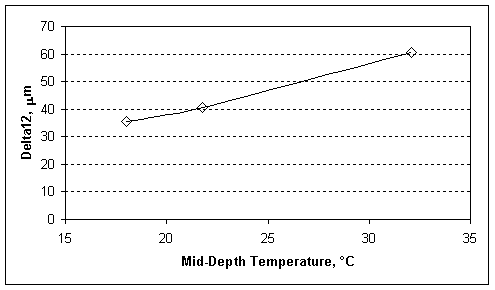
Figure 23. Delta12 factors from Figure 22 vs. Temperature
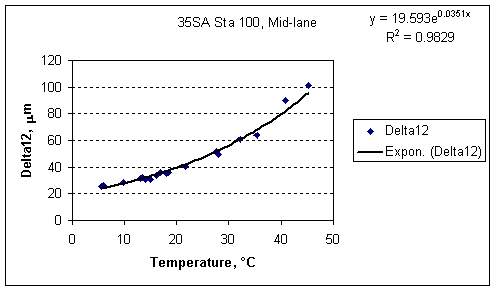
Figure 24. Delta12 versus temperature for a single test location
The LTPP SMP data was used to develop regression equations relating the Delta basin shape factors to pavement characteristics including the thickness of the HMA layer, the temperature at the mid-depth of the HMA layer, the 9 kip load-normalized deflection at the 36 in. offset (which provides a substitute for subgrade stiffness) and the latitude (which is used as a surrogate for binder stiffness).
Delta8
Log(Delta8) = 3.02 - 1.49*Log(ac) + 0.541*Log(theta) + 0.394*Log(defl36) - 0.0230*T + 0.0111*T*Log(ac)*Log(theta)
Delta12
Log(Delta12) = 3.45 - 1.59*Log(ac) + 0.489*Log(theta) + 0.449*Log(defl36) - 0.0275*T + 0.012*T*Log(ac)*Log(theta)
Delta18
Log(Delta18) = 4.18 - 1.52*Log(ac) + 0.317*Log(theta)*Log(defl36) - 0.0265*T + 0.0112*T*Log(ac)*Log(theta)
Delta24
Log(Delta24) = 3.30 - 1.32*Log(ac) + 0.514*Log(theta)*Log(defl36) - 0.00622*T*Log(theta)*Log(defl36) + 0.00838*T*Log(ac)*Log(theta)
Delta36
Log(Delta36)= 3.05 - 1.13*Log(ac) + 0.502*Log(theta)*Log(defl36) - 0.00487*T*Log(theta)*Log(defl36) + 0.00677*T*Log(ac)*Log(theta)
Delta60
Log(Delta60)= 2.67 - 0.770*Log(ac) + 0.650*Log(defl36) + 0.00290*T*Log(ac)
Where:
ac = Total thickness of the HMA, mmtheta = Latitude of the pavement section
defl36 = Deflection (load-normalized to 40.5 kN (9 kip)) at 915 mm (36 in.) from the center of the load plate, µm
T = Temperature at mid-depth of the HMA, °C
The Delta factors decrease as the log of the thickness of the AC increases and increase as the temperature of the HMA increases (the second term with T dominates the first term with T). The latitude is a substitute for the stiffness of the binder used in the HMA mix. The Delta factors increase as the latitude increases because, generally, softer binders are used in north and harder binders are used in the south. The coefficient on the terms where the latitude appears are positive, indicating that as the latitude increases, the Delta12 factor increases, which is consistent with the relationship between the Delta factors and stiffness. The coefficient for the term with the defl36 variable is positive, indicating an increase in defl36increases the Delta factors. The defl36 varies inversely with the subgrade stiffness, so as defl36 increases, the subgrade stiffness decreases.
Use of the Delta basin factors generally will require that the calculated Delta values be adjusted for temperature. Temperature adjustment factors can be calculated by using the respective Delta equation to calculate an Delta factor for the pavement tested using the mid-depth HMA temperature at the time of the test (Tm). The Delta is then calculated again using the mid-depth HMA temperature, or reference temperature (Tr) that it is to be adjusted to. The Basin Adjustment Factor for Deltax, or BAFDeltax, is the Deltax at the reference temperature divided by the Deltax at the measured temperature. This procedure is illustrated in the following equation:
BAFDeltax = Deltax, Tr / Deltax, Tm
Where:
BAFDeltax = Basin Adjustment Factor for DeltaxDeltax, Tr = Deltax factor calculated for the reference temperature
Deltax, Tm = Deltax factor calculated for the reference temperature
Source code for implementing the Delta8, Delta12, Delta18, Delta24, Delta36 and Delta60 temperature regression equations is included, as is sample data for checking code.
Source code for implementing the basin adjustment factors for Delta8, Delta12, Delta18, Delta24, Delta36 and Delta60 is also included.