Evaluation and Analysis of LTPP Pavement Layer Thickness Data

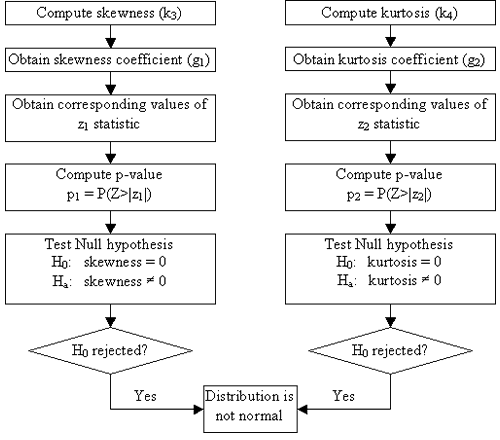
Figure 27 in page 73 shows the flowchart of the kurtosis and skewness test procedures for the test of layer thickness distribution normality. On the left of the chart, the test procedure for skewness starts with the computing of skewness (k3) defined in Figure 76 in page 133, computing skewness coefficient (g1) defined in Figure 78 in page 133, obtaining the skewness statistic (z1) defined in Figure 87 in page 135 based on k3 and g1, and computing the p-value (p1) which is the maximum probability that the null hypothesis: skewness = 0 will be rejected by looking up the standardized normal table when Z is greater than the absolute value of z1. If p1 is greater than the specified risk level of 1 or 5 percent, then the null hypothesis will be rejected. Similarly, on the right of the chart, the test procedure for kurtosis starts with the computing of kurtosis (k4) defined in Figure 77 in page 133, computing kurtosis coefficient (g2) defined in Figure 79 in page 134, obtaining the kurtosis statistic (z2) defined in Figure 93 in page 136 based on k4 and g2, and computing the p-value (p2) which is the maximum probability that the null hypothesis: kurtosis = 0 will be rejected by looking up the standardized normal table when Z is greater than the absolute value of z2. If p2 is greater than the specified risk level of 1 or 5 percent, then the null hypothesis will be rejected. The normality assumption of layer thickness distribution will not sustain if either the skewness or the kurtosis null hypothesis is rejected.

Back