U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-02-095 |
Previous | Table of Contents | Next
| where: |
PAYADJ = appropriate payment adjustment for new pavement or overlay (same units as C). C = present total cost of resurfacing. (typical value = $23.92/m2). D = design life of pavement or initial overlay (typically 20 years for new pavement, 10 years for overlay). E = expected life of pavement or overlay (variable). O = expected life of successive overlays (typically 10 years). R = (1 + INF) / (1 + INT). INF = long-term annual inflation rate in decimal form (typically 0.04). INT = long-term annual interest rate in decimal form (typically 0.08). |
The standard LCC equation is given by equation 73:
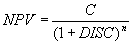 |
| where: |
NPV = the net present value. C = the present cost of the action in question. DISC = the annual discount rate in decimal form. n = the number of years in the future that the action will take place. |
Equation 73 is a very close approximation of what actually happens, and a slightly more accurate expression can be derived. If C is the cost of an action today, then its cost n years in the future is given by Cn = C (1 + INF)n in which INF is the annual inflation rate expressed as a decimal. The net present value of this future action is NPV = Cn / (1 + INT)n in which INT is the annual interest rate in decimal form. Combining these two equations produces
NPV = C (1 + INF)n / (1 + INT)n which, by defining R = (1 + INF) / (1 + INT), becomes
| NPV = C Rn |
To demonstrate that equation 74 produces almost exactly the same result as the standard LCC equation given by equation 73, typical long-term values of INF = 0.04 and INT = 0.08 will be used. Since the discount rate is conventionally treated as the difference between interest and inflation, DISC = 0.08 - 0.04 = 0.04 for this example. The following comparison can then be made for an action n = 10 years in the future:
equation 73: 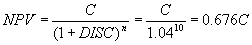 ¬
¬
equation 74: R = (1 + INF) / (1 + INT) = 1.04 / 1.08 = 0.963 NPV = C (0.963)10 = 0.686 C ¬
It is seen that the results are virtually identical, thus explaining the common practice in LCC analysis of defining the discount rate as the difference between the interest and inflation rates. Because equation 74 is slightly more accurate, it is used in the derivation that follows. However, it is first used to demonstrate that equation 72 is valid.
One way to check the validity of a derived expression is to create a hypothetical test case that can readily be calculated by hand, and then compare it to the result obtained with the derived equation. A convenient test case for equation 72 is the case in which a new pavement, designed to last D = 20 years, fails at exactly E = 10 years at which time it will be resurfaced. Historical data have shown that an overlay typically lasts about 10 years. Therefore, this unplanned-for overlay will restore the pavement to its originally intended design life of 20 years, after which it will continue to receive overlays at approximate 10-year intervals. In this special case, the only added expense beyond what has already been anticipated is the extra overlay in the 10th year. Using a more accurate value of R = (1 + INF) / (1 + INT) = 1.04 / 1.08 = 0.96296, the net present cost of this additional overlay can be determined by equation 72 (the derived equation) as
PAYADJ = -23.92 (0.9629620 - 0.9629610) / (1 - 0.9629610) = -$16.40/m2
or, by equation 74 (the more accurate version of the standard LCC analysis equation) as
PAYADJ = -23.92 (0.96296)10 = -$16.40/m2.
The exact agreement between the more accurate version of the standard LCC analysis approach and the derived equation provides convincing evidence that the derived equation will also provide the correct answer in other situations for which the standard LCC analysis method is not convenient, or would require an assumption about residual value. However, the actual proof is contained in the derivation that follows.
To derive equation 72, it is convenient to first write the expression for the net debit resulting from the rescheduling of any particular future overlay. For example, if a 20-year design pavement fails after 15 years, the two primary LCC analysis components associated with the rescheduling of the 20th-year overlay can be expressed as follows using equation 74 and the terms previously defined:
DEBIT (1) = C R15 |
| CREDIT(1) = C R 20 |
The net debit due to the rescheduling of the first overlay is then the difference of these two values or NETDEBIT(1) = C (R20 - R15). The series of debits due to the successive rescheduling of the future overlays, which are expected to occur at approximate 10-year intervals, is as follows:
NETDEBIT(1) = C (R20 - R15) |
| NETDEBIT(2) = C (R30 - R25) |
| NETDEBIT(3) = C (R40 - R35) |
NETDEBIT(4) = etc.
The total value in net-present-value terms is the sum of all the individual debits that, by segregating positive and negative terms, can be written as follows:
NPV = C [(R20 + R30 + R40 + _) - (R15 + R25 + R35 + _)] |
At this point it is convenient to write the equation in general terms:
| NPV = C [(RD + RD + O + RD + 2O + _) - (RE + RE + O + RE + 2O +... _)] |
This can be factored and rearranged as follows:
| NPV = C [RD(1 + RO + R2O + _) - RE(1 + RO + R2O + _)] | (82) |
| NPV = C (RD - RE) (1 + RO + R2O + _) |
The last term in parentheses in equation 83 is recognizable as a geometric progression. Because long-term inflation rates are always less than long-term interest rates, the ratio R will always be less than unity, thus causing the geometric progression to have a finite sum, as given by equation 84. (30)
1 + RO + R2O + _ = 1 / (1 - RO) |
Substituting this back into equation 83 completes the derivation, as shown in equation 85. In equation 72, the term PAYADJ is used in place of NPV because this equation applies to situations in which the change in expected life is estimated from construction characteristics that are under the contractor's control, thus providing the basis for rational payment-adjustment schedules. It should be noted that, in addition to justifying payment reductions for deficient quality, it appropriately awards incentive payments when superior quality extends the expected life of the pavement beyond the intended design life.
NPV = C (RD - RE) / (1 - RO) |
Two factors have been ignored in this derivation. One is relatively minor, but the other could have a substantial impact on the true costs. Routine annual maintenance costs have not been included because they are relatively small in comparison to construction costs, and may change very little when the overlays are rescheduled. User delay costs, however, may not only be large, they may be magnified when premature failure results in additional, unplanned-for overlays. Although they are difficult to quantify, it is quite apparent that delay costs can only add to the true cost of premature failure, suggesting that payment adjustments even larger than those produced by equation 72 are justified.
Using typical long-term values for interest and inflation of 0.08 and 0.04, respectively, the ratio R is found to be 1.04/1.08 = 0.963. Using this in either of equations 72 or 85, and assuming a present total cost of resurfacing of $23.97/m2, a design life for resurfacing of 10 years, and a typical overlay life of 10 years, the values in table 43 are obtained. It is seen from this table that the cost of premature failure can be substantial, terminating in this case at the initial cost of resurfacing of $23.92 $/m2 for zero expected life.
|
Expected Life, years |
Appropriate Payment Adjustment, $/m2 |
|---|---|
|
12 | +3.79 |
|
10 (Design) | 0.00 |
|
8 | -4.09 |
|
6 | -8.50 |
|
4 | -13.27 |
|
2 | -18.40 |
|
0 | -23.92 |