U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-046 Date: October 2004 |
Previous | Table of Contents | Next
As part of the acceptance procedures and requirements, one question that must be answered is "Who is going to perform the acceptance tests?" The agency may either decide to do the acceptance testing, assign the testing to the contractor, have a combination of agency and contractor acceptance testing, or require a third party to do the testing.
The decision as to who does the testing usually emanates from the agency's personnel assessment, particularly in the days of agency downsizing. Many agencies are requiring the contractor to do the acceptance testing. This is at least partially because of agency staff reductions. What has often evolved is that the contractor is required to perform both QC and acceptance testing. If the contractor is assigned the acceptance function, the contractor's acceptance tests must be verified by the agency. The agency's verification sampling and testing function has the same underlying function as the agency's acceptance sampling and testing-to verify the quality of the product. Statistically sound verification procedures must be developed that require a separate verification program. There are several forms of verification procedures and some forms are more efficient than others. To avoid conflict, it is in the best interests of both parties to make the verification process as effective and efficient as possible.
The sources of variability are important when deciding what type of verification procedures to use. This decision depends on what the agency wants to verify. Independent samples (i.e., those obtained without respect to each other) contain up to four sources of variability: material, process, sampling, and testing. Split samples contain variability only in the testing method. Thus, if the agency wishes to verify only that the contractor's testing methods are correct, then the use of split samples is best. This is referred to as test method verification. If the agency wishes to verify the contractor's overall production, sampling, and testing processes, then the use of independent samples is required. This is referred to as process verification. Each of these types of verification is evaluated in the following sections.
Before discussing the various procedures that can be used for test method verification or process verification, two concepts must be understood: hypothesis testing and level of significance. When it is necessary to test whether or not it is reasonable to accept an assumption about a set of data, statistical tests (called hypothesis tests) are conducted. Strictly speaking, a statistical test neither proves nor disproves a hypothesis. What it does is prescribe a formal manner in which evidence is to be examined to make a decision regarding whether or not the hypothesis is correct.
To perform a hypothesis test, it is first necessary to define an assumed set of conditions known as the null hypothesis (H0). Additionally, an alternative hypothesis (Ha) is, as the name implies, an alternative set of conditions that will be assumed to exist if the null hypothesis is rejected. The statistical procedure consists of assuming that the null hypothesis is true and then examining the data to see if there is sufficient evidence that it should be rejected. The H0 cannot actually be proved, only disproved. If the null hypothesis cannot be disproved (or, to be statistically correct, rejected), it should be stated that we fail to reject, rather than prove or accept, the hypothesis. In practice, some people use accept rather than fail to reject, although this is not exactly statistically correct.
Verification testing is simply hypothesis testing. For test method or process verification purposes, the null hypothesis would be that the contractor's tests and the agency's tests have equal means, while the alternate hypothesis would be that the means are not equal.
Hypothesis tests are conducted at a selected level of significance, α, where α is the probability of incorrectly rejecting the H0 when it is actually true. The value of α is typically selected as 0.10, 0.05, or 0.01. For example, if α = 0.01 and the null hypothesis is rejected, then there is only 1 chance in 100 that H0 is true and was rejected in error.
The performance of hypothesis tests, or verification tests, can be evaluated by using OC curves. OC curves plot either the probability of not detecting a difference (i.e., accepting the null hypothesis that the populations are equal) or the probability of detecting a difference (i.e., rejecting the null hypothesis that the populations are equal) versus the actual difference between the two populations being compared. Curves that plot the probability of detecting a difference are sometimes call power curves because they plot the power of the statistical test procedure to detect a given difference.
Just as there is a risk of incorrectly rejecting the H0 when it is actually true, which is called the type I (or α) error, there is also a risk of failing to reject the H0 when it is actually false. This is called the type II (or β) error. The power is the probability of rejecting the H0 when it is actually false and it is equal to 1 - β. Both α and β are important and are used with the OC curves when determining the appropriate sample size to be used.
The procedures for verifying the testing procedures should be based on split samples so that the testing method is the only source of variability present. The two procedures used most often for test method verification are: (1) comparing the difference between the split-sample results to a maximum allowable difference, and (2) the use of the t-test for paired measurements (i.e., the paired t-test). In this report, these are referred to as the maximum allowable difference and the paired t-test, respectively, and each is discussed below.
This is the simplest procedure that can be used for verification, although it is the least powerful. In this method, usually a single sample is split into two portions, with one portion tested by the contractor and the other portion tested by the agency. The difference between the two test results is then compared to a maximum allowable difference. Because the procedure uses only two test results, it cannot detect real differences unless the results are far apart.
The value selected for the maximum allowable difference is usually selected in the same manner as the D2S limits contained in many American Association of State Highway and Transportation Officials (AASHTO) and American Society for Testing and Materials (ASTM) test procedures. The D2S limit indicates the maximum acceptable difference between two results obtained on test portions of the same material (and thus applies only to split samples) and is provided for single- and multi-laboratory situations. It represents the difference between two individual test results that has approximately a 5-percent chance of being exceeded if the tests are actually from the same population.
Stated in general statistical terminology, the maximum allowable difference is set at two times the standard deviation of the distribution of the differences that would be obtained if the two test populations (the contractor's and the agency's) were actually equal. In other words, if the two populations are truly the same, there is approximately a 0.05 chance that this verification method will find them to be not equal. Therefore, the level of significance is 0.05 (5 percent).
OC Curves: OC curves were developed to evaluate the performance of the maximum allowable difference method for test method verification. In this method, a test is performed on a single split sample to compare the agency's and the contractor's test results. If we assume that both of these split test results are from normally distributed subpopulations, then we can calculate the variance of the difference and use it to calculate two standard deviation limits (approximately 95 percent) for the sample difference quantity.
Suppose that the agency's subpopulation has a variance ![]() and the contractor's subpopulation has a variance
and the contractor's subpopulation has a variance ![]() .
Since the variance of the difference in two independent random variables is
the sum of the variances, the variance of the difference in an agency's observation
and a contractor's observation is
.
Since the variance of the difference in two independent random variables is
the sum of the variances, the variance of the difference in an agency's observation
and a contractor's observation is ![]() +
+ ![]() .
The maximum allowable difference is based on the test standard deviation, which
may be provided in the form of D2S limits. Let us call this test standard deviation
.
The maximum allowable difference is based on the test standard deviation, which
may be provided in the form of D2S limits. Let us call this test standard deviation
![]() .
Under an assumption that
.
Under an assumption that ![]() ,
this variance of a difference becomes 2
,
this variance of a difference becomes 2![]() .
.
The maximum allowable difference limits are set as two times the standard deviation
of the test differences (i.e., approximately 95-percent limits). This, therefore,
sets the limits at ![]() ,
which is
,
which is ![]() (or
(or ![]() .
Without loss of generality, we can assume
.
Without loss of generality, we can assume ![]() ,
along with an assumption of a mean difference of 0, and use the standard normal
distribution with a region between -2.8284 and +2.8284 as the acceptance region
for the difference in an agency's test result and a contractor's test result.
With these two limits fixed, we can calculate the power of this decisionmaking
process relative to various true differences in the underlying subpopulation
means and/or various ratios of the true underlying subpopulation standard deviations.
,
along with an assumption of a mean difference of 0, and use the standard normal
distribution with a region between -2.8284 and +2.8284 as the acceptance region
for the difference in an agency's test result and a contractor's test result.
With these two limits fixed, we can calculate the power of this decisionmaking
process relative to various true differences in the underlying subpopulation
means and/or various ratios of the true underlying subpopulation standard deviations.
These power values can
conveniently be displayed as a three-dimensional surface. If we vary the mean
difference along the first axis and the standard deviation ratio along a second
axis, we can show power on the vertical axis. The agency's subpopulation, the
contractor's subpopulation, or both, could have standard deviations that are smaller,
about the same, or larger than the supplied ![]() value. To develop OC
curves, these situations were represented in terms of the minimum standard
deviation between the contractor's population and the agency's population as
follows:
value. To develop OC
curves, these situations were represented in terms of the minimum standard
deviation between the contractor's population and the agency's population as
follows:
Figures 45 through 47 show the OC
curves for each of the above cases. The power values are shown where the ratio
of the larger of the agency's or the contractor's standard deviation to the
smaller of the agency's or contractor's standard deviation is varied over the
values 0, 1, 2, 3, 4, and 5. The mean difference given along the horizontal
axis (values of 0, 1, 2, and 3) represents the difference in the agency's and
contractor's subpopulation means expressed as multiples of ![]() .
.
In figure 45, which shows the case when the minimum standard
deviation equals the test standard deviation (![]() ), even when the ratio of the contractor's and agency's
standard deviations is 5 and the difference between the contractor's and the agency's
means is three times the value for
), even when the ratio of the contractor's and agency's
standard deviations is 5 and the difference between the contractor's and the agency's
means is three times the value for ![]() , there is less than a 70-percent chance of detecting the
difference based on the results from a single split sample. As would be
expected, the power values decrease when the minimum standard deviation is half
of
, there is less than a 70-percent chance of detecting the
difference based on the results from a single split sample. As would be
expected, the power values decrease when the minimum standard deviation is half
of ![]() (figure 46) and
increase when the minimum standard deviation is twice
(figure 46) and
increase when the minimum standard deviation is twice ![]() (figure 47).
(figure 47).
As is the case with any method based on a sample size = 1, the D2S method does not have much power to detect the differences between the contractor's and the agency's populations. The appeal of the maximum allowable difference method lies in its simplicity, rather than in its power.
Average Run Length: The maximum allowable difference method was also evaluated based on the average run length. The average run length is the average number of lots that it takes to identify a difference between dissimilar populations. As such, the shorter the average run length, the better.
Various actual differences between the contractor's and the agency's population means and standard deviations were considered in the analysis. In the results that are presented, i refers to the difference (in units of the agency's population standard deviation) between the agency's and the contractor's population means. Also, j refers to the ratio of the contractor's population standard deviation to the agency's population standard deviation. In the analyses, i values of 0, 1, 2, and 3 were used, while the j values used were 0.5, 1.0, 1.5, and 2.0. Some examples of these i and j values are illustrated in figure 48.
Figure 45. OC surface for the maximum allowable difference test method verification method (assuming the
smaller σ = ![]() ).
).
Figure 46. OC surface for the maximum allowable difference test method verification method (assuming the smaller σ = 0.5 ![]() ).
).
Figure 47. OC surface for the maximum allowable difference test method verification method (assuming the
smaller σ = 2 ![]() ).
).
Figure 48a. Example 1 of some of the cases considered in the average run length analysis for the maximum allowable difference method.
Figure 48b. Example 2 of some of the cases considered in the average run length analysis for the maximum allowable difference method.
Figure 48c. Example 3 of some of the cases considered in the average run length analysis for the maximum allowable difference method.
The results of the analyses are presented in table 31 and figure 49. These values are based on 5000 simulated projects. As shown in the table, when i = 0 and j = 1.0 (meaning that the contractor's and the agency's populations are the same), the average run length is approximately 21.5 project lots. This is consistent with what would be expected. Since the limits are set at 2 standard deviations and since there is only 0.0455 chance of a value outside of 2 standard deviations, there is only 1 chance in 22 of declaring the populations to be different for this situation. It should also be noted in the table that the standard deviation values are nearly as large as the average run lengths. This means that for any individual simulated project, the run length could have varied greatly from the average. Indeed, for this case, the individual run lengths varied from 1 to more than 200.
Table 31 clearly shows that as the difference between the population means (i) increases, the average run length decreases since it is easier to detect a difference between the two populations. This is also true for the ratio of the population standard deviations (j).
Table 31. Average run length results for the single split-sample method (5000 simulated lots).
| Mean Difference, units of agency's σ | Contractor's σ |
Run Length | |
|---|---|---|---|
| Average | Std. Dev. | ||
| 0 | 0.5 | 85.57 | 85.44 |
| 1.0 | 21.55 | 20.88 | |
| 1.5 | 8.43 | 8.04 | |
| 2.0 | 4.83 | 4.19 | |
| 1 | 0.5 | 19.16 | 19.11 |
| 1.0 | 9.86 | 9.14 | |
| 1.5 | 5.83 | 5.25 | |
| 2.0 | 4.07 | 3.53 | |
| 2 | 0.5 | 4.38 | 3.82 |
| 1.0 | 3.58 | 3.03 | |
| 1.5 | 3.10 | 2.56 | |
| 2.0 | 2.67 | 2.09 | |
| 3 | 0.5 | 1.77 | 1.14 |
| 1.0 | 1.85 | 1.27 | |
| 1.5 | 1.88 | 1.29 | |
| 2.0 | 1.88 | 1.30 | |
Since the maximum allowable difference is not a very powerful test, another procedure that uses multiple test results to conduct a more powerful hypothesis test can be used. For the case in which it is desirable to compare more than one pair of split-sample test results, the t-test for paired measurements (i.e., the paired t-test) can be used. This test uses the differences between pairs of tests and determines whether the average difference is statistically different from zero. Thus, it is the difference within the pairs, not between the pairs, that is being tested. The t-statistic for the paired t-test is:
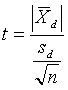 (7)
(7)
where: ![]() = average of the differences between the split-sample test results
= average of the differences between the split-sample test results
Sd = standard deviation of the differences between the split-sample test results
n = number of split samples
The calculated t-value is then compared to the critical value (tcrit) obtained from a table of t-values at a level of α/2 and n - 1 degrees of freedom. Computer programs, such as Microsoft® Excel, contain statistical test procedures for the paired t-test. This makes the implementation process straightforward.
OC Curves: OC curves can be consulted to evaluate the performance of the paired t-test in identifying the differences between population means. OC curves are useful in answering the question, "How many pairs of test results should be used?" This form of the OC curve, for a given level of α, plots on the vertical axis the probability of either not detecting (β) or detecting (1 - β) a difference between two populations. The standardized difference between the two population means is plotted on the horizontal axis.
For a paired t-test, the standardized difference (d) is measured as:
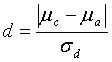 (8)
(8)
where: ![]() = true absolute difference between the mean
= true absolute difference between the mean ![]() of the contractor's test result population (which is unknown) and the mean
of the contractor's test result population (which is unknown) and the mean ![]() of the agency's test result population (which is unknown)
of the agency's test result population (which is unknown)
![]() = standard deviation of the true population of signed differences between the paired tests (which is unknown)
= standard deviation of the true population of signed differences between the paired tests (which is unknown)
The OC curves are developed for a given level of significance (α). OC curves for α values of 0.05 and 0.01 are shown in figures 49 and 50, respectively. It is evident from the OC curves that for any probability of not detecting a difference (β (value on the vertical axis)), the required n will increase as the difference (d) decreases (value on the horizontal axis). In some cases, the desired β or difference may require prohibitively large sample sizes. In that case, a compromise must be made between the discriminating power desired, the cost of the amount of testing required, and the risk of claiming a difference when none exists.
To use this OC curve, the true standard deviation of the signed differences (![]() ) is assumed to be known (or approximated based on past data or published literature). After experience is gained with the process,
) is assumed to be known (or approximated based on past data or published literature). After experience is gained with the process, ![]() can be more accurately defined and a better idea of the required number of tests can be determined.
can be more accurately defined and a better idea of the required number of tests can be determined.
As an example of how to use the OC curves, assume that the number of pairs of split-sample tests for verification of some test method is
desired. The probability of not detecting a difference (β) is chosen as 10 percent or 0.10. (Some OC curves, which are often called power curves, use 1 - β (known as the power of the test) on the vertical axis; however, the only difference is the scale change (in this case, 1 - β) being 90 percent or 0.90.) Assume that the absolute difference between ![]() and
and ![]() should not be greater than 20 units, that the standard deviation of the differences is 20 units, and that α is selected as 0.05. This produces a d value
of 20
should not be greater than 20 units, that the standard deviation of the differences is 20 units, and that α is selected as 0.05. This produces a d value
of 20 ![]() 20 = 1.0. Reading this value on the horizontal axis and a β of 0.20 on the vertical axis shows that about 10 paired split-sample tests are necessary for the comparison.
20 = 1.0. Reading this value on the horizontal axis and a β of 0.20 on the vertical axis shows that about 10 paired split-sample tests are necessary for the comparison.
Figure 49. OC curves for a two-sided t-test ( α = 0.05) (Natrella, M.G., "Experimental Statistics," National Bureau of Standards Handbook 91, 1963).
Figure 50. OC curves for a two-sided t-test ( α = 0.01) (Natrella, M.G., "Experimental Statistics," National Bureau of Standards Handbook 91, 1963).
Procedures to verify the overall process should be based on independent samples so that all of the components of variability (i.e., process, materials, sampling, and testing) are present. Two procedures for comparing independently obtained samples appear in the AASHTO Implementation Manual for Quality Assurance.(2) These two methods appear in the AASHTO manual in appendix G, which is based on the comparison of a single agency test with 5 to 10 contractor tests, and in appendix H, which is based on the use of the F-test and t-test to compare a number of agency tests with a number of contractor tests. These methods are referred to as the AASHTO appendix G method and the AASHTO appendix H method, respectively. Each of these methods is discussed and analyzed in the following sections.
In this method, a single agency test result must fall within an interval that
is defined from the average and range of 5 to 10 contractor test results. The
allowable interval within which the agency's test must fall is ![]() ,
where
,
where ![]() and
R are the mean and range, respectively, of the contractor's tests,
and C is a factor that varies with the number of contractor tests.
The factor C is the product of a factor to estimate the sample standard
deviation from the sample range and the t-value for the 99th
percentile of the t-distribution. This is not a particularly efficient
approach, although this statement can be made for any method that is based on
the use of a single agency test. Table 32 indicates the allowable interval based
on the number of contractor tests.
and
R are the mean and range, respectively, of the contractor's tests,
and C is a factor that varies with the number of contractor tests.
The factor C is the product of a factor to estimate the sample standard
deviation from the sample range and the t-value for the 99th
percentile of the t-distribution. This is not a particularly efficient
approach, although this statement can be made for any method that is based on
the use of a single agency test. Table 32 indicates the allowable interval based
on the number of contractor tests.
Table 32. Allowable intervals for the AASHTO appendix G method.
| Number of Contractor Tests | Allowable Interval |
|---|---|
| 10 | |
| 9 | |
| 8 | |
| 7 | |
| 6 | |
| 5 | |
OC Curves: Computer simulation was used to develop OC curves (plotted as power curves) that indicate the probability of detecting a difference between test populations with various differences in means and in the ratios of their standard deviations. The differences between the means of the contractor's and the agency's population
(![]() ),
stated in units of the agency's standard deviation, were varied from 0 to 3.0.
Various ratios of the contractor's standard deviation to the agency's standard
deviation (
),
stated in units of the agency's standard deviation, were varied from 0 to 3.0.
Various ratios of the contractor's standard deviation to the agency's standard
deviation (![]() )
were varied from 0.50 to 3.00.
)
were varied from 0.50 to 3.00.
Since there are two parameters that varied, OC surfaces were plotted, with each surface representing a different number of contractor tests (5 to 10) that were compared to a single agency test. These OC surfaces are shown in figure 51. As shown in the plots, the power of this procedure is quite low, even when a large number of contractor tests are used and when there are large differences in the means and standard deviations for the contractor's and the agency's populations. For example, for five contractor tests, even when the contractor's standard deviation is three times that of the agency and the contractor's mean is three of the agency's standard deviations from the agency's mean, there is less than a 50-percent chance of detecting a difference. Even if the number of contractor tests is 10, the probability of detecting a difference is still less than 60 percent.
Average Run Length: The method in appendix G was also evaluated based on the average run length. Various actual differences between the contractor's and the agency's population means and standard deviations were considered in the analysis. In the results that are presented, i refers to the difference (stated in units of the agency's population standard deviation) between the agency's and the contractor's population means. Also, j refers to the ratio of the contractor's population standard deviation to the agency's population standard deviation. In the analyses, i values of 0, 1, 2, and 3 were used, while j values of 0.5, 1.0, 1.5, and 2.0 were used.
The results of the simulation analyses, for the case of five contractor tests and one agency test per lot, are presented in table 33. The use of 5 and 10 contractor tests represents the upper and lower bounds, respectively, for the results since these are the fewest and most tests for the procedure. As shown in table 33, the run lengths can be quite large, particularly when the contractor's population standard deviation is larger than that of the agency. The values in the table are based on 5000 simulated projects.
Also note that the use of 10 tests gives a better performance than that of 5 tests when the contractor's standard deviation is equal to or less than that of the agency (ratios of 1.0 and 0.5). However, the opposite is true when the contractor's standard deviation is greater than that of the agency (ratios of 1.5 and 2.0). This is contrary to the desire to use a larger sample to identify the differences between the contractor's and the agency's populations.
Figure 51a. OC Surfaces (also called power surfaces) for the appendix G method for 5 contractor tests compared to a single agency test.
Figure 51b. OC surfaces (also called power surfaces) for the appendix G method for 6 contractor tests compared to a single agency test.
Figure 51c. OC surfaces (also called power surfaces) for the appendix G method for 7 contractor tests compared to a single agency test
Figure 51d. OC surfaces (also called power surfaces) for the appendix G method for 8 contractor tests compared to a single agency test.
Figure 51e. OC surfaces (also called power surfaces) for the appendix G method for 9 contractor tests compared to a single agency test.
Figure 51f. OC surfaces (also called power surfaces) for the appendix G method for 10 contractor tests compared to a single agency test.
Table 33. Average run length results for the appendix G method (5000 simulated lots).
| Mean Difference, units of agency's σ | Contractor's σ |
Run Length | ||
|---|---|---|---|---|
| Average | Std. Dev. | |||
| 5 Contractor Tests and 1 Agency Test | ||||
| 0 | 0.5 | 7.92 | 7.57 | |
| 1.0 | 43.30 | 42.68 | ||
| 1.5 | 124.19 | 126.40 | ||
| 2.0 | 234.45 | 234.56 | ||
| 1 | 0.5 | 4.04 | 3.51 | |
| 1.0 | 18.04 | 17.78 | ||
| 1.5 | 54.78 | 53.93 | ||
| 2.0 | 114.63 | 114.98 | ||
| 2 | 0.5 | 1.82 | 1.24 | |
| 1.0 | 6.21 | 5.69 | ||
| 1.5 | 17.61 | 17.23 | ||
| 2.0 | 39.30 | 38.33 | ||
| 3 | 0.5 | 1.22 | 0.51 | |
| 1.0 | 2.88 | 2.34 | ||
| 1.5 | 7.23 | 6.80 | ||
| 2.0 | 16.23 | 15.74 | ||
| 10 Contractor Tests and 1 Agency Test | ||||
| 0 | 0.5 | 5.15 | 4.70 | |
| 1.0 | 40.50 | 39.90 | ||
| 1.5 | 230.83 | 226.93 | ||
| 2.0 | 887.62 | 882.77 | ||
| 1 | 0.5 | 2.74 | 2.18 | |
| 1.0 | 12.76 | 12.04 | ||
| 1.5 | 62.33 | 61.14 | ||
| 2.0 | 229.00 | 227.47 | ||
| 2 | 0.5 | 1.39 | 0.73 | |
| 1.0 | 3.76 | 3.32 | ||
| 1.5 | 13.30 | 12.61 | ||
| 2.0 | 46.17 | 46.19 | ||
| 3 | 0.5 | 1.07 | 0.28 | |
| 1.0 | 1.75 | 1.20 | ||
| 1.5 | 4.46 | 3.94 | ||
| 2.0 | 12.77 | 12.15 | ||
This procedure involves two hypothesis tests where the null hypothesis for each test is that the contractor's tests and the agency's tests are from the same population. In other words, the null hypotheses are that the variability of the two data sets is equal for the F-test and that the means of the two data sets are equal for the t-test.
The procedures for the F-test and the t-test are more complicated and involved than that for the appendix G method discussed above. The F-test and the t-test approach also requires more agency test results before a comparison can be made. However, the use of the F-test and the t-test is much more statistically sound and has more power to detect actual differences than the appendix G method, which relies on a single agency test for the comparison. Any comparison method that is based on a single test result will not be very effective in detecting differences between data sets.
When comparing two data sets that are assumed to be normally distributed, it is important to compare both the means and the variances. A different test is used for each of these comparisons. The F-test provides a method for comparing the variances (standard deviations squared) of the two sets of data. The differences in the means are assessed by the t-test. To simplify the use of these tests, they are available as built-in functions in computer spreadsheet programs such as Microsoft® Excel. For this reason, the procedures involved are not discussed in this report. The procedures are fully discussed in the QA manual that was prepared as part of this project.(1)
A question that needs to be answered is: What power do these statistical tests have, when used with small to moderate sample sizes, to declare that various differences in the means and variances are statistically significant? This question is addressed separately for the F-test and the t-test with the development of the OC curves in the following sections.
F-Test for Variances (Equal Sample Sizes): Suppose that we have two sets of measurements that are assumed
to come from normally distributed populations and we wish to conduct a test to see if they come from populations that have the same variances (i.e., ![]() ). Furthermore, suppose that we select a level of significance of α = 0.05, meaning that we are allowing up to a 5-percent chance of incorrectly deciding that the variances are different when they are really the same. If we assume that these two samples are x1, x2,...xnx and y1, y2,...yny, we can calculate the sample variances and s2x and s2y construct:
). Furthermore, suppose that we select a level of significance of α = 0.05, meaning that we are allowing up to a 5-percent chance of incorrectly deciding that the variances are different when they are really the same. If we assume that these two samples are x1, x2,...xnx and y1, y2,...yny, we can calculate the sample variances and s2x and s2y construct:
![]() (9)
(9)
and ![]() accept for the values of F in the interval
accept for the values of F in the interval ![]() .
.
For this two-sided or two-tailed test, figure 52 shows the probability that we have accepted the two samples as coming from populations with the same variability. This probability is usually referred to as β and the power of the test is usually referred to as 1 - β. Notice that the horizontal axis is the quantity λ, where λ = σx/σy, the true standard deviation ratio. Thus, for λ = 1, where the hypothesis of equal variance should certainly be accepted, it is accepted with a probability of 0.95, reduced from 1.00 only by the magnitude of our type I error risk (α). One significant limiting factor for the use of figure 52 is the restriction that nx = ny = n. This limitation is addressed in subsequent sections of the report.
Example: Suppose that we have nx = 6 contractor tests and ny = 6 agency tests, conduct an α = 0.05 level test and accept (or fail to reject) that these two sets of tests represent populations with equal variances. What power did our test have to discern whether the populations from which these two sets of tests came were really rather different in variability? Suppose that the true population standard deviation of the contractor's tests (σx) was twice as large as that of the agency's tests (σy), giving λ = 2. If we enter figure 52 with λ = 2 and nx = ny = 6, we find that β ≈ 0.74 or that the power (1 - β) is 0.26. This tells us that with samples of nx = 6 and ny = 6, we only have a 26-percent chance of detecting a standard deviation ratio of 2 (and, correspondingly, a fourfold difference in variance) as being different.
Suppose that we are not comfortable with the power of 0.26, so subsequently we increase the number of tests used. Then suppose that we now have nx = 20 and ny = 20. If we again consider λ = 2, we can determine from figure 52 that the power of detecting these sets of tests as coming from populations with unequal variances to be more than 0.80 (approximately 82 to 83 percent). If we proceed to conduct our F-test with these two samples and conclude that the underlying variances are equal, we will certainly feel much more comfortable with our conclusions.
Figure 53 gives the appropriate OC curves to be used if we choose to conduct an α = 0.01 level test. Again, we see that for equal variances ![]() and
and ![]() (i.e., λ = 1), that β = 0.99, reduced from 1.00 only by the size of α.
(i.e., λ = 1), that β = 0.99, reduced from 1.00 only by the size of α.
F-Test for Variances (Unequal Sample Sizes): Up to now, the discussions and OC curves have been limited to equal sample sizes. Routines were developed for this project to calculate the power for this test for any combination of sample sizes nx and ny. There are obviously an infinite number of possible combinations for nx and ny. Thus, it is not possible to present OC curves for every possibility. However, three sets of tables were developed to provide a subset of power calculations using some sample sizes that are of potential interest for comparing the contractor's and the agency's samples. These power calculations are presented in table form since there are too many variables to be presented in a single chart, and the data can be presented in a more compact form in tables than in a long series of charts. Table 34 gives power values for all combinations of sample sizes of 3 to 10, with the ratio of the two subpopulation standard deviations = 1, 2, 3, 4, and 5. Table 35 gives power values for the same sample sizes, but with the standard deviation ratios = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0. Table 36 gives power values for all combinations for sample sizes = 5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, and 100, with the standard deviation ratio = 1, 2, or 3.
Figure 52. OC curves for the two-sided F-test for level of significance α = 0.05 (Bowker, A.H., and G.J. Lieberman, Engineering Statistics).
Figure 53. OC curves for the two-sided F-test for level of significance α = 0.01 (Bowker, A.H., and G.J. Lieberman, Engineering Statistics).
Table 34. F-test power values for n = 3-10 and s-ratio λ = 1-5.
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 3 | 3 | 0.05000 |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 4 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 5 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 6 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 7 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 8 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 9 | 3 | 0.05000 |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 10 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 2 | 3 | 3 | 0.09939 |
| 4 | 0.09753 | ||
| 5 | 0.09663 | ||
| 6 | 0.09620 | ||
| 7 | 0.09600 | ||
| 8 | 0.09590 | ||
| 9 | 0.09586 | ||
| 10 | 0.09585 | ||
| 4 | 3 | 0.14835 | |
| 4 | 0.15169 | ||
| 5 | 0.15385 | ||
| 6 | 0.15544 | ||
| 7 | 0.15668 | ||
| 8 | 0.15767 | ||
| 9 | 0.15848 | ||
| 10 | 0.15915 | ||
| 5 | 3 | 0.19036 | |
| 4 | 0.20240 | ||
| 5 | 0.21041 | ||
| 6 | 0.21622 | ||
| 7 | 0.22064 | ||
| 8 | 0.22413 | ||
| 9 | 0.22694 | ||
| 10 | 0.22926 | ||
| 6 | 3 | 0.22309 | |
| 4 | 0.24464 | ||
| 5 | 0.25968 | ||
| 6 | 0.27093 | ||
| 7 | 0.27968 | ||
| 8 | 0.28669 | ||
| 9 | 0.29243 | ||
| 10 | 0.29722 |
| λ | ny | nx | Power |
|---|---|---|---|
| 2 | 7 | 3 | 0.24820 |
| 4 | 0.27854 | ||
| 5 | 0.30055 | ||
| 6 | 0.31744 | ||
| 7 | 0.33086 | ||
| 8 | 0.34179 | ||
| 9 | 0.35087 | ||
| 10 | 0.35853 | ||
| 8 | 3 | 0.26768 | |
| 4 | 0.30567 | ||
| 5 | 0.33401 | ||
| 6 | 0.35619 | ||
| 7 | 0.37410 | ||
| 8 | 0.38888 | ||
| 9 | 0.40129 | ||
| 10 | 0.41187 | ||
| 9 | 3 | 0.28308 | |
| 4 | 0.32758 | ||
| 5 | 0.36144 | ||
| 6 | 0.38837 | ||
| 7 | 0.41036 | ||
| 8 | 0.42869 | ||
| 9 | 0.44421 | ||
| 10 | 0.45752 | ||
| 10 | 3 | 0.29549 | |
| 4 | 0.34549 | ||
| 5 | 0.38414 | ||
| 6 | 0.41521 | ||
| 7 | 0.44081 | ||
| 8 | 0.46230 | ||
| 9 | 0.48060 | ||
| 10 | 0.49639 | ||
| 3 | 3 | 3 | 0.19034 |
| 4 | 0.19354 | ||
| 5 | 0.19556 | ||
| 6 | 0.19696 | ||
| 7 | 0.19798 | ||
| 8 | 0.19875 | ||
| 9 | 0.19934 | ||
| 10 | 0.19981 | ||
| 4 | 3 | 0.31171 | |
| 4 | 0.33525 | ||
| 5 | 0.35007 | ||
| 6 | 0.36030 | ||
| 7 | 0.36777 | ||
| 8 | 0.37347 | ||
| 9 | 0.37795 | ||
| 10 | 0.38157 |
Table 34. F-test power values for n = 3-10 and s-ratio λ = 1-5 (continued).
| λ | ny | nx | Power |
|---|---|---|---|
| 3 | 5 | 3 | 0.39758 |
| 4 | 0.44454 | ||
| 5 | 0.47603 | ||
| 6 | 0.49872 | ||
| 7 | 0.51588 | ||
| 8 | 0.52931 | ||
| 9 | 0.54011 | ||
| 10 | 0.54899 | ||
| 6 | 3 | 0.45403 | |
| 4 | 0.51906 | ||
| 5 | 0.56396 | ||
| 6 | 0.59696 | ||
| 7 | 0.62225 | ||
| 8 | 0.64225 | ||
| 9 | 0.65846 | ||
| 10 | 0.67186 | ||
| 7 | 3 | 0.49230 | |
| 4 | 0.57007 | ||
| 5 | 0.62436 | ||
| 6 | 0.66443 | ||
| 7 | 0.69516 | ||
| 8 | 0.71943 | ||
| 9 | 0.73906 | ||
| 10 | 0.75523 | ||
| 8 | 3 | 0.51945 | |
| 4 | 0.60623 | ||
| 5 | 0.66693 | ||
| 6 | 0.71159 | ||
| 7 | 0.74565 | ||
| 8 | 0.77236 | ||
| 9 | 0.79378 | ||
| 10 | 0.81129 | ||
| 9 | 3 | 0.53955 | |
| 4 | 0.63285 | ||
| 5 | 0.69797 | ||
| 6 | 0.74560 | ||
| 7 | 0.78161 | ||
| 8 | 0.80958 | ||
| 9 | 0.83177 | ||
| 10 | 0.84970 | ||
| 10 | 3 | 0.55494 | |
| 4 | 0.65311 | ||
| 5 | 0.72136 | ||
| 6 | 0.77092 | ||
| 7 | 0.80803 | ||
| 8 | 0.83654 | ||
| 9 | 0.85890 | ||
| 10 | 0.87675 |
| λ | ny | nx | Power |
|---|---|---|---|
| 4 | 3 | 3 | 0.29251 |
| 4 | 0.30367 | ||
| 5 | 0.31010 | ||
| 6 | 0.31427 | ||
| 7 | 0.31717 | ||
| 8 | 0.31930 | ||
| 9 | 0.32093 | ||
| 10 | 0.32222 | ||
| 4 | 3 | 0.46558 | |
| 4 | 0.51179 | ||
| 5 | 0.54104 | ||
| 6 | 0.56126 | ||
| 7 | 0.57608 | ||
| 8 | 0.58742 | ||
| 9 | 0.59637 | ||
| 10 | 0.60363 | ||
| 5 | 3 | 0.56455 | |
| 4 | 0.63665 | ||
| 5 | 0.68356 | ||
| 6 | 0.71649 | ||
| 7 | 0.74084 | ||
| 8 | 0.75955 | ||
| 9 | 0.77437 | ||
| 10 | 0.78638 | ||
| 6 | 3 | 0.62143 | |
| 4 | 0.70759 | ||
| 5 | 0.76314 | ||
| 6 | 0.80150 | ||
| 7 | 0.82932 | ||
| 8 | 0.85027 | ||
| 9 | 0.86652 | ||
| 10 | 0.87943 | ||
| 7 | 3 | 0.65697 | |
| 4 | 0.75074 | ||
| 5 | 0.81002 | ||
| 6 | 0.84993 | ||
| 7 | 0.87808 | ||
| 8 | 0.89866 | ||
| 9 | 0.91416 | ||
| 10 | 0.92613 | ||
| 8 | 3 | 0.68090 | |
| 4 | 0.77901 | ||
| 5 | 0.83976 | ||
| 6 | 0.87961 | ||
| 7 | 0.90692 | ||
| 8 | 0.92628 | ||
| 9 | 0.94042 | ||
| 10 | 0.95100 |
| λ | ny | nx | Power |
|---|---|---|---|
| 4 | 9 | 3 | 0.69798 |
| 4 | 0.79871 | ||
| 5 | 0.85988 | ||
| 6 | 0.89907 | ||
| 7 | 0.92520 | ||
| 8 | 0.94321 | ||
| 9 | 0.95598 | ||
| 10 | 0.96525 | ||
| 10 | 3 | 0.71073 | |
| 4 | 0.81311 | ||
| 5 | 0.87423 | ||
| 6 | 0.91256 | ||
| 7 | 0.93751 | ||
| 8 | 0.95427 | ||
| 9 | 0.96583 | ||
| 10 | 0.97399 | ||
| 5 | 3 | 3 | 0.39165 |
| 4 | 0.41270 | ||
| 5 | 0.42481 | ||
| 6 | 0.43266 | ||
| 7 | 0.43815 | ||
| 8 | 0.44219 | ||
| 9 | 0.44530 | ||
| 10 | 0.44776 | ||
| 4 | 3 | 0.58713 | |
| 4 | 0.64932 | ||
| 5 | 0.68814 | ||
| 6 | 0.71467 | ||
| 7 | 0.73394 | ||
| 8 | 0.74858 | ||
| 9 | 0.76007 | ||
| 10 | 0.76932 | ||
| 5 | 3 | 0.68068 | |
| 4 | 0.76196 | ||
| 5 | 0.81171 | ||
| 6 | 0.84479 | ||
| 7 | 0.86811 | ||
| 8 | 0.88527 | ||
| 9 | 0.89836 | ||
| 10 | 0.90860 | ||
| 6 | 3 | 0.72975 | |
| 4 | 0.81790 | ||
| 5 | 0.86956 | ||
| 6 | 0.90223 | ||
| 7 | 0.92409 | ||
| 8 | 0.93936 | ||
| 9 | 0.95041 | ||
| 10 | 0.95864 |
| λ | ny | nx | Power |
|---|---|---|---|
| 5 | 7 | 3 | 0.75893 |
| 4 | 0.84940 | ||
| 5 | 0.90024 | ||
| 6 | 0.93086 | ||
| 7 | 0.95030 | ||
| 8 | 0.96318 | ||
| 9 | 0.97201 | ||
| 10 | 0.97824 | ||
| 8 | 3 | 0.77800 | |
| 4 | 0.86909 | ||
| 5 | 0.91845 | ||
| 6 | 0.94695 | ||
| 7 | 0.96423 | ||
| 8 | 0.97513 | ||
| 9 | 0.98225 | ||
| 10 | 0.98704 | ||
| 9 | 3 | 0.79133 | |
| 4 | 0.88238 | ||
| 5 | 0.93024 | ||
| 6 | 0.95690 | ||
| 7 | 0.97244 | ||
| 8 | 0.98184 | ||
| 9 | 0.98772 | ||
| 10 | 0.99150 | ||
| 10 | 3 | 0.80115 | |
| 4 | 0.89188 | ||
| 5 | 0.93838 | ||
| 6 | 0.96351 | ||
| 7 | 0.97767 | ||
| 8 | 0.98594 | ||
| 9 | 0.99092 | ||
| 10 | 0.99400 |
Table 35. F-test power values for n = 3-10 and s-ratio λ = 0-1.
| λ | ny | nx | Power |
|---|---|---|---|
| 0.0 | 3 | 3 | 1.00000 |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 4 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 5 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 6 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 7 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 8 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.0 | 9 | 3 | 1.00000 |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 10 | 3 | 1.00000 | |
| 4 | 1.00000 | ||
| 5 | 1.00000 | ||
| 6 | 1.00000 | ||
| 7 | 1.00000 | ||
| 8 | 1.00000 | ||
| 9 | 1.00000 | ||
| 10 | 1.00000 | ||
| 0.2 | 3 | 3 | 0.39165 |
| 4 | 0.58713 | ||
| 5 | 0.68068 | ||
| 6 | 0.72975 | ||
| 7 | 0.75893 | ||
| 8 | 0.77800 | ||
| 9 | 0.79133 | ||
| 10 | 0.80115 | ||
| 4 | 3 | 0.41270 | |
| 4 | 0.64932 | ||
| 5 | 0.76196 | ||
| 6 | 0.81790 | ||
| 7 | 0.84940 | ||
| 8 | 0.86909 | ||
| 9 | 0.88238 | ||
| 10 | 0.89188 | ||
| 5 | 3 | 0.42481 | |
| 4 | 0.68814 | ||
| 5 | 0.81171 | ||
| 6 | 0.86956 | ||
| 7 | 0.90024 | ||
| 8 | 0.91845 | ||
| 9 | 0.93024 | ||
| 10 | 0.93838 | ||
| 6 | 3 | 0.43266 | |
| 4 | 0.71467 | ||
| 5 | 0.84479 | ||
| 6 | 0.90223 | ||
| 7 | 0.93086 | ||
| 8 | 0.94695 | ||
| 9 | 0.95690 | ||
| 10 | 0.96351 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.2 | 7 | 3 | 0.43815 |
| 4 | 0.73394 | ||
| 5 | 0.86811 | ||
| 6 | 0.92409 | ||
| 7 | 0.95030 | ||
| 8 | 0.96423 | ||
| 9 | 0.97244 | ||
| 10 | 0.97767 | ||
| 8 | 3 | 0.44219 | |
| 4 | 0.74858 | ||
| 5 | 0.88527 | ||
| 6 | 0.93936 | ||
| 7 | 0.96318 | ||
| 8 | 0.97513 | ||
| 9 | 0.98184 | ||
| 10 | 0.98594 | ||
| 9 | 3 | 0.44530 | |
| 4 | 0.76007 | ||
| 5 | 0.89836 | ||
| 6 | 0.95041 | ||
| 7 | 0.97201 | ||
| 8 | 0.98225 | ||
| 9 | 0.98772 | ||
| 10 | 0.99092 | ||
| 10 | 3 | 0.44776 | |
| 4 | 0.76932 | ||
| 5 | 0.90860 | ||
| 6 | 0.95864 | ||
| 7 | 0.97824 | ||
| 8 | 0.98704 | ||
| 9 | 0.99150 | ||
| 10 | 0.99400 | ||
| 0.4 | 3 | 3 | 0.14221 |
| 4 | 0.22806 | ||
| 5 | 0.29564 | ||
| 6 | 0.34398 | ||
| 7 | 0.37868 | ||
| 8 | 0.40429 | ||
| 9 | 0.42380 | ||
| 10 | 0.43906 | ||
| 4 | 3 | 0.14250 | |
| 4 | 0.24034 | ||
| 5 | 0.32488 | ||
| 6 | 0.38884 | ||
| 7 | 0.43614 | ||
| 8 | 0.47159 | ||
| 9 | 0.49879 | ||
| 10 | 0.52015 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.4 | 5 | 3 | 0.14291 |
| 4 | 0.24808 | ||
| 5 | 0.34448 | ||
| 6 | 0.42028 | ||
| 7 | 0.47749 | ||
| 8 | 0.52079 | ||
| 9 | 0.55411 | ||
| 10 | 0.58029 | ||
| 6 | 3 | 0.14332 | |
| 4 | 0.25345 | ||
| 5 | 0.35863 | ||
| 6 | 0.44371 | ||
| 7 | 0.50889 | ||
| 8 | 0.55851 | ||
| 9 | 0.59674 | ||
| 10 | 0.62671 | ||
| 7 | 3 | 0.14369 | |
| 4 | 0.25739 | ||
| 5 | 0.36934 | ||
| 6 | 0.46187 | ||
| 7 | 0.53357 | ||
| 8 | 0.58837 | ||
| 9 | 0.63057 | ||
| 10 | 0.66355 | ||
| 8 | 3 | 0.14399 | |
| 4 | 0.26041 | ||
| 5 | 0.37772 | ||
| 6 | 0.47638 | ||
| 7 | 0.55351 | ||
| 8 | 0.61261 | ||
| 9 | 0.65804 | ||
| 10 | 0.69341 | ||
| 9 | 3 | 0.14424 | |
| 4 | 0.26278 | ||
| 5 | 0.38447 | ||
| 6 | 0.48825 | ||
| 7 | 0.56996 | ||
| 8 | 0.63266 | ||
| 9 | 0.68076 | ||
| 10 | 0.71805 | ||
| 10 | 3 | 0.14445 | |
| 4 | 0.26470 | ||
| 5 | 0.39001 | ||
| 6 | 0.49813 | ||
| 7 | 0.58375 | ||
| 8 | 0.64952 | ||
| 9 | 0.69984 | ||
| 10 | 0.73868 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.6 | 3 | 3 | 0.07564 |
| 4 | 0.10273 | ||
| 5 | 0.12665 | ||
| 6 | 0.14614 | ||
| 7 | 0.16173 | ||
| 8 | 0.17425 | ||
| 9 | 0.18444 | ||
| 10 | 0.19283 | ||
| 4 | 3 | 0.07283 | |
| 4 | 0.10212 | ||
| 5 | 0.13003 | ||
| 6 | 0.15430 | ||
| 7 | 0.17470 | ||
| 8 | 0.19170 | ||
| 9 | 0.20593 | ||
| 10 | 0.21791 | ||
| 5 | 3 | 0.07120 | |
| 4 | 0.10174 | ||
| 5 | 0.13222 | ||
| 6 | 0.15988 | ||
| 7 | 0.18396 | ||
| 8 | 0.20461 | ||
| 9 | 0.22225 | ||
| 10 | 0.23736 | ||
| 6 | 3 | 0.07022 | |
| 4 | 0.10157 | ||
| 5 | 0.13386 | ||
| 6 | 0.16407 | ||
| 7 | 0.19107 | ||
| 8 | 0.21472 | ||
| 9 | 0.23528 | ||
| 10 | 0.25314 | ||
| 7 | 3 | 0.06960 | |
| 4 | 0.10153 | ||
| 5 | 0.13516 | ||
| 6 | 0.16736 | ||
| 7 | 0.19675 | ||
| 8 | 0.22292 | ||
| 9 | 0.24600 | ||
| 10 | 0.26628 | ||
| 8 | 3 | 0.06919 | |
| 4 | 0.10155 | ||
| 5 | 0.13622 | ||
| 6 | 0.17003 | ||
| 7 | 0.20139 | ||
| 8 | 0.22972 | ||
| 9 | 0.25499 | ||
| 10 | 0.27741 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.6 | 9 | 3 | 0.06891 |
| 4 | 0.10161 | ||
| 5 | 0.13711 | ||
| 6 | 0.17223 | ||
| 7 | 0.20526 | ||
| 8 | 0.23545 | ||
| 9 | 0.26265 | ||
| 10 | 0.28698 | ||
| 10 | 3 | 0.06870 | |
| 4 | 0.10168 | ||
| 5 | 0.13786 | ||
| 6 | 0.17409 | ||
| 7 | 0.20854 | ||
| 8 | 0.24035 | ||
| 9 | 0.26925 | ||
| 10 | 0.29529 | ||
| 0.8 | 3 | 3 | 0.05467 |
| 4 | 0.06163 | ||
| 5 | 0.06758 | ||
| 6 | 0.07248 | ||
| 7 | 0.07649 | ||
| 8 | 0.07980 | ||
| 9 | 0.08255 | ||
| 10 | 0.08487 | ||
| 4 | 3 | 0.05202 | |
| 4 | 0.05929 | ||
| 5 | 0.06587 | ||
| 6 | 0.07156 | ||
| 7 | 0.07642 | ||
| 8 | 0.08057 | ||
| 9 | 0.08412 | ||
| 10 | 0.08719 | ||
| 5 | 3 | 0.05017 | |
| 4 | 0.05755 | ||
| 5 | 0.06448 | ||
| 6 | 0.07067 | ||
| 7 | 0.07612 | ||
| 8 | 0.08090 | ||
| 9 | 0.08508 | ||
| 10 | 0.08875 | ||
| 6 | 3 | 0.04883 | |
| 4 | 0.05626 | ||
| 5 | 0.06340 | ||
| 6 | 0.06995 | ||
| 7 | 0.07584 | ||
| 8 | 0.08109 | ||
| 9 | 0.08577 | ||
| 10 | 0.08994 |
| λ | ny | nx | Power |
|---|---|---|---|
| 0.8 | 7 | 3 | 0.04785 |
| 4 | 0.05529 | ||
| 5 | 0.06258 | ||
| 6 | 0.06938 | ||
| 7 | 0.07560 | ||
| 8 | 0.08124 | ||
| 9 | 0.08633 | ||
| 10 | 0.09092 | ||
| 8 | 3 | 0.04709 | |
| 4 | 0.05453 | ||
| 5 | 0.06193 | ||
| 6 | 0.06893 | ||
| 7 | 0.07541 | ||
| 8 | 0.08136 | ||
| 9 | 0.08680 | ||
| 10 | 0.09175 | ||
| 9 | 3 | 0.04650 | |
| 4 | 0.05393 | ||
| 5 | 0.06141 | ||
| 6 | 0.06856 | ||
| 7 | 0.07527 | ||
| 8 | 0.08148 | ||
| 9 | 0.08721 | ||
| 10 | 0.09248 | ||
| 10 | 3 | 0.04603 | |
| 4 | 0.05345 | ||
| 5 | 0.06099 | ||
| 6 | 0.06827 | ||
| 7 | 0.07516 | ||
| 8 | 0.08159 | ||
| 9 | 0.08757 | ||
| 10 | 0.09312 | ||
| 1.0 | 3 | 3 | 0.05000 |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 4 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 1.0 | 5 | 3 | 0.05000 |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 6 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 7 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 8 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 9 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 | ||
| 10 | 3 | 0.05000 | |
| 4 | 0.05000 | ||
| 5 | 0.05000 | ||
| 6 | 0.05000 | ||
| 7 | 0.05000 | ||
| 8 | 0.05000 | ||
| 9 | 0.05000 | ||
| 10 | 0.05000 |
Table 36. F-test power values for n = 5-100 and s-ratio λ = 1-3.
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 5 | 5 | 0.05 |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 10 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 15 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 |
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 20 | 5 | 0.05 |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 25 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 30 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 |
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 40 | 5 | 0.05 |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 50 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 60 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 |
Table 36. F-test power values for n = 5-100 and s-ratio λ = 1-3 (continued).
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 70 | 5 | 0.05 |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 80 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 90 | 5 | 0.05 | |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 |
| λ | ny | nx | Power |
|---|---|---|---|
| 1 | 100 | 5 | 0.05 |
| 10 | 0.05 | ||
| 15 | 0.05 | ||
| 20 | 0.05 | ||
| 25 | 0.05 | ||
| 30 | 0.05 | ||
| 40 | 0.05 | ||
| 50 | 0.05 | ||
| 60 | 0.05 | ||
| 70 | 0.05 | ||
| 80 | 0.05 | ||
| 90 | 0.05 | ||
| 100 | 0.05 | ||
| 2 | 5 | 5 | 0.21041 |
| 10 | 0.22926 | ||
| 15 | 0.23658 | ||
| 20 | 0.24043 | ||
| 25 | 0.24281 | ||
| 30 | 0.24442 | ||
| 40 | 0.24646 | ||
| 50 | 0.24770 | ||
| 60 | 0.24853 | ||
| 70 | 0.24913 | ||
| 80 | 0.24958 | ||
| 90 | 0.24993 | ||
| 100 | 0.25022 | ||
| 10 | 5 | 0.38414 | |
| 10 | 0.49639 | ||
| 15 | 0.55109 | ||
| 20 | 0.58353 | ||
| 25 | 0.60501 | ||
| 30 | 0.62027 | ||
| 40 | 0.64053 | ||
| 50 | 0.65336 | ||
| 60 | 0.66221 | ||
| 70 | 0.66869 | ||
| 80 | 0.67363 | ||
| 90 | 0.67753 | ||
| 100 | 0.68068 |
| λ | ny | nx | Power |
|---|---|---|---|
| 2 | 15 | 5 | 0.45487 |
| 10 | 0.62152 | ||
| 15 | 0.70573 | ||
| 20 | 0.75560 | ||
| 25 | 0.78820 | ||
| 30 | 0.81099 | ||
| 40 | 0.84054 | ||
| 50 | 0.85870 | ||
| 60 | 0.87092 | ||
| 70 | 0.87969 | ||
| 80 | 0.88626 | ||
| 90 | 0.89137 | ||
| 100 | 0.89545 | ||
| 20 | 5 | 0.49087 | |
| 10 | 0.68548 | ||
| 15 | 0.78230 | ||
| 20 | 0.83747 | ||
| 25 | 0.87192 | ||
| 30 | 0.89495 | ||
| 40 | 0.92304 | ||
| 50 | 0.93906 | ||
| 60 | 0.94918 | ||
| 70 | 0.95606 | ||
| 80 | 0.96099 | ||
| 90 | 0.96468 | ||
| 100 | 0.96753 | ||
| 25 | 5 | 0.51241 | |
| 10 | 0.72299 | ||
| 15 | 0.82516 | ||
| 20 | 0.88085 | ||
| 25 | 0.91389 | ||
| 30 | 0.93485 | ||
| 40 | 0.95864 | ||
| 50 | 0.97099 | ||
| 60 | 0.97817 | ||
| 70 | 0.98272 | ||
| 80 | 0.98578 | ||
| 90 | 0.98795 | ||
| 100 | 0.98955 |
Table 36. F-test power values for n = 5-100 and s-ratio λ = 1-3 (continued).
| λ | ny | nx | Power |
|---|---|---|---|
| 2 | 30 | 5 | 0.52669 |
| 10 | 0.74730 | ||
| 15 | 0.85174 | ||
| 20 | 0.90637 | ||
| 25 | 0.93725 | ||
| 30 | 0.95585 | ||
| 40 | 0.97551 | ||
| 50 | 0.98476 | ||
| 60 | 0.98968 | ||
| 70 | 0.99256 | ||
| 80 | 0.99436 | ||
| 90 | 0.99556 | ||
| 100 | 0.99639 | ||
| 40 | 5 | 0.54439 | |
| 10 | 0.77664 | ||
| 15 | 0.88220 | ||
| 20 | 0.93379 | ||
| 25 | 0.96067 | ||
| 30 | 0.97548 | ||
| 40 | 0.98924 | ||
| 50 | 0.99462 | ||
| 60 | 0.99702 | ||
| 70 | 0.99821 | ||
| 80 | 0.99886 | ||
| 90 | 0.99923 | ||
| 100 | 0.99945 | ||
| 50 | 5 | 0.55491 | |
| 10 | 0.79358 | ||
| 15 | 0.89881 | ||
| 20 | 0.94770 | ||
| 25 | 0.97160 | ||
| 30 | 0.98387 | ||
| 40 | 0.99414 | ||
| 50 | 0.99757 | ||
| 60 | 0.99888 | ||
| 70 | 0.99943 | ||
| 80 | 0.99969 | ||
| 90 | 0.99982 | ||
| 100 | 0.99989 |
| λ | ny | nx | Power |
|---|---|---|---|
| 2 | 60 | 5 | 0.56187 |
| 10 | 0.80456 | ||
| 15 | 0.90914 | ||
| 20 | 0.95588 | ||
| 25 | 0.97764 | ||
| 30 | 0.98820 | ||
| 40 | 0.99632 | ||
| 50 | 0.99869 | ||
| 60 | 0.99948 | ||
| 70 | 0.99977 | ||
| 80 | 0.99989 | ||
| 90 | 0.99995 | ||
| 100 | 0.99997 | ||
| 70 | 5 | 0.56683 | |
| 10 | 0.81224 | ||
| 15 | 0.91614 | ||
| 20 | 0.96120 | ||
| 25 | 0.98137 | ||
| 30 | 0.99073 | ||
| 40 | 0.99745 | ||
| 50 | 0.99921 | ||
| 60 | 0.99972 | ||
| 70 | 0.99989 | ||
| 80 | 0.99996 | ||
| 90 | 0.99998 | ||
| 100 | 0.99999 | ||
| 80 | 5 | 0.57053 | |
| 10 | 0.81791 | ||
| 15 | 0.92118 | ||
| 20 | 0.96490 | ||
| 25 | 0.98387 | ||
| 30 | 0.99235 | ||
| 40 | 0.99810 | ||
| 50 | 0.99947 | ||
| 60 | 0.99984 | ||
| 70 | 0.99994 | ||
| 80 | 0.99998 | ||
| 90 | 0.99999 | ||
| 100 | 1.00000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 2 | 90 | 5 | 0.57339 |
| 10 | 0.82226 | ||
| 15 | 0.92497 | ||
| 20 | 0.96762 | ||
| 25 | 0.98564 | ||
| 30 | 0.99345 | ||
| 40 | 0.99851 | ||
| 50 | 0.99962 | ||
| 60 | 0.99989 | ||
| 70 | 0.99997 | ||
| 80 | 0.99999 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 100 | 5 | 0.57568 | |
| 10 | 0.82571 | ||
| 15 | 0.92793 | ||
| 20 | 0.96968 | ||
| 25 | 0.98696 | ||
| 30 | 0.99425 | ||
| 40 | 0.99879 | ||
| 50 | 0.99972 | ||
| 60 | 0.99993 | ||
| 70 | 0.99998 | ||
| 80 | 0.99999 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 3 | 5 | 5 | 0.47603 |
| 10 | 0.54899 | ||
| 15 | 0.57700 | ||
| 20 | 0.59187 | ||
| 25 | 0.60108 | ||
| 30 | 0.60736 | ||
| 40 | 0.61537 | ||
| 50 | 0.62026 | ||
| 60 | 0.62355 | ||
| 70 | 0.62593 | ||
| 80 | 0.62772 | ||
| 90 | 0.62911 | ||
| 100 | 0.63024 |
| λ | ny | nx | Power |
|---|---|---|---|
| 3 | 10 | 5 | 0.72136 |
| 10 | 0.87675 | ||
| 15 | 0.92836 | ||
| 20 | 0.95158 | ||
| 25 | 0.96404 | ||
| 30 | 0.97154 | ||
| 40 | 0.97985 | ||
| 50 | 0.98420 | ||
| 60 | 0.98681 | ||
| 70 | 0.98853 | ||
| 80 | 0.98973 | ||
| 90 | 0.99062 | ||
| 100 | 0.99130 | ||
| 15 | 5 | 0.78336 | |
| 10 | 0.93786 | ||
| 15 | 0.97640 | ||
| 20 | 0.98918 | ||
| 25 | 0.99431 | ||
| 30 | 0.99669 | ||
| 40 | 0.99860 | ||
| 50 | 0.99928 | ||
| 60 | 0.99957 | ||
| 70 | 0.99972 | ||
| 80 | 0.99980 | ||
| 90 | 0.99985 | ||
| 100 | 0.99988 | ||
| 20 | 5 | 0.80975 | |
| 10 | 0.95808 | ||
| 15 | 0.98816 | ||
| 20 | 0.99597 | ||
| 25 | 0.99841 | ||
| 30 | 0.99930 | ||
| 40 | 0.99982 | ||
| 50 | 0.99994 | ||
| 60 | 0.99998 | ||
| 70 | 0.99999 | ||
| 80 | 0.99999 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 3 | 25 | 5 | 0.82417 |
| 10 | 0.96743 | ||
| 15 | 0.99254 | ||
| 20 | 0.99797 | ||
| 25 | 0.99936 | ||
| 30 | 0.99977 | ||
| 40 | 0.99996 | ||
| 50 | 0.99999 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 30 | 5 | 0.83321 | |
| 10 | 0.97267 | ||
| 15 | 0.99463 | ||
| 20 | 0.99877 | ||
| 25 | 0.99968 | ||
| 30 | 0.99990 | ||
| 40 | 0.99999 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 40 | 5 | 0.84390 | |
| 10 | 0.97822 | ||
| 15 | 0.99654 | ||
| 20 | 0.99938 | ||
| 25 | 0.99987 | ||
| 30 | 0.99997 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 3 | 50 | 5 | 0.84999 |
| 10 | 0.98107 | ||
| 15 | 0.99738 | ||
| 20 | 0.99960 | ||
| 25 | 0.99993 | ||
| 30 | 0.99999 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 60 | 5 | 0.85393 | |
| 10 | 0.98279 | ||
| 15 | 0.99783 | ||
| 20 | 0.99971 | ||
| 25 | 0.99996 | ||
| 30 | 0.99999 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 70 | 5 | 0.85668 | |
| 10 | 0.98394 | ||
| 15 | 0.99812 | ||
| 20 | 0.99976 | ||
| 25 | 0.99997 | ||
| 30 | 1.00000 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 |
| λ | ny | nx | Power |
|---|---|---|---|
| 3 | 80 | 5 | 0.85871 |
| 10 | 0.98476 | ||
| 15 | 0.99831 | ||
| 20 | 0.99980 | ||
| 25 | 0.99998 | ||
| 30 | 1.00000 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 90 | 5 | 0.86026 | |
| 10 | 0.98537 | ||
| 15 | 0.99844 | ||
| 20 | 0.99983 | ||
| 25 | 0.99998 | ||
| 30 | 1.00000 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 | ||
| 100 | 5 | 0.86150 | |
| 10 | 0.98584 | ||
| 15 | 0.99855 | ||
| 20 | 0.99985 | ||
| 25 | 0.99998 | ||
| 30 | 1.00000 | ||
| 40 | 1.00000 | ||
| 50 | 1.00000 | ||
| 60 | 1.00000 | ||
| 70 | 1.00000 | ||
| 80 | 1.00000 | ||
| 90 | 1.00000 | ||
| 100 | 1.00000 |
From these tables, it is obvious that the limiting factor in how well the F-test will be able to identify differences will be the number of agency verification tests. The power of the F-test is limited not by the larger of the sample sizes, but by the smaller of the sample sizes. For example, in table 34, when nx = 3 and ny = 10, the power is only about 20 percent, even when there is a threefold difference in the true standard deviations (i.e., λ = 3). The limiting aspect of the smaller sample size is also noticeable in table 36 for larger sample sizes. For example, for λ = 2 and for ny = 100, the power when nx = 5 is only about 25 percent. The power increases to 68 percent for nx = 10, 90 percent for nx = 15, and 97 percent for nx = 20. Since the agency will have fewer verification tests than the number of contractor tests, the agency's verification sampling and testing rate will determine the power to identify variability differences when they exist.
t-Test for Means: As with the appendix G method, the performance of the t-test for means can be evaluated with OC curves or by considering the average run length.
OC Curves: Suppose that we have two sets of measurements that
are assumed to be from normally distributed populations and that we wish to
conduct a two-sided or two-tailed test to see if these populations have equal
means (i.e., m x = m y).
Suppose that we assume that these two samples are from populations with unknown,
but equal, variances. If these two samples are x1, x2...,
xnx, with sample mean ![]() and
sample variance s2x, and y1, y2,..., yny, with
sample mean
and
sample variance s2x, and y1, y2,..., yny, with
sample mean ![]() and sample variance s2y, we can calculate:
and sample variance s2y, we can calculate:
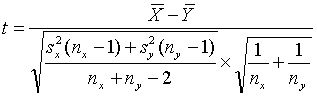 (10)
(10)
and accept H0: μx = μ x for values of t in the interval [-t α/2, n x+ny-2, t α/2, n x+ny-2].
For this test, figure 49 or 50, depending on the α value, shows the probability that we have accepted the two samples as coming from populations with the same means. The horizontal axis scale is:
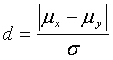 (11)
(11)
where: σ = σx = σ y = true common population standard deviation
We can access the OC curves in figure 49 or 50 with a value for d of d* and a value for n of n'
where:
![]() (12)
(12)
and
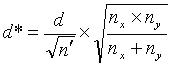 (13)
(13)
Example: Suppose that we have nx = 8 contractor tests and ny = 8 agency tests, conduct an α = 0.05 level test and accept that these two sets of tests represent populations with equal means. What power did our test really have to discern if the populations from which these two sets of tests came had different means? Suppose that we consider a difference in these population means of 2 or more standard deviations as a noteworthy difference that we would like to detect with high probability. This would indicate that we are interested in d = 2. Calculating
![]() (14)
(14)
and
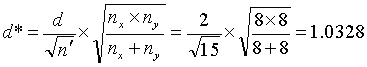 (15)
(15)
we find from figure 50 that β ≈ 0.05, so that our power of detecting a mean difference of 2 or more standard deviations would be approximately 95 percent.
Now suppose that we consider an application where we still have a total of 16 tests, but with nx = 12 contractor tests and ny = 4 agency tests. Suppose that we are again interested in the t-test performance in detecting a means difference of 2 standard deviations. Again, calculating
![]() (16)
(16)
but now
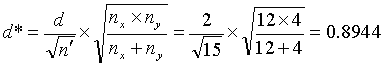 (17)
(17)
we find from figure 50 that β ≈ 0.12, indicating that our power of detecting a mean difference of 2 or more standard deviations would be approximately 88 percent.
Figure 51 gives the appropriate OC curves for use in conducting an α = 0.01 level test on the means. This figure is accessed in the same manner as described above for figure 50.
Average Run Length: The effectiveness of the t-test procedure was evaluated by determining the average run length in terms of project lots. The evaluation was performed by simulating 1000 projects and determining, on average, how many lots it took to determine that there was a difference between the contractor's and the agency's population means.
The results of the simulation analyses, for the case of five contractor tests and one agency test per lot, are presented in table 37. The results are shown only for the case where five contractor tests and one agency test are performed on each project lot. Similar results were obtained for cases where fewer and more contractor tests were conducted per lot. As shown in table 37, when there is no difference between the population means, the run lengths are quite large (as they should be). The values with asterisks are biased on the low side, because to speed up the simulation time, the maximum run lengths were limited to 100. Therefore, the actual average run length would be greater than those shown in the table since the maximum cutoff value was reached in more than half of the 1000 projects simulated for each i and j combination.
The average run lengths become relatively small as the actual difference between the contractor's and the agency's population means increases. This is obviously what is desired.
Table 37. Average run length results for the appendix H method (5 contractor tests and 1 agency test per lot) for 1000 simulated lots.
| Mean Difference, units of agency's σ | Contractor'sσ |
Run Length | |
|---|---|---|---|
| Average | Std. Dev. | ||
| 0 | 0.5 | 55.47* | 46.01* |
| 1.0 | 70.15* | 41.91* | |
| 1.5 | 77.78* | 36.95* | |
| 2.0 | 75.72* | 38.56* | |
| 1 | 0.5 | 4.83 | 4.05 |
| 1.0 | 5.75 | 4.28 | |
| 1.5 | 8.63 | 5.70 | |
| 2.0 | 9.83 | 5.94 | |
| 2 | 0.5 | 2.60 | 1.18 |
| 1.0 | 2.64 | 1.02 | |
| 1.5 | 3.51 | 1.52 | |
| 2.0 | 4.40 | 2.03 | |
| 3 | 0.5 | 2.35 | 0.73 |
| 1.0 | 2.10 | 0.37 | |
| 1.5 | 2.36 | 0.66 | |
| 2.0 | 2.88 | 1.03 | |
*These values are lower than the actual values. To reduce the simulation processing time, the maximum number of lots was limited to 100. For these cases, more than half of the projects were truncated at 100 lots.
Based on the analyses that were conducted and were summarized in this chapter, the following recommendations were made:
The comparison of a single split sample by using the maximum allowable limits (such as the D2S limits) is simple and can be done for each split sample that is obtained. However, since it is based on comparing only single data values, it is not very powerful for identifying differences where they exist. It is recommended that each individual split sample be compared using the maximum allowable limits, but that the paired t-test also be used on the accumulated split-sample results to allow for a comparison with more discerning power. If either of these comparisons indicates a difference, then an investigation to identify the cause of the difference should be initiated.
Since they are both based on five contractor tests and one agency test per lot, the results in tables 33 and 37 can be used to compare the appendix H and appendix G methods. The average run lengths for the appendix H method (t-test) were better than those for the appendix G method (single agency test compared to five contractor tests). Compared to the appendix G method, the appendix H method had longer average run lengths where there was no difference in the means and shorter lengths where there was a difference in the means. This is what is desirable in the verification procedure. The appendix H method is recommended for use in verifying the contractor's test results when the agency obtains independent samples for evaluating the total process.
From the OC curves that were developed, it is apparent that the number of agency verification tests will be the deciding factor when determining the validity of the contractor's overall process. When using the OC curves in figure 50 or 51, the lower the value of d*, the lower the power of the test for a given number of test results. The value for d* will decrease as the agency's portion of the total number of tests declines (this is shown in equation 13). If, in the expression under the square root sign, the total number of tests (nx + ny) is fixed, then the value of d* will decrease as the value of either nx or ny goes down.
An example will illustrate this point. Suppose that the total of nx + ny is fixed at 16, then the maximum value under the square root sign will be when nx = ny = 8. This is true because the denominator is fixed at 16 and 8 ' 8 = 64 is larger than any other combination of numbers that total 16. As one of the values gets smaller (and the other gets correspondingly larger), the product of the two numbers will decrease, thereby decreasing d* and reducing the power of the test.
The amount of verification sampling and testing is a subjective decision for each individual agency. However, with the OC (or power) curves and tables in this chapter, an agency can determine the risks that are associated with any frequency of verification testing and can make an informed decision regarding this testing frequency.
When using the appendix H method, first, an F-test is used to determine whether or not the variances (and, hence, standard deviations) are different for the two populations. The result of the F-test determines how the subsequent t-test is conducted to compare the averages of the contractor's and the agency's test results. Given some of the low powers associated with small sample sizes in tables 34 through 36, it could be argued that an agency will rarely be able to conclude from the F-test that a difference in variances exists. Given this fact, it may be reasonable to just assume that the populations have equal variances and run the t-test for equal variances and ignore the F-test altogether. This argument has some merit. However, with the ease of conducting the F-test and the t-test by computer, once the test results are input, there is essentially no additional effort associated with conducting the F-test before the t-test.