U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-127 Date: January 2006 |
Previous | Table of Contents | Next
Chapter 3 of the first volume in this report series documents the models that were identified and the ones selected for incorporation into HIPERPAV II. This appendix provides a detailed description of the models that were selected. The models incorporated are divided into:
A number of potential model enhancements were identified over the course of previous implementation efforts of HIPERPAV I. In this section, early-age behavior models incorporated into HIPERPAV II are presented. These models are divided in the following categories:
All other models in HIPERPAV I that were kept in HIPERPAV II are not presented here because they have been defined previously elsewhere.(1, 2, 3) Figure 1 shows a schematic of the enhancements made to the early-age behavior models in HIPERPAV II.
During the development of this project, the project team closely followed recent developments by the University of Texas at Austin on characterization of cement and admixtures. Based on these findings, improved models capable of predicting the hydration development of concrete mixes based on chemical composition of the cement and mix proportions were incorporated in HIPERPAV II. These models are based on a database of U.S. cements as shown in table 4. (4)
* Improved models
Figure 1. HIPERPAV early-age behavior framework showing improved models in HIPERPAV II.
| Calibration Data Sources |
Portland Cement Association (PCA)—Lerch and Ford(5) |
Schindler(4) Materials Characterization Phase |
|---|---|---|
| U.S. cements sources. Eight Type I, five Type II, three Type III, three Type IV, one Type V. All cement properties known. Well known and recognized data source. Conduction calorimeter heat of solution tests. |
Texas materials. Three different cement sources. Different fineness. Class C and F fly ash. GGBF slag. All cement properties known. Semiadiabatic testing. |
|
| Validation Data Sources |
Kjellsen et al.(6) | Schindler(4) Field Work Phase |
| Swedish cements source. All cement properties known. Type I cement. Nonevaporable water calculations. |
Texas materials. Typical paving mixtures. Different cements. All cement properties known. Field data collected. Mixed usage of Class C and F fly ash, and GGBF slag. Semiadiabatic testing. |
The model used in HIPERPAV II to predict the hydration of a cementitious mixture is presented below. The degree of hydration is defined as in equation 1:
where,
![]() (te) = degree of hydration at equivalent age, te,
(te) = degree of hydration at equivalent age, te,
te = equivalent age at reference temperature (21.1°C), (hours (h)),
u = ultimate degree of hydration,![]() = hydration time parameter (h), and
= hydration time parameter (h), and![]() = hydration shape parameter.
= hydration shape parameter.
The rate of heat liberation is defined as in equation 2:
where,
Qh(te) = rate of heat liberation at equivalent age, te, (Watts per cubed meter (W/m3)),
E = AE (J/mol),
R = universal gas constant (8.3144 J/mol/°C),
Tc = nodal PCC temperature (°C),
Tr = reference PCC temperature (°C),
Cc = cementitious materials content (kilogram per cubed meter (kg/m3)), and
Hu = total heat of hydration of cementitious materials at 100 percent hydration (J/kg), defined as in equation 3:
where,
pSLAG = slag mass ratio to total cementitious content,
pFA = fly ash mass ratio to total cementitious content,
pFA-CaO = fly ash CaO mass ratio to total fly ash content,
pcem = cement mass ratio to total cementitious content, and
Hcem = heat of hydration of the cement, defined by Bogue as in equation 4:(7)
where,
pi = mass ratio of i-th component to total cement content.
To predict the ultimate degree of hydration, and time and shape parameters in equation 1, multivariate nonlinear regression models were developed as shown in equations 5, 6, and 7:
where,
PC3A = weight ratio of tricalcium aluminate to total cement content,
PC3S= weight ratio of tricalcium silicate to total cement content,
PSO3 = sulfate weight ratio to total cement content,
Blaine = Blaine value, specific surface area of cement (m2/kg), and
w/cm = the water-cementitious material ratio.
The above models are based on heat of solution, conduction calorimeter, and semiadiabatic calorimeter test data. From a multivariate analysis, an r2 of 0.988 was achieved. The isothermal curing temperature considered for the test data was 21.1 °C.
The recommended AE model (E) is defined in equation 8:
where,
PC3A = weight ratio of tricalcium aluminate Bogue compound,
PC4AF = weight ratio of tetracalcium aluminoferrite Bogue compound,
Blaine = Blaine value, specific surface area of cement (m2 /kg), and
fE = AE modification factor for mineral admixtures, defined as in equation 9:
where,
pFA= mass ratio replacement of the fly ash,
pFACaO = mass ratio of the CaO content in the fly ash, and
pSLAG = mass ratio replacement of the GGBF slag.
A sensitivity analysis of the effect of temperature on the hydration of the cement was performed over a temperature range of 4.4 to 40.6 °C. From this analysis, the AE (E) model was found to be independent of curing temperature.
The limitations and assumptions to the model above presented are:
| C3S (%) | C2S (%) | C3A (%) | C4AF (%) | SO3 (%) | Free CaO (%) | MgO (%) | Alkalis | Blaine (m2/kg) | |
|---|---|---|---|---|---|---|---|---|---|
| Average | 52.5 | 20.8 | 8.4 | 9.3 | 2.6 | 1.4 | 1.8 | 0.6 | 373.7 |
| Min | 20.0 | 9.3 | 3.5 | 5.5 | 1.2 | 0.1 | 0.6 | 0.2 | 289.1 |
| Max | 64.5 | 55.0 | 13.2 | 16.6 | 4.4 | 2.9 | 4.0 | 1.1 | 579.5 |
* Equivalent alkalis as per ASTM C150 = Na2O + 0.658 K2O
| w/cm | Fly Ash CaO (%) | Fly Ash SiO2 (%) | Fly Ash Alkalis (%) | Fly Ash Dosage (%) | GGBF Slag Dosage (%) | |
|---|---|---|---|---|---|---|
| Average | 0.42 | – | – | – | – | – |
| Min | 0.36 | 10.8 | 35.8 | 0.3 | 0.0 | 0.0 |
| Max | 0.54 | 24.3 | 54.1 | 1.4 | 45.0 | 50.0 |
Based on the empirical results reported, the degree of hydration at initial and final set are determined as shown in equations 10 and 11:
where,
![]() i = degree of hydration at initial set,
i = degree of hydration at initial set,
![]() f = degree of hydration at final set, and
f = degree of hydration at final set, and
w/cm = water-cementitious materials ratio.
With equations 10 and 11, the equivalent age at setting can directly be determined from the hydration parameters. The closed form solutions are shown in equations 12 and 13. They are very useful, since the setting time at the reference temperature can now be obtained.
where,
![]() ei = equivalent age at initial set (hours),
ei = equivalent age at initial set (hours),
![]() ef = equivalent age at final set (hours), and
ef = equivalent age at final set (hours), and
w/cm = water-cementitious materials ratio.
It is customary to express the effect of chemical admixtures on cement mixes in terms of their effect on initial set at different temperatures. With equation 12, the initial set time for the cement without a chemical admixture can be estimated. Next, the effect recommend by the supplier of the chemical admixture can be added to the calculated initial set time. In the case of retarders, the initial set time will be increased, and with accelerators, the initial set time will be reduced. With this approach, it is assumed that only the hydration time parameter is affected by the chemical admixtures. Then, the new hydration time parameter can be determined that includes the use of chemical admixtures, as shown in equation 14:
where,
![]() chem = adjusted hydration time parameter to include the effect of retarder or accelerators (h),
chem = adjusted hydration time parameter to include the effect of retarder or accelerators (h),
![]() ei = equivalent age at initial set of the cement without chemical admixtures determined from equation 12 (h), and
ei = equivalent age at initial set of the cement without chemical admixtures determined from equation 12 (h), and
![]() chem = effect of mineral admixture on the time at initial set at the reference temperature (21.1 °C), where positive retards and negative accelerates.
chem = effect of mineral admixture on the time at initial set at the reference temperature (21.1 °C), where positive retards and negative accelerates.
In HIPERPAV I, a one-dimensional finite-element technique was used, but this procedure has proven to be a computational burden, and may not be appropriate for the large number of time-steps involved in long-term analyses. The finite-difference method is another numerical technique that is available to solve the transient heat transfer problem. In HIPERPAV II, the previous finite-element procedure for heat transfer analysis was replaced with a finite-difference method after extensive calibration and validation. The finite-difference model is used for both early-age and long-term predictions of concrete temperature. A description of this model follows:
The basic equation of the heat transfer model with respect to distance, x, and time, t, can be written as shown in equation 15: (8)
where,
T = temperature (°C),
![]() = density (kg/m3),
= density (kg/m3),
cp = specific heat capacity (J/kg/°C),
QH = generated heat per unit time and volume (W/m3), and
k = thermal conductivity (W/m/°C).
With this approach, the concrete temperature can be evaluated at discrete times after placement. Boundary conditions have to be chosen to satisfy compatibility with field conditions.
In concrete placed under field conditions, heat will be transferred to and from the surroundings, and the temperature development in the concrete structure is determined by the balance between heat generation in the concrete and heat exchange with the environment. The surroundings could either be an additional source of heat or at a lower temperature than the hydrating concrete. Heat transfer with the surroundings may take place in four basic ways: conduction, convection, irradiation, and solar absorption. Figure 2 illustrates how each of these methods exchange heat in a pavement system. The evaporation of moisture from the pavement surface causes a change in phase, which reduces the surface temperature due to the withdrawal of latent heat of vaporization. The models that will be used to model each of the heat exchange mechanisms will now be discussed in more detail. Due to the scope of this project, the parameters were not determined through physical testing, but instead parameters were obtained from published research. Therefore, normal ranges found acceptable in previous calibration efforts of these models are used.
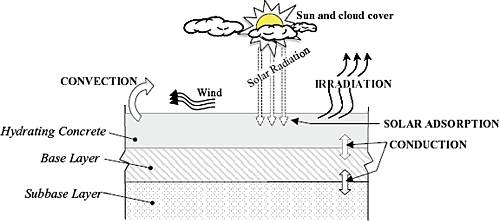
Figure 2. Heat transfer mechanisms between pavement and its surroundings.
Appropriate values for all the thermal material properties involved must be selected for the system. New methods to model early-age thermal properties and boundary conditions also were investigated.
The specific heat of a material can be defined as the ratio of the amount of heat required to raise a unit weight of a material 1 °C to the amount of heat required to raise the same weight of water by 1 °C. The International System (SI) units for specific heat are J/kg/°C, whereas the U.S. customary units are expressed in British Thermal Unites per pound per degrees Fahrenheit (BTU/lb/°F). Both the temperature of the concrete and the water content impact the specific heat of the mixture.(9,10)
Based on tests performed on hardening concrete, it is reported that the heat capacity is linear with the logarithm of time, which for common cement types is very similar to a linear decline with degree of hydration.(10, 11) Test data shows a 13 percent decrease in specific heat of concrete during hardening.(11) The following model shown in equation 16 is used in HIPERPAV II, as it accounts for the effect of temperature and mix proportions, and also decreases the specific heat as the concrete hardens:(12)
where,
cp = current specific heat of the concrete mixture (J/kg/°C),
![]() = unit weight of concrete mixture (kg/m3),
= unit weight of concrete mixture (kg/m3),
Wc, Wa, Ww = amount by weight of cement, aggregate, and water (kg/m3),
cc, ca, cw = specific heats of cement, aggregate, and water (J/kg/°C),
ccef = fictitious specific heat of the hydrated cement (J/kg/°C), determined as 8.4 Tc + 339, where Tc is the current concrete temperature (°C), and
![]() = degree of hydration.
= degree of hydration.
Based on the literature reviewed, the following specific heat values are recommended for cement, aggregate, and water (table 7):
| Material | Specific Heat (J/kg/°C) | Reference |
|---|---|---|
| Cement | 1140 | (13) |
| Water | 4187 | (9) |
| Limestone/dolomite | 910 | (14) |
| Sandstone | 770 | (14) |
| Granite/gneiss | 780 | (14) |
| Siliceous river gravel | 770 | (14) |
| Basalt | 900 | (14) |
To evaluate the proposed specific heat model, a mix design typically used in pavement construction was used.(1) The mix design per cubic meter consisted of 380 kg cement, 154 kg water, and 1631 kg of coarse and fine aggregate, which provided a unit weight of 2224 kg/m3. Figure 3 was developed based on the model shown in equation 16, and it may be concluded that it provides an adequate estimate of the specific heat as it fulfills the following requirements:
Figure 3. Concrete specific heat as influenced by the mixture constituents, temperature, and degree of hydration.
Thermal conduction is defined as heat transport in a material by transfer of heat between portions of the material that are in direct contact with each other. In a pavement system, conduction occurs between the pavement layers, and between the surface of the concrete slab and the surface protection (insulation) used at early ages, such as water fogging, plastic sheets, blankets, and urethane foams. The governing equation for thermal conduction reveals that heat transfer is a function of the thermal conductivity, density, and specific heat of the materials in contact.
Thermal conductivity of concrete (k) measures the ability of the concrete to transfer heat, and is defined as the ratio of the rate of heat flow to the temperature gradient.(9) The thermal conductivity is of great importance, since it determines the rate of penetration of heat into the concrete and hence the magnitude of temperature gradients and thermal stresses.(13) The SI units for thermal conductivity are W/m/°C, whereas the U.S. customary units are expressed in BTU/h/ft/°F.
It is reported that the water content, density, and temperature of the concrete may significantly influence the thermal conductivity.(9) The conductivity of ordinary concrete depends on its composition and especially the aggregate type used. Typical values proposed for the thermal conductivity of mature concrete are listed in table 8.
| Aggregate Type | Moist Density of Concrete (kg/m3) | Thermal Conductivity (W/m/°C) |
|---|---|---|
| Quartzite | 2350–2440 | 4.1–3.1 |
| Dolomite | 2500 | 3.3 |
| Limestone | 2450–2440 | 3.2–2.2 |
| Sandstone | 2400–2130 | 2.9 |
| Granite | 2420 | 2.6 |
| Basalt | 2520–2350 | 2.0–1.9 |
Thermal conductivity values, similar to the ones presented in table 8, are also recommended by ACI Committee 207.(15) In contrary to the values reported above, work performed at McGill University in Canada reports for normal strength concrete, thermal conductivity values of 1.723–1.740 W/m/°C for maturing concrete and values of 1.14–1.17 W/m/°C for hardened concrete.(10) These values are significantly lower than those listed in table 8. It was concluded that the average thermal conductivity of maturing concrete is 33 percent higher than that of the hardened concrete. This value is in agreement with that obtained by others, which showed a 21 percent decrease in thermal conductivity from the maturing state to the hardened state.(11)
From this information, assuming that the decline in this parameter is linear with the logarithm of time, which for common cement types is very similar to a linear decline with degree of hydration, a relationship that considers these initial and final values could be expressed as shown in equation 17:
where,
ki = current thermal conductivity of the concrete (W/m/°C),
k∞ = thermal conductivity of mature concrete (W/m/°C), and
![]() = degree of hydration.
= degree of hydration.
The temperature and properties of the base underlying the concrete have a significant influence on the temperature development of the hardening concrete. Tables 9 and 10 present typical thermal characteristics of some commonly used base materials.
| Base Material | Density (kg/m3) | Thermal Conductivity (W/m/°C) | Specific Heat (J/kg/°C) |
|---|---|---|---|
| Gravel, dry | 1703 | 0.52 | 838 |
| Gravel, moist | 1898 | 2.42 | 1047 |
| Asphalt | 2302 | 1.38 | 1047 |
| Base Material | Density (kg/m3) | Unfrozen Thermal Conductivity (W/m/°C) | Unfrozen Specific Heat (J/kg/°C) |
|---|---|---|---|
| Asphalt concrete | 2371 | 1.21 | 921 |
| Stabilized base | 2339 | 3.32 | 1005 |
| Cohesive subgrade | 2066 | 1.59 | 1214 |
During the development of the ICM,(18) different values for the thermal conductivity and specific heat was determined based on the moisture condition of the soil and three different material conditions—unfrozen, freezing, and frozen. The soil moisture content has a great influence upon the thermal conductivity and heat capacity of the soil. In later reports on the development of the ICM, the values listed in table 11 were recommended based on the AASHTO soil type classification.
| Soil Type | Dry Density (kg/m3) | Dry Thermal Conductivity (W/m ×°C) | Specific Heat Capacity (J/kg×°C) |
|---|---|---|---|
| Stabilized | 1188 | 1.50 | 1047 |
| A–1 | 1188 | 0.90 | 712 |
| A–2 | 950 | 0.81 | 712 |
| A–3 | 1045 | 1.02 | 838 |
| A–4 | 856 | 1.02 | 712 |
| A–5 | 808 | 0.45 | 712 |
| A–6 | 856 | 0.60 | 712 |
| A–7 | 760 | 0.30 | 712 |
Conduction further transpires between the surface coverings of the concrete slab commonly placed over during construction. These include insulation blankets, curing compound, plastic sheets, urethane foams, closed cell polystyrene foam, and many patented products. Insulation blankets often are used to provide a uniform temperature gradient, to prevent concrete freezing under cold weather conditions, and where opening requirements dictate very quick strength gain.(19) The use of blankets in cold weather conditions will increase the strength gain considerably, as some of the concrete heat generated during hydration is trapped, which allows concrete hydration at increased temperatures. It is also reported that when a period of less than 16 hours is required for early opening to traffic, the use of blankets become beneficial.(19) These blankets should be placed after the sawing operation and near the time the slab temperature begins its decent from the peak temperature.
Other membranes and surface coverings are also commonly placed over the concrete during construction. These include curing compound, plastic sheets, urethane foams, closed cell polystyrene foams, and many other products. The steady state heat transfer to the surrounding, excluding any radiation, can be expressed as shown in equation 18:(20)
where,
q = heat flux (W/m2),
h0 = overall heat transfer coefficient (W/m2/°C),
Ts = surface temperature (°C), and
Ta = air temperature (°C).
Where more than one layer of insulation is used, the overall heat transfer coefficient can be calculated, which is a single coefficient that defines the thermal resistance of all the materials. The overall heat transfer coefficient can be calculated as shown in equation 19:(20)
where,
h0 = overall heat transfer coefficient (W/m2/°C),
d1, d2, … dn = thickness of n successive layers (m), and
k1, k2, … kn = thermal conductivity of n successive layers (W/m/°C).
Table 12 contains some properties of various insulation materials that could be encountered during concrete construction operations.
| Base Material | Thermal Conductivity (W/m/°C) | Typical Thickness (mm) | Reference |
|---|---|---|---|
| No cover | 0 | 0 | – |
| Polyurethane foam | 0.035 | 25 | (21) |
| Plastic sheet | 0.043 | 0.1 | (22) |
| Water | 2.168 | Variable | (22) |
| Blankets: | |||
| Mineral fiber: |
0.039 | 75 | (22) |
| Textile organic fiber: |
0.043 0.033 |
25 25 |
(22) |
| Glass fibers: |
0.055 | 25 | (21) |
| Alumina fibers: |
0.058 | 25 | (21) |
| Cotton wool mats: |
0.042 | 25 | (20) |
| Mineral wool: |
0.039 0.042 |
50 50 |
(20) |
![]() = unit weight
= unit weight
Thermal convection is the heat transferred from a surface to a gas (or fluid), where convection is the movement of a mass of gas (or liquid) due to the temperature difference, and physical contact of the gas (or liquid) is the actual method of heat transfer. Convection is, therefore the mechanism of heat transfer between the concrete surface and the environment, and as illustrated above in figure 2, includes the effect of wind and evaporation. For flat surfaces such as concrete pavements, the wind velocity across the concrete surface determines whether convection is forced or free. In the case of free convection, the transport of heat is the result of temperature gradients. In HIPERPAV II convective heat transfer is modeled through the use of equation 20:(22)
where,
qc = heat transferred due to convection (W/m2),
hc = surface convection coefficient (W/m2/°C),
Ts = surface temperature (°C), and
Ta = air temperature (°C).
The rate of heat flow from a horizontal surface is controlled by the magnitude of the temperature difference, the speed of the air flow, and also the surface texture of the member. As heat is transferred from the warmer horizontal plate to the adjacent air, the air is heated, its density decreases, and it tends to rise. As the heated air rises, it is replaced by cooler air, which in turn is heated and rises; this is a continuous recurring process until the heat balance is eliminated. This complex phenomenon has been thoroughly investigated by numerous researches in the heat transfer field. From combinations of experimental work from Heilman and Langmuir, a model that is also used in ASTM C 680 is available for use on a smooth horizontal surface that is valid for both forced and free convection.(21, 22, 23) However, this model does not include any modification due to surface roughness, and it is recommended that the surface convection coefficient above be increased by 6 percent to account for this effect.(20) Therefore, the following model (shown in equation 21) was incorporated in HIPERPAV II:
where,
hc = surface convection coefficient (W/m2/°C),
C = constant depending on the shape and heat flow condition, equal to 1.79 for horizontal plates warmer than air, or 0.89 for horizontal plates cooler than air,
Ts = surface temperature (°C),
Ta = air temperature (°C), and
where w = windspeed (m/s).
In some programs that model the convection boundary conditions, it is common to use equations 22 and 23 to determine the magnitude of the convection coefficient:(24, 25, 26)
where,
hc = surface convection coefficient (kJ/m2/h/°C), and
w = windspeed (m/s).
These equations were obtained from experimental data for the flow of air at room temperature parallel to a smooth vertical copper plate.(20) The original equation presented by McAdams is very similar to equations 22 and 23, and after converted to similar units, is as shown in equations 24 and 25:(20)
These equations do not incorporate the fact that the surface convection coefficient is influenced by the magnitude of the temperature difference, as the tests were all performed at room temperature (21 °C). McAdams acknowledged this relationship, and recommended that the windspeed in the above equations be modified by a multiplier to account for this effect.(20) Using this form of the convection equation (equations 22 and 23) is, therefore, more appropriate to determine the effect of convection on vertical elements such as beam webs or retaining walls. However, the multiplier to the windspeed must be incorporated when the air temperature is above room temperature, and the effect of a rough concrete surface as opposed to a smooth plate must be taken into account. Figure 4 compares the surface convection coefficient associated with a vertical (equations 22 and 23) and horizontal plate (equation 21) as presented in this section. Note that with a vertical plate there is a significant increase in the amount of heat transferred as the windspeed is increased above a value of 5 m/s.
Figure 4. Comparison of different convection coefficients as influenced by the windspeed.
Because the heat transfer due to convection on the surface could occur simultaneously with the presence of surface insulations over the pavement top surface, the overall heat transfer coefficient that includes both these effects must be determined. The overall heat transfer coefficient can be calculated as shown in equation 26 (will all the parameters as defined elsewhere):
In some cases, liquid-curing membranes, water fogging of the pavement surface, or other porous coverings are used. When evaporation of the water on the surface occurs, the energy associated with the phase change is the latent heat of vaporization. Evaporation occurs when liquid molecules near the surface experience collisions that increase their energy above that needed to overcome the surface binding energy. The energy required to restrain the evaporation must come from the internal energy of the liquid, which then must reduce in temperature. The amount of energy transferred through evaporative cooling can be determined in equation 27: (27)
where,
qevap = heat flux due to latent heat of vaporization (W/m2),
Er = evaporation rate (g/m2/s), and
hlat = latent heat of vaporization (W×s/g).
In metric units, the latent heat of vaporization is the quantity of heat, in joules, required to evaporate 1 gram of water, and it varies with temperature.(22) The latent heat of vaporization can be defined as shown in equation 28:(22)
where,
hlat = latent heat of vaporization (W×s/g), and![]()
Ta = air temperature (°C).
Where curing membranes and water fogging are used, the duration of latent heat development can be identified by determining the evaporation rate per unit area and by knowing the thickness of the applied membrane. Most States specify the curing compound application rate, and ASTM C309(27) recommends a rate of application of 5 m2/l if the rate of application is not specified.
Solar absorption is the flux absorbed by the pavement surface through exposure to the incoming sunrays. In HIPERPAV II, the following simplified equation for solar absorption (equation 29) is used:
where,
qs = solar absorption heat flux (W/m2),
be = solar absorptivity,
If = intensity factor to account for angle of sun during a 24-hour day, and
qsolar = instantaneous solar radiation, (W/m2) as defined in table 13.
In HIPERPAV II, the solar radiation used is based on the 95 percentile value of solar radiation from historical records at any given weather station considered in the HIPERPAV II weather database. The solar radiation in the simulation varies with time of day, ranging from zero at sunrise and sunset to a peak value midday.
In table 13, the solar radiation is a function of the cloud cover, and even with an overcast sky, some of the longer wavelengths can still penetrate the sky and be a source of heat. During nighttime, the solar radiation is negligible. The intensity of solar radiation (If) is assumed to follow a sinusoidal distribution, with the simplifying assumption that the highest solar radiation occurs at 5 p.m.
The solar absorptivity of PCC is a function of the surface color, with typical values ranging from 0.5 to 0.6. An ideal white body would have a value of 0.0, and an ideal black body would have a value of 1.0.
| Sky Conditions | Solar Radiation (W/m2) |
|---|---|
| Sunny | 1000 |
| Partly cloudy | 700 |
| Cloudy (overcast) | 300 |
Irradiation is the reason that a frost occurs on a clear night even though the air temperature remains well above the freezing point. Irradiation heat transfer also affects the concrete surface, which is the heat transfer that is accomplished by electromagnetic waves between a surface and its surroundings. The Stefan-Boltzmann law is commonly used for this type of heat transfer, which is defined in equation 30:(20)
where,
qr = heat flux of heat emission from the surface (W/m2),
![]() = Stefan-Boltzmann radiation constant (5.67×10-8 W/m2/°C4),
= Stefan-Boltzmann radiation constant (5.67×10-8 W/m2/°C4),
![]() = surface emissivity of concrete,
= surface emissivity of concrete,
Tc = concrete surface temperature, (°C), and
T∞ = surrounding air temperature, (°C).
The surface emissivity is a function of the concrete's surface color. An “idealized” black surface would have a value of 1.0. A value of 0.88 was selected for use in HIPERPAV II.(28) However, in the above equation, T∞ is the temperature of the surrounding environment, and this value cannot arbitrarily be assumed to be equal to the ambient temperature. This equation would be valid for use in enclosed spaces, but where long wave radiation toward the open sky is involved, using this equation requires an appropriate estimate of the effective surrounding air temperature in terms of the atmosphere's ability to reflect and absorb the radiation. In figure 5, an idealized thermally black body with a surface temperature (Ts) equal to the air temperature is receiving and absorbing solar energy at a rate, qr. Because the plate is at the same temperature as the air, there will be no heat transfer through convection, but the plate will exhibit a radiation loss in the far infrared wavelength. The loss rate (R) is defined as the difference between the black body radiation (![]() s4) emitted by the surface and the incoming long wave atmospheric radiation (AR), which is striking the surface.(29)
s4) emitted by the surface and the incoming long wave atmospheric radiation (AR), which is striking the surface.(29)
Figure 5. Radiant energy exchanges between the sky and an exposed thermally black plate.(29)
Atmospheric radiation originates from gasses in the air. When radiation at the ground level is of concern, only water vapor and carbon dioxide are the main contributors, and water vapor is the most important.(29) Only the presence of these small gases prevents the atmosphere from being completely transparent in the far infrared. Therefore, to accurately model the radiation from the atmosphere to the surface, it is essential to determine the radiation expected from the gas mixture of water vapor and carbon dioxide. The fact that the composition, temperature, and pressure of these mixtures vary with height above ground level also must be considered.
The emissivity of a particular radiating gas is a function of the number of molecules of the radiating gas in the column of air under investigation. At a given temperature, the number of molecules of the radiating gas is linearly proportional to the density-length product, mg ≡ pgLg, where pg is the density of the gas and Lg is the length of the gas column.(29) The total emissivity (![]() w) of a column of water vapor and nonradiating gas is primarily a function of the following: the density-length product (mw) of the water vapor, the partial pressure (Pw) of the water vapor, the total pressure (PT) of the mixture, and the temperature of the mixture (T).(29) However, the total emissivity is not strongly influenced by either the partial pressure of the water or the temperature of the mix. When carbon dioxide is added to the gas mixture, the radiative behavior of the gas column is only slightly changed. Based on the established work from Hottel and Egbert,(30) Bliss expressed the total emissivity of moist atmospheric air as a function of mw, and the ratio of carbon dioxide to water vapor concentrations at a total pressure of 1 atmosphere and a temperature of 20 °C, which can mathematically be presented in equation 31 as:
w) of a column of water vapor and nonradiating gas is primarily a function of the following: the density-length product (mw) of the water vapor, the partial pressure (Pw) of the water vapor, the total pressure (PT) of the mixture, and the temperature of the mixture (T).(29) However, the total emissivity is not strongly influenced by either the partial pressure of the water or the temperature of the mix. When carbon dioxide is added to the gas mixture, the radiative behavior of the gas column is only slightly changed. Based on the established work from Hottel and Egbert,(30) Bliss expressed the total emissivity of moist atmospheric air as a function of mw, and the ratio of carbon dioxide to water vapor concentrations at a total pressure of 1 atmosphere and a temperature of 20 °C, which can mathematically be presented in equation 31 as:
where
where,
![]() atm = total atmospheric emissivity (unitless),
atm = total atmospheric emissivity (unitless),
mw = density-length product of the water vapor (mw ° pgLg = g/cm2), and
![]() c /
c /![]() w = ratio of carbon dioxide density to water vapor density (unitless).
w = ratio of carbon dioxide density to water vapor density (unitless).
In equation 31, the first term accounts for the emissivity of water vapor (moist air), and the second term accounts for the added emissivity caused by the presence of carbon dioxide. Figure 6 shows the individual contribution of the water vapor and carbon dioxide to the calculated emissivity of moist air. Note that the presence of carbon dioxide adds a maximum of only 0.185 to the overall emissivity. This figure further shows the effect of water vapor in the air, on the atmospheric emissivity. As the concentration of water vapor becomes less (dry air) the atmospheric radiation (total emissivity) decreases.
Figure 6. Emissivity of moist air at a total pressure of 1 atmosphere and a temperature of 20 °C.
The nature of the earth's atmosphere is that the pressure and temperature decreases with altitude, which, due to gas equilibrium principles, causes a change in the moisture condition of the body of gas. Therefore, to determine the total atmospheric emissivity, the earth's atmosphere should be considered as several layers, all at different temperatures, pressures, and moisture conditions. The composition of the atmosphere varies significantly, but it varies with height in typical ways. It can be shown that the variation of pressure with height above ground level can be determined by equation 32:(29)
where,
Pz = atmospheric pressure at height z (atm),
Pi = atmospheric pressure at ground level (atm), and
z = height above ground level (m).
As the total pressure is decreased, the emissivity of the gas is decreased. Equation 31 provided the total atmospheric emissivity at a pressure of 1 atmosphere, and by determining an adjusted density-length product of the water vapor, the effect of different pressures on emissivity can be incorporated. The adjusted density-length product of the water vapor (m'w) can be determined as in equation 33:(29)
where,
Pz = actual pressure of the moist air (atm), and
P0 = pressure of known emissivity versus water vapor relationship (1 atm).
The variation of temperature with height is less uniform, but it is reported that at heights above a few meters off the ground surface, it often obeys the following relationship in equation 34:(29)
where,
Tz = atmospheric temperature at height z (°C),
Ti = atmospheric temperature at ground level (°C), and
z = height above ground level (m).
As the total energy of a moist air column changes with a change in temperature, a temperature correction must be applied to the calculated total atmospheric emissivity. The total energy radiated by a gas of specified water-vapor content is function of its temperature only, and is directly proportional to the fourth power of its absolute temperature.(29) The temperature adjustment factor (Tf), which can be multiplied to the emissivity determined at a temperature different than the actual condition, can be determined as in equation 35:(29)
where,
Ti = actual temperature of the moist air (°C), and
T0 = assumed temperature during calculation of the emissivity (°C).
The water vapor density is variable with height, and the total precipitable water contained below a certain height (z) can be determined with the following relationship in equation 36:(29)
where,
![]() = total precipitable water contained below a height z (g/cm2),
= total precipitable water contained below a height z (g/cm2),
pwi = water vapor density at ground level (g/cm2), and
z = height above ground level (m).
In HIPERPAV II, the climatic conditions are defined in terms of the relative humidity and the air temperature (dry-bulb temperature). Through the use of established gas relationships, the water vapor density can be determined. The water vapor saturation pressure for a given dry-bulb temperature can be determined as in equations 37 and 38:(22)
For dewpoint range of -100 to 0 °C:
where,
pws = the water-vapor saturation pressure (atm),
TR = the dry-bulb temperature, (°R = °C *1.8 + 491.67),
C1 = -10214.165,
C2 = -4.8932428,
C3 = -0.0053765794,
C4 = -1.9202377 ´ 10-7,
C5 = 3.5575832 ´ 10-10,
C6 = -9.0344688 ´ 10-14, and
C7 = 4.1635019.
For dewpoint range of 0 to 200 °C:
where,
C8 = -10440.397,
C9 = -11.29465,
C10 = -0.027022355,
C11 = -1.289036 ´ 10-5,
C12 = -2.4780691 ´ 10-9, and
C13 = 6.5459673.
After the water vapor saturation pressure is determined, the water vapor pressure of the moist air can be determined from the known relative humidity (RH), as shown in equation 39.
The information above provides all the information needed to determine the apparent atmospheric emissivity with the following variables: surface atmospheric pressure (atm), dry-bulb temperature (°C), relative humidity, and the ratio of carbon dioxide to water vapor. The atmosphere is divided into different layers, and by using a step-wise procedure, the emissivity can be accumulated from each layer. After the apparent emissivity (![]() app) is determined, the intensity of atmospheric radiation (AR) can be determined in equation 40 (figure 5 above):
app) is determined, the intensity of atmospheric radiation (AR) can be determined in equation 40 (figure 5 above):
Now with the intensity of atmospheric radiation determined, the apparent surrounding air temperature (T∞) can be solved from equation 41:
As the apparent surrounding air temperature is now determined, the Stefan-Boltzmann law can be used to determine the heat transfer by irradiation (equation 30). Figures 7 to 9 illustrate the sensitivity of the effective surrounding temperature to all the various input variables with the following parameters as baseline values for the analysis: atmospheric pressure = 750 millibars, dry-bulb temperature = 30 °C, relative humidity = 20 percent, ratio of carbon dioxide to water vapor = 1.0. Under the conditions investigated, there is a significant reduction in the apparent surrounding temperature associated with a decrease in total pressure and the relative humidity. A change in the carbon dioxide content seems to have a minimal impact on the apparent surrounding temperature, and a ratio of 0.1 should be sufficient for most conditions.(29)
Figure 7. Sensitivity of the apparent surrounding temperature to changes in climatic conditions, atmospheric pressure.
Figure 8. Sensitivity of the apparent surrounding temperature to changes in climatic conditions, relative humidity.
Figure 9. Sensitivity of the apparent surrounding temperature to changes in climatic conditions, ratio of carbon dioxide to water vapor.
Although the initial temperature of the mix and temperature of the subbase are required inputs in HIPERPAV II, the finite-difference temperature model used in HIPERPAV II requires as an input the complete temperature profile including depths beyond the subbase. For this purpose, HIPERPAV II uses a simple closed form solution for prediction of pavement temperatures.(31) The 24-hour periodic temperature, T, at a given depth, x, can be predicted as in equation 42:(31)
where,
T = 24-hour periodic temperature of the mass, °C,
TM = mean effective air temperature, °C,
TV = maximum variation in temperature from the effective mean, °C,
t = time from beginning of cycle (one cycle = 24 h),
x = depth below surface, m,
H = h/k, where h is the surface convection coefficient, W/m2/°C, and k is the conductivity, W/m2/°C/m, and
C = (0.131/c)0.5, where diffusivity c = k/(sw), s is specific heat in J/kg/°C, and w is density in kg/m3.
As can be observed, the above model considers the climatic conditions and thermal properties of the materials for prediction of pavement temperature. To provide for temperature equilibrium with the environment, pavement temperatures are predicted for a total of 96 hours in advance up to the time of construction.
HIPERPAV II has been updated to include the prediction of autogenous shrinkage as well as drying shrinkage. The chosen autogenous shrinkage model was developed by Jonasson and Hedlund.(32) Likewise, the drying shrinkage model in HIPERPAV II has been updated from the RILEM B3 model previously used in HIPERPAV I to the Baźant-Panula model.(33) Now, shrinkage modeling is subdivided into two cases, when the w/cm is less than 0.40, and when it is greater than or equal to 0.40.
Autogenous shrinkage is defined by the Japanese Committee on Autogenous Shrinkage as “The macroscopic volume reduction of cementitious materials when cement hydrates after initial setting. Autogenous shrinkage does not include the volume change due to loss or ingress of substances, temperature variation, the application of an external force, and restraint.”(34) (p. 54). The magnitude of autogenous shrinkage depends on the w/cm in the concrete. The lower the w/cm, the greater the importance of autogenous shrinkage, as compared to drying shrinkage. From a practical viewpoint, Aїtcin recommends that when w/cm < 0.40, autogenous shrinkage cannot be neglected.(34) For a w/cm of 0.30, the autogenous shrinkage can represent 50 percent of the total shrinkage, with total shrinkage equaling drying shrinkage plus autogenous shrinkage.
The shrinkage model selected for incorporation in HIPERPAV II was developed by Jonasson and Hedlund. In developing this mechanistic-empirical model, experimental test data for high-performance concrete (HPC) with a w/cm < 0.40 and 28-day compressive strength of equal to or greater than 80 MPa were used. The total shrinkage strain—autogenous shrinkage for the whole system plus drying shrinkage due to drying and wetting deformation at the surface—for the concrete's cross section is expressed in equation 43 as:(32)
where,
t = time after casting (days),
![]() cs (t) = total external shrinkage strain (×106
cs (t) = total external shrinkage strain (×106 ![]()
![]() ),
),
![]() cs0 (t) = autogenous shrinkage under sealed conditions (see equation 44), and
cs0 (t) = autogenous shrinkage under sealed conditions (see equation 44), and
![]() csd (t) = additional strain due to drying/wetting caused by humidity change with the environment (see equation 45).
csd (t) = additional strain due to drying/wetting caused by humidity change with the environment (see equation 45).
Autogenous shrinkage is modeled as:
where,
![]() s0 (t) = time distribution of autogenous shrinkage (equation 45) and
s0 (t) = time distribution of autogenous shrinkage (equation 45) and
![]() s0∞ = final value of autogenous shrinkage (equation 46).
s0∞ = final value of autogenous shrinkage (equation 46).
Autogenous shrinkage measurements were initiated 24 hours after casting. The authors state that, prior to 24 hours, the concrete is plastic, but assume that the stresses and deformations begin after this time period. This expression for the time distribution of autogenous shrinkage starts at zero, 24 hours after casting.
where,
ts0 = 5 days (constant for HPC) and
tstart = 1 day (start time of autogenous shrinkage).
The time distribution of autogenous shrinkage is not a function of the concrete's w/cm. Instead w/cm is incorporated into the ultimate autogenous shrinkage. It is expressed in the following empirical equation as:
where,
w = water content (kg/m3) and
B = cement content + silica fume content (kg/m3).
Drying shrinkage is a surface concept. The external humidity exchange occurs only in the outer shell of the structural member, called “surface layer drying.” The portion of the cross section affected by surface layer drying, ![]() sd (figure 10), is assumed to be constant with time and is calculated using equation 47:
sd (figure 10), is assumed to be constant with time and is calculated using equation 47:
where,
u = perimeter of the cross section in contact with environmental humidity,
Ac= cross section perpendicular to water flow, and
lsd = typical length of surface for water exchange, given by equation 48:
where,
lsd,ref = 0.0045 m, the reference depth of surface layer drying for HPC.
This term tends to infinity when the w/B ratio is 0.5. It can only be used when w/B < 0.50, which is one of the constraints of using this model.
Figure 10. Surface layer zone subjected to drying shrinkage for a slip-formed pavement.
There are two cases, when ![]() sd = 1 and when
sd = 1 and when ![]() sd < 1, as shown for typical pavement cross sections,
sd < 1, as shown for typical pavement cross sections,
![]() sd < 1. However, for some cylinders,
sd < 1. However, for some cylinders, ![]() sd = 1, for example, for cylinders with diameters of 100 mm and w/B = 0.32.
sd = 1, for example, for cylinders with diameters of 100 mm and w/B = 0.32.
Case I (equation 49): ![]() sd = 1.
sd = 1.
where,
![]() sd,all (t) = drying shrinkage (plus autogenous shrinkage) when the whole specimen is affected by drying,
sd,all (t) = drying shrinkage (plus autogenous shrinkage) when the whole specimen is affected by drying,
![]() sd,tot = final drying shrinkage (see equation 51),
sd,tot = final drying shrinkage (see equation 51),
![]() sd,RH = coefficient depending on relative humidity (see equation 56), and
sd,RH = coefficient depending on relative humidity (see equation 56), and
![]() sd (t) = time development of drying shrinkage, expressed by equation 50:
sd (t) = time development of drying shrinkage, expressed by equation 50:
where,
t – ts = time after start of drying and wetting (days),
ts = age of concrete at start of drying and wetting (≥ 1 day), and
tsd = 200 days, time reflecting the typical rate of humidity exchange.
This total shrinkage ![]() sd,tot is the same order of magnitude for HPC as for normal strength concrete. The empirical relationship is:
sd,tot is the same order of magnitude for HPC as for normal strength concrete. The empirical relationship is:
Case II (equation 52): ![]() sd < 1.
sd < 1.
When ![]() sd is less than 1, a moisture exchange is taking place between the surface of the structural layer and the environment, and there is an inner part that is affected only by self-desiccation. Using a force balance and assuming that plane sections remain plane (equation 52),
sd is less than 1, a moisture exchange is taking place between the surface of the structural layer and the environment, and there is an inner part that is affected only by self-desiccation. Using a force balance and assuming that plane sections remain plane (equation 52),
Combining with equation 49, equation 53 results,
setting equation 54,
yields equation 55,
where,
![]() csd (t) = additional strain due to drying/wetting of the concrete with the environment,
csd (t) = additional strain due to drying/wetting of the concrete with the environment,
![]() sd∞ = final external strain due to drying shrinkage (see equation 54),
sd∞ = final external strain due to drying shrinkage (see equation 54),
![]() sd (t) = time development of drying shrinkage (see equation 50), and
sd (t) = time development of drying shrinkage (see equation 50), and
![]() sd,RH = coefficient depending on relative humidity (see equation 56).
sd,RH = coefficient depending on relative humidity (see equation 56).
To describe the shrinkage of HPC as a function of relative humidity:
where,
RH = actual environmental relative humidity,
RH0 = relative humidity at sealed conditions (80 percent for w/cm ≤ 0.4), and
RHref = chosen relative humidity at a typical indoors environment (60 percent when w/cm ≤ 0.4).
In addition, it has been found for normal strength concrete, and can be applied to HPC, that when the relative humidity is less than the reference relative humidity, it can be assumed that drying shrinkage is not affected by relative humidity, as seen in equation 57.
The effect of changing the w/c on the total shrinkage according to the Jonasson model is shown in figure 11. The lower w/c, the higher the total shrinkage.
Figure 11. Influence of w/cm on total shrinkage predicted by the Jonasson model.
The Baźant-Panula shrinkage model was selected to model the concrete when its w/cm ![]() 0.40. It models total shrinkage, which is autogenous shrinkage plus drying shrinkage, and it takes into account the composition of the mix and other empirical dependences.(35) It was also found to match the experimental drying shrinkage data better than the B3 model previously used in HIPERPAV I as described in section D.3.2.
0.40. It models total shrinkage, which is autogenous shrinkage plus drying shrinkage, and it takes into account the composition of the mix and other empirical dependences.(35) It was also found to match the experimental drying shrinkage data better than the B3 model previously used in HIPERPAV I as described in section D.3.2.
The drying shrinkage strain is expressed by equation 58:(35)
where,
![]() sh = shrinkage strain (me),
sh = shrinkage strain (me),
t = time (days),
t0 = age when drying begins (days), assumed to be the concrete's set time,
![]() = duration of drying (days),
= duration of drying (days), ![]() ,
,
![]() sh∞ = ultimate shrinkage strain (me) (see equation 63),
sh∞ = ultimate shrinkage strain (me) (see equation 63),
kh = humidity dependence (see equation 65), and
S(![]() ) = time dependence (see equation 59).
) = time dependence (see equation 59).
The time dependence is shown in equation 59:
where,
![]() sh = shrinkage half-time (equation 60).
sh = shrinkage half-time (equation 60).
The size dependence of the diffusion type is:
where,
ks= shape factor, ks = 1 for infinite slab, 1.15 for infinite cylinder, 1.25 for infinite square prism, 1.30 for sphere and 1.55 for cube (If the length of a cylinder or prism is 3 times its width, then it can be assumed to be infinitely long. For a finite length cylinder less than 3 times its width, its ks can be determined by linearly interpolating between the ks value for a sphere or prism and its corresponding ks for an infinitely long member),
D = effective cross section thickness (mm), = 2 v/s, with v = volume and s = surface area, (D is thickness/2 based on calibrations using the HIPERPAV I field sites (see section D.3.2). The same calibration factor was also reported by Persson.(36)),
C1ref = 10 mm2/day, and
C1(t0) = age dependence (mm2/day), given by equation 61:
where,
C7 = empirical reference diffusivity at 7 days (mm2/day) (see equation 66) and
k'T = temperature dependence coefficient, given by equation 62:
where,
T = temperature (Kelvin) and
T0 = reference temperature 23 °C (in Kelvin).
This model was calibrated using laboratory data. Since it will be used to model drying shrinkage that occurs in the field at temperatures that are not found in the laboratory, the effect of k'T will be neglected. T will be set to 23 °C in the modeling.
Ultimate shrinkage is given by equation 63:
where,
es∞ = empirical shrinkage given in equation 67.
where,
E(28) = 28-day modulus of elasticity.
Humidity dependence is the same as it is in the B3 model, as shown in equation 65:
where,
h = relative humidity (0 ≤ h ≤ 1).
The empirical dependences of drying shrinkage on concrete strength and composition of the mix are defined in the following equations. The reference diffusivity C7 (mm2/day) is shown in equation 66:
if C7 < 7, C7 = 7, and if C7 > 21, C7 = 21.
Final shrinkage ![]() s∞(10-6) is defined as shown in equation 67:
s∞(10-6) is defined as shown in equation 67:
where, as shown in equations 68 and 69,
else z = 0, with,
c = cement content (kg/m3),
w/c = w/c by weight, or w/cm,
a/c = total aggregate (coarse + fine)-to-cement ratio by weight,
g/s = coarse aggregate-to-fine aggregate ratio by weight,
s/c = sand-to-cement ratio by weight, and
f'c = 28-day compressive strength (MPa).
Brooks investigated the effect of admixtures on shrinkage.(37) He found that shrinkage was not greatly affected by fly ash, GGBF slag, or silica fume (5–15 percent). As a result, these additives will not be added to the cementitious materials content when calculating the drying shrinkage with the Baźant-Panula model.
The Baźant-Panula model does not take into account the cement type (![]() 1) and the specimen curing (
1) and the specimen curing (![]() 2) factors that were included in the B3 model. They were added to equation 67, as shown in equation 70:
2) factors that were included in the B3 model. They were added to equation 67, as shown in equation 70:
where, as shown in equations 71 and 72,
and
As shown in figure 12, increasing the w/c causes the total shrinkage to increase, as predicted by the Baźant-Panula model.
Figure 12. Effect of w/c on total shrinkage predicted by the Baźant-Panula model.
It is necessary to investigate the difference in the Baźant-Panula and Jonasson-Hedlund models when the w/cm is at and below 0.4. This is shown in figure . It is apparent that the shrinkage predicted by the Baźant-Panula model is greater, in some cases by 140 ![]()
![]() . After experimental data are collected for pavement mixes with w/cm < 0.40, the Jonasson-Hedlund model can be calibrated.
. After experimental data are collected for pavement mixes with w/cm < 0.40, the Jonasson-Hedlund model can be calibrated.
Figure 13. Comparison of the Baźant-Panula and Jonasson-Hedlund shrinkage models.
The influence of the start time on the Jonasson-Hedlund also was investigated. Changing tstart (equation 45) and ts (equation 50) to the set time allows the model to predict shrinkage at times less than 24 hours. This modification was made for HIPERPAV II predictions, since autogenous shrinkage has been documented to begin at times less than 24 hours.(34)
In this new approach, the predicted total shrinkage in HIPERPAV II is the greater of the shrinkage predicted by the Jonasson-Hedlund and the Baźant-Panula models.
Recognizing the nonlinear restraint effect imposed by some subbases, such as hot-mix asphalt (HMA) subbases, a nonlinear model was included in HIPERPAV II in addition to the current linear one to provide for the characterization of such behavior. The nonlinear model is of the following form, shown in equation 73:
where,
![]() f = friction stress (kPa),
f = friction stress (kPa),
uc = PCC axial displacement (m),
![]() f = axial displacement at sliding (m),
f = axial displacement at sliding (m),
C2= maximum friction stress (kPa), and
n = nonlinear power coefficient (dimensionless).
Typical values of the above coefficients can be obtained by performing friction tests. The procedure for these tests is described elsewhere. (See references 38, 39, 40, and 41.)
Recognizing that thermal gradients through the slab depth are nonlinear for the most part, the model developed by Mohamed and Hansen is used in HIPERPAV II to determine an equivalent linear gradient as a function of a nonlinear one as follows in equation 74:(42)
where,
![]() Teq = equivalent linear temperature gradient, °C,
Teq = equivalent linear temperature gradient, °C,
h = slab thickness, m,
![]() = PCC CTE, m/m/°C, and
= PCC CTE, m/m/°C, and
M* = constant dependent on the temperature distribution expressed as shown in equation 75:
where,
z = distance from slab midplane (z is positive downward), m, and
![]() (z) = strain profile, m/m.
(z) = strain profile, m/m.
The equivalent linear gradient from top to bottom of the slab determined with the above model was developed with the objective of producing the same curvature as the Westergaard and Bradbury linear gradient solution.(42)
In HIPERPAV II, the strain profile is determined as shown in equation 76:
where,
Tz = current temperature at slab depth z, °C, and
Tz,set = temperature at slab depth z, at time of set, °C.
The creep model described below was not incorporated in HIPERPAV II due to lack of data for validation. However, it is presented here because researchers in this project made major efforts that could make incorporating the creep model relatively easy in the future when enough data for validation are available.
When load is applied to a concrete member, it responds with an immediate elastic deformation (![]() el), followed by a time-dependent creep response (
el), followed by a time-dependent creep response (![]() cr), which is shown in figure 14 . This time-dependent response is best modeled by viscoelastic theory.(43) To obtain a reasonably accurate estimate of the stresses at early ages, the amount of creep must be taken into account.
cr), which is shown in figure 14 . This time-dependent response is best modeled by viscoelastic theory.(43) To obtain a reasonably accurate estimate of the stresses at early ages, the amount of creep must be taken into account.
Figure 14. Time-dependent deformation at time t, for a loading at time t0.(43)
In modeling of time-dependent deformation, creep compliance formulation is generally the preferred method. In this method, the total linear time-dependent deformation, ![]() (t), is expressed as mathematically as shown in equation 77 below and illustrated in figure 14 above.
(t), is expressed as mathematically as shown in equation 77 below and illustrated in figure 14 above.
where,
J(t,t0) = creep compliance defined as the response at time t after loading at time t0 and
![]() (t0) = applied stress at time t0.
(t0) = applied stress at time t0.
The instantaneous and time-dependent components of the total deformation can be separated as shown in equation 78:
where,
![]() (t0) = the instantaneous modulus of elasticity at time t0,
(t0) = the instantaneous modulus of elasticity at time t0,
![]() (t,t0) = the creep coefficient (ratio of creep to elastic strain), and
(t,t0) = the creep coefficient (ratio of creep to elastic strain), and
Eeff = the effective modulus of elasticity at time t.
Few models are available to model the time-dependent deformation and creep compliance of concrete at early ages. The Extended Triple Power Law model is developed from the Double Power Law and the Triple Power Law.(35, 44) The Double Power Law is perhaps the most well known compliance function, and has been used by many authors because it is based on extensive laboratory test results. The Triple Power Law was developed to provide a more accurate description of the long-term creep. As is commonly done, it will also be assumed that the creep response in tension is equal to the creep in compression.
Neither the Double nor the Triple Power Laws were calibrated for loading at early ages, and they were not intended to predict creep for young concrete.(45) Westman estimated that the Double and Triple Power Laws are only valid for loading ages larger than about 2 days.(43) Therefore, the Triple Power Law was adjusted first by Emborg(45) and then by Westman(43) to account for loading at ages less than about 2 days. The Extended Triple Power Law, as documented by Westman, provides good agreement with early-age test data, and accounts for all the factors that could influence the time-dependent deformation, such as:
In 1989, Emborg extended the Triple Power Law with two additional functions, which Westman(43) modified in 1999. For loading ages less than about 2 days, the function ![]() 1(t0) models the age dependence of the instantaneous deformation, and
1(t0) models the age dependence of the instantaneous deformation, and ![]() 2(t,t0) models the increase of creep when the load has been applied. The purpose of the two new terms,
2(t,t0) models the increase of creep when the load has been applied. The purpose of the two new terms, ![]() 1(t0) and
1(t0) and ![]() 2(t,t0), are shown schematically in figure 15 . The creep compliance according to the Extended Triple Power Law is as shown in equations 79 through 90:
2(t,t0), are shown schematically in figure 15 . The creep compliance according to the Extended Triple Power Law is as shown in equations 79 through 90:
where,
t = concrete age,
t0 = equivalent age when the load is applied (days),
E0 = negative asymptotic modulus of elasticity at time t0 (psi), (1 psi = 6.89 kPa)
(E0 may be determined from the 28-day modulus, E0 ![]() 1.5×E28),
1.5×E28),
w/c = water-to-cement ratio,
f'c = 28-day cylinder compressive strength (MPa),
where,
a/c = total aggregate/cement ratio,
s/c = sand/cement ratio,
a/g = coarse aggregate/cement ratio, and
a1 = 1.00 for Type I or II cement,
0.93 for Type III cement, and
1.03 for Type IV cement.
B(t,t0;n) is a binomial integral and may be evaluated by the following power series (equations 85 and 86):
with
Furthermore, if t0 ![]() t1,
t1,
if t0 ![]() t1,
t1,
and if t0 ![]() t3,
t3,
If t0 > t3,
where,
ts = the apparent setting time of the concrete (days),
t1 , t3 = time limits for adjustment at early ages (days),
t2 , a2 = parameter for the development of the time function (days),
![]() 1 = initial value of function
1 = initial value of function ![]() 1(t0) at t0 = ts,
1(t0) at t0 = ts,
![]() 2 = initial value of function
2 = initial value of function ![]() 2(t,t0). at t0 = ts,
2(t,t0). at t0 = ts,
a1 = parameter modifying the shape of ![]() 1(t0), and
1(t0), and
a3 = parameter modifying the end value of ![]() 2(t,t0).
2(t,t0).
Figure 15. A schematic of the additional ![]() 1(t0) and
1(t0) and ![]() 2(t,t0) functions to extend the Triple Power Law for the early-age creep response.(43)
2(t,t0) functions to extend the Triple Power Law for the early-age creep response.(43)
The dependence of creep on different curing temperatures that are constant for the time of interest may be modeled with the coefficients ![]() T and jT instead of n and
T and jT instead of n and ![]() 1, as shown in equations 91 through 97:(35)
1, as shown in equations 91 through 97:(35)
where,
![]() , (T measured in Kelvin), and (92)
, (T measured in Kelvin), and (92)
where,
where,
toT= age of the concrete when the temperature T is applied.
The age of the concrete at time of loading, t0, is here expressed as shown in equation 98:
where,
t'e = equivalent hydration period, and equation 99,
where,
T0 = the reference temperature (293 °K).
In the documentation provided by Westman, the necessary values for each of the parameters listed in this section are provided to allow the implementation of this model.(43) Based on the characteristics of the different mixtures tested by Westman, the mixture corresponding to a typical pavement mixture was selected. The characteristics of this mix are as follows: w/c = 0.40, 330 kg/m3 cement, 5.6 percent air content, and a 28-day compressive strength of about 47.2 MPa. Based on the test results with this mixture design, it is recommended that the following parameters for the Extended Triple Power Law be used:
| t1 = 1.5 days | |
| t3 = 1.5 days | |
| t2 = 0.02 days | a1 = 5 |
| a2 = 0.2 | a3= 5 |
To obtain a reasonably accurate estimate of the stresses at early ages, the amount of relaxation that occurs must be taken into account. It is recommended that the Extended Triple Power Law be used to determine the creep compliance at early ages, as this model has been developed to characterize early-age response.
In the implementation of creep compliance formulation, there are two possible approaches, and both methods have their advantages and disadvantages. The methods can briefly be described as follows:
If this model is incorporated in future versions of HIPERPAV, it is recommended that the first method be used, since the approach is less likely to produce conversion problems during analysis. The following sections will provide further details on the solution to this procedure.
Using the principle of superposition, the strain history ![]() (t) caused by an arbitrary history of applied stress
(t) caused by an arbitrary history of applied stress ![]() (t) can be determined by assuming the stress history is composed of infinitesimal step functions as shown in figure 16 .(46) The total strain can be calculated as shown in equation 100.(45,46) This equation is a general uniaxial constitutive relation defining concrete as an aging viscoelastic material.
(t) can be determined by assuming the stress history is composed of infinitesimal step functions as shown in figure 16 .(46) The total strain can be calculated as shown in equation 100.(45,46) This equation is a general uniaxial constitutive relation defining concrete as an aging viscoelastic material.
where,
J(t,t0) = creep compliance defined as the response at time t after loading at time t0,
d![]() (t0) = stress increment at time t0, and
(t0) = stress increment at time t0, and
![]() 0 (t) = stress-independent strain increment at time t.
0 (t) = stress-independent strain increment at time t.
Figure 16. Decomposition of stress history into stress steps.
When the history of strain is prescribed, equation 100 can be solved by a step-by-step numerical solution, where time is subdivided into discrete time steps, tr (r = 0,1,2, … n) with time steps, ![]() tr = tr – tr-1.(46) A schematic for the numerical solution is shown in figure 17, and the steps for the algorithm are as follows:
tr = tr – tr-1.(46) A schematic for the numerical solution is shown in figure 17, and the steps for the algorithm are as follows:
Step 1: At time tr, determine the equivalent age ter, and the change in equivalent age as: ![]() ter = ter – ter-1.
ter = ter – ter-1.
Step 2: Determine the applied strain, ![]() r, and calculate the change in strain as: D
r, and calculate the change in strain as: D![]() r =
r = ![]() r –
r – ![]() r-1.
r-1.
Step 3: Determine the incremental elastic modulus, E″r= 1/ J(r,r – ½). Subscript r, refer to the discrete time ter, and J(r,r – ½) may be interpreted as J(ter,ter – ![]() ter/2).
ter/2).
Step 4: Determine the incremental strain, ![]()
![]()
![]() r, as shown in equation 101.
r, as shown in equation 101.
where,
![]()
![]() s = ss – ss-1,
s = ss – ss-1, ![]()
![]() 0r =
0r = ![]() 0r –
0r – ![]() 0r-1, and
0r-1, and
![]() Jr = J(r,s – ½) – J(r – 1,s – ½).
Jr = J(r,s – ½) – J(r – 1,s – ½).
Step 5: Finally, the stress increment (![]()
![]() r) for the time step,
r) for the time step, ![]() tr can be determined as shown in equation 102:
tr can be determined as shown in equation 102:
NOTE: Due to the nature of the summation required in equation 101, and the fact that the value J(x,x) is not singular, the start of the numerical iteration (r = 0, and r = 1) requires some initial calculations other than those presented above. Iteration interval r = 0, should be taken to occur at time, t = t0, and r = 1 should be taken to occur at time, t = to+ 0.01 (hours). The following calculations are necessary for r = 0 and r = 1 (equations 103 and 104, respectively):
At r = 0:
At r = 1:
Figure 17. Discreet subdivision of time for numerical creep analysis.
Figures 18–20 show a schematic of how strains could be superimposed to model strain levels of varying intensities. Creep recovery at unloading could be overestimated by this principle, as the plastic flow component of the irrecoverable time-dependent deformation is not taken into accounted.(43)
Based on typical inputs, and the strains that were calculated with the HIPERPAV I program, the numerical procedure outlined above was programmed into Mathcad™ to verify the results of the models. The results are shown in figure 21 . With no relaxation modeled, the strains and the stresses cross the zero-stress level at the same time (approximately 22 hours). However, when the effects of relaxation are accounted for, the stress at ages less than 22 hours are significantly less, and the zero-stress level occurs earlier at an age of about 19 hours. Because much of the early tension has been relaxed, the magnitude of compressive forces between ages of 19 and 32 hours also is increased.
Figure 18. Superposition of various strains intensities: Loading.
Figure 19. Superposition of various strains intensities: Unloading.
Figure 20. Superposition of various strains intensities: Net applied strains.
Figure 21. Comparison of the results of the relaxation model and model without relaxation.
To obtain a reasonably accurate estimate of the stresses at early ages, the amount of relaxation that occurs must be taken into account. It is recommended that the Extended Triple Power Law be used to determine the creep compliance at early ages, as this model has been developed extensively to characterize early-age response. A numerical technique to model the time-dependent response for concrete at early ages is also presented. The principle of superposition is used, where the strain history ![]() (t) caused by an arbitrary history of applied stress
(t) caused by an arbitrary history of applied stress ![]() (t), is determined by assuming the stress history is composed of infinitesimal step functions.(46)
(t), is determined by assuming the stress history is composed of infinitesimal step functions.(46)
A brief description of the primary JPCP long-term performance models incorporated in HIPERPAV II is provided in the following sections. These models are divided in the following categories:
Environmental models are used to predict the temperature and moisture gradient through the pavement structure. Long-term materials properties models are used to predict the development of strength and stiffness at ages beyond 28 days. Structural models are used to predict the pavement behavior in terms of stress, strain, and deflection due to environmental and traffic loadings. Finally, distress models are used to predict the distress progression as a function of environmental and traffic loads.
As stated in section B.1.2 , the finite-difference method is used for prediction of long-term concrete temperatures in HIPERPAV II. A detailed description of this model is presented in that section. However, because pavement temperatures undergo seasonal changes in the long term, and because HIPERPAV II predicts PCC temperatures only at isolated periods of time for every season, the initial pavement temperature profile is required as an input in the finite-difference method for predicting the subsequent PCC temperatures for that season. HIPERPAV II uses the closed form solution developed by Barber described in section B.1.2.6 for this purpose.
This section summarizes the assumptions and limitations of the moisture model incorporated in HIPERPAV II. The model provides a simple method to predict the average monthly moisture content in pavement base materials using site-dependent climate conditions, soil data, and some pavement geometries.(18)
The required inputs for the model are given below.
The THMI is a correlation between rainfall and the potential for water loss through evaporation and transpiration.
High rainfall totals do not necessarily equate to a high THMI values because climatic conditions may dictate that the moisture is lost before it is absorbed into the soil.(47) A current practice is to group climate types according to moisture and winter temperature.(48) Table 14 gives a range of THMI values for specific locations in each of these climate types.
| City | THMI | Moisture | Winter Temperature |
|---|---|---|---|
| Chicago, IL | 30 | Wet | Cold |
| Fargo, ND | −5 | Moderate | Cold |
| Reno, NV | −40 | Dry | Cold |
| Washington, DC | 60 | Wet | Moderate |
| Oklahoma City, OK | 0 | Moderate | Moderate |
| Las Vegas, NV | −42 | Dry | Moderate |
| Atlanta, GA | 55 | Wet | Warm |
| Dallas, TX | 0 | Moderate | Warm |
| San Antonio, TX | −18 | Dry | Warm |
Default soil characteristics that provided values for lesser known parameters were included with the model. Table 15 gives these values.
| USC | %Clay | wsat – PL | SucPL | Gs |
|---|---|---|---|---|
| CH | 70 | 26.2 | 3.5 | 2.68 |
| CL | 40 | 8.4 | 3.2 | 2.7 |
| MH | 30 | 5.3 | 3 | 2.7 |
| ML | 20 | 2.2 | 2.8 | 2.71 |
| SC | 30 | 4.4 | 2.9 | 2.65 |
| SM | 25 | 2.4 | 2.7 | 2.65 |
| SP–SC | 12 | 1.5 | 2.6 | 2.65 |
| SW–SC | 12 | 1.5 | 2.6 | 2.65 |
| SP–SM | 10 | 0.5 | 2.4 | 2.65 |
| SW–SM | 10 | 0.5 | 2.4 | 2.65 |
| SP | 5 | 0.3 | 2.4 | 2.64 |
| SW | 5 | 0.3 | 2.4 | 2.66 |
| GW–GC | 12 | 1.1 | 2.2 | 2.65 |
| GP–GC | 12 | 1.1 | 2.2 | 2.65 |
| GW–GM | 10 | 0.6 | 2 | 2.65 |
| GP–GM | 10 | 0.6 | 2 | 2.65 |
| GP | 5 | 0.2 | 1.8 | 2.65 |
| GW | 5 | 0.2 | 1.8 | 2.65 |
The model makes a series of four calculations to predict the average monthly moisture content.
Reference Suction: The reference suction, Sucref, is based on the %Clay and THMI. The magnitude of reference suction is determined as shown in equations 105 through 110:
If %Clay ≤ 6 percent:
If 6 percent < %Clay < 40 percent:
If %Clay ≥ 40 percent:
Average Monthly Rainfall: The average monthly rainfall, rainavg, is calculated by taking the average of the maximum, rainmax, and minimum, rainmin, monthly rainfall totals for the design year (equation 111).
Suction Variation: The following steps in equations 112 through 114 are made to calculate the monthly soil suction, Sucmo: (112)
where,
![]() = 0.25 for paved shoulders and
= 0.25 for paved shoulders and
![]() = 0.50 for unpaved shoulders.
= 0.50 for unpaved shoulders.
Calculation of Moisture Content: The final step in the model is to correlate the monthly suction value to moisture content, as shown in equations 115 through 117.
If Sucmo < SucPL:
A sensitivity analysis was performed on the continuity of the reference suction calculations and the influence of climate and rainfall.
B.2.1.2.3.1 Reference Suction
A quick analysis on the continuity of the reference suction calculation was performed by choosing values just above and below the calculation thresholds. This analysis is not included, but it indicated that the reference suction calculation is continuous. Six sets of values for %Clay and THMI were used to evaluate the six possible reference suction calculations. The effect of paved shoulders was also examined for each scenario. Constant monthly rainfall totals were used during this portion of the sensitivity analysis even though the THMI varied between runs. Table 16 shows the factorial for this portion of the experiment. The following sections summarize the results according to soil classifications.
| Scenarios | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Thornthwaite Moisture Index (THMI) | −15 | −15 | 10 | 10 | −15 | −15 | 10 | 10 | −15 | −15 | −10 | −10 |
| Soil class | CL | CL | CL | CL | GW-GM | GW-GM | GW-GM | GW-GM | GW | GW | GW | GW |
| %Clay | 40 | 40 | 40 | 40 | 10 | 10 | 10 | 10 | 5 | 5 | 5 | 5 |
| w(PL) – w(sat) | 8.4 | 8.4 | 8.4 | 8.4 | 0.6 | 0.6 | 0.6 | 0.6 | 0.2 | 0.2 | 0.2 | 0.2 |
| w(sat) | 23.4 | 23.4 | 23.4 | 23.4 | 15.6 | 15.6 | 15.6 | 15.6 | 10.2 | 10.2 | 10.2 | 10.2 |
| Plastic limit | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 10 | 10 | 10 | 10 |
| Liquid limit | 40 | 40 | 40 | 40 | 21 | 21 | 21 | 21 | 15 | 15 | 15 | 15 |
| Plasticity index | 25 | 25 | 25 | 25 | 6 | 6 | 6 | 6 | 5 | 5 | 5 | 5 |
| Suction(PL) | 3.2 | 3.2 | 3.2 | 3.2 | 2 | 2 | 2 | 2 | 1.8 | 1.8 | 1.8 | 1.8 |
| Paved shoulder (Y/N) | Y | N | Y | N | Y | N | Y | N | Y | N | Y | N |
Lean Clay (CL): Results for the CL soil are presented in figure 22 and table 17. Table 17 reports the monthly moisture content for scenarios 1–4 as outlined in table 15. The fifth (1–2) and sixth (3–4) columns examine the effect of paved shoulders on moisture content. The final two columns (1–3 and 2–4) examine the effect of changing the formula for reference suction calculation by a change in the THMI. The average and standard deviation for the effects of these changes are also given. Figure 22 shows the monthly variations in moisture content. The THMI value appears to control the general vertical location in this figure, while rainfall and paved/unpaved shoulders control variability. The presence of a paved shoulder appears to reduce moisture content variation throughout the year.
| Scenario | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Month | Rain (mm) | 1 | 2 | 3 | 4 | 1–2 | 3–4 | 1–3 | 2–4 |
| Jan | 81 | 10.31 | 10.02 | 14.18 | 13.89 | 0.29 | 0.29 | 3.87 | 3.87 |
| Feb | 93 | 10.56 | 10.53 | 14.43 | 14.39 | 0.04 | 0.04 | 3.87 | 3.87 |
| Mar | 64 | 9.95 | 9.31 | 13.82 | 13.18 | 0.64 | 0.64 | 3.87 | 3.87 |
| Apr | 89 | 10.49 | 10.37 | 14.35 | 14.24 | 0.11 | 0.11 | 3.87 | 3.87 |
| May | 173 | 12.23 | 13.86 | 16.91 | 19.75 | 1.63 | 2.84 | 4.68 | 5.89 |
| Jun | 59 | 9.85 | 9.10 | 13.72 | 12.97 | 0.75 | 0.75 | 3.87 | 3.87 |
| Jul | 155 | 11.85 | 13.11 | 16.26 | 18.45 | 1.26 | 2.19 | 4.40 | 5.34 |
| Aug | 108 | 10.87 | 11.14 | 14.74 | 15.01 | 0.27 | 0.27 | 3.87 | 3.87 |
| Sep | 17 | 8.97 | 7.34 | 12.83 | 11.20 | 1.63 | 1.63 | 3.87 | 3.87 |
| Oct | 129 | 11.30 | 12.00 | 15.29 | 16.51 | 0.70 | 1.22 | 3.99 | 4.51 |
| Nov | 168 | 12.12 | 13.65 | 16.72 | 19.38 | 1.52 | 2.66 | 4.60 | 5.73 |
| Dec | 83 | 10.35 | 10.11 | 14.22 | 13.98 | 0.25 | 0.25 | 3.87 | 3.87 |
| Average | 0.76 | 1.07 | 4.05 | 4.37 | |||||
| Std. Dev | 0.61 | 1.02 | 0.32 | 0.81 | |||||
Figure 22. Monthly moisture content variation for lean clay (CL), scenarios 1–4.
Well-Graded Silty Gravel (GW–GM): Results for the GW–GM soil are presented in figure 23 and table 18. These scenarios also show that the moisture content value is dictated by the THMI, but the variability is dictated by rainfall and shoulder conditions. The variability of the GW–GM soil is noticeably less than the CL soil. This shows that the model accounts for changes in particle size, which directly affects the suction parameters used in the moisture content calculations. Smaller particle sizes or higher %Clay typically mean that the soil does not drain as well and is more susceptible to moisture content variation. As shown in figure 23 and in the previous section, the model predicts that a paved shoulder lessens the variability of moisture content throughout the year.
| Scenario | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Month | Rain (mm) | 5 | 6 | 7 | 8 | 5–6 | 7–8 | 5–7 | 6–8 |
| Jan | 81 | 11.05 | 10.86 | 13.10 | 12.91 | 0.19 | 0.19 | 2.05 | 2.05 |
| Feb | 93 | 11.22 | 11.20 | 13.27 | 13.25 | 0.02 | 0.02 | 2.05 | 2.05 |
| Mar | 64 | 10.82 | 10.40 | 12.87 | 12.45 | 0.42 | 0.42 | 2.05 | 2.05 |
| Apr | 89 | 11.17 | 11.10 | 13.22 | 13.15 | 0.07 | 0.07 | 2.05 | 2.05 |
| May | 173 | 12.32 | 13.39 | 14.37 | 15.60 | 1.07 | 1.23 | 2.05 | 2.21 |
| Jun | 59 | 10.75 | 10.26 | 12.80 | 12.31 | 0.49 | 0.49 | 2.05 | 2.05 |
| Jul | 155 | 12.07 | 12.90 | 14.12 | 14.95 | 0.83 | 0.83 | 2.05 | 2.05 |
| Aug | 108 | 11.42 | 11.60 | 13.47 | 13.65 | 0.18 | 0.18 | 2.05 | 2.05 |
| Sep | 17 | 10.17 | 9.10 | 12.22 | 11.15 | 1.07 | 1.07 | 2.05 | 2.05 |
| Oct | 129 | 11.70 | 12.16 | 13.75 | 14.21 | 0.46 | 0.46 | 2.05 | 2.05 |
| Nov | 168 | 12.25 | 13.25 | 14.30 | 15.42 | 1.00 | 1.12 | 2.05 | 2.17 |
| Dec | 83 | 11.08 | 10.92 | 13.13 | 12.97 | 0.16 | 0.16 | 2.05 | 2.05 |
| Average | 0.50 | 0.52 | 2.05 | 2.07 | |||||
| Std. Dev | 0.40 | 0.44 | 0.00 | 0.06 | |||||
Figure 23. Monthly moisture content variation for well-graded silty gravel (GW–GM), scenarios 5–8.
Well-Graded Gravel (GW): Results for the GW soil are presented in figure 24 and table 19. The effects of THMI, paved shoulders, and rainfall are less pronounced for the GW soil. THMI changes did not alter the vertical placement in figure 24 as in the previous scenarios, which caused all four moisture contents to be in the same ranges throughout the design year. One explanation is that the model of GW soil contains only 5 percent clay and drains freely. Therefore, the evaporation and transpiration accounted for by the THMI do not have as great an affect as soils with higher percentages of clay. In these scenarios, the presence of a paved shoulder reduces the moisture content variability, but not in the same range as those in the previous scenarios.
| Scenario | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Month | Rain (mm) | 9 | 10 | 11 | 12 | 9–10 | 11–12 | 9–11 | 10–12 |
| Jan | 81 | 9.61 | 9.49 | 9.72 | 9.60 | 0.12 | 0.12 | 0.11 | 0.11 |
| Feb | 93 | 9.71 | 9.70 | 9.82 | 9.81 | 0.01 | 0.01 | 0.11 | 0.11 |
| Mar | 64 | 9.46 | 9.19 | 9.57 | 9.30 | 0.27 | 0.27 | 0.11 | 0.11 |
| Apr | 89 | 9.68 | 9.63 | 9.79 | 9.74 | 0.05 | 0.05 | 0.11 | 0.11 |
| May | 173 | 10.20 | 10.20 | 10.20 | 10.20 | 0.00 | 0.00 | 0.00 | 0.00 |
| Jun | 59 | 9.42 | 9.11 | 9.53 | 9.22 | 0.31 | 0.31 | 0.11 | 0.11 |
| Jul | 155 | 10.20 | 10.20 | 10.20 | 10.20 | 0.00 | 0.00 | 0.00 | 0.00 |
| Aug | 108 | 9.84 | 9.95 | 9.95 | 10.14 | 0.11 | 0.19 | 0.11 | 0.19 |
| Sep | 17 | 9.05 | 8.37 | 9.16 | 8.49 | 0.68 | 0.68 | 0.11 | 0.11 |
| Oct | 129 | 10.04 | 10.20 | 10.20 | 10.20 | 0.16 | 0.00 | 0.16 | 0.00 |
| Nov | 168 | 10.20 | 10.20 | 10.20 | 10.20 | 0.00 | 0.00 | 0.00 | 0.00 |
| Dec | 83 | 9.62 | 9.52 | 9.74 | 9.63 | 0.10 | 0.10 | 0.11 | 0.11 |
| Average | 0.15 | 0.14 | 0.09 | 0.08 | |||||
| Std. Dev | 0.19 | 0.20 | 0.06 | 0.06 | |||||
Figure 24. Monthly variation for well-graded gravel (GW), scenarios 9–12.
B.2.1.2.3.2 Climate and Rainfall
The second part of the sensitivity analysis evaluated two specific soils at five locations. The soil parameters used in this analysis were derived from Lytton's default values for CL and GW–GM soil types.(48) THMI and monthly rainfall values for each location were identified using historical climate data from the National Climate Data Center (NCDC).(49) Table 20 shows the factorial used for this aspect of the analysis.
| Location | City | THMI | Moisture | Winter Temperature |
|---|---|---|---|---|
| 1 | Chicago, IL | 30 | Wet | Cold |
| 2 | San Antonio, TX | −18 | Dry | Warm |
| 3 | Oklahoma City, OK | 0 | Moderate | Moderate |
| 4 | Atlanta, GA | 55 | Wet | Warm |
| 5 | Reno, NV | −40 | Dry | Cold |
Table 21 gives the soil data for the CL and GW–GM soils used in the analysis.
| Property | Soil 1 | Soil 2 |
|---|---|---|
| Soil class | CL | GW–GM |
| %Clay | 40 | 10 |
| w(PL) – w(sat) | 8.4 | 0.6 |
| w(sat) | 26.4 | 15.6 |
| Plastic limit | 18 | 15 |
| Liquid limit | 38 | 21 |
| Plasticity index | 20 | 6 |
| Suction(PL) | 3.2 | 2 |
| Gs | 2.7 | 2.65 |
Table 22 gives the monthly rainfall totals for each of the five locations. Notice that the THMI value does not depend directly upon rainfall.
| Month | Chicago, IL | San Antonio, TX | Oklahoma City, OK | Atlanta, GA | Reno, NV |
|---|---|---|---|---|---|
| Jan | 36.6 | 43.4 | 28.7 | 120.4 | 27.2 |
| Feb | 32.5 | 46.0 | 39.6 | 121.9 | 25.1 |
| Mar | 63.8 | 38.6 | 68.8 | 146.6 | 18.0 |
| Apr | 89.4 | 63.5 | 70.4 | 108.2 | 9.7 |
| May | 79.8 | 107.2 | 132.8 | 109.0 | 17.5 |
| Jun | 92.5 | 96.8 | 109.5 | 90.4 | 11.7 |
| Jul | 89.4 | 54.9 | 66.3 | 127.3 | 7.1 |
| Aug | 105.9 | 64.5 | 66.0 | 93.0 | 8.1 |
| Sep | 87.4 | 86.6 | 97.5 | 86.9 | 9.9 |
| Oct | 58.4 | 80.5 | 82.0 | 77.5 | 9.7 |
| Nov | 72.6 | 66.5 | 50.3 | 98.0 | 22.1 |
| Dec | 61.5 | 38.4 | 35.6 | 110.0 | 25.1 |
| Total | 869.7 | 787.1 | 847.1 | 1289.1 | 191.0 |
Lean Clay (CL): The results from the CL soil are given in table 23 and figure 25. This soil showed a large amount of variability between climate types. Atlanta, GA, and Chicago, IL, have the highest THMI values and have the highest predicted moisture contents. Reno, NV, has the lowest THMI and subsequently has the lowest predicted moisture content. These findings reinforce earlier observations that the vertical placement in figure 25 is directly related to THMI and the monthly variation is due to rainfall.
| Month | Chicago, IL | San Antonio, TX | Oklahoma City, OK | Atlanta, GA | Reno, NV |
|---|---|---|---|---|---|
| Jan | 17.46 | 10.04 | 14.48 | 22.64 | 6.26 |
| Feb | 17.25 | 10.20 | 14.89 | 22.73 | 5.84 |
| Mar | 19.06 | 9.77 | 15.99 | 24.35 | 4.47 |
| Apr | 20.64 | 11.19 | 16.04 | 21.83 | 2.82 |
| May | 20.05 | 13.66 | 18.45 | 21.87 | 4.34 |
| Jun | 20.84 | 13.08 | 17.52 | 20.66 | 3.20 |
| Jul | 20.65 | 10.69 | 15.89 | 23.08 | 2.35 |
| Aug | 21.67 | 11.25 | 15.88 | 20.82 | 2.53 |
| Sep | 20.52 | 12.51 | 17.06 | 20.43 | 2.86 |
| Oct | 18.73 | 12.16 | 16.49 | 19.81 | 2.83 |
| Nov | 19.61 | 11.36 | 15.29 | 21.16 | 5.28 |
| Dec | 18.92 | 9.75 | 14.73 | 21.94 | 5.85 |
| Average | 19.62 | 11.30 | 16.06 | 21.78 | 4.05 |
| Std. Dev. | 1.37 | 1.31 | 1.18 | 1.29 | 1.46 |
Figure 25. Monthly variation for lean clay (CL) in five U.S. cities.
Well-Graded Silty Gravel (GW–GM): The results from the analysis of the GW–GM soil type are shown in table 24 and figure 26. The prediction for this soil shows less variation than the CL soil. This also reinforces earlier observations that the model assumes soils with higher clay contents will fluctuate more than granular soils that drain more freely. Even with less variation, the moisture contents varied according to the THMI value at each location.
| Month | Chicago, IL | San Antonio, TX | Oklahoma City, OK | Atlanta, GA | Reno, NV |
|---|---|---|---|---|---|
| Jan | 10.04 | 10.01 | 11.96 | 14.75 | 9.63 |
| Feb | 10.20 | 10.09 | 12.18 | 14.79 | 9.40 |
| Mar | 9.77 | 9.86 | 12.78 | 15.60 | 8.64 |
| Apr | 11.19 | 10.64 | 12.82 | 14.37 | 7.74 |
| May | 13.66 | 11.99 | 14.10 | 14.39 | 8.58 |
| Jun | 13.08 | 11.67 | 13.62 | 13.82 | 7.95 |
| Jul | 10.69 | 10.36 | 12.73 | 14.96 | 7.48 |
| Aug | 11.25 | 10.67 | 12.73 | 13.90 | 7.58 |
| Sep | 12.51 | 11.36 | 13.37 | 13.71 | 7.76 |
| Oct | 12.16 | 11.17 | 13.06 | 13.42 | 7.75 |
| Nov | 11.36 | 10.73 | 12.40 | 14.05 | 9.09 |
| Dec | 9.75 | 9.85 | 12.10 | 14.42 | 9.40 |
| Average | 11.30 | 10.70 | 12.82 | 14.35 | 8.42 |
| Std. Dev. | 1.31 | 0.72 | 0.64 | 0.61 | 0.80 |
Figure 26. Monthly variation for well-graded silty gravel (GW–GM) in five U.S. cities.
The model was evaluated using historical weather data from the NCDC and soil data from the American Association of State Highway Officials (AASHO) road test.(49 ,50 ,51) The pavement in loop 1 (untrafficked control lanes) was used for the analysis. Three layers of soil were compacted beneath the pavement. These layers are referred to as the embankment, subbase, and base layers. Published average spring and summer moisture contents from the road test were compared to the results from the model.(51) Some problems may have occurred in estimating the parameters needed by the model from the given soil data. Table 25 shows the gradation for each soil layer.
| % Passing | Embankment | Subbase | Base |
|---|---|---|---|
| 3.8 cm | 100 | 100 | 100 |
| 2.5 cm | 100 | 100 | 90 |
| 1.9 cm | 100 | 96.9 | 81 |
| 1.3 cm | 100 | 89.7 | 68 |
| No. 4 | 99 | 71.2 | 48 |
| No. 10 | 96.8 | – | 35 |
| No. 40 | 91 | 27 | 20 |
| No. 60 | 87.7 | – | – |
| No. 100 | – | – | 13.5 |
| No. 200 | 80.6 | 7.5 | 10 |
To run the model, soil parameters were estimated from the gradation and other data included in the AASHO road test reports.(50, 51) The gradation was used to determine the soil type and the corresponding default values included with the model were then used. Table 26 gives the actual values used in the model.
| Property | Embankment | Subbase | Base |
|---|---|---|---|
| Soil class | CL | SW–SM | GW–GM |
| %Clay | 81 | 7 | 10 |
| w(PL) – w(sat) | 8.4 | 0.5 | 0.6 |
| w(sat) | 24.9 | 7.5 | 7.6 |
| Plastic limit | 16.5 | 7 | 7 |
| Liquid limit | 29.4 | 10 | 9 |
| Plasticity index | 13.6 | 3 | 2 |
| Suction(PL) | 3.2 | 2.4 | 2 |
| Gs | 2.71 | 2.65 | 2.65 |
| Paved shoulder (Y/N) | Y | Y | Y |
Figure 27 compares the predicted moisture content using the aforementioned soil data and average rainfall totals from the NCDC and the measured values during the AASHO road test. The predicted measurements were typically within 2 to 3 percent in moisture content from the measured values. The lack of rainfall data from the time of measurement and error in the estimated soil properties could lead to deviation from the measured values.
Figure 27. Comparison of predicted and measured values from the AASHO road test.
The model also was evaluated using soil and weather data from DataPave 2.0, Beta Version (April 1999) and compared with moisture contents calculated in a FHWA time-domain reflectometry study.(53) The sites used for this purpose were in Texas (48–1068) and Maine (23–1026). Table 27 gives the climatic data for each site.
| Location | THMI | Moisture | Winter Temperature |
|---|---|---|---|
| Texas | 10 | Moderate | Warm |
| Maine | 80 | Wet | Cold |
As for the AASHO road test analysis, some soil properties had to be estimated from the given data. Missing soil data from the LTPP database had to be estimated to run the model. Soil types were recorded according to the AASHTO classification and had to be correlated to the Unified Soil Classification system to obtain certain properties. Figures 28 and 29 compare the predicted moisture contents and the values obtained from the FHWA study for the sites in Texas and Maine, respectively. The values from the FHWA study had to be estimated from charts and seemed to have questionable reliability.
Figure 28. Texas LTPP site comparison.
The subgrade for the Texas site is a lean clay (CL, A–7–6) and the subbase is a well-graded silty gravel (GW–GM, A–2–4). For this location, the moisture content prediction compared very well with the data from the FHWA study, although no data for the subgrade were found in the database.
Figure 29. Maine LTPP site comparison.
The Maine site has a lean silty soil (ML, A–4) in the subgrade and a well-graded silty gravel (GW–GM, A–1–A) in the subbase. The model predicted the subgrade to be saturated throughout the year and the subbase to be saturated from March to September. The saturated water content was an estimated parameter for these soils, which signals the need for quality soil property assumptions to ensure the reliability of the model.
This model appears to be able to predict monthly moisture content based on a few simple assumptions regarding THMI, %Clay, and presence of paved shoulders. Since the model is fairly simple, estimated soil and weather parameters can directly affect the outcome and accuracy of the model, as indicated by the Maine LTPP site comparison. The following trends were noticed from evaluating the model and should be noted before the model is used further:
The following items are not included in the model and can affect the moisture conditions beneath pavements:
Mechanical properties used in HIPERPAV II for long-term PCC characterization include modulus of elasticity and any of the following three strengths: tensile, flexural (modulus of rupture), or compressive. During the pavement life, the PCC slab is exposed to various stresses, such as curling and warping stresses, thermal axial stresses, and wheel load stresses. In the long term, one of the major failure modes is cracking due to fatigue. This generally has been found to be a function of the tensile stress to strength ratio at the bottom of the layer, implying that tensile strength is a significant characterization property. Unlike most concrete structures, JPCP does not rely on steel to withstand tensile stresses and is, therefore, typically designed using a specified tensile strength. Because concrete is much weaker in tension than in compression, tensile strength is the most critical strength characteristic.
The elastic modulus is an estimate of the slope of the stress-strain curve in the elastic region and a good indicator of the overall structural stiffness of the concrete. Because stresses and strains are related through the elastic modulus under assumptions of linear elasticity, it is important that this property be characterized. The model incorporated in HIPERPAV II is described in reference 54.
The following test methods are used to characterize PCC strength and stiffness.
In this section, recommended relationships between the different PCC pavement (PCCP) strength test methods are presented.
Melis et al. investigated the (fST/fR) ratio with different mix properties that are representative of concretes normally used in concrete pavements in Texas.(55) Altogether, 720 beams and 1260 cylinders were tested during this study. For this study, centerpoint loading according to ASTM C 293 was used to determine the rupture modulus of the concrete. Hence, all the correlations with regard to the flexural strength determined in this study will have to be converted to incorporate the loading configuration's effect on the tested concrete strength. The correlation between the splitting tensile and flexural strengths were determined for different concrete mixes, and the following mix variables were investigated:
Table 28 provides a summary of the test results achieved. Based on the results summarized in table 28, it was concluded that the transformation equation from the centerpoint-loaded modulus of rupture (fRC) to the splitting tensile strength should be as shown in equation 118:
| Splitting Tensile (152-mm x 305-mm Cylinder) | Modulus of Rupture | (fST/ fRC) Ratio |
|||
|---|---|---|---|---|---|
| Average Strength (MPa) | C.V. ( % ) | Average Strength (MPa) | C.V. ( % ) | ||
| 4 days | 2.69 | 6 | 4.34 | 6 | 0.62 |
| 7 days | 2.86 | 6 | 4.62 | 6 | 0.62 |
| 28 days | 3.24 | 6 | 5.31 | 6 | 0.62 |
| 56 days | 3.52 | 6 | 5.38 | 5 | 0.66 |
| Average | 2.86 | 6 | 4.59 | 6 | 0.62 |
Melis et al. made the following final conclusions and recommendations based on their test results(55) (pp. 75–76):
The recommendation from Melis et al. was based on centerpoint-loaded flexural beams, and to use their conversion formula, a conversion between the third point and centerpoint-loaded flexural specimens isare required. Carrasquillo and Carrasquillo performed a study with more than 700 beam specimens cast from 14 different mixes to investigate the use of centerpoint loading versus the third point loading in determining the flexural strength of concrete.(56)
The correlation between a specimen loaded at its center as opposed to its third point, for coarse aggregate sizes normally used in concrete pavement construction, was determined to be as shown in equation 119:
The relationship found above is also of the same order of magnitude with earlier findings from Kellermann, which concluded that the third point loading strength of a beam is about 88 percent of that found when it is loaded at its centerpoint.(57) Based on the fact that the tests performed by Carrasquillo and Carrasquillo were done more recently on typical concrete mix designs used for concrete pavements, it is reasoned that their conversion between the two loading configurations should be used.
Based on the results obtained by Carrasquillo and Carrasquillo, the conversion presented in equation 118 can be modified to account for the reduced flexural strength obtained when the third point loading configuration is used as opposed to the centerpoint-loading configuration. Using the conversion that the third point flexural strength is 86.4 percent of the centerpoint-loading, the following ratio (equation 120) between the splitting tensile strength and the third point-loaded modulus of rupture can be derived:
The fairly common relationship, shown in equation 121, between the modulus of rupture and compressive strength recommended by ACI is:(58)
However, it has been shown that the ACI equation provides a lower bound estimate (5th percentile) of the flexural strength, which is on the conservative side when designing reinforced concrete structures against cracking. It is not appropriate to use the ACI equation, therefore, when a conversion between average pavement strength is necessary. It also has been recommended that the relationship between the compressive strength and modulus of rupture is better predicted with expressions as a function of (f'c2/3) as compared to those expressions as a function of (f′c1/2).(59)
Raphael investigated the relationship between the flexural and compressive strength of concrete.(60) In this study, 12,000 individual test results gathered by 4 independent researchers were investigated together with the authors' own test results. The regression analysis that best fit the data can be seen in figure 30, and was determined to be as shown in equation 122:
![]() (in psi, 1 psi = 6.89 kPa) (122)
(in psi, 1 psi = 6.89 kPa) (122)
Figure 30. Comparison of test results with the correlation proposed in equation 122.(60)
In Texas, 306 compressive and 306 flexural tests were performed on concrete specimens made from five different pavement mix designs. Two different aggregate types were used for these projects—limestone and river gravel. The relationship between the compressive and flexural strength as presented in equation 123 was determined to provide the best fit, and an r2 value of 0.79 was obtained.
![]() (in psi, 1 psi = 6.89 kPa) (123)
(in psi, 1 psi = 6.89 kPa) (123)
Note that equations 122 and 123 are nearly identical and that they were developed from independent test results. Figure 31 shows the comparison of the equation developed by Raphael (equation 122) with regard to the test results measured in Texas. This figure demonstrates that Raphael's equation provides a good fit for the test data. This figure further shows the conservative nature of the ACI equation with regard to estimating the concrete's modulus of rupture. Based on the data presented in this section, it is recommended that equation 122 be used to describe the relationship between flexural and compressive strength.
Figure 31. Modulus of rupture versus compressive strength for Texas data.
The well-established relationship between modulus of elasticity (Ec) and compressive strength (fc) as recommended by the ACI will be used in this project. The conversion is shown in equation 124, and it can be seen that it is a function of the unit weight of the concrete. As the coarse aggregate accounts for 50–70 percent of the concrete by volume, the unit weight of the mix is determined mostly by the type of aggregate used in the mix.
where,
Ec = modulus of concrete in MPa and
wc = unit weight of concrete in kg/m3.
Note that equation 124 is only valid for values of wc between 1500 to 2500 kg/m3. To complete the conversion, the unit weight of the concrete must be determined. Popovics provides the following simplified equation (equation 125) to estimate the concrete unit weight.(61)
where,
wc = unit weight of concrete in kg/m3,
SG = average specific gravity of aggregate, and
Air = percent air content.
The average specific gravity of aggregate depends on the specific gravity of the mineral of which the aggregate is composed and also the amount of voids. The average specific gravity for different natural aggregates is presented in table 29.(62)
| Aggregate Type | Specific Gravity |
|---|---|
| Limestone | 2.66 |
| Sandstone | 2.69 |
| Granite | 2.69 |
| River gravel | 2.72 |
| Basalt | 2.80 |
Based on a typical air content of 4 percent and the specific gravities listed in table 29, the unit weights of the different aggregate types are as presented in table 30.
| Aggregate Type | Unit Weight (wc) (kg/m3) |
|---|---|
| Limestone | 2344 |
| Sandstone | 2365 |
| Granite | 2365 |
| River gravel | 2385 |
| Basalt | 2440 |
The long-term model forms recommended in the CEB-FIP Model Code 1990 are used in HIPERPAV II.(54) The equations in the model apply to concrete with normal weight aggregates with no appreciable amount of entrapped air other than intentionally entrained air.
The model calculates the values for strength and elastic modulus relative to the desired 28-day value. Application of the equations provides reasonable values for ages beyond 28 days. Figure 32 shows the curves for tensile strength and elastic modulus from 0 to 20,000 days (50 years) based on 28-day values of 700 psi for tensile strength and 4000 ksi for elastic modulus, reasonable 28-day values for a concrete pavement. Using the CEB-FIP model, there is a 23 percent gain in tensile strength from 28 days to 3 years. Elastic modulus increases 11 percent during the same time period. After 50 years, the gains are 27 percent and 13 percent for tensile strength and elastic modulus, respectively, over the 28-day values.
Figure 32. Tensile strength and elastic modulus values calculated using the CEB-FIP equation.
The development of strength with time depends on the type of cement, temperature, and curing conditions. The models assume a mean curing temperature of 20 °C and curing in accordance with the International Organization for Standardization (ISO) 2736/2. Equation 126 is used:
where,
ft(t) = the tensile strength at time t,
ft(28) = the desired 28-day tensile strength, and, as shown in equation 127,
where,
s = coefficient that depends on the type of cement,
0.20 for rapid hardening high strength cements,
0.25 for normal and rapid hardening cements, and
0.38 for slowly hardening cements,
t = time in days, and
t1 = 1 (for 1 day).
CEB-FIP recommends that the gain in other concrete properties, such as the modulus of rupture, compressive strength, and modulus of elasticity, be calculated using the same ![]() (t) factor. This is the approach used in HIPERPAV II to determine the concrete properties at ages other than 28 days.
(t) factor. This is the approach used in HIPERPAV II to determine the concrete properties at ages other than 28 days.
The CEB-FIP model code provides general equations for concrete structures. The equations were developed from a compilation of available data and, as such, background and original references for the models are not provided in the CEB-FIP document. Although the equations are not specific to concrete pavements, they provide reasonable values for tensile strength and elastic modulus over the long term. However, the general nature of the equations dictates that the values calculated for curing times beyond 28 days be considered as only approximations to actual values.
The validation data for the tensile strength model were published in the ACI Materials Journal, by Ghafoori and Bucholc.(63) This validation shows an excellent correlation between the calculated and measured values with an r2 of 0.995.
The validation data for the elastic modulus model were published in the ACI Materials Journal, by Khan, et al.(10) The measured values from the study at 14 different curing times during the first 100 days were compared to values calculated using the CEB-FIP model at the same ages and forced through the measured 28-day value. There was a good correlation between the calculated and measured values for most ages during the first 100 days of curing, with an overall r2 value of 0.92. Although there is not a strong correlation between the measured and calculated values for the first 10 days, HIPERPAV II uses a maturity-based model for this purpose.(1)
To predict the response of a rigid pavement due to external wheel loads accurately, a model is needed to assess the behavior of the pavement structure in the vicinity of discontinuities such as cracks and joints. This section describes the theoretical LTE model for both doweled and nondoweled JCP, and the midslab stress and deflection prediction models used along with the LTE model. These models were incorporated into HIPERPAV II.
The transfer of a wheel load across joints must be considered when mechanistically modeling the performance of a JCP. The LTE characterizes how traffic wheel loading is transferred from one section of JCP to the adjacent section. For a nondoweled JCP joint, load transfer can be attributed solely to aggregate interlock. If dowels are used, then both the dowels and the aggregate interlock contribute to the LTE of the joint. The theoretical LTE model presented here characterizes the load transfer across a joint as either a deflection transfer (LTE![]() ), or as a stress transfer (LTE
), or as a stress transfer (LTE![]() ).
).
If the deflection LTE of a joint is 100 percent efficient, both slabs will deflect the same amount. This is illustrated in figure 33, where both slabs deflect the same amount (![]() /2).
/2).
Figure 33. Schematic of deflection load transfer (LTEd) for a doweled JCP.
For the stress LTE (LTE![]() ), the stress in the pavement due to wheel loading is transferred across the joint.
), the stress in the pavement due to wheel loading is transferred across the joint.
The following sections present the theoretical equations that can be used to calculate LTE for doweled or nondoweled sections of JCP. The model is based primarily on work conducted by Westergaard.(64, 65) This model calculates LTE immediately after construction. The effect of repetitive loading on the joint and how this influences the LTE with regard to wearout and dowel looseness is discussed in subsequent sections.
The following sections describe the detailed formulation of the LTE model. To present this formulation in a logical and straightforward manner, the model is divided into the following calculation components:
The dimensional parameters affect all of these components directly, except for the loaded stress and deflection, and the LTE, which are affected indirectly by these parameters. The remaining nine components work linearly, as illustrated in figure 34.
Figure 34. Schematic of LTE model logic.
These models identify dimensional parameters that are used in the majority of the remaining models. The first variable is the radius of the contact area (a). It is defined in equation 128 from basic geometry as:(64)
where,
a = radius of the contact area (m),
P = wheel load (N), and
pt = tire pressure (MPa).
The radius of relative stiffness (l) of the pavement system is defined in equation 129 as follows:(64)
where,
l = radius of relative stiffness (m),
Ec = PCC elastic modulus (MPa),
h = PCC slab thickness (m),
![]() c = PCC Poisson's ratio (unitless), and
c = PCC Poisson's ratio (unitless), and
k = slab support reaction modulus (MPa/m).
A number of the following formulae will use the dimensionless ratio of these two parameters.
To determine the influence of dowels on the overall load transfer, a model based on the theory of Timoshenko and Lessels is used.(66) A summary of this theory can be found in a subsequent ACI publication.(67)
A number of variables are required for this characterization. The first is the bending moment of inertia (ID) of the dowel. This is defined in equation 130 as:(68)
where,
ID = bending moment of inertia of a circular dowel (m4), and
![]() D = diameter of the dowel (m).
D = diameter of the dowel (m).
The cross-sectional area of a circular dowel (AD) is defined in equation 131 as:(68)
where,
AD = cross-sectional area of the dowel (m2).
An adjustment is made of the cross-sectional area to account for its use in shear calculations.(69) The result is an effective cross-sectional area (ADz), defined in equation 132 as:
where,
ADz = effective cross-sectional area of the dowel (m2), and
AD = cross-sectional area of the dowel (m2) from equation 131.
The shear modulus of the dowel bar (GD) can possibly be a user input. However, it is more practical to estimate this value based on the assumption that it is a homogeneous, isotropic material, as shown in equation 133:(68)
where,
GD = shear modulus of the dowel (MPa),
ED = elastic modulus of the dowel (MPa), and
![]() D = Poisson's ratio of the dowel (unitless).
D = Poisson's ratio of the dowel (unitless).
This formula should not be used when the dowels are constructed with anisotropic materials, such as fiberglass.
To calculate the contribution of dowel stiffness to the LTE, five additional parameters must be calculated. The first is a correction factor for deep-beam shear deformation (![]() ), defined in equation 134 as:(69)
), defined in equation 134 as:(69)
where,
![]() = deep-beam shear deformation correction factor (unitless),
= deep-beam shear deformation correction factor (unitless),
ID = bending moment of inertia of a circular dowel (m4), from equation 130,
GD = shear modulus of the dowel (MPa), from equation 133,
ADz = effective cross-sectional area of the dowel (m2), from equation 132, and
w = joint opening (m).
Secondly, the relative stiffness (or characteristic) of the dowel-concrete system (![]() ) is calculated in equation 135 as:(69)
) is calculated in equation 135 as:(69)
where,
![]() = characteristic of the dowel-concrete system (m-1), and
= characteristic of the dowel-concrete system (m-1), and
KD = effective modulus of dowel support (MPa/m).
The shear stiffness of the dowel (C) is then defined in equation 136 as:(69)
where,
C = dowel (beam) shear stiffness (N/m), and
![]() = deep-beam shear deformation correction factor (unitless), from equation 134.
= deep-beam shear deformation correction factor (unitless), from equation 134.
The dowel-concrete interaction parameter (DCI) is then calculated in equation 137 as:(69)
where,
DCI = dowel-concrete interaction parameter (N/m), and
![]() = characteristic of the dowel-concrete system (m-1), from equation 135.
= characteristic of the dowel-concrete system (m-1), from equation 135.
Finally, the dowel shear stiffness (D![]() ) is calculated in equation 138 as:(69)
) is calculated in equation 138 as:(69)
where,
D![]() = dowel shear stiffness (N/m),
= dowel shear stiffness (N/m),
DCI = dowel-concrete interaction parameter (N/m), from equation 137, and
C = dowel (beam) shear stiffness (N/m), from equation 136.
To characterize the joint stiffness contribution due to aggregate interlock, a new model has been developed. This model is based on data collected by the Portland Cement Association (PCA) on a controlled load transfer experiment.(70)
The LTE model described here was employed in developing the new aggregate interlock model. To accomplish this, the agg/kl parameter (to be described) was “solved” as an unknown variable. The remaining (known) variables first were fixed, and the agg/kl parameter was solved for a known (reported) joint transfer efficiency (JTE). The dowel and joint opening variables were not needed in this analysis, and the remaining known variables are given in table 31.
| Variable | Description | Units | Value(s) |
|---|---|---|---|
| Ec | PCC elastic modulus | MPa | 30,337 *1 |
| PCC Poisson's ratio | none | 0.15 *2 | |
| H | PCC slab thickness | mm | 178 and 229 |
| tsaw | Sawcut depth | mm | 0 |
| P | Wheel load | N | 40,034 |
| pt | Tire pressure | MPa | 0.31 *3 |
| K | Slab support reaction modulus | MPa/m | 24.2 (clay) 39.4 (sand-gravel subbase) 122.7 (cement-treated subbase) |
Notes:
*1 – PCC modulus estimated from given compressive strength of 41.4 MPa
*2 – Assumed
*3 – Calculated from given load radius of 203 mm
JTE is a parameter that describes the percent of a load that is transferred from a loaded slab to an adjoining unloaded slab through load transfer. In the case of this experiment, aggregate interlock was the only mechanism. Additional information on this parameter will be given in a subsequent section. For the PCA experiment, JTE results for five combinations of the inputs in table 31 were reported. Within these five combinations, results for a number of crack openings were given. In total, 15 combinations of crack opening, slab thickness, and k-value were tested. From these combinations, agg/kl values were backcalculated using the LTE model. The results from these backcalculations are given in figure 35.
Figure 35. Relationship between the calculated agg/kl and measured JTE.
As can be seen from figure 35, the relationship between these two variables is quite pronounced. The next step in the development of an aggregate interlock characterization model was to identify a relationship between the backcalculated agg/kl values and the measured crack opening. Figure 36 illustrates the results of this comparison.
Figure 36. Relationship between measured crack opening and the calculated agg/kl.
From figure 36, two distinct relationships were identified corresponding to the two slab thicknesses used in the experiment. On a semilog scale, the relationships appear to be linear, and the two trends appear to be roughly parallel. As a result, a simple model form was selected with an exponential base, a constant slope, and a variable intercept. The final model is of the form shown in equation 139:
where,
agg/kl = the dimensionless aggregate interlock parameter (unitless),
![]() = aggregate interlock model intercept (unitless), defined below,
= aggregate interlock model intercept (unitless), defined below,
e = base of natural logarithm (» 2.71828…), and
w = crack opening (mm).
Through calibration, the aggregate interlock model intercept (g from equation 139) for the two known thicknesses was found to be 122 for the 229-mm slabs, and 37 for the 178-mm slabs. Based on engineering judgment, it is assumed that this intercept value would yield zero agg/kl as the thickness decreased in an exponential form and would increase linearly after an effective slab thickness of 178 mm. As a result of this assumption, the equations 140 and 141 were derived for the prediction of the intercept value as a function of the intact slab thickness (defined as the slab thickness minus the sawcut depth):
For h – tsaw < 178 mm:
For h – tsaw > 178 mm:
where,
![]() = aggregate interlock model intercept (unitless),
= aggregate interlock model intercept (unitless),
h = PCC slab thickness (mm), and
tsaw = sawcut depth (mm).
This model should be considered preliminary. One inherent deficiency in the model is the lack of a larger factorial of data for calibration. It is recommended that additional data be collected to conduct a more refined calibration. Subsequently, the model should be validated using an independent data set.
Although not required in the subsequent formulation, the variable defining the aggregate interlock (agg) can be calculated from the agg/kl value by simply multiplying by the slab support modulus (k) and by the radius of relative stiffness (l) as shown in equation 142:
where,
agg = aggregate interlock (MPa),
agg/kl = the dimensionless aggregate interlock parameter (unitless),
k = slab support reaction modulus (MPa/m), and
l = radius of relative stiffness (m), from equation 129.
To derive a common method to include the impacts of both dowels and aggregate interlock, a joint stiffness parameter is calculated. The joint stiffness parameter, or J value, is employed directly in a continuation of Westergaard's formulation for load transfer developed by Skarlatos, and reported subsequently by Ioannides and Hammons.(65, 71, 72)
For purposes of this model, the contribution to joint stiffness due to the presence of dowels (JD) is defined in equation 143:(69)
where,
JD = dimensionless joint stiffness due to dowels (unitless),
D![]() = dowel shear stiffness (N/m), from equation 138,
= dowel shear stiffness (N/m), from equation 138,
sD = dowel spacing (m),
k = Slab support reaction modulus (MPa/m), and
l = radius of relative stiffness (m), from equation 129.
The contribution of aggregate interlock to joint stiffness is simply defined as agg/kl, defined previously in equation 139. For nomenclature purposes, this variable is redefined in equation 144:
where,
Jagg = dimensionless joint stiffness due to aggregate interlock (unitless), and
agg/kl = the dimensionless aggregate interlock parameter (unitless), from equation 139.
The sum of these two parameters is the overall joint stiffness (J), which is defined in equation 145:
where,
J = overall dimensionless joint stiffness (unitless),
JD = dimensionless joint stiffness due to dowels (unitless), from equation 143, and
Jagg = dimensionless joint stiffness due to aggregate interlock (unitless), from equation 144.
The free edge deflection for a JCP is defined as the critical concrete deflection induced by a wheel load when applied on a theoretically long pavement edge with no adjoining slab. This is illustrated graphically in figure 37. This stress is commonly calculated using Westergaard's classical formulation.(65) For purposes of this model, a modified form is adopted here that has been enhanced by Ioannides and Hammons.(72) These authors have revisited the Westergaard solutions for pavement deflections and stresses, and have enhanced them using sophisticated numerical methods that were not available when the original solutions were developed.
Figure 37. Free edge loading of JCP.
For edge deflections, a dimensionless free edge deflection (![]() ) is calculated as shown in equation 146:
) is calculated as shown in equation 146:
where,
![]() = dimensionless free edge deflection (unitless),
= dimensionless free edge deflection (unitless),
B3,B4,B5 = Westergaard coefficients for free edge deflection (unitless), defined below,
a = radius of the contact area (m), from equation 128, and
l = radius of relative stiffness (m), from equation 129.
The three Westergaard coefficients (B3, B4, and B5) are defined in equations 147, 148, and 149:
where,
B3,B4,B5 = Westergaard coefficients for free edge deflection (unitless), and
![]() c = Poisson's ratio of the PCC.
c = Poisson's ratio of the PCC.
The free edge deflection (![]() f) can then be calculated from the dimensionless free edge deflection (
f) can then be calculated from the dimensionless free edge deflection (![]() ) as shown in equation 150:
) as shown in equation 150:
where,
![]() f = free edge deflection (m),
f = free edge deflection (m),
![]() = dimensionless free edge deflection (unitless), from equation 146,
= dimensionless free edge deflection (unitless), from equation 146,
P = wheel load (m),
k = slab support reaction modulus (MPa/m), and
l = radius of relative stiffness (m), from equation 129.
The free edge stress is calculated in a manner similar to that of the free edge deflection. A dimensionless free edge stress (![]() ) is first calculated in equation 151 as the sum of two components:
) is first calculated in equation 151 as the sum of two components:
where,
![]() = dimensionless free edge stress (unitless),
= dimensionless free edge stress (unitless),
![]() = first component of the dimensionless free edge stress (unitless), defined below, and
= first component of the dimensionless free edge stress (unitless), defined below, and
![]() = second component of the dimensionless free edge stress (unitless), defined below.
= second component of the dimensionless free edge stress (unitless), defined below.
The two components of the dimensionless stress function are calculated in equations 152 and 153:
where,
![]() = first component of the dimensionless free edge stress (unitless),
= first component of the dimensionless free edge stress (unitless),
![]() = second component of the dimensionless free edge stress (unitless),
= second component of the dimensionless free edge stress (unitless),
![]() c = Poisson's ratio of the PCC (unitless),
c = Poisson's ratio of the PCC (unitless),
a = radius of the contact area (m), from equation 128, and
l = radius of relative stiffness (m), from equation 129.
The constants employed in equation 153 are based on the assumption that the Poisson's ratio of the PCC is equal to 0.15. As a future enhancement to this model, it may be possible to rederive these constants for other values of Poisson's ratio. However, due to the overall sensitivity of this parameter, this exercise may be of secondary importance.
Based on the dimensionless free edge stress, the actual free edge stress can be calculated in equation 154:
where,
![]() f = free edge stress (MPa),
f = free edge stress (MPa),
![]() = dimensionless free edge stress (unitless), from equation 151,
= dimensionless free edge stress (unitless), from equation 151,
P = wheel load (N), and
h = PCC slab thickness (m).
The unloaded edge deflection is based on the same derivations previously described for the free edge deflection. In the case of the unloaded edge deflection, the value is equal to the deflection of the unloaded side of two adjoining slabs. Figure 38 illustrates this, where the unloaded and loaded edge deflections are defined graphically.
Figure 38. Loaded and unloaded deflections of a JCP.
The dimensionless unloaded edge deflection is given in equation 155:
where,
![]() = dimensionless unloaded edge deflection (unitless),
= dimensionless unloaded edge deflection (unitless),
B![]() 3,B
3,B![]() 4 = Westergaard coefficients for unloaded edge deflection (unitless), defined below,
4 = Westergaard coefficients for unloaded edge deflection (unitless), defined below,
a = radius of the contact area (m), from equation 128,
l = radius of relative stiffness (m) – from equation 129, and
J = overall dimensionless joint stiffness (unitless), defined in equation 145.
The Westergaard coefficients for this equation are defined in equations 156 and 157:
where,
B![]() 3,B
3,B![]() 4 = Westergaard coefficients for unloaded edge deflection (unitless).
4 = Westergaard coefficients for unloaded edge deflection (unitless).
The unloaded edge deflection (du) can then be calculated from the dimensionless unloaded edge deflection (![]() ) in equation 158:
) in equation 158:
where,
![]() u = unloaded edge deflection (m),
u = unloaded edge deflection (m),
![]() = dimensionless unloaded edge deflection (unitless), from equation 155,
= dimensionless unloaded edge deflection (unitless), from equation 155,
P = wheel load (N),
k = slab support reaction modulus (MPa/m), and
l = radius of relative stiffness (m), from equation 129.
The dimensionless unloaded edge stress can be calculated in equation 159:
where,
![]() = dimensionless free edge stress (unitless),
= dimensionless free edge stress (unitless),
B![]() 1,B
1,B![]() 2,B
2,B![]() 9= Westergaard coefficients for unloaded edge stress (unitless),
9= Westergaard coefficients for unloaded edge stress (unitless),
![]() c = Poisson's ratio of the PCC (unitless),
c = Poisson's ratio of the PCC (unitless),
a = radius of the contact area (m), from equation 128, and
l = radius of relative stiffness (m), from equation 129.
The Westergaard coefficients for this equation are defined in equations 160, 161, and 162:
where,
B![]() 1,B
1,B![]() 2,B
2,B![]() 9= Westergaard coefficients for unloaded edge stress (unitless), and
9= Westergaard coefficients for unloaded edge stress (unitless), and
J = overall dimensionless joint stiffness (unitless), defined in equation 145.
Based on the dimensionless unloaded edge stress, the actual unloaded edge stress can be calculated as shown in equation 163:
where,
![]() u = unloaded edge stress (MPa),
u = unloaded edge stress (MPa),
![]() u = dimensionless unloaded edge stress (unitless), from equation 159,
u = dimensionless unloaded edge stress (unitless), from equation 159,
P = wheel load (N), and
h = PCC slab thickness (m).
The loaded edge deflection and stress can easily be derived based on the corresponding free and unloaded edge responses. The loaded edge deflection can be calculated as shown in equation 164:
dl = loaded edge deflection (m),
df = free edge deflection (m), from equation 150, and
du = unloaded edge deflection (m), from equation 158.
The loaded edge stress can similarly be calculated as shown in equation 165:
where,
sl = loaded edge stress (MPa),
sf = free edge stress (MPa), from equation 154, and
su = unloaded edge stress (MPa), from equation 163.
Three LTE responses can be derived from the above referenced formulation: JTE, deflection LTE, and stress LTE.
JTE is defined as the percent of a load that is transmitted across a discontinuity (joint) due to the load transfer mechanisms present. Using the derived parameters, this can be calculated in equation 166:
where,
JTE = joint transfer efficiency (often reported as a percent),
![]() u = unloaded edge deflection (m), from equation 158, and
u = unloaded edge deflection (m), from equation 158, and
![]() l = loaded edge deflection (m), from equation 164.
l = loaded edge deflection (m), from equation 164.
The JTE is the value that was reported by the PCA in the aggregate interlock experiment for which the new aggregate interlock model is presented.(70)
Deflection LTE (LTE![]() ) is the ratio of the deflections of the unloaded to the loaded slabs. It is defined mathematically in equation 167:
) is the ratio of the deflections of the unloaded to the loaded slabs. It is defined mathematically in equation 167:
where,
LTE![]() = deflection LTE (often reported as a percent).
= deflection LTE (often reported as a percent).
Finally, the stress LTE is similarly calculated and is defined as the ratio of the stress induced in the unloaded slab to the stress in the loaded slab (equation 168):
where,
LTEs = stress LTE (often reported as a percent),
![]() u = unloaded edge stress (MPa), from equation 163, and
u = unloaded edge stress (MPa), from equation 163, and
![]() l = loaded edge stress (MPa), from equation 165.
l = loaded edge stress (MPa), from equation 165.
The relationship between the various LTE indicators is of interest. For example, it can be demonstrated in equation 169 that the relationship between JTE and LTE![]() is:
is:
where,
LTEd = deflection LTE (often reported as a percent), from equation 167, and
JTE = joint transfer efficiency (often reported as a percent), from equation 166.
where
Figure 39 illustrates this relationship. It can be seen, that the relationship does falls below the line of equity, demonstrating the nonlinear relationship in equation 169.
Figure 39. Relationship between JTE and LTEd.
As expected, the relationship between LTEd and LTEs is more complex. This is due to the complex nature of the formulation previously described. However, figure 40 illustrates that the relationship between these two parameters is a function of the a/l ratio, defined previously in equation 159.
Figure 40. Relationship between LTEs and LTEd.
The wearout model takes into account the effect of traffic loading on LTE. The wearout model is based on experimental deflection testing evaluation of laboratory controlled slabs subjected to loading at a joint capable of transferring load through aggregate interlock only.(70)
Equation 139 models aggregate interlock at the beginning of the loading period. The LTE model depends on du and dl that, in turn, depend on the joint stiffness for aggregate interlock.(73)
Figure 41 shows the JTE results obtained from the experimental work performed by Colley and Humphrey as a function of loading cycles of a 4086-kg load.(70)
Figure 41. JTE results obtained from the experimental work performed by Colley and Humphrey as a function of loading cycles of a 4086-kg load.(70)
The initial JTE at the beginning of the loading period is modeled with the initial aggregate interlock previously developed. To model JTE as a function of loading cycles, an exponential function was fitted to the backcalculated agg/kl obtained for each one of the curves shown in figures 42 and 43. The resulting model for wearout is of the form shown in equation 170:
where,
agg/klwear = Dimensionless aggregate interlock parameter at N loadings,
agg/klasymptote = Dimensionless aggregate interlock parameter at an infinite number of loading cycles,
agg/klinit = Dimensionless aggregate interlock parameter at the beginning of the loading period,
N = Noncalibrated cumulative traffic loading, and
s = Shape parameter, approximately 44,000 for the 229-mm slab and 91,000 for the 178-mm slab, on average.
To use the above model practically, the agg/klasymptote parameter was estimated based on the backcalculated agg/kl values at the end of the experimental loading period from reference 70 . Figure 44 shows the resulting agg/ klasymptote as a function of joint opening for the two slab thicknesses evaluated.
Figure 42. Influence of joint opening on JTE, 229-mm concrete slab, 152-mm gravel subbase.(70)
Figure 43. Influence of joint opening on JTE, 178-mm concrete slab, 152-mm gravel subbase.(70)
Figure 44. Asymptote dimensionless joint stiffness as a function of joint opening.
From the above data, a simple model was developed to predict the agg/klasymptote parameter as a function of joint opening as shown in figure 171:
where,
![]() = aggregate interlock asymptote model intercept (unitless), and
= aggregate interlock asymptote model intercept (unitless), and
w = joint opening (mm).
The ![]() intercept was found to depend on the slab effective thickness. The model was calibrated to have the same slope for both known thicknesses. This slope was assumed to have an exponential trend for h – tsaw
intercept was found to depend on the slab effective thickness. The model was calibrated to have the same slope for both known thicknesses. This slope was assumed to have an exponential trend for h – tsaw ![]() 178 mm and increase linearly thereafter. The resulting model for the
178 mm and increase linearly thereafter. The resulting model for the ![]() intercept is shown in equations 172 and 173:
intercept is shown in equations 172 and 173:
For h – tsaw ![]() 178 mm:
178 mm:
For h – tsaw > 178 mm:
The data used to develop the above wearout model are based on laboratory controlled testing of experimental slabs. The following limitations are encountered in the application of the above model:
It is therefore recognized that, although the above model provides a reasonable approach to characterizing LTE as a function of traffic loading and joint opening, investigation of a larger factorial of thicknesses, materials, and environmental conditions is required.
Several selection criteria were considered in selecting each individual JPCP distress model. One criterion included the preference for mechanistic models. Another selection criterion was that the model had been previously validated. Finally, the most important criterion (with respect to the HIPERPAV II effort), was that the model take into account early-age indicators for distress prediction such as joint opening, built-in curling, and/or delamination.
The faulting model for JCPs without dowels at the joints incorporated into HIPERPAV II, was developed using the combined Concrete Pavement Evaluation System (COPES) and Performance/Rehabilitation of Rigid Pavements (RIPPER) databases.(75) The pavements are subdivided by their environmental regions of origin in the United States (wet-freeze, wet-no freeze, dry-freeze, and dry-no freeze) and by their design features in table 32.
| Climatic Region | None/AGG | CTB/ATB | LCB | PERM |
|---|---|---|---|---|
| Wet-freeze | 5 | 5 | 2 | 2 |
| Wet-no freeze | 14 | 82 | – | – |
| Dry-freeze | 2 | 86 | – | – |
| Dry-no freeze | 3 | 127 | 14 | – |
NOTE: None: no base, AGG: aggregate, ATB: asphalt-treated base, CTB: cement-treated base,
LCB: lean concrete base and PERM : permeable stabilized or permeable nonstabilized base.
A mechanistic-empirical faulting model has been developed for nondoweled JCPs. The faulting equation is provided in equation 174:
where,
FAULT = mean faulting across the transverse joint (inches), The primary reference is not clear in defining mean faulting across the transverse joint. However, because the Distress Identification Manual for the Long-Term Pavement Performance Project was used for performing the condition surveys in that study, mean faulting is understood as the average faulting for a pavement section at the transverse joints after a given number of ESALs,(15,72)
ESAL = cumulative 18,000-lb equivalent single-axle loads in traffic lane (millions),
OPENING = average transverse joint opening of the analysis pavement section, computed for the maximum climatic temperature drop throughout the year (inches), and
DEFLAMI = Ioannides' pavement corner deflection (inches) = equation 175:
where,
![]() = radius of relative stiffness (inches),
= radius of relative stiffness (inches),
P = applied wheel load (~9000 lb),
a = radius of applied load (~5.64 inches, assuming a tire pressure of 90 psi),
KSTAT = modulus of subgrade reaction on top of base (psi/inch),
FI = freezing index (degree-days), and
BTERM = base type factor, which equals equation 176:
where,
GB = variable for dense-graded aggregate base (1 if aggregate base, else 0),
CTB = variable for dense-graded cement-treated base (1 if cement-treated base, else 0),
ATB = variable for dense-graded asphalt-treated base (1 if asphalt-treated base, else 0),
OGB = variable for open-graded aggregate or asphalt-treated base (1 if open-graded base, else 0),
LCB = variable for lean concrete base (1 if lean concrete base, else 0),
EDGESUP = index for edge support (0 if no edge support exists, else 1),
STYPE = index for AASHTO subgrade soil classification (0 if A–4 to A–7 or 1 if A–1 to A–3), and
DRAIN = index for drainage condition (0 if no edge subdrain exists, else 1).
(1 inch = 25.4 mm, 1 lb = 0.454 kg, 1 psi = 6.894 KPa)
The r2 statistic for this model is 0.81, and 398 slabs were used in its development.
Although this model is not truly mechanistic, it does contain a number of fundamental input parameters. In addition, the selected model has been validated using an extensive data set. Finally, the use of joint opening in this model, which is considered to be an important early-age indicator for distress prediction, was one of the primary factors for its selection.
The faulting model for JCPs with dowels incorporated in HIPERPAV II was also developed using the combined COPES and RIPPER databases.(75) The distribution of these pavement sections throughout the United States by climatic region and by subbase type is shown in table 33.
| Climatic Region | None/AGG | CTB/ATB | LCB | PERM |
|---|---|---|---|---|
| Wet-freeze | 257 | 44 | – | 5 |
| Wet-no freeze | 11 | 35 | 4 | – |
| Dry-freeze | 141 | 10 | – | 1 |
| Dry-no freeze | – | – | 1 | 1 |
NOTE: None: no base course, AGG: aggregate, ATB: asphalt-treated base, CTB: cement-treated base,
LCB: lean concrete base and PERM : permeable stabilized or permeable nonstabilized base.
The erosion of concrete from around dowels through repeated loading contributes to faulting in doweled pavements. In addition, pavement curling and warping increases deflection at the joint, further stressing the dowels. It has been recommended that the bearing stresses at the joint be less than 10.4 MPa to limit faulting.(64) The mechanistic-empirical faulting equation (equation 177) is given as:
where,
FAULT = mean transverse joint faulting (inches),
ESAL = cumulative equivalent 18,000-lb single axle loads in lane (millions), and
BSTRESS = maximum dowel-bearing stress on concrete using closed form solution (psi), shown in equation 178:
where,
BETA = relative stiffness of the dowel-concrete system,
![]() = a distribution factor (included in reference 75),
= a distribution factor (included in reference 75),
P = applied wheel load (~9000 lb),
T = percent transferred load (set to 0.45),
I = moment of inertia of dowel bar cross section (inches4),
Kd = modulus of dowel support (~1,500,000 psi/inch),
OPENING = average transverse joint opening (inches),
ES= modulus of elasticity of the dowel bar (set to 29,000,000 psi),
AVJSPACE = average pavement joint spacing,
KSTAT = effective modulus of subgrade reaction on top of the base (psi/inch),
DRAIN = index for drainage condition (0 if no edge subdrain exists, else 1),
EDGESUP = index for edge support (0 if no edge support exists, else 1), and
STYPE = index for AASHTO subgrade soil classification (0 if A–4 to A–7, else 1 if A–1 to A–3).
(1 in = 25.4 mm, 1 lb = 0.454 kg, 1 psi = 6.894 KPa)
The r2 statistic for this model is 0.67, and 559 slabs were used in its development.
For the case of faulting with dowels, the use of bearing stress (related to joint opening) in the above model was one of the primary factors for its selection. In addition, although this model is not truly mechanistic, it contains a number of fundamental input parameters. Another factor influencing the selection of this model is that it has been validated using an extensive data set.
The faulting models incorporated in HIPERPAV II (for both doweled and nondoweled JPCP) include inputs for joint opening. However, these faulting models were originally developed and calibrated based on a unique definition of joint opening.
The joint opening prediction made by HIPERPAV II is based on a different approach than the FHWA model. The FHWA model is closed form and rather simple prediction, while the HIPERPAV II model is based on a more sophisticated finite-difference-based analysis. Therefore, to use the joint prediction made by HIPERPAV II in predicting long-term faulting, a submodel was developed to convert from the HIPERPAV II-predicted joint opening to the joint opening parameter used in the FHWA faulting model.(75)
A parametric sensitivity analysis was performed on both the doweled and nondoweled faulting models. For the sensitivity analysis, joint opening was varied from 0.1 mm to 12.7 mm, and traffic loading from 0 to 50 million 80 KN ESALs. Plots of the results are in figures 45 and 46. As expected, these figures show that sensitivity to the faulting prediction exists as a function of both joint opening and traffic loading.
Figure 45. Sensitivity of faulting to joint opening and cumulative traffic loading for nondoweled JPCP (MESAL = 1,000,000 ESAL).
Figure 46. Sensitivity of faulting to joint opening and cumulative traffic loading for doweled JPCP (MESAL = 1,000,000 ESAL).
In the original FHWA report, joint opening is defined as in equation 179:(75)
where,
OPENING = joint opening, in inches (1 inch = 25.4 mm),
CON = frictional restraint adjustment factor (unitless) (0.65 for stabilized subbases, 0.80 for aggregate subbases),
AVJSPACE = average joint spacing in feet, (1 ft = 0.3048 m),
ALPHA = PCC CTE in inch/inch/°F, (1 inch/inch/degree Fahrenheit (°F) = 0.56 m/m/°C ),
TRANGE = annual temperature range in °F, (1 °F = 0.56 °C ), and
![]() = PCC drying shrinkage coefficient (in microstrains).
= PCC drying shrinkage coefficient (in microstrains).
Since the free strain of the PCC is defined in the last term, equation 179 can be simplified into equation 180:
The slab-base restraint model in HIPERPAV II is based on a finite-difference solution of the axial movement-restraint phenomenon.(1) It is currently one of the key models in predicting the critical stress in the concrete during the early-age period. However, this same model also can be used to predict the joint opening as a function of a number of variables, including those listed in table 34.
| Variable | Definition | Typical Value |
|---|---|---|
| h | PCC slab thickness | 305 mm |
| L | Average joint spacing | 4.6 m |
| Ec | PCC elastic modulus | 27,579 MPa |
| Free strain | 300 ´ 10-6 m/m | |
| Movement at maximum friction | 0.5 mm | |
| Fmax | Maximum friction force | 27.6 KPa |
The calculation of the joint opening in HIPERPAV II is not a closed form, as is that in the FHWA model (shown in equations 179 and 180), therefore the formulae for its calculation are not given here for brevity.(1)
Before even a cursory comparison of these two models for the prediction of joint opening, selecting “equivalent” inputs for the degree of slab-base restraint is required. The FHWA model includes a CON variable that is assigned a value of either 0.65 or 0.8, depending on the subbase type. The HIPERPAV II model is more sophisticated; it requires two parameters that define a bilinear relationship between the slab movement and corresponding force required for the movement. The intersection of the bilinear relationship is how the two parameters are defined. Extensive documentation on various subbase types was drawn upon to define equivalent values of subbase restraint that correspond to the two CON values given in the FHWA report. The final selection of these values, used in this analysis, is given in table 35.
| Subbase Type | CON Value for FHWA Model | δcrit Value for HIPERPAV Model | Fmax Value for HIPERPAV Model |
|---|---|---|---|
| Stabilized base | 0.65 | 0.254 mm | 55.2 KPa |
| Aggregate base or LCB with bond breaker | 0.80 | 0.508 mm | 27.6 KPa |
To compare the predictive ability of the joint opening models, a factorial was established that consisted of 1920 combinations of the various model inputs. The variables and the ranges selected for this factorial are included in table 36.
| Variable | Minimum Value | Maximum Value |
|---|---|---|
| Slab thickness | 50.8 mm | 406 mm |
| Average joint spacing | 0.9 m | 12.2 m |
| PCC elastic modulus | 20,700 MPa | 41,400 MPa |
| Free strain | 50 |
2000 |
| Slab-subbase restraint | CON = 0.65 Fmax = 55.2 KPa |
CON = 0.80 Fmax = 27.6 KPa |
The joint openings, using both the FHWA and the HIPERPAV II models, then were calculated for each of the factorial combinations. The results are given in figure 47. As can be seen in the figure, the predictions using the two models do not coincide. In all cases, the HIPERPAV II model predicts a greater joint opening than does the FHWA model. However, this is not surprising, due to the fundamental differences in the predictive methodology.
Figure 47. Relationship between joint opening model predictions.
Because the FHWA faulting model has been developed and calibrated based on a unique definition of joint opening, it is critical to the proper use of the model to find a relationship that can convert the HIPERPAV II prediction to the FHWA prediction.
It was decided that the most practical means of implementing a submodel to convert the HIPERPAV II joint opening to the FHWA joint opening is by calculating a ratio between the two. A nonlinear regression analysis was performed on the 1920 combinations given in the last section to predict the ratio of the FHWA to the HIPERPAV II joint opening. The result of this regression analysis is as shown in equation 181:
Equation 181 has an r2 of 0.926 and a Standard Error of the Estimate (SEE) of 0.020. Using this equation, the HIPERPAV II joint openings in figure 47 were converted to their equivalent HIPERPAV II joint opening predictions. The results are illustrated in figure 48.
Figure 48. Relationship between revised joint opening model predictions.
This section describes models for accumulating damage and models for predicting cracking in PCCP slabs. A short description also is given of three other models considered by the research team responsible for reference 76 in choosing appropriate fatigue damage and slab cracking models.
The first type of model is concrete fatigue damage resulting from load applications that induce stresses in the pavement slab. The four proposed models in reference 76 regarding concrete fatigue damage are (references 77, 78, 79, and 80 are the original sources for each of these models):
Corps of Engineers and ERES Consultants, Inc. (ERES/COE) Model (equation 182):(77)
NCHRP 1–26 Model (equation 183):(78)
Zero-Maintenance Model (equation 184):(79)
Austin Research Engineers, Inc. (ARE) Model (equation 185):(80)
where,
N = number of allowable load applications,
SR = stress-to-strength ratio (![]() /MR),
/MR),
![]() = adjusted Westergaard critical stress in psi (1 psi = 6.89 KPa),
= adjusted Westergaard critical stress in psi (1 psi = 6.89 KPa),
MR = PCC modulus of rupture in psi (1 psi = 6.89 KPa), and
P = probability of failure.
Figure 49 shows the four models' prediction of allowable loads as a function of stress-to-strength ratio. The figure shows the four models above, and includes the NCHRP 1–26 model based on both 50 percent and 5 percent probability of failure. The comparison in reference 76 fixed the probability term in the NCHRP 1–26 model at 50 percent.
The evaluation of the four models in reference 76 determined that the ERES/COE model was the best candidate, so it was chosen for use in the HIPERPAV II damage and cracking model. It should be noted, however, that the NCHRP 1–26 model is virtually identical to the chosen model when the probability term is set at 15 percent chance of failure, or an 85 percent reliability level.
Figure 49. Allowable loads versus stress-to-strength ratio.
The following paragraphs are taken from the discussion and critique of models in reference 76.
ERES/COE model—this model was developed from U.S. Army Corps of Engineers data from 51 full-scale field sections. The edge load stress was calculated using H–51 program (computerized Pickett and Ray charts) and multiplied by 0.75 to account for the edge support in the sections.
NCHRP 1–26 model—this model was developed using the COE and AASHO road test data. This model is also based on edge load stress.
Zero-Maintenance model—this model is based on laboratory testing results of 140 beams.
ARE model—this model was developed based on the AASHO road test data. The actual loads were converted to 18-kip ESALs, and the maximum midslab stresses were calculated using elastic layer theory.
Yu et al. recognize that the first two models (ERES/COE and NCHRP 1–26) are very similar in form and that they give similar results at specific values of the probability term.(76) The report stated that the Zero-Maintenance model gave the most scatter, and that the ARE model gave the narrowest range of damage values but does not show a logical trend. Later, the report selects the ERES/COE model, stating that the damage results of the NCHRP 1–26 model were shifted to the left of the ERES/COE model by one magnitude. Results from the ERES/COE model are in a more conventional range (about 50 percent cracking at fatigue damage of 1.0).
The ERES/COE model was incorporated in HIPERPAV II. This model could be changed in the future as new developments (such as those under the NCHRP 1–37a study) become available.
The second model discussed in this section is the slab cracking model. Yu et al. developed a percent cracking model based on the accumulated damage.(76) This model was incorporated in HIPERPAV II and is given as equation 186:
where,
FD = accumulated fatigue damage. As shown in equation 187,
where,
n = actual number of loads for load group i, and
N = allowable number of loads for load group i.
In the classic damage model form, using Miner's law, damage from individual loads is accumulated to produce an aggregate damage value with which the level of cracking is predicted.
Figure 50 shows the fit of the data to the model in equation 186. As can be seen in the figure, when accumulated damage equals 1, the slab cracking approaches 40 percent. This is one of the reasons Yu et al. selected the model.(76)
Figure 50. Fatigue cracking model with associated data.(76)
B.2.4.4.2.1 Assumptions
The form of the model was selected because it represents the theoretical characteristics of cracking progression in a PCC pavement section. Two theoretical boundary conditions are: 1) there will be 0 percent cracking when fatigue damage = 0, and 2) 100 percent of the slabs will be cracked as fatigue damage approaches infinity. This form of the model and the given boundary conditions ignore the possibility of environment-related cracking before any traffic-related fatigue damage, and the fact that 100 percent of the slabs may crack at a finite level of damage.
A good aspect of the model is that it seems to have been developed using sections both with and without cracked slabs. Some models can only consider sections with at least some cracking, and thus do not properly represent all possible data points in a set of data.
Other assumptions include the aggregate effects of curling and loading stresses and ability of the researchers to calculate stresses and fatigue damage accurately. The latter will be discussed in greater detail in the “Limitations” section below. The stress induced by traffic loads is adjusted for thermal curling, but other conditions such as drying shrinkage and other sources of curling and warping are not considered. Yu et al. state that climate can have a significant effect on cracking prediction due to the thermal and moisture gradients to which the slab is subjected.(76) The report references these effects, but other than the difference between temperature in the slab top and bottom, there is no way to account for these conditions.
B.2.4.4.2.2 Limitations
There are several limitations on this model, including the use of reliability, the necessity of calculating of fatigue damage rather than directly measuring it, the use of regression models rather than mechanistic-empirical models, and the use of the model without the curling component.
The first limitation mentioned above, the fact that reliability is not considered directly, is a drawback that the NCHRP 1–26 model does not have. In that model, as mentioned previously, the probability of failure is specifically included. This probability of failure can be considered analogous to the inverse of the probability of success. Given a 50 percent probability of failure, as the one considered in reference 76, the model also predicts a 50 percent probability of success. Given a 15 percent probability of failure, an 85 percent probability of success is implied (which is more reasonable for pavements on less important facilities). For this reason, the NCHRP 1–26 model was seriously considered for this project.
The need to calculate rather than measure fatigue damage directly is a limitation of this and any model. To validate a model, predictions of stress and accumulated damage must be made by other means. Perhaps a more reliable method of validating a combination of damage and cracking models could be made by comparing the inputs to the stress model described in the following section to the level of cracking predicted and observed. In that way, the entire stress-damage-cracking model system can be evaluated and validated.
A third limitation is the use of regression models. Although it is recognized that mechanistic models are much more difficult to develop, validate, and calibrate, new research should advance the state of the art so that such models are more reliable and accurate. As new models become available, the project team will evaluated them, and those that improve the predictive capability of the computer guidelines will be adopted.
The fourth limitation listed at the beginning of this section is the statement in reference 76 that “(w)hen this model is used without considering the built-in upward curling of slabs, the model is likely to predict an excessively high amount of cracking.” (p. 78) Although it is not expected that this will be the case, it is a limitation of the model that should be considered.
This section describes the model incorporated for midslab cracking prediction in HIPERPAV II. The model's background, characteristics, assumptions, and limitations, and a description of the validation efforts are included here.
B.2.4.4.3.1 Model Identification
The edge stress adjustment model is taken from a combination of papers submitted to TRB, ASCE, and the 6th International Conference of Concrete Pavements. (See references 81, 82, 83, and 84.) Each of the papers discussed in this section are based on the same principles, but contain different aspects of stress adjustment that the overall model addresses. This section combines the concepts and components of the various papers and demonstrates how they are all used together to modify the Westergaard free edge stress.
B.2.4.4.3.2 Model Characteristics
The model was derived from multiple runs of the ILLISLAB FEA program. The basis for this approach is that FEA can consider the effects of finite slab size and the possible loss of support due to linear temperature differentials. Theoretical (Westergaard) solutions that are based on infinite slab and full contact assumptions cannot consider the reality of slab size and temperature and moisture differentials.
The models presented in these papers were developed using multiple FEA runs with varying pavement designs and conditions. The resulting stresses predicted by the FEA were compared to the theoretical Westergaard solutions using the same conditions. Adjustment factors were developed to account for the differences in the two sets of solutions. In this way, a closed form solution was developed to represent the results of the FEA.
The papers claim that the models developed have been carefully validated and are readily implementable in spreadsheets or computer programs. They claim that the models are properly formulated to satisfy applicable engineering boundary conditions and that they are simple, easy to comprehend, and dimensionally correct. They further claim that the models can be extrapolated to wider ranges of input parameters.
One of the papers is an attempt to revise the PCA thickness design methodology and maintains adjustment factors for the placement of truck loads relative to the slab edge, and for the concrete's increased strength beyond 28 days.(82) Since HIPERPAV II includes strength gain prediction models beyond 28 days, this factor was omitted from this model. HIPERPAV II predicts this strength, eliminating the need to adjust the stress to account for increased strength.
The model developers reduced the Westergaard edge loading and deflection solutions to three dimensionless terms given by equations 188, 189, and 190:(81)
where,
![]() = Westergaard's edge stress, FL-2,
= Westergaard's edge stress, FL-2,
![]() = Westergaard's edge deflection, L,
= Westergaard's edge deflection, L,
q = subgrade vertical stress, FL-2,
h = slab thickness, L,
P = single wheel load, F,
k = modulus of subgrade reaction, FL-3, and
l = radius of relative stiffness of the slab-subgrade system, L.
The three dimensionless terms all depend on the normalized load radius a/l, assuming a constant Poisson's ratio of 0.15. Indeed, virtually all the models developed for these papers include an a/l term and other terms normalizing length dimensions to the radius of relative stiffness, such as W/l (slab width), L/l (slab length), and Do/l (distance of wheel load to slab edge).
B.2.4.4.3.3 Logic
The term ![]() eq, or equivalent stress, means the Westergaard edge stress adjusted for the specific design and conditions relating to the pavement in question. This stress is determined by equation 191:
eq, or equivalent stress, means the Westergaard edge stress adjusted for the specific design and conditions relating to the pavement in question. This stress is determined by equation 191:
where,
![]() e= equivalent edge stress prediction, FL-2,
e= equivalent edge stress prediction, FL-2,
![]() we = Westergaard edge stress, FL-2,
we = Westergaard edge stress, FL-2,
![]() ce = Westergaard/Bradbury edge curling stress, FL-2,
ce = Westergaard/Bradbury edge curling stress, FL-2,
R1 = wheel configuration factor (single or dual tire and single, tandem, or tridem axle),
R2 = finite slab length and width factor,
R3 = tied concrete shoulder factor,
R4 = widened outer lane factor,
R5 = bonded or unbonded second layer factor,
RT = adjustment factor for the combined effect of loading and thermal curling, and
f1 = PCA adjustment factors for the effect of truck placement on the edge (see table 37).
| Percent Trucks at Edge | Adjustment Factor f1 |
|---|---|
| 1 | 0.825 |
| 2 | 0.855 |
| 3 | 0.870 |
| 4 | 0.880 |
| 5 | 0.890 |
| 6 | 0.894 |
| 7 | 0.901 |
The Westergaard closed form edge stress equation is given as equation 192, and the Westergaard/Bradbury curling stress equation is given in equation 193.
where,
![]() = concrete Poisson's ratio,
= concrete Poisson's ratio,
E = concrete elastic modulus, FL-2, and
a = radius of the applied load, L.
where,
![]() = concrete CTE, T-1,
= concrete CTE, T-1,
![]() T = temperature differential through slab thickness, T,
T = temperature differential through slab thickness, T,
C = curling stress coefficient, which equals the formula shown in equation 194:
![]() = the formula shown in equation 195:
= the formula shown in equation 195:
W = slab width, L.
These equations are used to determine a free edge stress, which is later modified by factors developed through the FEA performed by the authors of the referenced papers. (See references 81, 82, 83, and 84).
The researchers identified several dimensionless mechanistic variables with which they performed regression analysis on the ILLISLAB FEA results. The sets of variables are different under the loading-only condition and the loading-plus-thermal-curling analysis. The following variables (shown in equations 196 and 197) were identified:
Loading-only condition:
Loading-plus-thermal-curling analysis:
where,
s = transverse wheel spacing, L,
t = longitudinal axle spacing, L,
Do = offset distance between the outer face of the wheel and the slab edge, L,
AGG = aggregate interlock factor, FL-2,
heff = effective thickness of two unbonded layers, L, which equals the formula shown in equation 198:
h1 = thickness of top slab, m, (also signified as h),
h2 = thickness of second concrete slab, m,
E1 = concrete elastic modulus of top slab, MPa, (also signified as E), and
E2 = concrete modulus of second slab, MPa.
For the midslab (edge) stress, the daytime curling condition is critical. An early version of the model was developed to account for the edge stress under nighttime curling conditions, where the curling counteracts the effect of traffic loading.(81) However, the most recent version of the model omits the nighttime condition. Models for adjustment factors considering both conditions are included in reference 84. The model also includes equations for curling-only conditions. These components are not for use in a fatigue cracking model, but were developed for validation purposes. They are included in this section to maintain the integrity of the model as it appeared in the references.
B.2.4.4.3.4 Assumptions
The papers and models presented in this section take the original Westergaard stress equations, along with their assumptions of infinite slab size and medium slab thickness, and compare their results to stresses predicted by ILLISLAB, an FEA computer program. The FEAs were performed under various load configurations, slab sizes, and other conditions that alter the configurations assumed by Westergaard in his original work. The resulting stresses predicted by ILLISLAB were then compared to the Westergaard stresses, and appropriate adjustment factors were developed by the authors. A basic assumption the authors made is that of a constant concrete Poisson's ratio of ![]() = 0.15, which greatly simplified the model development.
= 0.15, which greatly simplified the model development.
By using the FEA, the authors were able to eliminate the Westergaard assumption of full contact between the pavement slab and the subgrade. An important assumption in doing this, however, and one that is not mentioned by the authors of references 81 through 84 is that the nature of the stress model may change when a slab lifts off the subgrade, or when a void is otherwise present under the slab. The authors simply predict the adjustment factor for those conditions. This may be appropriate, but an addition to the model may be necessary to predict slab liftoff and then calculate the stresses in a different way, possibly using beam theory or further FEA.
B.2.4.4.3.5 Limitations
These models have several limitations that are not discussed by the authors, but these may impact the models' validity. The first and easiest to correct is that many typographical errors were found in the presentation of these models in the various publications. In fact, each publication in which the models were presented has at least some errors that were identified, but it is not known if other errors exist in the presentation of the models and their coefficients. Another limitation is that some of the models in the different publications have entirely different coefficients or have differences in their construction. This means, for example, that the model for adjusting Westergaard edge stresses affected by the presence of a tandem axle (single wheel) configuration was changed after it was originally published in Transportation Research Record No. 1568 to when it was published in the 6th International Conference of Concrete Pavement proceedings.(82, 84) No explanation was given for this and other change, while other models in the same group were not changed.
Another limitation of these models is that each one has limits on the dimensions or configuration that can be analyzed with them. For example, the ratio of dual wheel spacing to radius of relative stiffness (l) cannot be less than 0.2 nor greater than 4.0. Similar restrictions are placed on slab length to l, axle spacing to l, etc. The restrictions arise from the limitations on the model development, but the authors seem to indicate that the models can be extrapolated beyond these limits.(81) It is not difficult to construct a set of conditions that violate the restrictions placed on the individual models, increasing the probability that the user of a design procedure may violate those same restrictions with a normal design problem. Further investigation should be made to determine the extent to which the restrictions may be violated safely.
A limitation on the validity of the entire set of models is maintained by the fact that the models were developed using ILLISLAB and that the same finite-element program was used to validate the models. The paper in reference 81 indicates that a series of ILLISLAB runs was performed to validate the models. It states that factorial runs were totally independent of previous modeling processes. It seems, however, that to use the same methods for model development and validation necessarily introduces bias in the results of the validation. To verify and validate these models further, the project team has performed FEAs by using LS-DYNA. The models have been compared to the results from LS-DYNA which, together with the ILLISLAB validation, have provided some confidence in the validation claims of the authors.
B.2.4.4.3.6 Slab Stress, Damage, and Cracking Model Integration
This section describes the integration of the midslab and corner stress adjustment models (section B.2.4.4.3) with the PCC fatigue damage and cracking model (sections B.2.4.4.1 and B.2.4.4.2) and with the overall long-term performance analysis module in HIPERPAV II. In general, the cracking module contains four embedded loops. The first two loops are for the time of day and the season of the year. Within these two loops a third loop over each axle configuration, from which the Westergaard free edge and free corner stresses are computed. The fourth loop adjusts the load group. For each combination, the edge and corner stresses are adjusted, midslab and corner fatigue damage is accumulated, and then cracking for each case is determined.
The stress and damage integration module is essentially a damage accumulation model. The appropriate damage for individual load groups, axle configurations, seasons, and times of day are accumulated, and at the end of each season, the total damage is used to calculate the level of cracking from the date of construction to the current time.
For midslab cracking, the stress adjustments are determined, as described in section B.2.4.4.3. The Westergaard stresses are determined for both the longitudinal and transverse free edge, given other conditions such as load, slab thickness, concrete elastic modulus, and the modulus of subgrade support. The stresses are then modified to account for load transfer to adjacent slabs (section B.2.3.1) and by applying the adjustment factors. Then, for each combination of season, time of day, axle, and load, the fatigue damage for both longitudinal and transverse cracking is accumulated. At the end of each season, the accumulated fatigue damage is used in the cracking model described above to predict the accumulated level of cracking, both in the transverse and longitudinal directions.
Figure 51 shows a flowchart describing the stress-fatigue-cracking integration module. The flowchart applies to each season for which the analysis is performed. For each season, the analysis is performed two times a day to capture the effects of upward and downward curling. Within each of the two times, the analysis loops over the axle and load groups, as described above. The total accumulated fatigue damage and percent slab cracking values are then returned to the main analysis routine.
For Each of Four Seasons Per Year
Figure 51. Flowchart of stress, damage, and cracking module.
The values that will be calculated and returned by this routine include the accumulated and incremental damage as well as the total cracking for the current season.
Measuring the roughness of pavements is one of the most economical methods used to predict pavement serviceability. Two common roughness indicators are the present serviceability index (PSI) and the IRI. An evaluation of PSI and IRI models available in the literature and the models incorporated in HIPERPAV are presented in the following sections.
Present serviceability is defined as the ability of a specific section of pavement to serve high-speed, high-volume, mixed traffic in its existing condition.(64) The PSI originally was developed at the AASHO road test in 1960. PSI is a rating scale from 0 to 5, where 4 to 5 represent very good pavement, 3 to 4 is good, 2 to 3 is fair, 1 to 2 poor, and 0 to 1 is very poor. This rating is a function of the pavement's physical measurements of roughness and distress (e.g., cracking, faulting, patching). It depends on the pavement's longitudinal profile, where cracking, patching, and faulting are likely to contribute. The longitudinal profile can be expressed as the mean slope variance (deviation of the record from a baseline). These measurements are combined to formulate PSI.
The original equation (equation 199) for the PSI of rigid pavements is based on 49 rigid sections:(64)
where,
PSI = present serviceability index,
SV = slope variance measured using a profiler (10-6 rad),
C = cracking in ft/1,000 ft2 (1 ft = 0.3048 m), and
P = patching (ft2/1,000 ft2).
The influence of faulting and spalling were also measured, but these did not have a statistically significant influence on the pavement serviceability. The r2 for this model is 0.92.
This equation contains several limitations:
A 1990 study to predict PSI in JPCPs developed the following regression model, shown in equation 200:(85)
where,
TFAULT = cumulative transverse joint faulting in inches per mile (1 inch per mile (inch/mi) = 15.8 mm/km),
SPALL = number of deteriorated (medium and high severity) transverse joints per mile (1 mi = 1.609 km),
TCRKS = number of transverse cracks (all severities) per mile (1 mi = 1.609 km), and
FDR = number of full depth repairs per mile.
For this model, the r2 is 0.58 using 282 pavements. This model is a linear regression of multiple variables collected according to the Distress Identification Manual for the Long-Term Pavement Performance Project.(85) The intercept (4.536) is the maximum PSI allowed when all distresses equal zero. As the distresses accumulate, PSI decreases. Since the model sensitivity to FDR is relatively small and difficult to model, it can be omitted. The model incorporated in HIPERPAV II is shown in equation 201:
This model has some limitations, including:
Using the model presented in equation 201, the model's sensitivity to the faulting, spalling, and transverse cracking input parameters was assessed. An analysis was completed to calculate how each distress influences the PSI. To reduce PSI to 2.0 from the initial 4.536, each distress was increased while the other two distresses were kept at zero. As seen in figure 52, faulting has the greatest influence on PSI, spalling next, followed by transverse cracks. PSI depends on faulting 6 times more than spalling, and almost 12 times more than transverse cracking.
Figure 52. Amount of each individual distress required to reach a PSI of 2.0.
The IRI was developed at the International Road Roughness Experiment held in Brazil in 1982.(64) It is currently the standard for the FHWA Highway Performance Monitoring System database.(64) IRI describes the longitudinal surface profile in the wheel path, and it is defined as the average rectified slope (ratio of the accumulated suspension motion to the distance traveled) obtained from a mathematical model of a standard quarter car traversing a measured profile at a speed of 80 km/h. It is computed from surface elevation data collected by a topographical survey or mechanical profiler. The measurements should be calibrated to the measurement standard because roughness is sensitive to tire type, tire pressure, load, vehicle suspension system, and vehicle speed.
IRI can be estimated as a function of the PSI. Using linear regression, a contractor developed an IRI model using the LTPP GPS–3 sections. IRI is correlated to PSI as shown in equation 202.
The r2 is 0.76 for 3199 pavement sections. This equation only depends on PSI, so a sensitivity analysis is not needed. A plot of IRI versus PSI is shown in figure 53.
Figure 53. Shape of IRI versus PSI curve.
It may be necessary to develop a more sophisticated model that includes pavement design and location features in a later IRI calculation, as shown in equation 203.
The initial roughness (IRIo) also can be incorporated into the relationship as shown in equation 204:
where,
![]() IRI = the change in IRI due to traffic loading and weather conditions.
IRI = the change in IRI due to traffic loading and weather conditions.
Other relationships have been developed for IRI that use the JCP distress data as input. This section will compare these relationships, documented in FHWA–RD–97–147, FHWA–RD–00–130 and in the Guide for Mechanistic Design of Pavements developed under NCHRP study 1-37A to the one developed by the contractor, described above.(88, 89, 90)
B.2.4.5.3.1 FHWA–RD–97–147
For nondoweled JCP in the LTPP database, IRI is related to faulting as shown in equation 205.(88)
where,
TFAULT = total faulting (mm) per LTPP section.
This equation has an r2 of 0.48 for 51 sections and is plotted in figure 54.
Figure 54. Effect of faulting on IRI.
B.2.4.5.3.2 FHWA–RD–00–130
This IRI model was developed to improve the prediction models for PCC pavement performance-related specifications.(89) This IRI model is based on pavement distresses and also a site parameter that accounts for climate, age, and other factors that influence IRI, as shown in equation 206.
where,
IRI = smoothness (m/km),
IRI0 = initial smoothness measured as IRI (m/km),
%CRACKED = percent slabs with transverse cracking and corner cracks (all severities) (0–100 percent),
%SPALL = percent joints with spalling (medium and high severity) (0–100 percent),
TFAULT = total joint faulting cumulated per km (mm),
SITE = site factor, as shown in equation 207:
AGE = pavement age,
FI = freezing index (°C-days), and
P0.075 = percent subgrade material passing 0.075 mm (No. 200) sieve (0–100 percent).
The statistics for this model are N = 183, r2 = 0.70 and SEE = 0.35 m/km. This model is compared to the others in figures 55 to 57.
B.2.4.5.3.3 1-37A Guide for Mechanistic Design of Pavements—TRB 2000 Presentation
An IRI model was presented at the 2000 TRB session for the 1-37A Guide for Mechanistic Design of Pavements.(90) It is given in equation 208:
where,
IRI = smoothness (m/km),
IRI0 = initial IRI (m/km),
TransCk = transverse cracking (all severities) (assumed to be 0–100 percent),
JtSPALL = percent joints with spalling (all severities) (0–100 percent),
PATCH = percent of area with flexible or rigid patching (all severities) (assumed to be 0–100 percent),
CorBreak = percent joints with corner breaks (all severities),
AGE = pavement age (years), and
TFAULT = total joint faulting (mm/km).
No information on the modeling statistics (i.e., N and r2) was provided.
B.2.4.5.3.4 1–37A Guide for Mechanistic Pavement Design—TRB Presentation in 2001
In the 2001 TRB conference, the IRI (smoothness) model was modified from its past version presented at the 2000 TRB conference.(91) It more closely resembles the FHWA–RD–00–130 model, but it contains a term for patching. The general form of the equation is shown in equation in 209:
where,
S(t) = pavement smoothness,
S0 = initial IRI,
D(t) = distress,
SF = site factor to address site conditions,
M = maintenance activities, and
A, B, C = regression coefficients.
The model regression coefficients are as shown in equation 210:
where,
IRI = pavement smoothness (m/km),
IRIi = initial IRI (m/km),
CRK = percent slabs with cracking (all severities transverse and corner breaks),
SPALL = percent of joints with spalling (medium and high severities),
PATCH = area with flexible or rigid patching (all severities) (m2),
SF = site factor, as shown in equation 211:
AGE = pavement age (years),
FI = freezing index (°C-days),
P0.075 = percent subgrade material passing 0.075-mm sieve, and
TFAULT = total joint faulting (mm/km).
No information on the modeling statistics (i.e., N and r2) was provided.
The five models are summarized below in table 38. The units and dependent variables included in the models are listed. In the following parametric studies, only the distress variables for faulting, cracking, spalling, patching, and the initial IRI0 will be examined. The other variables will be held constant.
| IRI Models | FHWA–RD–97–147 | FHWA–RD–00–130 | 1–37A Guide (2000 TRB) | 1–37A Guide (2001 TRB) | Contractor |
|---|---|---|---|---|---|
| Units | inches/mi | m/km | m/km | m/km | m/km and inches/mi |
| Initial IRI: IRI0 | Constant | Variable | Variable | Variable | Constant |
| Distress Variables | TFAULT | TFAULT | TFAULT | TFAULT | TFAULT |
| – | Spalls | Spalls | Spalls | Spalls | |
| – | Cracks | Cracks | Cracks | Cracks | |
| – | – | Corner Breaks | – | – | |
| – | – | PATCH | PATCH | – | |
| Other Variables | – | AGE | AGE | AGE | – |
| – | FI | – | FI | – | |
| – | P0.075 | – | P0.075 | – |
To perform the comparison, control variables for the models have been chosen. Because model FHWA–RD–97–147 only has a faulting term, faulting will first be varied in all four models between 0 to 1200 mm. For both the FHWA–RD–00–130 and 1–37A models, IRI0 of 0.5 m/km is assumed, as is AGE of 10 years. Likewise, a freezing index of 300 °C-days and percent subgrade materials passing the No. 200 sieve of 40 percent are assumed. These are the control variables used in the model reference.(89) To convert the number of distresses per mile in the contractor's model to a percentage, an average joint spacing of 5.1 m is used. This is the average joint spacing for all the GPS–3 sections in the LTPP database. The comparison is shown graphically in figure 55.
As can be seen in figure 55, the slope of the IRI versus faulting models tend to be similar for all the prediction equations. One of the major distinctions is the high initial IRI0 of the FHWA–RD–97–147 model. The FHWA–RD–00–130 model and the contractor's model are very similar, as are the two 1–37A models.
Figure 55. Comparison of faulting influence between the various IRI models.
Now the influence of cracking and spalling will be assessed using the IRI models. The FHWA–RD–97–147 model will not be included because it is dependent only on faulting. By varying the percent cracking between 0 percent and 100 percent, the plots for IRI versus percent cracking can be produced (figure 56). Similarly, the influence of spalling will be assessed; this is shown in figure 57. For both of these plots, the level of faulting is assumed to be 600 mm.
Figure 56. Effect of percent cracked slabs on FHWA–RD–00–130, 1–37A Guide, and contractor IRI models.
Increasing percent cracked slabs in figure 56 causes a marked increase in IRI according to the 1–37A model presented in 2000 at TRB. Its effect on the other three models is not as severe.
Figure 57. Effect of percent spalling on FHWA–RD–00–130, 1–37A Guide, and contractor IRI models.
Increasing the percent spalling causes a slight increase in IRI for all four models. The slopes of the FHWA–RD–00–130 and 1–37A IRI models are approximately the same.
Patching is only a factor in the 1–37A models. The other models do not account for it. Its influence on IRI is shown below in figure 58 . The 1–37A model presented in 2000 is more sensitive to patching than is the one presented in 2001.
Figure 58. Effect of percent patching on IRI for the 1–37A models.
To assess the influence of initial roughness on the IRI models, IRI0 is varied in the FHWA–RD–00–130 and 1–37A models in figure 59. It is apparent that the slopes of all the models are the same. This is expected because IRI0 is an additive term. The contractor model cannot account for initial IRI, but it can be modified to do so in the future. In these modeling predictions, percent spalling and cracking are assumed to be 30 percent, and faulting is assumed to be 600 mm.
Figure 59. Effect of initial IRI0 on FHWA–RD–00–130, 1–37A, and contractor IRI models.
It appears, based on the parametric analysis, that the FHWA–RD–00–130 and the 1–37A models are the most versatile. They account for the pavement distresses and also allow for an initial roughness (IRI0). The simpler model by the contractor does not include an initial IRI0 term. The two models that are the most similar are the FHWA–RD–00–130 model and the 1–37A model presented in 2001. Because documentation on the development of the latter model was scarce when the HIPERPAV II was developed, the IRI model described in FHWA–RD–00–130 was incorporated into HIPERPAV II for its versatility and validation.
The long-term JPCP module of the HIPERPAV II system was developed to optimize early-age strategies based on how they perform in the long term. With this objective in mind, two early-age strategies can be analyzed in the long term under the same long-term environmental and traffic conditions.
Accurate predictions of long-term performance require accurate and detailed information on pavement structural factors, materials characterization, environmental conditions, and traffic data. Because the HIPERPAV II long-term module is intended to help the user optimize early-age strategies rather than serve as a tool for pavement design, a number of considerations were made to simplify the data entry.
No long-term input of seasonal adjustment factors for the k-value is required. The k-value used in the long-term module is the k-value input from the early-age analysis. This k-value represents the subgrade support conditions during construction. The k-value varies seasonally as a function of soil moisture and temperature, among other factors, and this may have a significant effect on pavement performance.
Loss of support is an important factor that affects the performance of the pavement. Loss of support depends highly on the erodibility of the subbase materials, presence of water, slab deflection, and magnitude and amount of traffic loads.(64) Available loss of support (pumping) models have limited applicability to mechanistic models such as the one used in HIPERPAV II to predict midslab cracking. For example, pumping models developed during the AASHO road test account for subbase materials highly susceptible to erosion and are thus not currently used. COPES models do not consider the subbase type as a factor.(64) Given the lack of a sound loss-of-support model, and considering that the HIPERPAV II long-term analyses are made to compare early-age factors, no loss-of-support model was incorporated. It is therefore important to emphasize that the effect of the structural support provided by the subbase must be evaluated with a pavement design procedure such as the one developed by the NCHRP 1–37A study.
Also, to minimize the number of inputs, no input for soil type is required. The soil type input required for the faulting prediction model has been hard coded to AASHTO classification A–2–6. Although the effect of soil type on faulting prediction for JPCP with no dowels is minimal, a significant effect on the faulting prediction for JPCP with dowels is observed. Given that the comparisons of early-age strategies are made under the same conditions of LTE in the long term, the results of the comparative analysis should be unaffected by this factor.
Loading position for analysis of longitudinal cracking is assumed at midslab along the transverse joint as required by the Westergaard stress model. No stress adjustment is made to account for the fact that the loading position rather than at midslab occurs at the wheel path.
No lift-off of the concrete slab from the subbase due to curling is considered, and the bond between the PCC slab and subbase layer is not taken into account.
The model that is used to predict average monthly moisture content in the pavement layers underneath the slab is rather simplistic. This model uses site-dependent climatic conditions, soil data, and some pavement geometry, but does not consider information on the drainage system.
The faulting prediction models require input on whether edge subdrains are used. The condition for no subdrains is hard coded for this model.
Input of accurate load spectra information requires of significant data entry time. To ease entry of traffic inputs, a number of assumptions are made:
Early-age strategies are compared under the same traffic conditions in the long term. Therefore, it is assumed that the effect of traffic distribution on these comparisons is minimal.
A spalling model was not included in the long-term prediction module because of the complexity required to account for all possible factors that affect spalling distress. These include the moisture state in the pavement slab, concrete evaporation, sawcutting procedures, and dowel-bearing stresses, among other factors.
Because no spalling distresses are predicted, serviceability and IRI may be underpredicted, as they are a function of the level of distresses present.
The selected model for prediction of CRCP early-age behavior in HIPERPAV II is the CRCP–8 model developed by the CTR of the University of Texas at Austin, TX . CRCP–8 is a mechanistic model based on equilibrium of internal forces in the reinforced concrete for predicting concrete and steel stresses as a function of the concrete mechanical properties, temperature development, and restraint imposed by the subbase and the steel. Similar to the JPCP module in HIPERPAV II, stresses in the concrete are compared to the strength development at any time step for prediction of crack formation.
Figure 60 shows a schematic representation of the one-dimensional model for analysis of concrete and steel stresses in a CRCP basic analysis unit bounded by two adjacent transverse cracks and longitudinal joints.(93)
Figure 60. Schematic representation of analysis of concrete and steel stresses in CRCP–8.
The complete model derivation is described in detail in reference 93; only the primary governing equations are presented here. For derivation of the governing equations of the CRCP system, a number of assumptions are made:
Since concrete stress is zero at cracks, considering that the steel stresses that develop at the crack location must be in equilibrium with the subbase restraint and the stresses in the concrete at any point in the slab, the following relationship is derived in equation 212:(93)
where,
x = coordinate distance from midslab,
![]() sx = stress in the steel at location x,
sx = stress in the steel at location x,
![]() cx = stress in the concrete at location x,
cx = stress in the concrete at location x,
ps = ratio of cross sectional area of steel (As) to area of concrete (Ac),
![]() sc = stress in the steel at a crack,
sc = stress in the steel at a crack,
L = one-half of the slab segment length,
Fi = friction force per unit length along the slab, and
D = thickness of the concrete slab.
Equation 213 is used to determine the stresses in the concrete at any location along the slab.
where,
Ec = modulus of elasticity of the concrete,
n = Ec/Es,
Es = modulus of elasticity of the steel,
![]() c = thermal coefficient of expansion of the concrete,
c = thermal coefficient of expansion of the concrete,
![]() s = thermal coefficient of expansion of the steel,
s = thermal coefficient of expansion of the steel,
![]() T = temperature change, and
T = temperature change, and
![]() sh = drying shrinkage of the concrete.
sh = drying shrinkage of the concrete.
Steel stress at the crack is determined as shown in equation 214:
with terms as previously defined.
Depending on the relative displacements between the steel and the concrete, two zones are identified: 1) a fully bonded zone at the middle of the geometric model where concrete and steel displacement are zero, and 2) a bond development zone, in proximity to the cracks, where steel displacement is zero, but concrete displacement occurs, and is a function of the material properties and environmental conditions. With the above conditions, for the fully bonded zone, the rate of steel and concrete stress is primarily a function of subbase restraint as shown in equations 215 and 216. For the bond development zone, the rate of steel and concrete stress is primarily a function of the bond stress as shown in equations 217 and 218.
where,
fb(x) = bond stress at location x along the steel-concrete interface and
![]() = diameter of steel bar.
= diameter of steel bar.
To solve the above system of equations, it is necessary to define a boundary condition for the steel stress at the crack location. It is assumed that the steel stress at cracks is the same regardless of the slab length. The steel stress is determined for a slab length with a mean crack spacing, Xbar, as shown in equation 219:
In addition to the above boundary condition, relationships for the bond stress and bond development length are derived as a function of the steel stress at the crack location. A simplified coordinate system with origin at the location where bond slippage begins is used, as shown in figure 61, to derive the bond stress and bond development length relationships in equations 220–222.
Figure 61. Simplified coordinate system for development of bond stress distribution functions.
where,
s = coordinate distance from the location where bond slippage begins,
K = bond stiffness (bond stress per unit slip),
W(s) = bond slip at location s,
C,D,E = constants that are functions of the boundary conditions (derived in reference 93), and
b = bond development length.
where,
c = b(aK)0.5,
![]() =
= ![]() /(EcD),
/(EcD),
![]() = slope of the subbase frictional stress distribution,
= slope of the subbase frictional stress distribution,
A = constant that is a function of the boundary conditions (derived in reference 93), and
a = distance from the location where bond slippage begins to midslab.
A second relationship between the steel stress at a crack and the bond development length is derived as shown in equations 223–225:
where,
An iterative process is used to solve equations 222 and 223 that provides the same bond development length for a given ![]() sc. With the bond development length and steel stress at the crack, concrete and steel stresses along the slab length are computed with the above relationships for both the fully bonded zone and the bond development zone. Initially, no subbase restraint is assumed, and an iterative process is used to solve for it. The subbase restraint stress distribution is approximated by a linear function of the distance from midslab.
sc. With the bond development length and steel stress at the crack, concrete and steel stresses along the slab length are computed with the above relationships for both the fully bonded zone and the bond development zone. Initially, no subbase restraint is assumed, and an iterative process is used to solve for it. The subbase restraint stress distribution is approximated by a linear function of the distance from midslab.
In CRCP–8, the Monte Carlo method is used to simulate the PCC strength variability. By assuming a normal distribution for the PCC tensile strength, the Monte Carlo method is used to probabilistically assign different values of tensile strength along the pavement length. A comparison of the concrete stress and the simulated concrete tensile strength at any point is performed for prediction of crack formation. In this fashion, crack spacing is predicted with an inherent variability.(93)
As an enhancement to the CRCP–8 model, in this study, similar to the strength prediction for JPCP, the maturity method is used in the CRCP HIPERPAV II module to predict the early-age strength.
In CRCP–8, the minimum and maximum PCC temperatures are an input for the days after construction until concrete reaches full strength (assumed to be 28 days) and for the coldest time of the year. As an enhancement to the CRCP–8 model, in this study the required PCC temperatures are predicted with the finite-difference temperature model described in section B.1.2.
The CRCP model used in HIPERPAV II is a one-dimensional mechanistic model with the following limitations:
Selection of the FHWA mix optimization study was described in Volume I of this report series. This study was incorporated in the HIPERAPV II system in the form of a module termed Concrete Optimization, Management, Engineering, and Testing (COMET). COMET is a simplified derivation of the Concrete Optimization Software Tool (COST) software originally developed by FHWA and the National Institute of Standards and Technology. A two-stage analysis process is involved.
Stage I: Trial Batches
A limited number of factors (or decision variables) are determined by providing bound values and a midpoint value. Specific gravity and unit cost of the constituents (e.g., cement, admixture, aggregate) are defined by the user. Desirability curves for responses or objective functions (e.g., cost, 28-day strength) are defined.
Trial batches, whose number is based on the number of factors plus replicates, then are generated. The predicted responses are obtained from default predictive models. However, the predicted responses may be overwritten using actual trial batch test results.
Stage II: Virtual Batches
A full quadratic model is fitted for each response based on the responses from the trial batches. Virtual mixes are then generated using a finer grid (i.e., adding more combinations within the operability region of the variable space). The responses of virtual mixes are subsequently predicted by the fitted quadratic models. Scores for all virtual mixes are calculated and ranked. The top N virtual mixes are then recommended as optimized mixes, where N is defined by the user.
Since COMET is a simplified version of the FHWA COST software, its usability is enhanced while hiding the inherent complexity of the analysis. (See references 94, 95, 96, and 97.) This is not to deter users who have limited statistical backgrounds. However, flexibility and detailed statistical reports for all analysis stages are not available, nor is the more robust analysis that is provided by COST.
COMET uses FORTRAN in the back-end coding while it uses Microsoft® Visual Basic®/HTML in the front-end coding. COMET uses four fixed factors: percent coarse aggregate of total aggregate weight, cementitious content, percent pozzolan of total cementitious, and w/c. COMET uses three fixed responses: cost, early-age strength, and 28-day strength. Property desirability curves (with six data points) are user-defined for each response.
Face-centered design methodology is used to generate 29 trial mixes based on equation 226:
where,
k = number of factors (four in this case),
x = number of centerpoints (five in this case),
NB = number of trial batches,
AP = number of axial points,
CP = number of central points, and
FP = number of factorial points.
The trial batches may be increased if number of factors is increased. The current version of COMET utilizes eight evenly spaced design points between the limits of each factor. This generates a combination of 4096 virtual mixes (i.e., 84). A full quadratic model is used in model fitting. Fifteen terms are contained in this model. The 29 face-centered design points are used for model fitting, with predicted responses calculated for each of the 4096 points.
The central composite design (CCD) is a very efficient experiment design technique to fit second-order response models. It uses a two-level factorial or fraction combined with axial and centerpoints. The factorial points describe “a variance-optimal design for a first-order model or a first-order + two-factor interaction model”.(98) (p. 322) The centerpoints capture the curvature in the system. If curvature exists, axial points will help in the approximation of quadratic terms efficiently. In summary, CCD is very efficient at providing information on variable effects and overall experimental error while minimizing the number of required runs.
To calculate concrete compressive strength as a function of w/c, Abrams' equation is used.(61) The most basic form of this equation (equation 227) relates compressive strength directly to w/c.
where,
fc = compressive strength, in KPa,
w/c = water-to-cement ratio, and
AA, BA, and CA = empirical coefficients that are independent of strength and w/c. CA commonly is set to zero.
The empirical coefficients depend on the units, materials, test method used, age of testing, and the conditions of validity for Abrams' rule. Abrams' rule states that:
The strengths of comparable concrete depend solely on their w/c's regardless of their compositions. Abrams' rule is valid, provided that the following 10 assumptions hold:
The compressive strength prediction model formulated for COMET must account for the influence of w/c, pozzolans, and aggregate contents, in addition to concrete age. The relationships between these inputs and compressive strength are listed below.
A basic model for compressive strength at 28 days is given in equation 228: (61)
(1 ksi = 6.89 MPa)
An augmented model, which accounts directly for cement content, is given in equation 229:(61)
where,
c = cement content in pcy (1 lb/yd3 = 0.594 kg/m3).
Figure 62 compares these two models. At low w/c's (w/c < 0.3), the compressive strength continues to increase according to the basic model. This relationship would be correct for fully compacted concrete, but at lower w/c's, it is difficult to achieve full compaction.(13) The augmented model, used in COMET, provides a more reasonable prediction of compressive strength.
Figure 62. Compressive strength as a function of w/c and cement content.
When investigating the effect of fly ash and age on the concrete's compressive strength, the relative change in strength (frel) can be calculated within the limits of Abrams' rule (equation 230).
where,
concrete strength f is related to w/c and
concrete strength f1 is related to w/c1.
Assuming AA = AA1, equation 231 follows:
Abrams' rule is valid for blended cements. When a portion of the cement has been replaced by fly ash, the following approximation of BA has been derived in equation 232.
where,
c = mass of cement and
p = mass of fly ash that has been added to the cement.
To use this equation to predict the 28-day compressive strength of concrete, the w/cm of w/(c + p) applies. Also, it is only applicable for the range of p/c = 0 to 1. Although there is not a similar relationship for concretes containing silica fume, it is likely that Abrams' rule is still valid. Its effect on BA has yet to be developed.
It is also possible to relate the 28-day compressive strength to its early-age values at a specific time t using Abrams' rule. As given in Popovics:(61)
For Type I cement (equation 233):
For Type III cement (equation 234):
This hyperbolic function approximates the strength gain of the concrete well within the limits of 3 days and 1 year. The values, however, are too low at 1 day.
To develop the relationship between compressive strength and aggregate content, the importance of aggregate gradation was recognized. According to Gilkey, concrete strength is influenced by: 1) the ratio of cement to mixing water, 2) the ratio of cement to aggregate, 3) grading, surface texture, shape, strength and stiffness of aggregate particles, and 4) maximum size of the aggregate.(61) For concretes with identical w/c's, the compressive strength increases as the maximum particle size decreases.
The following ratio (equation 235) was developed to account for the effect of aggregate:
where,
FA = fine aggregate content and
CA = coarse aggregate content.
Equation 235 was calibrated using the data provided by Ganju.(99)
Combining the effects of w/c, pozzolan content, aggregate content, and age on compressive strength yields the relationship shown in equation 236:
where,
f![]() c = compressive strength that includes the effects of age, pozzolan content, and aggregate content,
c = compressive strength that includes the effects of age, pozzolan content, and aggregate content,
fc = compressive strength calculated using only the w/c,
RatioAge = factor that incorporates the influence of time on the compressive strength,
RatioPozzolan = factor that includes the effect of pozzolan content on compressive strength, and
RatioAggregate = factor that accounts for aggregate content on compressive strength.
This relationship is used in COMET to predict concrete compressive strength.
Limitations of this equation are:
Dowel bars are subjected to combined environmental loading and dynamic traffic loading at the joint during the pavement's lifetime. The dowel bar module in HIPERPAV assesses how the dowel bars affect the early-age performance of JPCP. If the bearing stress is greater than the concrete's early-age compressive strength, then it is probable that the dowel will loosen over the lifetime of the pavement at a faster rate than if the bearing stress is less than the concrete's compressive strength. The model that predicts the early-age dowel bar bearing stress is summarized below.
To calculate the dowel bar bearing stress, several inputs are needed in the model. These inputs are listed in table 39 .
| Input Category | Parameter | Units | Variable |
|---|---|---|---|
| Dowel bar | Diameter | m | dD |
| Poisson ratio | Unitless | nD | |
| Modulus | MPa | ED | |
| Effective modulus of dowel support | MPa/m | KD | |
| Joint | Opening | MPa | w |
| Slab | Modulus | MPa | Ec |
| Poisson ratio | Unitless | nc | |
| CTE | m/m/°C | ||
| Length | m | L | |
| Thickness | m | h | |
| Load and support | Linear temperature gradient | °C/m | |
| Slab support reaction modulus | MPa/m | k |
For the system, the radius of relative stiffness is calculated in equation 237:
as are the dowel moment of inertia, ID, in equation 238:
and the relative stiffness of the dowel-concrete system, b. Equations 237–239 can be found in Huang.(64)
A dowel at the joint is subjected to moments Mo, as shown in figure 63.
Figure 63. Schematic of dowel deformation and loading at the joint.
To model the behavior of the dowel at the joint, some assumptions are made. Two cases are shown in figure 64. In the first case, the gray dowel depicts behavior at the joint, assuming that the concrete underneath it does not deform, or that there is no concrete compliance. In the second case, the concrete has deformed under the black dowel.
Figure 64. Schematic of dowel deformation without concrete compliance and with concrete compliance at the joint.
To relate the angles of the dowels as they leave the concrete to the deflection of the dowel at the slab face, yo, the relationship in equation 240 is used:
where,
![]() = slope of the dowel without concrete compliance,
= slope of the dowel without concrete compliance,
![]()
![]() = slope of the dowel with concrete compliance, and
= slope of the dowel with concrete compliance, and
yo = deflection of the dowel at the slab face.
According to Timoshenko and Lessels, and as reported by Friberg, the deflection of the dowel at the slab face yo|x=0 when it is subjected to a moment is as shown in equation 241:(66, 100)
From Westergaard, the slope of the dowel without concrete compliance can be calculated. Westergaard solved for the deflection of a curled pavement, z.(101) Adjusted for the coordinate system presented here, it is shown in equation 242:
where, as defined in equations 243–246,
Taking the differential of the deflection with respect to x yields the slope. With the small angle assumption, the slope of the dowel approximates the angle of the dowel, ![]() , under deformation when it leaves the slab (equation 247):
, under deformation when it leaves the slab (equation 247):
To determine ![]()
![]() , the dowel is modeled as a cantilever beam. The angle of the deflected dowel shape,
, the dowel is modeled as a cantilever beam. The angle of the deflected dowel shape, ![]()
![]() , at the center of the joint is given by equation 248, as derived by Timoshenko and Lessels.(66)
, at the center of the joint is given by equation 248, as derived by Timoshenko and Lessels.(66)
Mo, the moment causing the dowel to deflect at an angle of ![]()
![]() now must be determined. Combining equation 248 with Friberg's (equation 241) and the geometric relationship (equation 240), equation 249 for the moment is derived as a function of
now must be determined. Combining equation 248 with Friberg's (equation 241) and the geometric relationship (equation 240), equation 249 for the moment is derived as a function of ![]() .
.
The resulting dowel bar bearing stress, from Huang, is shown in equation 250:
The effect of varying nine of the model input are shown in figures 65 to 73 and is summarized in table 40.
Figure 65. Effect of varying the dowel diameter (dD) on the bearing stress.
Figure 66. Effect of varying the effective modulus of dowel support (KD) on the bearing stress.
Figure 67. Effect of varying the joint opening on the bearing stress.
Figure 68. Effect of varying the concrete modulus (Ec) on the bearing stress.
Figure 69. Effect of varying the concrete CTE (ac) on the bearing stress.
Figure 70. Effect of varying the slab length (L) on the bearing stress.
Figure 71. Effect of varying the slab thickness (h) on the bearing stress.
Figure 72. Effect of varying the modulus of subgrade reaction (k) on the bearing stress.
Figure 73. Effect of varying the linear temperature gradient (T) on the bearing stress.
| Input Parameter | Influence on Bearing Stress | Influence on Bearing Stress According to Friberg(100) |
|---|---|---|
| Dowel diameter (dD) |
||
| Effective modulus of dowel support (KD) |
– | |
| Joint opening (w) |
||
| Concrete modulus (Ec) | – | |
| Concrete CTE ( |
– | |
| Slab length (L) |
– | |
| Slab thickness (h) |
– | |
| Modulus of subgrade reaction (k) |
– | |
| |Temperature gradient| ( |
– |
When the joints in pavements are loaded in shear (Pslab in MPa/m) as illustrated in figure 74, the dowel bars resist this loading (Pdowel in MPa/m). The free edge deflection, yo (in meters), is restrained by twice the value of y1 (in meters) due to the dowels.
Figure 74. Schematic representation of slabs loaded in shear.
The resulting load on the dowel is shown in equation 251:
where,
C = Huang's spring constant (MPa).(64)
Derived from Hetenyi's beam theory, the load on the slab is shown in equation 252:(102)
where,
k = slab support reaction modulus (MPa/m),
![]() b = beam characteristic (m-1), and
b = beam characteristic (m-1), and
l = radius of relative stiffness (m).
Further proof of this derivation was provided by Skarlatos (equation 253):(71)
Equilibrium (equation 254) is achieved when:
Solving for y1 in term of yo yields equation 255:
Since yois known from Westergaard theory, Pdowel can be calculated using equation 256:
Then the deflection of the dowel at the joint face (![]() face in m) can be determined by equation 257:
face in m) can be determined by equation 257:
where,
![]() , w, E, and I are previously defined.
, w, E, and I are previously defined.
The dowel-bearing stress (sb in MPa) can now be calculated in equation 258:
where,
Kdowel was previously defined in table 39.
This bearing stress is plotted in the HIPERPAV dowel bar module and compared to the concrete's compressive strength.
A screen capture of the dowel analysis module in HIPERPAV II is shown in figure 75. The calculated results are for the HIPERPAV II default input.
Figure 75. HIPERPAV II screen capture showing typical output from the dowel bar module.