U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-127 Date: January 2006 |
Previous | Table of Contents | Next
Although the CRCP early-age behavior models and long-term JPCP models selected for use in this project have already undergone extensive validation efforts, modification to some of the models to reflect specific early-age conditions and to integrate well with the overall system warrant further validation.
Validation focuses on determining the reliability of the model. Model reliability determines if the model is a good one or a poor one. If there is significant scatter in the data as compared to the prediction, then the model is possibly poor. Less scatter implies that the model is reliable. The reliability of the individual models in the long-term JPCP and early-age CRCP modules in HIPERPAV II was assessed under this concept.
Two levels of validation were undertaken for both the long-term JPCP and early-age CRCP models incorporated into HIPERPAV II. The first level of validation was performed with the use of databases. The second level of validation consisted of selecting pavement sites and obtaining the necessary information for the validation analysis.
The database validation efforts are discussed in section D.1, and the field validation work is discussed in more detail in section D.2. Additional validation also was performed for general early-age behavior enhanced models such as the finite-difference temperature prediction model and the improved drying shrinkage model. Also, initial attempts to incorporate an improved relaxation-creep model were performed. Validation of each of these early-age behavior models is presented in section D.3.
The primary databases used for this purpose were the database maintained by LTPP and the Texas CRCP database.(105, 106) The wider geographical distribution and variety of pavement sections in the LTPP database were determinant factors for its use, while the extensive amount of early-age data for CRCP in the Texas rigid pavement database was a major factor for its selection. Other databases, such as the COPES and the RIPPER databases, were investigated; however, lack of early-age information and monitoring records made the validation efforts difficult.(107, 108)
Information in the LTPP database was used exclusively for validation of the JPCP structural response models. Provided the LTE model has not been previously calibrated as a whole, pavement sections in the LTPP database were used for model calibration. Subsequently, validation of the JPCP long-term performance predictions was performed with information collected from existing field sites. Calibration of the LTE model is described in this section, and field validation of JPCP existing sites is discussed in section D.2.1.
As previously presented in section B.2.3.1, a model for the prediction of stress and deflection transfer across JPCP joints due to traffic loads was incorporated in HIPERPAV II. Prediction of LTE for JPCP is a function of a number of factors including the presence of dowels, aggregate interlock, pavement geometry, PCC mechanical properties, slab support, and environmental conditions.(69, 70, 73) The seasonal monitoring program (SMP) under the LTPP program includes monitoring of JPCP sections to observe the effects of temperature and moisture on the pavement structure and its response to loads.(109) Evaluation of LTE for SMP sections with enough information on the factors mentioned above was useful in better understanding structural behavior of JPCP and provided the basis for calibrating the pavement response LTE model incorporated in HIPERPAV II.
As part of the SMP study, joint movement is monitored along with PCC temperatures and deflections obtained with FWD equipment.(109) This information is believed to be useful in understanding the effect of joint opening on LTE. Lee and Stoffels reported several findings on analysis of joint movement information for the SMP sections.(110) The following observations from that study are of particular interest:
Although joint opening is not directly measured in the SMP study, it is believed that monitoring of the joint movement during hot weather may capture the temperature of joint closure, as was the case for some of the sections analyzed by Lee and Stoffels.(110)
To determine the temperature of closure, an important parameter in the LTE analysis, the procedure developed by Lee and Stoffels was followed for this study.(110) JPCP LTPP sections were investigated and the effective ratio of joint movement to change in PCC temperature (ER) determined. The effective ratio is understood as a reduction in joint opening, in millimeters, for a 100 °C increase in PCC temperature. For this analysis, the information was obtained from the LTPP DataPave 3.0. Table 75 presents the ER statistics for each of the 12 sections investigated. From the analysis summarized here, although slight differences in the computed ER for a few sections were observed, similar findings were obtained to those presented by Lee and Stoffels. In addition to the JPCP sections previously investigated by Lee and Stoffels, SMP sections 39-0204 and 32-0204 were evaluated.
| Section ID | Avg. ER (mm/100°C) |
Min. ER (mm/100°C) | Max. ER (mm/100°C) | Locked Joints | Closure Temp | Observations |
|---|---|---|---|---|---|---|
| 04-0215 | −5.82 | −7.7 | −3.9 | 1 of 8 | 32.3 | - |
| 06-3042 | - | - | - | - | - | No correlation of PCC temperature to joint opening |
| 13-3019 | −5.35 | −8.7 | −3.4 | 2 of 6 | 13.8 | - |
| 18-3002 | - | - | - | - | - | No PCC temperature records in DataPave 3.0 for joint opening dates |
| 31-3018 | −5.09 | −6.8 | −3.5 | 0 of 6 | NR | - |
| 32-0204 | −11.72 | −23.6 | −3.8 | 3 of 6 | NR | Many joints appear locked |
| 37-0201 | −2.84 | −5.2 | −1.8 | 2 of 6 | NR | - |
| 39-0204 | −2.85 | −6.6 | −1.6 | 0 of 6 | NR | - |
| 49-3011 | −5.25 | −7.0 | −3.3 | 0 of 8 | 30.5 | - |
| 53-3813 | - | - | - | - | - | No correlation of PCC temperature to joint opening |
| 83-3802 | −9.99 | −28.9 | −1.4 | 1 of 6 | 4.8-14.5 | Most joints with small ER |
| 89-3015 | −6.22 | −12.1 | −3.4 | 2 of 5 | NR | - |
ER = reduction in joint opening, in millimeters, for a 100 °C increase in PCC temperature.
NR = temperature of closure not observed within range of temperatures monitored.
The following are some comments on the findings obtained:
As part of this study, predictions with the HIPERPAV II joint opening model were made for the SMP sections evaluated. The HIPERPAV II joint opening model is documented elsewhere.(1, 3)
For prediction of joint movement with the HIPERPAV II joint opening model, the following factors are required:
Figure 111 compares of the measured versus predicted joint movement for the investigated sections. In general, it can be observed that the HIPERPAV II joint opening model slightly overpredicted joint movement for most of the sections.
Figure 111. Measured versus predicted joint opening.
During this exercise, no attempt was made to predict the erratic and large joint movements measured for section 32-0204, since no CTE information for this section was found in DataPave 3.0. However, to match the measured average joint movement for section 83-3802, a 9.8-m joint spacing had to be assumed to account for the joint freezing effect observed for this section. The largest ER ratio for this section could be matched with a 28.4-m joint spacing. The last value would indicate that five joints were locked up, contributing to the large joint opening.
To perform the LTE analysis, information for the SMP sections in study was obtained from the following tables in DataPave 3.0:
In most cases, manual readings and automatic temperature readings differed for less than 3 °C. In cases when both manual PCC temperature measurements and automatic thermistor measurements were available, the PCC temperature reported by the thermistors was used. It was assumed that automatic monitoring would give less room to measurement error than manual readings.
A number of points were discarded for this analysis based on the following criteria:
Table 76 shows the total number of points used after the above filtering process was performed.
| Section ID | Points in Database | Points Used for LTE Analysis | Points Used for LTE Analysis (%) | Points with Computed LTE > 100% | Points with Computed LTE > 100% (%) |
|---|---|---|---|---|---|
| 04-0215 | 754 | 604 | 80.1 | 3 | 0.5 |
| 06-3042 | 660 | 597 | 90.5 | 14 | 2.3 |
| 13-3019 | 793 | 611 | 77.0 | 3 | 0.5 |
| 18-3002 | 383 | 329 | 85.9 | 0 | 0.0 |
| 31-3018 | 719 | 650 | 90.4 | 1 | 0.2 |
| 32-0204 | 405 | 404 | 99.8 | 6 | 1.5 |
| 37-0201 | 774 | 718 | 92.8 | 10 | 1.4 |
| 39-0204 | 422 | 381 | 90.3 | 12 | 3.1 |
| 49-3011 | 1038 | 971 | 93.5 | 3 | 0.3 |
| 53-3813 | 635 | 470 | 74.0 | 10 | 2.1 |
| 83-3802 | 868 | 845 | 97.4 | 35 | 4.1 |
| 89-3015 | 737 | 679 | 92.1 | 16 | 2.4 |
The LTE across joints was evaluated based on the deflection ratio using the procedure documented by Teller and Sutherland (equation 262):(113)
where,
LTE = load transfer efficiency, percent,
Wu = deflection on the unloaded slab, and
Wl = deflection on the adjacent loaded slab.
Figure 112 shows a typical plot of PCC temperature versus joint LTE for a doweled section. It is observed that for high PCC temperatures the joint LTE remains high, typically above 80 percent. However, there is a threshold temperature below which LTE is significantly reduced, most likely due to the loss of aggregate interlock as the joint opens.
Figure 112. Typical plot of PCC temperature versus joint LTE, section 37-0201.
Table 77 shows some computed LTE statistics for the sections analyzed and some design and construction characteristics. In this table, the JPCP sections are sorted as a function of the average computed LTE, from lowest to highest. From this sorting procedure, the following observations are made:
| Section ID | Min. LTE (%) | Max. LTE (%) | Avg. LTE (%) | CV (%) | T after which LTE > 80% | T min. | T max. | Closure Temperature | Construction Date | Joint Spacing (m) | D (mm) | Climate | Dowels | Base |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31-3018 | 18.6 | 100.0 | 58.6 | 33.0 | 30 | −3.3 | 32.6 | Not within range | May 1985 | 4.7 | 302 | WF | No | Soil cement |
| 49-3011 | 9.2 | 106.4 | 63.1 | 38.5 | 25 | −4.2 | 41.6 | 30.5 | May 1986 | 4.6 | 259 | DF | No | CAM |
| 06-3042 | 14.6 | 102.5 | 75.5 | 26.5 | 25 | 2.9 | 36.7 | - | Jun 1979 | 4.7 | 224 | DNF | No | CAM |
| 83-3802 | 30.0 | 104.7 | 77.3 | 26.9 | 22 | −16.0 | 31.6 | 4.8-14.5 | Sep 1985 | 4.6 | 249 | WF | No | Subgrade |
| 53-3813 | 39.9 | 105.2 | 88.2 | 14.7 | 20 | 1.9 | 44.1 | - | Aug 1966 | 4.6 | 203 | WNF | No | Coarse soil agg. mixture |
| 37-0201 | 46.8 | 105.5 | 85.9 | 15.0 | 26 | 0.2 | 39.7 | Not within range | Nov 1993 | 4.6 | 229 | WNF | Yes | Crushed stone |
| 04-0215 | 45.2 | 104.7 | 86.3 | 12.8 | 36 | 12.3 | 48.4 | 32.3 | Sep 1993 | 4.6 | 287 | DNF | Yes | Crushed gravel |
| 18-3002 | 63.1 | 99.1 | 90.5 | 7.6 | 17 | −1.7 | 36.9 | - | Aug 1976 | 4.7 | 241 | WF | Yes | Crushed stone |
| 13-3019 | 53.9 | 101.9 | 91.3 | 9.4 | 17 | −0.5 | 43.0 | 13.8 | Dec 1981 | 6.1 | 231 | WNF | Yes | Crushed stone |
| 32-0204 | 82.7 | 102.5 | 93.8 | 3.3 | all | −0.9 | 34.4 | Not within range | Jul 1995 | 4.6 | 300 | DF | Yes | crushed gravel |
| 89-3015 | 62.3 | 111.9 | 95.2 | 3.4 | 6 | −17.0 | 32.7 | Not within range | Sep 1984 | 6.0 | 208 | WF | Yes | Crushed stone |
| 39-0204 | 80.0 | 105.5 | 95.6 | 3.6 | all | 0.1 | 30.8 | Not within range | Aug 1995 | 4.6 | 282 | WF | Yes | Crushed stone |
CAM - Cement-aggregate mixture, CV - Coefficient of variation, D - Thickness, DF - Dry freeze, DNF - Dry-no freeze, T - Temperature (°C), WF - Wet freeze, WNF - Wet-no freeze
*Random joint spacing
For a number of sections, a large variability was found, as can be seen from the LTE CV in table 77. A large variability of LTE for JPCP sections in the LTPP database has been reported previously.(114) A more detailed analysis of section 49-3011 with the highest CV was performed to try to determine the reason for the large variability. Figure 113 shows a plot of PCC temperature versus LTE for that section. It is evident that several factors affect the variability of this section.
Figure 113. Computed LTE versus PCC temperature for section 49-3011.
The most remarkable factor from figure 113 is the effect of PCC temperature. As discussed before, above a certain threshold temperature (in this case, 25 °C), the LTE for this section remains above 80 percent. This is believed to be associated with the slabs expanding and causing a reduction in joint opening. Below that PCC temperature, the aggregate interlock is lost as the joint opens, and the LTE decreases significantly. It is also interesting to note that below freezing (PCC temperature < 0 °C), LTE is slightly higher than at PCC temperatures immediately above freezing. It is possible that the freezing effect provides higher soil support, therefore maintaining high LTE values. It is also hypothesized that ice in the joint can lead to a bridging effect. However, in figure 113, it is not quite clear why, for the range of temperatures above freezing and below 25 °C, a high variability occurs. Other factors that are believed to have an effect on LTE are pavement age, type of LTE test (load on approach slab or load on leave slab), variability in joint opening (figure 113 includes LTE tests for all joints monitored in that section), season of the year, and joint spacing (this section has random spacing).
To further investigate the possible impact of the above factors, the LTE measurements for section 49-3011 were individually analyzed for each joint as a function of type of LTE test, and date LTE tests were performed. Figure 114 shows the average LTE computed for each joint. For each joint, the computed LTE was grouped into two categories: tests performed before 1996, and tests performed in 1996 and thereafter. The Joint ID in figure 114 includes the type of LTE test (load positioned on approach slab-LTPP designation J4, or load positioned on leave slab-LTPP designation J5), distance from the start of the section to the joint in meters, and testing date group. An evident decrease in LTE is noted for the tests performed after 1996 as compared to the tests performed in previous years. It is also interesting to note that the approach slab tests show a lower average LTE than the leave slab tests for most of the joints, except for the joint located 8.95 m from the start of the section, where the trend is reversed.
Figure 114. Average LTE above freezing and below 25 °C, section 49-3011.
A statistical analysis for the average LTE is presented in table 78. The percent decrease in LTE for tests performed before 1996 and tests performed after 1996 is included along with a paired t-test to determine whether or not the means belong to the same population. It is observed that for most of the joints, except for joints −9.25 and 19.65 for the leave slab test, the null hypothesis that the mean LTE for tests performed before and tests performed after 1996 is the same is rejected at the 5 percent confidence interval. Therefore, quantitative evidence is obtained suggesting that age is a significant factor in joint LTE. The average decrease in LTE for tests after 1996 for all joints analyzed is 15.3 percent. The dates considered in the analysis range from November 1993 to September 1997.
Table 78 also shows the difference in LTE for approach slab tests and leave slab tests. For most of the joints, higher LTE values are observed for the leave slab test than for the approach slab test. On average, the leave slab tests show 9.8 percent higher LTE values.
A large variability in LTE also was noted between individual joints that also contribute to the overall LTE variability for that section. A typical example of the variability between joints is presented in figure 115. In general, lower values of LTE are noted for the joint located at −9.25 m from the start of the section than for the joint located at 8.95 m (for LTE tests below 25 °C). In addition, the variability for the joint at 8.95 m is notoriously higher than that for the joint at −9.25 m, as implied by the lower coefficient of determination (r2) for that joint, determined with a linear regression analysis.
| Type of LTE Test | Joint Location (m) | Date | Average LTE (%) | Standard Deviation | Coefficient of Variation | Change in Average LTE | t-test for Means | Difference in LTE (J5-J4) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J4 | −9.25 | before 96 | 0.471 | 0.173 | 36.6% | −10.1% | 2.0% | - | |||||
| after 96 | 0.370 | 0.100 | 27.1% | ||||||||||
| J5 | −9.25 | before 96 | 0.614 | 0.242 | 39.5% | −4.8% | 10.1% | 14.3% | |||||
| after 96 | 0.565 | 0.292 | 51.7% | 19.5% | |||||||||
| J4 | 1.35 | before 96 | 0.548 | 0.140 | 25.4% | −16.8% | 0.0% | - | |||||
| after 96 | 0.380 | 0.119 | 31.4% | ||||||||||
| J5 | 1.35 | before 96 | 0.644 | 0.159 | 24.7% | −20.9% | 0.0% | 9.6% | |||||
| after 96 | 0.436 | 0.183 | 42.0% | 5.5% | |||||||||
| J4 | 5.35 | before 96 | 0.709 | 0.174 | 24.5% | −26.6% | 0.0% | - | |||||
| after 96 | 0.442 | 0.119 | 26.9% | ||||||||||
| J5 | 5.35 | before 96 | 0.766 | 0.175 | 22.8% | −23.3% | 0.0% | 5.7% | |||||
| after 96 | 0.533 | 0.189 | 35.5% | 9.0% | |||||||||
| J4 | 8.95 | before 96 | 0.695 | 0.177 | 25.5% | −17.1% | 0.2% | - | |||||
| after 96 | 0.524 | 0.139 | 26.6% | ||||||||||
| J5 | 8.95 | before 96 | 0.640 | 0.220 | 34.4% | −9.3% | 1.5% | −5.4% | |||||
| after 96 | 0.547 | 0.232 | 42.5% | 2.3% | |||||||||
| J4 | 14.15 | before 96 | 0.594 | 0.222 | 37.3% | −23.0% | 0.0% | - | |||||
| after 96 | 0.365 | 0.143 | 39.2% | ||||||||||
| J5 | 14.15 | before 96 | 0.700 | 0.251 | 35.9% | −16.6% | 1.1% | 10.6% | |||||
| after 96 | 0.534 | 0.280 | 52.5% | 16.9% | |||||||||
| J4 | 19.65 | before 96 | 0.546 | 0.156 | 28.6% | −10.2% | 3.7% | - | |||||
| after 96 | 0.443 | 0.187 | 42.1% | ||||||||||
| J5 | 19.65 | before 96 | 0.667 | 0.217 | 32.6% | −4.8% | 38.0% | 12.1% | |||||
| after 96 | 0.620 | 0.221 | 35.7% | 17.6% | |||||||||
| −15.3% | 9.8% | ||||||||||||
Figure 115. Variability of LTE for individual joints, section 49-3011.
In addition, as noted in table 77, section 49-3011 has a random joint spacing. Since the point location corresponds to the distance from the start of the section, and since most of these joints are consecutive to each other, individual joint spacings could be determined. Figure 116 shows the results of evaluating the effect of joint spacing on LTE for that section. Although a slight decrease in LTE is observed for larger joint spacings, a rather low r2 is obtained. It must be noted that a similar variability between joints also was noted for sections with constant joint spacing. It is believed that the pavement age at which the crack formed at the joint may also play an important role on joint opening, and therefore on LTE. From previous experience, it has been noted that after construction, the joints that crack first tend to have larger joint openings than joints that crack later.
Figure 116. Effect of joint spacing on LTE, section 49-3011.
Figures 117 through 126 present the LTE computed for the remaining nondoweled and doweled sections in the SMP study, respectively. Individual analyses for each section showed similar trends in LTE, with testing date and type of LTE test, to those observed for section 49-3011. However, sections 04-0215 and 83-3802 showed reversed trends of LTE versus testing date. For these two sections, a higher LTE was observed for LTE tests after 1996. Although the increase in load transfer could be attributed to an improvement of the load transfer, records in DataPave 3.0 show no load transfer restoration for these sections nor any other rehabilitation activity of this sort.
The temperature at joint closure and ER can be used to determine the joint openings at different temperatures for the sections in study.
Figure 127 shows a plot of LTE versus joint opening for an individual joint in section 49-3011. For this section, the temperature of closure could be clearly identified from the joint opening analysis. In figure 127, testing dates are split in LTE tests before and after 1996. A linear fit is used to differentiate between testing dates. This figure corroborates some of the findings previously presented.
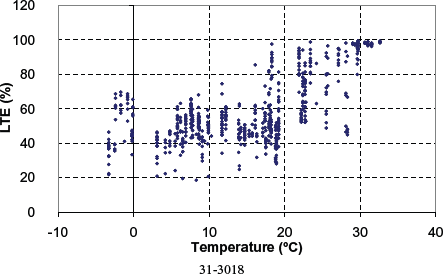
Figure 117. Computed LTE versus PCC temperature for nondoweled section 31-3018.
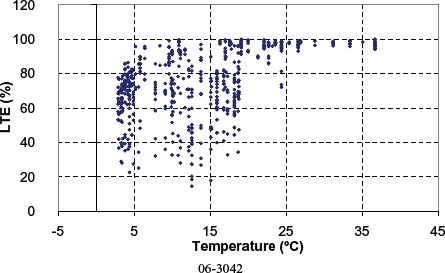
Figure 118. Computed LTE versus PCC temperature for nondoweled section 06-3042.
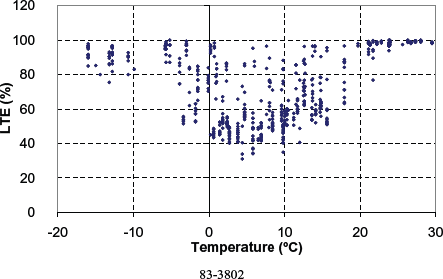
Figure 119. Computed LTE versus PCC temperature for nondoweled section 83-3802.
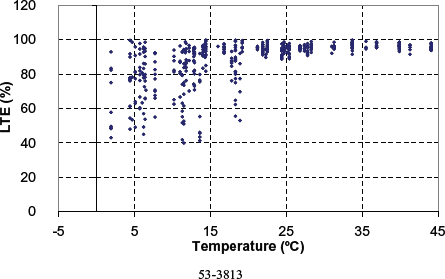
Figure 120. Computed LTE versus PCC temperature for nondoweled section 53-3813.
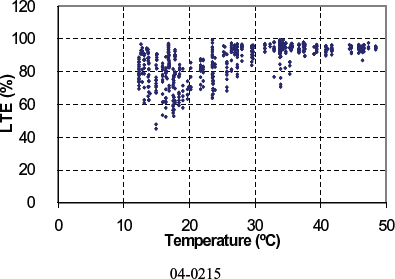
Figure 121. LTE versus PCC temperature for doweled section 04-0215.
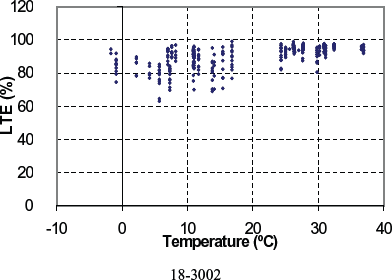
Figure 122. LTE versus PCC temperature for doweled section 18-3002.
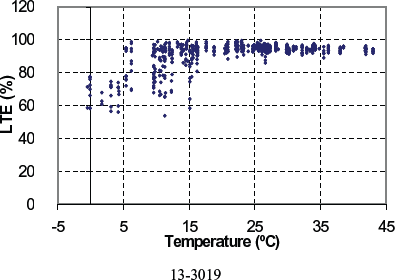
Figure 123. LTE versus PCC temperature for doweled section 13-3019.
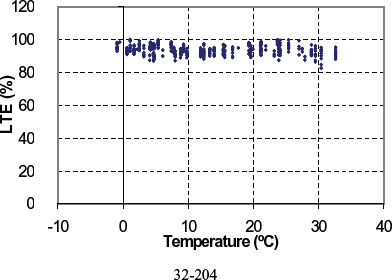
Figure 124. LTE versus PCC temperature for doweled section 32-0204.
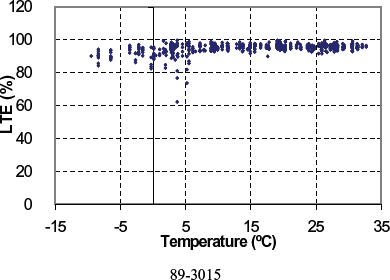
Figure 125. LTE versus PCC temperature for doweled section 89-3015.
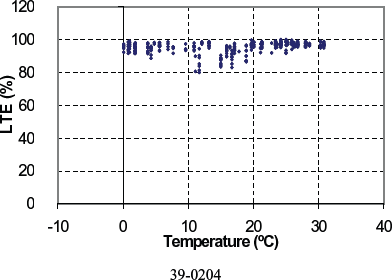
Figure 126. LTE versus PCC temperature for doweled section 39-0204.
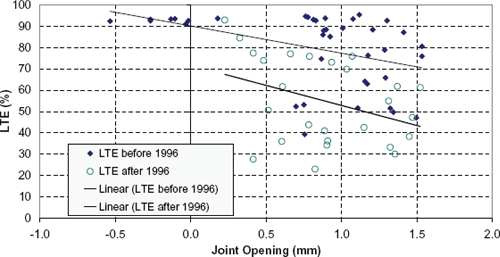
Figure 127. LTE versus joint opening for section 49-3011, joint at 5.5 m from start of section.
A number of analyses were performed to understand the effect of various parameters on joint LTE. An analysis was performed with LTPP data from SMP sections to determine the effect of temperature on joint movement and to identify the temperature of closure necessary in determining the joint opening. In addition, the computed LTE from the SMP sections was evaluated, and a number of factors were found to have a significant effect on LTE. These factors include:
It is believed that the procedures used in this investigation are effective in better understanding the effects of various factors on LTE.
For calibration of the LTE model, LTE was predicted as a function of joint opening and compared to the computed LTE from FWD tests. The temperature at closure and ER were used to determine the joint openings at different temperatures for the sections in study.
For sections where the temperature at joint closure could not be identified, this temperature was estimated based on a subjective assessment of the effect on LTE with change in temperature. It was noted that in most sections with information on temperature at joint closure, the LTE remained above 90 percent for joint openings smaller than 0.5 mm. Assuming this same behavior would hold true for the remaining sections with no joint closure information, the temperature at closure was backcalculated in such a way as to observe that drop below 90 percent on LTE at a joint opening of approximately 0.5 mm.
Figure 128 shows a plot of predicted versus computed LTE at a representative joint on section 31-3018. The LTE tests presented for this section date from 1995 to 2000. Because LTE prediction changes with load applications, the LTE tests were separated into two different periods: LTE tests on 1996 and before, and LTE tests after 1996. It can be observed in figure 128 that at the same joint opening, tests performed before 1996 show higher LTE values than those performed after 1996. However, a significant variability is noted, which makes it slightly difficult to determine a clear difference between testing dates.
The predicted LTE values are also shown in figure 128 at different load applications. LTE was predicted for the following loads: 0, 250,000, 500,000, and 12,400,000 ESALs. The last load level was obtained from traffic records in the LTPP database as the estimated cumulative ESALs at the end of 1996 for section 31-3018. Looking at figure 128 however, the predicted LTE at 250,000 ESALs seems to better match the computed LTE from tests at the end of 1996. After 500,000 ESALs, the predicted LTE seems to have very little variation with cumulative traffic.
Figure 128. Predicted versus computed LTE for section 31-3018, joint 5.5 m from start of section.
It was mentioned in section B.2.3.1.12 that the laboratory testing data used to develop the aggregate wearout model is based on slabs of small dimensions to which 9-kip loads were applied. The 9-kip loads subjected the slabs to higher deflections than normally observed in the field. It is possible that the 250,000 ESALs entered in the model represent the 12,400,000 ESALs actually applied to that section. That is, the model would need an ESALs multiplication factor of 0.02 to predict LTE properly.
The above exercise was repeated for all the sections in study to determine the number of load applications and ESALs correction factor that better matched the computed LTE in each case. Figures 129 through 132 present the LTE predictions at different levels of cumulative ESAL applications. A representative joint is shown with LTE tests for two different loading periods: before 1996 and after 1996.
Figure 129. Predicted versus computed LTE for section 49-3011, joint 5.5 m from start of section.
Figure 130. Predicted versus computed LTE for section 06-3042, joint 148.1 m from start of section.
Figure 131. Predicted versus computed LTE for section 83-3802, joint 149.7 m from start of section.
Figure 132. Predicted versus computed LTE for section 53-3813, joint 0.0 m from start of section.
Note from the above plots that, except for section 83-3802, the LTE test showed lower values for the period after 1996. Again, this seems to corroborate the effect of traffic loads on LTE. Although not indicated in the LTPP database maintenance records for section 83-3802, it is believed that some possible rehabilitation of this section could have been performed that resulted in the increased LTE after 1996.
As performed for section 31-3018, the number of ESALs that fit the LTE for 1996 was estimated with the LTE model in a rather subjective fashion. Table 79 presents the cumulative ESALs for every section on the analysis year along with the ESALs used in the model to fit the results from LTE tests. The last column presents the ESALs multiplication factor necessary to convert from the actual ESALs to the ESALs number required by the model to produce a good fit of the computed LTE. The average multiplication factor for all the sections analyzed was 0.048. However, a large variation of this factor was found among sections.
It is believed that although the LTE model is capable of producing the same trends in LTE as observed in the field, an accurate prediction will be possible only after a major investigation of the many factors that could affect these predictions such as aggregate type, aggregate shape, slab support conditions, and slab thickness is performed.
| Section | Year | Cumulative ESALs | ESAL fit | ESALs Multiplication Factor |
|---|---|---|---|---|
| 31-3018 | 1996 | 12,409,440 | 250,000 | 0.020 |
| 49-3011 | 1996 | 8,088,833 | 280,000 | 0.035 |
| 06-3042 | 1996 | 29,065,803 | 180,000 | 0.006 |
| 83-3802 | 1995 | 1,973,712 | 300,000 | 0.152 |
| 53-3813 | 1996 | 3,792,431 | 100,000 | 0.026 |
Figure 133 shows the results of a sensitivity analysis of the LTE model for nondoweled joints. It is observed that, according to this model, the most predominant factors affecting LTE are joint opening, cumulative load applications, and slab thickness. No major effect from PCC stiffness, wheel load, pressure, nor k-value were observed on LTE. As previously mentioned, factors that are not included in the model but that are believed to somehow affect the development of load transfer at joints include the aggregate type and shape, as well as slab curling and warping.
It was found during the verification process that, although the LTE model predictions follow the general trends of LTE as computed from FWD tests, further investigation of a number of factors are necessary to be able to predict LTE with more accuracy.
Figure 133. Sensitivity analysis of LTE model for nondoweled pavements.
In this section, an attempt to calibrate the LTE model for SMP doweled sections is performed. Similar to the nondoweled sections, LTE is predicted as a function of joint opening. The temperature at closure, and ER was used to determine the joint openings at different temperatures for the sections in study.
For sections where the temperature at joint closure could not be identified, this temperature was estimated based on a subjective assessment of the effect on LTE with change in temperature as described in the calibration of nondoweled sections.
For doweled sections, in addition to the PCC and support properties, the dowel characteristics are inputs to the LTE model. Among these characteristics, dowel looseness is one of the factors that has a significant effect on load transfer, as can be seen in the sensitivity analysis results presented in figure 134.
Figure 134. LTE model sensitivity for doweled sections.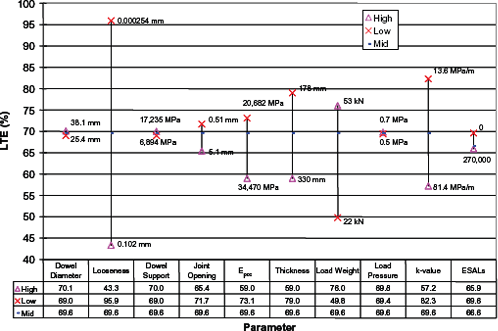
Teller and Cashell explored the effect of dowel looseness under repeated loading.(115) They reported an increase in dowel looseness as a function of the load cycles. They also found some correlations of dowel diameter to dowel looseness. In this study, the correlations presented in equations 263 and 264 were made with the data reported by Teller and Cashell.
where,
DL0 = dowel looseness after construction and
![]() = dowel diameter (mm).
= dowel diameter (mm).
where,
DLN = dowel looseness after N cumulative loading and
ESALS = cumulative 8.2-ton single axle load applications.
Figure 135 shows a plot of predicted versus computed LTE at a representative joint on section 37-0201. The computed LTE presented for this section dates from 1994 to 2001. Because LTE has been observed to decrease with load applications, LTE tests were separated into two different periods: LTE tests in 1996 and before, and LTE tests after 1996. Although it can be observed that measurements after 1996 show lower LTE values, some variability is noted, which makes it difficult to determine differences between measurement dates clearly.
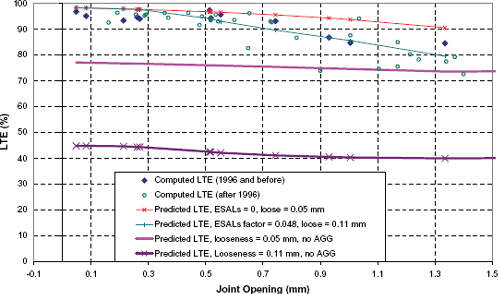
Figure 135. Predicted versus computed LTE for section 37-0201, joint 145.1 m from start of section.
The predicted LTE values at different load applications are also shown in figure 136. LTE was predicted for no loads and for 1593,467 ESALs (load level at the end of 1996 obtained from LTPP traffic records) adjusted by the multiplication factor of 0.048 previously determined for nondoweled sections. From equations 263 and 264, the predicted dowel looseness for those two load levels is 0.0018 and 0.0044, respectively. Figure 136 also includes the predicted LTE, assuming no aggregate interlock for the above looseness levels. For the looseness level with no traffic (0.0018), an LTE between 74 percent and 77 percent is obtained for the actual range of joint movement. For the looseness level at the end of 1996, the LTE varies between 40 percent and 45 percent. Given that the LTE for aggregate interlock is higher than the LTE for dowel support, it is difficult to verify the goodness of fit for the dowel looseness model in this LTPP section.
The above exercise was repeated for all the other sections in study to verify the accuracy of the ESALs multiplication factor for LTE determination and to verify the accuracy of the dowel looseness prediction model. Figures 137 through 140 present the LTE predictions at different levels of cumulative ESAL applications. For each section, a representative joint is shown with LTE measurements for two different loading periods: before 1996 and after 1996.
Figure 136. Predicted versus computed LTE for section 04-0215, joint 144.5 m from start of section.
Figure 137. Predicted versus computed LTE for section 13-3019, joint 21.3 m from start of section.
Figure 138. Predicted versus computed LTE for section 32-0204, joint 8.5 m from start of section.
Figure 139. Predicted versus computed LTE for section 89-3015, joint 36.3 m from start of section.
Figure 140. Predicted versus computed LTE for section 39-0204, joint 0.0 m from start of section.
Table 80 shows the cumulative ESALs for every section and the ESALs multiplication factor required to fit the computed LTE.
| Section | Year | Cumulative ESALs | ESALs Multiplication Factor |
|---|---|---|---|
| 37-0201 | 1996 | 1,593,467 | 0.048 |
| 04-0215 | 1996 | 3,395,341 | 0.074 |
| 13-3019 | 1996 | 1,553,000 | 0.090 |
| 32-0204 | 1996 | 559,708 | 0.048* |
| 89-3015 | 1996 | 4,195,817 | 0.048* |
| 39-0204 | 1998 | 1,967,539 | 0.048* |
* Possibly biased due to no dowel looseness.
From a comparative analysis of the LTE predictions for the above pavement sections, the following findings are observed:
From this analysis, it was possible to verify the trend in LTE as a function of joint opening and load applications for a number of doweled LTPP SMP sections. The average ESALs multiplication factor previously found for nondoweled sections seems to work reasonably for the doweled pavement sections evaluated here.
For the sections evaluated, it was rather difficult to determine the level of dowel looseness, because for half of the sections, LTE appears to be provided by aggregate interlock with some dowel looseness, while the remaining sections appear to have very little or no dowel looseness. Therefore, further work is required to verify the dowel looseness models presented. It is recommended that factors such as aggregate characteristics, dowel coatings, and compressive stresses at the dowel location due to curling stresses in the early ages be investigated.
Validation of the CRCP early-age behavior models had two objectives: validation of cracking behavior during the early age and validation of cracking behavior in the long term. Although, as its name implies, the CRCP module in HIPERAV should predict cracking behavior at early ages, long-term performance can be better estimated based on the cracking characteristics after the lowest temperature (typically after 1 year). Therefore, validation was also performed on existing CRCP sections with crack spacing information. Validation of cracking characteristics for existing CRCP sections is described in the following section. Validation of early-age cracking behavior was performed with information collected on construction field sites and is described in section D.2.2.
The CRCP-8 model included in HIPERPAV II has been validated extensively in the past.(106, 116, 117) However, during its incorporation into the HIPERPAV II system, new enhancements were made. These enhancements consisted of using the capabilities for pavement temperature prediction and development of mechanical properties in the HIPERPAV II system. The above enhancements warranted an additional validation of this module.
Provided the mechanistic nature of the CRCP-8 model, extensive information on the input parameters for a few sections was desired as opposed to limited information on several sections. For this reason, 16 sections on State Highway (SH)-6 in Houston, TX, that have been monitored continuously since construction were selected for this effort. Other CRCP sections also were investigated, such as the GPS-5 sections of the LTPP database; however, only limited early-age information was available for validation of the CRCP-8 model.(118, 119)
Reference 106 provides a detailed description of the section characteristics, construction, instrumentation, and testing procedures. A brief summary is presented below.
The test sections in study are located on SH-6 on two different segments, one placed during summer 1989 and other placed during winter 1990. For each segment, two different aggregate types were used with four different reinforcement designs for eight different design sections per construction season. Table 81 shows the factorial of designs used for both the summer and winter sections.
| Section ID | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Coarse Aggregate | SRG | SRG | SRG | SRG | LS | LS | LS | LS |
| Bar Size | #6 | #6 | #6 | #7 | #7 | #6 | #6 | #6 |
| Steel (%) | 0.63 | 0.53 | 0.42 | 0.53 | 0.63 | 0.52 | 0.61 | 0.68 |
SRG - Siliceous river gravel
LS - Limestone
To measure temperatures in the concrete, thermocouples were installed 25 mm from the surface, in the middle, and 25 mm from the bottom of the slab. In addition, DEMEC points were used to measure the magnitude of thermal changes in the concrete.
Condition surveys were performed during the month following construction to monitor crack spacing and crack width. In addition, long-term cracking characteristics have been monitored at different times throughout the pavement life.(106, 116, 117)
A number of cylinders were cast at the job to measure concrete splitting tensile strength, compressive strength, elastic modulus, drying shrinkage, and CTE under field and laboratory conditions at different ages.
Validation of the CRCP HIPERPAV II module required collecting information on all the input parameters considered. This information and assumptions made are presented below.
The CRCP design thickness for all sections was 279 mm. Since no construction information on thickness was reported, the design thickness was used in the analysis. A single layer of steel was used, with bar size and steel percentage as shown in table 81.
Slab support was provided by a 152-mm cement-treated base and 25-mm asphalt-stabilized base as a bond breaker. No restraint tests were reported. Typical restraint conditions for asphalt-stabilized bases were assumed for this exercise. A restraint stress of 41.4 kPa and movement at sliding of 0.63 mm were selected based on previous experiences by the authors.
As previously mentioned, the type of coarse aggregate used was SRG and limestone. The mix design information is reported by Suh et al. and is presented in table 82 below.(106)
| Project | SH-6 Summer | SH-6 Winter | ||
|---|---|---|---|---|
| Coarse aggregate type | SRG | LS | SRG | LS |
| Coarse aggregate-kg/m3 | 1,204 | 1,127 | 1,236 | 1,127 |
| Water-kg/m3 | 139 | 134 | 125 | 133 |
| Cement-kg/m3 | 230 | 251 | 203 | 230 |
| Fly Ash-kg/m3 | 63 | 68 | 95 | 63 |
| Fine Aggregate-kg/m3 | 658 | 722 | 640 | 746 |
| Entrained air (%) | 5 | 5 | 5 | 5 |
Test results on concrete properties were reported by Suh et al. and are summarized in tables 83 and 84 for summer and winter placements, respectively.(106)
| Property | Agg. Type | Value (Lab/Field) |
|---|---|---|
| 28-day splitting tensile (MPa) | SRG | 3.9/4.1 |
| LS | 3.6/3.4 | |
| 28-day modulus of elasticity (MPa) | SRG | 32884/37228 |
| LS | 36125/38124 | |
| 28-day compressive strength (MPa) | SRG | 44.8/43.1 |
| LS | 42.1/50.8 | |
| 28-day shrinkage ( |
SRG | 204.8/208.5 |
| LS | 196.3/170.8 | |
| CTE ( |
SRG | 8.6/9.9 |
| LS | 5.2/5.6 |
| Property | Agg. Type | Value (Lab/Field) |
|---|---|---|
| 28-day splitting tensile (MPa) | SRG | 4/3.8 |
| LS | 3.7/3.8 | |
| 28-day modulus of elasticity (MPa) | SRG | 37779/37848 |
| LS | 34746/37159 | |
| 28-day compressive strength (MPa) | SRG | 40.5/38.2 |
| LS | 47.4/46.5 | |
| 28-day shrinkage ( |
SRG | 90/115* |
| LS | 165/165 | |
| CTE ( |
SRG | -/11.9 |
| LS | -/6.8 |
* 30-day result
During construction, the placement temperature (temperature of the mix) was monitored, as was the time of day when construction began. This information is reported in tables 85 and 86, respectively.
| Section | Summer | Winter |
|---|---|---|
| Section A | 30 | 21 |
| Section B | 30 | 20 |
| Section C | 30 | 19 |
| Section D | 31 | 18 |
| Section E | 29 | 21 |
| Section F | 29 | 14 |
| Section G | 30 | 14 |
| Section H | 30 | 15 |
* Values in bold were reported, all other values were estimated.
| Section | Summer | Winter |
|---|---|---|
| Section length (m) | 70 | 70 |
| Section A | 6/16/1989 8:30 | 1/10/1990 13:00 |
| Section B | 6/16/1989 10:30 | 1/10/1990 15:00 |
| Section C | 6/16/1989 12:20 | 1/11/1990 10:00 |
| Section D | 6/16/1989 14:00 | 1/11/1990 12:30 |
| Section E | 6/19/1989 9:40 | 1/11/1990 16:00 |
| Section F | 6/19/1989 11:30 | 1/12/1990 10:00 |
| Section G | 6/19/1989 13:00 | 1/12/1990 11:20 |
| Section H | 6/19/1989 14:20 | 1/12/1990 14:00 |
* Values in bold were reported, all other values were estimated.
Curing method was not reported, and white curing compound was assumed; however, inconsistencies in the prediction of temperatures for sections G and H during winter placement lead to indications that polyethylene sheeting or cotton mats could have been used during the first few hours. This was based on the low temperatures observed during those days.
Historical air temperature, windspeed, relative humidity, and cloud cover data were retrieved from the National Oceanic and Atmospheric Administration (NOAA) database for the construction dates for every section. This information was obtained from the Houston Intercontinental Airport, the closest weather source to the site.
Crack spacing and crack width information has been monitored continuously for the sections on SH-6. During construction, condition surveys were performed during the first 30 days. In addition, condition surveys have been performed at 180, 500, 1000, 2500, 2800, and 4700 days for the summer sections and at 300, 800, 2300, 2600, and 4700 days for the winter sections (data provided by CTR of the University of Texas at Austin). Average crack spacings for the above survey dates are presented in figures 141 and 142. A typical trend of reduced crack spacing with age can be observed; however, for most sections, higher average crack spacings were reported for the surveying date at 4700 days than for previous dates. Since no rehabilitation has been reported for those sections, it is believed that the higher average crack spacings at 4700 days possibly may be due to omitted cracks during crack spacings measurement (this may be possible if the measurements were taken during a hot summer day when concrete expansion closes the cracks, making some of them imperceptible to the human eye). During hot days, hairline cracks are difficult to identify, which may result in cracks not included in the condition survey. For this reason, the crack spacing at 2500 days for the summer sections and 2600 days for the winter sections was selected for validation of the long-term crack spacings.
Figure 141. Crack spacing history for summer sections, SH-6.
Figure 142. Crack spacing history for winter sections, SH-6.
With the above information, each section was analyzed with the CRCP HIPERPAV II module to compare the measured crack spacings to the predicted values. Figure 143 shows the comparison results using the above input parameters as reported. Although a general slight overprediction of crack spacing is observed, a reasonably good r2 with respect to the 45° line was obtained (r2 = 0.82).
Figure 143. Preliminary long-term crack spacing prediction.
Given the reasonable fit obtained and because this validation effort was intended to determine if the differences in prediction are within reasonable limits rather than to calibrate the model, no model adjustments were performed.
Crack spacing during the early age was also compared to the predicted crack spacings with the CRCP HIPERPAV II module. Figure 144 shows the prediction results at 3 days from construction.
Figure 144. Crack spacing prediction at 3 days from construction.
For the early age, a generally poor prediction of crack spacings was observed. Similar results had been observed in previous validation efforts with this data set. Suh et al. had found good predictions for the first few months after construction; however, significant deviations were observed for the first 5 to 10 days.(106) This poor prediction may be attributed to a number of reasons:
Validation of the CRCP model during early ages is discussed further in section D.2.2.
Measurements of crack width 2 years after placement for the SH-6 test sections, were reported by Otero et al.(116) The HIPEPRAV CRCP module was used to predict crack widths at the temperature observed in the concrete during the crack width measurements. A comparison of the long-term crack width predictions against the measured values is presented in figure 145. Although a fair trend in crack width prediction is observed, all crack widths were largely overpredicted. This overprediction in crack widths had been observed in previous validation efforts.(116) Although Otero et al. proposed a new model for crack width prediction, the use of this model in this study did not show reasonable results. As has been previously reported, the overprediction may be because the CRCP-8 model does not account for the time when the crack forms, but rather depends on the predicted crack spacing, PCC thermal properties, and total shrinkage. As figure 146 illustrates, the drying shrinkage after crack formation depends on the concrete age when the crack occurs. It is believed that the residual drying shrinkage after the crack forms has a large effect on crack width.
Figure 145. Measured versus predicted crack widths, SH-6.
Figure 146. Conceptual representation of residual drying shrinkage effect (adapted from Otero et al.).(116)
The CRCP-8 crack width algorithm could be modified to account for the time of crack formation and residual drying shrinkage. However, such modification is out of the scope for this study, since additional data would be required for calibration and validation.
Only scattered information on crack widths during the early age was reported, and no attempt was made to perform validation with these data. It is believed that crack width information collected from the field sites evaluated in this study will shed some light on the accuracy of early-age crack width predictions.
During the database validation of the CRCP models in HIPERPAV II, good predictions of long-term crack spacing were observed. However, poor early-age crack spacing predictions were obtained. The inaccuracy in the early-age predictions is believed to be due to the nature of the stochastic algorithm used to predict crack spacings combined with the small length of the experimental sections (approximately 60 m) and the typically large crack spacings observed at early ages (from 2 to 8 m). Another possible reason contributing to the overprediction is the lack of information on curing procedures used. In the long term, the crack spacings were much smaller compared to the length of the experimental sections, with much better predictions achieved.
Four field sites were investigated for validation of the HIPERPAV II system:
It is believed that the number of field sites evaluated will provide the minimum level of information necessary to meet the objectives of this effort successfully. However, additional data from field sites in the future could be used for local customization. The objective of this section is to describe the steps performed for validation of both, the JPCP and CRCP pavement sites investigated. The detailed data collection procedures and data reduction are presented in appendix C.
The information collected from the pavement sections in Illinois and Ticuman, Mexico were used for validation of the long-term performance prediction models in HIPERPAV II. In this effort, the reliability of prediction for these two sites was evaluated. Several factors were considered in the validation of the long-term JPCP HIPERPAV II module for each field site. This validation included a comparison of measured and predicted mechanical properties, LTE, and long-term distresses. Validation of each factor is discussed in the following paragraphs.
As previously mentioned in section C.1.1, the Illinois site consisted of several pavement sections with different designs. Design features that were varied included the slab thickness, presence of longitudinal underdrain, and presence of sealant on longitudinal joint. Therefore, each of the sections evaluated was analyzed separately. In addition, to account for the effect of time of day of construction on performance, analyses for placement times at 2 a.m., 8 a.m., 2 p.m., and 8 p.m. were evaluated.
Information on pavement design, materials, and construction procedures was extracted from historical records for this site. Climatic information was extracted from NOAA records for the date of construction of every section for input into HIPERPAV II.
Information on concrete flexural strength is available from records at 14, 28, and 90 days.(103) In addition, the flexural strength almost 16 years after construction was estimated based on the splitting tensile strength obtained from cores extracted during the field visit in 2001. Figure 147 shows the flexural strength for these ages along with the early-age and long-term strength predicted with HIPERPAV II.
Figure 147. Comparison of measured and predicted strength, Illinois site.
In general, although the 90-day strength is slightly underpredicted, a reasonably good prediction of the measured long-term strength is obtained.
A similar analysis was performed for prediction of the elastic modulus. Figure 148 shows the measured modulus of elasticity at 28 days and the one obtained from concrete cores extracted from the field visit in 2001. While the predicted elastic modulus shows an increasing trend, the elastic modulus obtained from field cores in 2001 shows a slight decrease from the 28-day value. A significant difference in predicted versus measured elastic modulus is thus observed after 16 years. Although no further investigation was performed to determine the cause of the unexpected decrease in measured modulus of elasticity, possible reasons for this trend include variability in testing and in data interpretation, since the tests at 28 days and those in the long term were performed by different laboratories.
Figure 148. Comparison of measured and predicted modulus of elasticity, Illinois site.
LTE has been measured on this site at 8, 12, and 15 years of age. Figure 149 shows the measured and predicted LTE for the sections with 216-mm thickness. The predicted LTE is shown as continuous lines for four times of day: 2 a.m., 8 a.m., 2 p.m., and 8 p.m. The fluctuating trend observed is due to seasonal effects. Higher LTE values are observed for the summer months when the joints are tight due to the higher temperatures on those months. Both the approach and leave slab LTE is shown for the tests performed at 15 years. In general, a slight overprediction of LTE is observed for all testing ages.
Figure 149. Comparison of measured versus predicted LTE.
Figures 150 to 152 show typical early-age results for these sections in terms of strength and stress development for the first 72 hours after construction. In these figures, the results for the placement time at 2 p.m. are shown for sections AA, IA, and NA. It is particularly interesting to observe the excessive stresses for section NA. As previously mentioned in section C.1.1, a cement-aggregate mixture base was used under the slab, which is believed to have induced high restraint conditions. In addition, higher air temperatures for that day were observed from historical weather records. These analysis results suggest that the transverse cracking observed from condition surveys on these sections possibly originated in the early age rather than from fatigue cracking.
Figure 150. Early-age analysis for section AA, for placement at 2 p.m.
Figure 151. Early-age analysis for section IA, for placement at 2 p.m.
Figure 152. Early-age analysis for section NA for placement at 2 p.m.
In addition to the early-age analysis, materials characterization, and structural response evaluation above, a comparison of measured versus predicted long-term distresses was made to assess the accuracy of prediction of the HIPERPAV II long-term module. Individual runs were performed at 10 percent, 50 percent, and 90 percent reliability levels.
Figure 153 shows the predicted faulting for sections MA and NA with 191 mm of thickness. These predictions closely follow the observations made during the field visit in 2001, where no apparent faulting was reported.
Figure 153. Predicted faulting for sections MA and NA (191-mm thick).
Figures 154 to 156 show a comparison of measured and predicted midpanel cracking in the transverse direction for the sections evaluated. As previously mentioned in the early-age analysis for this site, it is believed that the amount of transverse cracking present is due to early-age factors rather than to fatigue cracking. The predicted fatigue cracking observed for these sections is minimal compared to the transverse cracking observed from surveys.
Figure 154. Comparison of measured and predicted transverse cracking (sections NA and MA).
Figure 155. Comparison of measured and predicted transverse cracking for sections (IA, JA, KA, LA).
Figure 156. Transverse cracking for section AA, thickness = 241 mm.
Figure 157 shows a comparison of transverse cracking for sections MA and NA with 191-mm thickness. Only one low severity longitudinal crack was observed for section NA. Similar to the transverse cracking present in some of these sections, the longitudinal cracking observed is believed to be due to thermal effects and restraint conditions. No longitudinal cracking was either predicted or observed in the fields for all other sections.
Figure 157. Comparison of measured and predicted longitudinal cracking (sections MA and NA)
No longitudinal cracking was observed for sections AA, IA, JA, KA, and LA. The model predictions for these sections showed no longitudinal cracking, either.
Figure 158 shows the IRI predicted for section NA. The average IRI for all sections for 1994, 1996, 1998, and 2001 also is shown in this figure. Because no data were available for the IRI after construction, an estimated IRI of 1.42 m/km was assumed for this analysis. From this figure, a high scatter in the measured IRI is observed.
Figure 158. Comparison of measured and predicted IRI (section NA).
Similar to the Illinois site, a comparison of the measured and predicted mechanical properties, structural response, and long-term performance distresses was made for the Ticuman bypass.
Figure 159 shows a comparison of the measured and predicted third-point flexural PCC strength for the Ticuman bypass. Flexural strength tests were performed at 1, 3, 7, 14, and 28 days of age. The long-term flexural strength value at 8 years of age was estimated from compressive and indirect tensile strength tests results obtained from cores extracted in the 2001 field evaluation. In general, a rather good prediction of the PCC strength was achieved.
Figure 159. Comparison of measured versus predicted flexural strength, Ticuman, Mexico.
Figure 160 shows a comparison of the measured versus predicted modulus of elasticity. The measured values correspond to 28 days and 8 years of age. A significant underprediction of the elastic modulus at 8 years of age is observed. While the predicted modulus of elasticity shows an increase of 12 percent from 28 days to 8 years, the measured value shows an increase of 55 percent. This finding is opposite to the one observed for the Illinois site, where the elastic modulus was overpredicted.
Figure 160. Comparison of measured versus predicted modulus of elasticity, Ticuman, Mexico.
LTE tests results are available for two instances: during the first few months after construction, and at 8 years of age. These results are compared to the model predictions in figure 161. As previously mentioned in section C.1.2.2, the low LTE test results observed in 1993 are attributed to the fact that some of the joints had not cracked, leading to wider joint widths and poor load transfer. In comparison, the LTE tests results at 8 years of age show a high LTE. Compared to the LTE predicted with HIPERPAV II, the LTE predicted is higher than the measured in 1993 and slightly lower than the one measured in 2001.
Figure 161. Comparison of measured versus predicted LTE, Ticuman, Mexico.
A total of 54 factorial runs were considered for analysis of the distresses at the Ticuman bypass. This factorial was to account for the variability on thickness observed at this site and the different times of placement. In addition, the factorial was expanded to account for different levels of reliability in the long-term analyses.
For the early-age scenarios, three different thicknesses were considered: 203, 229, and 254 mm. Each one of these scenarios was evaluated for placement times at 8 a.m., 2 p.m., and 6 p.m. For the long-term scenarios, three levels of reliability were considered: 10 percent, 50 percent, and 90 percent. Each strategy was analyzed under two conditions: curling stresses computed from thermal gradient at time of loading only, and curling stresses computed for the thermal gradient at time of loading plus built-in curling present at PCC set time.
Figure 162 shows the effect of built-in curling for longitudinal cracking on placement times at 10 a.m. and 6 p.m. For the 10 a.m. placement, the gradient at time of loading with no gradient built-in at set produces higher cracking than the condition with built-in curling. In contrast, the placement at 6 p.m. shows the opposite trend, with the condition with built-in curling showing higher longitudinal cracking. Further investigation into this effect shows that the slabs placed at 10 a.m. set with a positive built-in curling, while the slabs placed at 6 p.m. set with a negative built-in curling. In addition, the most critical loading condition in the long-term for both cases is found to be at 2 p.m., when the slab is being subjected to a positive thermal gradient. For the 10 a.m. placement, the positive thermal gradient built-in at set counteracts the positive thermal gradient during loading and thus reduces the total tensile stresses at the slab bottom for that condition. The opposite occurs for the placement at 6 p.m., where the negative built-in gradient adds to the positive thermal gradient at the time of loading, effectively increasing the stresses for this condition. Because the relaxation occurring on the curling shape of the slab with time, it is believed that the actual stress state at time of loading lies somewhere between these two conditions.
Figure 162. Analysis for 229-mm slab at different construction times and built-in gradient conditions, Ticuman bypass.
Faulting was measured for the Ticuman bypass on the field visit in 2001. Figure 163 shows a comparison of measured and predicted faulting for this site. The average measured faulting of 1.0 mm is lower than the faulting predicted at 50 percent reliability and above the faulting predicted at 10 percent reliability.
Figure 163. Comparison of measured versus predicted joint faulting, Ticuman, Mexico.
Figures 164 and 165 show the observed and predicted cracking in both, the transverse and longitudinal directions respectively. The amount of both, transverse and longitudinal cracking observed for this site is between the cracking predicted at 50 percent and 90 percent reliability.
Figure 164. Comparison of measured versus predicted transverse cracking, Ticuman, Mexico.
As previously mentioned in section C.1.2.3, the significant amount of cracking is attributed to the lack of maintenance and the excessive traffic loading on this road.
Figure 165. Comparison of measured versus predicted longitudinal cracking, Ticuman, Mexico.
Figure 166 show a comparison in terms of measured and predicted serviceability index. PSI measurements with Mays meter have been performed in 1993 just after construction, in 1995, and in 2001. The PSI in 2001 (after 8 years) is just above the PSI predicted at 90 percent reliability. However, this condition was also observed in 1995 (2 years after construction). While the predicted PSI shows a gradual decrease with time, the PSI measurements show a significant drop for the first few years, and then this condition is maintained.
Figure 166. Comparison of measured versus predicted present serviceability index, Ticuman, Mexico.
In summary, it can be concluded that reasonable predictions were obtained in terms of long-term performance for both field sites. Although limited, this validation was done with extensive and quality data on pavement design, materials, climatic, and construction inputs. It is recommended that continued validation of the models be made as more sites are available with enough information on materials characterization and construction.
This section presents the data reduction and analysis of the information collected for the CRCP instrumentation in Fort Worth, TX. Measured responses in terms of steel stresses, crack widths, and crack spacings for this site and those predicted with HIPERPAV II also are presented.
As documented in appendix C, a slab pushoff test was performed to determine the restraint conditions at the slab/subbase interface. Figure 167 shows a plot of the measured restraint values. The restraint curve observed was fitted with a nonlinear restraint power function with ultimate displacement of 3.8 mm, critical restraint stress of 58.6 kPa, and power coefficient of 3.5. The resulting fit is also shown in figure 167.
Figure 167. Restraint at the slab/subbase interface.
PCC set time is an important parameter, because the development of many concrete properties depends on it. It is anticipated that set time from laboratory testing and set time in the field will differ, since the aggregate matrix and environmental conditions are different. For determining PCC set time in the field, information from three sources was considered: laboratory testing, pulse velocity testing, and analysis of PCC strains from an unconfined specimen.
PCC set time tests were performed under laboratory conditions with materials collected from the Fort Worth, TX, CRCP site. The procedure and results from these tests are presented in section C.9. Under laboratory conditions, initial and final set times of 4.0 hours and 4.9 hours were obtained, respectively. Although attempts were made to maintain the temperature of the sample under the same environmental conditions than those observed in the field, slight differences were noted. Therefore, the equivalent time at set was obtained to determine the set time at 20 °C and determine the set time in the field corresponding to that equivalent time. Using the Arrhenius relationship for equivalent time, initial and final set times at 20 °C would occur at 8.8 hours and 11.3 hours, respectively. For the temperatures observed in the field, initial and final set for those equivalent ages correspond to 3.5 hours and 4.4 hours real time, respectively.
To corroborate the lab results, the pulse velocity readings were analyzed. For CRCP, pulse velocity time is affected by the presence of steel in the concrete. However, the rate of change of wave travel time still depends on stiffening of the concrete and can be related to set time. In figure 168, a significant decrease in wave travel can be observed between 2.5 and 5.0 hours, which indicates a significant stiffening of the concrete and initial set time occurrence. The estimated set times are indicated in this figure to be within the transition zone between the plastic and hardened state of concrete.
Figure 168. Determination of set time with pulse velocity equipment.
Analysis of the PCC strains in an unconfined concrete specimen also can be used to estimate PCC set time. Figure 169 shows a plot of observed PCC strain versus PCC temperature for an unconfined field concrete specimen instrumented with an embedded strain gage. When the strain gage is initially embedded in the concrete cylinder, relative strain readings do not follow a definitive trend with change in temperature, as the concrete is still plastic. As time progresses and the concrete stiffens, the strains tend to follow the temperature changes in the concrete. The transition, as observed in figure 169, occurs between 2.1 and 4.5 hours, corresponding to the set times from laboratory testing. After this time, the strains in the specimen follow a trend with temperature, fluctuating between contraction and expansion cycles.
Figure 169. PCC strains during PCC set time as a function of temperature changes.
It most be noted that during construction, joint sawing of the instrumented slab was performed shortly after the slab was strong enough to withstand the Soff-Cut equipment. This occurred at 3.25 hours of age, which is before the measured final set time of 4.4 hours as determined from laboratory testing. According to the pulse velocity readings and the observations of joint sawing in the field, it is evident that initial set time for the instrumented slab occurred approximately at 3.0 hours after placement.
The CTE was determined with two different procedures: laboratory testing according to AASHTO TP-60-00 and PCC strain analysis of a field unconfined concrete cylinder as a function of temperature. From laboratory testing, a CTE of 7.48 * 106 m/m/°C was reported. From the analysis of strains versus temperature, a CTE of 6.6 * 106 m/m/°C is determined (see figure 170). A slight difference is observed between testing procedures. It is believed that the difference in relative humidity conditions at which the CTE for each procedure was determined may have contributed to the difference in CTE.
Figure 170. Determination of PCC CTE with the use of PCC strains on an unconfined concrete cylinder.
Validation of the CRCP HIPERPAV II module required collection of information on all the input parameters. With the above information, the CRCP monitored section was analyzed with the CRCP HIPERPAV II module to compare the measured and predicted cracking characteristics.
D.2.2.1.4.1 Analysis of Steel Strains
Steel strains were evaluated at different distances from the crack, as observed in figure 171.
Figure 171. Steel strains at various distances from the crack location.
Note from this figure that steel strain increases at lower temperatures and also as a function of time. This last trend possibly is due to the increase in PCC drying shrinkage. Figure 172 shows a plot of steel strains along the slab length for the strain peaks observed at 21.0, 44.8, and 68.5 hours. The strain plotted is the average strain of the two strain gages installed at each distance.
Figure 172. Steel strain along the slab length at different ages.
From figure 172, the bond development length can be identified; this is the slab segment from the crack location for which the steel strain is variable. In this case, a bond development length of approximately 279 mm is observed for these ages.
D.2.2.1.4.2 Analysis of Concrete Strains
Concrete strains were analyzed to determine their influence on the stress development in the steel. Figure 173 shows the strains observed in the concrete at different distances from the crack. The time of crack formation can be clearly identified by the sharp increase in strains on the gages at 127 mm from the crack. The crack is observed to occur close to 12 hours after construction, which also coincides with the significant development in steel strain at the crack seen in figure 171.
Figure 173. Concrete strains at middepth along slab length.
Comparing the individual ages of 21.0, 44.8, and 68.5 hours with steel strains, the average concrete strains for those ages are 4.4 * 10-6 m/m, −26.7 * 10-6 m/m, and −40.6 * 10-6 m/m. A negative trend in PCC strain is observed, which can be attributed to the decreasing temperature in the concrete and to drying shrinkage. The drying shrinkage observed on an unrestrained PCC cylinder in the field after subtracting temperature effects is presented in figure 174.
Figure 174. Drying shrinkage observed in the field on an unrestrained PCC cylinder.
Figure 175 shows the steel strains in the concrete and in the steel at 68.5 hours after construction. The strains in the concrete appear almost constant along the slab at approximately 40 microstrains. The strains in the steel also appear within the same order of magnitude along most of the slab, except near the crack, where they increase significantly.
Figure 175. Strains in concrete and steel at 68.5 hours after construction.
Assuming a strain level in the steel similar to the one observed in the concrete at midslab and integrating the strains along the slab length, the displacement of concrete and steel is plotted in figure 176.
Figure 176. Displacements in steel and concrete along slab length at 68.5 hours.
D.2.2.1.4.3 Evaluation of Stress and Bond Development Length
The bond development length predicted with HIPERPAV II for this site for the first 3 days of age varied from 0.56 to 0.79 m. The bond development length predicted is significantly higher than the measured one of approximately 279 mm.
From the strains measured, the steel stress is computed and is shown in figure 177 for the age of 68.5 hours. The steel stress at the crack is 246.8 MPa. The steel stress computed by HIPERAV for that age is 392.3 MPa at the crack location. The predicted stress is also shown in this figure. It is believed that the difference in predicted and measured bond development length and steel stress is related to the limitations in the bond-slip relationships assumed in the CRCP-8 model. These limitations have been previously identified by Palmer et al.(120)
Figure 177. Steel stress along the slab at 68.5 hours.
D.2.2.1.4.4 Analysis of Crack Widths
Crack width data were evaluated as a function of pavement age and also as a function of pavement depth. Table 87 shows the crack widths observed during the first 3 days after construction for the top, middle, and bottom of the slab.
| Age | Measured Top | Measured Middle | Measured Bottom | Predicted Middle |
|---|---|---|---|---|
| Day 1 | 0.005 | 0.003 | 0.002 | 0.027 |
| Day 2 | 0.009 | 0.004 | - | 0.042 |
| Day 3 | 0.010 | 0.005 | - | 0.050 |
A large discrepancy in measured and predicted crack width is observed. The predicted crack width is overpredicted by a factor of 5 compared to the average crack width at the top, and by a factor of 10 compared to the crack width measured at middepth.
Crack width tends to increase as a function of time. In addition, larger crack widths are observed at the top of the slab compared to middepth and bottom; this is attributed to increased drying shrinkage at the slab surface. Crack width measurements were obtained at the slab edge. The crack width at the steel location was not measured. It is believed that, due to the steel restraint, the crack width near the steel is smaller than those reported here and therefore increasing the overprediction.
The limitations in crack width prediction have been discussed in section D.1.2.10. The differences in steel stress and bond development length found in this analysis also are believed to contribute to the overprediction of crack widths.
D.2.2.1.4.5 Crack Spacing Validation Results
Table 88 shows a comparison of measured versus predicted crack spacings for the first 3 days after construction. Although the measured crack spacings show a slight decreasing trend, the predicted crack spacing is constant for the early ages and is reduced to an average crack spacing of 1.55 m after 1 year. However, the average crack spacing predicted of 3.32 m matches very closely the measured average crack spacing of 3.59 m at 3 days of age. The predicted crack spacing at 1 year for this site is 1.55 m.
| Age | Measured (m) | Predicted (m) |
|---|---|---|
| Day 1 | 4.36 | 3.32 |
| Day 2 | 3.99 | 3.32 |
| Day 3 | 3.60 | 3.32 |
| After construction traffic | - | 2.71 |
| 1 year | - | 1.55 |
The crack spacing distributions are presented in figure 178. Although a reasonably good fit for the crack spacings observed after 3 days is achieved, it is believed that the bond slip relationships in the CRCP-8 program must be further investigated to predict steel stresses and crack widths accurately.
Figure 178. Measured versus predicted crack spacing at 3 days of age, Fort Worth, TX.
This section presents the data reduction and analysis of the information collected for the CRCP instrumentation in South Dakota. Measured responses in terms of steel stresses, crack widths, and crack spacings for this site and those predicted with HIPERPAV II also are presented.
Although no pushoff test was performed for this site, the subbase restraint conditions were observed to be typical of an unbonded aggregate base. Default values for this subbase type were selected.
For determination of PCC set time in the field, information from two sources was considered: laboratory testing and analysis of PCC strains from an unconfined specimen.
PCC set time tests were performed under laboratory conditions with materials collected from the South Dakota CRCP site. The procedure and results from these tests are presented in appendix C. Under laboratory conditions, initial and final set times of 5.1 hours and 6.6 hours were obtained, respectively. However, given the inability to relate laboratory set time to the time set occurred in the field for the South Dakota site, set time was identified with the analysis of PCC strains from an unconfined specimen. With this procedure, a set time of approximately 6 hours was measured.
The equivalent time at set was obtained to determine the set time at 20 °C and determine the set time in the field corresponding to that equivalent time. Using the Arrhenius relationship for equivalent time, initial and final set times at 20 °C would occur at 4.9 hours and 6.4 hours, respectively. For the temperatures observed in the field, set times for those equivalent ages correspond to approximately 4.0 hours and 5.0 hours in real time, respectively.
Analysis of the PCC strains in an unconfined concrete specimen used can also be to estimate PCC set time. Figure 179 shows a plot of observed PCC strain versus PCC temperature for an unconfined field concrete specimen instrumented with an embedded strain gage. When the strain gage is initially embedded in the concrete cylinder, relative strain readings do not follow a definitive trend with change in temperature, as the concrete is still plastic. As time progresses and the concrete stiffens, the strains tend to follow the temperature changes in the concrete. The transition, as observed in figure 179, occurs between 2.8 hours and 6.5 hours. The initial and final set times from laboratory tests fall within this range. After this time, the strains in the specimen follow a trend with temperature, fluctuating between contraction and expansion cycles.
Figure 179. PCC strains during PCC set time as a function of temperature changes.
According to the above analysis, the initial and final set times of 4.0 hours and 5.0 hours, respectively, were used for analysis.
The CTE was determined with two different procedures: laboratory testing according to AASHTO TP-60-00 and PCC strain analysis of a field unconfined concrete cylinder as a function of temperature. From laboratory testing, a CTE of 10.9 * 106 m/m/°C was reported. From the analysis of strains versus temperature, a CTE of 11.6 * 106 m/m/°C is determined (see figure 180). A slight difference is observed between testing procedures. It is believed that the difference in relative humidity conditions at which the CTE for each procedure was determined may have contributed to the difference observed.
Figure 180. Determination of PCC CTE with the use of PCC strains on an unconfined concrete cylinder.
Validation of the CRCP HIPERPAV II module required collecting information on all the input parameters. With the above information, the CRCP monitored section was analyzed with the CRCP HIPERPAV II module to compare the measured and predicted cracking characteristics.
D.2.2.2.4.1 Analysis of Steel Strains
Steel strains were evaluated at different distances from the crack as observed in figure 181. Gages were installed on two different bars and are identified as either "A" or "B" in the figure. The crack occurred 108 mm from the expected location, thus shifting the location of the gages by that amount. In addition, a second crack was noticed later 356 mm from midslab, leaving the gages at that location at that distance from the new crack. Crack occurrences can be identified clearly by the sharp change in strain at approximately 19, 34, and 40 hours from placement.
Similar to the Fort Worth, TX, site, the strain gages closer to the crack recorded higher strains than those far from the crack. However, the gages at 356 mm from the second crack did not show a significant increase in strain after crack occurrence, as would be expected. However, it most be noted that, for the Fort Worth, TX, site, the bond development length was smaller than 356 mm. Therefore, it is possible that the bond development length for the second crack could have been less than 356 mm.
Figure 181. Steel strains at various distances from the crack location.
Figure 182 shows a plot of steel strains along the slab length for the strain peaks observed at 20.3, 43.2, and 67.2 hours. The strain plotted is the average strain of the two strain gages installed at each distance.
Figure 182. Steel strain along the slab length at different ages.
From figure 182, the bond development length can be identified; this is the slab segment from the crack location for which the steel strain is variable. In this case, a bond development length of approximately 0.5 to 0.6 m is observed for these ages. Extrapolating the steel strains to estimate the strain at the crack yields 550 microstrains at 20.3 hours and 1200 to 1500 microstrains for the other two ages.
D.2.2.2.4.2 Analysis of Concrete Strains
Concrete strains were analyzed to determine their influence on the stress development in the steel. Figure 183 shows the strains observed in the concrete at different distances from the crack. The time of crack formation can be identified clearly by the sharp increase in strains on the gages at 235 mm from the crack. The cracks are observed to occur close to 19, 34, and 40 hours after construction, which also coincide with the significant development in steel strain seen in figure 181.
Figure 183. Concrete strains at middepth along slab length.
In the above figure, the concrete strains at 20.3, 43.2, and 67.2 hours are compared with the steel strains; the average concrete strains for those ages are 0.2 * 10-6, −34.7 * 10-6, and −44.3 * 10-6. Similar to the Fort Worth, TX, site, a negative trend in PCC strain is observed. The drying shrinkage observed on an unrestrained PCC cylinder in the field after subtracting temperature effects is presented in figure 184.
Figure 184. Drying shrinkage observed in the field on an unrestrained PCC cylinder.
Figure 185 shows the steel strains in the concrete and in the steel at 67.2 hours after construction. The strains in the concrete appear almost constant along the slab at approximately 40 microstrains. The strains in the steel also appear within the same order of magnitude along most of the slab, except near the crack, where they increase significantly.
Figure 185. Strains in concrete and steel at 67.2 hours after construction.
D.2.2.2.4.3 Evaluation of Stress and Bond Development Length
A comparison of measured and predicted bond development lengths for this site is presented in figure 186. The bond development length predicted with HIPERPAV II for this site for the first 3 days of age varied from 0.48 to 0.66 m. A rather good prediction is observed on the bond development length for this site.
Figure 186. Comparison of measured and predicted bond development length.
From the strains measured, the steel stress is computed and is shown in figure 187 for the age of 67.2 hours.
Figure 187. Steel stress along the slab at 67.2 hours.
In general, a rather good prediction of stresses at the steel were observed for this site.
D.2.2.2.4.4 Analysis of Crack Widths
Crack width data were evaluated as a function of pavement age and also as a function of pavement depth.
Table 89 shows the crack widths observed during the first 3 days after construction for the top, middle, and bottom of the slab.
| Age | Measured Top | Measured Middle | Predicted Middle |
|---|---|---|---|
| Day 1 | - | 0.002 | 0.018 |
| Day 2 | - | 0.008 | 0.025 |
| Day 3 | 0.010 | 0.008 | 0.029 |
A large discrepancy in measured and predicted crack width is observed. The predicted crack width is overpredicted by a factor of three compared to the average crack width measured at middepth.
Similar trends to the Fort Worth, TX site in terms of increasing crack widths with time also are observed for this site. Crack width measurements were obtained at the slab edge. The crack width at the steel location was not measured. It is believed that due to the steel restraint, the crack width near the steel is smaller than those reported here, therefore increasing the overprediction.
D.2.2.2.4.5 Crack Spacing Validation Results
Table 90 shows a comparison of measured versus predicted crack spacings for the first 3 days after construction. Although the measured crack spacings show a slight decreasing trend, the predicted crack spacing is constant for the early ages and is reduced to an average crack spacing of 1.25 m after 1 year. However, the average crack spacing predicted of 3.47 m matches very closely the measured average crack spacing of 3.08 m at 3 days of age. The predicted crack spacing at 1 year for this site is 1.25 m.
| Age | Measured (m) | Predicted (m) |
|---|---|---|
| Day 1 | 5.33 | 3.47 |
| Day 2 | 3.32 | 3.47 |
| Day 3 | 3.08 | 3.47 |
| 1 year | - | 1.25 |
The crack spacing distributions are presented in figure 188. Although a reasonably good fit for the crack spacings observed after 3 days is achieved, the predictions for earlier ages do not follow the measurements in the field. Inaccuracy to match earlier ages also was reported on the validation for the Fort Worth, TX, site.
Figure 188. Measured versus predicted crack spacing at 3 days of age, Sioux Falls, SD.
Improvements to the concrete pavement temperature prediction, drying shrinkage, and creep-relaxation models were investigated in this study. Results of the validation efforts for this models are presented below.
Over the course of its development, HIPERPAV has employed two different temperature prediction models. Originally, the temperature prediction model was a transient two-dimensional FEM. However, this procedure had proven to require excessive solution times. The model has since been replaced by a one-dimensional finite-difference approach, which allows quicker execution without a compromise in accuracy. However, the accuracy of the finite-difference model needed to be verified by comparison with field data. Verification of the temperature predictions with the improved model is presented in appendix E.
Using the field data collected from the five early-age HIPERPAV I field sites, the calibration factor (Deff) for the Baźant-Panula shrinkage model could be determined.(121) The vibrating wire strain gages placed at midslab 25 mm from the pavement surface and 152 mm from the edge, in the transverse direction, were used for the calibration. The restraint strains induced by the subbase would be small at this location, allowing the drying shrinkage strains to be modeled. Calibration results are presented below.
All of the slabs in field were cured with white curing compound (![]() 2 = 1.1), and the cement types varied between Type I and Type II (
2 = 1.1), and the cement types varied between Type I and Type II (![]() 1 = 1 and 0.85). The coarse aggregate used at the sites had a relatively low CTE. In Minnesota, limestone and gravel were mixed. In Nebraska and Texas, limestone was used. In North Carolina, slate was used. In Arizona, a gravel basalt was used. The Baźant-Panula shrinkage model was developed for similar aggregate types to those found in the HIPERPAV I sites, so relatively good fits resulted. Fly ash content was not included in the mix components input to the model, since it does not greatly influence concrete shrinkage.(37)
1 = 1 and 0.85). The coarse aggregate used at the sites had a relatively low CTE. In Minnesota, limestone and gravel were mixed. In Nebraska and Texas, limestone was used. In North Carolina, slate was used. In Arizona, a gravel basalt was used. The Baźant-Panula shrinkage model was developed for similar aggregate types to those found in the HIPERPAV I sites, so relatively good fits resulted. Fly ash content was not included in the mix components input to the model, since it does not greatly influence concrete shrinkage.(37)
The Deff values determined for each site are listed in table 91. Deff for Nebraska is 0.6; this is the highest value. The Nebraska mix was not typical; more sand/fine aggregate was used than coarse aggregate. Averaging all of the sites yields an average Deff of 0.45 with a standard deviation of 0.09. A Deff of 0.50 has also been reported by Persson, and it is used to account for specimen shape in HIPERPAV II drying shrinkage calculations.(36)
| Site Location | Deff Without Fly Ash |
|---|---|
| Arizona | 0.35 |
| Minnesota | 0.40 |
| Nebraska | 0.60 |
| North Carolina | 0.45 |
| Texas | 0.46 |
The fit of the Baźant-Panula shrinkage model to these five field sites is shown in the following plots (figures 189-193).
Figure 189. Drying shrinkage results for North Carolina site.
Figure 190. Drying shrinkage results for Texas site.
Figure 191. Drying shrinkage results for Arizona site.
Figure 192. Drying shrinkage results for Nebraska site.
Figure 193. Drying shrinkage results for Minnesota site.
To calibrate the size factor Deff for CRCP, 28-day drying shrinkage predictions from the Baźant-Panula model were matched to the experimentally measured drying shrinkage values taken in concrete placed on SH-6 in winter and summer.(106) Limestone was the coarse aggregate. At 28 days, the drying shrinkage was 171 me in the summer and 165 ![]()
![]() in the winter. These values were matched using an Deff of 0.2. A comparison of drying shrinkage predictions at different ages are shown in figures 194 and 195 as a function of Deff. The drying shrinkage measured for the Houston, TX, sections is presented in these figures with its corresponding calibration factor.
in the winter. These values were matched using an Deff of 0.2. A comparison of drying shrinkage predictions at different ages are shown in figures 194 and 195 as a function of Deff. The drying shrinkage measured for the Houston, TX, sections is presented in these figures with its corresponding calibration factor.
Figure 194. Calibration of drying shrinkage factor for Houston, TX, sections constructed in summer.
Figure 195. Calibration of drying shrinkage factor for Houston, TX, sections constructed in winter.
Attempts to validate the creep model based on the extended Triple Power Law presented in appendix B were made. However, preliminary sensitivity analyses showed that, in some instances, tensile stresses were being overpredicted significantly as compared to results from the previous validation efforts of the current prediction models in HIPERPAV II. Possible reasons for inaccuracy are:
Further work is required to validate this method properly. It is believed that, after calibrated and validated, it will prove helpful in properly determining creep and relaxation effects for stress prediction, built-in curling prediction, and possibly determining the curled slab shape.