U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| TECHBRIEF |
| This techbrief is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-14-030 Date: February 2014 |
Publication Number: FHWA-HRT-14-030 Date: February 2014 |
PDF files can be viewed with the Acrobat® Reader®
FHWA Publication No. of this TechBrief: FHWA-HRT-14-030 |
This document is a technical summary of the unpublished Federal Highway Administration report, Lightweight Concrete: Development of Mild Steel in Tension (FHWA-HRT-14-029) available through the National Technical Information Service, www.ntis.gov.
NTIS Accession No. of the report covered in this TechBrief: PB2014-100627
Objective
Concrete with a unit weight between that of traditional lightweight concrete (LWC) and normal weight concrete (NWC) is not covered in the American Association of State Highway Transportation Officials (AASHTO) LRFD Bridge Design Specifications.(1) This research program includes a significant number of bond strength tests on this type of concrete. The results from this research project are included in a database that covers a broader range of unit weights in order to determine trends for LWC as a function of unit weight. New design expressions for the development length of mild steel in tension are proposed for LWC that include a modification factor for LWC based on unit weight.
Introduction
Much of the fundamental basis for the current lightweight concrete provisions in the AASHTO LRFD Bridge Design Specifications is based on research of LWC from the 1960s. (See references 1–5.) The LWC that was part of this research used traditional mixes of coarse aggregate, fine aggregate, portland cement, and water. Broad-based advancement in concrete technology over the past 50 years has given rise to significant advancements in concrete mechanical and durability performance. Research during the past 30 years, including the recent NCHRP studies on different aspects of high-strength concrete, has resulted in revisions to the AASHTO LRFD Bridge Design Specifications to capitalize on the benefits of high-strength, NWC. However, as described by Russell, many of the design equations in the AASHTO LRFD Bridge Design Specifications are based on data that do not include tests of LWC specimens, particularly with regard to structural members with compressive strengths in excess of 6 ksi (41 MPa).(6)
The Federal Highway Administration (FHWA) at the Turner-Fairbank Highway Research Center (TFHRC) has executed a research program investigating the performance of LWC with concrete compressive strengths in the range of 6 to 10 ksi (41 to 69 MPa) and equilibrium densities between 0.125 to 0.135 kcf (2,000 to 2,160 kg/m3). The research program used LWC with three different lightweight aggregates that are intended to be representative of those available in North America. The program included tests from 27 precast/prestressed LWC girders to investigate topics including transfer length and development length of prestressing strand, time-dependent prestress losses, and shear strength of LWC. The development and splice length of mild steel reinforcement used in girders and decks made with LWC was also investigated using 40 reinforced concrete (RC) beams. While much of the research program focused on structural behavior, it also included a material characterization component wherein the compressive strength, elastic modulus, and splitting tensile strength of the concrete mixes used in the structural testing program were assessed. One key outcome of the research program is to recommend changes to the AASHTO LRFD Bridge Design Specifications relevant to LWC.
This document summarizes the results of bond strength tests conducted on RC beams. The bond strength of LWC tested in this study is included in a database of tests on LWC and NWC that was collected from test results available in the literature. This document also summarizes the database and the analysis of database. Design expressions in ACI 318-11 and the ACI Committee 408 report are compared to the database.(7,8) Potential revisions to the AASHTO LRFD Bridge Design Specifications relating to development length of mild steel in tension are presented.
LWC Splice Beam Tests Conducted at TFHRC
LWC Mix Designs
The Expanded Shale, Clay, and Slate Institute (ESCSI) assisted FHWA in obtaining LWC mixes that had been used in production. One of the criteria for this research project was to use lightweight aggregate sources that were geographically distributed across the United States. Additional selection criteria included mixes using a large percentage of the coarse aggregate as lightweight coarse aggregate, mixes using natural sand as the fine aggregate, and mixes with a target equilibrium density between 0.125 and 0.135 kcf (2,000 and 2,160 kg/m3). The concrete density needed to be in the range of densities not currently covered by the AASHTO LRFD Bridge Design Specifications.(1)
Three mix designs were selected with a design compressive
strength greater than or equal to
6.0 ksi (41.4 MPa) to represent concrete that could be used for bridge girders.
Another mix design was selected that had a design compressive strength less
than 6.0 ksi (41.4 MPa) to represent concrete that could be used for a bridge
deck. The mix designs selected are shown in table 1. Each uses partial
replacement of the coarse aggregate with lightweight aggregate to achieve their
reduced unit weight. The lightweight aggregates in the mixes were Haydite, an
expanded shale from Ohio, Stalite, an expanded slate from North Carolina, and
Utelite, an expanded shale from Utah. The normal weight coarse aggregate was
No. 67 Nova Scotia granite. Natural river sand was used as the fine aggregate. Type
III portland cement was used to obtain the high early strengths typically
required in high-strength precast girders. Admixtures included a water reducer,
an air entrainer, and a high-range water reducer.
Table 1. Selected concrete mix designs.
|
Cast Date |
Haydite Girder (HG) |
Stalite Girder (SG) |
Utelite Girder (UG) |
Stalite Deck (SD) |
|
Design 28-Day Strength (ksi) |
6.0 |
10.0 |
7.0 |
4.0 |
|
Design Release Strength (ksi) |
3.50 |
7.5 |
4.2 |
— |
|
Target Unit Weight (kcf) |
0.130 |
0.126 |
0.126 |
0.125 |
|
Water/Cementitious Materials Ratio |
0.36 |
0.31 |
0.34 |
0.43 |
— Indicates no value was recorded.
1.0 ksi = 6.89 MPa
0.001 kcf = 16.01 kg/m3
Experimental Program
The experimental program consisted of testing to failure 40 splice beam specimens. Key test parameters include the lightweight aggregate, the bar size (#4, #6, #8, and #11), the splice length (short versus long ℓs/db ratio), and the presence of transverse reinforcement (as stirrups). Twelve splice beam designs were developed to evaluate the effect of the key parameters. A set of 12 splice beams was cast for each of three different concrete mixes intended to represent typical LWC for girders. Table 2 gives the nominal beam dimensions and reinforcement size and splice length for the 12 different specimens using girder concrete mixes. Four additional splice beam specimens were developed for a concrete mix intended to represent typical LWC for bridge deck applications. The nominal beam dimensions and reinforcement details for the specimens using the deck concrete mix are given in table 3.
Table 2. Nominal splice beam dimensions—girder concrete mixes.
|
Beam |
Bar Size |
Splice Length (inch) |
No. of Stirrups† |
Nominal Cross Section Dimensions (width × height) (inch) |
Beam Length (inch) |
Support Spacing (inch) |
|
1 |
#6 |
16 |
0 |
9 × 18 |
168 |
60 |
|
2 |
#6 |
24 |
0 |
9 × 18 |
168 |
60 |
|
3 |
#6 |
16 |
2 |
9 × 18 |
168 |
60 |
|
4 |
#6 |
24 |
3 |
9 × 18 |
168 |
60 |
|
5 |
#8 |
24 |
0 |
12 × 18 |
180 |
72 |
|
6 |
#8 |
32 |
0 |
12 × 18 |
180 |
72 |
|
7 |
#8 |
24 |
3 |
12 × 18 |
180 |
72 |
|
8 |
#8 |
32 |
4 |
12 × 18 |
180 |
72 |
|
9 |
#11 |
32 |
0 |
18 × 18 |
192 |
84 |
|
10 |
#11 |
48 |
0 |
18 × 18 |
192 |
84 |
|
11 |
#11 |
32 |
4 |
18 × 18 |
192 |
84 |
|
12 |
#11 |
48 |
6 |
18 × 18 |
192 |
84 |
† #3 bar at 8-inch (203.2-mm) spacing.
1.0 inch = 25.4 mm
Table 3. Nominal splice beam dimensions—deck concrete mix.
|
Beam |
Bar Size |
Splice Length (inch) |
No. of Stirrups |
Nominal Cross Section Dimensions (width × height) (inch) |
Beam Length (inch) |
Support Spacing (inch) |
|
1 |
#4 |
12 |
0 |
9 × 18 |
168 |
60 |
|
2 |
#4 |
16 |
0 |
9 × 18 |
168 |
60 |
|
3 |
#6 |
12 |
0 |
9 × 18 |
168 |
60 |
|
4 |
#6 |
16 |
0 |
9 × 18 |
168 |
60 |
1.0 inch = 25.4 mm
The splice beams had three adjacent bottom-cast splices. The specimens were inverted prior to testing so that the splices were at the top face, and then simply supported with ends cantilevered. Equal loads were applied at each end resulting in a constant moment region between the supports. Stirrups were placed in the cantilevered ends to prevent a shear failure. Eighteen beams had stirrups spaced along the splice. A sketch of the splice beams is shown in figure 1.
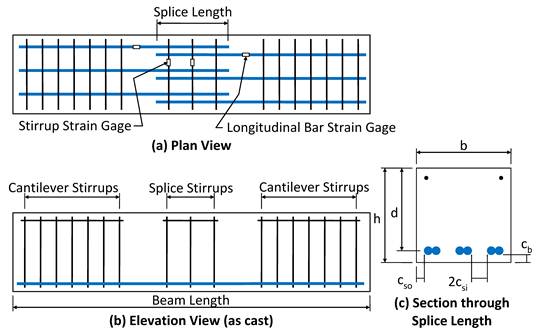
Figure 1. Illustration. Splice beam specimen dimensions.
Material Properties
The girders were fabricated at a concrete precasting plant in Mobile, AL. The fabricator was asked to prescriptively produce the concrete mixes, without trying to adjust them for target strengths or unit weight. This was intended to remove batch-to-batch variations as a variable in the study. The lightweight aggregates were stored in three piles at the plant and watered continuously using a sprinkler on each pile.
Compression tests were performed on 4-by-8-inch (102-by-203-mm) cylinders. The indirect tensile strength was measured on 4-by-8-inch (102- by-203-mm) cylinders using the splitting tensile test. Density measurements were made to determine the air-dry density of cylinders used for compression testing. Average compressive strength, splitting tensile strength, and air-dry unit weight for each concrete mix are given in table 4.
Table 4. Mean concrete properties from tests on 4-by-8-inch (102-by-203-mm) cylinders.
|
Concrete Mix |
Compressive Strength, 28 Day (ksi) |
Compressive Strength, Test Day (ksi) |
Splitting Tensile Strength (ksi) |
Air-Dry Density (kcf) |
|
HG |
8.0 |
9.8 |
0.685 |
0.133 |
|
SG |
10.6 |
12.2 |
0.716 |
0.126 |
|
UG |
9.6 |
10.9 |
0.764 |
0.131 |
|
SD |
5.7 |
7.6 |
— |
0.138 |
— Indicates no value was recorded.
1.0 ksi = 6.89 MPa
0.001 kcf = 16.01 kg/m3
The reinforcing bars were ASTM A615, Grade 60.(9) The mechanical properties were tested under displacement control in a 100 kip (445 kN) testing machine. Strain was measured with an 8-inch (203-mm) extensometer. The yield strength was determined using the 0.2 percent offset method. The average yield strength and the ultimate strength of the two bars in each size tested are given in table 5.
Table 5. Reinforcing bar properties.
|
Bar Measurement |
Nominal Bar Size |
|||
|
#4 |
#6 |
#8 |
#11 |
|
|
Nominal Diameter (inch) |
0.50 |
0.75 |
1.00 |
1.41 |
|
Yield Strength† (ksi) |
65.7 |
67.6 |
73.8 |
66.5 |
|
Ultimate Strength (ksi) |
105.3 |
107.1 |
109.3 |
‡ |
† Calculated using 0.2 percent offset method.
‡ Beyond capacity of testing machine.
1.0 inch = 25.4 mm
1.0 ksi = 6.89 MPa
Splice Beam Test Procedure
The splice beams were inverted so that the spliced bars were on the top face during testing. Load was applied on the top face at each cantilevered end using a 120‑kip (534-kN) hydraulic jack. The load at each end was measured using a 100‑kip (445-kN) loadcell. The beams were supported on 6-inch (152-mm)-diameter rollers located 4 ft (1.220 m) from the applied loads.
Displacement measurements were taken using two string potentiometers at each end and two linear variable differential transformers (LVDTs) at mid-span as shown in figure 2. The strain in a spliced reinforcing bar was measured using two electronic resistance strain gages, one on each side of the splice, approximately 6 inches (150 mm) from the supports (outside of the splice) as shown in figure 1. The strain in the stirrups was also measured, with one strain gage on a stirrup near the middle of the splice and one on a stirrup near the outside of the splice.
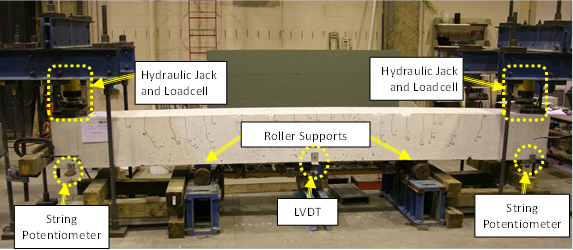
The cross section of each splice beam was measured at each end of the lap splice prior to beginning a test. After the test was complete, measurements of the top cover and side cover were made from pieces of concrete that had spalled from the specimen during the test.
Figure 2. Photo. Splice beam test setup.
Test Results
The first flexural crack typically occurred at one end of the splice. Additional flexural cracks developed over the support before the first flexural crack opened along the length of the splice. The first splitting cracks opened directly over the spliced bars at the ends of the splice as shown in figure 3. The green and blue lines show the approximate locations of the ends of the splice and stirrups, respectively. The black lines in the photograph indicate cracks that were perpendicular to the rebar direction and assumed to be flexural cracks. The red lines are parallel or inclined to the rebar direction and were assumed to be splitting cracks. As the load increased, the new splitting cracks opened up closer to the middle of the splice. Near failure, there was a high density of splitting cracks near the ends of the bars, and few splitting cracks, if any, in the middle half of the splice. In members without transverse reinforcement (stirrups), failure was sudden and brittle.
In specimens with stirrups, the progression of the splitting cracks towards the middle of the splice was delayed at each stirrup. As the load was increased, additional splitting cracks would form closer to the middle of the splice, but would again be limited by the next stirrup. Figure 4 shows the region of the lapped bars after failure for a specimen with stirrups.
A splitting tensile failure occurred in 36 of the splice beam tests. Yielding of the spliced bars occurred in 4 of the 22 specimens without transverse reinforcement and in all but 2 of the 18 specimens with stirrups. A flexural compression failure occurred in four specimens after significant yielding of the spliced reinforcement. Detailed results of the splice beam tests including the bar stress at failure is included in the full report covering this test program.(9)

Figure 3. Photo. First splitting cracks in splice beam
with HG mix and stirrups
(top surface and side of beam shown).
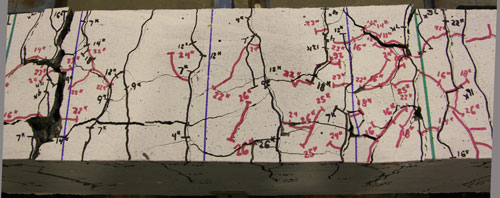
Figure 4. Photo. Cracking in splice
beam with HG mix and stirrups after failure
(top surface of beam shown).
Summary of Experimental Results
The bar stresses at failure were compared to expressions based on design expressions for development length of rebar. The mean test-to-prediction ratio for all specimens was 0.94 for the AASHTO LRFD Bridge Design Specifications expression, 1.18 for the ACI 318-11 expression, and 1.15 for the ACI 408‑03 expression.(1,7,8) This indicates that the bar stresses were slightly overestimated by the AASHTO LRFD Bridge Design Specifications expression, and slightly underestimated by the ACI 318-11 expression and ACI 408-03 expression. These predictions of bar stress do not include a modification factor for LWC or the safety factors applied for the design of splices. The design expressions showed a decrease in the test-to-prediction ratio with increases in compressive strength, and uniform test-to-prediction ratios with increases in splitting tensile strength.
TFHRC LWC DATABASE
A thorough literature review was performed to find published journal papers, conference papers, technical reports, and university dissertations that included tests, analysis, or discussions of LWC. Over 500 references were found in the literature that mentioned LWC. These references were reviewed for data from tests that measured the development of mild steel in tension. Tests included in the database were limited to data from beam-end specimens, splice beam specimens, tension beam specimens, and development beam specimens. Only test data from published reports was included in the database.
The TFHRC Mild Steel Development Database consists of data from 474 tests on LWC and NWC. More information about the tests in the database and a full list of references for the database is included in the associated report.(10)
Proposed Expressions for Bar Stress Based on ACI 318-11 and a Revised ACI 408-03
The test-to-prediction ratio is the ratio of the bar stress at failure (fs) to the predicted bar stress determined using a design expression. A slight revision was made to the ACI 408-03 expression in the approach used to include the LWC modification factor. Table 6 indicates that the ACI 318‑11 expression gave larger test-to-prediction ratios than the revised ACI 408-03 expression regardless of the presence of stirrups. The scatter in the test-to-prediction ratios for the ACI 318-11 expression, as indicated by the COV, is very high (50 percent) for specimens without stirrups. For the same specimens, the revised ACI 408-03 was still high (31 percent), but the scatter was still less than the ACI 318-11 expression.
Test-to-prediction ratios for the ACI 318-11 expression are shown compared to an ℓs/db ratio in figure 5 for specimens without stirrups and in figure 6 for specimens with stirrups. Figure 7 and figure 8 show the test-to-prediction ratios for the revised ACI 408-03. Least-squares linear regression lines are shown for each concrete mixture type. The number of specimens in each group is shown in parentheses after the group label. Also, regression lines are shown for all specimens with stirrups (“All N”) and all specimens without stirrups (“All T”). The regression lines in figure 5 and figure 6 show that the test-to-prediction ratios determined using the ACI 318‑11 expression are much larger than 1.0 (i.e., under-estimate bar stress) for short splice lengths and the ratios become smaller as splice length increases. Figure 7 and figure 8 show the regression lines for the test-to-prediction ratios determined using the revised ACI 408-03 expression. The regression line for the specimens without stirrups is slightly greater than 1.0 and has almost no slope. This indicates that the prediction given by ACI 408-03 provides a consistent result that slightly underestimates the bar stress over the range of splice lengths tested.
Table 6. Test-to-prediction ratio of bar stress using ACI 318-11 and revised ACI 408-03.
|
Concrete Mixture Type† |
Design Expression |
Mean |
COV |
Max. |
Min. |
Percent < 1.0 (%) |
Percent < 0.8 (%) |
|
LWC Specimens |
ACI 318 |
1.59 |
47.7 |
4.10 |
0.38 |
17.5 |
2.8 |
|
ACI 408-rev |
1.11 |
28.1 |
1.92 |
0.31 |
33.6 |
17.1 |
|
|
LWC Specimens without Atr (156) |
ACI 318 |
1.70 |
49.5 |
4.10 |
0.38 |
18.6 |
3.8 |
|
ACI 408-rev |
1.11 |
30.3 |
1.92 |
0.31 |
36.5 |
18.6 |
|
|
LWC Specimens with Atr (55) |
ACI 318 |
1.27 |
18.8 |
1.76 |
0.85 |
14.5 |
0.0 |
|
ACI 408-rev |
1.11 |
21.0 |
1.53 |
0.52 |
25.5 |
12.7 |
† Number of specimens given in parentheses.
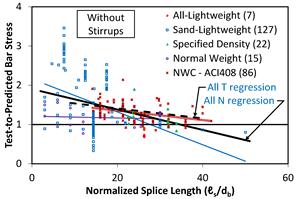
Figure 5. Graph. Bar stress test-to-prediction ratio compared to splice length for ACI 318‑11 expression for specimens without stirrups.
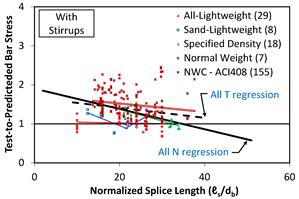
Figure 6. Graph. Bar stress test-to-prediction ratio compared to splice length for ACI 318‑11 expression for specimens with stirrups.
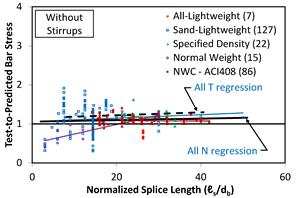
Figure 7. Graph. Bar stress test-to-prediction ratio compared to splice length for revised ACI 408-03 expression for specimens without stirrups.
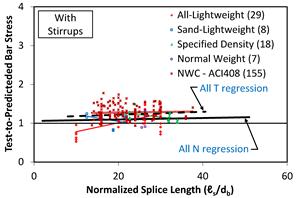
Figure 8. Graph. Bar stress test-to-prediction ratio compared to splice length for revised ACI 408-03 expression for specimens with stirrups.
Preliminary Recommendations for AASHTO LRFD bridge design Specifications
A set of preliminary recommended changes to the AASHTO LRFD Bridge Design Specifications were developed in this research effort. The first two recommended changes regarding the definition of LWC and the introduction of a LWC modification factor (λ-factor) were previously described in a related document concerning the mechanical properties of LWC and are presented again for clarity.(11,12) Additional recommended changes to the AASHTO LRFD Bridge Design Specifications are based upon the analysis described in this document. These additional recommendations build upon the two previous recommendations.
The analysis of the TFHRC Database included an evaluation of design expressions for development length given in the ACI 318-11 building code, and the expression in the ACI Committee 408 report (ACI 408-03).(7,8) An additional expression based on a revision to the expression in the ACI Committee 408 report was evaluated. This section presents a recommended change to the AASHTO LRFD Bridge Design Specifications based on the revised ACI 408 expression.
AASHTO Subcommittee on Bridges and Structures (SCOBS) Technical Committee 10 (T-10) is currently considering a change to the design expression for mild steel development length in the AASHTO LRFD Bridge Design Specifications. This change is based on the design expression in ACI 318-11 building code as recommended by NCHRP Project 12-60.(13) The design expression based on ACI 318-11 will also be presented here as an alternative recommendation.
The design expressions for development length include the recommended new expression for the λ-factor. The λ-factor is not based on the proportions of constituent materials and includes tests from types of mix designs that are not explicitly permitted by the current edition of the AASHTO LRFD Bridge Design Specifications.(1) These mix types include specified density LWC (typically a blend of lightweight and normal weight coarse aggregate) and inverted mixes (normal weight coarse and lightweight fine aggregate). The recommended new expression for the λ-factor is instead based on unit weight and splitting tensile strength and as a result the definitions of sand-lightweight concrete and all-lightweight concrete would no longer be needed.
The definition for LWC in Article 5.2 of the AASHTO LRFD Bridge Design Specifications limits the unit weight for LWC to 0.120 kcf (1,920 kg/m3) and includes definitions for sand-lightweight and all-lightweight concrete. The proposed definition for LWC expands the range of unit weights and eliminates the definitions for terms relating to the constituent materials in LWC. The proposed definition for LWC is as follows:
Lightweight Concrete—Concrete containing lightweight aggregate and having an equilibrium density not exceeding 0.135 kcf (2,160 kg/m3), as determined by ASTM C567.(14)
Proposed Expression for LWC Modification Factor
The concept of including a modification factor for LWC in expressions for predicting nominal resistance is included in many articles of the AASHTO LRFD Bridge Design Specifications. However, a single unified expression or LWC modification factor is not specified. This section proposes a new term, the λ-factor, to quantify the modification in nominal resistance that could be included in any expression for nominal resistance. The λ-factor relates to the material properties of structural LWC so the new article for the definition for the λ-factor could be located in Article 5.4.2 “Normal Weight and Structural Lightweight Concrete.” The λ-factor will be referred to as Article 5.4.2.8 in the present document. The proposed text for the λ‑factor is as follows:
Where lightweight aggregate concretes are used, the LWC modification factor, λ, shall be determined using the equation in figure 9 where fct is specified.
![]()
Figure 9. Equation. Expression for λ-factor with fct specified.
Where fct is not specified, λ shall be determined using the equation in figure 10.
![]()
Figure 10. Equation. Expression for λ-factor with fct not specified.
Where:
λ = LWC modification factor.
fct = Concrete splitting tensile strength in ksi.
f 'c = Compressive strength in ksi.
wc = Concrete unit weight in kcf.
Proposed Design Expression for Development Length
The determination of the development length of mild steel in tension consists of evaluating an expression that includes modification factors that either increase or decrease the development length. Unlike the design expression in AASHTO LRFD Bridge Design Specifications, the factors are not separated from an expression for basic tension development length.
The proposed design expression for development length is as follows:
The tension development length, ℓd,, in inches shall not be less than:
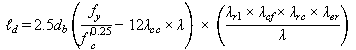
Figure 11. Equation. Proposed expression for ℓd.
Where:
λcc = Concrete cover factor.
λrl = Reinforcement location factor.
λcf = Coating factor.
λrc = Reinforcement confinement factor.
λer = Excess confinement factor.
λ = Proposed LWC modification factor.
TThe modifications given by the λrl, λcf, and λer
factors are in Articles 5.11.2.1.2 and 5.11.2.1.3 of AASHTO LRFD Bridge Design Specifications. The
concrete cover factor (λcc) and the
reinforcement confining factor (λrc) are
new modification factors. The concrete cover factor and reinforcement confining
factor can decrease development length. The proposed expressions are as
follows:
The tension development length,ℓd, modified by the factors as specified in Article 5.11.2.1.2, may be modified by the following factors, where:
For cover to the nearest concrete surface that is not equal to the side cover or one-half the center-to-center spacing of the bars, λer may be taken as:
![]()
Figure 12. Equation. Expression for λcc.
In which:
cmax = The larger of cc and cs.
cmin = The lesser of cc and cs.
cs = The lesser of cso and csi + 0.25 inch.
Where:
cc = Cover to the nearest concrete surface.
cso = Side clear cover.
csi = One-half of the clear spacing of the bars.
The value of the confinement factor, λrc, for the reinforcement being developed in the length under consideration satisfies the following:
![]()
Figure 13. Equation. Expression for λrc.
In which:
Ktr = 16 trtdAtr √f’c/(sn).
tr = 9.6 Rr + 0.28 ≤ 1.72.
td = 0.78 db + 0.22.
Where:
Ktr = Transverse reinforcement index.
cb = The smaller of the distance from center of bar or wire being developed to the nearest concrete surface and one-half the center-to-center spacing of the bars or wires being developed (inch).
Atr = Total cross-sectional area of all transverse reinforcement within spacing s that crosses the potential plane of splitting through the reinforcement being spliced or developed (inch2).
s = Maximum center-to-center spacing of the stirrups withℓd(inch).
n = Number of bars or wires being spliced or developed along the plane of potential splitting.
Rr = Relative rib area of the reinforcement. For conventional reinforcement, tr may be taken as 1.0.
The bar stress of the specimens in the TFHRC database without stirrups is shown in figure 14. The prediction given by the proposed expression based on ACI 408-03 for concrete with a compressive strength of 5 ksi (34 MPa) and 9 ksi (62 MPa) is shown in the figure. The mean compressive strength of the all-lightweight concrete, sand-lightweight concrete, and NWC specimens in the ACI Committee 408 database is 5 ksi (34 MPa). The mean compressive strength of the specified density concrete and NWC specimens found in the literature is 9 ksi (62 MPa). A prediction for 5 ksi (34 MPa) concrete and a λ-factor of 0.75 is shown in the figure. The shaded region indicates the range of possible predicted bar stress for 5 ksi (34 MPa) concrete with a modification factor for LWC varying from 1.00 to 0.75. Note that nearly all of the regression line from LWC experimental data points is within the shaded region, which indicates the possible range of LWC predictions.
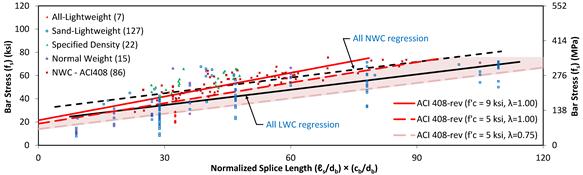
Figure 14. Graph. Bar stress for the proposed expression based on ACI 408-03.
If desired, the proposed expression for development length could also be simplified to eliminate some of the factors that appear to have lesser impact on the overall prediction. The simplification would include eliminatingλcc, the factor tr, and the term Rr. Eliminatingλcc would simplify the expressions forλrc andℓd. Eliminating tr in the expression for Ktr would also eliminate the need for the new term Rr that is used for reinforcing bars with large deformations. After simplification, the main differences between the proposed expression given in this document and the proposed expression currently being considered by SCOBS T-10 would be expressions for ℓdand Ktr.
Proposed Alternative Design Expression for Development Length
Based on the anticipated 2014 revisions to the AASHTO LRFD Bridge Design Specifications, an alternate design expression was also developed. The proposed alternative design expression for development length is as follows:
The tension development length, ℓd, shall not be less than the product of the basic tension development length,ℓdb, specified herein and the modification factor or factors specified in Articles 5.11.2.1.2 and 5.11.2.1.3.
The tension development length,ℓd , in inches shall be taken as:
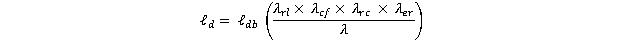
Figure 15. Equation. Proposed alternative expression for ℓd .
In which:
ℓ db = 2.4 dbfy /√f ‘c
Where:
ℓ db = Basic development length.
λrl = Reinforcement location factor.
λcf = Coating factor.
λrc = Reinforcement confinement factor.
λer = Excess confinement factor.
λ = Proposed LWC modification factor.
The modifications given by theλrl,λcf, andλer factors are in Article 5.11.2.1.2 and 5.11.2.1.3 of AASHTO LRFD Bridge Design Specifications. The reinforcement confining factor (λrc) is a new modification factor. The expression forλrc used by the proposed alternative is similar to the expression given previously.
The bar stress of the specimens in the TFHRC Database without
stirrups is shown in figure 16. The prediction given by the proposed expression
based on ACI 318-11 for concrete with a compressive strength of 5 ksi
(34 MPa) and 9 ksi (62 MPa) is shown in the figure. The mean
compressive strength of the all-lightweight concrete, sand-lightweight
concrete, and NWC specimens in the ACI Committee 408 Database is 5 ksi
(34 MPa). The mean compressive strength of the specified density concrete
and NWC specimens found in the literature is 9 ksi (62 MPa). A prediction
for 5 ksi (34 MPa) concrete and a ![]() -factor of 0.75 is shown in the
figure. The shaded region indicates the range of possible predicted bar stress
for 5 ksi (34 MPa) concrete with a modification factor for LWC
varying from 1.00 to 0.75.
-factor of 0.75 is shown in the
figure. The shaded region indicates the range of possible predicted bar stress
for 5 ksi (34 MPa) concrete with a modification factor for LWC
varying from 1.00 to 0.75.
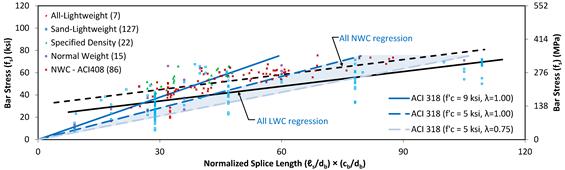
Figure 16. Graph. Bar stress for the proposed expression based on ACI 318-11.
Conclusion
This document describes bond strength tests on LWC, summarizes a database of LWC and NWC bond tests, and presents potential revisions to the AASHTO LRFD Bridge Design Specifications relating to the development length of mild steel in tension. The proposed design expressions for development length were compared to tested values in a database collected as part of this research effort. A full description of the database and the development and evaluation of prediction expressions is included in the full report.(10) Future phases of this research program and analysis effort will focus on other structural performance attributes as related to LWC. The test results will be compared to the prediction expressions for nominal resistance in the AASHTO LRFD Bridge Design Specifications incorporating appropriate proposed revisions for LWC mechanical properties.
References
1. AASHTO (2012). “AASHTO LRFD Bridge Design Specifications, Customary U.S. Units, 6th Edition,” American Association of State Highway and Transportation Officials, Washington, DC.
4. Ivey, D.L. and Buth, E. (1966), “Splitting Tension Test of Structural Lightweight Concrete,” ASTM Journal of Materials, Vol. 1, No.4, pp. 859–871.
7. ACI Committee 318 (2011). “Building Code Requirements for Reinforced Concrete (ACI 318-11) and Commentary,” American Concrete Institute, Farmington Hills, MI.
11. Greene, G. and Graybeal, B. (2013). Lightweight Concrete: Mechanical Properties, Report No. FHWA-HRT-13-062, Federal Highway Administration, U.S. Department of Transportation, McLean, VA.
Researchers—This study was led by Ben Graybeal at FHWA Turner-Fairbank Highway Research Center. It was conducted by Gary Greene of PSI, Inc. and Trine University through laboratory support contract DTFH61‑10‑D‑00017. For additional information, contact Ben Graybeal at (202) 493-3122 or at the FHWA Office of Infrastructure Research and Development, 6300 Georgetown Pike, McLean, VA, 22101-2296.
Distribution—The report (PB2014-10067) covered in this TechBrief is being distributed through the National Technical Information Service at www.ntis.gov.
Availability—This TechBrief may be obtained from the FHWA Product Distribution Center by email to report.center@dot.gov, fax to (814) 239-2156, phone to (814) 239-1160, or online at https://www.fhwa.dot.gov/research.
Key Words—LWC, lightweight concrete, bridge design, LRFD design specifications.
Notice—This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for the use of the information contained in this document. The U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers’ names appear in this TechBrief only because they are considered essential to the objective of the document.
Quality Assurance Statement—The Federal Highway Administration provides high-quality information to serve Government, industry, and the public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement.