Measured Variability Of Southern Yellow Pine - Manual for LS-DYNA Wood Material Model 143
PDF files can be viewed with the Acrobat® Reader®
2.2 DESCRIPTION OF PROPERTIES
Wood is generally considered an orthotropic material with different properties in the longitudinal, tangential, and radial directions. This is a transversely isotropic model (simplification of orthotropic) in which the properties in the tangential and radial directions are modeled the same. For simplicity, the longitudinal direction is referred to as the parallel-to-the-grain direction and the tangential and/or radial directions as the perpendicular-to-the-grain direction. This is an elastoplastic damage model with rate effects. Separate elliptical yield surfaces and scalar damage formulations are modeled for the parallel and perpendicular modes. The damage formulations admit progressive degradation of the tensile and shear stress components while retaining perfect plasticity in compression. Hardening formulations are available, based on a translating yield surface, to model nonlinearity in compression. Evaluation of the model through correlations with wood post data (static and dynamic) is given in Murray and Reid.(2) Clear wood data for pine, available as default material properties, are given in Green and Kretschmann.(14)
| 1. |
|
EL is the normal modulus of the undamaged wood parallel to the grain. The subscript L refers to the longitudinal direction of the wood. Typical units for moduli are GPa, MPa, or lbf/inch2.
|
| 2. |
|
ET is the normal modulus of the undamaged wood perpendicular to the grain. The subscript T refers to the tangential direction, which, for a transversely isotropic material, is modeled the same as the ‘R’ radial direction.
|
| 3. |
|
GLT is the shear modulus of the undamaged wood parallel to the grain.
|
| 4. |
|
GTR is the shear modulus of the undamaged wood perpendicular to the grain.
|
| 5. |
|
nLT is the major Poisson’s ratio parallel to the grain. A transversely isotropic material has three ratios, only one of which is independent. The minor Poisson’s ratio parallel to the grain, nTL, is calculated internally within the model as nTL = nLT (ET / EL). The Poisson’s ratio perpendicular to the grain (in the isotropic plane) is calculated internally as nTR = nRT = (ET – 2GTR) / 2GTR.
|
| 6. |
|
Inputs XT, XC, and S|| are the strengths, parallel to the grain, in uniaxial tensile stress, uniaxial compressive stress, and pure shear stress, respectively. Together, these three strengths form an irregular elliptical surface for modeling failure or yielding parallel to the grain. These three strengths form the ultimate yield surface. The compressive strength is also scaled back to form the initial yield surface when prepeak hardening is requested. Yielding is initiated once the stress state exceeds the yield surface. In this case, a plasticity algorithm with associated flow returns the stress state to the yield surface (normal return). Typical units for strength are GPa, MPa, or lbf/inch2.
|
| 7. |
|
Inputs YT, YC, and S^ are the strengths, perpendicular to the grain, in uniaxial tensile stress, uniaxial compressive stress, and pure shear stress, respectively. The yield surface for the perpendicular modes is separate from the yield surface for the parallel modes.
|
| 8. |
|
Gf I || and Gf II || are the fracture energies in uniaxial tensile stress and pure shear stress parallel to the grain. The fracture energy is the area under the stress-displacement curve as it softens from peak stress to zero stress. The softening model incorporates fracture energy and element size (passed to the wood model internally) in order to regulate mesh-size sensitivity. The result is a softening response that is independent of element size. This is accomplished by keeping the fracture energy constant from element to element, regardless of size. Typical units are GPa-mm, MPa-cm, or lbf/inch2-inch.
|
| 9. |
|
B is the parallel-to-the-grain softening parameter. It sets the shape of the softening curve plotted as stress-strain or stress-displacement. B is unitless. A typical value is B = 30.
|
| 10. |
|
dmax|| is the maximum damage that can accumulate parallel to the grain. Damage accumulation is based on an undamaged elastic strain energy norm formulated from the parallel strains. No damage threshold is required as input. The threshold is internally calculated and stored once the parallel yield criterion is satisfied. Thus, damage initiates with plastic yielding and accumulates if the energy norm of the current time step exceeds the energy norm of the previous time step. dmax|| is unitless and ranges from 0 (no damage) to 1 (100-percent damaged). A value of dmax|| = 0.9999 is typical.
|
| 11. |
|
Gf I ^ and Gf II ^ are the fracture energies in tension and shear perpendicular to the grain. Typical units are GPa-mm, MPa-cm, or lbf/inch2-inch.
|
| 12. |
|
D is the perpendicular-to-the-grain softening parameter. It sets the shape of the softening curve plotted as stress-strain or stress-displacement. D is unitless. A typical value is D = 30.
|
| 13. |
|
dmax^ is the maximum damage that accumulates perpendicular to the grain. Damage accumulation is based on an undamaged elastic strain energy norm formulated from the perpendicular strains. Perpendicular damage accumulates separately from parallel damage. dmax^ is unitless. A value of dmax^ = 0.99 is typical.
|
| 14. |
|
Inputs h||, hc||, and n|| are rate-effect parameters that increase the parallel strengths of wood as a function of strain rate via shifted surface formulations. Dynamic strength is equal to the static strength plus an overstress. The overstress is equal to EL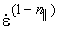 h|| in tension, GLT h|| in tension, GLT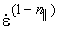 h|| in shear, and EL h|| in shear, and EL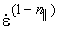 hc|| in compression, where hc|| in compression, where 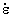 is the effective strain rate. The products is the effective strain rate. The products 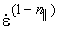 h|| and h|| and 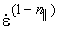 hc|| are unitless. Values for n|| range from 0 to less than 1, with a typical value of n|| = 0.1. hc|| are unitless. Values for n|| range from 0 to less than 1, with a typical value of n|| = 0.1.
|
| 15. |
|
Inputs h^, hc^, and n^ are rate-effect parameters that increase the perpendicular strengths of wood as a function of strain rate. Strength increases for the perpendicular stresses are modeled separately from strength increases for the parallel stresses. The overstress is equal to ET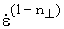 h^ in tension, GTR h^ in tension, GTR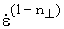 h^ in shear, and ET h^ in shear, and ET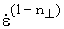 hc^ in compression. hc^ in compression.
|
| 16. |
|
Inputs N|| and c|| are the hardening parameters for modeling prepeak nonlinearity in compression parallel to the grain. The hardening formulation translates an initial yield surface until it coincides with the ultimate yield surface that is formulated from the parallel strengths. The parameter N|| determines the location of the initial yield surface. The parameter c|| determines the rate of translation. Both parameters are unitless. Typical values are N|| = 0.5 with c|| = 1000.
|
| 17. |
|
Inputs N^ and c^ are the hardening parameters for modeling prepeak nonlinearity in compression perpendicular to the grain. Perpendicular hardening is formulated separately from parallel hardening.
|
| 18. |
|
Input GHARD is an additional hardening parameter that allows each translating yield surface to surpass the ultimate yield surface. A positive value will produce continued hardening in excess of the yield strengths. A zero value will produce perfect plasticity in compression. A small positive value (e.g., GHARD = 0.02) is recommended if computational difficulties are suspected because of perfect plasticity.
|
Previous | Table of Contents | Next
|
