• Federal Highway Administration >
• Publications >
• Research Publications >
• 05042 >
• Chapt.Cfm
• Safety Effects of Differential Speed Limits

Safety Effects of Differential Speed Limits

PDF files can be viewed with the Acrobat® Reader®

INTRODUCTION

The Surface Transportation and Uniform Relocation Assistance Act (STURAA), enacted on April 2, 1987, permitted individual States to raise rural interstate speed limits from the previously mandated national speed limit of 89 kilometers per hour (km/h) (55 miles per hour (mi/h)) to 105 km/h (65 mi/h) on rural interstate highways. Of those that changed their speed limits, some States raised the limits for passenger cars but not trucks while other States raised the limits for both passenger cars and trucks. The former category, with different speed limits for cars and trucks, is known as differential speed limits (DSL). The latter category, which mandates the same speed limits for cars and trucks, is known as uniform speed limits (USL). The 1995 repeal of the national maximum speed limit gave States additional flexibility in setting their limits, such that by 2002, several States had experimented with both DSL and USL. Figure 1 shows the types of speed limits throughout the 1990s for rural interstate highways used in this study.

Proponents of DSL note that heavy trucks require a larger stopping distance and stopping time than passenger cars. Thus, a lower speed for trucks would reduce the risk of crashes that would otherwise be associated with these larger vehicles traveling at high speeds. Proponents of USL contend that different limits could increase speed variance, resulting in more conflicts between trucks and other types of vehicles, especially rear-end and sideswipe collisions. Advocates of a uniform limit also suggest that the higher driver position in a truck provides a greater sight distance than would be the case for a passenger car, giving truck drivers more time to stop.

Studies conducted during the early 1990s to compare the safety impacts of USL and DSL were constrained because of the limited data available at that time. Most such studies compared effects at different physical sites, such as Interstate 64 in the western portion of Virginia and the adjacent section of Interstate 64 in the eastern portion of West Virginia, where, in 1990 the former had a uniform limit and the latter had a differential limit. With more than a decade having elapsed since the passage of STURAA, however, the Federal Highway Administration (FHWA) requested that a longitudinal study be conducted, focusing especially on States that had changed their limits from USL to DSL or vice versa.

PURPOSE AND SCOPE

The purpose of this study is to compare the safety impacts of DSL and USL on rural interstate highways. Thus, the study’s objectives are twofold:

• To compare the effect of DSL and USL on crashes.
• To compare the effect of DSL and USL on vehicle speeds.

The scope of this study is limited to crash and speed data available in the U.S. on rural interstate highways between the period 1991and 2000.

LITERATURE REVIEW

One of FHWA’s justifications for a longitudinal study was the lack of consistent findings from previous research. Previous authors had focused on three main indicators of safety: speed, speed variance, and the crashes themselves. Some studies found no difference between DSL and USL, and some studies found one or the other to be a better policy choice. Because it was thought that a new methodological approach might help resolve these inconsistencies, literature suggesting the empirical Bayes approach was also reviewed.

Impact of DSL on Mean Speed

In 1990, Freedman and Williams analyzed speed data collected at 54 sites in 11 Northeastern States to determine the effect of DSL on mean and 85th percentile speeds.⁽¹⁾ Six States had retained a uniform limit of 89 km/h (55 mi/h), three had raised speed limits for all vehicles to a uniform value of 105 km/h (65 mi/h), and two States employed a differential limit for cars and trucks of 105/89 km/h (65/55 mi/h), respectively. The results showed that for passenger cars, the mean speed and 85th percentile speed for the two DSL States were not significantly different from the States with a uniform limit of 105 km/h (65 mi/h). Further, the mean and 85th percentile truck speeds in DSL states were close to those of the USL States. Similar results were obtained when comparing the percentage of vehicles complying with the speed limit. Harkey and Mera also found there to be no significant difference between passenger car and truck mean speeds when comparing DSL and USL.⁽²⁾ Garber and Gadiraju, however, did find a significant difference between truck mean speeds under DSL and USL, as well as an increase in passenger cars’ mean speed when the speed limits for those vehicles were raised.⁽³⁾

Impact of DSL on Speed Variance

Garber and Gadiraju also found that speed variance for all types of vehicles were significantly greater at DSL sites than at non-DSL sites.⁽³⁾ The implication of increased variance is that of increased interactions between vehicles and, thus, a potential in some types of crashes. While researchers found differences in truck speed variance in 10 of 13 comparisons between a USL site and DSL site, Harkey and Mera found no significant differences were between car speed variances at the DSL and USL sites.⁽²⁾ Furthermore, they found no difference between the speed distributions for both cars and trucks for the 105/97 km/h (65/60 mi/h) and 105/105 km/h (65/65 mi/h) speed limits.

Impact of DSL on Crashes

Harkey and Mera also looked at crash results from 26 sites in 11 States, where the sites were grouped into pairs.⁽²⁾ Each pair was comprised of a USL site with a speed of 105 km/h (65 mi/h) or 89 km/h (55 mi/h) and a DSL site with a speed of 105/89 km/h (65/55 mi/h) or 105/97 km/h (65/60 mi/h). The study investigated the percentage of different collision types for the total number of crashes for each of four types of speed limits. Three types of collisions were taken into consideration: rear end, sideswipe, and all other crashes. Table 1 shows that a higher proportion of car-into-truck and truck-into-car crashes occurred in USL States than in DSL States, with the exception of rear-end crashes where more car-into-truck collisions happened in the DSL group.

In contrast, Garber and Gadiraju, who had compared sites in three DSL States (California, Michigan, and Virginia) against two USL States (Maryland and West Virginia) found no statistically significant differences between crash rates when stratifying by collision type and crash severity.⁽³⁾ Council, Duncan, and Khattack in 1998 found that for rear-end collisions between cars and trucks, a high speed differential increases the severity of the crash.⁽⁴⁾ A simulation study by Garber reported a potential for an increase in crash rates for facilities using DSL, especially in the case of high vehicle volumes and truck percentages.⁽⁵⁾ Further, a 1991 study found no evidence indicating that the increase of the speed limit to 105 km/h (65 mi/h) for trucks at the test sites resulted in a significant increase in fatal, injury and overall accident rates.⁽⁶⁾ In that study, comparisons of crash rates in the adjacent States of Virginia (DSL) and West Virginia (USL) showed relatively more rear-end crashes in Virginia, suggesting that DSL might have a negative impact on safety.

Lending credence to the use of speed variance as a surrogate for crashes, Garber and Gadiraju found that crash rates increased with increasing speed variance for all classes of roads.⁽⁷⁾ A 1974 study by Hall and Dickinson showed that speed differences contributed to crashes, primarily rear-end and lane-change collisions.⁽⁸⁾ The existence of a posted DSL, however, was not found to be related to the occurrence of truck crashes. The study also noted that lower rates of truck crashes could be expected with higher speed limits and hence the study recommended an increase of truck speed limits to 105 km/h (65 mi/h) for highways carrying a higher truck percentage. Finally, an evaluation conducted by the Idaho Department of Transportation found that a change from USL to DSL did not increase crashes.⁽⁹⁾

Modified Empirical Bayes Methodology

Because of the discrepancies in findings in the literature with respect to the safety impacts of DSL versus USL, the investigators considered a new conceptual approach that had been refined during the past decade. The empirical Bayes method, developed by Ezra Hauer and modified by the investigators because of data issues specific to this analysis, was applied because recent literature suggested it could delineate between random variation and variation that resulted from some policy change (such as DSL to USL) more clearly than is the case with conventional methods.⁽¹⁰⁾ Specifically, four advantages of the empirical Bayes approach have been cited in the literature:

• It employs the correct mathematical distribution for crashes. Many conventional statistical tests are predicated on the assumption of normality; however, previous studies have indicated that the error or residuals (difference between predicted values and actual values) structure of the negative binomial distribution is a better description of the variation of crash frequency between sites. (See references 10, 11, 12 , and 13.)
• It does not assume that other conditions remain constant. The estimated number of crashes at a particular site usually does not remain constant from one year to the next because of variation in traffic volumes, traffic flow characteristics, weather conditions, driver attitudes, and a host of other factors beyond the control of the researcher. While conventional methods strive to control for these factors by either judiciously selecting sites that are common in most characteristics except that being studied (such as USL versus DSL) or using a control group, the empirical Bayes technique provides for the use of trend data. It has been shown that this method can be used to evaluate safety impacts even when yearly data are not available. Although yearly trend information is lost, researchers still benefit from the use of reference groups to pinpoint which effects are significant.⁽¹⁴⁾
• It does not assume a proportional relationship between crashes and average daily traffic (ADT). Instead, the number of crashes, or crash frequency, is used to reflect highway safety, given that empirical studies have suggested that a percentage change in ADT will not necessarily have the same percentage change in crashes, even if all other factors were constant.
• Crash estimation models are used to account for the fact that the observed crash frequency is just a point observation from some underlying distribution. In sum, the actual number of crashes observed may not be an unbiased estimator of the expected number of crashes. Thus, in lieu of this point estimate, a crash estimation model (CEM) is employed to statistically predict the best estimator of crash frequency. The generalized linear modeling (GLM) technique has been suggested as a way of determining parameters for the crash estimation model, although recently the generalized estimating equation (GEE) has been proposed as an alternative. (See references 10, 11, 14, 15, 16, and 17.)

METHODOLOGY

Four general steps comprised the methods used to compare the safety impacts of DSL and USL. First, crash and speed data were synthesized from 17 States that had been recommended by FHWA, were recommended by other researchers, or were thought to have changed their speed limits at least once during the 1990s from USL to DSL or vice versa. Second, conventional statistical approaches, such as the analysis of variance (ANOVA) were used to analyze speed monitoring data from these States. Third, comparable approaches were used to evaluate crash data from these States. Last, the empirical Bayes procedure was applied to these crash data.

Data Synthesis

As shown in appendix A, crash, speed, and volume data were solicited from multiple States by phone and e-mail. Raw data formats varied widely. Some data were only available in hardcopy format and were manually entered. Moreover, the detail of electronic data sets also varied widely. For example, some States provided detailed speed data in 8.0 km/h (5 mi/h) bins, whereas other States only provided a mean speed. During this data synthesis, data records that appeared likely to contain errors were removed. As an illustration, consider the 24-hour ADTs available from one State. The available data were the number of axles per vehicle, the vehicle speed, and the distance between the axles. There were a few records that showed both a speed of less than 8.0 km/h (5 mi/h), and a total axle-distance less than 1.2 meters (m) (4 feet); thus, these were removed from the data. In some cases, State data were not used because of concerns about the data quality. For example, after data had been partially synthesized for one State, practitioners from that State told investigators that the location system for the speed limits was so imprecise that the data were not reliable; thus, that State was omitted from the analysis. In other cases, local knowledge suggested that a facility should be excluded. For example, an experienced Virginia Transportation Research Council (VTRC) technician noted that although Interstate 66 had been designated as a "rural" section, the high volumes on that segment caused it to function as an urban section. In a few cases, the data were of good quality but the time required for reformatting the data for the purposes of this analysis was prohibitive. However, repeated telephone calls were helpful for clarifying the meaning of the data elements within the individual data sets.

Table 2 shows that the States that provided data used in this study may be divided into four policy groups based on their speed limits during the 1990s:

1. States that maintained a uniform limit for cars and trucks.
2. States that maintained a differential limit for cars and trucks.
3. States that changed from a uniform to a differential limit.
4. States that changed from a differential to a uniform limit.

Note: "x" indicates that the correspondent data are available.

Table 4 shows the categories of crash data obtained from the different States used in this study.

Note: "x" indicates that the correspondent data are available.

Analysis of Speed Data

To the extent possible with available data, annual changes in five speed variables (mean speed, speed variance, 85th percentile speed, median speed, and noncompliance rates) were compared within individual States. The Analysis of Variance (ANOVA) was used to determine if the change between the USL and DSL periods was significant. For those States that never changed their policy, the data were categorized into two virtual groups, 1990-1995 and 1996-2000, to determine whether significant changes occurred over time even without a policy shift between USL and DSL.

ANOVA was also used to look at speed changes on a yearly basis within every State. When a significant difference at the 5 percent confidence level was detected for these yearly changes, then, as shown in figure 2, three additional statistical tests were employed. Levene’s test served as a screening procedure to determine if the groups had equal variances. If so, then Tukey’s test was used to determine whether the differences were significant, while Dunnett’s test was used for samples with unequal variances, since the former assumes equal variances and the latter does not.^{(18, 19, 20)} The Levene, Tukey, and Dunnett tests were performed with the SPSS software following ANOVA test; hence, they are referred to as the "post hoc analysis" in figure 2.

Analysis of Crash Data Using Conventional Statistical Approaches

The same procedure employed for evaluating the speed data was employed for evaluating the crash data, using the ANOVA, Levene, Tukey, and Dunnett tests. Six types of crash rates were studied: total, fatal only, rear-end only, total truck-involved, fatal truck involved, and truck-involved rear-end. The crash rate was computed as shown in figure 3, where the annual crash frequency was simply the annual number of crashes; ADT was the average daily traffic.⁽²¹⁾

Analysis of Crash Data Using the Empirical Bayes Technique

A fundamental reason for applying the empirical Bayes technique is that a traditional before/after test, which simply compares the number of crashes on a facility before and after some type of treatment, may not necessarily have been the result of the treatment. Figure 3 illustrates how the use of a reference population can assist in making this determination, provided the reference group is judiciously selected.⁽¹⁰⁾ To understand the impact of assumptions, it is helpful to trace how the available crash data can be mapped to figure 4.

Conceptual Overview

Consider a State such as Arkansas that changed from a uniform limit to a differential limit in the mid 1990s. If the shift to DSL is viewed as a treatment, then figure 4 shows that years 1 to Y refer to the before-treatment portion and years Y+1 to Y+Z refer to the after-treatment portion, such that the before period has a duration of Y years and the after period has a duration of Z years. For each roadway segment within the State, there is sequence of crash counts K for year 1 to year Y; thus, the number of crashes at a particular site i during a year y may be designated as K_i,y. To evaluate how this treatment affected safety, there must be a prediction as to what the expected crash frequency m would have been in the after period had there had been no such treatment and then compare this would-have-been value to the actual number of crashes that occurred during the after period.

To determine this would-have-been value, a single multivariate crash estimation model (CEM) was developed to estimate the mean E(m_i,y) and the variance VAR(m_i,y) of the expected crash frequency m for each year y and at each site i during the before and after periods. For the treated entity with covariate values available, the multivariate model was applied to calculate the E(mi,y) and VAR(m_i,y) for the before and after years. The expected crash frequency m was then calculated from the E(m_i,y) from the before year values. Finally, these frequencies (m) of the before years then serve as a basis to obtain the predictions of the frequencies (m) of the after years of treated entities, with the use of the multivariate model. These steps are illustrated in the subsections that follow.

Development of the Crash Estimation Model

The CEM predicts the mean of the expected frequency of crashes E(m_i,y) and is especially relevant for predicting would-have-been crashes. The ideal CEM will account for all sources of variation other than the treatment being studied, which in this case are the DSL and USL policies. Thus, the ideal CEM would account for effects such as operational changes (e.g., volume growth, enforcement modifications, and the installation of safety service patrols), geometric changes (e.g., work zones, median barriers, or new interchange construction), and driver changes pertaining to behavior, licensing, and vehicle maintenance. Unfortunately, the data for these other sources of variation either were not available, or at best were very limited. The research team, therefore, had to develop the crash estimation models based on the available data. For example, in Virginia, the before data were from 1991-1994 and the after data were from 1995-1999. Unfortunately, there is no perfect technique for selecting the data from which to build the crash estimation model for the after period. Given this, there are two options for acquiring these data:

• Use data from the same time period but from a different State. In Virginia’s case, the researchers could select crash data for the period from 1995 to 1999 from a different State with comparable geometric and volume characteristics. The advantage is that if there is some temporal trend that applies nationwide, the reference group will capture that trend. The disadvantage is that the chosen State would need characteristics comparable to those of Virginia.
• Use data from the before period but for the same State. The advantages and disadvantages are the reverse of the previous option. In this case, the researchers are guaranteed of having the right geometric characteristics, but may miss temporal trends that are present in the after years, but not present in the before years.

The investigators chose the latter course of action, deeming the disparity between States as being greater than the disparity between time periods and using as an example a comparison of two crash models from the before periods for Virginia and Washington State from the same time period of 1991-1993. Both States maintained a differential speed limit at the time.

Visual inspection of the plots of the crash estimation models, shown in figure 7 below for a fixed length of 8 km (5 mi) and a range of ADTs, confirms that a different number of crashes at a given site with a given volume could be predicted. For example, if an 8-km (5-mi) site registered an ADT of 10,000, then the CEM for Virginia would have predicted approximately 9 crashes, whereas the CEM for Washington would have predicted almost 25 crashes.

Generally, the variation between States in terms of the crash estimation models was found to be relatively large, even among States with similar speed limit policies. Thus, for this specific application, it appeared that capture of nontreatment sources of variation was best accomplished by using CEMs developed within the same State, which is a significant departure from the empirical Bayes formulation as given in the literature. For that reason, the nomenclature modified empirical Bayes will be used for the remainder of this report to acknowledge that the selection of comparison sites herein deviates from that original methodology.

The crash estimation model took the form shown in figure 8, where the expected mean value of crashes for a roadway segment during a given year was the function of the length and ADT. As recommended in the literature, the maximum likelihood technique was used to estimate the parameters since the crash distribution was thought to follow a negative binomial distribution.⁽¹⁷⁾ Note parameters β1 and β2 do not imply a proportionate effect of ADT and length unless equal to unity, since others have suggested that such an effect cannot be assumed.^(22,23)

Estimation of the parameters was done with the GENSTAT software package (release 4.2.1). The procedure also gives the variance, VAR(m_i,y) of expected crash frequency for each section, which enables researchers to determine an aggregation parameter, shown as k, which describes the underlying crash distribution as k approaches infinity, when the distribution moves from negative binomial to Poisson. Theoretical explanations of k and techniques for estimating k are given in the literature. (See references 12, 13, 17, and 24.) Software for estimating k used for this effort was developed by Persaud and Lord.⁽¹⁷⁾

It should be noted that the equation for this effort shown in figure 8 was chosen after investigators considered a variety of formulations and determined that this formulation could be applied most consistently for each State’s data set. To ascertain whether the model was appropriate, the method of cumulative residuals may be used.⁽¹⁷⁾ (The cumulative residual is the difference between actual crash counts and model estimated crash counts. If the cumulative residuals oscillate around zero within the range of the two plots of two standard deviations, a good quality of fit is reflected.)^(17,25) Figures 9 and 10, for example, show the cumulative residual plots with respect to section length and annual ADT (AADT) for Virginia. Although there existed several sites where the cumulative residuals exceed the range of two standard deviations, the overall figures show a good quality of fit.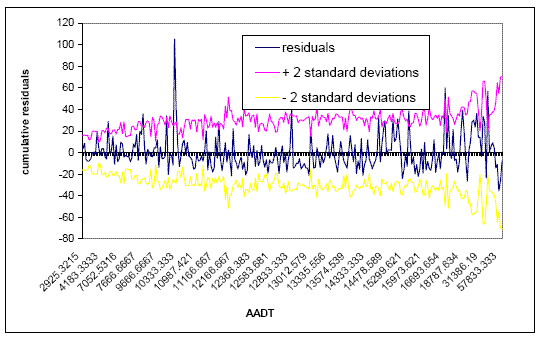

Note: top line is +2 standard deviations, middle line is residuals, bottom line is -2 deviations.

Figure 9. Chart. Plot of goodness of fit for the crash estimation model versus ADT.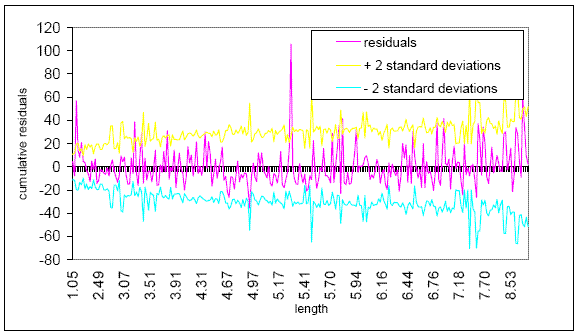

Note: top line is +2 standard deviations, middle line is residuals, bottom line is -2 deviations.

Figure 10. Chart. Plot of goodness of fit for the crash estimation model versus length.

An alternative crash estimation model that was explored in the course of this work entailed the use of yearly trend analysis and is given in figure 10, where α_y indicates the yearly trend. This expression was ultimately not used because reliable estimates could not be obtained for the after years for the States that changed from USL to DSL or from DSL to USL. That is, for a State such as Virginia, which changed from DSL to USL in 1994, calibration of this model would indeed yield a coefficients for the before period (α₁₉₉₁, α₁₉₉₂, α₁₉₉₃, and α₁₉₉₄); however, data were not available to estimate the appropriate coefficients for the after years, e.g., α₁₉₉₇, α₁₉₉₈, and α₁₉₉₉. In short, the formulation shown in figure 8 proved advantageous over the formulation below because it required less data.

In terms of specific software, general estimating equation (GEE) and generalized linear modeling (GLM) can accommodate both expressions, but the investigators used GEE for all States because it considers the possibility of temporal correlation between the years of the analysis.

In sum, several considerations governed the crash estimation model formulation used in this study. First, using total crashes for Virginia as a case study, four different formulations were considered (the equation in figure 8 using GEE and figure 8 using GLM, figure 11 using GEE and using GLM), and it was found with the Virginia case that the equation in figure 7 using the GEE approach was most suitable. As shown in tables 5 and 6, the parameters for these formulations were quite similar, but GEE was chosen over GLM because it accounts for temporal correlation; and the equation in figure 8 was chosen over the one in figure 11 because it meshed better with the data available for the study. Second, the method of cumulative residuals showed that, for total crashes in Virginia, both variables were indeed appropriate. The Genstat software used to implement the GEE method also showed that the t-statistics for length and ADT exceeded the critical values; thus both variables are significant. Third, the equation in figure 8 using the GEE software was applied for the remaining States and crash types.

Tables 5 and 6 illustrate the parameters for the equations in figures 8 and 11 with GLM and GEE respectively. A fifth formulation based on 3-year averages was also considered in the course of this study as shown in the rightmost columns of tables 5 and 6; however, this model ultimately was not used because ADT variation by year is not included therein.

The equation shaded in tables 5 and 6 was ultimately used in this study. The standard error are lower than those shown for GLM because GEE accounts for the possibility of correlation between years.

Critical Assumptions of the Crash Estimation Model

It is important to recognize two critical characteristics of the crash frequency distribution that affect the form of the crash estimation model.

• For any particular site i, such as an 8-km (5-mi) segment of rural interstate highway, the annual number of crashes for year y will follow the Poisson rather than the normal distribution. Thus, in the equations that follow, the crash frequency variable K_i,y obeys the Poisson distribution.
• For any particular year y, such as 1995, the crash frequency variable K_i,y for sites i follows the negative binomial distribution rather than the Poisson distribution.

Although recent studies have indicated that the negative binomial distribution is a better descriptor for crash frequencies between sites, the investigators confirmed this by comparing the actual crash frequencies for Arizona, Idaho, North Carolina, and Virginia with theoretical frequencies using the Poisson and negative binomial distributions. Appendix C shows that the negative binomial distribution is a valid descriptor of these data sets.

Application of the Crash Estimation Model with the Before Data

After CEM was developed, the expected crash frequency m₁, m₂,... m_y for the treated segments for the after years were determined. To accomplish this, the following steps were undertaken in sequence:

• CEM was applied to the before years data to obtain E(m_i,y), as shown in figure 8. (Recall that E(m_i,y) is the mean of the estimated crash frequency of site i during year y.)
• The ratio C_i,y was then computed for each of these before years from y=1, 2, ….Y. Thus C_i,y is the ratio of the current E(m_i,y) to the first year E(m_i,1).

Figure 12. Equation. CEM for before years.

Note that in the application of figure 12, the literature points out it is not essential that the first year of the before period be the denominator.⁽¹⁰⁾ Appendix D confirms this view by illustrating that the use of another year rather than the first year for Virginia would not affect the results.

• Recall that k was determined from the calibration process for the crash estimation model and essentially reflects the type of crash distribution reflected in the model. (On the other hand, recall that K_i,y represents the actual crashes observed at site i in year y.) The expected crash frequency m_i,y and its variance VAR(m_i,y) for years of y=1, 2, ....Y are then calculated from the next four equations.⁽¹⁰⁾

Figure 13. Equation. Expected crash frequency m for period 1.

Figure 14. Equation. Variance of expected crash frequency m for period 1.

Figure 15. Equation. Expected crash frequency m for period y.

Figure 16. Equation. Variance of expected crash frequency m for period y.

Application of the Crash Estimation Model with the After Data

With the expected crash frequency m₁, m₂,... m_y estimated for before period for each treated entity from figure 15, investigators can compute the "would have been crash frequency" m_Y+1, mY+2,...m_Y+Z for the after period as if there had been no such treatment using the following sequential steps.

• The crash estimation model from figure 8 is applied to the after years data in order to obtain E(m_i,y) for from y=Y + 1 to y=Y + Z.
• The ratios Ci,y are be computed using the equation in figure 12 for the years from y=Y + 1 to y=Y + Z.
• The values for m_i,y and VAR(m_i,y) are computed using equations 6 and 7 for the years from y=Y + 1 to y=Y + Z. These mi,y are the crashes that would have occurred had no treatment been made.

Thus, this process is very similar to application of the crash estimation model for the before years, with the exception of figures 13 and 14, used to compute m_i,1 and its variance VAR(m_i,1) do not need to be repeated since the quantities m_i,1 and VAR(m_i,1) have already been determined. (That is, m_i,1 and VAR(m_i,1) refer to year 1 as designated in the subscript m_i,1.)

Quantifying the Safety Impact of the Speed Limit Change

The effect of the treatment, which in this case is a change in the speed limit for Arkansas from uniform to differential, is quantified by comparing the would-have-been crashes (shown above as m_i,y for y ranging from Y + 1 to Y + Z) to the actual crashes in the after period (shown above as K_i,y with y ranging from Y + 1 to Y + Z). The would-have-been crashes at each site i during the after period are denoted as Π_i while the actual crashes at each site during the after period are denoted as Λ_i. Figures 17 and 18 are used to sum the crashes from the individual sites as Π and Λ.

Figure 17. Equation. Would-have-been crashes, had there been no speed limit change.

Figure 18. Equation. Actual crashes, given that the speed limit did change.

Then, the literature suggests two alternative formulations for assessing the safety impact, based on a comparison of Π and Λ.¹⁰

• Reduction in the expected number of crashes. Figure 19 computes δ as the difference between would-have-been and actual crashes, such that a positive value of δ indicates that the treatment had a desirable effect of reducing the number of crashes. Figures 20 and 21 show the computation of the variance and the resultant confidence intervals for δ.

Figure 19. Equation. The difference between would-have-been and actual crashes.

Figure 20. Equation. Variance for δ.

^*The investigators acknowledge that, in theory, the K_i,y are themselves random observations that could be replaced by a crash estimation model that smoothes the annual data. The investigators felt that using CEM would add additional confusion when interpreting the results; thus the actual K_i,y were used as indicators of the actual crashes in the after period.

Figure 21. Equation. Confidence intervals for δ.

• Ratio of actual to would-have-been crashes. Figure 22 computes this ratio, also known as the index of effectiveness (θ), such that a value of θ less than 1.0 indicates that the speed limit change improved safety. The unbiased estimator, however, is not the equation in figure 22 but rather the one in figure 23 as shown below.⁽¹⁰⁾ Figures 24 and 25 show the variance and confidence bounds, respectively.

Figure 22. Equation. Reduction in the expected number of crashes.

Figure 23. Equation. Ratio of actual to would-have-been crashes.

Figure 24. Equation. Variance of ratio of actual to would-have-been crashes.

Figure 25. Equation. Confidence intervals for θ.

The confidence bounds, shown in figures 21 and 25, are used to determine whether the values for δ and θ show a statistically significant safety impact. If the confidence bounds for δ and θ contain 0 and 1 respectively, then the safety impact computed by figures 20 and 24 are not significant; thus, it cannot be said that the treatment had a measurable effect.

RESULTS, DISCUSSION, AND LIMITATIONS

The results of the analysis are presented across three key areas: vehicle speeds as collected from speed monitoring data and evaluated using conventional statistical approaches, crash rates that were evaluated using conventional statistical approaches, and crashes as evaluated with the empirical Bayes technique.

Vehicle Speeds

The five types of speed data (mean speeds, speed variance, 85th percentile speeds, median speeds, and noncompliance rates) were analyzed for all States where such speed monitoring data were readily available. Furthermore, because Idaho provided a large number of speed monitoring sites and was a State that had changed its type of speed limit (from USL to DSL), speed data from that State were studied in detail.

Mean Speeds: An Example of How the Data May Be Assessed

Figure 26 illustrates the trends in mean speeds among five States from which speed data were analyzed. Two observations that arise from examination of figure 26 are, that with the exception of Virginia, speeds appear to be increasing over time (whether or not the differences are practically or statistically significant) and, unfortunately, data cannot always be obtained for all time periods.

Tables 7 and 8 illustrate the two types of analyses that were conducted for all speed and crash data: a before-after analysis to determine whether the speeds from the before period were significantly different from the after period at the 95 percent confidence level, and a year-by-year analysis, to determine whether individual years showed a significant difference. For this report, p values of 0.05 or lower were considered significant and are designated by an asterisk (*).

Table 7 shows two sets of results for Idaho since its speed limits were changed twice: first, a raising of its uniform limits and second, a lowering of truck speeds only. In table 8, the Levene test showed the variances to be significantly different; Dunnett’s test was used to compare annual mean speeds because it does not require comparison groups to have similar variances.

Examination of the statistics in table 7 shows that the mean speed of Iowa, a State that maintained a uniform limit, increased by 3.6 km/h (2.2 mi/h), which was significant. The mean speed change for Idaho, which maintained a uniform speed limit but increased that limit by 16 km/h (10mi/h) for all vehicles, was also significant with an increase of 9.2 km/h (5.7 mi/h). In Illinois and Indiana, which maintained DSL, their mean speeds increased by 1.2 km/h (0.8 mi/h) and 3 km/h (1.9 mi/h), respectively, which were not significant. Also, Idaho’s second change, which was a shift from USL to DSL, resulted in a slight decrease in the mean speed of 0.18 km/h (0.11 mi/h), but this decrease was not significant. The mean speed in Virginia, which changed from DSL to USL by increasing the speed limit for trucks by 16 km/h (10 mi/h), decreased by 1.15 km/h (0.71 mi/h), which was insignificant. In examining the results of the year-to-year analysis shown in table 8, the mean speed in Iowa for 1999, after the change from USL to DSL, was significantly higher than that for 1996 before the change, and that for 2001 was significantly lower than for 1995.

Appendix E discusses, in detail, whether the sample size used in testing for statistical significance should be the number of speed monitoring sites or the number of vehicles. As explained in that appendix, the investigators chose to use the number of sites for speed monitoring, although this decision had a pragmatic rather than a theoretical justification.

Graphical Overview of Changes in Speed Variance, 85th Percentile Speed, Median Speed, and Noncompliance Rates

Figures 26-29 give a pictorial understanding of how speeds changed from 1991 to 2000 for the States where data were available. These figures facilitated the observations of three general phenomena. First, there appear to be some correlations among the speed variables where data are available. For example, the mean and median speeds for Virginia are similar to one another, and the same can be said for Indiana. Likewise, the mean speeds and 85th percentile speeds for Idaho show similar trends. Although this is not surprising, it should not be taken for granted, since differences can sometimes be observed in the 85th percentile speed even though no differences are observed in mean speeds.⁽²⁶⁾ Second, there is not a clear difference in behavior between uniform and differential States. For example, Iowa (always a uniform limit) and Illinois (always a differential limit) show similar peaks in 1999, followed by a decreasing trend with respect to speed variance. Similarly, most States tended to show an overall increase in speeds. Virginia (the one State that went from differential to uniform) did show a decrease in mean speeds. However, table 6 shows that this difference was not significant. (Furthermore, table 8 shows that decreases in Virginia for the 85th percentile and median speeds were also not significant). Last, figure 29 suggests, but does not prove, that there may be a correlation between speed variance and noncompliance rates. The small amount of data available do not justify firm conclusions, but do suggest a relationship worthy of further study.

Figure 27. Chart. 85th Percentile speeds and median speeds.

Statistical Results of Changes in Speed Variance, 85th Percentile Speed, Median Speed, and Noncompliance Rates

Table 9 highlights the results of the statistical analysis and suggests that while increasing speeds were observed in most cases, these were not usually significant. (Idaho and Iowa are exceptions, which definitely do show a significant increase in speeds; it should be noted, however, that Iowa had a small number of sites.) The fact that no State showed a significant decrease in speeds and that States from all four policy groups showed either a significant or insignificant increase lends weight to the idea that changes in speed as a result of a differential or uniform speed limit were not supported by this study.

Comparison of Six Interstate Highway Segments in Idaho

It could be argued that the five different States shown in table 9 may have masked impacts of speed limit changes because of differences among them. Fortunately, one State-;Idaho-had six sites where speed data were available; some of these sites had DSL and some had USL. Thus, the changes in the 85th percentile speed and mean speeds were compared at these sites. As shown in table 10, a shift from a uniform limit to a differential limit occurred at the three rural sites meant that researchers could look closely at how speeds at those sites changed after 1998.

Statistical tests of these data show that, while significant differences were observed in the Idaho speeds when comparing yearly data, none of the differences were significant when comparing DSL to USL, as shaded in tables 10 and 11. The finding is that, although some factors clearly caused Idaho interstate mean speeds and 85th percentile speeds to change, a decrease in the truck speed limit (changing that limit from USL to DSL) for the three rural segments clearly did not affect these speeds. For example, for the first site shown in table 11 (Interstate 84 at milepost 14.9), it is clear that the first speed limit change, which raised the USL by 16.1 km/h (10 mi/h), significantly increased the mean and 85th percentile speeds (p=0.000). Yet the second speed limit change for that site, which is shown in table 10, a change to DSL, did not significantly change the mean or 85th percentile speeds as shaded in table 11. Shaded results indicate that there was no significant change in the mean or 85th percentile speeds.

Given that this is a regulatory change and assuming the statistical test is accurate, three implications are possible: the lowering of the speed limit was ignored by trucks; trucks were a relatively small percentage of the ADT such that the behavior of trucks did not influence speeds in an observable way; or increases in car speeds offset decreases in truck speeds. (Table 11 could be viewed as evidence that a shift to DSL can decrease speeds, since all changes in speed limits lead to statistically significant increases except the change to DSL. However, the only way to make this determination would be to evaluate changes at non-DSL sites during 1998.)

Discussion of Speed Impacts

Several inferences become apparent in examining these speed data:

• Significant increases in mean speed for Idaho and Iowa were observed over the study period. The other States tended to show insignificant increases. This trend suggests that the mean speed tended to increase over the 1990s regardless of whether the speed limit was uniform or differential. The 85th percentile speeds and median speeds showed a comparable upward trend, although fewer data were available for those two variables.
• Idaho’s first speed limit change, from a uniform limit of 105 km/h (65 mi/h) to a uniform limit of 121 km/h (75 mi/h), resulted in a significant increase in both the mean speed and the 85th percentile speed.
• Idaho’s second speed limit change, from a uniform limit of 121 km/h (75 mi/h) to a differential limit of 121/105 km/h (75/65 mi/h) did not significantly change either the mean speed or the 85th percentile speed, although these did decrease slightly.
• In Illinois, where no speed limit changes were implemented, the noncompliance rate increased steadily. Given the increasing mean speed of Illinois, this could be due to drivers desiring to travel at a higher speed.

Crash Rates (Analyzed by Conventional Methods)

Table 4 showed that crash rate data could be obtained from five States (Arizona, Arkansas, Idaho, North Carolina, and Virginia). Six types of crash rates (total crash rate, fatal crash rate, rear-end crash rate, total truck-involved crash rate, truck-involved fatal crash rate, and truckinvolved rear-end crash rate) were evaluated. As was done with the speed data, both a beforeafter comparison and a year-pair comparison were performed. (Again, for those States that never changed their policy, the data were categorized into two virtual groups, 1990-1995 and 1996- 2000.)

Figure 31 graphically compares the total crash rate in the five States for all sites, while table 12 indicates which changes were significant. Of the two States that maintained USL, one (North Carolina) showed a significant increase in the total crash rate, whereas only Arizona showed an insignificant increase. None of the other States, all of which had either changed from DSL to USL or from USL to DSL, showed a significant change in the total crash rate.

Note that speed limits changed in Arkansas (1996), Idaho (1996, 1998), and Virginia (1994)

Table 12 shows the before versus after period change in the six types of crash rates of the five States, with the p values from the ANOVA test given in parentheses. In examining table 12, there were 27 cases where both an ADT and a crash rate were available. There was a significant difference between the before and after period in 3 of those 27 cases.

Table 12 also shows that, as was the case with the speed analysis, there is no consistent trend in crash rates matching the change in speed limits. For example, Virginia and Arkansas, two States that were diametrically opposed in terms of their policies (Arkansas changed to DSL and Virginia changed from DSL), both showed statistically insignificant increases in rear-end crashes with almost identical p-values.

On the basis of the limited data available, there is potential evidence that the change to USL (as in Virginia) resulted in an increase in the number of rear-end crashes since the number of these crashes increased in Virginia, albeit insignificantly. This viewpoint, however, is tempered by two observations: first, such an increase was insignificant; and second, there was no corresponding decrease in the States that shifted from USL to DSL. In fact, the States that made such a shift (Idaho and Arkansas) saw an increase (albeit insignificant) in the number of rear-end crashes. Virginia observed a reduction in the fatal crash rates after the change from DSL to USL, and Idaho observed an increase in the fatal crash rate after changing from USL to DSL, although both of these changes were insignificant.

The most striking feature of table 12 is that, despite all four combinations of speed limit policies (maintaining USL, maintaining DSL, changing from USL to DSL, or changing from DSL to USL), not a single State saw a significant decrease in any of the various crash rate categories. Crash rates either did not change significantly or significantly increase.

Because crash data were available for five interstate segments in Virginia, these crash data were scrutinized to see if patterns could be gleaned from an examination of the sites grouped by interstate. A snapshot of these data is shown in figure 32, which illustrates that no single segment dominated the statewide average for total truck-involved crash rate. Figure 31 does, however, show a slight increase over time for the crash rates on the interstate segments.

Crashes (Analyzed by the Modified Empirical Bayes Method)

Because the empirical Bayes approach is best suited for a before/after scenario where one State undergoes some type of treatment—such as a change in the speed limits—the results are presented first for the policy group 3 and 4 States, where States changed from either a differential limit to a uniform limit or from a uniform to a differential limit.

Virginia Crashes (DSL to USL))

For the 266 sites that comprised the Virginia study data, the length of the sites ranged from 1.7 km to 22.9 km (1.05 mi to 14.25 mi) in length, and substantial variation in ADT was observed, as shown in table 13. The minimum, maximum, and total crashes per segment are shown for each crash type and reveal substantial variation, as well.

Calibration of the parameters for the crash estimation model of the form shown in figure 8 as E(m)=α(Length)^β₁ (ADT)^β₂ are shown in table 14 for the Virginia data. The fact that β₂ is less than 1.0 for all crash types means that the model presumes that ADT does not have an equal proportional effect on crashes. Instead, a certain percentage increase in ADT will result in a small percentage increase in the number of crashes. In short, an increase in ADT should yield a lower crash rate according to the model. Similarly, the β₁ values below 1.0 mean that an increase in section length, according to the model, will increase crashes by a smaller percentage. (For all States, the β₁ exponent usually was also almost always less than 1.0, meaning that as the section length increases, the number of crashes forecasted by the crash estimation model will correspond to a lower crash rate.)

The application of equations in figures 17-20 is reflected in table 15. The application of figure 18 results in the actual crash data for each year being shown in the "λ;" column with the cumulative values of λ; shown in the "Cumu λ;" column. Similarly, the application of the equation in figure 17 shows the predicted would-have-been crash data for each year during the after period listed in the fourth column ("π"), with the cumulative values of these would-havebeen crashes shown in the fifth column ("Cumu π"). The variance of π was calculated for each year during the after period and listed in the sixth column ("VAR(π)"), with the cumulative values of VAR(π) listed in the next column ("Cumu VAR(π)"). The equation in figure 19 means that the evaluation was conducted using the difference between the would-have-been after crashes and the actual after crashes, shown as "Excess δ" and tabulated by year in the "Cumu δ" column. The evaluation was also investigated using figure 22—by obtaining the ratio of the actual after crashes to the would-have-been after crashes for each year ("θ") and the total values of ("Cumu θ"). Variances for both the difference δ and the ratio θ are also calculated and listed to the right of table 15 as an application of figures 20 and 25.

Table 15 shows that the ratio θ for total crashes in Virginia was larger than 1.0. Furthermore, when the empirical confidence bounds are selected in accordance with the equation in figure 25, it is clear that the upper and lower bounds for θ are very close to 1.15 and certainly do not include 1.0 within that range. Thus, according to the empirical Bayes technique, because the ratio of the actual after crashes (λ;) to the would-have-been after crashes (π) is greater than 1.0, then the treatment (a change from a differential limit to a uniform limit) resulted in an increase in the number of crashes. In fact, for all Virginia crash types, θ is greater than 1.0. If the analysis is restricted to Virginia alone and used only the empirical Bayes method, then the interpretation would be that the change to a uniform speed limit increased the number of crashes. However, as is explained in the following sections, data from other States do not support this interpretation.

Table 16 shows a comparable analysis except that it is restricted to fatal crashes in Virginia. Statistically, application of the equation in figure 25 shows that the cumulative value of θ is 1.06 for total fatal crashes. Close examination of table 16 shows inconsistent performance from year to year. Although θ is greater than 1.0 for 1995 and 1997, it is less than 1.0 for 1996 and 1999.

Arkansas Crashes (USL to DSL)

Arkansas is of special interest because it is the reverse of Virginia in that the State changed from USL to DSL. The Arkansas data shown in table 17 are from 10 interstate sections in Arkansas, each 16 km (10 mi) in length.

As shown in table 18, the β₁ parameter was assumed to be 1.0 since all sections were of the same length and the β₂ parameter was found to be less than 1.0 for all crash types except that of rear-end crashes. The 1.774 coefficient from table 18 means that, according to the model, a certain increase in ADT would increase crashes by a larger proportion. In short, at a given site, increasing the ADT will increase the crash rate.

Except for rear-end crashes, all crash types for Arkansas showed that θ was significantly greater than 1.0, meaning that the shift (from USL to DSL) increased the number of crashes. Rear-end crashes were the only crash type that did not follow this trend because such crash types showed θ less than 1.0 in table 19; moreover, as shown in table 18, only rear-end crashes had a β₂ ADT coefficient that was greater than 1.0. Table 20 shows the application of the empirical Bayes approach for the total number of crashes on Arkansas rural interstate highways. Another important finding, which supports the statistical analysis, is that although both Virginia and Arizona showed an increase in the fatal crashes after the changes in the speed policies, the crashes in Virginia increased by only 6 percent. (See table 21 that shows Arkansas had a 60-percent increase when the State changed from DSL to USL. There is some variation in the Arkansas results, however, with θ being greater than 1.0 for 2 of the 3 years.)

Finally, the total number of fatal crashes for Arkansas was only 30 during the after period. Certainly, this small sample size contributes to the width of the corresponding confidence interval shown in table 25. Yet, the exceptionally low value of calibration parameter β₂ shown in table 24 may be a result of the fact that, for the specific case of Arkansas fatal crashes, the low calibration parameter of β₂ for Arkansas was not significant, as shown in table 26. Overall, the effect of that low value is to make the effect of increasing ADT almost negligible in terms of increasing crash risk. Arguably, this is a reasonable impact for fatal truck crashes, and the extraordinarily low value of that parameter relative to that of the other crash types makes one hesitant to draw conclusions from that set of truck-involved fatal crashes for Arkansas. (For Arkansas only, all β₁ values were set to 1.0 because lengths for all Arkansas sites were identical.)

Idaho Crashes (USL to DSL)

Similar to Arkansas, Idaho changed its speed limit from uniform to differential. Table 22 shows that 1996 was chosen as the before period and 1999-2000 were chosen as the after period, such that 32 sections from Interstates 15, 84, 86, and 90 comprised the study group. Section lengths ranged from 0.16 km to 139 km (0.1 mi to 86.1 mi).

With β₁ and β₂ parameters of 0.81 and 0.75 respectively for total crashes, Idaho data suggest that the total number of crashes was approximately 29 percent higher than would have occurred, had the uniform limit been retained. The variation of θ, shown in the far right column of table 23, suggests that these results are statistically significant. In fact, θ values were greater than 1.0 and significant for all types of Idaho crashes. There were cases where the variance of θ was not always so low. For example, for Idaho truck rear-end crashes, the variance of θ was computed as approximately 0.5. In that instance, however, θ had been found to be about 2.35, meaning that the impact of a speed limit change on the number of Idaho truck rear-end crashes was still significant according to the empirical Bayes method.

Crashes from the States of Arizona, Missouri, North Carolina, and Washington

Table 24 shows the values of θ that were obtained when evaluating the effect of maintaining the same speed limit in four other States. For comparison purposes, the values from Arkansas, Idaho, and Virginia are shown as well. In most cases, table 24 shows that θ was greater than 1.0. On examining these θ values for individual States, it seems that, although the ratio for total crashes in Virginia (changed from DSL to USL) is higher than that for Arkansas (changed from USL to DSL), it is lower than that for Idaho, which, like Arkansas, also changed from USL to DSL. An important factor in the case of Virginia is that the total fatal crash ratio is 1.06, whereas that for Arkansas was 1.61. All ratios for Idaho were much higher than those for Virginia. This suggests that, although there was an overall trend for an increase in crashes, the percentage of increases, particularly for fatal crashes, tended to be higher in States that changed from USL to DSL.

On the other hand, the data from table 24 are not consistent. For total crashes, θ remained approximately 1.0 for the one State that maintained DSL (Washington), whereas it was greater than 1.0 for States that maintained USL, Arizona and North Carolina. At first glance, the results might be interpreted to mean that maintaining DSL caused no change in crashes while maintaining USL caused an increase in the number of crashes. Examination of the fatal crashes shows inconsistency in those States that maintained USLs where fatal crash data were available; in these cases, θ was greater than 1.0 for Arizona, but less than 1.0 for North Carolina.

Table 25 presents confidence intervals for the expected percentage crash increase for each type of crash and for each State according to the empirical Bayes method. For example, consider the category of "total crash with truck involved." Table 24 shows θ values of 1.31 and 1.25 for Arkansas and Virginia, respectively, suggesting that there was a 31 percent increase in Arkansas and a 25 percent increase in Virginia as a result of the changes in the speed limit policies. However, these percentage increases are not perfect, given the variability that can occur in crashes. Thus, table 25 is used to suggest that the confidence interval for Arkansas is between 18.9 percent and 42.8 percent, and between 20.0 percent and 29.8 percent for Virginia. Clearly, larger sample sizes tended to lead to smaller confidence intervals.

Generally, the standard interpretation of confidence intervals is to declare the change insignificant if the confidence interval includes zero. Using the Virginia example, it can be inferred that according to this application of the empirical Bayes methodology, the change from DSL to USL in Virginia did not affect truck-involved fatal crashes (since that confidence interval runs from -12.5 percent to +38.4 percent and thus includes zero), but that it did cause total crashes to significantly increase (since the corresponding confidence interval is 12.9 percent to 17.2 percent and thus does not include zero.)

Interestingly, confidence intervals associated with the use of the empirical Bayes method in table 25 showed either increases in crashes or no change in crashes for all States and for all categories of crashes regardless of the speed policy change, with only one exception—fatal crashes in North Carolina, a State which maintained USL.

^*Shaded values were not significant at the 95 percent confidence level

Finally, table 26 shows the T-statistics associated with the β₁ and β₂ values used in the crash estimation model. An interpretation of table 26 is that, for all States and crash types, either section length, section ADT, or both were significant determinants of the number of crashes with three exceptions: total crashes in Washington, total crashes with truck involved in Arkansas, and fatal crashes in Arkansas. For the State of Washington, the corresponding confidence interval from table 25 had shown no change in crashes; in that sense, the results from table 26 are not surprising. For the case of Arkansas fatal crashes, the results from table 26 show that the crash estimation model for that particular case was probably spurious. In that sense, the decision from table 24 (that, because of the abnormally low value for β₂ observed for Arkansans fatal crashes in table 24, one should be cautious about inferences for this particular case) is confirmed by the corresponding T-statistic in table 26.

Relating Speed and Crash Changes

The logical question is whether any relationship exists between crashes or crash rate changes and changes in speed. Accordingly, researchers may compare the speed results shown in table 9 to the crash results shown in table 24, and/or the crash rate results shown in table 12. The States that intersect both speed-related data in table 8 and either of the crash tables (tables 12 or 24) are Idaho and Virginia. From those two States, investigators can glean three sets of changes in speed policy: Idaho increasing its USL, Idaho changing from USL to DSL, and Virginia changing from DSL to USL. Yet even these results are inconclusive:

• When Idaho raised its USL, there was an increase in both the mean speed and the 85th percentile speed (other speed data were not available), as expected. Yet there was no significant change in the crash rate.
• When Idaho changed USL to DSL, there was no significant change in its speed or its crash rate. There was, on the other hand, an increase in the number of crashes as reflected in tables 24 and 25. (Except for the category of truck-involved rear-end crashes, the upper and lower confidence bounds for all Idaho crash rate categories were positive. To the extent that having the 95 percent confidence interval not include zero indicates statistical significance, therefore, one would say that the Idaho crash rate increases for all categories except rear-end with truck involved were significant. For the category of rear-end with truck involved, research could deduce no significant change because the confidence interval includes zero. The lower confidence interval is less than zero, and the upper confidence interval is greater than zero.)
• When Virginia changed DSL to USL, there were no significant changes in any speed measures except for one—the rate of noncompliance significantly dropped (generally viewed as a positive development). There was a significant increase in two of five crash rate categories (rear-end and total truck involved) and an increase in three of the five categories for the number of crashes via the empirical Bayes method (the other two categories showed no change in crash rates).

Looking at only these three bullets, a logical inference based on these changes in speed policy would find no relationship between changes in speed and safety changes. Idaho’s first change saw an increase in speeds but no adverse safety impacts, whereas Idaho’s second change and Virginia’s change each saw no change in most measures of speed and adverse safety impacts. The only exception was Virginia’s decreased rate of noncompliance—accompanied by an increase in the number of crashes. Certainly, it is plausible that the indicators of speed used in this study are simply not useful measures of crash risk.

Acceptance of this outcome—that there is no relationship between changes in speed indicators and crash changes—however, requires two logical steps. First, there must be the tacit acceptance that crashes (as measured by the empirical Bayes method) are a better indicator of safety than crash rates (thereby simplifying the second and third bullets), but that crash rates are a better measure of safety than nothing (thereby simplifying the first bullet). Second, tables 24 and 25 must be accepted as true even though they generally tended to show increasing crash risk, regardless of the policy speed limit change. In sum, this study offers some tendency for speed indicators and crash indicators to not be correlated. However, because these inferences are based on observations from only two States, such results prevent investigators from using this study to make that conclusion.

STUDY LIMITATIONS

Caveats About the Use of the Empirical Bayes Method

Several data limitationsmay have influenced the values shown in tables 24 and 25. These data limitations apply to the investigators’ use of the modified empirical Bayes method and not necessarily to the application of the empirical Bayes method in other situations.

First, table 24 shows the corresponding exponent β₂ for each crash type and State, where β₂ reflects the impact of a change in ADT according to the crash estimation model developed for that State and crash type. A plausible explanation for this is that, in most States, ADT increases over time, so with a β₂ less than 1.0 the would-have-been crashes predicted by the crash estimation model will correspond to a lower crash rate. As β₂ approaches zero, large increases in ADT tend to only increase crashes by a disproportionately small amount, with the effect being that the would-have-been crash rate is so low that it is virtually impossible for any policy change to show a θ less than 1.0, which would be an improvement in safety. In sum, a low value of β₂ far from unity renders the model very insensitive to changes in ADT from the before scenario (in the sense that a low value of β₂ means that large additional ADT should only increase crashes slightly). Thus, the interpretation that Arkansas fatal crashes increased as a result of the change from USL to DSL should be tempered by the very low β₂ value of 0.00355 shown in table 24, which would mean that almost any change would probably result in a θ value greater than 1.0. Alternatively, one can cite that the insignificance of the crash estimation model, based on table 26, for the specific case of Arkansas fatal crashes, is also a reason not to rely solely on inferences from Arkansas fatal crashes.

Second, comparison groups are imperfect. Ideally, the comparison (control) group would have been selected from the same State at the same time as the studied group. For example, in Virginia, if after the statewide differential speed limit of the early 1990s was repealed, one section of Interstate 81 could have been kept at DSL and another section of the highway could have been changed to DSL. Unfortunately, not only were comparison groups composed of different roadways, but they also drew from different States altogether. Thus, since the actual Virginia reference group was an extrapolation of the temporal trend that occurred during the before period from 1991 to 1993, later aberrations in this trend may not have been identified. In other words, if some significant change occurred in one year that increased the crashes but had nothing to do with speed limits policy change, then unfortunately this change would not be captured in the comparison group and therefore would not be reflected in the models. In short, a problem would arise if the relationship between ADT and crashes had drastically changed from the before to the after period. When this relationship is based on multiple years of data and multiple sites, one can have some confidence in the model, but temporal changes in the after year are possible that might alter this relationship.

Third, although speed-monitoring data were available to clarify general speed trends throughout a State, specific speeds often were not available on every section of interstate that was a segment in the crash analysis. (In other words, for a given 322-km (200-mi) stretch of interstate, annual data indicating overall speed trends might be available from two speed-monitoring sites. While analyzing crashes on those interstates, however, if the interstates were divided into 20 sections for analysis, it would be best to have 20 speed-monitoring sites to include actual speeds in the crash estimation models.)

Next, the crash estimation models used identical treatment and comparison sites, which, as discussed earlier in the paper, was done to reduce error in the prediction of crashes by CEM. In traditional before/after studies, such a decision could possibly subject the study to what Hauer describes as "regression-to-mean (RTM) bias" or "selection bias."⁽¹⁰⁾ As explained by Hauer, RTM arises when "there is a link between the decision to treat an entity and its accident history."⁽¹⁰⁾ If the basis of site selection was those sites with the largest number of crashes in a single year, then it is possible that subsequent crash reductions would be erroneously attributed to the treatment when in fact such reductions were truly the result of random variation that would have transpired even without the treatment.† Two characteristics of this study likely eliminate the possibility of regression to the mean bias. First, the sites studied were generally not chosen by persons with an interest in testing the effects of USL and DSL; rather, the sites were those that had available data. Second, the sites did not show behavior expected in a study where regression to the mean occurs. Instead of seeing dramatic crash reductions, States generally saw crash increases. For the rate-based method, the increases were often not significant and for the modified empirical Bayes approach, the increases were sometimes significant. Had the bias been present, researchers would have expected to see crash reductions in lieu of increases.

Finally, the crash estimation model used only two variables, AADT and section length. This could have been the result of too few variables, in case other factors, such as the number of interchanges per mile, could have influenced crash rates. Other variables besides AADT and section length also may have been relevant. To mitigate the impact of this last problem, goodness of fit tests were conducted for the crash estimation model for total crashes for Virginia, as shown in figures 9 and 10. Based on the Virginia results, this model formulation was applied for other States. However, additional data elements, such as the number of interchanges per mile, might have helped reduce the amount of noise used throughout this analysis.

†In practice, RTM occurs when an agency identifies, based on a short period of data, the most unsafe locations and then makes subsequent engineering modifications to those locations. Since crash data have an element of probability, choosing the worst locations based on a short period of data may mean that investigators simply have identified sites that, at random, happened to exhibit a large number of crashes in a given year and would probably exhibit a lower number of crashes the following year, even if no change were made. Investigators seek to avoid this bias by selecting sites that have good and bad crash records and studying those accordingly with a new treatment.

General Caveats

There are six additional limitations that, unlike the concept of the comparison reference groups cited above, apply to all three sets of results: speed, crashes, and crash rates. As was the case with the limitations described for the application of the modified empirical Bayes method, these caveats arise because of the limited data available. Firstly, the sample size varied by State. For example, there may be less certainty for the North Carolina crash results (based on 26 sites) being representative of North Carolina than that of the Arizona crash results (based on 278 sites) being representative of Arizona. For the empirical Bayes method, Washington, which maintained a differential speed limit, comprised the only State in policy group 2 with nine sites. Secondly, the selected sites may be an unbiased sample; however, the investigators cannot control site selection; their randomness is a function of how individual States set up their individual speed monitoring programs. Thirdly, the durations used in this study are relatively short. Certainly 3 years is normal for a before/after study, but some of these States, notably Idaho, only had a speed limit in effect for 1 or 2 years. Fourthly, the rural interstates were analyzed at an annual level of detail, without stratification by time period or season. Fortunately, since congestion is usually lower for rural interstates, this annual approach should not have been as significant a problem as it would have been for urban interstates. Next, the speed data shown are based on all vehicles, not just trucks. Except for speed variance, researchers ideally want to know how truck speeds, not just all vehicle speeds, were affected by differential versus uniform speed limit policy. Similarly, when looking at truck-involved crashes, investigators would want to be able to delineate between crash types that are directly affected by DSL versus USL policy (e.g., car-intotruck collisions) and those that are indirectly affected by such a policy (e.g., truck-into-truck collisions).²⁷

Finally, the sample size used in the statistical tests associated with the speed analysis was defined as the number of speed monitoring sites. Although the investigators decided that this was appropriate to determine whether speed changes were meaningful, an argument can be made that the sample size should have been estimated as the number of vehicles at all of the sites combined. Acceptance of this latter view would give significance to many of the statistical tests shown in table 11 as insignificant, although there still would be no clear pattern as to the effect of DSL versus USL for speed. (A minor item is the need to make some assumptions regarding the underlying vehicle distribution since individual vehicle speeds were not available; appendix E discusses this issue further.) An extension of this argument arises in the computation of confidence intervals for the 85th percentile speed; hence, theoretical issues associated with determining significant differences in 85th percentile speed are discussed in appendix F but are not believed to influence the outcome of this study.⁽²⁸⁾

CONCLUSIONS

The original purpose of this study was to compare the safety impacts of DSL and USL, with safety impacts being assessed through crashes and speeds, and to that extent, findings may be presented across both those areas. An unforeseen outcome of this study, however, was to identify considerations in the application of the empirical Bayes methodology, both with respect to the formulation of the crash estimation model and the types of data necessary to conduct the analysis.

Safety Impacts of DSL Versus USL

1. Speed characteristics were generally unaffected by a DSL versus USL policy.Except for Virginia, the mean, 85th-percentile, and median speeds tended to increase over the 1990s regardless of whether the State maintained USL, maintained DSL, or changed from one to the other. In some cases, the difference was significant; in other cases, it was not.
2. Crash rates, when compared using conventional statistical methods, did not show an obvious relationship to the type of speed limit chosen.When States were stratified into four policy groups (USL, DSL, shift from USL to DSL, and vice versa), the changes in crash rates and crash rate types did not all correspond to one group.
3. Actual number of crashes, when compared using the modified empirical Bayes approach indicated that the percentage of increase of the fatal actual crashes over that for the wouldhave- been fatal crashes was higher for the States that changed from USL to DSL than for Virginia, which changed from DSL to USL.On the other hand, the same empirical Bayes approach showed that the percentage increase of the total actual crashes over the wouldhave- been total crashes was higher for the States that maintained USL than for the State that maintained DSL.
4. Measurable variation within speeds and crash rates by year and by State may confound any statistical tests employed.The performance of Illinois annual speed variances, as shown in figure 17, is indicative of the noise associated with random variation, where the annual speed variance has an insignificant but observable upwards and downwards trend despite the fact that Illinois made no policy changes to its speed limits.

Methodological Findings

1. In this study, most of the crash estimation models developed by the investigators for the modified empirical Bayes approach were very sensitive to changes in ADT. In most cases for this study, as time passed, the actual number of crashes for the after period was larger than the predicted would-have-been crashes. The investigators believe this to be the result of the less than unity exponent associated with the equation in figure 8.
2. Even within a single State, different trends are observed on different rural interstates. Examination of figure 19, for example, suggests that the between-interstate variation adds quite a bit of noise to any attempt to study statewide temporal trends. The reality may be that DSL and USL have different safety impacts, as might be implied by an imagined extrapolation of the shaded Idaho data in table 11 (beyond 1998) or the Virginia mean speed downward trend in figure 26 (beyond 2000 to 2001). This particular study, however, could not identify such a difference. It may be the case, therefore, that a detailed crash-by-crash evaluation at a few interstate segments may be able to reveal a more precise analysis, especially after a few more years of data have been collected at States such as Idaho that have recently made changes form USL to DSL.
3. The proportionality of crashes to ADT has been questioned but not resolved. The crash estimation models developed for this study showed a nonlinear effect of crashes to ADT, such that it was often the case that a large increase in ADT would, according to the crash estimation models, yield a small increase in the number of crashes. For that reason, investigators can state that a proportional relationship between crashes and ADT, which is presumed in the use of crash rates, is questionable. Yet, the same approach yielded contradictory results on a State-by-State basis. Some CEMs predicted, for example, that one policy adversely affected safety, whereas others predicted that the opposite policy adversely affected safety. For this reason, the highly nonproportionate effect of crashes to ADT may be overstated by the CEMs developed for this study—but these results cannot prove or disprove that assessment. Thus, because of the contradictory nature of these CEMs, the proportionality of crashes to ADT is not resolved.

4. To assist decisionmakers under conditions of sparse data availability, it may be productive to analyze safety impacts through both the traditional method of crash rates and the newer method of the empirical Bayes (or modified empirical Bayes) approach. If the aggregate results from the two methods are the same, then results can be presented using the method that is more familiar. If the aggregate results from the two methods are contradictory, then researchers have an indication that there may be a flaw in the analysis. For example, consider the States analyzed in this study:

   • Application of the modified empirical Bayes method showed no consistent trend among the States. Regardless of speed limit policy change, table 24 suggests a statistically significant increase in crashes for each State. The aggregate result of the modified empirical Bayes method, therefore, is that, because the State-by-State results are inconsistent, the modified empirical Bayes method does not show that changes in speed limit policy have a statistically significant impact on crashes.
   • Application of the traditional crash rate method, shown in table 12, also indicates that most State-by-State results were statistically insignificant. In the few cases where a statistically significant rate was found, results were not consistent among States in the same group. For example, one State that maintained USL saw a significant increase, whereas the other two States that maintained USL did not see a significant increase. The aggregate results of the traditional crash rate method may be stated thus: "Because most States saw insignificant changes in the crash rate and because there was no discernible pattern in the States that did have a significant change in the crash rate, the traditional crash rate method does not show that the changes in speed limit policy have a statistically significant impact on crash rates."

Because the two bulleted methods show the same conclusions, the investigator may have greater confidence that the analysis is correct than would be the case had the two bulleted methods yielded contradictory conclusions.

Previous | Table of Contents | Next