Prediction of the Expected Safety Performance of Rural Two-Lane Highways
4. ACCIDENT MODIFICATION FACTORS
The incremental effects of individual geometric design and traffic control elements are represented in the accident prediction algorithm by AMFs. This section describes the development of the AMFs and documents the AMFs for each geometric design and traffic control factor considered in the algorithm.
Development of Accident Modification Factors
AMFs are used in the accident prediction algorithm to represent the effects on safety of specific geometric design and traffic control features. The AMF for the nominal or base value of each geometric design traffic control feature has a value of 1.0. Any feature associated with higher accident experience than the nominal or base condition has an AMF with a value greater than 1.0; any feature associated with lower accident experience than the base condition has an AMF with a value less than 1.0. The multiplicative nature of the AMFs is illustrated in equations (13)and (14).
The AMFs were developed by two expert panels, one for roadway sections and one of at-grade intersections. These panels exercised expert judgment in reviewing the reported research findings concerning each geometric design and traffic control feature of interest and selecting an appropriate basis for an AMF. The members of the two expert panels that developed the AMFs are identified in appendix A.
Each expert panel selected a set of geometric and traffic control elements, including both roadway segment and at-grade intersection elements, as candidates for the development of AMFs. The candidates were selected based on the panel’s initial assessments of those roadway segment and intersection features that are generally considered to be related to safety. A critical review of published and unpublished safety literature related to each geometric design and traffic control element was then undertaken. Each panel met and used the findings of the literature review as the basis for (1) selecting the final set of geometric and traffic control elements for which AMFs could be developed; and (2) quantifying those AMFs. For roadway segments, the final AMFs included all of the variables in the roadway segment base models plus additional variables. For at-grade intersections, the final AMFs did not include all of the variables in the intersection base models because the expert panel found that reliable estimates of safety effects from the literature were lacking for some variables in the base models and others were judged to be of relatively less importance.
For some geometric design or traffic control elements, the expert panel selected the results of one particular study that they considered most credible to serve as the basis for the AMF. In other cases, the expert panel combined the results of two or more studies to develop an AMF. In other cases, where reliable research results were lacking, the panel exercised its collective judgment to estimate values for an appropriate AMF; this was done, for example, where the panel felt comfortable in establishing a bound, such as an appropriate maximum or minimum value, for an AMF.
AMFs were based on a variety of sources including results of before-and-after accident evaluations, coefficients or parameter values from regression models, and expert judgment. The expert panel considered well-designed before-and-after evaluations to be the best source for AMFs. However, relatively few well-designed before-and-after studies of geometric design elements were found in the literature and, therefore, the expert panel had to rely in many cases on other types of studies. Coefficients or parameter values from regression models are considered less reliable, but were used when no before-and-after study results were available and the value of the coefficient in question was considered by the panel to be credible. Expert judgment alone was exercised in limited cases where no better results were available; even where an AMF was based primarily on expert judgment, the panel used all relevant research results in making that judgment. FHWA has many promising before-and-after evaluations underway, and it is hoped that the AMFs recommended here will be updated with those analysis results when they become available.
The expert panels faced many difficult judgments in determining the appropriate values of the AMFs. A broad range of literature was reviewed and many studies were assessed. Many of the studies reviewed were similar in quality, and the selection of one study over another may have depended as much on consistency with other selected AMFs as on the relative merits of the studies. Thus, the omission of any particular study from the final AMFs should not necessarily be interpreted as disparagement of that particular study. The sources on which each AMF is based are documented in the following discussion. Section 8 of this report not only identifies the sources cited in the text but also includes a complete bibliography of all sources consulted in the development of the AMFs.
While the individual AMFs were based on the panel’s best judgment about the relative merits of the available research findings, the credibility of the model is supported by a sensitivity analysis whose results are presented in section 5 of this report.
The AMFs incorporated in the model include:
Roadway Segments
- Lane width.
- Shoulder width.
- Shoulder type.
- Horizontal curves:
-
- length;
- radius;
- presence or
- absence of spiral transitions;superelevation.
- Grades.
- Driveway density.
- Two-way left-turn lanes.
- Passing lanes/short four-lane sections.
- Roadside design.
At-Grade Intersections
- Skew angle.
- Traffic control.
- Exclusive left-turn lanes.
- Exclusive right-turn lanes.
- Intersection sight distance.
An explanation of each AMF for roadway sections and for at-grade intersections is presented below.
Roadway Segments
The AMFs for geometric design and traffic control features of roadway segments are presented below.
Lane Width
The nominal or base value of lane width is 3.6 m (12 ft). Thus, 3.6-m (12-ft) lanes are assigned an AMF of 1.00. Figure 2 illustrates the recommended values of the AMF for lane widths from 2.7 to 3.6 m (9 to 12 ft). The AMF for any lane widths within the range of 2.7 to 3.6 m (9 to 12 ft) would be interpolated between the lines shown in figure 2. Lanes less than 2.7 m (9 ft) in width would be assigned an AMF equal to that for 2.7-m (9-ft) lanes. Lanes greater than 3.6 m (12 ft) in width would be assigned an AMF equal to that for 3.6 m (12-ft) lanes. As shown in the figure, the AMFs for lanes less than 3.6 m (12 ft) in width would be constant for all ADTs above 2,000 veh/day, but would decrease to a substantially smaller value over the range of traffic volumes between 400 and 2,000 veh/day. The AMFs then have constant, but lower, values in the range of ADT below 400 veh/day.
If the lane widths for the two directions of travel on a roadway segment differ, the AMF should be determined separately for the lane width in each direction of travel and the resulting AMFs should then be averaged.
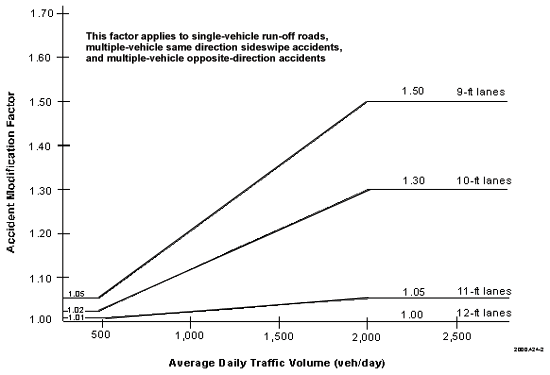
Figure 2. Recommended Accident Modification Factor for Lane Width.
The AMFs shown in figure 2 apply to single-vehicle run-off-the-road and multiple-vehicle head-on, opposite-direction sideswipe, and same-direction sideswipe accidents. The AMFs expressed on this basis must, therefore, be adjusted to total accidents within the accident prediction algorithm. This can be accomplished with the following equation:
|
AMF = (AMFra - 1.0) Pra +1.0
|
|
where:
| AMF |
= |
accident modification factor for total accidents; |
| AMFra |
= |
accident modification factor for related accidents (i.e., single-vehicle run-off-the-road and multiple-vehicle head-on, opposite-direction sideswipe, and same-direction sideswipe accidents), such as the accident modification factor for lane width shown in figure 2; |
| Pra |
= |
proportion of total accidents constituted by related accidents. |
The proportion of related accidents (Pra) is estimated as 0.35 (i.e., 35 percent) based on thedefault distribution of accident types presented in table 2. This default accident type distribution, and therefore the value of Pra, may be changed by a highway agency as part of the calibration process.
The AMFs for lane width for roadways with ADT greater than 2,000 veh/day are based on the results of Zegeer et al.(6) Furthermore, these values are reasonably consistent with the results of Zegeer et al.(7,8) and Miaou.(9) The AMF of 1.05 for 3.3-m (11-ft) lane widths on roadways with ADTs over 2,000 veh/day has been adjusted to a lower value than that indicated by Zegeer et al.(6) based on the expert panel’s assessment of a broader set of studies concerning the safety performance of roadways with 3.3-m (11-ft) lanes. The AMFs for lane widths on roadways with ADTs less than 400 veh/day are based on the results of Griffin and Mak.(10) The transition lines in the ADT range from 400 to 2,000 veh/day are based on a judgment by the expert panel.
Shoulder Width and Type
The nominal or base value of shoulder width and type is a 1.8-m (6-ft) paved shoulder, which is assigned an AMF value of 1.00. Figure 3 illustrates the recommended AMF for shoulder widths that differ from 1.8 m (6 ft). Another AMF, presented below, adjusts for differences between gravel, turf, or composite shoulders and paved shoulders. The modification factors in figure 3 illustrate that, for ADTs above 2,000 veh/day, the effect of a 0.6-m (2-ft) change in shoulder width is equivalent to the effect of a 0.3-m (1-ft) change in lane width. For ADTs below 400 veh/day, the effect of a 0.3-m (1-ft) change in shoulder width is equivalent to the effect of a 0.3-m (1-ft) change in lane width. A linear transition between these effects occurs over the range of ADTs from 400 to 2,000 veh/day. AMFs for shoulder widths between 0 and 2.4 m (0 and 8 ft) should be interpolated between the lines in figure 3. Shoulders greater than 2.4 m (8 ft) in width should be assigned AMFs equal to those for 2.4 m (8 ft). The AMFs shown in figure 3 apply only to single-vehicle run-off-the-road and opposite-direction accidents.
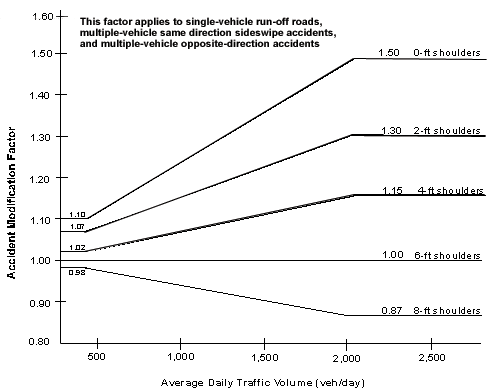
Figure 3. Accident Modification Factor for Shoulder Width.
The AMFs for shoulder width on rural two-lane highways with ADTs over 2,000 veh/day are based primarily on the results of Zegeer et al.(6) which suggests the 2:1 ratio between the effects of lane and shoulder widths. This finding is reasonably consistent with the results of Miaou(9,11) and Rinde.(12) The AMFs for roadways with ADTs less than 400 veh/day, which indicate a 1:1 ratio between the effects of lane width and shoulder width, are based on the work of Zegeer et al.(8) for low-volume roads. The transition curves in the ADT range from 400 to 2,000 veh/day are based on a judgment by the expert panel.
The nominal or base condition for shoulder type is the paved shoulder. Table 3 presents the recommended AMFs for gravel, turf, and composite shoulders as a function of shoulder width. The AMFs shown in table 3 apply to single-vehicle run-off-the-road and opposite-direction accidents.
Table 3. Accident Modification Factors for Shoulder Types on Two-Lane Highways.
Shoulder
type |
Shoulder width (ft) |
| 0 |
1 |
2 |
3 |
4 |
6 |
8 |
10 |
| Paved |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
| Gravel |
1.00 |
1.00 |
1.01 |
1.01 |
1.01 |
1.02 |
1.02 |
1.03 |
| Composite |
1.00 |
1.01 |
1.02 |
1.02 |
1.03 |
1.04 |
1.06 |
1.07 |
| Turf |
1.00 |
1.01 |
1.03 |
1.04 |
1.05 |
1.08 |
1.11 |
1.14 |
Conversion: 1 ft = 0.305 m
Note: The values for composite shoulders in this table represent a shoulder for which 50 percent of the shoulder width is paved and 50 percent of the shoulder width is turf.
The panel made a judgment that the shoulder type effect observed by Miaou (9) was appropriate to characterize the difference between gravel and paved shoulders and that the effect observed by Zegeer et al. (6) was appropriate to characterize the difference between turf and paved shoulders. The composite shoulders represented by table 3 represent a shoulder for which 50 percent of the shoulder width is paved and 50 percent of the shoulder width is turf. The AMFs for composite shoulders are averages of the AMFs for paved and turf shoulders.
Table 3 assumes that the base condition for shoulder type is a paved shoulder. In fact, the data base used to develop the base model for roadway sections shown in equation (4) consisted of approximately 67 percent paved and composite shoulders and 33 percent gravel shoulders. However, the difference in safety performance between paved and gravel shoulders is so small that the magnitude of the AMFs is only minimally affected by the proportion of gravel shoulders in the data base. Therefore, the use of table 3 without modification is recommended. If, at any future time, the base model for roadway sections is replaced or updated, it is recommended that either (1) the model be based solely on roadway sections with paved shoulders; or (2) that shoulder type appear explicitly in the base model.
If the shoulder types and/or widths for the two directions of travel on a roadway segment differ, the AMF should be determined separately for the shoulder type and width in each direction of travel and the resulting AMFs should then be averaged.
The AMFs for shoulder width and type apply only to single-vehicle run-off the-road and multiple-vehicle head-on, opposite-direction sideswipe, and same-direction sideswipe accidents. The AMFs expressed on this basis must, therefore, be adjusted to total accidents within the accident prediction algorithm. This can be accomplished with the following equation that is analogous to equation (15):
where:
|
AMF = (AMFwra AMFtra - 1.0) Pra + 1.0
|
|
| AMFwra |
= |
accident modification factor for related accidents based on shoulder width (from figure 4); and |
| AMFtra |
= |
accident modification factor for related accidents based on shoulder type (from table 3). |
The proportion of related accidents (Pra) is estimated as 0.35 (i.e., 35 percent) based on the default distribution of accident types presented in table 2. This default accident type distribution and therefore the value of Pra, may be changed by a highway agency as part of the calibration process.
Horizontal Curves
Length, Radius, and Presence or Absence of Spiral Transitions
The nominal or base condition for horizontal alignment is a tangent roadway section. An AMF has been developed to represent the manner in which accident experience of curved alignments differs from that of tangents. This AMF applies to total roadway segment accidents, not just the related accident types considered above for lane and shoulder widths.
The AMF for horizontal curves has been determined from the regression model developed by Zegeer et al.(13) The Zegeer model includes the effects on accidents of length of horizontal curve, degree of horizontal curve, and presence or absence of spiral transition curves. The Zegeer model could also be used to introduce an effect of lane width on horizontal curves that differs from the effect of lane width on tangents. No data are available to represent any differential effect of shoulder width between horizontal curves and tangents.
The AMF for horizontal curvature is in the form of an equation and, thus, might be termed an accident modification function rather than an accident modification factor. The AMF for length, radius, and presence or absence of spiral transitions on horizontal curves is:
| AMF = |
|
|
80.2
|
|
(17)
|
| |
1.55Le +
|
|
- 0.012S |
| |
|
R
|
|
1.55Le
|
| Lc |
= |
length of horizontal curve (mi); |
| R |
= |
radius of curvature (ft); and |
| S |
= |
1 if spiral transition curve is present
0 if spiral transition curve is not present. |
where:
In applying the accident modification functions for curves with spiral transitions, the length variable (Lc) should represent the length of the circular portion of the curve.
Superelevation
The nominal or base condition for the AMF for the superelevation of a horizontal curve is the amount of superelevation required by the AASHTO Green Book.(14) The superelevation required by the AASHTO Green Book must be determined taking into account the value of maximum superelevation rate, emax, established by highway agency policies. Policies concerning maximum superelevation rates for horizontal curves vary between highway agencies based on climate and other considerations. If no value of emax specified by the particular highway agency has been incorporated in the IHSDM, then emax = 0.06 will be assumed by default. The AMF for superelevation is based on the superelevation deficiency of a horizontal curve (i.e., the difference between the actual superelevation and the superelevation required by AASHTO policy). When the actual superelevation meets or exceeds that required by AASHTO policy, the value of the superelevation AMF is 1.00. The expert panel made a judgment that there would be no effect of superelevation deficiency on safety until the superelevation deficiency exceeds 0.01.
The general functional form of an AMF for superelevation is shown in figure 4, based on the work of Zegeer et al.(13,15) For a horizontal curve with 12-ft lanes and no spiral transitions, the Zegeer work suggests an AMF of the form:
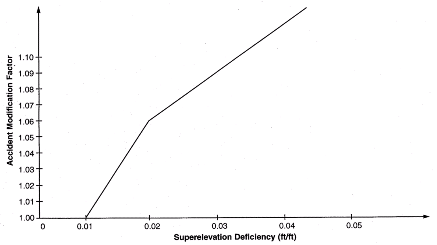
Figure 4. Accident Modification Factor for Superelevation Deficiency.
| AMF = |
|
|
1604
|
|
(18)
|
| |
1.22 +
|
|
+ 9.52SD |
| |
|
R
|
|
|
| |
|
1604
|
|
| |
1.22 +
|
|
|
|
|
|
R
|
|
where:
| SD |
= |
superelevation deficiency. |
However, the AMF in the form shown in equation (18) is not directly usable because it suggests that for any given superelevation deficiency, the value of AMF increases with increasing radius of curvature. In fact, it seems likely that the opposite should occur, with superelevation deficiencies being more important on curves with smaller radii.
Zegeer, et al. (15) indicate that the mean radius of horizontal curves in their study was 257.0 m (842.5 ft). For this mean radius, equation (18) indicates the following values of the AMF:
Superelevation
deficiency |
AMF |
| 0.02 |
1.06 |
| 0.03 |
1.09 |
| 0.04 |
1.12 |
| 0.05 |
1.15 |
Based on these values and the expert panel’s judgment that there is no effect on safety until the superelevation deficiency reaches 0.01, the following relationships which form the basis for figure 5 can be derived:
|
AMF = 1.00 + 6 (SD - 0.01) for 0.01 £ SD < 0.02
|
|
|
AMF = 1.06 + 3 (SD - 0.02) for SD ³ 0.02
|
|
This AMF applies to total roadway segment accidents for roadway segments located on horizontal curves.
Grades
The nominal or base condition for grade is a level roadway (0% grade). Table 4 presents the accident modification factor for grades based on an analysis of two-lane highway grades in Utah conducted by Miaou.(16) This analysis considered accident and geometric data for approximately 4,000 km (2,500 mi) of two-lane roads with 88.5 km/h (55-mi/h) speed limits, 3.6-m (12-ft) lanes, and tangent alignment. Two analysis approaches were used: univariate analysis using smoothing techniques and negative binomial regression modeling. Both methods estimated the effect of vertical grade on accidents as approximately a 1.6 percent increase in accidents per 1 percent increase in grade. However, both studies found this effect to be not statistically significant.
Despite the lack of statistical significance of the results, a decision was reached by the expert panel to use the observed effect as the basis for an AMF because the result appeared reasonable to the expert panel and because no more reliable results are available. Table 4 presents AMFs for grade based on the observed 1.6 percent increase in accidents per 1 percent increase in percent grade. The AMFs in table 4 are applied to each individual grade section on the roadway being evaluated without respect to the sign of the grade. The sign of the grade is irrelevant because each grade on a two-lane highway is an upgrade for one direction of travel and a downgrade for the other. The grade factors are applied to the entire grade from one point of vertical intersectional (PVI) to the next (i.e., there is no special account taken of vertical curves). The AMFs in table 4 apply to total roadway segment accidents.
Table 4. Accident Modification Factors for Grade of Roadway Sections
|
Grade (%)
|
| 0 |
2 |
4 |
6 |
8 |
| 1.00 |
1.03 |
1.07 |
1.10 |
1.14 |
Note: This factor can be expressed as an effect of 1.6 percent per percent grade.
Driveway Density
The nominal or base condition for driveway density is three driveways per km (five driveways per mi). The AMF for driveway density is based on the following equation derived from the work of Muskaug:(17)
|
AMF =
|
0.2 + [0.05 - 0.005 ln (ADT)] DD |
|
|
| 0.2 + [0.05 - 0.005 ln (ADT)] (5) |
where:
| ADT |
= |
annual average daily traffic volume of the roadway being evaluated (veh/day); and |
| DD |
= |
driveway density (driveways per mile). |
The Muskaug study deals with injury accidents only but the expert panel made a judgment that the AMF shown in equation (22) can be applied to total roadway accidents of all severity levels.
The expert panel considered the Norwegian study by Muskaug to be the best available study on the safety effects of driveway density on rural two-lane highways. The panel was concerned, however, about reliance on an international data source and undertook a further review of relevant U.S. literature. The most applicable U.S. reference appeared to be Transportation Research Circular 456, and an analysis concluded that its results were consistent with the findings of Muskaug.(18) Still another review of HSIS data from Minnesota concluded that the effect of driveway density in accidents is consistent with the results of the Muskaug study. Therefore, the Muskaug results were retained as the basis for the driveway density AMF.
Passing Lanes
The nominal or base condition for passing lanes is the absence of a lane (i.e., the normal two-lane cross section). The AMF for a conventional passing or climbing lane added in one direction of travel on a two-lane highway is 0.75 for total accidents in both directions of travel over the length of the passing lane from the upstream end of the lane addition taper to the downstream end of the lane drop taper. This value assumes that the passing lane is operationally warranted and that the length of the passing lane is appropriate for the operational conditions on the roadway. An IHSDM procedure other than the accident prediction algorithm should be used to warn users if a passing lane is not operationally warranted or if an inappropriate passing lane length is used. Passing lanes are known to have traffic operational effects that extend 5 to 13 km (3 to 8 mi) downstream of the passing lane; while it might be presumed that these operational effects provide analogous safety benefits over a similar length of highway, no such effect is included in the accident prediction algorithm for lack of quantitative evidence of such a benefit.
The AMF for short four-lane sections (i.e., side-by-side passing lanes provided in opposite directions on the same roadway section) is 0.65 for total accidents over the length of the short four-lane section. This AMF applies to any portion of roadway where the cross section has four lanes and where both added lanes have been provided over a limited distance to increase passing opportunities. This AMF does not apply to extended four-lane highway sections.
The AMF for passing lanes is based primarily on the work of Harwood and St. John, with consideration also given to the results of Rinde and Nettleblad.(19, 12, 20) The AMF for short four-lane sections is based on the work of Harwood and St. John.(19) These AMFs apply to total roadway segment accidents within the passing lane and short four-lane sections.
Two-Way Left-Turn Lanes
The installation of a center two-way left-turn lane (TWLTL) on a two-lane highway to create a three-lane cross section can reduce accidents related to turning maneuvers at driveways. The AMF for installation of a TWLTL is:
where:
| PD |
= |
driveway-related accidents as a proportion of total accidents; and |
| PLT/D |
= |
left-turn accidents susceptible to correction by a TWLTL as a proportion of driveway-related accidents. |
The value of PAP is estimated from the work of Hauer as:(21)
|
PD =
|
0.0047DD + 0.0024DD2
|
(24) |
|
| 1.199 + 0.0047DD + 0.0024DD2 |
The value of PLT/D was estimated by the expert panel as 0.5.
The expert panel considers that equations (23) and (24) provides the best estimate of the AMF for TWLTL installation that can be made without data on the left-turn volumes within the TWLTL. Realistically, such volumes are seldom available to highway agencies for use in such analyses. The AMF, as adjusted in equation (23), applies to total roadway segment accidents. Equation (24) was initially developed to represent total access point density (driveways plus unsignalized intersections). However, it is used here to determine an AMF for driveway density alone, because the effects of left-turn lanes at intersections are considered separately below.
The AMF for TWLTL installation should not be applied unless the driveway density is greater than or equal to three driveways per km (five driveways per mi). If the driveway density is less than three driveways per km (five driveways per mi), the AMF for TWLTL installation is 1.00. TWLTL installation would, in any case, be inappropriate for roadway segments with driveway densities lower than this threshold.
Roadside Design
For purposes of the accident prediction algorithm, the quality of roadside design is represented by the roadside hazard rating (1 to 7 scale) developed by Zegeer et al. (6) No studies were found in the literature that presented satisfactory relationships between the roadside hazard rating and accident experience for two-lane highways. Therefore, the AMF for roadside design was derived directly from the base model for roadway sections presented in equation (5). The nominal or base value of roadside hazard rating employed in the base model for roadway sections is 3. The AMF is based on the ratio of the accident experience predicted by base model using the actual roadway section in question to the accident experience predicted by the base model using the nominal value of roadside hazard rating equal to 3. The AMF is:
|
AMF =
|
exp(-0.6869 + 0.0668RHR)
|
(25) |
|
| exp (-0.4865) |
This AMF applies to total roadway segment accidents. Photographic examples and quantitative definitions for each roadside hazard rating (1 through 7) as a function of roadside design features such as side slope and clear zone width are presented in appendix D.
The expert panel encourages future development of AMFs for specific roadside design elements in as much detail as the roadway design factors in this accident prediction algorithm. For example, the algorithm could be made sensitive to the presence or absence of a guardrail at specific roadside slopes and at individual roadside obstacles. The Roadside Safety Analysis Program (RSAP) model currently being developed might be applied for this purpose rather than just as a benefit/cost tool for comparing roadside design alternatives.(22) However, the RSAP model is not yet complete and the consensus of the panel was that application of the RSAP model would be beyond the scope of this initial effort to develop the accident prediction algorithm.
At-Grade Intersections
The AMFs for geometric design and traffic control features of at-grade intersections are presented below. As explained above, AMFs have been developed only for those geometric design and traffic control features for which the expert panel found a suitable basis for quantifying an AMF.
Number of Intersection Legs
There is no separate AMF for the number of intersection legs. Instead, the effect of the number of intersection legs will be accounted for by the separate base models for three- and four-leg intersections like those presented in section 3 of this report. Base models have been developed for both three- and four-leg STOP-controlled intersections, while base models for signalized intersections have been developed for four-leg intersections only. No base models will be developed for intersections with more than four legs. Therefore, multi-leg intersections and three-leg signalized intersections will not be addressed by the initial version of the accident prediction algorithm.
Intersection Skew Angle
The nominal or base condition for intersection skew angle is 0 degrees of skew (i.e., an intersection angle of 90 degrees). The skew angle for an intersection was defined as the deviation from an intersection angle of 90 degrees and carries a positive or negative sign that indicates whether the minor road intersects the major road at an acute or obtuse angle. This sign was introduced into the base model because a Finnish study by Kulmala found that acute and obtuse skew angles affected safety differently.(23)
STOP-Controlled Intersections
The AMF for intersection angle at three-leg STOP-controlled intersections is derived from the base model for this intersection type. Because the intersection angle variable was not statistically significant at the 0.015 significance level, it did not appear in the base model in equation (7). Therefore, the base model presented in equation (49) in appendix B with additional variables, including the intersection angle variable, was used to derive the following AMF:
|
AMF =
|
exp(-12.15 + 1.001ln ADT1 + 0.406ln ADT2 + 0.0040SKEW3)
|
(26)
|
|
| exp(-12.15 + 1.001ln ADT1 + 0.406ln ADT2) |
where:
| ADT1 |
= |
average daily traffic volume for the major road; |
| ADT2 |
= |
average daily traffic volume for the minor road; and |
| SKEW3 |
= |
intersection angle (degrees) minus 90 for the angle between the major-road leg in the direction of increasing stations and a leg to the right; 90 minus intersection angle (degrees) for the angle between the major-road leg in the direction of increasing stations and a leg to the left. |
Equation (26) reduces to:
The AMF for intersection angle at four-leg STOP-controlled intersections is based directly on the base model presented as equation (9) for this intersection type:
|
AMF =
|
exp(-9.15 + 0.534ln ADT1 + 0.665ln ADT2 + 0.0054SKEW4)
|
(28)
|
|
| exp(-9.15 + 0.534ln ADT1 + 0.665ln ADT2 ) |
| SKEW4 |
= |
intersection angle (degrees) expressed as one-half of the angle to the right minus one-half of the angle to the left for the angles between the major-road leg in the direction of increasing stations and the right and left legs, respectively |
Equation (28) reduces to:
The opposite signs of the coefficients of skew angle in equations (27) and (29) are a concern because the difference in sign implies that positive and negative skew angles (as defined above for available SKEW3 and SKEW4) have opposite effects on safety at three- and four-leg intersections. On further review, the expert panel decided that the results of the Kulmala study alone did not provide a sufficient basis for challenging the widely accepted view that any intersection skew that departs from a 90-degree angle, whether positive or negative, is detrimental to safety. Therefore, equations (27) and (29) have been recast as shown below. For a three-leg STOP-controlled intersection:
For a four-leg STOP-controlled intersection:
where:
| SKEW |
= |
intersection skew angle (degrees), expressed as the absolute value of the difference between 90 degrees and the actual intersection angle. |
These AMFs apply to total intersection accidents.
Signalized Intersections
Skew angle is a much less important factor in the operation of signalized intersection than in the operation of STOP-controlled intersections. Since the traffic signal separates most movements from conflicting approaches, the risk of collisions related to the skew angle between the intersecting approaches is limited at a signalized intersection. Therefore, the AMF for skew angle at four-leg signalized intersections is 1.00 for all cases.
Intersection Traffic Control
The safety differences between STOP-controlled and signalized intersections are accounted for by use of separate base models rather than by an AMF. However, an AMF for the difference between minor-leg and all-way STOP-controlled intersections has been developed and is discussed below. The nominal base case for STOP-controlled intersections has STOP signs on the minor leg(s) only. An AMF is provided for intersection with all-way STOP control. Minor-road YIELD controlled intersections are treated identically to minor-road STOP-controlled intersections in the accident prediction algorithm.
All-way STOP control is most appropriate for lower-speed roadways with relatively equal traffic volumes on all legs of the intersection. The Manual on Uniform Traffic Control Devices (MUTCD) includes specific warrants for all-way STOP control.(24) All-way STOP control should not be considered for an intersection unless these warrants are met. The AMF for conversion from minor-road to all-way STOP-control is 0.53. This AMF applies to total intersection-related accidents. The AMF value of 0.53 implies that an all-way STOP-controlled intersection experiences 47 percent fewer accidents than a two-way STOP-controlled intersection. This AMF is based on the findings of Lovell and Hauer.(25) They collected data for three local agencies (San Francisco, Philadelphia, and Toronto) and one State agency (Michigan). Of these, only the Michigan data pertains to low-volume, high-speed, rural roads. However, since the Michigan data set is small and its results are similar to those for the other three agencies, the recommended AMF is based on the combined data for all four agencies. The expert panel recommended that some other IHSDM module, possibly the diagnostic review module for design of at-grade intersections, should make clear to IHSDM users that all-way STOP-control should be used only when the established warrants are met. This is necessary to discourage indiscriminate use of all-way STOP-control, because it is likely that the substantial safety benefits of all-way STOP control shown below can be attained only when the warrants are met.
Intersection Left-Turn Lanes
The nominal or base condition for intersection left-turn lanes is the absence of left-turn lanes on the major-road approaches. The AMFs for presence of left-turn lanes on the major road are presented in table 5. These AMFs apply to total intersection-related accidents. The expert panel did not find any well-designed before-and-after studies on the accident reduction effectiveness of left-turn lanes. Therefore, the AMFs in the table represent a judgment by the expert panel combining results from several sources. The AMFs for installation of left-turn lanes at STOP-controlled intersections are based on studies by Agent, Bauer and Harwood, California Department of Public Works, Creasy and Agent, Dale, Ermer, Glennon, McCoy et al., McCoy and Malone, and Smith et al. The AMFs for installation of left-turn lanes at signalized intersections are based on studies by Agent, California Department of Public Works, Datta, Smith et al., and McCoy and Malone.(26, 1, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37) The AMFs for installation of left-turn lanes on both approaches to a four-leg intersection are equal to the square of the corresponding AMF for installation of a left-turn lane on a single approach. No data are available to quantify the effect on safety of left-turn lanes on a minor road, so these will not be considered in the accident prediction algorithm.
Table 5. Accident Modification Factors for Installation of Left-turn Lanes on the Major-Road Approaches to Intersection Two-Lane Rural Highways.
| |
Number of major-road approaches on which left-turn lanes are installed |
|
Intersection type
|
Intersection traffic control
|
One approach |
Both approaches |
| Three-leg intersection |
STOP signa
|
0.78
|
-
|
|
Traffic signal
|
0.85
|
-
|
| Four-leg intersection |
STOP signa
|
0.76
|
0.58
|
|
Traffic signal
|
0.82
|
0.67 |
a STOP signs on minor-road approach(es).
Intersection Right-Turn Lanes
The nominal or base condition for intersection right-turn lanes is the absence of right-turn lanes on the major-road approaches. The AMF for the presence of right-turn lanes at STOP-controlled intersections is 0.95 for a right-turn lane on one major-road approach and 0.90 for right-turn lanes on both major road approaches. These AMFs apply to total intersection-related accidents. The expert panel did not find any well-designed before-and-after studies on the accident reduction effectiveness of right-turn lanes. Therefore, the values of the AMFs are based on a judgment by the panel based on the work of Vogt and Bared, Kulmala, and Elvik.(3, 4, 5, 23, 38) No data are available to quantify the effect on safety of right-turn lanes on a minor road, so these are not considered in the accident prediction algorithm. Also, no effect is considered for the provision of a paved shoulder on an intersection approach unless that paved shoulder is marked as a right-turn lane.
No studies that the expert panel considered appropriate were found concerning the accident reduction effectiveness of right-turn lanes at signalized intersections. Therefore, the panel made a judgment that the effectiveness of right-turn lanes at signalized intersections should be estimated as half that found at STOP-controlled intersections. Thus, the AMF for the presence of right-turn lanes at signalized intersections is 0.975 for a right-turn lane on one major-road approach and 0.95 for right-turn lanes on both major-road approaches. These AMFs also apply to total intersection-related accidents.
Intersection Sight Distance
The nominal or base condition for intersection sight distance is the availability of adequate intersection sight distance along the major road in all quadrants of the intersection. The AMFs for intersection sight distance at intersections with STOP control on the minor leg(s) are:
- 1.05 if sight distance is limited in one quadrant of the intersection.
- 1.10 if sight distance is limited in two quadrants of the intersection.
- 1.15 if sight distance is limited in three quadrants of the intersection.
- 1.20 if sight distance is limited in four quadrants of the intersection.
These AMFs apply to total intersection-related accidents.
Sight distance in a quadrant is considered limited if the available sight distance is less than the sight distance specified by AASHTO policy for a design speed of 20 km/h less than the major-road design speed. Only sight distance restrictions due to roadway alignment and terrain are considered by the accident prediction algorithm. Sight distance restrictions due to specific obstructions (e.g., trees, bushes, poles, and buildings) are not available in the CAD system and, therefore, are not to be considered by the accident prediction algorithm.
The AMFs for intersection sight distance apply only to two-way STOP-controlled or YIELD-controlled intersections. An AMF of 1.00 is applicable to signal-controlled and all-way STOP-controlled intersections.
There was no single evaluation of the effects of intersection sight distance on accidents that the panel found to be most credible. Therefore, the recommended AMF was determined from the panel’s best judgment based on the results of Kulmala, Brüde and Larsson, and Elvik.(39, 38) These results were assumed to represent sight distance improvements in all quadrants of an intersection. Therefore, this effect was proportioned on a per-quadrant basis for application in the accident prediction algorithm.
Previous | Table of Contents | Next
|
