Prediction of the Expected Safety Performance of Rural Two-Lane Highways
APPENDIX C
CALIBRATION PROCEDURE TO ADAPT THE ACCIDENT PREDICTION ALGORITHM TO THE DATA OF A PARTICULAR HIGHWAY AGENCY
This appendix presents a calibration procedure for use with the accident prediction algorithm. The purpose of the calibration procedure is to allow potential users of the algorithm to scale the accident predictions to be suitable for the roads under the jurisdiction of their agency.
The base models that form a key element of the accident prediction algorithm are based on data from several States. The roadway section base models were based on data from Minnesota and Washington, but are implemented in the accident prediction algorithm for Minnesota conditions (i.e., STATE=0 in Equation (42). The base models for STOP-controlled intersections are based on Minnesota data, and the base models for signalized intersections are based on combined data from California and Michigan. The development of these base models has been documented in appendix B of this report.
The calibration procedure provides a method for highway agencies other than those identified above to adapt the accident prediction algorithm to their own safety conditions. Because safety conditions change over time, even a state whose data were used in the development of the base models should consider applying the calibration procedure every 2 or 3 years.
The accident prediction algorithm applies to rural two-lane highways. Safety conditions and the resulting accident rates and distributions of accident severities and accident types, on rural two-lane highways, vary substantially from one highway agency to another. Some of these variations are due to geometric design factors, such as differences in the distributions of lane and shoulder width, and differences in terrain, which lead to differences in horizontal and vertical alignment. These geometric design factors are accounted for by the accident prediction algorithm and should not require calibration to allow the algorithm to be used by different agencies.
By contrast, there are several factors that lead to safety differences between highway agencies in different geographical areas that are not directly accounted for by the accident prediction algorithm. These include:
- Differences in climate (i.e., exposure to wet pavement and snow-and-ice-covered pavement conditions).
- Differences in animal populations that lead to higher frequencies of collision with animals in some States than in others.
- Differences in driver populations and trip purposes (i.e., commuter vs. commercial travel vs. recreational travel).
- Accident reporting thresholds established by State law (i.e., minimum property damage threshold that requires reporting of an accident).
- Accident investigation practices (i.e., some police agencies are much more diligent about investigating and reporting property-damage-only collisions than others).
The calibration procedure is intended to account for these differences and provide accident predictions that are comparable to the estimates that a highway agency would obtain from its own accident records system.
The tables for the calibration procedure are presented in this appendix using conventional units, because all of the underlying equations and data are in conventional units. A metric conversion chart is included for the convenience of those who wish to implement the calibration procedure in metric units.
How Does the Calibration Procedure Affect the Accident Predictions?
The calibration procedure is implemented by a highway agency by determining the value of calibration factors for roadway sections and at-grade intersections from comparison of their own data to estimates from the accident prediction algorithm. As shown in section 3 of this report, the calibration factors are incorporated in the accident prediction algorithm in the following fashion for roadway segments and at-grade intersections, respectively:
| Nrs = Nbr Cr (AMF1r AMF2r ... AMFnr) |
(72)
|
| Nint = Nbi Ci (AMF1i AMF2i ... AMFni) |
(73)
|
where:
| Cr |
= |
calibration factor for roadway sections developed for use by a particular highway agency; and |
| Ci |
= |
calibration factor for at-grade intersections developed for use by a particular highway agency. |
The procedures for estimating values of Cr and Ci for a particular highway agency are described later in this section.
The calibration procedure also permits a highway agency to modify the basic accident severity distribution for rural two-lane highways presented in table 1 and the basic accident type distribution for rural two-lane highways presented in table 2 based on their own data.
Who Should Perform the Calibration Procedure?
It is recommended that one division or office within a specific State highway agency should calibrate the accident prediction algorithm for subsequent use by all other highway agency employees and their contractors throughout the State. Because the calibration procedure requires the use of historical accident, roadway, and traffic data for State highways, it is further recommended that the calibration be performed by a division or office of the highway agency that has the following:
- Unrestricted access to the State traffic, accident, and roadway record system(s).
- Capability to generate estimates of roadway mileage and accident experience for various ADT levels.
- Expertise in highway safety analysis procedures.
It is not necessary to calibrate these models to different regions (or districts) within the State, although that certainly can be done if the highway agency wishes by stratifying mileage and accidents by region (or district) and applying the recommended calibration procedures for each region (or district).
Furthermore, since the accident analysis module is only applicable to rural two-lane highways at this time, the models currently cannot be calibrated for different urban areas within the State. As the models for multilane and urban roads are developed, calibration procedures that apply to individual urban areas may also be desirable.
Should the Accident Prediction Algorithm Be Used Without Calibration?
It is possible for a highway agency to use the accident prediction algorithm without calibration, but this is not recommended. Using the accident prediction algorithm without calibration requires the user to accept the assumption that for their agency Cr = 1.0, Ci = 1.0, and the accident severity and accident type distributions for two-lane highways are those shown in tables 1 and 2, respectively. These assumptions are unlikely to be correct for any highway agency and are unlikely to remain correct over time. Even a minimal calibration effort (referred to later in this appendix as level 1 calibration) is likely to produce far more satisfactory results than using the algorithm without calibration.
How Often Should the Accident Prediction Algorithm Be Calibrated?
The recommended calibration procedure uses the three most recent years of accident data for the highway agency’s rural two-lane highway system. Recalibration every year is not necessary because it is unlikely that adding a new year of data and dropping the oldest of the three years used for calibration in the previous year will change the calibration factors substantially. Recalibration every 2 or 3 years is recommended instead.
Recommended Calibration Procedures
It is neither necessary nor recommended for users of the accident prediction algorithm to generate new accident prediction models using accident, roadway, and traffic data from their State and appropriate statistical analysis procedures. It is definitely not recommended for users to change the accident modification factors in the accident prediction algorithm. These AMFs are based on a compilation of the best available research, and they will be updated by FHWA as new research becomes available. Rather, the recommended calibration procedure estimates the values of calibration factors that adapt the outputs from the accident prediction algorithm to the safety conditions experienced by an individual highway agency.
Calibrating the Roadway Segment Accident Prediction Algorithm
Optional levels are available to calibrate the roadway segment accident prediction algorithm. The levels vary in terms of the effort required and the availability of the following:
- Type of data elements maintained within the existing traffic records systems.
- Existence, quality and coverage of roadway, and traffic files.
- Availability and quality of accident data.
- Skills of personnel who will perform the calibration.
- Level of effort and personnel resources that a State is willing to commit to calibration.
The minimum data requirements and anticipated effort for each calibration process level are specified in table 51. Level 1 is deemed the minimum and, compared to the other level, the easier calibration to perform. Level 2 requires more effort, but with a corresponding gain in applicability of the accident prediction algorithm to a particular State's accident experience. It is strongly recommended that the models NOT be used without calibration. Attempting to calibrate using procedures less stringent than the level 1 procedure is strongly discouraged.
Table 51. Minimum Requirements for Calibration Levels 1 and 2
| Calibration process* |
Minimum requirements |
Anticipated effort for calibration |
| Level 1 |
The State must have the ability to:
(1) Stratify all two-lane rural roads by ADT; and
(2) Identify all non-intersection related accidents reported on those two lane rural roads. |
Minimal |
| Level 2 |
Level 1 requirements + the State must have the ability to: (3) Stratify all two-lane rural roads by ADT, shoulder width and lane width. |
Moderate |
* to be selected by the State.
While table 51 describes the minimum data requirements for each calibration level and shows how the calibration levels relate to each other, table 52 identifies the data elements that must be present within the State’s record systems to complete the calibration level. The procedures to perform levels 1 and 2 are described on the following pages.
The basic procedure to be followed in each level involves six steps shown in figure 7. The only difference in the two levels is that, in level 2, step 1 will develop estimates of miles of roadway by lane and shoulder width, as well as by curve and grade.
Road System to be Used in Calibration Process
It is important to recognize that there are differences in State highway agency record systems. Some States, such as California, include only roads under State jurisdiction in their record systems. Others, such as Minnesota, include local roads that are maintained by counties and municipalities. Calibration can be performed using whatever rural two-lane road system the user wishes to apply the accident prediction algorithm to as long as the data are accurate. Specifically, the following should exist:
- A reliable inventory of paved roads.
- Reliable counts of ADT and accidents that can be assigned to specific sections of a highway.
- Ability to stratify sections of highways into different highway types (i.e., the ability to distinguish rural two-lane highways from their highway types).
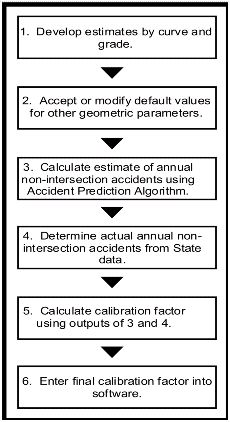
Figure 7. Flow Diagram of Calibration Process.
Table 52. Data Needs for Calibration Levels 1 and 2.
| |
Type of data |
Data element |
Level 1 |
Level 2A |
| Required |
Accident records |
Relationship of accidents to intersections or junctions |
X
|
X
|
| Traffic volume files |
ADT |
X
|
X
|
| Roadway inventory files |
Lane width |
|
X
|
| Shoulder width |
|
X
|
| Desirable |
Alignment inventory files |
Horizontal curve data; |
X
|
X
|
| Grade and vertical curve data |
X
|
X
|
| Access point |
Driveway |
X
|
X
|
It should be noted that the base models used in the accident prediction algorithm were developed for State primary routes that generally had 88-km/h (55-mi/h) speed limits.
If the State has accurate data for county highways and higher order routes but not for municipal highways, then the calibration process should not use municipal or township highways. Rather, data for only the county highways and higher order routes should be used. For example, Utah has data for 20,600 km (12,800 mi) of paved roadways under State jurisdiction and another 51,000 km (32,000 mi) of roadways not under State jurisdiction. A complete roadway inventory to which accidents can be linked is available for the 20,600 km (12,800 mi) system of state roadways, but the other 51,000 km (32,000 mi) have only “zone” records, that do not permit accident records to be linked to specific roadway sections. Consequently, any calibration of the accident prediction model by Utah should use only the 20,600 km (12,800 mi) of roadway under State jurisdiction.
Only paved two-lane highways should be considered in the calibration process.
Level 1 Calibration Process for Roadway Segment Accident Prediction Using ADT Only
Step 1. Develop Estimates of Pavel Rural Two-Lane Highway Mileage by Curve and Grade. The State will first need to estimate the following for all paved rural, two-lane highways in the State for each of five ADT groups:
- Number of miles of tangent roadway.
- Number of miles of roadway on horizontal curves.
- Average degree of curvature for horizontal curves.
- Number of miles of level roadway.
- Number of miles of roadway on grade.
- Average grade percent for roadway on grade.
For States with Alignment (Curve and Grade) Inventory Files
If the State has curve and grade inventory files for paved rural two-lane highways, then it will be possible to calculate the necessary alignment data to perform the calibration. Using their horizontal curve inventory data, the State should first calculate the number of miles of tangent roadway, the number of miles of curved roadway, and the average degree of curve for horizontal curves by ADT interval, using the format shown in table 53. Table 53, and subsequent tables in this section, are presented to illustrate the format in which the calibration calculations should be made; the blank spaces in the tables may be filled in by users of the calibration process. Using its vertical alignment (grade) inventory data files, the State should then calculate the number of miles of two-lane rural roads that are not on grade (e.g., level), the number of miles with non-zero grades, an average percent grade for the miles with non-zero grades, and an overall average percent grade as shown in table 54.
Table 53. Estimated Mileage by ADT Level and Horizontal Alignment.
| ADT Interval |
Number of Tangent Miles |
Number of Curved Miles |
Average Degree of Curvature for Curved Miles (D) |
Average Radius of Horizontal Curvea |
Average Length of Curve |
| < 1000 |
|
|
|
|
|
| 1,001- 3,000 |
|
|
|
|
|
| 3,001- 5,000 |
|
|
|
|
|
| 5,001- 10,000 |
|
|
|
|
|
| > 10,000 |
|
|
|
|
|
a Calculated as 5729.58 / (D).
Table 54. Estimate Mileage by ADT Level and Vertical Alignment.
| ADT Interval |
Number of Level Miles (Ml) |
Number of Miles on Grade (Mg) |
Average Percent Grade for Miles on Grade (Pg) |
Average Percent Gradea |
| < 1000 |
|
|
|
|
| 1,001- 3,000 |
|
|
|
|
| 3,001- 5,000 |
|
|
|
|
| 5,001- 10,000 |
|
|
|
|
| > 10,000 |
|
|
|
|
a Calculated as [(Ml ) * (0) + (Mg) * (Pg)] / [Ml + Mg].
For States without Alignment (Curve and Grade) Inventory Files
For States without curve or grade files, they can use an estimation procedure that will calculate “default” values for curve and grade mileages and average degree of curve and percent grade values based on the percent of rural two-lane miles that fall into each of the three terrain groups—flat, rolling, and mountainous. Thus, the State needs to estimate the mileage by ADT interval and the percentage of mileage in flat, rolling, and mountainous terrains, which could be derived from Highway Performance Monitoring System (HPMS) data. Then, the State will need to determine the mileages by ADT intervals and the percentages of level, rolling, and mountainous terrain.
Default values for percent of tangent and curved miles and the average degree of curve for the curved miles were based on analyses of States in the HSIS database which had both a curve file and terrain information. Based on these analyses, default values for proportion of two-lane rural miles that are curved and the average degree of curve for these miles are as follows:
- Flat: percent of non-tangent miles = 19 percent; average degree of curvature= 2°.
- Rolling: percent of non-tangent miles = 24 percent; average degree of curvature = 4°.
- Mountainous: percent of non-tangent miles = 38 percent; average degree of curvature =8 °.
Similarly, information on default values for percent of non-flat miles and average grade for non-flat mileage from HSIS States were used to calculate the following default values:
- Flat: percent of non-flat miles = 87 percent; average grade = 1.5 percent.
- Rolling: percent of non-flat miles = 91 percent; average grade = 2.0 percent.
- Mountainous: percent of non-flat miles = 97 percent; average grade = 3.7 percent.
Tables 55 and 56 illustrate the data that are required.
Table 55. Estimated Mileage by ADT Interval.
| ADT Interval |
Estimated miles of paved, two-lane rural highways |
| < 1000 |
|
| 1,001- 3,000 |
|
| 3,001- 5,000 |
|
| 5,001- 10,000 |
|
| > 10,000 |
|
Table 56. Estimated Proportion of Mileage by Terrain.
| Terrain |
Proportion of paved, two-lane rural highways (percentage) |
| Flat |
|
| Rolling |
|
| Mountainous |
|
| Total |
100%
|
These values in tables 55 and 56 will then be used by the calibration software to produce estimates of the following:
- Number of miles of tangent roadway.
- Number of miles of roadway on horizontal curves.
- Average degree of curvature for horizontal curves.
- Average radius of horizontal curves.
- Average length of horizontal curves.
- Number of miles if level roadway.
- Number of miles of roadway on grade.
- Average percent grade for roadway on grade.
- Statewide average percent grade.
Step 2. Accept or Modify Default Values for Other Geometric Parameters. In addition to the values of curvature and grade developed in the proceeding step, the calibration procedure requires other geometric parameters. Using data from a sample of States during the calibration procedure development, it has been found reasonable to use the following default values for these parameters:
- Shoulder type = paved.
- Driveway density = three driveways/km (five driveways/mi).
- Passing lane = not present.
- Short four-lane section = not present.
- Two-way left turn lanes = not present.
- Roadside hazard rating = 3.
- For horizontal curves:
- no spiral transition present; and
- superelevation is not deficient (e.g., AMF = 1.0).
For level 1 calibration (which does not require data to be input for lane width and shoulder width), the following default values were estimated based on average values for two-lane highways obtained from eight HSIS States and are recommended for use:
|
DEFAULT VALUES FOR LEVEL 1 CALIBRATION
|
| ADT Interval (Vehicles/day) |
ADT
(vehicles/day)
|
Lane Width
(ft)
|
Shoulder Width
(ft)
|
| < 1000 |
400
|
11
|
3.5
|
| 1,000 - 3,000 |
1800
|
11.5
|
5
|
| 3,001 - 5,000 |
3900
|
12
|
5
|
| 5,001 - 10,000 |
6900
|
12
|
6.25
|
| > 10,000 |
13800
|
12
|
6.5
|
The State may accept these defaults as presented and proceed onward. However, if a State has a better estimate for a value [e.g., if average driveway density is known to be equal to four driveways/km (seven driveways/mi), rather than three driveways/km (five driveways/mi)], or if the predominant two-lane roadway design used in a particular State differs from these assumed defaults (e.g., if the predominant rural two-lane highway shoulder type is unpaved, rather than paved), then the user should feel free to modify the defaults.
Step 3. Calculate Estimate of Annual Non-Intersectional Accidents Using the Accident Prediction Algorithm. Using the roadway segment accident prediction algorithm, calculate the estimated annual number of non-intersection accidents for tangents and horizontal curves. Then, sum the total. Table 57 illustrates how the predicted number of accidents per year can be determined by the calibration software.
Table 57. Calculate the Predicted Annual Number of Non-Intersection Accidents as a Function of ADT.
|
ADT (veh/day)
|
Assumed
mean of ADT interval* |
Mileage of rural two lane highways |
Predicted number of non-intersection accident per year** |
| Tangent |
Curve |
Total |
Tangent |
Curve |
Total |
| 1,000 |
400 |
|
|
|
|
|
|
| 1,000-3,000 |
1,800 |
|
|
|
|
|
|
| 3,001-5,000 |
3,800 |
|
|
|
|
|
|
| 5,001-10,000 |
7,000 |
|
|
|
|
|
|
| >10,000 |
13,500 |
|
|
|
|
|
|
* Generally the average is less than the midpoint of the ADT interval.
** Determined with the uncalibrated accident prediction algorithm for roadway segments
Step 4. Determine Actual Annual Non-Intersection Accidents from State Data.
Using data from the last 3 years, determine the actual number of non-intersection accidents per year that were reported on the rural two-lane highways. First, determine the number of total accidents on the selected rural two-lane highways. Then, deduct all accidents on those rural two-lane highways that were identified by the investigating officer as being “at intersection” or “intersection-related.”
With respect to this criterion, the State must determine the most appropriate field(s) to establish intersection-relatedness. for example, a State may have a field for “type of event location” or “site location” or “relationship to junction” on its accident report form that includes categories such as intersection, junction area, non-junction area, driveway access, and alley access. Some States have an explicit field for “relation to intersection” with categories for yes or no. The decision on which field to use is left to the user. It is important to note that driveway accidents are NOT considered intersection accidents and should NOT be excluded from the calibration data for roadway segments. Driveway accidents were included in the data set from which the roadway segment base model was developed and, therefore, driveway accidents should not be excluded with intersection accidents.
Step 5. Calculate Calibration Factor Using Outputs of Steps 3 and 4. Calculate the calibration factor (Cr) as the ratio of the total number of reported non-intersection accidents (from step 3) to the total number of predicted non-intersection accidents (from step 2).
Step 6. Enter Final Calibration Factor into Software. The preceding five steps will produce a calibration factor based on the user’s inputs. At this point, the user will usually accept the calibration factor as calculated. However, if the resulting factor appears unreasonable (perhaps because of data problems of which the user is aware), it may be modified before entry into the system. Once accepted by the user, the value of the calibration factor (Cr) should be entered into a file of default input values for the accident prediction algorithm. In subsequent applications of the accident prediction algorithm, this value of Cr will be used in applying equation (72). As discussed earlier, the user can, and should, update the calibration factor every 2 or 3 years.
Level 2 Calibration Process for Roadway Segment Accident Prediction Using ADT, Lane Width, and Shoulder Width
Step 1. Develop Estimates of Mileage by Curve and Grade and Lane and Shoulder Width. The State will first need to stratify the mileage of their paved rural, two-lane highways in the State by the following factors and associated levels:
- ADT
-
< 1000 veh/day
1,001 - 3,000 veh/day
3,001 - 5,000 veh/day
5,001 - 10,000 veh/day
>10,000 veh/day
- Lane Width
< 2.9 m (9.5 ft)
9.5-10.5 2.9-3.2 m (9.5-10.5 ft)
3.2-3.5 m (10.5-11.5 ft)
>3.5 m (11.5 ft)
- Shoulder Width
< 0.9 m (3 ft)
0.9-1.5 m (3-5 ft)
1.5-2.1 m (5-7 ft)
2.1 m (7 ft)
- Horizontal Alignment
For States with Alignment (Curve and Grade) Inventory Files
If the State has curve and grade inventory files, then it will be possible to calculate the necessary alignment data to perform the calibration. Using their horizontal curve inventory data, they should first estimate the number of miles of tangent roadway, the number of miles of curved roadway and the average degree of curve for horizontal curves for each unique combination of ADT interval, lane width and shoulder width. Table 58 illustrates this for a portion of all possible combinations.
Using their vertical alignment (grade) inventory data files, the State should then calculate the number of miles of two-lane rural roads that are not on grade (e.g., level), the number of miles with non-zero grades, an average percent grade for the miles with non-zero grades, and an overall average percent grade as shown in table 59.
For simplification purposes, it can be assumed that the average percent grade computed for an ADT interval is equally applicable across lane widths and shoulder widths within that interval. By way of an example, consider the case where 1.9 percent is computed as the average percent grade for all two-lane rural roads within the <1000 ADT interval. The 1.9 percent grade can be assumed for all lane and shoulder width combinations having ADTs less than 1,000 veh/day, as illustrated in table 60.
For States without Alignment (Curve and Grade) Inventory Files
For States without curve or grade files, they can use an estimation procedure that will calculate “default” values for curve and grade mileages and average degree of curve and percent grade values based on the percent of rural two-lane miles that fall into each of the three terrain groups—flat, rolling, and mountainous. Thus, the State needs to estimate the mileage by ADT interval, lane width and shoulder width, and the percentage of mileage in flat, rolling, and mountainous terrains, which could be derived from HPMS data. Then, the State will need to enter the mileages by ADT intervals and the flat, rolling, and mountainous percentages into the calibration software. Tables 61 and 62 illustrate the data that are required.
Default values for percent of tangent and curved miles and the average degree of curve for the curved miles were based on analyses of States in the HSIS database which had both a curve file and terrain information. Based on these analyses, default values for proportion of two-lane rural miles that are curved and the average degree of curve for these miles are as follows:
- Flat: percent of non-tangent miles = 19 percent; average degree of curvature = 2°.
- Rolling: percent of non-tangent miles = 24 percent; average degree of curvature = 4°.
- Mountainous: percent of non-tangent miles = 38 percent; average degree of curvature = 8°.
Table 58. Develop Estimates Required for Alignment Components of the Procedure.
| ADT interval |
Lane width (ft) |
Shoulder width (ft) |
Number of miles on tangent |
Number of miles on horizontal curves |
Average degree of curvature (D) |
Average radius of horizontal curvea (ft) |
Average length of curve (mi) |
| < 1000 |
< 9.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| 9.5 to 10.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| 10.5 to 11.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| > 11.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| 1,001 to 3,000 |
< 9.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| 9.5 to 10.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| 10.5 to 11.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
| > 11.5 |
< 3 |
|
|
|
|
|
| 3 to 5 |
|
|
|
|
|
| 5 to 7 |
|
|
|
|
|
| > 7 |
|
|
|
|
|
a Calculated as 5729.58 / (D).
Table 59. Estimate Mileage by ADT Level and Vertical Alignment
| ADT interval |
Number of miles of level roadway (Ml) |
Number of miles on grade (Mg) |
Average percent grade for miles of roadway on grade (Pg) |
Average percent gradea |
| < 1000 |
|
|
|
|
| 1,001-3,000 |
|
|
|
|
| 3,001-5,000 |
|
|
|
|
| 5,001-10,000 |
|
|
|
|
| > 10,000 |
|
|
|
|
a Calculated as [(Ml ) * (0) + (Mg) * (Pg)] / [Ml + Mg].
Table 60. Illustration of How Average Percent Grade Can Be Applied Across Lane and Shoulder Width Combinations.
| AADT (Vehicles per day) |
Average Percent Grade (%) |
| Lane Width |
| < 9.5 ft |
9.5 to 10.5 ft |
10.5 to 11.5 ft |
> 11.5 ft |
| Shoulder Width (ft) |
| < 3 |
3-5 |
5-7 |
> 7 |
< 3 |
3-5 |
5-7 |
> 7 |
< 3 |
3-5 |
5-7 |
> 7 |
< 3 |
3-5 |
5-7 |
> 7 |
| < 1,000 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
1.9 |
Table 61. Estimate Proportion of Mileage by Terrain
| Terrain |
Proportion of paved, two-lane rural highways (percentage) |
| Flat |
|
| Rolling |
|
| Mountainous |
|
| Total |
100% |
Table 62. Estimate Mileage by ADT Internal, Lane and Shoulder Width
| AADT (Vehicles per day) |
Mileage of paved, two-lane rural roads |
| Lane Width <9.5 ft |
9.5<Lane Width<10.5ft |
10.5<LaneWidth<11.5 ft |
Lane Width > 11.5 ft |
| Shoulder Width (ft) |
| <3 |
3-5 |
5-7 |
>7 |
<3 |
3-5 |
5-7 |
>7 |
<3 |
3-5 |
5-7 |
>7 |
<3 |
3-5 |
5-7 |
>7 |
| < 1,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1,001 - 3,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3,001 - 5,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5,001 - 10,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| > 10,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ft = 0.305 m
Similarly, information on default values for percent of non-flat miles and average grade for non-flat mileage from HSIS States were used to calculate the following default values:
- Flat: percent of non-flat miles = 87 percent; average grade = 1.5 percent.
- Rolling: percent of non-flat miles = 91 percent; average grade = 2.0 percent.
- Mountainous: percent of non-flat miles = 97 percent; average grade = 3.7 percent.
These values in tables 61 and 62 will then be used by the calibration software to produce estimates of the following:
- Number of tangent miles.
- Number of curved miles.
- Average degree of curvature for horizontal curves.
- Average radius of horizontal curve.
- Average length of curve.
- Number of level miles.
- Number of miles on grade.
- Average percent grade for miles on grade.
- Statewide average percent grade.
Step 2. Accept or Modify Default Values for Other Geometric Parameters. Next, the State will need to develop values for other input parameters of the roadway segment accident prediction algorithm. Values for average percent grade, average length of curve, and average radius of curve will have been developed in step 1. For the purposes of calibration, it has been found to be reasonable to assume the following default values:
- Shoulder type = paved.
- Driveway density = three driveways per km (five driveways per mile).
- Passing lane = not present.
- Short four-lane section = not present.
- Two-way left turn lanes = not present.
- Roadside hazard rating = 3.
- For horizontal curves: no spiral transition present; and superelevation is not deficient (e.g., AMF = 1.0).
Step 3. Calculate Estimate of Annual Non-Intersection Accidents Using the Accident Prediction Algorithm. Calculate the predicted annual number of non-intersection related accidents for tangents and curves using the roadway segment accident prediction algorithm. Then, sum the total. Table 63 illustrates the procedure. the predicted number of total non-intersection accident rates will then be the sum of the number predicted in each line of the table (i.e., sum all calculated values in the final table column for all combinations of ADT, lane width, shoulder width, curve, and grade).
Step 4. Detemine Actual Annual Non-Intersection Accidents from Sate Data. Determine the number of non-intersection accidents on rural two-lane highways using 3 years of accident data. This is the same as step 3 from the level 1 calibration process, which was previously described.
Step 5. Calculate Calibration Factor Using Outputs of Steps 3 and 4. Calculate the calibration factor (Cr) as the ratio total number of reported non-intersection accidents on rural two-lane highways (from step 4) to the predicted total number of non-intersection accidents on rural two-lane highways (from step 3).
Step 6. Enter Calibration Factor into Software. As in level 1, the preceding five steps will produce a calibration factor based on the user’s inputs. At this point, the user will usually accept the calibration factor as calculated. However, if the resulting factor appears unreasonable (perhaps because of data problems of which the user is aware), it may be modified before entry into the system. Once accepted by the user, the value of the calibration factor (Cr) should be entered into a file of default input values for the accident prediction algorithm. In subsequent applications of the accident prediction algorithm, this value of Cr will be used in applying equation (72). As discussed earlier, the user can, and should, update the calibration factor every 2 or 3 years.
Table 63. Predicting Total Non-Intersection Accidents as a Function of ADT, Lane Width, and Should Width
| ADT (veh per day) |
Lane width (ft) |
Shoulder width (ft) |
Calculated mean ADT for each combination of ADT, lane width, and shoulder width |
Mileage of rural two lane highways |
Predicted number of non-intersection accidents per year* |
| |
Tangent |
Curve |
Total |
Tangent |
Curve |
Total |
| < 1000 |
< 9.5 |
< 3 |
|
|
|
|
|
|
|
| 3.1 to 5.0 |
|
|
|
|
|
|
|
| 5.1 to 7.0 |
|
|
|
|
|
|
|
| > 7.0 |
|
|
|
|
|
|
|
| 9.5 to 10.5 |
< 3 |
|
|
|
|
|
|
|
| 3.1 to 5.0 |
|
|
|
|
|
|
|
| 5.1 to 7.0 |
|
|
|
|
|
|
|
| > 7 |
|
|
|
|
|
|
|
| 10.5 to 11.5 |
< 3 |
|
|
|
|
|
|
|
| 3.1 to 5.0 |
|
|
|
|
|
|
|
| 5.1 to 7.0 |
|
|
|
|
|
|
|
| > 7 |
|
|
|
|
|
|
|
| > 11.5 |
< 3 |
|
|
|
|
|
|
|
| 3.1 to 5.0 |
|
|
|
|
|
|
|
| 5.1 to 7.0 |
|
|
|
|
|
|
|
| > 7 |
|
|
|
|
|
|
|
| Continue Table for Other AADT Intervals |
|
Predicted total number of non-intersection accidents
|
1 ft = 0.305 m 1 mi = 1.61 km
| * |
Determined with the uncalibrated accident prediction algorithm for roadway segments. |
Calibrating the At-Grade Intersection Accident Prediction Algorithm
A calibration procedure for at-grade intersections has also been developed. Several alternative methodologies were developed, applied, and evaluated using California, Minnesota, and Maine data obtained from FHWA’s HSIS. The objective was to develop a calibration process that produces intuitively logical, accurate, reliable, and consistent calibration factors. Based on the results of the research, the following calibration process is recommended.
Step 1. Identify Intersection Sites. For each of the following intersection types, identify a sample of intersections for which both intersecting roads are paved rural two-lane highways:
- Three-leg, STOP-controlled intersections.
- Four-leg, STOP-controlled intersections.
- Four-leg, signalized intersections.
Separate values of the calibration factor (Ci) are obtained for each intersection type.
It should be recognized that the current IHSDM Accident Analysis Module does not currently contain prediction algorithms for other types of rural road intersections, such as (1) five-leg intersections; (2) traffic circles/rotaries; (3) three-leg signalized intersections; (4) intersections of two-lane roads with multi-lane roads; (5) uncontrolled or YIELD-controlled intersections; (6) intersections involving one-way streets; or (7) intersections (which are technically considered ramp terminals in the AASHTO Green Book) formed by the junction of freeway ramps and two-lane rural roads. In general, these types of intersections constitute a small percentage of all two-lane rural road intersections. There was insufficient data to develop reliable accident prediction algorithms for these types of intersections. As times goes on, more research may be conducted to develop additional accident prediction algorithms, which can then be integrated into the IHSDM.
The desirable minimum sample sizes are suggested in table 64.
Table 64. Minimum Sample Sizes by Type of Intersection.
| Type of Intersection |
Suggested Minimum Sample
Size |
| Three-leg STOP-controlled intersections |
100 |
| Four-leg STOP-controlled intersections |
100 |
| Four-leg signalized intersections |
25 |
The suggested minimum sample sizes are somewhat arbitrary in that they do not have a statistical basis. Clearly, more intersections should produce a more accurate and reliable calibration factor. However, more data collection translates into greater costs to the highway agency. It is believed that the minimum sample sizes presented in table above represent a reasonable compromise between accuracy and cost.
States should identify the sample of their two-lane rural road intersections based on selected characteristics for each of the three intersection types (e.g., three-leg STOP-controlled, four-leg STOP-controlled, and four-leg signalized intersections). The most important characteristic is ADT
It should be understood that there are other parameters used in the accident prediction algorithm such as intersection skew angle, number of major approaches with left-turn lanes, and number of major approaches with right-turn lanes, among others. Moreover, data on several of these variables may even be available within the State’s intersection inventory file. However, because the research has found that the ADTs had the strongest predictive relationship with accidents compared to the other variables, it was deemed that the sampling strategy should be based only on the ADTs.
For States with complete and accurate intersection inventory files, it may be possible to automate the sample identification process. For States without intersection inventory files, it will not be possible to sample in proportion to known intersection distributions. Hence, a different sampling procedure applies. The two procedures are discussed separately in the following sections.
Sample Selection for States with Intersection Inventory Files
If a State maintains an accurate and comprehensive intersection inventory file which includes attribute data about the ADTs on the mainline and the cross road, then the following process is applicable.
For all three- and four-leg STOP-controlled intersections, stratify intersections by ADT on the major road. Table 65 illustrates how this can be accomplished for the three- and four-leg STOP-controlled intersections. As shown, the State will calculate the proportions of, say, three-leg STOP-controlled intersections which fall into each major-road ADT group (see “Relative Percentage”). The needed sample of 100 intersections will be divided into groups using these proportions (i.e., see “Desired Sample”).
For four-leg signalized intersections, both the major- and minor-road ADTs have a significant effect on accidents. Hence, for four-leg signalized intersections, sampling should consider both the major-road ADT and the minor-road ADT. Given that there are expected to be relatively few rural signalized intersections in a State, the decision was made to combine major- and minor-road ADTs into a single factor, which can be subsequently used for sampling stratification. The factor is the sum of the average major-road ADT and the average minor-road ADT. Table 66 presents a numerical example of how this might be done for four-leg signalized intersections.
It is important to note that States can do much more with respect to selecting an appropriate sample of intersections. For example, additional factors can be considered and integrated into the sampling stratification strategy. In some States, there are distinct differences in climate, topography, and/or accident reporting practices such that the accident experience in certain parts of the State may significantly differ from other parts of the States. For example, a State’s western portion may be dominated by mountains while the eastern portion is primarily flat plains. In addition, there may be distinct differences in geometric design, maintenance practices, and traffic control as a function of highway district (or region). For example, District A may be “better” with respect to maintenance and traffic control devices than District Z, which may help to explain differences in average accident rates between the two districts. In any event, the State has the ability to integrate additional factors such as regional area, district, or terrain into the sampling strategy (provided that they have data for these factors in their intersection inventories).
Table 65. Example of Desired Sample Stratification of Three- and Four-Leg STOP-Controlled Intersections Based on Major Road ADT.
| Intersection type |
|
Intersections of two-lane rural roads |
| ADT on major road(vehicles/day) |
Number |
Relative
percentage |
Desired
sample |
| Three-leg STOP-controlled intersections |
< 1,000 |
1,095 |
18.3% |
18 |
| 1,001 - 3,000 |
1,443 |
24.1% |
24 |
| 3,001 - 5,000 |
1,641 |
27.4% |
27 |
| 5,001 - 10,000 |
887 |
14.8% |
15 |
| 10,001 - 15,000 |
574 |
9.6% |
10 |
| > 15,000 |
347 |
5.8% |
6 |
| Total |
5,987 |
100.0% |
100 |
| Four-leg STOP-controlled intersections |
< 1,000 |
874 |
21.0% |
21 |
| 1,001 - 3,000 |
777 |
18.6% |
19 |
| 3,001 - 5,000 |
1,219 |
29.2% |
29 |
| 5,001 - 10,000 |
489 |
11.7% |
12 |
| 10,001 - 15,000 |
544 |
13.1% |
13 |
| > 15,000 |
267 |
6.4% |
6 |
| Total |
4,170 |
100.0%
|
100 |
Table 66. Example of Desired Sample Stratification of Four-Leg Signalized Intersections Based on Major Road ADT.
| Four-leg, signalized intersections |
Sum of major- and minor-road ADTs |
Intersections of two-lane rural roads |
| Number |
Relative percentage |
Desired sample |
| < 15,000 |
49 |
36.0% |
9 |
| ³ 15,000 |
87 |
64.0% |
16 |
| Total |
136 |
100.0% |
25 |
By way of an example, consider a situation in which the State wants to sample intersections based on ADT and highway district. Table 67 illustrates how highway districts can be considered in the development of a sampling strategy for three-leg STOP-controlled intersections only in a State with 3 districts. The results of this table can be compared with the top portion of table 65 to illustrate how the desired stratification scheme for the sample can be further refined.
Table 67. Example of Desired Sample Stratification of Three-Leg STOP Controlled Intersections Based on Major-Road ADT and Highway District.
| ADT on major roads |
State
highway
district |
Intersections of two
two-lane rural roads |
| Number |
% within State |
Desired sample |
| < 1,000 |
District 1 |
620 |
10.4% |
10 |
| District 2 |
339 |
5.7% |
6 |
| District 3 |
136 |
2.3% |
2 |
| Subtotal |
1,095 |
18.4% |
18 |
| 1,001 - 3,000 |
District 1 |
435 |
7.3% |
7 |
| District 2 |
674 |
11.3% |
11 |
| District 3 |
334 |
5.6% |
6 |
| Subtotal |
1,443 |
24.2% |
24 |
| 3,001 - 5,000 |
District 1 |
592 |
9.9% |
10 |
| District 2 |
527 |
8.8% |
9 |
| District 3 |
522 |
8.7% |
9 |
| Subtotal |
1,641 |
27.4% |
28 |
| 5,001 - 10,000 |
District 1 |
363 |
6.1% |
6 |
| District 2 |
446 |
7.4% |
7 |
| District 3 |
78 |
1.3% |
1 |
| Subtotal |
887 |
14.8% |
14 |
| 10,001 - 15,000 |
District 1 |
185 |
3.1% |
3 |
| District 2 |
334 |
5.6% |
6 |
| District 3 |
55 |
0.9% |
1 |
| Subtotal |
574 |
9.6% |
10 |
| > 15,000 |
District 1 |
58 |
1.0% |
1 |
| District 2 |
289 |
4.8% |
5 |
| District 3 |
0 |
0.0% |
0 |
| Subtotal |
347 |
5.8% |
6 |
| Total for entire State |
|
5,987 |
|
100 |
After the sampling stratification is established, then the specific intersections within each of the cells must be identified. A random selection process should be employed. Within this context, the term random means that all intersection sites of the same type (e.g., either three-leg STOP-controlled intersections, four-leg STOP-controlled intersections, or four-leg signalized intersections) must have the same chance of being selected.
As an example, using the sampling stratification shown in table 65, the names of all three-leg STOP-controlled intersections with major-road ADT less than 1,000 veh/day could be put into a hat and the names of 18 intersections could be drawn at random. The same procedure would be followed for each of the other ADT levels, and then repeated again for four-leg STOP-controlled and signalized intersections. The same “random draw” could be accomplished with a computerized sample by assigning a number to each three-leg STOP-controlled intersection with major-road ADT less than 1,000 veh/day and determining a ratio by dividing the total number of intersections in the file by 18. The first intersection selected would be the intersection whose number is closest to that ratio, the second selected is the intersection whose number is closest to twice that ratio, etc. For example, if there were 90 total intersection from which 18 were to be selected every fifth intersection should be chosen (i.e., 90/18=5).
Sample Selection for States Without Intersection Inventory Files
For States without comprehensive or accurate intersection inventories, information about the existing distribution of intersections within a State may not be known. Hence, the task of identifying existing distributions on which to base the sampling strategy may be limited or even non-existent. Moreover, it may not be possible to identify every intersection of two-lane rural roads, although one expects traffic signal inventory data to be available to do so for signalized intersections.
When a comprehensive list of intersections is not available or cannot be created, then it will be necessary to identify and develop a sample of two-lane rural road segments. [It is assumed that the State has the capability to identify, sort and develop a random sample of all two-lane rural road segments.] Using an approach similar to one previously described for States with intersection inventories, a sample of 100 two-lane rural road segments should be identified based on either (1) ADT alone; or (2) ADT plus additional factors such as highway district that the State deems necessary. (Thus, using the results shown in table 65 for three- and four-leg STOP-controlled intersections in the lowest ADT groups, the State should sample approximately 20 intersections with ADTs less than 1,000 veh/day.)
The data collection teams should be dispatched to those two-lane rural road segments with instructions to collect data at the first three-leg STOP-controlled intersection and the first four-leg STOP-controlled intersection encountered on each segment. In this manner, data can be gathered on a sample of 100 intersections for two of the three intersection types.
As was noted earlier, it is reasonable to assume that traffic signal inventory information, even if in hard copy format, will be available to identify the locations of four-leg signalized intersections at which both the major and minor legs are two-lane rural roads. If the information is not adequate (e.g., cannot determine whether the intersecting roads are two-lane rural roads), then it may be necessary to use the random selection process described for three- and four-leg STOP-controlled intersections above. Based on the intersection inventory data from three HSIS States, there are relatively few four-leg signalized intersections of two-lane rural roads. Thus, the potential exists that the data collection team will have to drive long distances before encountering their first four-leg signalized intersection at which both legs are two-lane rural roads.
Additional Constraints with Respect to Final Selection of the Sample
It is important to recognize that regardless of how the sample is identified, the State should ensure that each selected site experienced no significant changes in geometry, traffic control, roadside improvements, or other factors during the 3-year period corresponding the accident data (which will be discussed in steps 4 and 5). In addition, it will be necessary to exclude intersections that have undergone changes since the end of that 3-year period because measurements of skew angle and intersection sight distance taken today may not be representative of conditions that existed during the 3-year period. By way of an example, assume that accident data from 1995, 1996, and 1997 are going to be used in the calibration. To be included in the sample, the intersection should not have undergone any major changes since January 1, 1995.
If an intersection is known to have had experienced a major change during the study period, then it should be excluded from the sample. Major changes at intersection sites include the following:
- Installation of traffic signal control.
- Widening to provide more approach lanes and/or turn lanes.
- Change from a two-way STOP control to an all-way STOP control.
- Changes in intersection geometry (e.g., alignment or cross-section).
Step 2. Collect Data a Selected Intersections. Collect the following information for each intersection in the selected sample:
- Average ADT of major road.
- Average ADT of minor road.
- Intersection skew angle.
- Number of quadrants with deficient sight distance.
- Number of major-road approaches with left turn lanes.
- Number of major-road approaches with right turn lanes.
- Type of traffic control applies (e. g., minor-road or all-way STOP control).
Several of these variables are described below in more detail.
Average ADT of Major Road and Average ADT of Minor Road pertain to the bidirectional (i.e., two-way) ADT on the mainline and cross road, respectively. For intersections where the ADT on one leg of the major road differs from the ADT of the other leg of the major road, the average of the two values should be used. Similarly, if the ADT on one leg of a cross road at a four-leg intersection differs from the ADT on the other leg of the crossroad, then the average of the two values should be used.
Most importantly, the ADT should correspond to the accident data. For example, if the calibration is to be performed using accident data from 1995, 1996, and 1997, then the ADTs to be used in the accident prediction algorithm should be the average of the 1995, 1996, and 1997 ADTs for the major and minor roads for the selected intersection. When data for selected years are missing or not available, then the State should use the mid-year if available, or the last year if the mid-year is not available.
The skew angle is described in the main text of this report. The skew angle is the deviation of the intersection angle from the nominal or base angle of 90 degrees (i.e., a right angle). For a four-leg intersection where the angles of the intersection legs to the left and the right of the major road differ, they are averaged. For example, if one leg forms a 60 degree angle and the other intersects at 90 degrees, then the average would be 15 degrees [e.g., |(60-90)| / 2].
Step 3. Execute Accident Prediction Algorithm. The data collected in step 2 will be entered into tables. Data for each intersection within each of the three intersection types will be entered in a row of the table by itself. The accident prediction algorithm will then be used to calculate the predicted number of annual intersection accidents for each intersection. The total number of predicted accidents for each of the three types of intersections will be obtained by summing the calculated predictions for all intersections of that type.
Step 4. Tally Reported Intersection Accidents. Determine the number of intersection-related accidents reported at these intersections over a period of 3 calendar years. An intersection-related accident is an accident that occurs at the intersection itself or an accident that occurs on an intersection approach with 76 m (250 ft) of the intersection and is related to the presence of the intersection. The State should exercise its judgment to develop the criteria that best apply this definition to their available data. Within each intersection type, the 3-year totals for intersection-related accidents will be divided by three to obtain annual counts. These annual counts will then be used in determining the calibration factor.
Step 5. Calculate Calibration Factors. For each intersection type, calculate the calibration factor (Ci) as the total number of reported annual intersection accidents (from step 4) divided by the total number of predicted annual intersection accidents (from step 3). As with the earlier roadway segment calibration, the user will then have the option of accepting the calculated factors or modifying them. Once accepted by the user, the values of the calibration factors for each intersection type should be entered into a file of default input values for the accident prediction algorithm. In subsequent applications of the accident prediction algorithm, these values of Ci will be used in applying equation (73). Again, it is suggested that the calibration factors be updated every 2 to 3 years. The same sample of intersections can be used at 2- to 3-year intervals for this purpose.
Calibration of Accident Severity Distribution
It is recommended that users of the accident prediction algorithm replace the default accident severity distribution shown in table 1 with values specifically applicable to the rural two-lane highways under a particular agency’s jurisdiction. In step 3 of the preceding calibration procedures for roadway segments and step 4 of the procedures for intersections, the user will have identified appropriate files of accidents for roadway segments and intersections. It is recommended that these accidents be used in determining the accident severity distributions to update table 1.
Calibration of Accident Type Distribution
The default accident type distribution shown in table 2 can be calibrated by a user to obtain values specifically applicable to the rural two-lane highways under a particular agency’s jurisdiction using a procedure that is entirely analogous to the procedure for accident severity distributions described above. The accident type distributions for both roadway segments and at-grade intersections in table 2 should be calibrated in this manner using the same accident data used to update table 1. It should be noted that the accident type distribution for roadway segments influences the AMFs for lane width, shoulder width, and shoulder type presented in section 4 of this report.
Calibration Factors for Subareas within a State
The calibration procedures presented earlier in this appendix for the roadway segment and intersection accident prediction algorithms will result in statewide calibration factors. If the State deems it necessary, then they can develop calibration factors for subareas in the State. For example, States may feel that it is necessary to developing unique sets of calibration factors for subareas within the State stratified by the following:
- Geographic area (e.g., upstate vs. downstate, plains vs. mountains, etc.).
- Terrain (e.g., flat areas, rolling areas, or mountainous areas).
- Highway district or region.
The calibration procedures previously described can be applied to develop multiple sets of calibration factors within the same State. If it is possible to stratify the State’s mileage of all two-lane rural highways into the associated categories or levels that define the subareas, then sets of calibration factors can be developed for each unique category or level. Of course, the effort required will also increase. As more cells are added to the stratification matrix, sample sizes for individual cells will decrease. If the sample size is too small, then the resulting calibration factors may not be reliable. It is recommended that calibration factors only be used for the following absolute minimum sample sizes:
| Type of intersection |
Absolute minimum sample size (number of intersections) |
| STOP-controlled intersections |
50 |
| Signalized intersections |
25 |
Local Calibration Factors
In addition to the calibration process described in this appendix, which can be thought of as a “global” calibration of the algorithms, another form of calibration is possible. Specifically, predictions made with the algorithm [including the calibration factors (Cr and Ci)] can be further “calibrated” to existing local conditions by means of the EB procedure, which is described in section 6 of this report. It is important to recognize that for projects in which existing accident histories can be used, weights are assigned to the outputs from the accident prediction algorithm and the site-specific accident history within the EB procedure. Thus, a greater degree of importance can be assigned to site-specific accident histories than to the algorithm-generated prediction.
For alternatives primarily on new alignment, the EB procedure does not apply because the site-specific accident history of the old alignment is not necessarily representative of conditions on the new alignment. Thus, such projects should be analyzed without the EB procedure, but using the applicable calibration factors, Cr and Ci. If the analyst is concerned that safety conditions in a particular local area may differ substantially from the conditions represented by the “global” calibration factors, a special calibration study for a local area (possibly with a reduced sample size of roadway segments and/or intersections) can be performed using the procedures presented in this appendix. This might be particularly suitable for smaller areas with distinct populations or climate conditions.
Previous | Table of Contents | Next
|
