• Federal Highway Administration >
• Publications >
• Research Publications >
• 02045 >
• 3a.Cfm >
• IHSDM Intersection Diagnostic Review Model

IHSDM Intersection Diagnostic Review Model

3.10   Decision Sight Distance for Vertical Curves

Applicability

In geometric design, SSD is usually sufficient to ensure safety unless drivers are confronted with a complex or unexpected situation. Decision sight distance (DSD) is applied on approaches to intersections and other locations where drivers need generous sight distance because they may be called upon to make decisions. DSD is an extended version of SSD that is employed in areas where drivers face multiple demands.

The DSD model for vertical curves is applied in IDRM wherever the driver's view of an intersection or potentially conflicting vehicle is limited by a crest vertical curve. All crest vertical curves within the intersection influence area, as defined in Section 2.2, should be considered. A similar DSD model is applied when the sight restriction is the inside of a horizontal curve (see Section 3.11).

Basis

At crest vertical curves, the pavement at some point in the vertical curve may become an obstruction that limits the driver's view of the road ahead. When the driver encounters an intersection, he or she is faced with a more complex situation. The model used to determine the distance ahead that a driver can see and make a decision on the course of action, as limited by crest vertical curves, is based on the DSD model used in geometric design. The 2001 AASHTO Green Book presents the criteria for DSD calculations.

The length of a crest vertical curve to provide the adequate sight lines for any specified value of DSD can be determined as follows:

When DSD is less than L,

Equation 3.10.1

When DSD is greater than L,

Equation 3.10.2

where:

The recommended value for driver's eye height (h₁) is 1080 mm and the recommended value for object height (h₂) is also 1080 mm (to ensure that the approaching driver can see other vehicles at the intersection).

On horizontal tangents, the obstruction that limits the driver's sight distance is the road surface at some point on a crest vertical curve.

Input Parameters

The source of data for those input parameters whose values are not specified above are as follows:

Evaluation Procedure

The DSD model is applied to evaluate crest vertical curves as follows:

1. Determine V_act, the higher of the actual 85th percentile speeds of traffic on the selected curve in two directions of travel. V_act can be determined from field data, from a speed prediction model like those developed for the IHSDM design consistency module, or from an engineering judgment by the user. The objective is to base the value of V_act, to the maximum possible extent, on actual field conditions rather than on an arbitrary design speed.

2. Determine DSD_des by entering Table 10 with V_act. The columns in Table 10 are defined as follows:

• Column A – applies to any curve on a stop- or signal-controlled approach in a rural area
• Column B – applies to any curve on a stop- or signal-controlled approach in an urban or suburban area
• Column C – applies to any curve on a major-road (uncontrolled) approach to an intersection in a rural area
• Column D – applies to any curve on a major-road (uncontrolled) approach to an intersection in a suburban area
• Column E – applies to any curve on a major-road (uncontrolled) approach to an intersection in an urban area

In IDRM, which deals with rural two-lane highways, only Columns A and C in Table 10 are needed. Column A should be applied in determining DSD for stop- and signal-controlled approaches. Column C should be applied in determining DSD on major-road (uncontrolled) approaches to unsignalized intersections.

Interpolation in Table 10 should be performed linearly for values of V_act between 50 and 120 km/h. For values of V_act less than 50 km/h, interpolate linearly between the value in Column A or C and zero. For values of V_act greater than 120 km/h, use the value in Column A or C for 120 km/h.

Table 10. Decision Sight Distance (Table III-3 in 1994 Green Book)

3. Calculate L₁ (when DSD_des is less than L) and L₂ (when DSD_des is greater than L):

Equation 3.10.3

Equation 3.10.4

where:

4. Determine L_des, the length of vertical curve needed to provide DSD_des:

If DSD_des £ L₁, then L_des = L₁.
If DSDdes > L₂, then Ldes = L₂.

5. If Lact ³Ldes, then there is not a potential problem present. Proceed to Step 9.

6. If L_act < L_des, then compute DSD_act from the appropriate equation:

When DSD_des is less than L_act,

Equation 3.10.5

When DSD_des is greater than L_act,

Equation 3.10.6

7. Determine V_eff by entering Table 10. Use Column A or C of Table 10, as appropriate. V_eff can be determined by linear interpolation for values within the range from 50 to 120 km/h. When the value of DSD_act is less than the value in Column A or C of Table 10 corresponding to 50 km/h, interpolate linearly between 0 and 50 km/h to determine V_eff. When the value of DSD_act is greater than the value in Column A or C of Table 10 corresponding to 120 km/h, set V_eff equal to 120 km/h.

8. Calculate the difference between V_eff and V_act. Assess the need to trigger a DSD advisory message by referring to threshold values presented in Section 4.

9. Proceed to consideration of the next vertical curve.

The equations in the previous steps are applicable to isolated vertical curves. IDRM actually uses an equivalent numerical method that can address not only isolated vertical curves, but also more complex situations such as compound vertical curves and vertical curves followed by short straight grades. This numerical procedure is also used in the IHSDM PRM and has been documented in the PRM Functionality Document.

Model Output

The model output is the effective speed for which DSD is provided, V_eff. The criticality of V_eff is judged by comparison to V_act as described in Section 4.

References

1. American Association of State Highway and Transportation Officials, Washington, DC, 1994.
2. McGee, H.W., W. Moore, B.G. Knapp, and J.H. Sanders. Decision Sight Distance for Highway Design and Traffic Control Requirements, Report No. FHWA-RD-78-078. Federal Highway Administration, Washington, DC, 1978.

3.11   Decision Sight Distance for Horizontal Curves

Applicability

In geometric design, SSD is usually sufficient to ensure safety unless drivers are confronted with a complex or unexpected situation. Decision sight distance (DSD) is applied on approaches to intersections and other locations where drivers need generous sight distance because they may be called upon to make decisions. DSD is an extended version of SSD that is employed in areas where drivers face multiple demands.

DSD model for horizontal curves is applied in IDRM wherever the driver's view of an intersection or potentially conflicting vehicle is limited by an obstruction on the inside of a horizontal curve. All horizontal curves within the intersection influence area, as defined in Section 2.2, should be considered. A similar DSD model is applied when the sight restriction is the crest of a vertical curve (see Section 3.10).

Basis

At horizontal curves, sight obstructions (such as walls, cut slopes, trees, buildings, and longitudinal barriers) on the inside of the curves may limit the driver's view of the road ahead. When the driver encounters an intersection, he or she is faced with a more complex situation. The model used to determine the distance ahead that a driver can see and make a decision on the course of action, as limited by the horizontal sight obstruction, is based on the DSD model used in geometric design. The 2001 AASHTO Green Book presents the criteria for DSD calculations.

Input Parameters

The input parameters used in the DSD model are:

The source of data for those input parameters whose values are not specified above are as follows:

Evaluation Procedure

The DSD model is applied to evaluate a horizontal curve as follows:

1. Determine V_act, the actual 85th percentile speed of traffic on the selected curve in the direction of travel toward the intersection. V_act can be determined from field data, from a speed prediction model like those developed for the IHSDM design consistency module, or from engineering judgment by the user. The objective is to base the value of V_act, to the maximum possible extent, on actual field conditions rather than on an arbitrary design speed.

2. Determine the desired DSD from Table 10 in the same way this was done in Step 2 for vertical curves.

3. Compute the desired obstruction offset on the inside of the horizontal curve, CSW_des.

For a horizontal curve to the right for which the length of curve (L_c) ³ DSD_des:

Equation 3.11.1

where:

For a horizontal curve to the left for which L_c > DSD_des:

Equation 3.11.2

For a horizontal curve to the right for which L_c < DSD_des:

Equation 3.11.3

For a horizontal curve to the left for which L_c < DSD_des:

Equation 3.11.4

4. Obtain the obstruction offset available (CSW_avail) on the inside of the horizontal curve from the roadway file or ask the user to enter it.

5. If CSW_avail ³CSW_des, then there is no potential problem present. Proceed to Step 8.

6. If CSW_avail < CSW_des, then calculate the effective speed (V_eff) for which DSD is available by backsolving the appropriate equation from among Equations 3.11.5 through 3.11.6 to determine DSD_act and then using Table 10 to determine V_eff in the same manner described for Step 8 in Section 3.10 .

7. Calculate the difference between V_eff and V_act. Access the need to trigger a DSD advisory message by reference to threshold values presented in Section 4.

8. Proceed to consideration of the next horizontal curve.

The equations in the previous steps are applicable to isolated horizontal curves. IDRM actually uses an equivalent numerical method that can address not only isolated horizontal curves, but also more complex situations such as compound horizontal curves or horizontal curves followed by short tangents. This numerical procedure has also been used in the IHSDM PRM and has been documented in the PRM Functionality Document.

Model Output

The model output is the effective speed for which DSD is provided, V_eff. The criticality of V_eff is judged by comparison to V_act as described in Section 4.

References

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994.
2. McGee, H.W., W. Moore, B.G. Knapp, and J.H. Sanders. Decision Sight Distance for Highway Design and Traffic Control Requirements, Report No. FHWA-RD-78-078. Federal Highway Administration, Washington, DC, 1978.

3.12   Clearance Time for Skewed Intersection

Applicability

Clearance time models are proposed for use in IDRM for skewed intersection approaches at both signalized and unsignalized intersections.

Similar considerations also apply to intersections where the approach alignment differs between opposing approaches, at multileg intersections, and at intersections with more than one minor-road approach on the same side of the major road.

Basis

A clearance time model is required to address safety and operational issues that arise from the additional distance (and time) that vehicles require to cross skewed intersections versus right-angle intersections.

At unsignalized intersections, the need for additional clearance time is safety-related. Additional clearance time is required for stopped vehicles on the minor approach to cross the intersection, resulting in greater exposure of the vehicle to conflict. The sight distance for a crossing maneuver from one minor-road leg to the other is based on the time it takes for the stopped vehicle to clear the intersection. The time gap for ISD for crossing the major road at an unsignalized intersection should thus be increased by Dt at a skewed intersection.

At signalized intersections, the additional time needed to cross the skewed intersection is more of an operational issue than a safety issue. Increased crossing time at a skewed intersection will have a negative effect on the operational efficiency of a signalized intersection by requiring an increase in the yellow and/or all-red clearance time. The function of the all-red clearance time is to allow the vehicle that has entered the intersection to safely clear the intersection before the conflicting movement is released.

Input Parameters

The following input data are required to utilize the clearance time model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Intersection angle (degrees).
• Length of design vehicle (m) – data may be obtained from 1994 AASHTO Policy, Table II-1.
• Major approach lane width (m).
• Major approach turn bay width (m).
• Distance vehicle stops behind stop bar on minor approach (m).
• Acceleration rate from a stopped condition (m/s²) – data may be obtained from NCHRP Report 383.
• Actual approach travel speed of vehicle on major approach (m/s).

Evaluation Procedure

The following rationale is used by IDRM to calculate additional clearance time at skewed intersections. Two cases of clearance time models at skewed intersections are considered: unsignalized intersections and signalized intersections. Each of these cases is discussed below.

At an unsignalized intersection at which the major- and minor-road legs intersect at an angle other than 90 degrees, the clearance time analysis applies to the minor-road legs (i.e., the stop-controlled legs). The sight distance for a crossing maneuver from one minor-road leg to the other is based on the time it takes for the stopped vehicle to clear the intersection. This clearance time is increased by the intersection skew. Thus, for crossing maneuvers at skewed intersections, the S distance (the distance that the crossing vehicle must travel to clear the major highway) is larger than for right-angle intersections (see Figure 5 below). That is, the roadway width on the path of the crossing vehicle, W, is the actual traveled way width divided by the sine of the intersection angle:

Equation 3.12.1

where:

Figure 5. Skewed Intersection

The time to accelerate from a stop and travel distance w at a right-angle intersection is:

Equation 3.12.2

where:           

While the time to accelerate from a stop and travel distance W at a skewed intersection is:

Equation 3.12.3

where:

the additional time required to cross the intersection is:

Signalized Intersections

The same model applies to signalized intersections. At signalized intersections, however, the additional time needed to cross the skewed intersection is more of an operational issue than a safety issue. Increasing the crossing time will reduce the operational efficiency of a signalized intersection.

The efficiency of an approach depends on the ratio of effective green to the cycle length (g/C ratio). A higher ratio represents greater efficiency for that approach. The additional time needed for a vehicle to cross a skewed intersection, Dt , will be provided during the all-red clearance time. The function of the all-red clearance time is to allow the vehicle that has entered the intersection to safely clear the intersection before the conflicting movement is released. The design vehicle for computing the length of the all-red clearance time is a truck and is computed as:

Equation 3.12.4

where:    

This equation demonstrates that an increase in the crossing width of a skewed intersection increases the all-red clearance time. An increase in the all-red clearance time represents an increase in an approach's unused time or, for a given cycle length, a decrease in an approach's effective green time. This results in a lower g/C ratio for that particular approach.

At skewed intersections, drivers at all four approaches encounter longer crossing distances and need additional time to cross. This Dt will be taken from the effective green of all four approaches, resulting in a lower g/C ratio or a lower operating efficiency for the entire intersection.

Model Output

Model output is summarized in the tables presented below. Data provided is the additional time required for a vehicle to cross skewed intersections relative to a 90-degree intersection. Model output is provided for both the unsignalized and signalized conditions.

Change in clearance time (s) for a skewed intersection relative to a 90-degree intersection (with median/turn bay on major approaches):

Change in clearance time (s) for a skewed intersection relative to a 90-degree intersection (without median/turn bay on major approaches):

Signalized Intersections

Change in clearance time (s) for a skewed intersection relative to a 90-degree intersection (with median/turn bay on major approaches [3.6-m lanes]):

For values of V_act less than 50 km/h, use the 50-km/h value from the appropriate column. For values of V_act greater than 120 km/h, use the value from the appropriate column for 120 km/h.

Change in clearance time (s) for a skewed intersection relative to a 90-degree intersection (without median/turn bay on major approaches [3.6-m lanes]):

For values of V_act less than 50 km/h, use the 50-km/h value from the appropriate column. For values of V_act greater than 120 km/h, use the value from the appropriate column for 120 km/h.

References

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994 (Table II-1: Design Vehicle Dimensions, p. 21).
2. Harwood, D.W., J. Mason, R. Brydia, M. Pietrucha, and G. Gittings. Intersection Sight Distance, NCHRP Report 383. Transportation Research Board, Washington, DC, 1996(acceleration rate from a stop).

3.13   Left-Turn Lane Warrants

Applicability

Left-turn lane warrant models are proposed for use in IDRM for the situation where left-turn lanes are not present on the major unstopped approach. This model does not address the geometric design characteristics of the turn lane, such as length, taper design, etc., which are addressed in the PRM.

Basis

A model is required to identify the need for left-turn lanes at intersections and to highlight locations where lack of left-turn lanes presents a potential safety concern. For rural, unsignalized intersections along the through or unstopped approach, left-turn lanes serve a safety and operational efficiency function by removing decelerating and stopped vehicles waiting to turn from the higher speed through lanes.

Input Parameters

The following input data are required to utilize the left-turn lane warrant model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Peak- or design-hour traffic volume, by movement, on each unstopped approach.
• Vehicle approach operating speed on the major unstopped approach.

Evaluation Procedure

The following general steps would be undertaken by IDRM to evaluate the left-turn lane warrants:

1. For each unstopped approach to an intersection, determine whether a left-turn lane is present or not.
2. From data provided by the designer, determine the peak-hour volume of each unstopped approach. If peak-hour volume is not available, use design-hour volume.
3. Determine the 85^th percentile speed. The speed can be determined from actual data, from a speed prediction model like those developed for the IHSDM design consistency module, or from engineering judgment by the user. (Note that both directions of travel need to be evaluated.)
4. Look up the appropriate warranting condition and display an appropriate message.

No formulas or calculations are required to obtain output from the left-turn lane warrant model. Model output is obtained via a look-up table.

Model Output

Model output is summarized in Table 15 . Determination of whether a left-turn lane is warranted is based on consulting the table for a particular operating speed and opposing design-hour volume. If the advancing volume is greater than the value shown (for a given percentage of left turns), a left-turn lane is warranted.

  Table 15. Volume Warrants for Left-Turn Lanes    

References

1. A Policy on Geometric Design of Highways and Street (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994 (Table II-1: Design Vehicle Dimensions, p. 21).
2. Intersection Channelization Design Guide, NCHRP Report 279. Transportation Research Board, Washington, DC (Figure 4-12 [Harmelink study]).

3.14   Right-Turn Lane Warrants

Applicability

Right-turn lane warrant models are proposed for use in IDRM for the situation where right-turn lanes are not present on the major unstopped approach.

Basis

A model is required to identify the need for right-turn lanes at intersections and to highlight locations where lack of right-turn lanes presents a potential safety concern. For rural, unsignalized intersections along the through or unstopped approach, right-turn lanes serve a safety and operational efficiency function by removing decelerating vehicles waiting to turn from the higher speed through lanes.

Input Parameters

The following input data are required to utilize the right-turn lane warrant model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Peak- or design-hour traffic volume, by movement, on each intersection approach.

Evaluation Procedure

The following general steps would be undertaken by IDRM to evaluate the right-turn lane warrants:

1. For each unstopped approach to an intersection, determine whether a right-turn lane is present or not.
2. From data provided by the designer, determine the peak-hour volume of each unstopped approach. If peak-hour volume is not available, use design-hour volume.
3. Look up the appropriate warranting condition and display an appropriate message.

No formulas or calculations are required to obtain output from the right-turn lane warrant model. Model output is obtained via the table below.

Model Output

Model output is summarized in Table 16 below. Determination of whether a right-turn lane is warranted is based on a comparison of the approach design-hour volume (DHV) and the actual right-turn volume. If the actual right-turn volume is greater than that in the table, an exclusive right-turn lane is warranted.

Table 16. Threshold Volumes for Right-Turn Lane

References

1. The Development of Criteria for the Treatment of Right-Turn Movements on Rural Roads. Virginia Highway and Transportation Council, March 1981.

3.15   Left-Turn Lane Length for Closely Spaced Intersections

Applicability

The left-turn lane length model is proposed for use in IDRM to deal with the adequacy of storage lengths, deceleration lengths, and taper lengths for back-to-back left-turn lanes between closely spaced intersections on the major road.

Basis

A model is required to address safety and operational issues that arise from the often restricted dimension along a major road between closely spaced intersections. Drivers turning off a highway at an intersection are usually required to reduce their speed before turning.   When rapid deceleration takes place directly on the highway through lanes, it disrupts the flow of through-lane traffic. Another function of left-turn lanes is to store vehicles waiting to turn off a major roadway. Intersections with high turning-traffic volumes and/or opposing-traffic volumes generally require greater storage lengths. This model will provide guidance as to the minimum required dimension between intersections.

Input Parameters

The following input data are required to utilize the left-turn lane length for the closely spaced intersections model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Spacing between intersections (from edge of pavement to edge of pavement).
• Vehicle approach speed (posted speed or predicted speed from DCM).
• Left-turn lane width.
• Left-turn queue length (output from queue prediction model).

Evaluation Procedure

The following procedures would be used by IDRM to calculate the minimum required dimension between intersections. As part of this process, three components of left-turn lane length are reviewed: storage length, deceleration length, and taper length. Each of these components is discussed below.

For the case with back-to-back left-turn lanes on the major road between closely spaced intersections, threshold values of storage length are based on total left-turn volumes at both intersections. The anticipated number of queued vehicles at each intersection is converted to a dimension and compared to the available storage dimension provided at the respective intersection.

Deceleration Length

At closely space intersections, the left-turn lane may not be of sufficient length to enable a driver to maneuver a vehicle into it properly and make the necessary reduction in speed. For this scenario, threshold values for the minimum spacing between intersections are based on AASHTO deceleration lengths for V_act.

 The required deceleration lengths for various values of V_act are as follows:

For IDRM, the model will assume that no deceleration occurs in the through lanes and that the taper is not part of the deceleration length.

For minimum taper length, the Green Book refers to the Manual on Uniform Traffic Control Devices, which recommends that the minimum length of taper can be calculated as:

Equation 3.15.1

Equation 3.15.2

where:

Note: For programming purposes the second equation will be used when V_act < 70.

Model Output

Model output is summarized in Figure 6 . Determination of a minimum distance between closely spaced intersections is obtained by consulting the chart using the approach speed of the vehicle and the expected queue condition at the intersection.

Figure 6. Minimum Distance Between Closely Spaced Intersections

References

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994 (deceleration length requirements, p. 780).
2. Manual on Uniform Traffic Control Devices. U.S. Department of Transportation, Federal Highway Administration, Washington, DC, 1988 (Figure 3-10, Typical lane transition markings, p. 3B-13).
3. Highway Capacity Manual. Transportation Research Board, 1997 (Chapter 10, Unsignalized Intersections).
   

3.16   Intersection Conflict Index

Applicability

Intersection conflict index models are proposed for use in IDRM to characterize both the absolute and relative safety of a multileg intersection configuration. Multileg intersections are potential problems in that they produce a greater number of conflict points relative to four-leg intersections.

Basis

The intersection conflict index is used to measure the relative safety of an intersection configuration as a function of the number and types of intersection conflicts. Intersection conflict analysis is a well-understood means of addressing intersection safety. For example, it has long been known that three-leg intersections operate more safely than four-leg intersections because three-leg intersections have fewer conflict points at which conflicting traffic streams cross, merge, or diverge. Intersection conflicts reflect the crossing or conflicting paths of vehicles moving from one leg to another. Depending on the type of movement (right or left turn, crossing the intersection), any one vehicle can encounter or create one or more different conflicts. The different types of conflicts include diverging, merging, or crossing conflicts.

It is proposed to extend the same concept to the evaluation of multileg intersections. The intersection conflict index proposed for IDRM recognizes two principles of intersection conflicts and accidents. First, conflicts (and the associated risk of a particular type of crash) are related to the traffic volume of the conflicting movements. Second, the different conflicts have differing importance. This is a reflection of the severity of crashes associated with a conflict type.

Input Parameters

The following input data are required to utilize the intersection conflict index model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Design-hour traffic volume, by movement, on each intersection approach.
• Type of traffic control.

Evaluation Procedure

The following procedures would be used by IDRM to calculate the intersection conflict index.

The intersection conflict index (ICI) is defined as follows:

Equation 3.16.1

where:    

ICI is computed by systematic consideration of all pairs of turning movements at the intersection (i.e., through, left-turn, and right-turn movements from each approach) that conflict with one another. Turning movements would be considered conflicting whenever their paths cross.

The weight factor (W_k) is used to incorporate the concept that not all conflicting movements are equally likely to result in a crash. Proposed weights are shown in Table 18 below. Higher weights are assigned to pairs of conflicting movements that appear to have the highest risk of a crash. Zero weight is assigned to traffic streams that do not cross or that represent negligible risk.

ICI is based on the assumption that a traffic signal separates conflicts in time; hence, the only conflicts of interest related to signalized intersection configuration are diverging conflicts. This assumes the use of protected phasing for all movements. If the traffic signal phasing is such that particular movements do conflict, then the same weights as for unsignalized intersections should be used.

Model Output

Model output is a dimensionless numerical value based on the equation described above in detail. This number can then be compared to the established ICI threshold values, noted in Section 4.22, to determine if the designer should be shown a Level 1 or Level 2 alert message.

References

1. Manual on Uniform Traffic Control Devices. U.S. Department of Transportation, Federal Highway Administration, Washington, DC, 1988 (traffic signal warrants, pp. 4C-1 through 4C-12).

3.17   Minor-Road Profile

Applicability

The minor-road profile model is proposed for use in IDRM at intersections with a discontinuous minor-road profile through the intersection with the major road.

Basis

The profile of minor roads at intersections can present operational problems if not properly designed. Often, designers are focused on achieving an optimal profile for the major, unstopped road, but have less concern about the minor road.   Issues of concern where there is not continuity of the minor-road profile through an intersection include:

• Pavement elevations and drainage patterns across the intersection result in flat spots at corners or through the intersection.
• Amount of grade change from the minor road to the major road may result in an alignment that is uncomfortable to drive, necessitating lower speeds.
• Presence of a reasonable platform for drivers stopped on the minor approach.
• Presence of vertical curves connecting significantly different grades that may result in vehicles "bottoming out".

Input Parameters

The following input data are required to utilize the minor-road profile model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Centerline grade of the through road.
• Centerline grade of each stopped approach.
• Typical cross section of the major road, including normal cross-slope, or slope if superelevated.
• Edge of pavement elevations for all curb returns.
• Horizontal plan, lane width, and other geometry for the intersection.
• Traffic volume on the minor approach and major, unstopped road.

Evaluation Procedure

The following general steps would be undertaken by IDRM to utilize the minor-road profile model:

1. Determine each minor-road stopped approach.
2. Determine the grade within 100 m of the centerline intersection of the two roadways on each minor approach.
3. Refer to the traffic volume and determine the desirability or need for a "platform" for drivers stopped on the minor approach. The criteria for a platform is considered to be any local grade of ± 2 percent. Display appropriate message.
4. Determine the cross-slope of the major road through the intersection.
5. For each minor road, determine the relative difference in grades between the cross-slope of the major road and the minor road. Refer to Table 19 below, which relates to design controls on grade; produce message as appropriate.
6. Check the presence of a vertical curve where grade changes are significant (see table notes); produce message as appropriate.

Table 19. Design Controls on Difference Between Major- and Minor-Road Slopes

Note: Vertical curves are not required for the "Desirable" grade in each case, but are recommended (10 ft to 50 ft in length). For the "Maximum" grade change, vertical curves are required (minimum length, 10 ft) to prevent significant vehicle bounce and scraping of the chassis [1 ft = 0.305 m].

Model Output

Model output is guidance provided to the designer via the messages generated by applying the procedure documented above.

References

1. Planning and Design Guide for At-Grade Intersections (Course workbook developed by Jack E. Leisch and Associates), 1990.
   

3.18   Intersection Pavement Area

Applicability

The intersection pavement area model is proposed for use in IDRM to deal with the large, open pavement areas associated with multileg intersections, skewed intersections, and intersections on a horizontal curve. Additional pavement is also required to serve large trucks.

Basis

Intersections with large, open pavement areas can produce operational problems. Large, open pavement areas generally occur at multileg intersections, skewed intersections, and intersections on a horizontal curve. Larger intersections are more costly to construct and maintain. The open pavement areas can be more difficult to drain, which may create icing or other vehicle control problems. In addition, large open pavement areas at intersections may also be difficult for unfamiliar drivers to navigate.

The need to accommodate the operation of long and wide vehicles also produces special problems at intersections. Vehicle turning paths, which are a function of the characteristics of the vehicles, take up considerable space as the vehicle makes either a right or a left turn.   The amount of space and potential impacts on the operation and safety of the intersection are influenced by the type of large vehicle and the angle of the intersection. The types and severity of potential turning path problems are based on the frequency of large vehicle turns and which approach legs (i.e., stopped or unstopped) are skewed.   Turning-path requirements are a concern at all intersections, but are particularly important at skewed and multileg intersections. An intersection on a relatively sharp horizontal curve will also result in one or more turning movements occurring through a skew.

Both left- and right-turning geometric elements are affected by the turning paths of large vehicles. For right-turning vehicles, the design of the curb return (simple radius curve, multi-centered curve, or other variations), the width of the roadway the vehicle is turning onto, and the proximity and type of opposing lane are features of concern. For left-turning vehicles, the type of traffic control (signal versus stop) and the width of roadway the vehicle is turning onto are also factors.

Input Parameters

The following input data are required to utilize the intersection pavement area model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Intersection angle (degrees).
• Type of design vehicle.
• Length of design vehicle (m) – data may be obtained from 1994 AASHTO Policy, table II-1.
• Percentage of heavy vehicles in the traffic stream.
• Major approach lane width (m).
• Major approach turn-bay width (m).
• Minor approach lane width (m).

Evaluation Procedure

The following general steps would be undertaken by IDRM to utilize the intersection pavement area model:

1. Check if the intersection is a multileg intersection; display appropriate message to the designer.
2. Compute the intersection skew angle and compare to threshold value presented in Section 4.24; display appropriate message to the designer.
3. Check the intersection design vehicle and compare to threshold design vehicle presented in Section 4.24; display appropriate message to the designer.
4. Compute the percentage of heavy vehicles on each approach leg and compare to threshold values presented in Section 4.24; display appropriate message to the designer.

Model Output

Model output is guidance provided to the designer via the messages generated by applying the procedure documented above. The following figure was used to determine the skew angle threshold. Refer to Section 4.24 Basis for more details.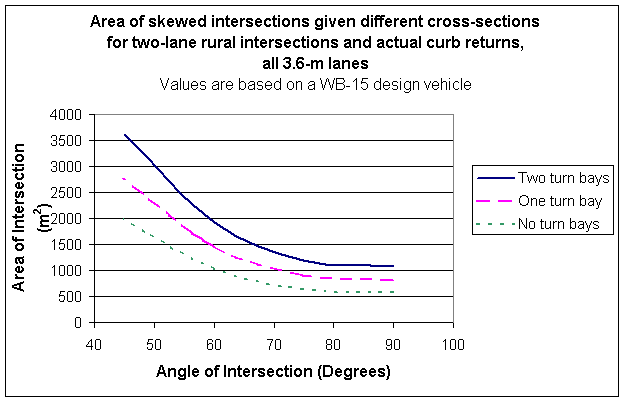

 

Figure 7. Area of Skewed Intersections for Two-Lane Rural Intersections

References

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994 (Table IX-1, Minimum edge of traveled way designs for turns at intersections, pp. 648-649).

3.19   Change in Approach Alignment Between Opposing Approaches

Applicability

The change in approach alignment model is proposed for use in IDRM to deal with forced directional changes for through vehicles as they proceed through an intersection. Forced directional changes may be difficult for unfamiliar drivers to navigate.

Basis

Intersections with substantial changes between approach alignments can produce operational and safety problems. Forced path changes for through vehicles violate driver expectations.

Input Parameters

The following input data are required to utilize the change in approach alignment model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Intersection angle (degrees).
• Design speed for each approach leg (km/h) or 85^th percentile speed (km/h).

Evaluation Procedure

The following general steps would be undertaken by IDRM to utilize the change in approach alignment model:

1. Obtain the design speed or 85th percentile speed for the approach leg(s) being examined.
2. Compute the deflection angle between intersection legs for each direction of travel.
3. Compare the angle with the threshold values; display appropriate message to the designer.

Model Output

Model output is a calculated value of the difference in angles between opposing intersection legs.

References

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994.

3.20   Queue Length Prediction

Applicability

Aqueue length prediction model is proposed for use in IDRM to characterize locations where there may be inadequate queue storage on a major road between intersections or where stopped drivers on an approach may be hidden from other drivers on the same approach.

Basis

A traffic operational model is needed to identify situations in which expected queues of vehicles (e.g., at a stopped approach) will pose an unusual hazard because of the presence of a particular geometric condition or feature. A queue prediction model would estimate a level of queuing for a given approach-traffic volume and translate that volume to a design dimension.

Example cases in which a queue prediction model would be useful

• Determining critical dimensions at offset T intersections (with left turns queued between each intersection).
• Determining critical dimensions on stopped approaches with limiting geometric features such as vertical curves, horizontal curves, or steep grades on the approach.
• Flagging critical operational conditions where queued turning traffic without the benefit of a left-turn lane may occur frequently enough to pose an unusually great hazard.

Input Parameters

The following input data are required to utilize the queue length prediction model. Data can be obtained from the IHSDM roadway model or by prompting the user for relevant input data.

• Design-hour traffic volume, by movement, on each major, unstopped intersection approach.

Evaluation Procedure

Highway Capacity Manualprocedures for unsignalized intersections (1997 edition, chapter 10) were used as the basis for queue prediction model development. The procedures were used to translate volume and geometric conditions into an expected number of queued vehicles.

Use the left-turn design-hour traffic volume and the sum of through and right-turning vehicles for each unstopped approach when reading Figure 8 below.

Model Output

Model output is summarized in Figure 8. An estimate of the number of vehicles queued is obtained by consulting the chart using design-hour volume for the left turn and the opposing through/right volumes for a major, unstopped approach to a stop-controlled intersection.

References

1. Highway Capacity Manual. Transportation Research Board, 1997 (Chapter 10, Unsignalized Intersections).

3.21   Horizontal Curve Design for Braking and Cornering

Applicability

A horizontal curve review procedure for the adequacy of cornering and braking friction is applied in IDRM wherever there is a horizontal curve on an intersection approach within the influence area of the intersection for the direction of travel leading toward the intersection. The purpose of this procedure is to determine whether the combination of braking and cornering that may occur when an intersection is on or near a curve is likely to result in vehicle loss of control due to skidding.

Basis

Horizontal curves are designed to ensure that a driver can not only traverse a horizontal curve (i.e., make a cornering maneuver) without loss of control, but also do so within tolerable limits of lateral acceleration that have been set to ensure driver comfort. The compliance of any horizontal curve with these tolerable limits of lateral acceleration is checked by the PRM.

Where an intersection is located in a horizontal curve or a horizontal curve is present on the intersection approach, the ability of an approaching driver to brake in response to the actions of other vehicles approaching the intersection is reduced because the driver may be simultaneously braking and cornering.

The purpose of this procedure is to determine whether the combination of braking and cornering that may occur when an intersection is on or near a curve is likely to result in loss of vehicle control due to skidding. Checks for such combinations of braking and cornering are not addressed by the PRM and, therefore, are included in IDRM.

Input Parameters

The source of data for those input parameters whose values are not specified above are as follows:

Evaluation Procedure

The specific procedure will be formulated as follows:

1. Determine V_act, the actual 85th percentile speed of traffic on the selected major-road approach. V_act can be determined from field data, from a speed prediction model like those developed for the IHSDM design consistency module, or from engineering judgment by the user. The objective is to base the value of V_act, to the maximum possible extent, on actual field conditions rather than on an arbitrary design speed.

2. Estimate the available coefficient of cornering friction (f_cor) for wet-pavement conditions at V_act as:

Equation 3.21.1

The estimated value of SN₄₀, the skid number at 64 km/h (40 mi/h), should be 35. This value is consistent with revised AASHTO criteria for SSD design.

3. Estimate the maximum braking friction demand (f_brake) at V_act as:

Equation 3.21.2

The estimated value of SN₄₀ for this application should also be 35.

4. Determine the speed at impending skid (V_skid) for combined cornering and braking on wet pavement:

Equation 3.21.3

where:

5.      Compute the margin of safety (V_ms) as V_skid - V_act, procedures to compare VMS to appropriate threshold values are presented in Section 4.27.

Model Output

The model output is the speed margin of safety against skidding, VMS The criticality of VMS is judged by comparison to threshold values as described in Section 4.27.

1. A Policy on Geometric Design of Highways and Streets (Green Book). American Association of State Highway and Transportation Officials, Washington, DC, 1994.