| << Previous | Contents | Next >> |
Geotechnical Aspects of Pavements Reference Manual
Chapter 5.0 Geotechnical Inputs For Pavement Design (continued)
5.4 Mechanical Properties
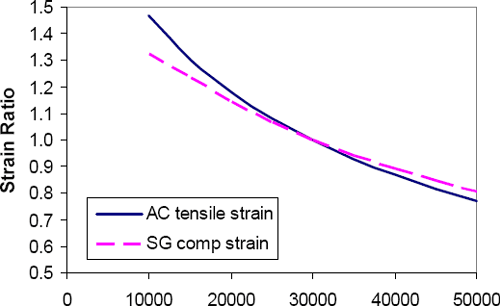
Stiffness is the most important mechanical characteristic of unbound materials in pavements. The relative stiffnesses of the various layers dictate the distribution of stresses and strains within the pavement system. Figure 5-10 and Figure 5-11 illustrate respectively how the stiffnesses of the subgrade and the unbound base layer influence the horizontal tensile strain at the bottom of the asphalt and the compressive vertical strain at the top of the subgrade for a simple three-layer flexible pavement system. These pavement response parameters are directly related to asphalt fatigue cracking and subgrade rutting performance, respectively.
Figure 5-10. Influence of subgrade stiffness on critical pavement strains. (Elastic solution, 6 in./150 mm AC over 18 in./450 mm granular base. Reference elastic moduli: EAC = 500,000 psi/3450 MPa; EBS = 30,000 psi/207 Mpa; ESG = 3000 psi/20.7 MPa. Load: 10 kip/44.5 kN single-wheel load, 100 psi/690 kPa contact pressure.)
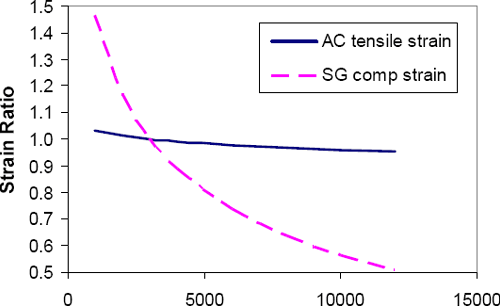
Figure 5-11. Influence of granular base stiffness on critical pavement strains. (Elastic solution, 6 in./150 mm AC over 18 in./450 mm granular base. Reference elastic moduli: EAC = 500,000 psi/3450 MPa; EBS = 30,000 psi/207 Mpa; ESG = 3000 psi/20.7 MPa. Load: 10 kip/44.5 kN single wheel load, 100 psi/690 kPa contact pressure.)
It may seem odd that stiffness rather than strength is considered the most important unbound material property for pavements. Pavement structural design is usually viewed as ensuring sufficient load-carrying capacity for the applied traffic - i.e., providing sufficient pavement strength. However, the stress levels in well-designed asphalt or PCC-surfaced pavement are well below the strength of the unbound materials, and thus failure under any given load application is not an issue. The situation for aggregate-surfaced roads is, of course, a bit different: strength of the aggregate surface will directly influence the road's durability and performance. Subgrade strength is also an important issue during pavement construction.
The preferred method for characterizing the stiffness of unbound pavement materials is the resilient modulus MR (Section 5.4.3), which is defined as the unloading modulus in cyclic loading. The AASTHO Design Guides beginning in 1986 have recommended the resilient modulus for characterizing subgrade support for flexible and rigid pavements and for determining structural layer coefficients for flexible pavements. The resilient modulus is also the primary material property input for unbound materials in the NCHRP 1-37A Design Guide for both flexible and rigid pavements.
Both the AASHTO and NCHRP 1-37A design procedures recognize the need for backward compatibility with other properties used in the past to characterize unbound materials, in particular the California Bearing Ratio and the Stabilometer R-value. These index material properties continue to be used by many highway agencies. Correlations are provided in both design procedures for relating CBR and R-values to MR (or, in the case of the AASHTO Guides, to the structural layer coefficients ai). The modulus of subgrade reaction (k) used in the AASHTO Guides is also correlated to MR.
Laboratory and field methods (where appropriate) for determining the stiffness and other relevant mechanical properties of unbound materials in pavement systems are described in the following subsections and tables. Typical values for each property are also summarized. The soil mechanical properties described here are:
- Index properties
- California Bearing Ratio (Section 5.4.1)
- Stabilometer R-Value (Section 5.4.2)
- Structural Layer Coefficients (Section 5.4.5)
- Stiffness properties
- Resilient Modulus (Section 5.4.3)
- Poisson's Ratio (Section 5.4.4)
- Modulus of Subgrade Reaction (Section 5.4.6)
- Other properties
- Interface Friction (Section 5.4.7)
- Permanent Deformation (Section 5.4.8)
- Coefficient of Lateral Pressure (Section 5.4.96)
5.4.1 California Bearing Ratio (CBR)
The California Bearing Ratio or CBR test (Table 5-27) is an indirect measure of soil strength based on resistance to penetration by a standardized piston moving at a standardized rate for a prescribed penetration distance (Figure 5-12). CBR values are commonly used for highway, airport, parking lot, and other pavement designs based on empirical local or agency specific methods (i.e., FHWA, FAA, AASHTO). CBR has also been correlated empirically with resilient modulus and a variety of other engineering soil properties.
CBR is not a fundamental material property and thus is unsuitable for direct use in mechanistic and mechanistic-empirical design procedures. However, it is a relatively easy and inexpensive test to perform, it has a long history in pavement design, and it is reasonably well correlated with more fundamental properties like resilient modulus. Consequently, it continues to be used in practice.
| Description | The California Bearing Ratio or CBR is an indirect measure of soil strength based on resistance to penetration. |
| Uses in Pavements |
|
| Laboratory Determination | AASTHO T 193 or ASTM D 1883. CBR is based on resistance to penetration by a standardized piston moving at a standardized rate for a prescribed penetration distance (Figure 5-12). CBR is defined as the ratio of the load required to cause a certain depth of penetration of a piston into a compacted specimen of soil at some water content and density, to the standard load required to obtain the same depth of penetration on a standard sample of crushed stone (usually limestone). Typically soaked conditions are used to simulate anticipated long term conditions in the field.
The CBR test is run on three identically compacted samples. Each series of the CBR test is run for a given relative compaction and moisture content. The geotechnical engineer must specify the conditions (dry, at optimum moisture, after soaking, 95% relative compaction, etc.) under which each test should be performed. |
| Field Measurement | ASTM D 4429. Test procedure is similar to that for laboratory determination. |
| Commentary | Most CBR testing is laboratory based; thus, the results will be highly dependent on the representativeness of the samples tested. It is also important that the testing conditions be clearly stated: CBR values measured from as-compacted samples at optimum moisture and density conditions can be significantly greater than CBR values measured from similar samples after soaking, for example.
For field measurement, care should be taken to make certain that the deflection dial is anchored well outside the loaded area. Field measurement is made at the field moisture content while laboratory testing is typically performed for soaked conditions, so soil-specific correlations between field and laboratory CBR values are often required. |
| Typical Values | See Table 5-28. For AASHO Road Test, CBR ≈ 100 for the granular base layer and about 30 for the granular subbase. |
Figure 5-12. California Bearing Ratio test device (http://www.ele.com/geot/cali.htm).

| USCS Soil Class | Field CBR |
|---|---|
| GW | 60 - 80 |
| GP | 35 - 60 |
| GM | 40 - 80 |
| GC | 20 - 40 |
| SW | 20 - 40 |
| SP | 15 - 25 |
| SM | 20 - 40 |
| SC | 10 - 20 |
| ML | 5 - 15 |
| CL | 5 - 15 |
| OL | 4 - 8 |
| MH | 4 - 8 |
| CH | 3 - 5 |
| OH | 3 - 5 |
5.4.2 Stabilometer (R-Value)
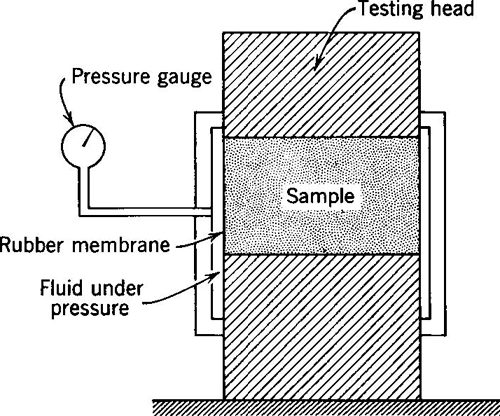
The Stabilometer or R Value test (Table 5-29) was developed by the California Division of Highways for use in their in-house empirical pavement design method. The R-value measured in this test is a measure of the resistance to deformation and is expressed as a function of the ratio of the induced lateral pressure to the applied vertical pressure as measured in a triaxial-type loading device (Figure 5-13):
(5.7)| R = 100 - | 100 |
| ( 2.5 / D2 ) [ ( Pv / Ph ) - 1 ] + 1 |
in which
| R | = | resistance value |
| Pv | = | applied vertical pressure (160 psi) |
| Ph | = | transmitted horizontal pressure |
| D2 | = | displacement of stabilometer fluid necessary to increase horizontal pressure from 5 to 100 psi, measured in revolutions of a calibrated pump handle |
A kneading compactor is used to prepare the test samples, as specimens fabricated by this method are thought to develop internal structures most similar to those in actual field compacted materials.
The R Value is used either directly or translated into more common factors (i.e., CBR) through correlation charts to be used with other more common design methods (i.e., AASHTO). Like CBR, however, it is not a fundamental material property and thus is unsuitable for use in mechanistic and mechanistic-empirical design procedures.
| Description | The R-value is a measure of the ability of a soil to resist lateral deformation under vertical load. |
| Uses in Pavements |
|
| Laboratory Determination | Measurement of the R value of a soil is done with a stabilometer (AASHTO T 190 or ASTM D 2844). A stabilometer (Figure 5-13) is similar to a triaxial device consisting of a metal cylinder in which there is a rubber membrane; the annular space between the two is filled with oil that transmits lateral pressure to the specimen.
Compacted, unstabilized, or stabilized soils and aggregates can be tested. Samples are compacted using a special kneading compaction device. When the specimen is vertically loaded, a lateral pressure is transmitted to the soil, which can be measured on a pressure gage. The R value is determined for the vertical to lateral pressure ratio and the displacement. |
| Field Measurement | Not applicable. |
| Commentary | The test also allows the measurement of swell pressure of expansive soils (see Section 5.3.3). The swell pressure or expansion pressure data is used in determining the suitability of expansive soils for use under pavements and the magnitude of overburden pressure needed to control the expansion of these soils. |
| Typical Values | Dense graded crushed stone: 80+ High compressibility silts: 15 - 30 For the AASHO Road Test, R ≈ 85 for the granular base layer and about 60 for the granular subbase. |
Figure 5-13. Schematic of stabilometer test setup for measuring R-value (Yoder and Witczak, 1975).
5.4.3 Elastic (Resilient) Modulus
Pavement thickness design prior to the 1986 AASHTO Design Guide was based on experience, soil classification, and the plastic response of pavement materials to static load, e.g., Marshall stability for asphalt concrete and CBR for unbound materials. The potential for fatigue cracking of asphalt concrete and the accumulation of permanent deformations in the unbound materials in flexible pavements under essentially elastic deformation conditions were not considered. Many expressed concerns about this approach, including Professor A. Casagrande (Burmeister, 1943):
"Irrespective of the theoretical method of evaluation of load tests, there remains the important question as to what extent individual static load tests reflect the results of thousands of dynamic load repetitions under actual traffic. Experience and large-scale traffic tests have already indicated that various types of soils react differently, and that the results of static load tests by no means bear a simple relation to pavement behavior."
Investigators in the 1950s began using repeated load triaxial tests in the laboratory to evaluate the stiffness and other behavior of pavement materials under conditions that more closely simulated real traffic loadings in the field. Substantial pioneering contributions in this area were made by Seed, Chan, and Monismith (1955), Seed and McNeill (1956), and Seed, Chan, and Lee (1963) in their work on the deformation characteristics and resilient modulus of compacted subgrades. They found significant differences between values of initial tangent modulus measured from single-cycle unconfined compression tests as compared to values of resilient modulus as determined from repeated cyclic unconfined compression loading. The conclusion from this work was that the behavior of soils under traffic loading should be obtained from repeated load tests whenever possible. This conclusion was substantiated by field data obtained by the California Department of Highways that showed the marked difference in pavement deflections occurring under standing and slowly moving wheel loads.
The culmination of this work was the adoption of resilient modulus testing by AASHTO in 1982. The AASHTO T274 standard was the first modern test protocol for resilient modulus. The concept of resilient modulus was subsequently incorporated into the 1986 and AASHTO Guide for Design of Pavement Structures.
Unbound Materials
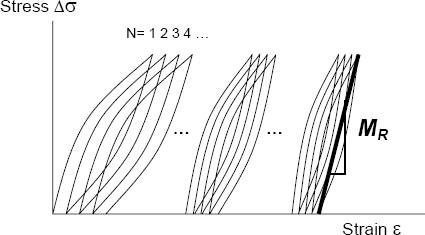
The elastic modulus for unbound pavement materials is most commonly characterized in terms of the resilient modulus, MR. The resilient modulus is defined as the ratio of the applied cyclic stress to the recoverable (elastic) strain after many cycles of repeated loading (Figure 5-14) and thus is a direct measure of stiffness for unbound materials in pavement systems. It is the single most important unbound material property input in most current pavement design procedures. Beginning in 1986, the AASTHO Design Guides have recommended use of resilient modulus for characterizing subgrade support for flexible and rigid pavements and for determining structural layer coefficients for flexible pavements. The resilient modulus is also the primary material property input for unbound materials in the NCHRP 1-37A Design Guide for both flexible and rigid pavements. It is an essential input to mechanistic pavement response models used to compute stresses, strains, and deformations induced in the pavement structure by the applied traffic loads.
Figure 5-14. Resilient modulus under cyclic loading.
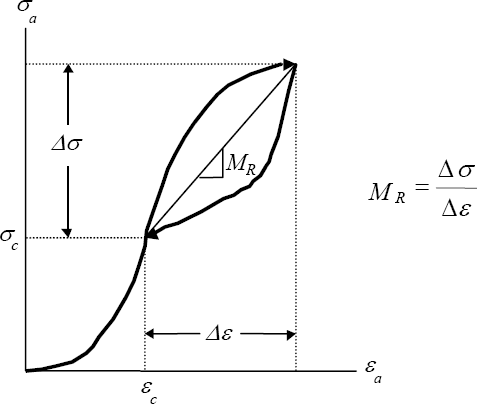
The definition of the resilient modulus as measured in a standard resilient modulus cyclic triaxial test is shown in Figure 5-15, in which σa and εa are the stress and strain in the axial (i.e., cyclic loading) direction. The sample is initially subjected to a hydrostatic confining pressure (σc), which induces an initial strain (εc). This initial strain is unmeasured in the test, but it is assumed the same in all directions for isotropic material behavior. The axial stress is then cycled at a constant magnitude (Δσ), which during unloading induces the cyclic resilient axial strain (Δε). The resilient modulus (MR) is defined simply as the ratio of the cyclic axial stress to resilient axial strain:
(5.8)| MR = | Δ σ |
| Δ εa |
Figure 5-15. Definition of resilient modulus MR for cyclic triaxial loading.
Although resilient modulus of unbound pavement materials is most commonly evaluated in the laboratory using a conventional triaxial cell, other test equipment/methods include the simple shear test, torsional resonant column testing, hollow cylinders, and true (cubical) triaxial tests. The pros and cons of these less-commonly employed testing procedures are described in Barksdale et al. (1996) and in LTPP (2003). The reasons that the triaxial device is most commonly used for resilient modulus testing include the following:
- Equipment availability. Resilient modulus testing can be performed using triaxial testing equipment commonly found in many pavement materials laboratory. This equipment is virtually identical to that found in most geotechnical laboratories except for the requirement of larger specimen sizes (up to 6 in./150 mm diameter by 12 in./300 mm tall) for coarse-grained base and subbase materials.
- Stress state. The stress conditions within the specimen on any plane are defined throughout the triaxial test. The stress conditions applied in resilient modulus testing are similar in magnitude to those that occur when an isolated wheel loading is applied to the pavement directly above the element of material simulated in the test.
- Specimen drainage. The triaxial test permits relatively simple, controlled drainage of the specimen in the axial and/or radial directions. Pore pressures can also be easily measured at the ends of the specimen, or, with more difficulty, within the specimen.
- Strain measurement. Axial, radial, and volumetric strains can all be measured relatively easily in the triaxial test.
- Availability and robustness of test protocols. The testing protocols for triaxial resilient modulus have been improved steadily over the years. Good summaries of the evolution of the various protocols and their advantages and disadvantages can be found in Andrei (1999) and Witczak (2004).
In addition to the above advantages, undisturbed tube samples of the subgrade obtained from the field can be extruded and tested with a minimum amount of specimen preparation. Finally, the triaxial cell used for the repeated load triaxial test can also be employed in static testing.
The most severe limitation of the triaxial cell is its ability to simulate rotation of the principal stress axes and shear stress reversal. Both of these phenomena apply when a wheel load moves across the pavement. Additionally, the intermediate principal stress applied to a specimen cannot be controlled in the triaxial test.
The laboratory-measured resilient modulus for most unbound pavement materials is stress dependent. The dominant effect for coarse-grained materials is an increase in MR with increasing confining stress, while the dominant effect for fine-grained soils is a decrease in MR with increasing shear stress. Many nonlinear MR models have been proposed over the years for incorporating the effects of stress level on the resilient modulus (Andrei, 1999; Witczak, 2004). The stress-dependent MR model implicitly included in the 1993 AASHTO Guide for granular base and subbase materials is (see Section 5.4.5 for more details):
(5.9)MR = k1 θk2
in which
| q | = | bulk stress = σ1 + σ2 + σ3 (psi) |
| k1, k2 | = | material properties |
Guidance is provided in the 1993 AASHTO Guide for estimating the values of k1 and k2 for unbound base and subbase layers. Typical ranges of k1 and k2 are given in Table 5-30.
The more general stress-dependent MR model adopted in the NCHRP 1-37A Design Guide is:
(5.10)| MR = k1 pa | θ | k2 | τoct | + 1 | k3 | ||||
| pa | pa |
in which
| θ | = | bulk stress | = | σ1 + σ2 + σ3 (same units as pa) | |||||||
| τoct | = | octahedral shear stress | = |
| |||||||
| pa | = | atmospheric pressure (to make equation dimensionless) | |||||||||
| k1, k2, k3 | = | material properties with constraints k1 > 0, k2 ≥ 0, k3 ≤ 0 | |||||||||
Equation (5.10) combines both the stiffening effect of the confinement or bulk stress (the term under the k2 exponent) for coarse-grained materials and the softening effect of shear stress (the term under the k3 exponent) for fine-grained soils.
The seasonal variation of unbound material properties is often significant, particularly for moisture-sensitive fine-grained soils or for locations with significant freeze-thaw cycles. Both the 1993 AASHTO Guide and the NCHRP 1-37A design procedures include provisions for including seasonal variations of unbound material properties in the design. The procedure in the 1993 AASHTO Guide for incorporating seasonal variations into the effective subgrade (MR) can be briefly summarized as follows:
- Determine an MR value for each time interval during a year. Typically, time intervals of two weeks or one month duration are used for this analysis. Methods for determining the MR value for each time interval include:
- laboratory measurement at the estimated in-situ water content for the time interval.
- backcalculation from FWD tests performed during each season. Mohammad et al. (2002) and Andrei (2003) provide some useful correlations between MR, moisture content, and other soil parameters.
- Estimate a relative damage ur corresponding to each seasonal modulus value using the empirical relationship:
(5.11)
uf = 1.18 × 108 ( MR )-2.32
- Compute the average relative damage uf as the sum of the relative damage values for each season divided by the number of seasons.
- Determine the effective subgrade MR from using the inverse of Eq. (5.11):
(5.12)
MR = 3015 ( uf )-0.431
This procedure can also be used to incorporate seasonal variations into the effective base and subbase MR values used to estimate structural layer coefficients in the 1993 AASHTO Guide (see Section 5.4.5).
There are two options for incorporating the seasonal variation of unbound material properties in the NCHRP 1-37A design procedure. The first is the direct input of monthly MR values. The second method combines moisture and freeze/thaw predictions from the Enhanced Integrated Climate Model (EICM) with models relating MR to environmental conditions. The EICM and MR environment models are built into the NCHRP 1-37A Design Guide software; details are provided in Appendix D.
Details of the procedures for determining MR for unbound paving materials are given in Table 5-31. Laboratory determination of MR is recommended for new construction and reconstruction projects. For rehabilitation projects, backcalculation of layer and subgrade MR from FWD testing is the preferred approach (see Section 4.5.4), although calibrating backcalculated estimates with laboratory-measured values is a good practice (see Table 5-32).
| Material | k1 (psi) | k2 |
|---|---|---|
| Granular base | 3000 - 8000 | 0.5 - 0.7 |
| Granular subbase | 2500 - 7000 | 0.4 - 0.6 |
| Description | The resilient modulus (MR) is the elastic unloading modulus after many cycles of cyclic loading. | ||||||||||
| Uses in Pavements |
| ||||||||||
| Laboratory Determination | There currently are five test protocols in use for resilient modulus testing in the laboratory:
The harmonized protocol developed in NCHRP Project 1-28A attempts to combine the best features from all of the earlier test methods with a new loading sequence that minimizes the potential for premature failure of the test specimen. All of the test procedures employ a closed loop electro-hydraulic testing machine to apply repeated cycles of a haversine shaped load-pulse. Load pulses are typically a 0.1 second loading time followed by a 0.9 second rest time for base/subbase materials, and a 0.2 second loading time followed by an 0.8 second rest time for subgrade materials. A triaxial set-up for the resilient modulus test is shown in Figure 5-16. Axial deformation is best measured on the sample using clamps positioned one quarter and three quarters from the base of the test specimen. For very soft specimens, the displacement may be measured between the top and bottom plates. Different specimen sizes, compaction procedures, and loading conditions are usually recommended for granular base/subbase materials, coarse-grained subgrades, and fine-grained subgrades. These different procedures reflect the different particle sizes of the materials, the state of stress specific to each layer in the pavement structure, and the mechanical behavior of the material type. Detailed comparisons of the various resilient modulus test protocols is presented in Witczak (2004). | ||||||||||
| Field Measurement | In-situ resilient modulus values can be estimated from backcalculation of falling weight deflectometer (FWD) test results (Section 4.5.4) or correlations with Dynamic Cone Penetrometer (DCP) values (Section 4.5.5; see also Table 5-34). | ||||||||||
| Commentary | No definitive studies have been conducted to date to provide guidance on differences between measured MR from the various laboratory test protocols.
Field MR values determined from FWD backcalculation are often significantly higher than design MR values measured from laboratory tests because of differences in stress states. The 1993 AASHTO Guide recommends for subgrade soils that field MR values be multiplied by a factor of up to 0.33 for flexible pavements and up to 0.25 for rigid pavements to adjust to design MR values. NCHRP 1-37A recommends adjustment factors of 0.40 for subgrade soils and 0.67 for granular bases and subbases under flexible pavements. More detailed guidance for adjusting backcalculated modulus values to design MR values is given in Table 5-32. The 1993 AASHTO Guide includes procedures for incorporating seasonal variations into an effective MR for the subgrade. Seasonal variations of material properties are included directly in the NCHRP 1-37A M-E design methodology. The Level 1, 2, and 3 MR inputs in the NCHRP 1-37A design methodology are functions of pavement and construction type, as summarized in Table 5-33. | ||||||||||
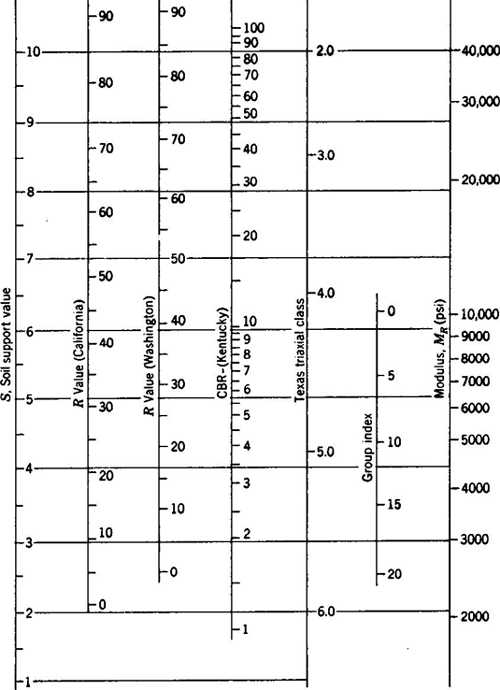
| Typical Values | Correlations between MR and other soil properties include the following:
AASHTO 1993 Guide
Additional useful correlations for subgrade MR are provided in Figure 5-17. NCHRP 1-37A (Level 2 Inputs) See Table 5-34 for correlations between MR and various material strength and index properties. The correlations in Table 5-34 are in rough order of preference; correlations of MR with CBR have the longest history and most supporting data and thus are most preferable. NCHRP 1-37A (Level 3 Inputs) See Table 5-35 for typical ranges and default values as functions of AASHTO and USCS soil class. Note that these values are for soils compacted at optimum moisture and density conditions; the NCHRP 1-37A analysis software adjusts these for in-situ moisture and density conditions. |
Figure 5-16. Triaxial cell set-up for resilient modulus test.

Figure 5-17. Correlations between subgrade resilient modulus and other soil properties (1 psi = 6.9 kPa; from Huang, 1993, after Van Til et al., 1972).
Click here for text version of image
| Layer Type and Location | Mean ER/MR Ratio | |
|---|---|---|
| Unbound Granular Base and Subbase Layers | Granular base/subbase between two stabilized layers (cementitious or asphalt stabilized materials). | 1.43 |
| Granular base/subbase under a PCC layer. | 1.32 | |
| Granular base/subbase under an HMA surface or base layer. | 0.62 | |
| Embankment and Subgrade Soils | Embankment or subgrade soil below a stabilized subbase layer or stabilized soil. | 0.75 |
| Embankment or subgrade soil below a flexible or rigid pavement without a granular base/subbase layer. | 0.52 | |
| Embankment or subgrade soil below a flexible or rigid pavement with a granular base or subbase layer. | 0.35 | |
- ER = Elastic modulus backcalculated from deflection basin measurements.
- MR = Elastic modulus of the in-place materials determined from laboratory repeated load resilient modulus test.
| Project Type | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Flexible Pavements | |||
| New/reconstruction | Laboratory-measured MR with stress dependence-Eq. (5.10) | MR correlations with other properties (Table 5-34) | Default MR based on soil type (Table 5-35) |
| Rehabilitation | Backcalculated MR from FWD deflections | MR correlations with other properties (Table 5-34) | Default MR based on soil type (Table 5-35) |
| Rigid Pavements | |||
| New/reconstruction | Not available | MR correlations with other properties (Table 5-34) | Default MR based on soil type (Table 5-35) |
| Rehabilitation | Backcalculated modulus of subgrade reaction (k) from FWD deflections (see Section 5.4.6) | MR correlations with other properties (Table 5-34) | Default MR based on soil type (Table 5-35) |
| Strength/Index Property | Modela | Comments | Test Standard | ||||
|---|---|---|---|---|---|---|---|
| California Bearing Ratiob | MR (psi) = 2555 ( CBR )0.64 MR (MPa) = 17.6 ( CBR )0.64 | CBR = California Bearing Ratio (%) | AASHTO T193-The California Bearing Ratio | ||||
| Stabilometer R-value | MR (psi) = 1155 + 555R MR (MPa) = 8.0 + 3.8R | R = R-value | AASHTO T190-Resistance R-Value and Expansion Pressure of Compacted Soils | ||||
| AASHTO layer coefficient | MR (psi) = 30,000 ( ai / 0.14 )3 MR (MPa) = 207 ( ai / 0.14 )3 | ai = AASHTO layer coefficient | AASHTO Guide for the Design of Pavement Structures (1993) | ||||
| Plasticity index and gradation |
|
wPI = P200 * PI P200 = % passing No. 200 sieve size PI = plasticity index (%) | AASHTO T27-Sieve Analysis of Coarse and Fine Aggregates AASHTO T90-Determining the Plastic Limit and Plasticity Index of Soils | ||||
| Dynamic Cone Penetrationc | CBR = 292 / ( DCP1.12 ) | CBR = California Bearing Ratio (%) DCP = Penetration index, in./blow | ASTM D6951-Standard Test Method for Use of the Dynamic Cone Penetrometer in Shallow Pavement Applications |
- Correlations should be applied to similar conditions - i.e., CBR measured at optimum moisture and density vs. soaked conditions correlates to MR at corresponding moisture and density conditions.
- NCHRP 1-37A strongly recommends against use of the older Heukelom and Klomp (1962) correlation Eq. (5.13) between MR and CBR specified in the 1993 AASHTO Design Guide.
- Estimates of CBR are used to estimate MR.
| Material Classification | MR Range (psi)* | Typical MR (psi)* |
|---|---|---|
| AASHTO Soil Class | ||
| A-1-a | 38,500 - 42,000 | 40,000 |
| A-1-b | 35,500 - 40,000 | 38,000 |
| A-2-4 | 28,000 - 37,500 | 32,000 |
| A-2-5 | 24,000 - 33,000 | 28,000 |
| A-2-6 | 21,500 - 31,000 | 26,000 |
| A-2-7 | 21,500 - 28,000 | 24,000 |
| A-3 | 24,500 - 35,500 | 29,000 |
| A-4 | 21,500 - 29,000 | 24,000 |
| A-5 | 17,000 - 25,500 | 20,000 |
| A-6 | 13,500 - 24,000 | 17,000 |
| A-7-5 | 8,000 - 17,500 | 12,000 |
| A-7-6 | 5,000 - 13,500 | 8,000 |
| USCS Soil Class | ||
| GW | 39,500 - 42,000 | 41,000 |
| GP | 35,500 - 40,000 | 38,000 |
| GM | 33,000 - 42,000 | 38,500 |
| GC | 24,000 - 37,500 | 31,000 |
| GW-GM | 35,500 - 40,500 | 38,500 |
| GP-GM | 31,000 - 40,000 | 36,000 |
| GW-GC | 28,000 - 40,000 | 34,500 |
| GP-GC | 28,000 - 39,000 | 34,000 |
| SW | 28,000 - 37,500 | 32,000 |
| SP | 24,000 - 33,000 | 28,000 |
| SM | 28,000 - 37,500 | 32,000 |
| SC | 21,500 - 28,000 | 24,000 |
| SW-SM | 24,000 - 33,000 | 28,000 |
| SP-SM | 24,000 - 33,000 | 28,000 |
| SW-SC | 21,500 - 31,000 | 25,500 |
| SP-SC | 21,500 - 31,000 | 25,500 |
| ML | 17,000 - 25,500 | 20,000 |
| CL | 13,500 - 24,000 | 17,000 |
| MH | 8,000 - 17,500 | 11,500 |
| CH | 5,000 - 13,500 | 8,000 |
*Multiply by 0.069 to convert to MPa.
Fractured PCC Slabs
Rehabilitation designs for AC overlays over badly damaged PCC existing pavement frequently require fracturing (crack and seat, etc.) or rubblizing of the existing concrete slabs. The net effect of the fracturing or rubblization process is to turn the slabs into a very coarse unbound granular material. Table 5-36 summarizes recommended design values for the modulus of the fractured slab, Efs, for Level 1 characterization in the NCHRP 1-37A Design Guide. These recommended design values, which are functions of the anticipated variability of the slab fracturing process, were developed based on NDT data on fractured slab projects contained in NAPA IS-117 (NAPA, 1994). When using these design values, NDT of the fractured slab must be performed to ensure that not more than 5 percent of the in-situ fractured slab modulus values exceed 1000 ksi. The Level 1 design values may be used for all methods of fracture (crack and seat or rubblize for JPCP, break and seat or rubblize for JRCP, or rubblize for CRCP).
Table 5-37 summarizes recommended design values for the modulus of the fractured slab, Efs, for Level 3 characterization in the NCHRP 1-37A Design Guide. These values, which are functions of the fracture method used and the nominal fragment size, were developed by applying conservatism to the relationship of Efs versus nominal fragment size published in the 1986 AASHTO Design Guide and NAPA IS-117. Level 3 should not be used with JRCP unless it is certain that full debonding of the steel and concrete occurs.
| Expected Control on Slab Fracture Process | Anticipated Coefficient of Variation for the Fractured Slab Modulus, % | Design Modulus |
|---|---|---|
| Good to Excellent | 25 | 600 ksi (4.1 GPa) |
| Fair to Good | 40 | 450 ksi (3.1 GPa) |
| Poor to Fair | 60 | 300 (2.1 GPa) |
| Type of Fracture | Design Modulus |
|---|---|
| Rubblization | 150 ksi (1.0 GPa) |
| Crack and Seat | |
| 12-in crack spacing | 200 ksi (1.4 GPa) |
| 24-in crack spacing | 250 ksi (1.7 GPa) |
| 36-in crack spacing | 300 ksi (2.1 GPa) |
Note: For JRCP, Level 1 should be used unless agency experience dictates otherwise.
Bedrock
Shallow bedrock under an alignment can have a significant impact on the pavement's mechanical responses and thus needs to be considered in mechanistic-empirical design. Shallow bedrock is also an important factor in the backcalculation of layer moduli for rehabilitation design. While a precise value of bedrock stiffness is seldom required, the effect of high bedrock stiffness must nonetheless be incorporated into the analysis. Recommended values from NCHRP 1-37A for the elastic modulus of bedrock are as follows:
- Solid, massive bedrock:
- E = 750 - 2,000 ksi (5.2 - 13.8 GPa)
- Default = 1,000 ksi (6.9 GPa)
- Highly fractured/weathered bedrock:
- E = 250 - 1,000 ksi (1.7 - 6.9 GPa)
- Default = 500 ksi (3.4 GPa)
5.4.4 Poisson's Ratio
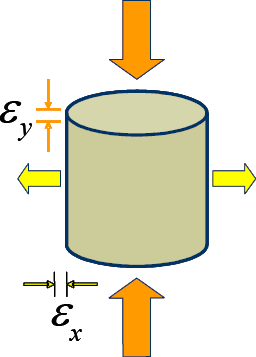
| Description | Poisson's ratio ν is defined as the ratio of the lateral strain εx to the axial strain εy due to an axial loading (Figure 5-18). |
| Uses in Pavements |
|
| Laboratory Determination | Determined as part of resilient modulus test (see Section 5.4.3.). |
| Field Measurement | Not applicable. |
| Commentary | The influence of ν on computed pavement response is normally quite small. Consequently, use of assumed values for ν often gives satisfactory results, and direct measurement in the laboratory is usually unnecessary. |
| Typical Values | Poisson's ratio for isotropic elastic materials must be between 0 and 0.5. Typical values of ν for pavement geomaterials are given in Table 5-30. |
Figure 5-18. Illustration of Poisson's ratio.
| Material Description | ν Range | ν Typical |
|---|---|---|
| Clay (saturated) | 0.4 - 0.5 | 0.45 |
| Clay (unsaturated) | 0.1 - 0.3 | 0.2 |
| Sandy clay | 0.2 - 0.3 | 0.25 |
| Silt | 0.3 - 0.35 | 0.325 |
| Dense sand | 0.2 - 0.4 | 0.3 |
| Coarse-grained sand | 0.15 | 0.15 |
| Fine-grained sand | 0.25 | 0.25 |
| Bedrock | 0.1 - 0.4 | 0.25 |
| << Previous | Contents | Next >> |

