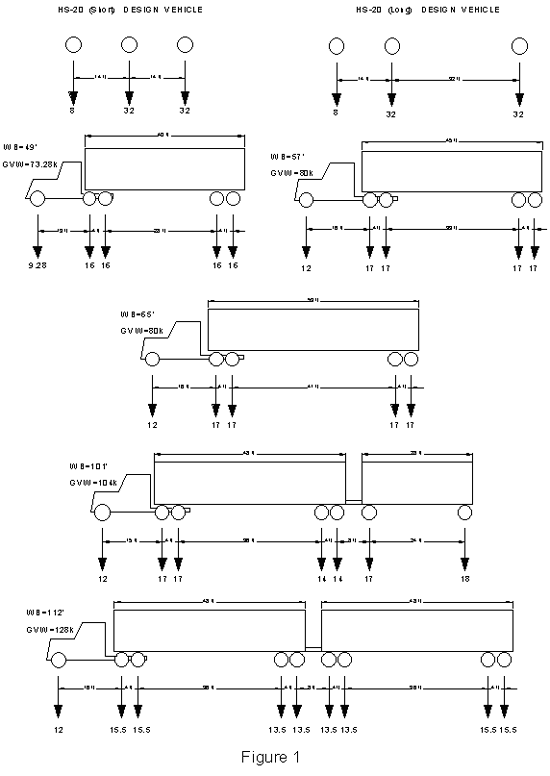
This appendix describes in detail why, for example, a simple maximum gross vehicle weight (GVW) limit would not sufficiently protect bridges. It also shows for which types of bridges the Federal Bridge Formula B (BFB) works and for which types it does not.
Consider the following table. This table presents the analysis of two trucks of equal weight; one is a 72,000 pound four axle dump truck with an 18-foot wheelbase and the second is a 72,000 pound 5-axle tractor semitrailer with a 64-foot wheelbase. The sample bridges are simple span steel girder bridges with spans of 40, 60, 80, 100 and 120 feet. The values shown are the ratios of the moments of the selected truck to the HS20 vehicle.
| Span Length (feet) |
4 Axle Dump Truck 72,000 lbs. Wheel base = 18 feet |
5-axle Tractor Semitrailer 72,000 lbs. Wheel base = 64 feet |
|---|---|---|
| 20 | 1.210 | 0.790 |
| 40 | 1.123 | 0.778 |
| 60 | 1.086 | 0.791 |
| 80 | 1.066 | 0.843 |
| 100 | 1.053 | 0.891 |
| 120 | 1.044 | 0.922 |
This analysis shows that using a straightforward GVW standard will not adequately protect bridges. For short spans the dumb truck produces a moment, and therefore a stress, 21 percent greater than the HS20 design vehicle and 53 percent (1.21 ÷ 0.79) greater than that of the "eighteen wheeler," even though the GVWs are identical. As expected, as the span length becomes greater, the difference between the two trucks decreases. However, more than 50 percent of the bridges nationwide have span lengths less than 60 feet.
Consequently, a better and fairer standard was needed. Federal Bridge Formula B (BFB) is a formula with which one can calculate the maximum allowable weight on any group of axles. It is function of the number of axles and axle spacing:
(1)W = [LN/N-1 + 12N + 36]
where:
W = the maximum weight in pounds that can be carried by a group of two or more axles to the nearest 500 pounds
L = the distance between the outer axles of the group
N = the number of axles in the considered group
The concept of a bridge formula evolved a half a century ago, and it went through several revisions. Even before the Federal formula was implemented, a number States adopted this or a similar formula in the 1960s and early 1970s. As significant numbers of trucks began to get heavier, Congress established the national implementation of Formula B for Interstate highways in 1974.49 At the same time Congress raised the maximum allowable Gross Vehicle Weight (GVW) on the Interstate system to 80,000 pounds the maximum single axle load to 20,000 pounds, and maximum tandem axle load to 34,000 pounds. In 1982 Congress prohibited any State from establishing a maximum GVW less than the Federal 80,000 pound “cap”. By the mid-1980s effectively all the States established the Federal BFB, but some States allowed trucks to exceed the 80,000 pound cap on the non-Interstate systems as long as the trucks met BFB. Furthermore, a few States were allowed “grandfather” rights to allow trucks greater than 80,000 pounds on the Interstate system, usually for a relatively nominal annual permit fee. Nonetheless, most all States require even the “grandfathered” combination trucks to comply with BFB.
The guideline followed by the developers of BFB was that a typical HS20 rated bridge would not be overstressed by more than 5 percent by the typical combination truck with one trailer. At the time it was implemented, Formula B worked quite well in protecting the bridges on the Interstate system. It also worked quite well in keeping single unit trucks and single trailer combination trucks from damaging bridges in those States that applied the formula to the non-Interstate systems.
Although the analyses conducted in developing Bridge Formula B considered only simply supported superstructures,50 the resulting formula was generally applicable since the lengths and weights of most trucks in the then current fleet did not differ significantly from the HS20 design vehicle, and because the structural capacity of continuous bridges to accommodate typical single combination trucks is similar to that of simply supported structures subjected to these same loads. However, the moments caused by longer and heavier trucks on continuously supported bridges are much greater than the moments on simply supported bridges of equal rating and of equal span lengths.
To demonstrate this, consider the total (live load plus dead load) moments of seven different vehicles, assuming steel girder bridges, the single most common highway bridge type. The vehicles include the HS20 Short and HS20 Long design vehicles, a 73,280-pound 5-axle tractor semitrailer, an 80,000-pound 5-axle tractor semitailer, an 80,000-pound 5-axle tractor semitailer with a 53-foot trailer, a typical Rocky Mountain Double and a Turnpike Double, see Figure A-1. These vehicles were chosen because they represent typical single trailer trucks from both before and after the 1982 increase in the cap from 73,280 pounds to 80,000 pounds and before and after the increase in trailer length to 53-feet. Also included are two typical double trailer trucks, the Rocky Mountain Double and the Turnpike Double. All of these vehicles comply with Formula B.
Table A-2, presents the ratio of the moments of these selected vehicles to that of the HS20 (short) design vehicle for simply supported bridges and for 2-span and 3-span continuous bridges with spans lengths varying from 20 to 180 feet in 20 foot increments. The ratio in the fourth column is, of course, 1.0 because it is the ratio of the moments of the HS20 (short) design vehicle to itself (i.e., the inventory rating). Single trailer combination trucks do not overstress (i.e., the ratio is < 1.0) simply supported bridges for any span lengths. For continuously supported multi-span bridges, except as noted below, these conventional single trailer combinations weighing up to 80,000 pounds also cause no greater stresses than the HS20 design vehicle (i.e., the inventory rating). However, on continuous bridges with main spans in the 50-70 foot range, these combinations operating at 80,000 pounds have moments (and therefore produce stresses) up to 10 percent greater than the HS20 design vehicles. Since the Inventory Rating of the bridge is HS20, then the 10 percent is probably acceptable, because of the large factor of safety associated with the Inventory Rating.
Longer combination trucks overstress both simply supported and continuously supported bridges. Turnpike doubles are worse than Rocky Mountain doubles at the weights assumed in this analysis. On simply supported bridges Turnpike Doubles overstress the bridge up to 13 percent more than the HS20 design vehicle while Rocky Mountain Doubles overstress up to 8 percent greater. Even this level of overstress is usually acceptable. However, overstresses caused by LCVs are even greater on continuously supported bridges. Turnpike Doubles cause stresses up to 22 percent greater than the HS20 design vehicle and Rocky Mountain Doubles up to 15 percent greater.
Bridge Formula B thus does not provide the same protection against damaging overloads by LCVs as it does for single-trailer combinations, especially on continuously supported bridges. For most span lengths the overstress exceeds the inventory rating significantly and that, for the worst cases, e.g., Turnpike Doubles on 2 span continuous bridges with span lengths equal to 80-feet, this overstress reaches 25 percent. Although this level of overstress is less than the operating rating, the overall factor of safety designed into bridges would be substantially reduced with the continuous use of such LCVs.
| Bridge Type | Length of Main Span (ft) | Total Length (ft) | HS20 (Short) | HS20 (Long) | 3S2 w/40' trailer 73,280 lbs | 3S2 w/45' trailer 80,000 lbs | 3S2 w/53'trailer 80,000 lbs | 3S2 2 Rocky Mtn Dbl 104,000 lbs | 3S2 4 Turnpike Dbl 128,000 lbs. |
|---|---|---|---|---|---|---|---|---|---|
| Simple | 20 | 20 | 1.00 | 1.00 | 0.85 | 0.89 | 0.89 | 0.89 | 0.83 |
| Simple | 30 | 30 | 1.00 | 0.95 | 0.88 | 0.89 | 0.89 | 0.95 | 0.95 |
| Simple | 40 | 40 | 1.00 | 0.84 | 0.80 | 0.82 | 0.82 | 0.86 | 0.90 |
| Simple | 50 | 50 | 1.00 | 0.80 | 0.78 | 0.80 | 0.80 | 0.83 | 0.88 |
| Simple | 60 | 60 | 1.00 | 0.82 | 0.77 | 0.80 | 0.80 | 0.82 | 0.87 |
| Simple | 70 | 70 | 1.00 | 0.86 | 0.82 | 0.80 | 0.80 | 0.85 | 0.87 |
| Simple | 80 | 80 | 1.00 | 0.88 | 0.85 | 0.84 | 0.81 | 0.87 | 0.88 |
| Simple | 90 | 90 | 1.00 | 0.91 | 0.88 | 0.88 | 0.82 | 0.89 | 0.90 |
| Simple | 100 | 100 | 1.00 | 0.92 | 0.90 | 0.90 | 0.86 | 0.93 | 0.93 |
| Simple | 110 | 110 | 1.00 | 0.93 | 0.92 | 0.92 | 0.88 | 0.96 | 0.97 |
| Simple | 120 | 120 | 1.00 | 0.94 | 0.93 | 0.94 | 0.91 | 0.99 | 1.00 |
| Simple | 130 | 130 | 1.00 | 0.95 | 0.94 | 0.95 | 0.92 | 1.01 | 1.03 |
| Simple | 140 | 140 | 1.00 | 0.96 | 0.95 | 0.96 | 0.94 | 1.03 | 1.06 |
| Simple | 150 | 150 | 1.00 | 0.96 | 0.96 | 0.97 | 0.95 | 1.04 | 1.07 |
| Simple | 160 | 160 | 1.00 | 0.96 | 0.96 | 0.98 | 0.96 | 1.05 | 1.09 |
| Simple | 170 | 170 | 1.00 | 0.97 | 0.96 | 0.98 | 0.96 | 1.06 | 1.10 |
| Simple | 180 | 180 | 1.00 | 0.97 | 0.97 | 0.99 | 0.97 | 1.06 | 1.11 |
| 2-span Cont | 20 | 40 | -1.00 | -1.05 | -0.93 | 0.92 | 0.92 | -0.92 | 0.91 |
| 2-span Cont | 30 | 60 | 1.00 | -1.02 | -0.96 | -0.93 | 0.86 | -0.92 | 0.91 |
| 2-span Cont | 40 | 80 | 1.00 | -0.99 | -1.00 | -1.01 | -0.94 | -1.03 | -1.03 |
| 2-span Cont | 50 | 100 | 1.00 | -0.98 | -1.01 | -1.08 | -1.07 | -1.16 | -1.19 |
| 2-span Cont | 60 | 120 | -1.00 | -0.95 | -0.99 | -1.07 | -1.10 | -1.25 | -1.23 |
| 2-span Cont | 70 | 140 | -1.00 | -0.92 | -0.94 | -1.03 | -1.07 | -1.24 | -1.22 |
| 2-span Cont | 80 | 160 | -1.00 | -0.94 | -0.92 | -0.99 | -1.03 | -1.21 | -1.25 |
| 2-span Cont | 90 | 180 | -1.00 | -0.95 | -0.94 | -0.95 | -1.00 | -1.18 | -1.25 |
| 2-span Cont | 100 | 200 | -1.00 | -0.96 | -0.95 | -0.96 | -0.97 | -1.15 | -1.24 |
| 2-span Cont | 110 | 220 | -1.00 | -0.97 | -0.96 | -0.98 | -0.95 | -1.12 | -1.23 |
| 2-span Cont | 120 | 240 | -1.00 | -0.98 | -0.97 | -0.99 | -0.97 | -1.09 | -1.21 |
| 2-span Cont | 130 | 260 | -1.00 | -0.98 | -0.98 | -1.00 | -0.98 | -1.09 | -1.19 |
| 2-span Cont | 140 | 280 | -1.00 | -0.98 | -0.98 | -1.01 | -0.99 | -1.11 | -1.17 |
| 2-span Cont | 150 | 300 | -1.00 | -0.98 | -0.99 | -1.01 | -1.00 | -1.12 | -1.15 |
| 2-span Cont | 160 | 320 | -1.00 | -0.99 | -0.99 | -1.02 | -1.00 | -1.13 | -1.17 |
| 2-span Cont | 170 | 340 | -1.00 | -0.99 | -0.99 | -1.02 | -1.01 | -1.14 | -1.18 |
| 2-span Cont | 180 | 360 | -1.00 | -0.99 | -0.99 | -1.02 | -1.01 | -1.14 | -1.20 |
| 3-span Cont | 20 | 60 | 1.00 | -1.02 | -0.96 | -0.92 | 0.86 | -0.95 | 0.92 |
| 3-span Cont | 30 | 90 | 1.00 | -1.00 | -0.99 | -1.00 | -0.92 | -1.01 | -1.03 |
| 3-span Cont | 40 | 120 | -1.00 | -0.98 | -1.00 | -1.06 | -1.04 | -1.12 | -1.16 |
| 3-span Cont | 50 | 150 | -1.00 | -0.92 | -0.96 | -1.03 | -1.04 | -1.16 | -1.16 |
| 3-span Cont | 60 | 180 | -1.00 | -0.91 | -0.92 | -0.99 | -1.02 | -1.16 | -1.14 |
| 3-span Cont | 70 | 210 | -1.00 | -0.94 | -0.91 | -0.96 | -0.99 | -1.15 | -1.18 |
| 3-span Cont | 80 | 240 | -1.00 | -0.95 | -0.94 | -0.94 | -0.97 | -1.13 | -1.19 |
| 3-span Cont | 90 | 270 | -1.00 | -0.96 | -0.95 | -0.96 | -0.95 | -1.11 | -1.19 |
| 3-span Cont | 100 | 300 | -1.00 | -0.97 | -0.96 | -0.98 | -0.94 | -1.08 | -1.18 |
| 3-span Cont | 110 | 330 | -1.00 | -0.98 | -0.97 | -0.99 | -0.96 | -1.06 | -1.17 |
| 3-span Cont | 120 | 360 | -1.00 | -0.98 | -0.98 | -1.00 | -0.98 | -1.09 | -1.16 |
| 3-span Cont | 130 | 390 | -1.00 | -0.98 | -0.98 | -1.01 | -0.99 | -1.11 | -1.15 |
| 3-span Cont | 140 | 420 | -1.00 | -0.98 | -0.98 | -1.01 | -1.00 | -1.12 | -1.15 |
| 3-span Cont | 150 | 450 | -1.00 | -0.99 | -0.99 | -1.02 | -1.00 | -1.13 | -1.16 |
| 3-span Cont | 160 | 480 | -1.00 | -0.99 | -0.99 | -1.02 | -1.01 | -1.14 | -1.18 |
| 3-span Cont | 170 | 510 | -1.00 | -0.99 | -0.99 | -1.02 | -1.01 | -1.14 | -1.19 |
| 3-span Cont | 180 | 540 | -1.00 | -0.99 | -0.99 | -1.02 | -1.01 | -1.14 | -1.20 |