U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-033 Date: May 2015 |
Publication Number: FHWA-HRT-15-033 Date: May 2015 |
Cohesive soils generally include fine-grained silt and clay mineral particles passing the No. 200 sieve (less than 0.003 inches (0.075 mm)). These particles usually have a shape of small flat plates, needles, or tubes with a high specific area defined as the ratio of surface area to volume.(1) In the presence of water, these particles are subjected to physicochemical forces that are large in comparison with their weight, which tends to hold the soil mass together. These physicochemical forces are more dominant than the submerged particle weight in resisting erosion (scour). However, attempting to apply an understanding of the physicochemical forces on the micro level is challenging and may not yield practical results because erosion of cohesive soils generally occurs at the more macro scale of clumps of soil rather than individual particles.
Many parameters influence the erosion of cohesive soils. These parameters include the physical and chemical properties of soil, as well as the physical, chemical, and mechanical characteristics of the eroding fluid.
The physical and chemical properties of soil include the following:
The following physical, chemical, and mechanical characteristics of the eroding fluid may contribute to erosion:
The scope of this study does not include consideration of the erosion effects of the physical or chemical characteristics of the eroding fluid and assumes that they are constant for the laboratory testing of erosion.
Another soil loss process that may occur when a soil is not saturated and then exposed to flowing water is slaking. This mechanism will be discussed separately from the soil erosion process because it is a distinctly different process that can accelerate erosion.
Hydraulic Engineering Circular 18 (HEC-18) provides a conceptual framework (shown here in figure 1) relating shear stress, soil types, and erosion rates for a variety of materials, including cohesive soils.(2) Erodibility is divided into six categories for materials ranging from very highly erodible fine sands and non-plastic silts to non-erosive rock. However, this broad categorization is not directly useful for site-specific erosion or scour computations because of the wide range in types of soils and the wide range of erosion rates for a given type of soil. (The two-letter soil type codes are from the Unified Soil Classification System (USCS) that is discussed later.)
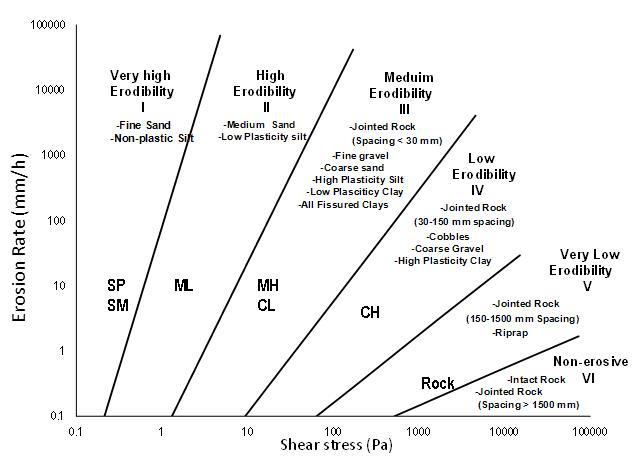
1 inch = 25.4 mm.
1 lbf/ft2 = 47.8 Pa.
Figure 1. Graph. Generalized relationships for erosion in cohesive materials
One of the few strategies available today for the design engineer to determine site-specific soil erosion rates is to conduct erosion tests on the specific soil. Because the appropriate range of shear stresses needed for a range of soil types may vary by orders of magnitude, a single device is unlikely to be able to adequately test all materials. Figure 2 illustrates a division of the shear stress axis into five shear stress ranges and suggests the types of materials that could be tested using a device capable of delivering those shear stresses. This report describes a device targeted to the second (highlighted) of the five shear stress ranges, which should be capable of measuring erosion rates for many soils classified as ML (inorganic silts, very fine sands, rock flour, silty or clayey fine sands) and CL (inorganic clays of low to medium plasticity, gravelly clays, sandy clays, silty clays, lean clays).
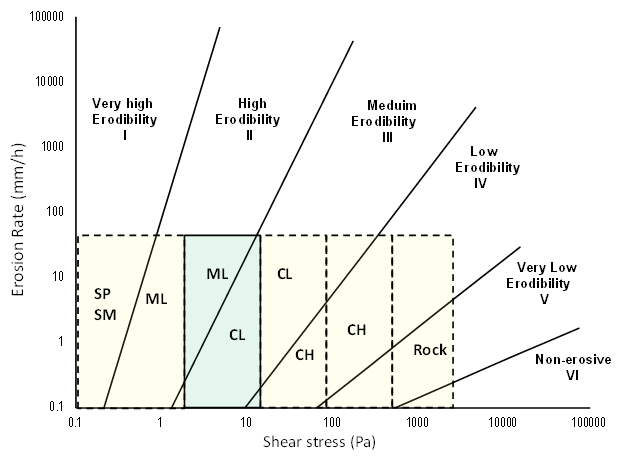
1 inch = 25.4 mm.
1 lbf/ft2 = 47.8 Pa.
Figure 2. Graph. Division of materials into zones for specific devices
Experimental modeling remains an indispensable method for understanding the erosion mechanism. In addition to flume modeling, several small-scale devices have been developed for the specific purpose of testing soil/rock erodibility. However, these devices may simulate flow conditions that do not mimic the conditions experienced with open channel flow, particularly the velocity distribution. Because different flow conditions will generate distinct dynamic forces on the tested cohesive soils, the type of testing apparatus and bed size may influence the test results. In some cases, such testing may result in designs for scour prediction that are not protective of the traveling public.
Therefore, a device that can simulate the open channel flow profile approximated by the log-law velocity profile is urgently needed. If a testing device reproduces the log-law velocity profile, then it will be capable of generating hydrodynamic forces on the bed similar to those in an open channel and, therefore, better mimicking the erosion process.
Development of sensors that can accurately and reliably measure the forces acting on the bed is another key challenge in developing a small-scale erosion testing device. Direct force measurements with a servo-controlled mechanism are available to instantaneously measure hydrodynamic forces on soil specimens and can be incorporated into erosion testing devices.
HEC-18 provides an approach for estimating scour in cohesive materials for contraction scour (chapter 6) and pier scour (chapter 7). Although equations for estimating contraction and pier scour are presented, quantification of essential soil parameters to use in the methods is not provided. Rather, HEC-18 provides qualitative graphs describing expected soil parameters and describes several types of instrumentation that have been used, with varied degrees of success, to quantify these soil parameters.
For contraction scour, HEC-18 provides the equation in figure 3 for ultimate scour:
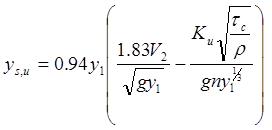
Figure 3. Equation. Ultimate contraction scour
Where:
ys,u = Ultimate scour depth, ft (m).
y1 = Upstream average flow depth, ft (m).
V2 = Average flow velocity in the contracted section, ft/s (m/s).
g = Acceleration due to gravity, ft/s2 (m/s2).
n = Manning’s roughness coefficient, dimensionless.
ρ = Density of water, lb/ft3 (kg/m3).
𝜏c = Critical shear stress, lbf/ft2 (N/m2).
Ku = Unit conversion, 1.486 for U.S. customary units and 1.0 for S.I.
The need addressed in this research is the estimate of critical shear stress for cohesive soils. In addition, HEC-18 provides a framework for estimating the time rate of scour for contraction, as seen in figure 4:
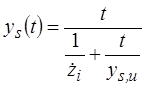
Figure 4. Equation. Time rate of contraction scour
Where:
ys(t) = Scour depth at time, t, ft (m).
t = Duration of flow, h.
![]() i = Initial rate of scour, ft/h (m/h).
i = Initial rate of scour, ft/h (m/h).
To apply this equation, an initial rate of scour, and subsequent rates of scour when conditions change, is needed. This requirement is also addressed in this research.
For ultimate pier scour, HEC 18 provides the equation in figure 5:
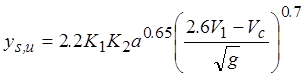
Figure 5. Equation. Ultimate pier scour
Where:
K1 = Correction factor for pier nose shape, dimensionless.
K2 = Correction factor for angle of attack of flow, dimensionless.
a = Pier diameter (or width), ft (m).
V1 = Mean velocity of flow directly upstream of the pier, ft/s (m/s).
Vc = Critical velocity for initiation of erosion of the cohesive material, ft/s (m/s).
Determination of the critical velocity for a soil is needed to apply this equation. Critical velocity is related to critical shear stress and the hydraulic parameters of the stream as shown in figure 6. Therefore, no additional soil information is required for computation of pier scour beyond that required for contraction scour. Time rate of pier scour is computed in the same manner described for time rate of contraction scour.
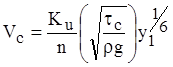
Figure 6. Equation. Critical velocity and critical shear stress
Where:
y1 = Depth of water approaching the pier, ft (m).
Therefore, the need addressed by this research is to provide quantitative tools for determining critical shear stress, c, and erosion rate, , for cohesive soils. The critical shear stress is essential for determining an ultimate scour depth and, in many situations, may be all that is required. For situations where a more detailed assessment is needed, the erosion rate may be used for a time-dependent scour assessment.
This study has two objectives. The first objective is to introduce and demonstrate the effectiveness of a new ex situ erosion testing device that can mimic the near-bed flow of open channels to erode cohesive soils within a specified range of shear stresses. The new ex situ scour test device (ESTD) uses a moving belt and a pump to generate a log-law velocity profile in a channel. The ESTD is designed to maintain a constant bed shear stress throughout the test period. Cohesive soil samples mixed with Red Art clay (Illite), silt, and sands were created in the laboratory and tested in the ESTD to demonstrate the operations and effectiveness of the device.
The second objective is to develop a method for estimating the key erosion parameters of a limited range of cohesive soils based on more easily obtained soil parameters so that direct erosion testing is not needed in all cases. General relations are proposed in this report.
Chapter 2 features a brief literature review of erosion processes in cohesive soils. Chapter 3 describes the design and operation of the ESTD. Chapter 4 describes how the log-law velocity profile is reproduced in the test channel and how boundary shear stress is measured with the device. Chapter 5 details the preparation of soil specimens and the soil sample properties. Chapter 6 describes erosion tests and results. Chapter 7 discusses the factors affecting erosion and summarizes the analytical development of the recommended design relations. Chapter 8 includes conclusions and future research recommendations.