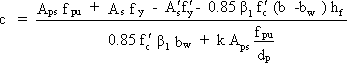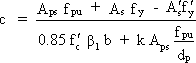Comprehensive Design Example for Prestressed Concrete (PSC) Girder Superstructure Bridge
Design Step 5 Design of Superstructure
Design Step 5.5 Stress in Prestressing Strands
Design Step 5.5.1 - Stress in prestressing strands at nominal flexural resistance
The stress in prestressing steel at nominal flexural resistance may be determined using stress compatibility analysis. In lieu of such analysis a simplified method is presented in S5.7.3.1.1. This method is applicable to rectangular or flanged sections subjected to flexure about one axis where the Whitney stress block stress distribution specified in S5.7.2.2 is used and for which fpe, the effective prestressing steel stress after losses, is not less than 0.5fpu. The average stress in prestressing steel, fps, may be taken as:
| fps | = fpu[1 - k(c/dp)] (S5.7.3.1.1-1) |
| where: | |
| k = 2(1.04 - fpy /fpu) (S5.7.3.1.1-2) | |
The value of "k" may be calculated using the above equation based on the type and properties of prestressing steel used or it may be obtained from Table SC5.7.3.1.1-1.
The distance from the neutral axis to the compression face of the member may be determined as follows:
for T-section behavior (Eq. S5.7.3.1.1-3):
for rectangular section behavior (Eq. S5.7.3.1.1-4):
T-sections where the neutral axis lies in the flange, i.e., "c" is less than the slab thickness, are considered rectangular sections.
From Table SC5.7.3.1.1-1:
k = 0.28 for low relaxation strands
Assuming rectangular section behavior with no compression steel or mild tension reinforcement:
c = Apsfpu /[0.85f′cβ1b + KAps(fpu /dp)]
For the midspan section
| Total section depth, h | = girder depth + structural slab thickness = 72 + 7.5 = 79.5 in. |
| dp | = h - (distance from bottom of beam to location of P/S steel force) = 79.5 - 5.0 = 74.5 in. |
| β1 | = 0.85 for 4 ksi slab concrete (S5.7.2.2) |
| b | = effective flange width (calculated in Section 2 of this example) = 111 in. |
| c | = 6.73(270)/[0.85(4)(0.85)(111) + 0.28(6.73)(270/74.5)] = 5.55 in. < structural slab thickness = 7.5 in. The assumption of the section behaving as a rectangular section is correct. |
Notice that if "c" from the calculations above was greater than the structural slab thickness (the integral wearing surface is ignored), the calculations for "c" would have to be repeated assuming a T-section behavior following the steps below:
Assume the neutral axis lies within the precast girder flange thickness and calculate "c". For this calculation, the girder flange width and area should be converted to their equivalent in slab concrete by multiplying the girder flange width by the modular ratio between the precast girder concrete and the slab concrete. The web width in the equation for "c" will be substituted for using the effective converted girder flange width. If the calculated value of "c" exceeds the sum of the deck thickness and the precast girder flange thickness, proceed to the next step. Otherwise, use the calculated value of "c".
Assume the neutral axis is below the flange of the precast girder and calculate "c". The term "0.85 f′cβ1(b - bw)" in the calculations should be broken into two terms, one refers to the contribution of the deck to the composite section flange and the second refers to the contribution of the precast girder flange to the composite girder flange.
fps = fpu[1 - k(c/dp)] (S5.7.3.1.1-1)
= 270[1 - 0.28(5.55/74.5)]
= 264.4 ksi
Design Step 5.5.2
| Transfer and development length | = 60(Strand diameter) (S5.11.4.1) 60(0.5 in.) = 30 in. |
Development Length = ld ≥ κ[fps - (2/3)fpe]db (S5.11.4.2-1)
From earlier calculations:
| fps | = 264.4 ksi (Design Step 5.4.8) |
| fpe | = 162.83 ksi (Design Step 5.5.1) |
From S5.11.4.2, κ = 1.6 for fully bonded strands
From S5.11.4.3, κ = 2.0 for partially debonded strands
For fully bonded strands (32 strands):
ld ≥ 1.6[264.4 - (2/3)162.83](0.5) = 124.7 in. (10.39 ft. or 10'-4 11/16")
For partially debonded strands (two groups of 6-strands each):
ld ≥ 2.0[264.4 - (2/3)162.83](0.5) = 155.8 in. (12.98 ft. or 12'-11 ¾")
Design Step 5.5.3 - Variation in stress in prestressing steel along the length of the girders
According to S5.11.4.1, the prestressing force, fpe, may be assumed to vary linearly from 0.0 at the point where bonding commences to a maximum at the transfer length. Between the transfer length and the development length, the strand force may be assumed to increase in a parabolic manner, reaching the tensile strength of the strand at the development length.
To simplify the calculations, many jurisdictions assume that the stress increases linearly between the transfer and the development lengths. This assumption is used in this example.
As shown in Figures 2-5 and 2-6, each beam contains three groups of strands:
Group 1: 32 strands fully bonded, i.e., bonded length starts 9 in. outside the centerline of bearings of the noncomposite beam
Group 2: 6 strands. Bonded length starts 10 ft. from the centerline of bearings of the noncomposite beam, i.e., 10'-9" from the end of the beam
Group 3: 6 strands. Bonded length starts 22 ft. from the centerline of bearings of the noncomposite beam, i.e., 22'-9" from the end of the beam
For each group, the stress in the prestressing strands is assumed to increase linearly from 0.0 at the point where bonding commences to fpe, over the transfer length, i.e., over 30 inches. The stress is also assumed to increase linearly from fpe at the end of the transfer length to fps at the end of the development length. Table 5.5-1 shows the strand forces at the service limit state (maximum strand stress = fpe) and at the strength limit state (maximum strand stress = fps) at different sections along the length of the beams. To facilitate the calculations, the forces are calculated for each of the three groups of strands separately and sections at the points where bonding commences, end of transfer length and end of development length for each group are included in the tabulated values. Figure 5.5-1 is a graphical representation of Table 5.5-1.
Table 5.5-1 - Prestressing Strand Forces
| Dist. from Grdr End (ft) |
Dist. from CL of Brg (ft) |
Initial Prestressing Force at Transfer | |||
|---|---|---|---|---|---|
| Group 1 (k) |
Group 2 (k) |
Group 3 (k) |
Total (k) | ||
| 0* | -0.75* | 0.0 | 0.0 | ||
| 0.75 | 0.00 | 277.3 | 277.3 | ||
| 2.50 | 1.75 | 924.4 | 924.4 | ||
| 7.75 | 7.00 | 924.4 | 924.4 | ||
| 10.39 | 9.64 | 924.4 | 924.4 | ||
| 10.75** | 10.00** | 924.4 | 0.0 | 924.4 | |
| 11.75 | 11.00 | 924.4 | 69.3 | 993.7 | |
| 13.25 | 12.50 | 924.4 | 173.3 | 1,097.7 | |
| 17.25 | 16.50 | 924.4 | 173.3 | 1,097.7 | |
| 22.75*** | 22.00*** | 924.4 | 173.3 | 0.0 | 1,097.7 |
| 23.73 | 22.98 | 924.4 | 173.3 | 67.9 | 1,165.6 |
| 25.25 | 24.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 28.25 | 27.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 33.75 | 33.00 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 35.73 | 34.98 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 39.25 | 38.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 44.75 | 44.00 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 50.25 | 49.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 55.25 | 54.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 55.75 | 55.00 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 61.25 | 60.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 66.75 | 66.00 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 72.25 | 71.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 74.77 | 74.02 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 77.75 | 77.00 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 83.25 | 82.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 85.25 | 84.50 | 924.4 | 173.3 | 173.3 | 1,271.0 |
| 86.77 | 86.02 | 924.4 | 173.3 | 67.9 | 1,165.6 |
| 87.75+++ | 87.00+++ | 924.4 | 173.3 | 0.0 | 1,097.7 |
| 88.75 | 88.00 | 924.4 | 173.3 | 1,097.7 | |
| 94.25 | 93.50 | 924.4 | 173.3 | 1,097.7 | |
| 97.25 | 96.50 | 924.4 | 173.3 | 1,097.7 | |
| 99.75++ | 99.00++ | 924.4 | 0.0 | 924.4 | |
| 100.11 | 99.36 | 924.4 | 924.4 | ||
| 103.25 | 102.50 | 924.4 | 924.4 | ||
| 108.00 | 107.25 | 924.4 | 924.4 | ||
| 109.75 | 109.00 | 277.3 | 277.3 | ||
| 110.5+ | 109.75+ | 0.0 | 0.0 | ||
*, **, *** - Point where bonding commences for strand Groups 1, 2, and 3, respectively
+, ++, +++ - Point where bonding ends for strand Groups 1, 2, and 3, respectively
Table 5.5-1 (cont.) - Presstressing Strand Forces
| Dist. from Grdr End (ft) |
Dist. from CL of Brg (ft) |
Prestressing Force After Losses | Force at the Nominal Flexural Resistance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Group 1 (k) |
Group 2 (k) |
Group 3 (k) |
Total (k) |
Group 1 (k) |
Group 2 (k) |
Group 3 (k) |
Total (k) | ||
| 0* | -0.75* | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 0.75 | 0.00 | 239.0 | 239.0 | 239.0 | 239.0 | ||||
| 2.50 | 1.75 | 797.2 | 797.2 | 797.2 | 797.2 | ||||
| 7.75 | 7.00 | 797.2 | 797.2 | 1,128.1 | 1,128.1 | ||||
| 10.39 | 9.64 | 797.2 | 797.2 | 1,294.5 | 1,294.5 | ||||
| 10.75** | 10.00** | 797.2 | 0.0 | 797.2 | 1,294.5 | 0.0 | 1,294.5 | ||
| 11.75 | 11.00 | 797.2 | 59.8 | 857.0 | 1,294.5 | 59.8 | 1,354.3 | ||
| 13.25 | 12.50 | 797.2 | 149.5 | 946.7 | 1,294.5 | 149.5 | 1,444.0 | ||
| 17.25 | 16.50 | 797.2 | 149.5 | 946.7 | 1,294.5 | 185.1 | 1,479.6 | ||
| 22.75*** | 22.00*** | 797.2 | 149.5 | 0.0 | 946.7 | 1,294.5 | 234.0 | 0.0 | 1,528.5 |
| 23.73 | 22.98 | 797.2 | 149.5 | 58.6 | 1,005.3 | 1,294.5 | 242.7 | 58.6 | 1,595.8 |
| 25.25 | 24.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 149.5 | 1,686.7 |
| 28.25 | 27.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 176.2 | 1,713.4 |
| 33.75 | 33.00 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 225.1 | 1,762.3 |
| 35.73 | 34.98 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 39.25 | 38.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 44.75 | 44.00 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 50.25 | 49.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 55.25 | 54.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 55.75 | 55.00 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 61.25 | 60.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 66.75 | 66.00 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 72.25 | 71.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 74.77 | 74.02 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 242.7 | 1,779.9 |
| 77.75 | 77.00 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 216.2 | 1,753.4 |
| 83.25 | 82.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 167.3 | 1,704.5 |
| 85.25 | 84.50 | 797.2 | 149.5 | 149.5 | 1,096.2 | 1,294.5 | 242.7 | 149.5 | 1,686.7 |
| 86.77 | 86.02 | 797.2 | 149.5 | 58.6 | 1,005.3 | 1,294.5 | 242.7 | 58.6 | 1,595.8 |
| 87.75+++ | 87.00+++ | 797.2 | 149.5 | 0.0 | 946.7 | 1,294.5 | 234.0 | 0.0 | 1,528.5 |
| 88.75 | 88.00 | 797.2 | 149.5 | 946.7 | 1,294.5 | 225.1 | 1,519.6 | ||
| 94.25 | 93.50 | 797.2 | 149.5 | 946.7 | 1,294.5 | 176.2 | 1,470.7 | ||
| 97.25 | 96.50 | 797.2 | 149.5 | 946.7 | 1,294.5 | 149.5 | 1,444.0 | ||
| 99.75++ | 99.00++ | 797.2 | 0.0 | 797.2 | 1,294.5 | 0.0 | 1,294.5 | ||
| 100.11 | 99.36 | 797.2 | 797.2 | 1,294.5 | 1,294.5 | ||||
| 103.25 | 102.50 | 797.2 | 797.2 | 1,096.6 | 1,096.6 | ||||
| 108.00 | 107.25 | 797.2 | 797.2 | 797.2 | 797.2 | ||||
| 109.75 | 109.00 | 239.0 | 239.0 | 239.0 | 239.0 | ||||
| 110.5+ | 109.75+ | 0.0 | 0.0 | 0.0 | 0.0 | ||||
*, **, *** - Point where bonding commences for strand Groups 1, 2, and 3, respectively
+, ++, +++ - Point where bonding ends for strand Groups 1, 2, and 3, respectively
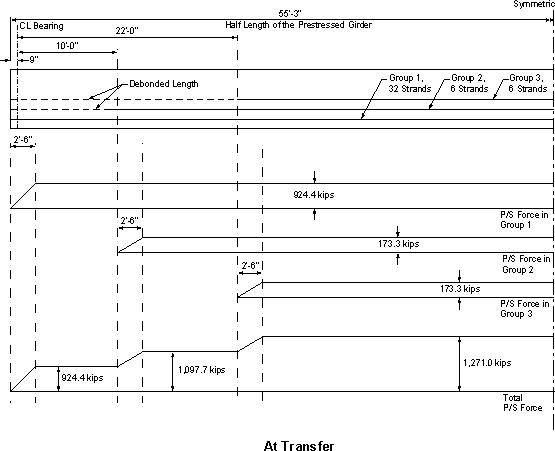
Figure 5.5-1 - Prestressing Strand Forces Shown Graphically
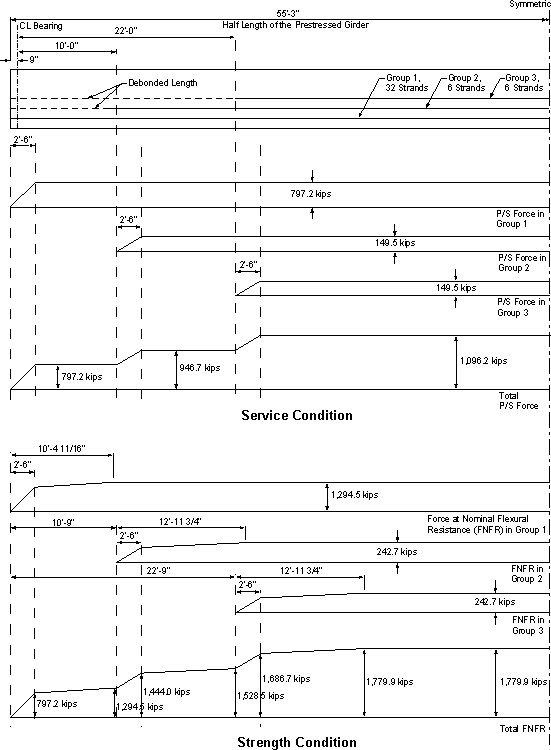
Transfer length = 30 in.
Development length, fully bonded = 124.7 in.
Development length, debonded = 155.8 in.
Figure 5.5-1 (cont.) - Prestressing Strand Forces Shown Graphically
Design Step 5.5.4 - Sample strand stress calculations
Prestress force at centerline of end bearing after losses under Service or Strength
Only Group 1 strands are bonded at this section. Ignore Group 2 and 3 strands.
Distance from the point bonding commences for Group 1 strands = 0.75 ft < transfer length
| Percent of prestressing force developed in Group 1 strands | = 0.75/transfer length = (0.75/2.5)(100) = 30% |
Stress in strands = 0.3(162.83) = 48.8 ksi
Force in strands at the section = 32(0.153)(48.8) = 239 kips
Prestress force at a section 11 ft. from the centerline of end bearing after losses under Service conditions
Only strands in Group 1 and 2 are bonded at this section. Ignore Group 3 strands.
The bonded length of Group 1 strands before this section is greater than the transfer length. Therefore, the full prestressing force exists in Group 1 strands.
Force in Group 1 strands = 32(0.153)(162.83) = 797.2 kips
Distance from the point bonding commences for Group 2 strands = 1.0 ft. < transfer length
| Percent of prestressing force developed in Group 2 strands = | 1.0/transfer length = (1.0/2.5)(100) = 40% |
Stress in Group 2 strands = 0.4(162.83) = 65.1 ksi
Force in Group 2 strands at the section = 6(0.153)(65.1) = 59.8 kips
Total prestressing force at this section = force in Group 1 + force in Group 2 = 797.2 + 59.8 = 857 kips
Strands maximum resistance at nominal flexural capacity at a section 7.0 ft. from the centerline of end bearing
Only Group 1 strands are bonded at this section. Ignore Group 2 and 3 strands.
Distance from the point bonding commences for Group 1 strands, i.e., distance from end of beam = 7.75 ft. (7'- 9")
This distance is greater than the transfer length (2.5 ft.) but less than the development length of the fully bonded strands (10.39 ft.). Therefore, the stress in the strand is assumed to reach fpe, 162.83 ksi, at the transfer length then increases linearly from fpe to fps, 264.4 ksi, between the transfer length and the development length.
| Stress in Group 1 strands | = 162.83 + (264.4 - 162.83)[(7.75 - 2.5)/(10.39 - 2.5)] = 230.41 ksi |
| Force in Group 1 strands | = 32(0.153)(230.41) = 1,128.1 kips |
Strands maximum resistance at nominal flexural capacity at a section 22 ft. from centerline of end bearing
Only strands in Group 1 and 2 are bonded at this section. Ignore Group 3 strands.
The bonded length of Group 1 strands before this section is greater than the development length for Group 1 (fully bonded) strands. Therefore, the full force exists in Group 1 strands.
Force in Group 1 strands = 32(0.153)(264.4) = 1,294.5 kips
The bonded length of Group 2 at this section = 22 - 10 = 12 ft.
| Stress in Group 2 strands | = 162.83 + (264.4 - 162.83)[(12 - 2.5)/(12.98 - 2.5)] = 254.9 ksi |
Force in Group 2 strands = 6(0.153)(254.9) = 234.0 kips
| Total prestressing force at this section | = force in Group 1 + force in Group 2 = 1,294.5 + 234.0 = 1,528.5 kips |