Use of Contractor Test Results in the Acceptance Decision, Recommended Quality Measures, and the Identification of Contractor/Department Risks
T 6120.3
August 9, 2004
Par.
- What is the purpose of this Technical Advisory?
- Does this Technical Advisory supersede other Federal Highway Administration (FHWA) guidance?
- What is FHWA's policy on the use of contractor's quality control test results for acceptance?
- Is there any existing FHWA guidance regarding 23 CFR 637B, the use of quality measures, and the identification of contractor and department risks?
- What is the background on quality assurance and quality assurance specifications?
- Where can I find definitions for the terms used within this Technical Advisory?
- Do any of the terms need additional explanation?
- What are the requirements for the use of independent samples?
- Who is required to perform verification sampling and testing?
- What are the validation procedures performed on independent samples?
- What are the test method comparison procedures performed on split samples?
- When should split samples be used?
- Can contractor split sample test results be used in the acceptance decision?
- What are the recommended quality measures?
- What quality measures are not recommended?
- What are contractor and department risks?
- Are there any conflicts between American Association of State Highway and Transportation Officials (AASHTO) quality assurance publications and FHWA regulations?
- Are there any reference materials on quality assurance, risks, and statistics?
What is the purpose of this Technical Advisory? This Technical Advisory provides guidance and recommendations for the use and validation of contractor's test results for acceptance, the use of quality measures, and the identification of contractor and department risks.
Does this Technical Advisory supersede other Federal Highway Administration (FHWA) guidance? Yes. This Technical Advisory supersedes previous guidance provided in the following:
Memorandum from Director, Office of Engineering, to Regional Administrators, "INFORMATION: Quality Assurance Procedures for Construction - 23 CFR 637 - Sampling for Verification Testing," March 28, 1997.
Memorandum from Chief, Highway Operations Division, to Regional Administrators, Division Administrators, Federal Lands Highway Program Administrator, "INFORMATION: Quality Assurance Guide Specification and Implementation Manual for Quality Assurance," August 2, 1996.
What is FHWA's policy on the use of contractor's quality control test results for acceptance? The FHWA policy on the use of contractor's quality control test results for acceptance requires validation of all data not generated by the State transportation department (STD) or its designated agent if used in the acceptance decision. The requirements are codified in Title 23 Code of Federal Regulations Part 637 Subpart B (23 CFR 637B), located at http://www.access.gpo.gov/nara/cfr/waisidx_03/23cfr637_03.html. (Note that the use of STD is in line with 23 CFR 637 B, as of April 1, 2003. In this Technical Advisory, all references to State Highway Agency (SHA) or "agency" have been replaced with STD or "department.")
Is there any existing FHWA guidance regarding 23 CFR 637B, the use of quality measures, and the identification of contractor and department risks? Yes. Existing FHWA guidance is provided in the following:
FHWA Materials Notebook: Chapter 1 - Materials Sampling and Testing 23 CFR 637, "23 CFR 637 ACTION: Final Rule and Questions & Answers on the Regulation," https://www.fhwa.dot.gov/pavement/materials_notebook/1sec1.htm.
Publication No. FHWA-RD-02-095 "Optimal Procedures for Quality Assurance Specifications" (see paragraph 18b), http://www.tfhrc.gov/pavement/pccp/pubs/02095/.
Memorandum from Chief, Highway Operations Division, to Resource Center Directors, Division Administrators, "INFORMATION: Laboratory Qualification," October 9, 1998, https://www.fhwa.dot.gov/pavement/labqual.htm.
Memorandum from Chief, Highway Operations Division, to Resource Center Directors, Division Administrators, Acting Federal Lands Highway Program Administrator, "INFORMATION: Technician Qualification," July 17, 1998, https://www.fhwa.dot.gov/pavement/techqual.htm.
What is the background on quality assurance and quality assurance specifications?
One of the fundamental concepts in quality assurance (QA) specifications is the separation of the functions of quality control (QC) and acceptance. In QA specifications, the contractor is responsible for the QC and the STD is responsible for obtaining and conducting verification tests and making the acceptance decision. Although QA is a combination of QC and acceptance, the separation of these two functions is important.
Due to the evolutionary nature of QA specifications, QC and acceptance functions often have been combined or intermingled. This has been a major source of confusion. The intermingling of QC and acceptance can be traced to the first statistically based specifications that were used at a time when STDs had technicians at the contractor's materials plants. The STD technicians did testing and determined when the product was acceptable. Contractors rarely did their own QC testing, and they often made changes to the process when necessary based on the STD's test results. Although QC was often recognized as a separate item from acceptance, in reality, little separation occurred.
With the downsizing that took place within many STDs in the 1990s, inspection and testing personnel positions were reduced significantly and many technicians were removed from the contractors' materials plants. Although STDs often took it upon themselves to control most aspects of production and construction, reductions in staff made it more important to assign QC where it rightfully belonged so the STD could focus on acceptance testing and inspection. This resulted in the contractor having to conduct the QC tests and the STD examining options for requiring more of its functions to be undertaken by the contractor. Many STDs found ways to include contractor test results in the acceptance decision, and some have questioned why the regulations prohibit the contractor from conducting acceptance testing.
The Federal regulations on sampling and testing of materials for construction appear in 23 CFR 637B (see paragraph 18a). These regulations were revised on June 29, 1995. This revision included clarification on the use of contractor test results in an acceptance program. The regulations most recent revision occurred in the Federal Register on December 10, 2002.
Further evolution of QA specifications has introduced the use of incentive/disincentive provisions and pay adjustment systems that utilize pay factors to adjust the amount paid to a contractor based on the level of quality of the product provided. Several different statistical quality measures were developed and used in order to determine this level of quality. Some examples of quality measures are: percent within limits, percent defective, average deviation, average absolute deviation, conformal index, and moving average. Some of these quality measures have been implemented without fully understanding how they apply to acceptance or whether they conform to sound statistical principles.
Statistical QA specifications and acceptance procedures have been implemented without fully understanding the risks involved to both the STD and the contractor. The acceptable level of STD risk and contractor risk is a subjective decision that often varies between departments. It is estimated that few departments have developed and evaluated the risk levels associated with their acceptance plans.
State planning and research pooled fund study SPR-2(199) "Optimal Acceptance Procedures for Statistical Construction Specifications" was conducted in order to investigate the current use of QA specifications and provide recommendations for statistically sound QA procedures and balancing of risks. The pooled fund study was administered by FHWA and the results provided in publication no. FHWA-RD-02-095, "Optimal Procedures for Quality Assurance Specifications" (see paragraph 18b). This publication provides a guide for developing new or modifying existing acceptance plans and QA specifications.
Where can I find definitions for the terms used within this Technical Advisory? The definitions for terms used in this Technical Advisory are taken from the following sources (listed in order of precedence), unless otherwise specified:
23 CFR 637 (see paragraph 18a).
AASHTO R10 (see paragraph 18e).
Transportation Research Board (TRB) Circular (see paragraph 18f).
Do any of the terms need additional explanation? Some additional explanations of terms are provided below:
Difference Two-Sigma Limit (D2S Limit). The D2S method compares the contractor and department results from a single split sample. The D2S Limit indicates the maximum acceptable difference between two test results obtained on test portions of the same material (and thus, applies only to split samples), and it is provided for single and multi-laboratory situations. It represents the difference between two individual test results that has approximately a five percent chance of being exceeded if the tests are actually from the same population. The value provided by this procedure is contained in many AASHTO and American Society of Testing and Materials (ASTM) test procedures and is typically listed in the precision and bias statement as "Acceptable Range of Two Test Results" at the end of each test procedure.
F-test. The F-test provides a method for comparing the variances (standard deviations squared, σ2) of two sets of data by assessing the size of the ratio of the variances. The hypothesis is that the department's tests and the contractor's tests are from the same population and the variability of the two data sets are equal. The intent is to determine whether the differences in the variability of the contractor's tests and the department's tests are larger than might be expected by chance if they came from the same population. The calculated F-value is then compared to the critical value (Fcrit) obtained from a table of F-values at a chosen level of significance (α). The F-test can be used to compare either an equal or unequal number of contractor vs. department sample sizes.
Operating Characteristics (OC) Curves
(1) OC curves for statistical tests. OC curves can be developed to indicate the probability of rejecting a hypothesis. This type of curve shows the relation between the probability of rejecting a hypothesis that a sample belongs to a given population with a given characteristic and the actual population value of that characteristic. OC curves can also be developed to show either the probability of not detecting a difference, or detecting a difference, versus the actual difference between the two populations being compared. There are also OC curves available to provide guidance regarding the number of tests needed to achieve a certain probability of detecting a given difference when one actually exists. OC curves that plot the probability of detecting a difference are sometimes called power curves because they plot the power of the statistical test procedure to detect a given difference.
(2) OC curves for acceptance plans. OC curves can also be a graphical representation of an acceptance plan that shows a relationship between the actual quality of a lot and either (a) the probability of its acceptance (for accept/reject acceptance plans), or (b) the probability of its acceptance at various pay levels for acceptance plans that include pay adjustment provisions.
Paired t-test. The paired t-test compares contractor and department results from an equal number of split samples. When it is desirable to compare more than one pair of split sample test results, the t-test for paired measurements can be used. This test uses the differences between pairs of tests and determines whether the average difference is statistically different from zero. Thus, it is the difference within pairs, not between pairs, that is being tested. The calculated t-value is compared to the critical value (tcrit) obtained from a table of t-values at a specified level of significance and with n-1 degrees of freedom (see t-test in paragraph 7e).
t-test
(1) The t-test provides a method for comparing the means of two independent data sets and is used to assess the degree of difference in the means. The null hypothesis is that the department's tests and the contractor's tests are from the same population, and the means of the two data sets are equal. The desire is to determine whether it is reasonable to assume that the contractor's tests came from the same population as the department's tests. The t-test can be used to compare either an equal or unequal number of contractor vs. department sample sizes.
(2) Since the values used for the t-test are dependent upon whether or not the variances are assumed equal for the two data sets, it is necessary to test the variances (F-test) before the means (t-test). If it is determined that the variances are assumed to be equal (F<Fcrit), then the t-test is conducted based on the two sample sets using a pooled estimate for the variance and pooled degrees of freedom. If the sample variances are determined to be different (F≥Fcrit), then the t-test is conducted using the individual sample variances, the individual sample sizes, and the effective degrees of freedom. The calculated t-value is compared to the critical value (tcrit) obtained from a table of t-values at a specified level of significance.
What are the requirements for the use of independent samples? The regulation 23 CFR 637B requires the use of independent samples for verification sampling and testing in the acceptance program. In order to be considered independent, each sample must contain independent information reflecting all sources of variability associated with the material, process, sampling, and testing in the test results. This does not prevent split samples from being used in the acceptance decision if the data is used properly to provide validation of independent data (see paragraph 13). Some clarification of using contractor performed sampling for verification sampling and for use in the acceptance decision is found in paragraphs 9 through 13.
Who is required to perform verification sampling and testing?
The regulation requires STD personnel or their representatives to perform the verification sampling and testing. The regulation also specifically indicates that verification sampling and testing cannot be performed by contractor employees. However, there are situations where labor regulations, hazardous conditions, and liability issues may dictate some contractor involvement in verification sampling. In these situations, the involvement of contractor personnel should be limited so that they are not deemed to be in control of the sampling.
(1) The STD can use the services of the contractor's personnel to assist in obtaining independent verification samples when the following requirements are adhered to:
(a) The verification sample location or time has been randomly selected by the STD and is only given to the contractor immediately prior to sampling.
(b) The contractor's personnel are used only to provide labor to assist in physically obtaining the verification sample of the material.
(c) The STD is present to witness the taking of the verification sample.
(d) Both the STD witness and contractor labor are qualified sampling personnel.
(e) The STD witness controls the sampling process by choosing the location or timing and directing the taking of the verification sample.
(f) The STD witness immediately takes possession of the verification sample.
(2) STD verification sample independence and the intent of 23 CFR 637B are maintained when the above requirements are met. However, these situations should be the exception and not the rule. The verification sampling is expected to be performed entirely by STD personnel or their representative in the majority of situations.
Verification testing is required to be performed by the STD or its designated agent, excluding the contractor or vendor; therefore, verification testing cannot be based on contractor performed testing witnessed by the STD.
What are the validation procedures performed on independent samples? When comparing two data sets, such as department and contractor test results, it is important to compare both the variances and the means. The tests most often used are the F-test (comparison of variances) and the t-test (comparison of means), which are used together. A procedure that compares a single department test with 4 to 10 contractor tests is sometimes used but not recommended.
The F-test and t-test are the recommended methods because they have more power to detect actual differences than the method that relies on a single department test for the comparison. If either the F-test or the t-test show a significant difference (F≥Fcrit or t≥tcrit), it is questionable whether the data does truly come from the same population.
(1) The computational method used for the t-test differs depending on if the variances are found to be either equal or not equal. There is a t-test that corresponds with finding a difference in variances, F≥Fcrit (see paragraph 7e). This has lead to instances of incorrectly validating test results by finding no differences in the means (t<tcrit) after finding differences in the variances (F≥Fcrit). When a difference in the variances is identified then the test results have not been validated, even if no difference in the means has been identified.
(2) The source of the difference should be identified if it is determined that a significant difference is likely between either the variances or the means. The identification of a difference between either variances or means is simply a notice that a difference exists. Therefore, the source of the difference must still be determined.
The method of comparing a single department test to a number of contractor tests should not be used. Although simple, it suffers from the fact that only a single department test is used when making the comparison. Any comparison method that is based on a single test result is not effective in detecting differences between data sets. This is due to the high variability that is associated with individual values, as compared with mean values.
What are the test method comparison procedures performed on split samples?
The comparison of a single split sample by using the D2S limits is simple and can be done for each split sample that is obtained. However, since it is based on comparing only single data values, it is not very powerful for identifying differences when they exist. Thus, it cannot detect real differences unless the results are far apart. The appeal of the D2S method lies in its simplicity rather than its power.
Due to D2S method limitations, it is recommended that the paired t-test (see paragraph 7d) be used on the total accumulated split sample results to allow for a comparison with more discerning power. If either of these comparisons indicates a difference, then an investigation to identify the cause of the difference should be initiated.
-
When should split samples be used? The split sampling, testing, and comparison procedures (see paragraph 11) are primarily used as a function of an Independent Assurance (IA) program as outlined in 23 CFR 637B. The use of split samples in the IA program provides a check on testing equipment and procedures. The evaluation of split samples helps to identify where the cause of any differences may occur by isolating the testing components. This complements the QA program and ensures credibility of the testing program.
Can contractor split sample test results be used in the acceptance decision?
In order for contractor split sample test results to be used in the acceptance decision, the contractor's test results used in the acceptance decision must be independently validated by the STD. The validation is not required if the STD conducts all of the verification sampling and testing and does not wish to use the contractor's test results in the acceptance decision.
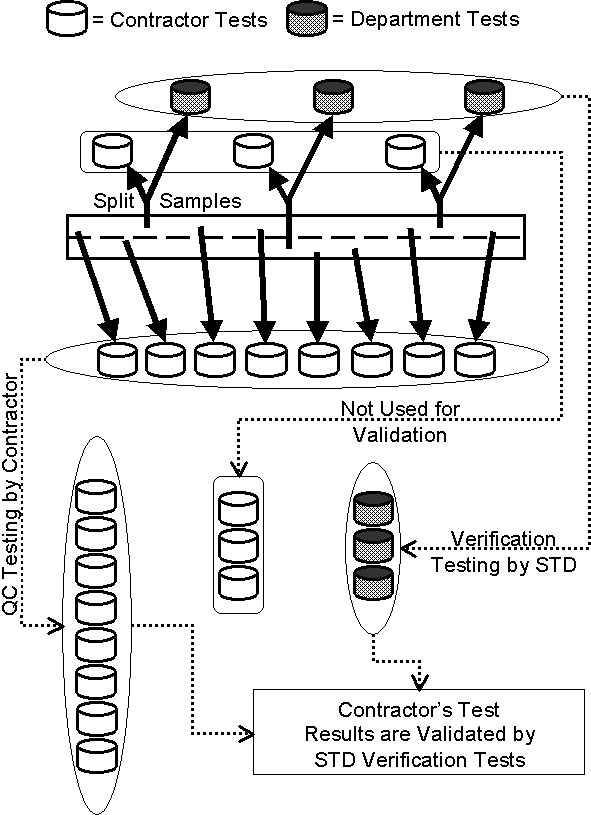
The contractor performs QC testing using independently obtained samples. The STD can perform verification testing using its half of the split samples when sampled as required in paragraph 9. The validation is accomplished by comparing the STD verification tests with the contractor's independently sampled QC tests (see Figure 1). The contractor's splits of the verification samples cannot be used for validation purposes because they are not independent of the STD samples. If both sets of split samples are used the only component of variability that can be compared is the testing variability. The split sample components of variability associated with materials, process, and sampling are the same, having come from the same location and sampler.
The contractor may or may not test their portion of the split sample. The validation procedure is the same in either case because the contractor's split samples cannot be used for validation (see Figure 1).
When the STD uses contractor personnel as labor to take verification samples as required in paragraph 9 and the STD then performs verification testing on these samples, the verification test results may be considered independent of the contractors test results. They may be considered independent because they have been sampled with control by the STD, independently tested, and independently compared to the contractor's independent QC test results (test results that do not include the contractor's set of split samples). Again, in order to be considered independent the two sets of samples must each contain the variability associated with the material, process, sampling, and testing.
If the contractor's independently sampled QC test results are validated by the STD verification test results, then the material can be accepted based on either:
(1) The total test results provided by the contractor that combine their independent QC test results and their split of the verification sample test results (see 2.1 in Figure 2),
(2) A combination of independent contractor QC test results excluding their split sample test results and the STD verification split test results (see 2.2 in Figure 2), or
(3) Only the contractor independent QC test results, excluding all split sample test results (see 2.3 in Figure 2).
The STD test results from their split portion of the verification samples and the contractor test results from their split portion of the of the verification samples cannot be combined for the acceptance decision (see 2.4 in Figure 2). If the two sets of split test results are combined, they are no longer independent and the population of the contractor's independent test results will be biased and result in an invalid comparison. In essence, a double counting of test results would occur if the two sets of split test results were combined. This is true even though the two sets of test results may have different values.
A scenario may exist where all samples are taken by the STD and split between the STD and contractor. In this scenario the STD only performs verification tests on a specified percentage of all the split samples they have in their possession. It is important to note, the validation must still be performed on independent sample data. Again, this is accomplished by comparing the STD verification test results with the contractor's independent test results. The contractor's independent test results cannot include the split tests that match with the STD verification tests.
(1) For example, if 11 samples were split, the contractor tests all 11 samples and the STD tests only 3 samples, the 3 STD test results would be compared against the contractor's remaining 8 test results. Independence of the two sets of data is maintained by excluding the contractor's three test results that match the STD test results.
(2) In essence, the validation shown in Figure 1 has occurred when the STD does not test all of the split samples that are in its possession. By taking possession of all the split samples, the STD does have additional material for an investigation if the contractor's results do not validate or for use in a dispute resolution system.
Although split samples have physically been taken, it is the method which the data from these samples is analyzed that allows independent validation and their use in the acceptance decision. The independent validation is accomplished by validation procedures performed on independent samples (see paragraph 10), not by test method comparison procedures performed on split samples (see paragraph 11).
What are the recommended quality measures? The percent within limits (PWL) or percent defective (PD) are the recommended quality measures to be used. It is necessary to measure both the center and spread when characterizing a lot of material. These quality measures use the mean and standard deviation to measure center and spread and then estimate the percentage of the lot that is within, PWL, or outside of, PD, the specification limits. Since PD and PWL can easily be converted to one another simply by subtracting from 100, they are equivalent quality measures. The preference on which of the two quality measures to use, PWL or PD, is typically based on the department's preference to highlight how much of the material meets the requirements as described with PWL, rather than how much is defective as described with PD.
What quality measures are not recommended?
The average deviation from the target value should not be used as the quality measure for QA acceptance plans. This approach often encourages the contractor to manipulate its process during the production of a lot. In effect, the contractor increases process variability by making frequent adjustments to the process in order to get the average of the test results to be at or near the target value.
The average absolute deviation (AAD) from the target value should not be used as the quality measure for QA acceptance plans. To avoid the problem of over-adjusting the process in response to early test results, the average absolute deviation from the target has been used instead of the average deviation. By taking the absolute value of the deviation from the target, the contractor cannot benefit by any strategy other than aiming for the target value. However, the variability of the material may not be adequately measured. Very different sets of test results can give identical AAD values. Not only must it be questioned if equal pay is appropriate for these widely different conditions, the use of AAD fails to document these differences that should be used for future modifications of the specification. Specifically, the means and populations may vary considerably for different sets of test results that can give identical AAD values. These mean and variability differences are disregarded with acceptance based on AAD.
The conformal index (CI) should not be used as the quality measure for QA acceptance plans. The CI is very similar in practice to the AAD and has the same disadvantages of not being appropriate for a one-sided specification and potentially having the same CI value for very different test results.
The moving average should not be used as the quality measure for QA acceptance plans. The moving average was developed as a QC measure and not developed for use as an acceptance approach. The use of the moving average is not consistent with the use of lot-by-lot acceptance. When acceptance is based on a lot, it is assumed that the various lots are independent of one another. Since each individual test result appears in several moving average calculations, the moving averages are correlated and the results of one average are not independent of the next; therefore, it is difficult to determine when or where a lot begins or ends. In addition, it is not easy to determine pay factors on a lot-by-lot basis since the successive moving averages are correlated and individual lots are not well defined. As a result, acceptance procedures based on moving averages often result in production shut downs and plant adjustments rather than determining appropriate pay factors for specific production lots.
What are contractor and department risks?
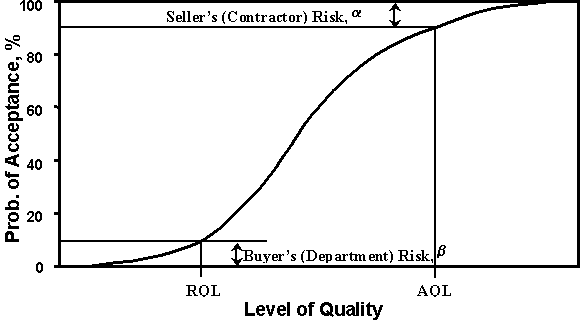
The two types of risks discussed in this section are the seller's (contractor) risk (α) and the buyer's (department) risk (β). The acceptable level of α and β risks is a subjective decision that can vary from department to department. A properly developed QA acceptance plan takes these risks into consideration in a manner that is fair to both the department and contractor. Too large a risk for either party undermines credibility.
(1) Table 1 of the AASHTO Material's Specification R 9-97(2000), "Acceptance Sampling Plans for Highway Construction" (see paragraph 18d), has suggestions for risk levels for both the seller and buyer that range from 0.001 (0.1 percent) to 0.200 (20 percent). It should be noted that large sample quantities, on the order of 10 to 20 or more, are needed to achieve some of the risk levels provided in this table. Larger sample quantities will provide this lower level of risk to both the department and contractor. The selection of the number of samples required by a department may need to be modified based on an analysis of risks.
(2) The sample size is the number of test results used to judge the quality of a lot, and therefore it is directly related to the lot size. One reason to use larger lot sizes is the potential resultant increase in sample size. This tends to provide a much lower level of risk to both the contractor and department. However, an assumption that all of the material and construction processes remain consistent throughout the lot is required. Small lot sizes may not be compatible with large sample sizes due to a large amount of required testing. Larger sample sizes can be used with large lot sizes to decrease risks of making incorrect acceptance decisions. However, the possibility of combining materials from different populations must be taken into consideration. The final decision regarding sample size per lot cannot be made until an evaluation of risks has been completed. An attempt should be made to balance the risk between the contractor and department while holding the risk to a reasonable level. This means that a large number of samples may be required. If the risks cannot be held to a reasonable level for both, the department may have to accept a disproportionate level of risk.
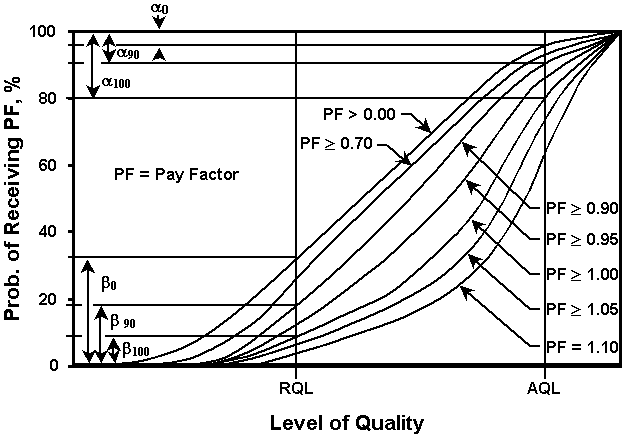
The α and β risks are very narrowly defined to occur at only two specific quality levels. The α risk is the probability of rejecting material that is exactly at the acceptable quality level (AQL), while β is the probability of accepting material that is exactly at the rejectable quality level (RQL). Therefore, they do not provide a very good indication of the risks over a wide range of possible quality levels that a contractor may operate. It is necessary to construct an OC curve that illustrates the probability of acceptance for any quality level for the acceptance plan under consideration (see Figure 3) to evaluate how the acceptance plan will actually perform in practice. Another step that is necessary to fully evaluate the risks for a pay adjustment acceptance plan is to plot OC curves associated with receiving various pay factors (see Figure 4).
The concept of α and β risks derives from statistical hypothesis testing where there is either a right or wrong decision. When α and β risks are applied to materials or construction, they are only truly appropriate for the case of a pass/fail or accept/reject decision. This may lead to considerable confusion if an attempt is made to apply them to the pay adjustment case.
(1) The evaluation of risks becomes more complicated when the acceptance system includes pay adjustment provisions. The α and β risks discussed do not fully incorporate the concept of pay adjustments. By itself, the α risk, defined as the probability that an acceptance plan will incorrectly reject acceptable quality material or construction, cannot reflect the fact that the material or construction may be accepted at any of the possible pay adjustments (full pay, increased or decreased pay). When working with a pay adjustment system, the contractor's risk may also be interpreted as the probability of acceptable material or construction being accepted at less than 100 percent pay. In order to avoid confusion in the terms when the contractor's risk is used in this manner, the risk is here called α100. However, it is computed in the same manner as α at the AQL. In addition, the β risk, defined as the probability that the owner incorrectly accepts rejectable quality material or construction, cannot reflect the impact of pay adjustments on determining the department's risk. When working with a pay adjustment plan, the department's risk may also be interpreted as the probability of accepting rejectable quality material or construction at 100 percent pay or greater. In order to avoid confusion in the terms when the department's risk is used in this manner, it is here called β100. There are α and β type risks (αPF and βPF) associated with any given level of pay adjustment or pay factor (PF) from zero through the bonus chosen by the STD. For example, at a pay factor of 0.90 (90 percent payment) the alpha and beta risks can be represented by α90 and β90. Likewise, at a pay factor of 1.05 (bonus of 5 percent) alpha and beta can be represented by α105 and β105.
(2) The use of α and β risks alone to evaluate pay adjustment acceptance plans is simply not sufficient. When developing a pay adjustment system the contractor's risk αPF and the department's risk βPF must also be considered for the entire range of risks associated with the system. If only one level of risk is evaluated alone, for example at 100 percent pay, some other risks associated with the system may be too high. Making any change to the system will change all risks involved.
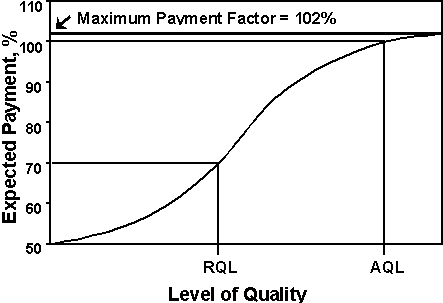
An additional method to properly evaluate the risks when pay adjustments are added to the acceptance decision is the expected pay (EP) curve (see Figure 5). The EP curve has the advantage of combining all of the possible levels into a single expected or long-term average pay for each given level of quality.
The EP curve can also be used to ensure that a department's acceptance plan will pay 100 percent for material that is accepted at the AQL. It is generally agreed that the average pay for AQL material should be 100 percent. An average pay of 100 percent cannot be achieved unless a bonus is allowed. If the department's pay equations or tables are not properly developed, the average pay factor may be above or below 100 percent at the AQL. This would result in the contractor either being underpaid or overpaid on average. If this is the case, the department should determine if an expected pay other than 100 percent is acceptable for AQL material.
While the average expected pay shown with an EP curve should be used in addition to considering α and β type risks, the use of EP curves alone is also not sufficient to fully evaluate an acceptance plan. The EP alone is not a complete measure of the likelihood that any individual lot will receive a correct pay factor. The variability of the individual pay factors about the EP curve must also be considered.
When a price adjustment acceptance plan is used, it is essential that the department develop an EP curve and multiple OC curves for the probability of receiving various pay factors over the total range of quality levels in addition to considering all levels of α and β type risks. Both OC and EP curves must be developed and analyzed to show how an acceptance plan was designed to function. In all cases, when pay adjustments are used in the acceptance decision, the OC curves should be constructed to confirm that the acceptance procedure is working as desired and, in particular, that the average pay factor at the AQL is 100 percent. The department may also want to look at computer simulation histograms of individual pay factors to obtain a picture of how much variability is associated with the pay factor determination.
It is important to note that for PWL or PD acceptance plans, computer simulation is almost always used to develop α and β risks, OC and EP curves. The OCPLOT computer program that was developed as a part of FHWA Demonstration Project No. 89 (see paragraph 18j) is able to develop OC and EP curves, run simulations on the effect of the variability of the individual lot pay factors on the final pay factor determination, and create histograms. This program can be found on the Federal Highway Administration Office of Pavement Technology website at https://www.fhwa.dot.gov/pavement/qasoft.htm.
Are there any conflicts between American Association of State Highway and Transportation Officials (AASHTO) quality assurance publications and FHWA regulations?
The companion reports "AASHTO Implementation Manual for Quality Assurance" (see paragraph 18h) and "AASHTO Quality Assurance Guide Specification"(see paragraph 18i) were published in February 1996 as reports of the AASHTO Highway Subcommittee on Construction. The Guide Specification is not an official AASHTO Specification and the Implementation Manual is not an official guide or voluntary standard because they have not been balloted and approved by the AASHTO Standing Committee on Highways and the AASHTO Board of Directors.
These reports provide uniform guidance to develop and implement quality assurance standard specifications. While these reports substantially follow 23 CFR 637B, some differences exist.
(1) One significant difference is that the reports provide for the use of either paired split (see paragraph 11) or independent (see paragraph 10) sample data comparisons for validation of contractor test results, while 23 CFR 637B allows only independent sample data for validation (see paragraph 8). The use of a paired split sample data comparison only verifies the test procedures and equipment, not the quality of the material (see paragraph 12). The use of independently obtained and tested samples assesses material, process, sampling and testing variability. Therefore, an acceptance program that uses paired split sample comparisons or witnessed tests for validation does not ensure the material quality and does not meet the requirements or intent of 23 CFR 637B.
(2) On the other hand, the use of split samples in the IA program provides a check on testing equipment and procedures. This complements the QA program and ensures the credibility of the testing program. The Implementation Manual offers the option of using either split or independent samples for IA. This does not agree with the regulation that IA testing may only be performed on split samples or proficiency samples. There is value to both split and independent samples; however, they do not provide interchangeable information.
Are there any reference materials on quality assurance, risks, and statistics? Yes. The following references apply to quality assurance, risks, and statistics.
"23 CFR Part 637," Subpart B - Quality Assurance Procedures for Construction, Federal Highway Administration, Federal Register, Washington, DC, April 2003, http://www.access.gpo.gov/nara/cfr/waisidx_03/23cfr637_03.html.
"Optimal Procedures for Quality Assurance Specifications," Publication No. FHWA-RD-02-095, Federal Highway Administration, Washington, DC, April 2003, http://www.tfhrc.gov/pavement/pccp/pubs/02095/.
StatSoft, Inc., Electronic Statistics Textbook, StatSoft, Tulsa, OK, 2003, http://www.statsoft.com/textbook/stathome.html.
"Acceptance Sampling Plans for Highway Construction," AASHTO Standard Specifications for Transportation Materials and Methods of Sampling and Testing, Part 1B Specifications: R 9-97 (2000), American Association of State Highway and Transportation Officials, 22nd Edition, 2002. (This is currently being evaluated and rewritten under the guidance of NCHRP Project 20-07, Task 164.)
"Definition of Terms for Specifications and Procedures," AASHTO Standard Specifications for Transportation Materials and Methods of Sampling and Testing, Part 1B Specifications: R 10-98 (2002), American Association of State Highway and Transportation Officials, 22nd Edition, 2002.
"Glossary of Highway Quality Assurance Terms," Transportation Research Circular No. E-C037, Transportation Research Board, Washington, DC, April 2002, http://trb.org/news/blurb_detail.asp?id=621.
Introduction to Statistical Quality Control, Fourth Edition, Douglas C. Montgomery, ISBN 0471316482, John Wiley & Sons, November 2000.
AASHTO Implementation Manual for Quality Assurance, AASHTO Construction/Materials Quality Assurance Task Force of the AASHTO Highway Subcommittee on Construction, American Association of State Highway and Transportation Officials, February, 1996.
AASHTO Quality Assurance Guide Specification, AASHTO Construction / Materials Quality Assurance Task Force of the AASHTO Highway Subcommittee on Construction, American Association of State Highway and Transportation Officials, February, 1996.
"Quality Assurance Software for the Personal Computer, Demonstration Project 89," Publication No. FHWA-SA-96-026, Federal Highway Administration, Washington, DC, May 1996, https://www.fhwa.dot.gov/pavement/qasoft.htm.
Statistical Quality Control, Seventh Edition, Eugene Grant and Richard Leavenworth, ISBN 0078443547, McGraw-Hill, January 1996.
Quality Control and Industrial Statistics, Fifth Edition, Acheson J. Duncan, ISBN 0256035350, McGraw-Hill, October 1994.
Report on Limits of Use of Contractor Performed Sampling and Testing in Federal Highway Administration Programs, Robert Bohman, et al, Federal Highway Administration, March 1993.
Materials Control and Acceptance - Quality Assurance, NHI Course Number 134042A, Federal Highway Administration, National Highway Institute, http://www.nhi.fhwa.dot.gov.
King W. Gee
Associate Administrator for Infrastructure
Figure 1 - Validation of Contractor's Tests
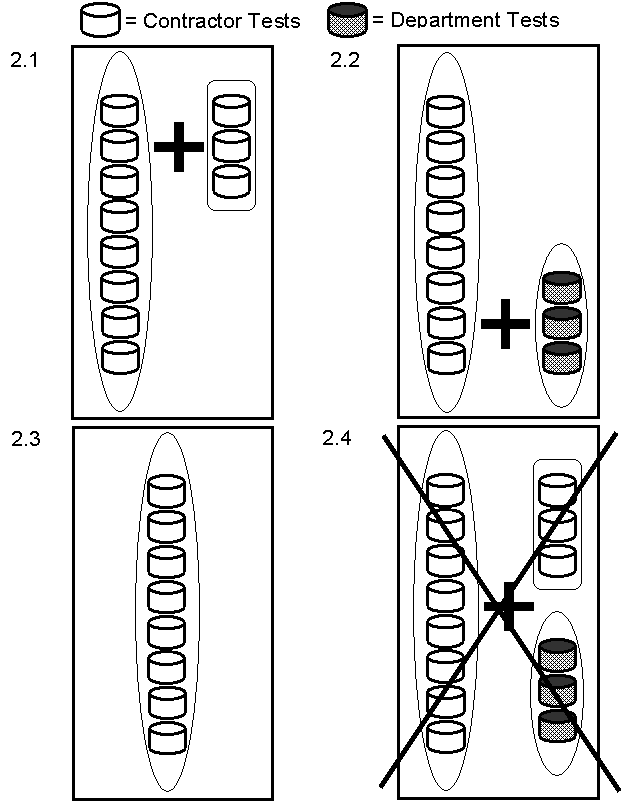
Figure 2 - Acceptance Based on Combined Test Results
(Using Sampling Plan in Figure 1)
Figure 3 - Typical Operating Characteristic (OC) Curve for an Accept/Reject Acceptance
Figure 4 - Typical Operating Characteristic (OC) Curves for an Acceptance Plan with Pay Adjustments
Figure 5 - Typical Expected Pay Curve