| << Previous | Contents | Next >> |
Geotechnical Aspects of Pavements Reference Manual
Appendix C: 1993 AASHTO Design Method
C.1 Introduction
The AASHTO Guide for Design of Pavement Structures (AASHTO, 1993) is the primary document used to design new and rehabilitated highway pavements. Approximately 80% of all states use the AASHTO pavement design procedures, with the majority using the 1993 version. All versions of the AASHTO Design Guide are empirical design methods based on field performance data measured at the AASHO Road Test in 1958-60.
Chapter 3 of this manual describes the evolution of the various versions of the AASHTO Design Guide. Geotechnical inputs to the 1993 AASHTO design procedure are detailed in Chapter 5. Chapter 6 provides some design examples using the 1993 AASHTO procedures.
The overall approach of the 1993 AASHTO procedure for both flexible and rigid pavements is to design for a specified serviceability loss at the end of the design life of the pavement. Serviceability is defined in terms of the Present Serviceability Index, PSI, which varies between the limits of 5 (best) and 0 (worst). Serviceability loss at end of design life, ΔPSI, is partitioned between traffic and environmental effects, as follows (see also Figure 3.8):
(C.1)ΔPSI = ΔPSITR + ΔPSISW + ΔPSIFH
in which ΔPSITR, ΔPSISW and ΔPSIFH are the components of serviceability loss attributable to traffic, swelling, and frost heave, respectively. The structural design procedures for swelling and frost heave are the same for both flexible and rigid pavements; these are detailed in Appendix G of the 1993 AASHTO Guide. The structural design procedures for traffic are different for flexible and rigid pavement types. These procedures are summarized below in Sections C.2 and C.3, respectively. For simplicity, only the design procedures for new construction are summarized here. The design procedures for reconstruction are similar, except that characterization of recycled materials may be required. See the 1993 AASHTO Guide for details of additional procedures (e.g., determination of remaining structural life for overlay design) relevant to rehabilitation design.
C.2 Flexible Pavement Structural Design
Design Equation
The empirical expression relating traffic, pavement structure, and pavement performance for flexible pavements is:
(C.2)log10 ( W18 ) = ZR S0 + 9.36 log10 ( SN + 1 ) - 0.20
| + | log10 | ΔPSI | + 2.32 log10 ( MR ) - 8.07 | |||
| 4.2 - 1.5 | ||||||
| 0.40 + | 1094 | |||||
| ( SN + 1 )5.19 | ||||||
in which:
| W18 | = | number of 18 kip equivalent single axle loads (ESALs) |
| ZR | = | standard normal deviate (function of the design reliability level) |
| S0 | = | overall standard deviation (function of overall design uncertainty) |
| ΔPSI | = | allowable serviceability loss at end of design life |
| MR | = | subgrade resilient modulus |
| SN | = | structural number (a measure of required structural capacity) |
The first five parameters typically are the inputs to the design equation, and SN is the output. Equation (C.2) must be solved implicitly for the structural number SN as a function of the input parameters. The structural number SN is defined as:
(C.3)SN = a1 D1 + a2 D2 m2 + a3 D3 m3
in which D1, D2, and D3 are the thicknesses (inches) of the surface, base, and subbase layers, respectively, a1, a2, and a3 are corresponding structural layer coefficients, and m2 and m3 are drainage coefficients for the base and subbase layers, respectively. Equation (C.3) can be generalized for additional bound and/or unbound layers. Note that there may be many combinations of layer thicknesses that can provide satisfactory SN values; cost and other issues must be considered to determine the optimal final design.
Design Inputs
Analysis Period
Performance period refers to the time that a pavement design is intended to last before it needs rehabilitation. It is equivalent to the time elapsed as a new, reconstructed, or rehabilitated pavement structure deteriorates from its initial serviceability to its terminal serviceability. The term "analysis period" refers to the overall duration that the design strategy must cover. It may be identical to the performance period. However, realistic performance limitations may require planned rehabilitation within the desired analysis period, in which case, the analysis period may encompass multiple performance periods. Analysis period in this context is synonymous with design life in the 1993 AASHTO Guide. AASHTO recommendations for analysis periods for different types of roads are summarized in Table C-1.
| Highway conditions | Analysis period (years) |
|---|---|
| High-volume urban | 30 - 50 |
| High-volume rural | 20 - 50 |
| Low-volume paved | 15 - 25 |
| Low-volume aggregate surface | 10 - 20 |
Traffic
Traffic is one of the most important factors in pavement design, and every effort should be made to collect accurate data specific to each project. Traffic analysis requires the evaluation of initial traffic volume, traffic growth, directional distribution, and traffic type.
The AASHTO Design Guide is based on cumulative 18 kip (80 KN) equivalent single-axle loads (ESALs). Detailed traffic analysis is beyond the scope of this reference manual. However, ESALs may be estimated using the following equation:
(C.4)ESAL = ( ADT0 ) ( T ) ( Tf ) ( G ) ( D ) ( L ) ( 365 ) ( Y )
in which:
| ADT0 | = | average daily traffic at the start of the design period |
| T | = | percentage of trucks in the ADT |
| Tf | = | truck factor, or the number of 18 kip ESALs per truck |
| G | = | traffic growth factor |
| D | = | directional distribution factor |
| L | = | lane distribution factor |
| Y | = | design period in years |
AASHTO (1993) and standard pavement engineering textbooks (e.g., Huang, 2004) provide details on the determination of all of these parameters and estimation of design ESALs.
Reliability
Design reliability is defined as the probability that a pavement section will perform satisfactorily over the design period. It must account for uncertainties in traffic loading, environmental conditions, and construction materials. The AASHTO design method accounts for these uncertainties by incorporating a reliability level R to provide a factor of safety into the pavement design and thereby increase the probability that the pavement will perform as intended over its design life. The levels of reliability recommended by AASHTO for various classes of roads are summarized in Table C-2.
| Functional classification | Recommended level of reliability | |
|---|---|---|
| Urban | Rural | |
| Interstate and other freeways | 85 - 99.9 | 80 - 99.9 |
| Principal arterials | 80 - 99 | 75 - 95 |
| Collectors | 80 - 95 | 75 - 95 |
| Local | 50 - 80 | 50 - 80 |
Note: Results base on a survey of AASHTO Pavement Design Task Force.
The reliability level is not included directly in the AASHTO design equations. Rather, it is used to determine the standard normal deviate ZR. Values of ZR corresponding to selected levels of reliability are summarized in Table C-3.
| Reliability (%) | Standard normal deviate (ZR) | Reliability (%) | Standard normal deviate (ZR) |
|---|---|---|---|
| 50 | 0.000 | 93 | -1.476 |
| 60 | -0.253 | 94 | -1.555 |
| 70 | -0.524 | 95 | -1.645 |
| 75 | -0.674 | 96 | -1.751 |
| 80 | -0.841 | 97 | -1.881 |
| 85 | -1.037 | 98 | -2.054 |
| 90 | -1.282 | 99 | -2.327 |
| 91 | -1.340 | 99.9 | -3.090 |
| 92 | -1.405 | 99.99 | -3.750 |
The AASHTO design equations also require specification of the overall standard deviation S0. For flexible pavements, values for S0 typically range between 0.35 and 0.50, with a value of 0.45 commonly used for design.
Serviceability
Serviceability is quantified by the Present Serviceability Index, PSI. Although PSI theoretically ranges between 5 and 0, the actual range for real pavements is between about 4.5 to 1.5.
The initial serviceability index po corresponds to road conditions immediately after construction. A typical value of po for flexible pavements is 4.2. The terminal serviceability index pt is defined as the lowest serviceability that will be tolerated before rehabilitation or reconstruction becomes necessary. A terminal serviceability index of 2.5 or higher is recommended for design of major highways. Thus, a typical allowable serviceability loss due to traffic for flexible pavements can be expressed as:
(C.5)ΔPSI = pt - po = 4.2 - 2.5 = 1.7
Subgrade Resilient Modulus
Pavement subgrade quality is defined in terms of its resilient modulus MR. The resilient modulus MR is a basic material property that can be measured directly in the laboratory, evaluated in-situ from nondestructive tests, or estimated using various empirical relations as detailed in Chapter 5. The 1993 AASHTO Design Guide also incorporates a procedure for considering seasonal fluctuations in MR to determine a seasonally averaged value for use in design. This procedure is summarized in Section 5.4.3.
Layer Properties
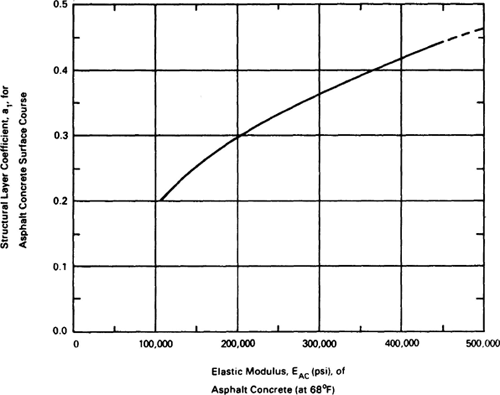
The material properties required for each layer are the structural layer coefficients ai and, for unbound materials, the drainage coefficients mi. Methods for evaluating the ai and mi values for unbound materials are detailed in Sections 5.4.5 and 5.5.1, respectively. The chart in Figure C-1 can be used to estimate the structural layer coefficient for asphalt concrete in terms of its elastic modulus at 68°F. Values of a1 between 0.4 and 0.44 are typically used for dense graded asphalt concrete.
Figure C-1. Chart for estimating structural layer coefficient of dense-graded asphalt concrete based on the elastic (resilient) modulus (AASHTO, 1993).
Click here for text version of image
Procedure
The steps in the 1993 AASHTO flexible pavement design procedure are summarized below in the context of the example baseline scenario presented in Section 6.2.1:
- Determine the analysis period. For the example design scenario, a 30-year design life is specified.
- Evaluate the design traffic: W18 = 11.6 million ESALs.
- Determine the design reliability factors: Reliability = 90% (usually set by agency policy), ZR = -1.282, S0 = 0.45.
- Determine the allowable serviceability loss due to traffic: ΔPSI = 1.7 (this may be reduced if frost heave or swelling soils are an issue).
- Evaluate the seasonally averaged subgrade resilient modulus MR using the procedures described in Section 5.4.3: MR = 7,500 psi.
- Determine the layer properties:
- Structural layer coefficients ai for all bound layers (see Section 0 for asphalt concrete, 1993 AASHTO Guide for other stabilized materials) and unbound layers (Section 5.4.5). Recommendations for appropriate ai values for rehabilitation design are given in Table 5-44 in Section 5.4.5. Values for example design:
a1 = 0.44, a2 = 0.17. - Drainage coefficients mi for all unbound layers (Section 5.5.1): m2 = 1.0.
- Structural layer coefficients ai for all bound layers (see Section 0 for asphalt concrete, 1993 AASHTO Guide for other stabilized materials) and unbound layers (Section 5.4.5). Recommendations for appropriate ai values for rehabilitation design are given in Table 5-44 in Section 5.4.5. Values for example design:
- Solve Eq. (C.2) for the required overall structural number: SN = 5.07.
- Determine the design layer thicknesses for the pavement section:
- Using Eq. (C.2) with MR set equal to the granular base resilient modulus EBS = 40,000 psi (from the correlation in Eq. 5.16), solve for the required structural number for the asphalt concrete surface layer: SN1 = 2.62.
- Convert SN1 to the required thickness of asphalt: D1 = SN1 / a1 = 5.95 → 6 inches1.
- Assign the remaining required structural number to the granular base layer:
SN2 = SN - D1 a1 = 2.43. - Convert SN2 to the required thickness of granular base: D2 = SN2 / m2 a2 = 14.3 → 14 inches.1
C.3 Rigid Pavement Structural Design
Design Equation
The empirical expression relating traffic, pavement structure, and pavement performance for rigid pavements is:
(C.6)log10 ( W18 ) = ZR So + 7.35 log10 ( D + 1 ) - 0.06
| + | log10 | ΔPSI | + ( 4.22 - 0.32 pt ) log10 | Sc Cd ( D0.75 - 1.132 ) | ||||||||
| 4.5 - 1.5 | ||||||||||||
| 1 + | 1.64 × 107 | 215.63 J | D0.75 - | 18.42 | ||||||||
| ( D + 1 )8.46 | ( Ec / k )0.25 | |||||||||||
in which:
| W18 | = | number of 18 kip equivalent single axle loads (ESALs) |
| ZR | = | standard normal deviate (function of the design reliability level) |
| S0 | = | overall standard deviation (function of overall design uncertainty) |
| ΔPSI | = | allowable serviceability loss at end of design life |
| pt | = | terminal serviceability |
| k | = | modulus of subgrade reaction (pci) |
| Sc | = | PCC modulus of rupture (psi) |
| Ec | = | PCC modulus of elasticity (psi) |
| J | = | an empirical joint load transfer coefficient |
| Cd | = | an empirical drainage coefficient |
| D | = | required PCC slab thickness (inches) |
The first ten parameters typically are the inputs to the design equation, and D is the output. Equation (C.6) must be solved implicitly for the slab thickness D as a function of the input parameters.
The design of JRCP and CRCP pavements also requires design of the steel reinforcement. Reinforcement design is beyond the scope of this manual; refer to the 1993 AASHTO Guide for details on this.
Design Inputs
Analysis Period
Same as for flexible pavements; see Section 0.
Traffic
Same as for flexible pavements; see Section 0. Note that the truck factor Tf will not in general be the same for rigid and flexible pavements. Refer to the 1993 AASHTO Design Guide or standard pavement engineering textbooks like Huang (2004) for determination of the truck factor.
Reliability
Similar to flexible pavements; see Section 0. For rigid pavements, values for S0 typically range between 0.3 and 0.45, with a value of 0.35 commonly used for design.
Serviceability
Similar to flexible pavements; see Section 0. A typical value of po for rigid pavements is 4.4. As for flexible pavements, a terminal serviceability index of 2.5 or higher is recommended for design of major highways. Thus, a typical allowable serviceability loss due to traffic for rigid pavements can be expressed as:
(C.7)ΔPSI = pt - po = 4.4 - 2.5 = 1.9
Modulus of Subgrade Reaction
The design modulus of subgrade reaction k is a computed quantity that is a function of the following properties:
- Subgrade resilient modulus MR
- Thickness of granular subbase DSB
- Resilient modulus of granular subbase ESB
- Depth to bedrock DSG (if shallower than 10 feet)
- Loss of Service LS (an index of the erodibility of the granular subbase)
See Section 5.4.6 for the procedure for determining the design value for the modulus of subgrade reaction k.
Other Layer Properties
Other layer properties include the modulus of rupture Sc and elastic modulus Ec for the Portland cement concrete slabs, an empirical joint load transfer coefficient J, and the subbase drainage coefficient Cd. The PCC parameters Sc and Ec are standard material properties; mean values should be used for the pavement design inputs. The joint load transfer coefficient J is a function of the shoulder type and the load transfer condition between the pavement slab and shoulders; recommended values are summarized in Table C-4. See Section 5.5.1 for determination of the drainage coefficient Cd.
| No Shoulders | Asphalt Shoulders | Tied PCC Shoulders | ||||
|---|---|---|---|---|---|---|
| With Load Transfer Devices | Without Load Transfer Devices | With Load Transfer Devices | Without Load Transfer Devices | With Load Transfer Devices | Without Load Transfer Devices | |
| JPCP / JRCP | 3.2 | 3.8 - 4.4 | 3.2 | 3.8 - 4.4 | 2.5 - 3.1 | 3.6 - 4.2 |
| CRCP | 2.9 | N.A. | 2.9 - 3.2 | N.A. | 2.3 - 2.9 | N.A. |
Procedure
The steps in the 1993 AASHTO rigid pavement design procedure are summarized below in the context of the example baseline scenario presented in Section 6.2.1:
- Determine the analysis period. For the example design scenario, a 30-year design life is specified.
- Evaluate the design traffic: W18 = 18.9 million ESALs
- Determine the design reliability factors: Reliability = 90% (usually set by agency policy), ZR = -1.282, S0 = 0.45.
- Determine the terminal serviceability and allowable serviceability loss due to traffic: pt = 2.5, ΔPSI = 1.9 (this may be reduced if frost heave or swelling soils are an issue).
- Evaluate the effective modulus of subgrade reaction k using the procedures described in Section 5.4.6. Specific design inputs to this procedure are the seasonally averaged subgrade resilient modulus MR = 7,500 psi, the assumed thickness of the granular subbase DSB, the seasonally averaged subbase resilient modulus ESB = 40,000 psi, the depth to bedrock DSG (if less than 10 feet-not the case for this example design), and the loss of service coefficient LS = 2.
- Specify the PCC properties: Sc = 690 psi, Ec = 4.4 × 106 psi (these would typically be from material specifications; mean values should be used for inputs).
- Determine the other input parameters: joint load transfer coefficient J = 3.2, drainage coefficient Cd = 1.0.
- Solve Eq. (C.6) for the required slab thickness: D = 10.55 ≈ 10.5 inches.
Note that the thickness assumed for the granular subbase in Step 5 can influence the required slab thickness computed in Step 8. If desired, several design alternatives can be evaluated to arrive at the optimal design.
C.4 Software
The empirical design equations for flexible and rigid pavements in Eqs. (C.2) and (C.6) are implicit relationships for the required structural number SN and slab thickness D, respectively. Consequently, an iterative solution algorithm is required. The 1993 AASHTO Design Guide provides nomographs for the graphical evaluation of these equations. They can also be evaluated easily using a spreadsheet, e.g., via the Solver tool in Microsoft Excel. DARWin, a comprehensive software program tied to the 1993 AASHTO Design Guide procedures, is also available through AASHTO. Additional information on DARWin can be found at http://darwin.aashtoware.org/.
C.5 References
- AASHTO (1993). AASHTO Guide for Design of Pavement Structures, American Association of State Highway and Transportation Officials, Washington, D.C.
- Huang, Y.H. (2004). Pavement Analysis and Design (2nd ed.), Prentice-Hall, Englewood Cliffs, NJ.
Notes
- After rounding to the nearest half-inch, per the recommendations in the 1993 AASHTO Design Guide. Unbound layer thicknesses are rounded to the nearest inch. Return to Text
| << Previous | Contents | Next >> |

