U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number:
FHWA-RD-03-048
|
Previous | Table of Contents | Next
In this chapter, an outline of the design methodology of MSEWs with geosynthetic reinforcement under static conditions is presented in accordance with AASHTO, Section 5.8, 1998 (AASHTO 98). The details of AASHTO design are given in "Demonstration Project No. 82: Mechanically Stabilized Earth Walls and Reinforced Soil Slopes, Design and Construction Guidelines," Federal Highway Administration (FHWA), 1997.
Current design of an MSEW is a multistep process based on limit equilibrium analysis (AASHTO 1998, Elias and Christopher 1997). Based on a detailed analysis of specific site constraints and project requirements (such as wall geometry, performance requirements, constructability, aesthetic, and environmental issues), a particular MSEW system is selected. The most important input design parameters of an MSEW are the type of reinforcing elements and facing. Design of a particular MSEW consists of the following steps:
The following input information is necessary to start the design:
Wall Parameters: total height (H); face inclination (i); type of facing (modular blocks, precast concrete, wrapped reinforcement, etc.); type of reinforcing elements (metal strips, bar mats, geogrid, geotextile, etc.).
Soil Parameters: layout/geology of the construction site; angle of internal friction (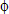 ) and unit weight (
) and unit weight (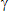 ) of the backfill material; shear strength parameters and unit weight of the retained soil; shear strength parameters and unit weight of the foundation soil.
) of the backfill material; shear strength parameters and unit weight of the retained soil; shear strength parameters and unit weight of the foundation soil.
Design Criteria: settlement requirements; factors of safety; design life; construction sequence; etc.
Based on field observations of existing MSEWs, the prescribed minimum length of the reinforcement is:
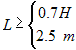
It is used as a preliminary width of a MSEW in the stability analysis.
External stability analysis of an MSEW is similar to the stability analysis of conventional retaining walls. It verifies whether the dimensions of an MSEW ensure its global stability under the loads induced by the retained soil. The reinforced mass is considered as a solid block, and only failure surfaces through the adjacent retained soil are considered. For a given wall, the external stability checks and the corresponding minimum factors of safety are as follows:
The direct sliding, eccentricity, and bearing capacity checks are based on the wedge failure mechanism. Deep-seated stability check is based on the rotational failure mechanism. As a result of external stability analysis, the total length of the reinforcement is verified and may be increased if necessary.
Internal stability analysis investigates the possibility of collapse within the reinforced soil due to insufficient strength or embedment length of the reinforcement. Planar slip surfaces developed through the toe and the reinforcement are investigated. If the wall front batter is greater than 10 degrees, the inclination of the slip surfaces is defined by Coulomb's earth pressure theory. If the wall front batter is less than or equal to 10 degrees, the inclination of the slip surfaces is defined by Rankine's earth pressure theory. Internal stability analysis yields the spacing and strength parameters of reinforcement necessary to ensure the integrity and internal stability of the reinforced soil. The major calculations are:
The check against reinforcement breakage is done at each level of reinforcement. It must ensure that the required tensile resistance of the reinforcement is less than the allowable long-term strength:
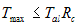
where: Tmax is the maximum required tensile force needed to resist the active lateral earth pressure at the face of the wall; Tal is the allowable tensile capacity per unit width of reinforcement; Rc is the coverage ratio. The allowable long-term tensile strength is calculated according to the type of the reinforcement. For geosynthetic reinforcement, the allowable tensile strength takes into account the reduction of the ultimate strength due to creep, degradation, and installation damage.
The capacity of the reinforcement to develop the required tensile resistance depends on its pullout resistance. The pullout resistance of the reinforcement is defined by the soil-reinforcement interaction and the anchorage length into stable soil. The check against reinforcement pullout is:
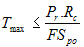
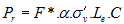
where: Tmax is the maximum required tensile
force needed to resist the active lateral earth pressure at the face of the
wall; Pr is the pullout resistance;
Rc is the coverage ratio; FSpo
is the safety factor against pullout; F*
is a pullout resistance factor, defined by the soil-reinforcement interaction;
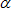 is a scale effect correction
factor taking into account the nonuniform mobilization of the pullout resistance
along the length of the reinforcement;
is a scale effect correction
factor taking into account the nonuniform mobilization of the pullout resistance
along the length of the reinforcement; 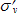 is the effective vertical stress at the reinforcement level; Le
is the anchorage length of reinforcement; and C
is the effective perimeter of reinforcement.
is the effective vertical stress at the reinforcement level; Le
is the anchorage length of reinforcement; and C
is the effective perimeter of reinforcement.
Usually in design, both calculations (against reinforcement breakage and pullout) are satisfied iteratively. First, the reinforcement layout and strength characteristics are specified based on constructability requirements or experience with similar structures, and then the anchorage length is checked. Equations (2.2)–(2.4) are combined as follows:
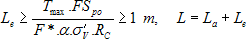
where: Le is the anchorage or embedment length of the reinforcement, that extends behind the adopted slip surface; La is the length of the reinforcement between the facing and the critical slip surface; L is the total length of the reinforcement.
The internal stability checks are made at each level of reinforcement, and the most critical state defines the final length, spacing and strength parameters of the reinforcement.
Connection design ensures that the forces at the connections can be sustained by both the reinforcement and the connection. The connection force in reinforcement is expressed by the active lateral earth pressure acting on the tributary area at the face of the wall.
The settlements and lateral displacements of MSEWs influence their serviceability and long-term performance. Since the limit equilibrium analysis is unable to predict displacements, their evaluation in design is often based on semi- empirical relations and field observations on existing structures. Usually it is assumed that the adequate selection of material properties and safety factors in design ensure acceptable displacements.
The design ends up with the following information (in addition to the design input):
According to the presented design methodology (AASHTO 1998), the internal stability calculations control the total dimensions of the wall and the reinforcement characteristics in most of the cases. This is due to the assumption that an internal slip surface always develops without taking into account the reinforcement spacing, reinforcement stiffness, and other factors that influence the behavior of MSEWs.
The program FLAC (Itasca Consulting Group, Inc., 1998) is a two- dimensional explicit finite difference program best suited to simulate the behavior of materials that may undergo plastic flow and large deformations when these materials' yield limits are reached. It is a powerful tool for solving a wide range of complex problems in continuum mechanics, due to its formulation based on dynamic equations of motion that use an explicit Lagrangian calculation scheme and a mixed- discretization zoning technique. FLAC's ability to model plastic collapse and flow of highly nonlinear materials such as soil and rock very accurately makes it a useful tool for numerical analysis in geotechnical and mining engineering. In addition to the basic ability to represent the mechanical response of various materials, including the ability to model groundwater flow and pore pressure dissipation, there are optional modules for dynamic analysis, thermal analysis and modeling of creep material behavior. Some of the program's major features are: 10 built-in material models; plane-strain (basic formulation), plane stress and axisymmetric geometry modes; 4 structural element models simulating structural support; interface elements simulating distinct planes along which slip or separation can occur; built-in programming language FISH; and an extensive facility for generating plots and slideshow movies. The built-in programming language, FISH, offers unique capabilities to tailor the analysis to the user, ranging from implementing user-defined constitutive models to overriding some of the FLAC calculation modules and replacing them with user- written ones.
FLAC formulation is based on the dynamic equations of motion using an explicit time-marching method to solve the algebraic equations that correspond to a given set of governing differential equations, and initial and boundary conditions. The calculation scheme follows two-step calculation cycles. The first step of each cycle uses the equations of motion (equilibrium equation) to derive new velocities and displacements from stresses and forces. At the second step, the stress-strain relation (constitutive equation) is applied, and the velocities calculated during the first step are used to derive new strain rates, and new stresses from strain rates. One cycle occupies one calculation timestep, which is small enough to ensure that the information cannot pass physically from one element to another in the chosen interval. The central concept of the calculation scheme is that the disturbances will propagate across the elements numerically as they would propagate physically; however, the calculational wave speed always keeps ahead of the physical wave speed. Major advantages of FLAC formulation are: numerical scheme is stable when the physical system is unstable; plastic collapse and flow are modeled very accurately; large two- dimensional models can be analyzed without excessive memory requirements (matrices are not formed, iterations are not necessary to compute stresses from strains); objects of any shape and different properties can be modeled; the material can yield and flow, and in large-strain mode, the grid deforms and moves with the represented material. However, FLAC solution requires many steps because of the typically small timestep.
In current study, the program FLAC (Version 3.40) was chosen to analyze the behavior of geosynthetic reinforced earth block wall up to failure because of its many advantages compared to other commercial programs, and particularly because of its ability to model accurately unstable states of soil systems.
The literature review is based on references relevant to the following aspects of the current study: design methodology of MSEWs; failure mechanisms of MSEW with modular block facing; and FLAC application in MSEW analysis.
The design methodology of MSEWs with geosynthetic reinforcement and modular block facing has been published in several FHWA and AASHTO documents (Elias and Christopher 1997, AASHTO 1998). Relevant issues are discussed in chapter 2.1. However, none of the existing methods considers the effects of reinforcement spacing on wall stability.
Leshchinsky et al. (1994) conducted a series of pullout experiments employing one and two reinforcement layers. The results demonstrated that the behavior of single- and double-layered systems was different and implied the idea of MSEW with closely spaced reinforcement. The experiments investigated the pullout response of multilayered systems with reference to single-layered systems. The most important observations were: the pullout resistance of single- and double-layered systems was nearly the same for confining pressures typical for actual walls; the front- end displacement corresponding to the maximum pullout force was much smaller for double-layered systems than for single-layered systems; and the displacement field of double-layered systems showed no differential movements within the soil confined between the reinforcement, except near the back end. The test results and observations implied that the material confined between the geogrid layers (double- layered systems) was stiffened for overburden pressures typical for actual walls and moved as a block. The study acknowledged the importance of reinforcement spacing in design with respect to the critical slip surface and critical failure mechanism. The major conclusion was that, if the reinforcement layers are closely spaced and are sufficiently stiff and strong, the reinforced soil can be treated as a composite mass, and the critical slip surface will develop behind it. The current numerical study was designed to investigate further the effects of reinforcement spacing on wall behavior using sophisticated numerical methods.
Bathurst and Hatami (1998) reported results of extensive numerical analysis of seismic response of a MSEW wall with continuous facing panel using FLAC. The effects of dynamic loading on reinforced soil structure, and the influence of reinforcement stiffness, number of reinforcement layers, base condition, and wall geometry on the earthquake response of the system were investigated. The numerical model of a continuous panel wall was 6 meters (m) high with 6 uniformly spaced reinforcement layers. The wall facing was modeled as a continuous concrete panel with a thickness of 0.14 m. The foundation soil was not modeled, and its effect on model response was investigated by specifying different boundary conditions along the base. The reinforcement layers were modeled using FLAC cable elements that were attached to a grid point of the continuous panel region (corresponding to unbreakable structural connections). The soil was modeled as a frictional material with a Mohr-Coulomb failure criterion. The elastic modulus of soil was kept constant using the values calculated at the end of construction before prop removal. The properties of the FLAC model were chosen to correspond to a reference finite element model (FEM) and represent values commonly used in design. The FLAC model represented the following construction sequence: the soil and reinforcement elements were constructed in layers, while the continuous panel was braced horizontally using external rigid supports; at the end of construction, the panel supports were released in sequence from top to bottom; and dynamic loading was applied. The FLAC model response under static loading was compared with the response of a similar model analyzed with FEM. The following parameters were analyzed: dynamic excitation; base conditions; type and location of the right-edge boundary; material dumping ratio; reinforcement stiffness; reinforcement length; and toe restraint condition. Important observations relevant to the current analysis were: for the given reinforcement layout and model properties, interior slip surfaces intersecting all reinforcement layers were not observed during all simulations; the accuracy of dynamic analysis was sufficient if the developed slip surface did not reach the right-edge boundary. The reported results are a major contribution to the analysis of dynamic response of precast facing MSEWs.
Hatami and Bathurst (1999) reported results from a numerical investigation of the influence of wall height, reinforcement stiffness, reinforcement length and toe restrained condition on the frequency response of MSEWs. This study used the same numerical model reported by Bathurst and Hatami (1998) in addition to equivalent models with wall heights equal to 3 m and 9 m. The numerical simulations results showed that the reinforcement stiffness, reinforcement length, and toe- restrained condition did not affect the fundamental frequency of the models. Some effects of the input ground motion were recorded. The stronger of the two input acceleration records gave lower fundamental frequencies of the models. As noted by the authors, the results are relevant only to the rigid foundation condition.
Lee (1999) reported strain and force distributions in reinforcement as results of FLAC analysis of the FHWA test walls built in Algonquin, IL. However, the model was not described. The focus of the analysis was on the earth pressure distribution within the reinforced soil and the corresponding earth pressure coefficient.
Leshchinsky (1997, 1999) proposed four failure mechanisms to be investigated in the design of geosynthetic reinforced steep slopes using the limit equilibrium method: two-part wedge mechanism (direct sliding analysis); rotational mechanism (deep-seated stability analysis and compound stability analysis); and log- spiral failure mechanism (internal stability or tieback analysis). These mechanisms closely correspond to the four failure modes identified numerically in the current study: external, deep-seated, compound, and connection mode.
Leshchinsky (1999) proposed a new concept related to the safety factor in stability analysis of reinforced steep slopes. The safety factor is directly related to the reinforcement strength, based on the fact that reinforced steep slopes are stable because of the reinforcement tensile resistance (i.e., the soil shear strength is fully mobilized, and stability is dependent entirely on reinforcement strength). The peak shear strength of soil is reduced, accounting for possible large deformations and progressive failure. This approach is implemented in the program MSEW 1.1 (ADAMA Engineering 1998) as an L-method for compound or deep-seated stability analysis. Compound stability analysis using the L-method demonstrated very good agreement with relevant FLAC predictions.