U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number:
FHWA-RD-03-048
|
Previous | Table of Contents | Next
The results are divided into two major sets. The first set includes results related to identification of failure mechanisms and influence of soil strength, reinforcement stiffness, foundation stiffness, and secondary reinforcement layers on wall behavior. The second set of results illustrates the influence of reinforcement length, secondary reinforcement layers, and soil dilatancy on wall stability. All tables and figures of chapter 4 are grouped at the end of the chapter in the order of their citing.
All results are presented with reference to three basic states of the modeled wall: failure, critical, and stable states. These states reflect the response of the model during the numerical simulations of construction. Each wall was modeled to reach failure by increasing its height in layers while keeping the reinforcement length equal to 1.5 m. In the process of numerical simulation, the wall reached the verge of failure, but its construction continued until the complete collapse was detected numerically. The state that corresponded to a wall at the verge of failure was termed a critical state. It was defined by analyzing numerical and physical parameters such as slip surface development, maximum cumulative displacement of the system during construction, number of calculation steps necessary to equilibrate the system after placing each layer, and history of maximum unbalanced force. The critical state was identified when at least three of the following events occurred simultaneously: (1) a slip surface was fully developed; (2) the maximum cumulative displacement increased nonlinearly; (3) the number of calculation steps per layer increased rapidly; and (4) the history of maximum unbalanced force indicated an abrupt change of the unbalanced force. The height and length-to-height ratio at the critical state were termed critical height (hcr) and critical length-to-height ratio (l/hcr). The critical wall height with respect to the prevailing mode of failure and soil strength for all cases are shown in figures 4.1 and 4.2. States corresponding to walls higher than the wall at the critical state were termed failure states. Stable states corresponded to walls with a height equal to the critical height but having a length-to-height ratio larger than the critical length-to-height ratio. The definition of failure, critical, and stable states of the numerical modeling is illustrated in figure 3.3. General information about runs corresponding to failure and critical states for all cases are given in table 3.9 and table 3.10.
The main purpose of this study was to investigate the behavior of MSEWs with modular block facing and geosynthetic reinforcement simulating construction sequence up to failure. It was important practically to identify the failure mechanisms as a function of geosynthetic spacing, the effects of soil strength, reinforcement stiffness, foundation stiffness, and secondary reinforcement layers. All numerical simulations used in the analysis are summarized in table 3.8.
Failure mechanisms were identified by monitoring the development of local plastic (or failure) zones in soil during wall construction, which were recorded incrementally by FLAC on plots in the form of movies. The observed displacement configuration and the type of the developed slip surface defined a failure mechanism. Four failure mechanisms were identified: external mode (direct sliding/toppling); deep-seated mode; compound mode; and connection mode. The slip surface types that corresponded to the identified failure mechanisms are shown in figure 4.3. A summary of results identifying the failure modes of all cases is given in table 4.1. The critical wall height and the prevailing mode of failure of all cases are given in table 4.2. Maximum forces in reinforcement (connection forces and maximum axial forces) for all cases at the critical and failure states are given in tables 4.3 and 4.4.
To gain further insight of wall behavior, stresses, and horizontal displacements at certain vertical sections of the wall were extracted and analyzed. The location of sections A, B, and C is shown in figure 4.4. These vertical sections were defined as Section A (0.1 or 0.15 m behind the facing), Section B (within the reinforced soil, 0.1 m apart from the end of reinforcement), and Section C (within the backfill soil, 0.1 or 0.15 m apart from the end of reinforcement).
The following models were considered as representative cases to illustrate each identified mode of failure:
Figure 3.9 shows the number of calculation steps per layer and the maximum cumulative displacements during wall construction that defined the critical wall height for these cases.
The major characteristic of this failure mode was the development of a sliding wedge behind the reinforced mass (figure 4.3–a). When failure was approached, plastic zones evolved within the bottom of reinforced mass. For cases with foundation soil that was stronger and stiffer than the reinforced soil, the slip surface at failure passed through the bottom of reinforced mass, and the lower reinforcement layers were overstressed. The reinforced mass behaved as a coherent block and failed by toppling against the toe or sliding along the base. This failure mechanism corresponded to toppling or direct sliding. The cases with identified external failure mode are shown in figure 4.1 and given in table 4.2. External failure mode was observed for cases with close reinforcement spacing, stronger reinforced soil, and stiffer foundation and reinforcement.
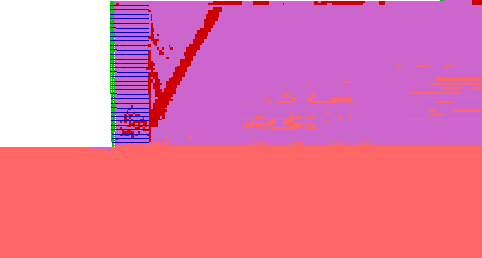
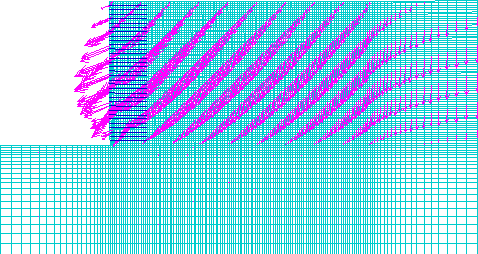
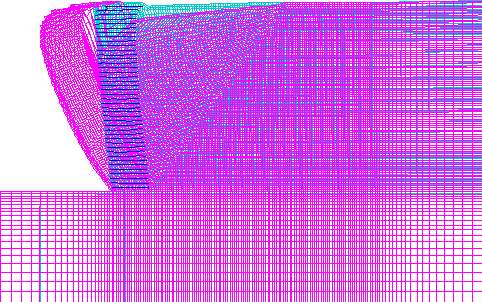
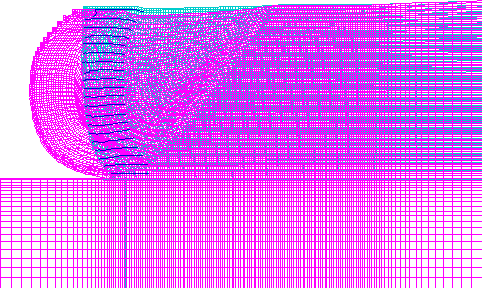
The model of case 1 (s=0.2 m, high strength soil, very stiff foundation) experienced external mode of failure, and the critical state was identified at wall height h=6.6 m. At the critical state, the failure zones defined an external slip surface that had developed only in the backfill soil (figure 4.5). The displacement field (figure 4.6) and the distorted grid (figure 4.7) confirmed the observation that the wall was toppling against the toe. The horizontal displacements along sections A and B demonstrated that the reinforced soil was moving as a block (figure 4.8). The axial force distribution along reinforcement layers showed that the reinforcement layers at the wall bottom were overstressed (figure 4.9). However, the forces in the first reinforcement layer were smaller than the forces of adjacent layers, because of a very stiff foundation.
Failure zone distributions of other models that experienced external mode of failure are shown on figures 4.10–4.14.
Deep-seated external mode of failure was characterized by a slip surface developed outside the reinforced mass and through the foundation soil (figure 4.3–b). As failure developed, plastic zones evolved within the bottom of the reinforced mass. This mode of failure was observed for cases with close reinforcement spacing and relatively weak foundation (table 4.2, figure 4.1–b). This failure mechanism corresponded to deep-seated sliding.
The model of case 10 (s=0.2 m, high strength reinforced soil, low strength backfill and foundation soil) experienced deep-seated mode of failure, and the critical state was identified at wall height h=3.2 m. At the critical state, the failure zones defined an external slip surface that developed outside the reinforced soil (figure 4.15). The displacement field (figure 4.16) and the distorted grid (figure 4.17) confirmed the observation that the wall was first sliding and then toppling against the toe as a result of the foundation's insufficient bearing capacity. The horizontal displacements along sections A and B demonstrated that the reinforced soil was moving as a block (figure 4.18). At the critical state, the displacements at the base of the wall were larger because of the sliding, while at failure, the displacements at the top were larger as a result of toppling. The axial force distribution along reinforcement layers showed that the forces in reinforcement layers increased with depth (figure 4.19). With the progress of failure, the forces in the bottom layers increased rapidly.
Case 5 (s=0.2 m, low strength soil, baseline foundation) also experienced deep-seated mode of failure, and the failure zones' distribution is shown on figure 4.20.
The compound mode of failure was characterized by a slip surface that developed through the reinforced soil and the backfill (figure 4.3–c). Plastic zones developed within the reinforced soil during early stages of construction. Significant deformations developed as failure approached. The reinforced mass did not behave as a coherent block. The walls failed due to sliding of a mass, defined by a compound slip surface. Compound mode of failure was observed for all cases with DR, and for cases with very stiff foundation and reinforcement spacing that varied from 0.2 m to 0.6 m.
The model of case 8–1 (s=0.4 m, high strength soil, very stiff foundation, DR) experienced compound mode of failure, and the critical state was identified at wall height h=5.0 m. At the critical state, the failure zones defined a compound slip surface that developed through the reinforced soil (figure 4.21). The displacement field (figure 4.22) and the distorted grid (figure 4.23) indicated significant deformations within the wall, particularly the bottom. The horizontal displacements along sections A and B demonstrated that the reinforced soil was not moving as a coherent block (figure 4.24). The axial force distribution along reinforcement layers (figure 4.25) showed that the forces in reinforcement layers increased with depth and reached their maximum values in the wall section intersecting the compound slip surface. The forces in the bottom reinforcement layer were smaller than the forces of the adjacent layers because of the effects of a very stiff foundation.
Failure zone distributions of models that also experienced compound mode of failure are shown on figures 4.26–4.31.
Connection mode of failure was characterized by a slip surface that developed entirely within the reinforced soil (figure 4.3–d). Plastic zones and significant deformations within the reinforced soil developed from the beginning of construction. The reinforced mass did not behave as a coherent mass. Due to the large deformations at the facing, a sliding wedge in the retained soil was observed in some cases. This failure mechanism corresponded to reinforcement pulled out of the facing.
The model of case 2 (s=0.6 m, medium strength soil, very stiff foundation) experienced connection mode of failure, and the critical state was identified at wall height h=2.6 m. At the critical state, the failure zone was defined by a slip surface that developed entirely within the reinforced soil (figure 4.32). The displacement field (figure 4.33) and the distorted grid (figure 4.34) indicated significant deformations within the wall, and particularly at facing. The horizontal displacements along sections A and B confirmed that there were significant differential movements between the facing blocks, and the reinforced soil was not moving as a block (figure 4.35). The axial force distribution along reinforcement layers showed that the forces in reinforcement layers increased with depth (figure 4.36). The force in the bottom reinforcement layer was smaller than forces in the adjacent layers as a result of the effects of a very stiff foundation.
Case 4 (s=0.6 m, high strength soil, baseline foundation) also experienced connection mode of failure, and the failure zones' distribution is shown in figure 4.37.
Mixed failure modes were observed for certain combinations of soil and reinforcement properties (table 4.1). In the current analysis, only the predominant mode of failure was considered.
The critical wall height and the predominant mode of failure for all cases are summarized in figures 4.1 and 4.2, and table 4.2.
The identified failure modes (external, deep-seated, compound, and connection mode) closely correspond to the following failure mechanisms investigated in the design of geosynthetic reinforced steep slopes using limit equilibrium method: two-part wedge mechanism (direct sliding analysis); rotational mechanism (deep- seated stability analysis and compound stability analysis); and log-spiral failure mechanism (internal stability or tieback analysis) (Leshchinsky 1997, 1999).
The reinforcement spacing was identified as a major factor controlling all aspects of wall behavior. The effects of reinforcement spacing on failure mechanisms were identified with respect to the critical wall height and the mode of failure.
All numerical simulations confirmed the general conclusion that wall stability increases as reinforcement spacing decreases. The critical wall height was defined as a general characteristic of wall stability. It was identified numerically and corresponded to the critical state when the wall was at the verge of failure. Analysis of all relevant cases showed that the critical wall height always increased when the reinforcement spacing decreased. The only exception was observed for case 10 (figure 4.1–b), when the failure was controlled by the strength of the foundation soil, and the wall failed as a result of deep-seated sliding. For this case, the critical wall height remained the same h=3.2 m for both models, with reinforcement spacing equal to 0.2 m and 0.4 m.
The numerical analysis confirmed that the reinforcement spacing also controlled the identified modes of failure. In general, it was observed that the mode of failure changed from external or deep-seated to compound and then to connection when the reinforcement spacing increased (figure 4.1, table 4.2). Most of the cases with reinforcement spacing at s=0.2 m experienced external or deep-seated modes of failure, and the reinforced soil moved as a solid body, showing no plasticity within the reinforced soil zone. Most of the cases with reinforcement spacing equal to 0.6 m or larger experienced connection mode of failure, and the reinforced soil did not move as a coherent mass. Most of the cases with reinforcement spacing equal to 0.4 m experienced a mixed mode of failure (table 4.1).
In the current analysis, the reinforcement spacing equal to 0.4 m was considered as a specific value that divided the reinforcement spacing range into two categories, with respect to wall behavior. Reinforcement spacing less than or equal to 0.4 m was considered "small" reinforcement spacing. The reinforcement spacing larger than 0.4 m was considered "large" reinforcement spacing. The walls with small reinforcement spacing were more stable than the walls with large reinforcement spacing. The failure of walls with large reinforcement spacing was always accompanied by some degree of instability within the reinforced soil mass.
The behavior of walls with small reinforcement spacing was similar to the behavior of a conventional gravity retaining wall. The identified modes of failure were external or deep-seated (table 4.2). At the critical state, a small number of local failure zones within the bottom part of the reinforced soil mass was observed (figures 4.5, 4.10–4.15, 4.26). The analysis of displacement fields (figures 4.6, 4.16), grid distortions (figures 4.7, 4.17) and horizontal displacement distributions along sections A and B (figures 4.8, 4.18) confirmed that the reinforced soil was internally stable and moved as a coherent mass. The analysis of axial force distributions in reinforcement showed a smooth change of force without abrupt differences within the reinforcement layers or within the wall, which is another indication of internal stability (figures 4.9, 4.19).
All walls with large reinforcement spacing experienced internal instability to some degree. The predominant mode of failure was the connection mode. The reinforced mass did not move as a solid block. Analysis of failure zone distributions (observed by movies produced by FLAC) showed that failure zones evolved first in the reinforced soil, initiating large deformations that led to connection breakage. At the critical state, the predominant part of the reinforced soil was at yield in shear or volume, while the backfill was affected minimally (figures 4.31, 4.32, and 4.37). At failure states, the failure zones propagated to the backfill because of the large deformations at the facing. The analysis of displacement fields (figure 4.33), grid distortions (figure 4.34) and horizontal displacement distributions along sections A and B (figure 4.35) of case 2 (s=0.6 m) confirmed that there were significant deformations in the reinforced soil.
The reinforcement spacing appears to control the failure mechanisms of MSEWs. In the subsequent discussion, all effects on wall behavior were identified with respect to reinforcement spacing.
Cases 1 to 6 were designed to investigate the effects of soil strength on failure mechanisms. For cases 1 to 3, the soil strength decreased from case 1 to case 3, and the foundation soil was modeled to represent a very stiff foundation (tables 3.2 and 3.7). The foundation soil of cases 4 to 6 was modeled to be the same as the reinforced and backfill soil. Soil properties were the same as those of cases 1 to 3, respectively.
The effect of soil strength on wall stability is illustrated in figures 4.1 and 4.2 by the change of critical wall height with respect to soil strength. The critical wall height decreased as soil strength decreased. An important observation was that, with smaller reinforcement spacing, the same or higher critical wall height can be achieved with lower strength soil. For example, the critical wall height of case 5 (s=0.2 m, medium strength soil) was 4.2 m, while the critical wall height of case 4 (s=0.6 m, high strength soil) was 3.8 m.
The effects of soil strength on failure mechanisms were different for the cases with very stiff foundations and the cases with baseline foundations. For very stiff foundations (cases 1–3), the deep-seated mode of failure was not identified. The decrease of soil strength changed the mode of failure from external to compound mode, or from compound to connection mode (table 4.2, figure 4.1–a). For the cases with baseline stiffness of the foundation soil (cases 4–6), all four modes of failure were observed. For cases 5 and 6 with reinforcement spacing of 0.2 m, and case 4 with reinforcement spacing of 0.2 m and 0.4 m, the decrease of soil strength changed the mode of failure from external to deep-seated. All models experienced connection mode of failure when the reinforcement spacing was equal to 0.6 m or larger.
For a given reinforcement spacing, soil strength affected the stability and, to some extent, the failure mechanism. A decrease of soil strength corresponded to a decrease of the critical wall height. A decrease of soil strength, however, did not always change the identified failure mechanism.
Effects of reinforcement stiffness on failure mechanisms were investigated by comparing cases with different reinforcement stiffness. The reinforcement stiffness characteristics of cases 1 (s=0.4 m), 2 (s=0.4 m), and 3 (s=0.2 m) were decreased 10 times, and new models were defined: case 8–1 (s=0.4 m), case 8–2 (s=0.4 m) and case 8–3 (s=0.2 m). Cases 1, 2, and 3 represented models with very stiff foundations and low, medium, and high strength soils, respectively. The largest reinforcement spacing corresponding to models experiencing mainly external mode of failure was chosen for each (table 4.1). The modes of failure of cases 1–3 were mixed. For case 1 (s=0.4 m), the external mode was predominant. For cases 2 (s=0.4 m) and 3 (s=0.2 m), the compound mode was predominant. The reinforcement of the modified cases 8–1, 8–2 and 8–3 was termed DR. The reinforcement of all other cases was termed BR. Material properties of the reinforcement are given in table 3.5.
The effects of reinforcement stiffness on wall response were identified by comparison between cases 1 (s=0.4 m, BR) and 8–1 (DR), cases 2 (s=0.4 m, BR) and 8–2 (DR), and cases 3 (s=0.2 m, BR) and 8–3 (DR). All comparisons were made for a wall height equal to the smaller critical height of the compared cases.
The effects of reinforcement stiffness on wall response in models with high strength soil and very stiff foundation were investigated by comparing case 1 (s=0.4 m, BR) and case 8–1 (DR). The most significant results are given in table 4.5.
For case 1, an external mode of failure prevailed, and the critical wall height was 6.0 m. The plastic zone distribution for wall height h=5.0 m (the critical height of case 8–1) shows that plasticity occurred at the bottom of the reinforced soil and behind it, but the slip surface was not developed fully yet (figure 4.38–a). The first plastic zones occurred within the backfill soil at wall height of 3.2 m, and the first slip surface was external and fully developed at a wall height of 5.8 m (table 4.1). For wall height h=5.0 m, the maximum forces in reinforcement were not at the connections (figure 4.38–b). They increased almost linearly with depth, reaching a maximum value of 6.46 kN at elevation 1.0 m, and then decreased in the lower reinforcement layers (figure 4.39). The connection force followed a similar pattern. Maximum horizontal displacement of 2.9 cm was observed at elevation of 2 to 2.5 m (figure 4.40).
For case 8–1, a compound mode of failure was identified, and the critical wall height was 5.0 m. At the critical wall height, a compound slip surface was fully developed, and plastic zones were located not only along the surface, but also within the reinforced soil (figure 4.21). The first plastic zone occurred within the reinforced soil at wall height of 1.6 m, and the first slip surface was internal and fully developed at wall height of 1.8 m. Maximum forces in reinforcement were at the connections (figure 4.25). They increased almost linearly with depth, reaching a maximum value of 5.51 kN at elevation 1.4 m, and then decreased in the lower reinforcement layers (figure 4.39). Maximum horizontal displacement of 7.3 cm was observed at an elevation 2 to 2.5 m (figure 4.40).
Comparing cases 1 and 8–1 (high strength soil) showed that the lower reinforcement stiffness allowed larger deformations within the reinforced soil and, as a consequence, failure mode changed from mixed (predominant external mode) to compound, critical wall height decreased, and plastic zones first occurred within the reinforced soil at much lower wall height. For case 8–1 (DR), the maximum reinforcement forces were lower and always located at the connections. The decrease of reinforcement forces at the bottom of the wall was a result of the effects of a very stiff foundation.
The effects of reinforcement stiffness on wall response in models with medium strength soil and very stiff foundations were investigated by comparing case 2 (s=0.4 m, BR) and case 8–2 (s=0.4 m, DR). The most significant results are given in table 4.6.
For case 2, the compound mode of failure prevailed, and the critical wall height was 4.4 m. The plastic zone distribution for wall height h=3.2 m (the critical height of case 8–2) shows that the plastic zones were located at the bottom of the reinforced soil and within a wedge of backfill soil (figure 4.41). The first plastic zone developed within the reinforced soil at wall height of 1.4 m, and the first slip surface was compound and fully developed at wall height of 2.8 m (table 4.6). For wall height h=3.2 m, the maximum forces in reinforcement were not at the connections (figure 4.42). They increased almost linearly with depth until they reached the maximum value of 4.51 kN at elevation 0.6 m, and then decreased in the first reinforcement layer (figure 4.43). Maximum horizontal displacement of 1.7 cm was observed at an elevation of 1.5 to 2.0 m (figure 4.40).
For case 8–2, a compound mode of failure was identified, and the critical wall height was 3.2 m. At the critical wall height, a compound slip surface was fully developed, and plastic zones were spread out within the reinforced soil (figure 4.29). The first plastic zone within the reinforced soil occurred at wall height of 1.4 m (the same wall height as for case 2), and the first slip surface was internal and fully developed at a wall height h=1.6 m (table 4.6). The maximum forces in reinforcement were at the connections in the middle part of the wall and in the bottom layer (figure 4.42). Forces increased almost linearly with depth until the layer at elevation 1.4 m, reaching a maximum value of 4.23 kN at elevation 1.0 m, and then decreased in the bottom reinforcement layer (figure 4.43). Maximum horizontal displacement of 5.2 cm was observed at an elevation of 1 to 1.5 m (figure 4.40).
Comparing cases 2 and 8–2 (medium strength soil) showed that the lower reinforcement stiffness of case 8–2 allowed larger deformations within the reinforced soil and, as a consequence, failure mode changed from mixed (predominant compound mode) to compound, and the critical wall height decreased. First plastic zone occurred at the same wall height for both cases. The maximum reinforcement forces for case 2 were not at the connections, while the forces for case 8–2 were at the connections in the middle part of the wall and in the bottom layer. For case 2 (BR), the maximum reinforcement forces in the middle part of the wall were slightly smaller, compared to case 8–2. This can be explained by the fact that the middle part of the wall was internally stable, almost no plastic zones developed (figure 4.41–a).
The effects of reinforcement stiffness on wall response in models with low strength soil and very stiff foundations were investigated by comparing case 3 (s=0.2 m, BR) and case 8–3 (s=0.2 m, DR). The most significant results are given in table 4.7.
For case 3, the compound mode of failure prevailed, and the critical wall height was 4.0 m. The plastic zone distribution for wall height h=2.2 m (the critical height of case 8–2) showed that few and scattered plastic zones developed behind the reinforced soil (figure 4.44–a). The first plastic zone occurred within the reinforced soil at a wall height of 1.2 m, and a compound slip surface developed at a wall height of 2.4 m (table 4.7). For wall height h=2.2 m, the maximum forces in reinforcement were not at the connections (figure 4.45–a). They increased almost linearly with depth, reaching the maximum value of 2.26 kN at elevation 0.8 m, and then decreased in the lower reinforcement layers (figure 4.46–a). Maximum horizontal displacement of 0.8 cm was observed at an elevation of 1.0 to 1.5 m (figure 4.40).
For case 8–3, a compound mode of failure was identified, and the critical wall height was 2.2 m. At the critical wall height, a compound slip surface was fully developed, and plastic zones developed also within the reinforced soil (figure 4.44–b). The first plastic zone occurred within the reinforced soil at a wall height of 1.2 m (the same wall height as for case 2), and a compound slip surface developed at wall height of 1.2 m (table 4.7). The maximum forces in reinforcement were near the connections (figure 4.45–b). They increased almost linearly with depth until elevation 1.4 m, reaching the maximum value of 4.23 kN at elevation 1.0 m, and decreasing in the bottom layer (figure 4.46–b). Maximum horizontal displacement of 5.2 cm was observed at an elevation of 1 to 1.5 m (figure 4.40).
Comparing cases 3 and 8–3 (low strength soil) showed that the lower reinforcement stiffness of case 8–3 allowed for larger deformations within the reinforced soil and, as a consequence, failure mode changed from mixed (predominant compound mode) to purely compound, and the critical wall height decreased. The first plastic zone occurred at the same wall height for both cases. The maximum reinforcement forces for both cases were not located at the connections.
Based on the comparison between cases representing different soil strength and reinforcement stiffness, researchers drew the following conclusions:
Three types of connections were modeled to investigate the effects of connection strength on failure mechanisms: frictional connection with baseline strength, frictional connection with low strength, and structural connection. Interface properties that modeled these types of connections are given in table 3.7.
The effects of connection strength on failure mechanisms were investigated by comparatively analyzing the following two sets of cases that represented models with small and large reinforcement spacing:
Case 1 (s=0.2 m, FCon–B), case 9 (s=0.2 m, FCon–L), and case 12 (s=0.2 m, SC) represent models with high strength soil, very stiff foundations, and small reinforcement spacing (s=0.2 m). Interfaces at the facing of case 1 were modeled with angle of friction 
int=30° and zero cohesion to represent frictional connection between the reinforcement and the blocks. This type of connection was defined as a baseline type and was used in all models except the models of cases 9 and 12. The models of cases 9 and 12 were prepared by changing the interface properties of case 1. Interfaces at the facing of case 9 were modeled with angle of friction int=20° and zero cohesion to represent frictional connection with lower strength. Interfaces at the facing of case 12 were modeled with angle of friction int=30° and cohesion cint=20 kPa to represent structural connection. All interface properties are given in table 3.6. The most significant results for case 1 (FCon–B), case 9 (FCon–L), and case 12 (SC) are given in table 4.8.
Comparing the results for cases 1, 9, and 12 (s=0.2 m) indicates that connection strength had insignificant influence on wall behavior for cases with small reinforcement spacing. All models experienced external mode of failure and reached a critical state at wall height of 6.6 m (table 4.8). For case 9, the first plastic zones in the backfill soil occurred at lower wall height, and the connection and maximum forces were large compared with cases 1 and 12. This can be explained with the larger displacements developed in the model of case 9 facilitated by the lower connection strength. The connection force and the maximum force in reinforcement for cases 1, 9 and 12 (s=0.2 m) are given on figures 4.47 and 4.48, respectively. The horizontal displacements along section A (0.1 m behind the facing) are shown in figure 4.49.
The comparison between cases 1, 9, and 12 with small reinforcement spacing (s=0.2 m) and different connection strengths revealed that the connection strength did not affect the wall behavior significantly.
Case 2 (s=0.6 m, FCon–B) and case 12 (s=0.6 m, SC) represented models with high strength soil, very stiff foundations, and large reinforcement spacing (s=0.6 m). Interfaces at the facing of case 2 were modeled with angle of friction ?int=30? and zero cohesion to represent frictional connection (frictional connection with baseline strength). The model of case 12 was prepared by changing the interface properties of case 2. Interfaces at the facing of case 12 were modeled with angle of friction ?int=30? and cohesion cint=20 kPa to represent structural connection between the reinforcement and the blocks. All interface properties are given in table 3.7. The most significant results for the compared cases are given in table 4.9.
Comparing the results for cases 2 and 12 (s=0.6 m) indicates that connection strength had significant influence on wall behavior for cases with large reinforcement spacing. Due to the higher strength of the structural connection, the mode of failure changed from connection mode (case 2) to compound mode (case 12), and the critical wall height increased from 2.6 m (case 2) to 4.6 m (case 12). For case 2, the first plastic zone occurred at lower wall height, the maximum force was larger, and the connection forces were smaller compared to case 12 (table 4.9, figures 4.50 and 4.51). This can be explained with the larger displacements at the facing developed in the model of case 2, caused by the lower connection strength. The horizontal displacements along section A (0.1 m behind the facing) are shown in figure 4.52. The uneven distribution of the horizontal displacements along section A for case 2 indicated that the frictional connection allowed differential movements between the facing blocks.
The comparison between cases 2 and 12 with large reinforcement spacing (s=0.6 m) and different connection strengths revealed that the connection strength affected the wall behavior significantly. The connection strength increase led to a failure mode change, an increase of the critical wall height, and decrease of wall displacements.
The analysis of cases with high strength soil, very stiff foundations, and different connection strengths indicates that the effects of connection strength on wall behavior can be significant for large reinforcement spacing. For cases with small reinforcement spacing, connection strength effects were insignificant.
Effects of foundation stiffness on failure mechanisms were investigated by changing the stiffness of foundation soil. Two major types of foundation were modeled: very stiff foundation and baseline foundation. In all numerical simulations, the elastic modulus of soil was updated after placing each soil layer and after equilibrium was attained using the hyperbolic stress-strain relationship given in Equation (3.2). Poisson's ratio was kept constant. The very stiff foundation soil was modeled with an artificially high cohesion (c=1000 kPa), and a hyperbolic model parameter K=270200 that was 1000 times larger than the value used to model the baseline soil stiffness (K=270.2, Ling et al. 2000). Soil properties that were used to model the soil stiffness are given in table 3.4.
Cases 1–6 and case 10 were designed to investigate the effects of foundation stiffness on failure mechanisms (tables 3.3, 3.4, and 3.8). Cases 1, 2, and 3 represent models with very stiff foundation soil, and soil strength of the reinforced and backfill soil that changed from high (case 1) to low (case 3). The models of cases 4, 5, and 6 were the same as those of cases 1, 2, and 3, respectively, but the foundation soil was modeled to be the same as the reinforced and backfill soil. For case 10, the soil stiffness was the same in all parts of the model, but the soil strength was different; the reinforced soil was of high strength, while the rest was of low strength.
The effects of foundation stiffness on wall behavior were identified by comparatively analyzing all cases with respect to failure mechanisms and wall stability. cases 1, 4, and 10 (s=0.2 m) were analyzed further, and the horizontal displacements along section A, stress distributions along section A, connection forces, and maximum forces in reinforcement were compared at wall height h=3.2 m. The effects of foundation stiffness on wall stability were identified by the change of the critical wall height for cases with different foundation soil. The comparison of the critical wall height for case 1 (HS=high strength soil, VSt=very stiff foundation), case 4 (HS, BSt=foundation soil with baseline stiffness) and case 10 (H&LS=high strength reinforced soil, and low strength soil in foundation and backfill) is shown in figure 4.53–a. The comparison of the critical wall height for cases 2 (MS=medium strength soil, VSt), 5 (MS, BSt), and 10 (H&LS) is shown in figure 4.53–b. The comparison of the critical wall height for cases 3 (LS=low strength soil, VSt), 4 (LS, BSt), and 10 (H&LS) is shown in figure 4.53–c. All comparisons show that the lower stiffness or lower strength of foundation soil led to smaller critical wall height. It is important to note that the comparison of cases 3 and 10 (s=0.4 m) does not contradict this conclusion. The model of case 3 (LS, VSt, s=0.4 m) experienced compound mode of failure, and because the foundation soil was very stiff and strong, the wall stability was controlled by the low strength of the reinforced soil. The model of case 10 (H&LS, s=0.4 m) experienced deep-seated mode of failure, and since the reinforced soil was with high strength, the wall stability was controlled by the low strength of the foundation soil. This was also true for case 10 (s=0.2 m). The models of case 10 with reinforcement spacing s=0.2 and 0.4 m had the same critical wall height h=3.2 m and behaved identically. This indicates that, because of the small reinforcement spacing and high strength of the reinforced soil, the reinforced soil moved as a coherent block, and failure is controlled by the low strength of the foundation soil.
The effect of foundation stiffness on failure mechanisms was different for the cases with very stiff foundations and the cases with baseline stiff foundations. For the very stiff foundation (cases 1, 2, and 3), decrease of soil strength changed the mode of failure from external to compound mode, or from compound to connection mode (figure 4.1–a). A deep-seated mode of failure was not identified. For the baseline foundation (cases 4, 5, and 6), all four modes of failure were observed. For cases with large reinforcement spacing, decrease of foundation soil strength changed the mode of failure from external to connection mode. For cases with small reinforcement spacing, the decrease of foundation soil strength changed the mode of failure from external to deep-seated.
The foundation stiffness affected the wall behavior by changing the failure mechanisms. The artificially high stiffness and strength of foundation soil prevented the development of deep-seated failure and increased wall stability. When the foundation soil was changed from baseline to very stiff soil, the cases with small reinforcement spacing that experienced deep-seated mode of failure exhibited compound failure mode. The current analysis implied that foundation effects should not be neglected in numerical analysis and design.
To express numerically the effects of foundation stiffness, the most significant results of cases 1, 4, and 10 (s=0.2 m) were analyzed (table 4.10). Horizontal displacements along section A, stress distributions along section A, connection forces, and maximum forces in reinforcement were compared at wall height h=3.2 m. The wall height of 3.2 m corresponded to the lowest critical height of all 3 cases.
The change of foundation stiffness from very stiff (case 1) to baseline soil (case 4) led to a decrease of the critical wall height from 6.6 (case 1) to 5.6 (case 4). The mode of failure for both cases was external, and distribution of plastic zones in the backfill soil was similar. For case 4 (baseline foundation), the plastic zones spread to the foundation soil under the toe, and the first zone in the reinforced and backfill soil occurred at lower wall height, compared to case 1. The very stiff foundation restrained the displacements at the bottom of the wall. The comparison between models of cases 1 and 4 with wall height h=3.2 m showed that the change of foundation soil from very stiff to baseline soil increased the horizontal displacements (figure 4.53–a) and maximum forces in reinforcement (figure 4.54). Forces in the reinforcement layers decreased at the bottom of the wall for both cases. Stress distributions along section A (0.15 m behind facing) showed a stress concentration at the bottom of the wall as a result of the toppling of the walls (figure 4.53–b).
The change of foundation strength from high strength (case 4) to low strength (case 10) led to a decrease of the critical wall height from 5.6 m (case 4) to 3.2 m (case 10), and to a change of failure mode from external to deep-seated. Plastic zones occurred predominantly in the backfill and foundation soil. For case 10 (low strength foundation soil), the first zone occurred at lower wall height compared to case 4 (high strength foundation soil) and were concentrated around the toe of the wall. The comparison between the models of cases 4 and 10 at wall height h=3.2 m showed that the change of foundation strength from high to low increased the horizontal displacements (figure 4.53–a) and the reinforcement forces (figure 4.53–b). Reinforcement forces of case 10 increased linearly with depth, and the maximum values were observed in the first layer. The reinforcement forces of case 4 increased linearly, reaching the maximum value at 0.6 m, and then decreased at the bottom of the wall. Stress distributions along section A (0.15 m behind facing) showed a stress concentration at the bottom of the wall due to the toppling (figure 4.53–c).
Foundation stiffness had significant effects on wall response. The decrease of foundation stiffness or strength decreased the critical wall height, changed the mode of failure, and increased the displacements and reinforcement forces. The current study confirmed that the modeling of foundation soil as very stiff significantly changed the wall response. The walls with large reinforcement spacing were more sensitive to the change of foundation properties than walls with small reinforcement spacing.
The effects of reinforcement length on wall stability were identified by additional numerical analysis of case 1 (s=0.2 m, external mode), case 8–1 (s=0.4 m, compound mode), and case 10 (s=0.2 m, deep-seated mode). The wall height of these models was kept constant and equal to the critical height, while the reinforcement length was increased to predetermined values. The state corresponding to walls with critical height and reinforcement length larger than l=1.5 m (baseline length), is termed "stable state." The effects of reinforcement length on reinforcement forces, stress distributions and horizontal displacements are presented graphically (figures 4.55–4.67).
The model of baseline case 1 (s=0.2 m, l=1.5 m, high strength soil, very stiff foundation) experienced external mode of failure and the critical state was identified at wall height h=6.6 m (l/h=0.23). Three stable states were investigated with the following reinforcement length: l=2.0 m (l/h
0.3); l=2.6 m (l/h0.4); and l=3.3 m (l/h=0.5). The distributions of horizontal and vertical stresses along section A (0.15 m behind the facing) and section C (0.15 m behind the reinforced soil) are shown on figures 4.55 and 4.56. The movements of the wall at failure corresponded to wall toppling (figure 4.5–a). This led to a stress concentration along the bottom of section A and smaller stresses along section C. When the reinforcement length was increased, the stresses along section A decreased and the stresses along section C increased. This was an indication that rotation against the toe decreased and wall stability increased. The horizontal displacements along sections A and C also decreased as reinforcement length increased (figure 4.57). However, displacements were small and implied a movement of the reinforced soil as a composite block. The maximum axial forces in reinforcement decreased with the increase of the reinforcement length (figure 4.58). For a given state, the maximum reinforcement forces increased with depth almost linearly, reaching a maximum value at an elevation of 0.8 to 1.2 m, and then decreased in the bottom layers. The connection forces changed in the same way (figure 4.59).
The model of baseline case 8–1 (s=0.4 m, l=1.5 m, high strength soil, DR) experienced compound mode of failure, and the critical state was identified at wall height h=5.0 m (l/h=0.3). Two stable states were investigated with the following reinforcement lengths: l=2.0 m (l/h=0.4); l=2.5 m (l/h=0.5). The distributions of horizontal and vertical stresses along section A (0.15 m behind the facing) and section C (0.15 m behind the reinforced soil) are shown in figures 4.60 and 4.61. The wall movements led to stress concentration along the bottom of section A and smaller stresses along section C. When the reinforcement length was increased, the stresses along section A decreased, and the stresses along section C increased. This indicated that rotation against the toe decreased, and wall stability increased. The horizontal displacements also decreased as reinforcement length increased (figure 4.62). The differences between the horizontal displacements along sections A and C increased as reinforcement length increased. The maximum difference was about 2 percent of the reinforcement length, indicating significant deformations within the reinforced soil. The maximum axial forces in reinforcement were at the connections and decreased as reinforcement length increased (figuBackfill Soilre 4.63). For a given state, the maximum reinforcement forces increased with depth almost linearly, reaching a maximum value at an elevation of 1.2 to 1.6 m, and then decreased in the bottom layers.
The model of baseline case 10 (s=0.2 m, l=1.5 m, high strength reinforced soil, low strength backfill and foundation soil) experienced deep-seated mode of failure, and the critical state was identified at wall height h=3.2 m (l/h=0.47). A stable state with reinforcement length l=2.2 m (l/h=0.7) was investigated. The distributions of horizontal and vertical stresses along section A (0.15 m behind the facing) and section C (0.15 m behind the reinforced soil) are shown in figures 4.64 and 4.65. When the reinforcement length was increased, the stresses along section A decreased, and the stresses along section C increased. This indicated that the wall stability increased. The differences between the horizontal displacements along sections A and C increased as reinforcement length increased. However, they were small and represented a movement of the reinforced soil as a composite block (figure 4.66). The maximum axial forces in reinforcement decreased as reinforcement length increased (figure 4.67). For a given state, the maximum reinforcement forces increased with depth almost linearly. The connection forces changed in the same way (figure 4.67).
The analysis of stable states of models representing external, compound, and deep-seated modes of failure indicates that increasing of reinforcement length improved wall stability and decreased wall displacements and reinforcement forces.
Effects of secondary reinforcement layers on wall behavior were investigated by comparing case 1 (s=0.6 m) and case 7 (s=0.6/0.2 m) (table 4.11, figure 3.12). The reinforcement layout of case 1 (s=0.2 m, medium strength soil, very stiff foundation) was changed to create the model of case 7 (figures 3.12 and 4.68). The reinforcement layers that corresponded to the reinforcement layout of case 2 (s=0.6 m) were kept the same and were termed "primary reinforcement." The other reinforcement layers were termed "secondary reinforcement." The cable part of secondary layers was divided into two parts with different properties. The cable part next to the facing was 0.3 m long and had the same properties as the primary reinforcement. The other cable part was 1.2 m long and was modeled with very low stiffness and strength to avoid influencing the model response. The values of cable elastic modulus, cable tensile yield strength, grout shear stiffness, and grout cohesive strength were chosen to be 100 times smaller than the values used to model the primary reinforcement, i.e.:
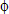g=5°The other properties of the cable were the same as the properties of the primary reinforcement (table 3.6).
The comparison between case 2 (s=0.6 m) and case 7 (s=0.6/0.2 m) shows that the intermediate reinforcement spacing changed the mode of failure from connection mode (case 2) to compound mode (case 7), and increased the critical wall height from 2.6 m (case 2) to 5.0 m (case 7). The comparison of plastic zones corresponding to wall height h=2.6 m demonstrates that secondary reinforcement increased internal stability of the reinforced soil, particularly at the facing (figures 4.28 and 4.69). The horizontal displacements along section A (0.1 m behind the facing) were larger for case 2 (s=0.6 m, h=2.6 m), particularly between the reinforcement layers (figure 4.70). The forces in the reinforcement were also larger for case 2 (figures 4.68 and 4.71).
Introducing secondary reinforcement layers in a model with large reinforcement spacing changed the wall behavior significantly. The following effects were identified: mode of failure changed; global wall stability and local stability at the wall facing increased; and displacements and reinforcement forces decreased. The secondary reinforcement layers increased the stability of the wall by redistributing the stresses and connection forces at the facing.
Influence of soil dilatancy on model response was investigated comparing the results of case 1 (s=0.2 m) and case 11. The model of case 11 was developed by setting dilation angle to zero for all soils in the model of case 1 (s=0.2 m). All other characteristics were the same in both models. The most significant results for the compared cases are given in table 4.12.
The comparison showed that soil dilatancy did not influence the observed mode of failure, but the model with zero dilation was less stable and experienced larger deformations and larger reinforcement forces. External mode of failure was identified for both cases (figures 4.5 and 4.13). The critical height of case 11 (h=6.0 m, zero dilation) was smaller than the critical height of case 1 (h=6.6 m) (table 4.13). Failure zones that developed during wall construction showed that plastic zones for case 11 were located in narrower bands, compared to case 1. The first plastic zone in the model of case 11 evolved at a later stage of construction, compared to case 1. With respect to numerical stability, the model with zero dilation (case 11) required longer run time and more calculation steps than the model with nonzero dilation (case 1).
The current results showed that soil dilatancy influenced the model's response. Decreasing the dilation angle increased the displacements and reinforcement forces, and decrease the critical wall height. Decreasing the dilation angle did not change the mode of failure.
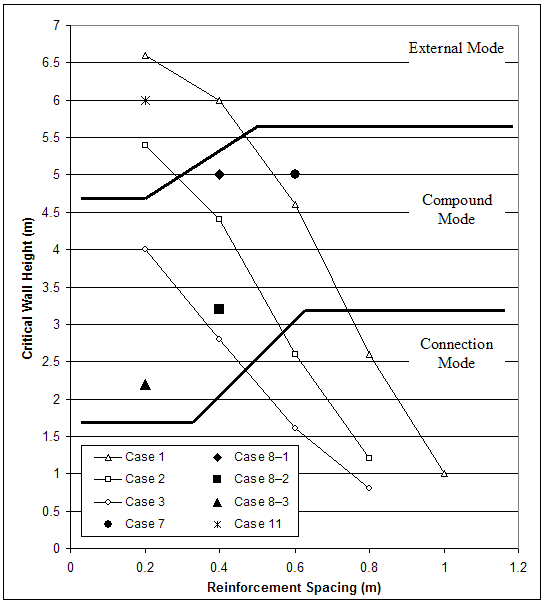
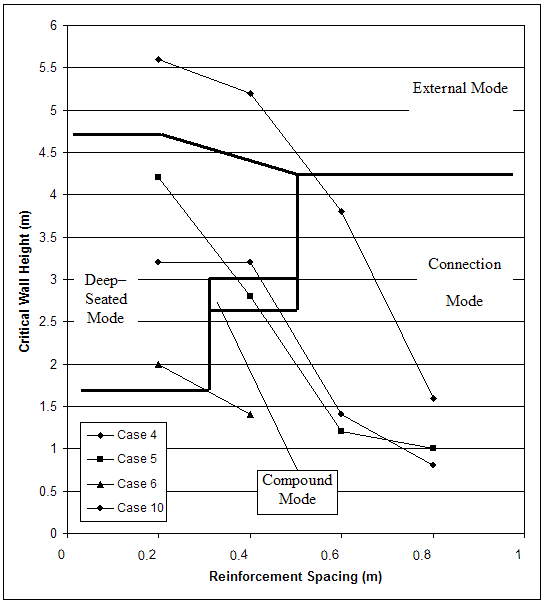
Figure 4.1 Critical Wall Height and Prevailing Mode of Failure: (a) Cases with Very Stiff Foundation; (b) Cases with Baseline Foundation.
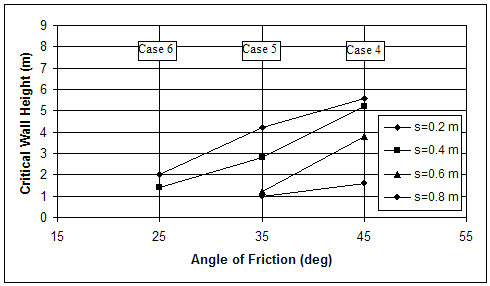
Figure 4.2 Change of Critical Wall Height with Respect to Soil Strength: (a) Cases with Very Stiff Foundation; (b) Cases with Baseline Foundation.
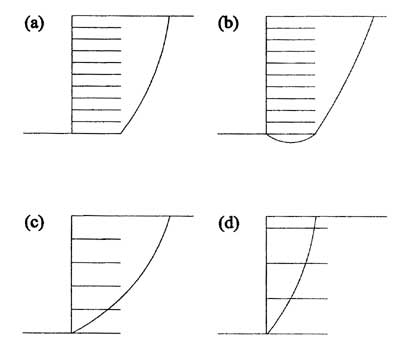
Figure 4.3 Slip Surface Types: (a) External Slip Surface; (b) Deep-Seated Slip Surface; (c) Compound Slip Surface; (d) Internal Slip Surface.
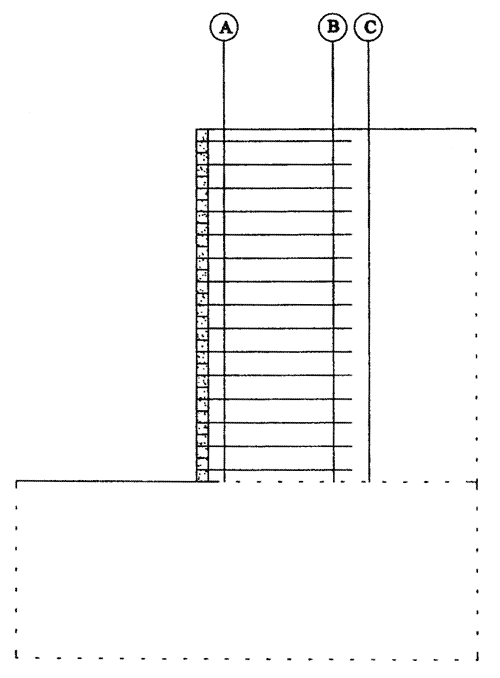
Figure 4.4 Definition of Vertical Sections A, B, and C along which Stress and Displacement Distributions Were Investigated.
Elastic  |
At Yield in Shear or Volume  |
Elastic, Yield in Past  |
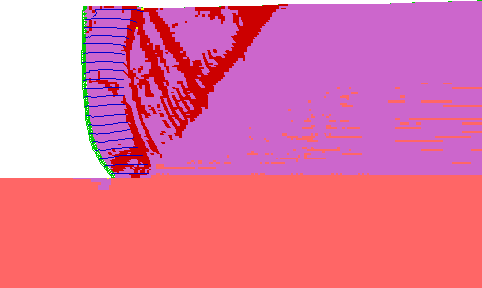
Figure 4.5 State of Soil for Case 1 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.6 m, l/h=0.17); (b) Critical State (h=6.6 m, l/h=0.23).
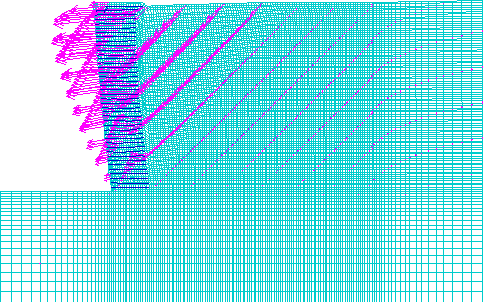
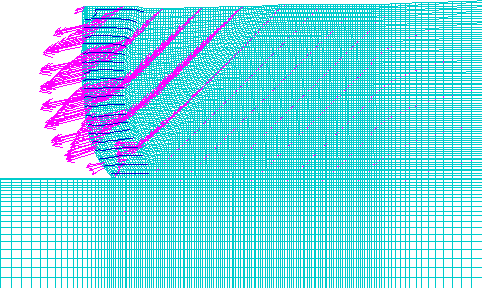
LEGEND: Maximum Vector
Figure 4.6 Displacement Vectors for Case 1 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.6 m, l/h=0.17); (b) Critical State (h=6.6 m, l/h=0.23).
LEGEND: Maximum Displacement
Figure 4.7 Distorted Grid for Case 1 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.6 m, l/h=0.17); (b) Critical State (h=6.6 m, l/h=0.23).
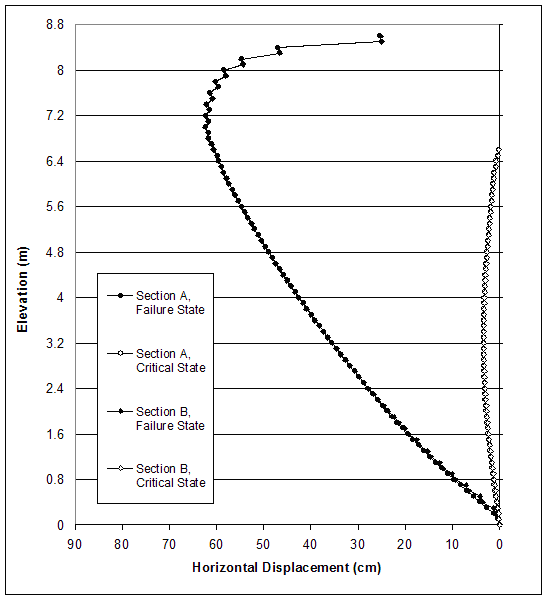
Figure 4.8 Cumulative Horizontal Displacements for Case 1 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.6 m, l/h=0.17); (b) Critical State (h=6.6 m, l/h=0.23).
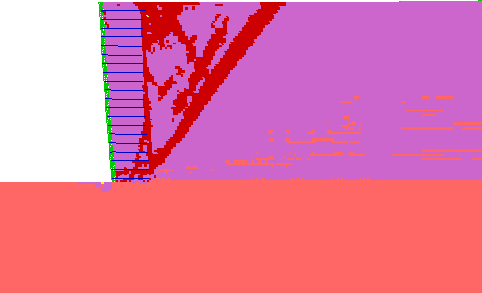
Figure 4.9 Axial Force Distribution in Reinforcement for Case 1 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.6 m, l/h=0.17); (b) Critical State (h=6.6 m, l/h=0.23).
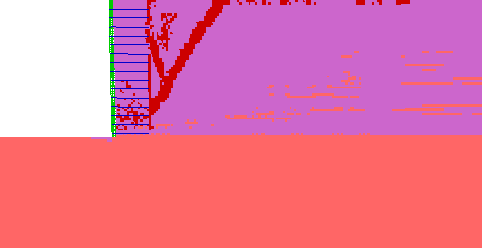
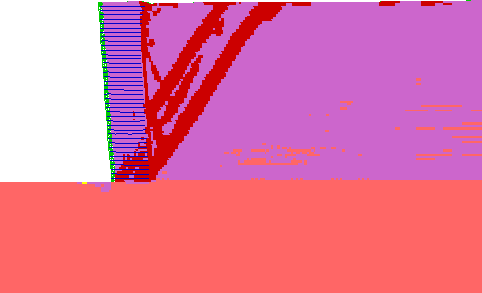
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
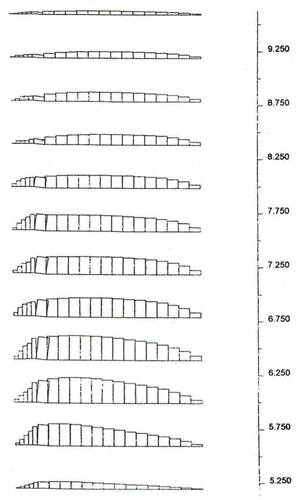
Figure 4.10 State of Soil for Case 1 (s=0.4 m, l=1.5 m): (a) Failure State (h=8.2 m, l/h=0.18); (b) Critical State (h=6.0 m, l/h=0.25).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.11 State of Soil for Case 4 (s=0.2 m, l=1.5 m): (a) Failure State (h=7.0 m, l/h=0.21); (b) Critical State (h=5.6 m, l/h=0.27).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.12 State of Soil for Case 9 (s=0.2 m, l=1.5 m): (a) Failure State (h=8.2 m, l/h=0.18); (b) Critical State (h=6.6 m, l/h=0.23).
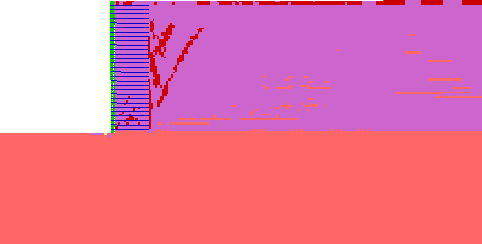
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.13 State of Soil for Case 11 (s=0.2 m, l=1.5 m): (a) Failure State (h=7.2 m, l/h=0.21); (b) Critical State (h=6.0 m, l/h=0.25).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.14 State of Soil for Case 12 (s=0.2 m, l=1.5 m): (a) Failure State (h=9.4 m, l/h=0.16); (b) Critical State (h=6.6 m, l/h=0.23).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.15 State of Soil for Case 10 (s=0.2 m, l=1.5 m): (a) Failure State (h=4.4 m, l/h=0.34); (b) Critical State (h=3.2 m, l/h=0.47).
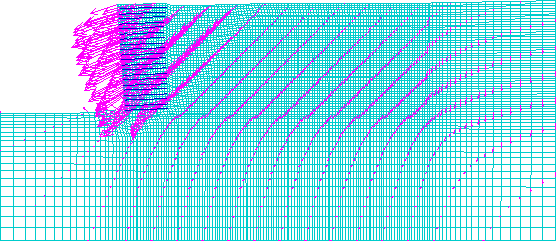
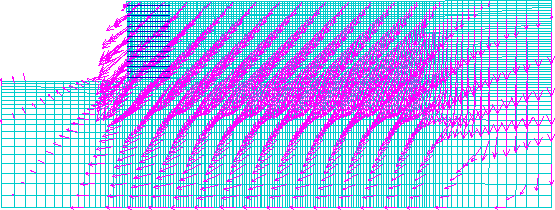
LEGEND: Maximum Vector
Figure 4.16 Displacement Vectors for Case 10 (s=0.2 m, l=1.5 m): (a) Failure State (h=4.4 m, l/h=0.34); (b) Critical State (h=3.2 m, l/h=0.47).
LEGEND: Maximum Displacement
Figure 4.17 Distorted Grid for Case 10 (s=0.2 m, l=1.5 m): (a) Failure State (h=4.4 m, l/h=0.34); (b) Critical State (h=3.2 m, l/h=0.47).
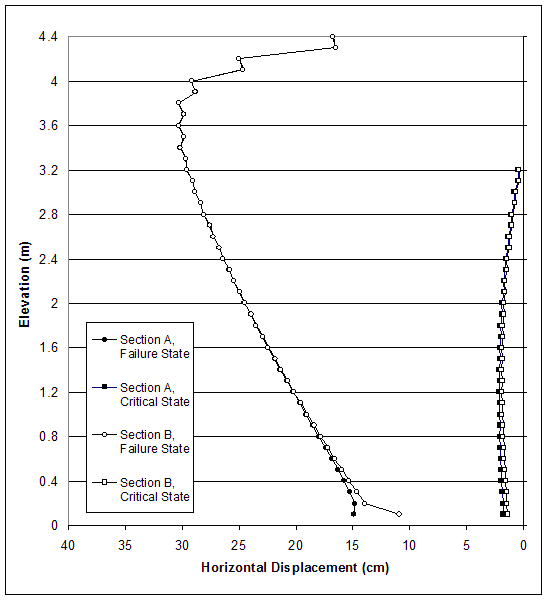
Figure 4.18. Horizontal Displacements for Case 10 (s=0.2 m, l=1.5 m) at Failure State (h=4.4 m, l/h=0.34) and Critical State (h=3.2 m, l/h=0.47).
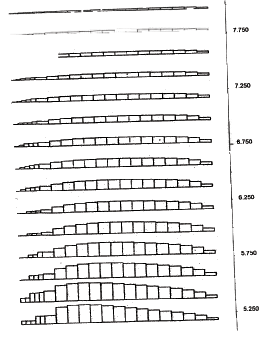
Figure 4.19 Axial Force Distribution in Reinforcement for Case 10 (s=0.2 m, l=1.5 m): (a) Failure State (h=4.4 m, l/h=0.34); (b) Critical State (h=3.2 m, l/h=0.47).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.20 State of Soil for Case 5 (s=0.2 m, l=1.5 m): (a) Failure State (h=5.4 m, l/h=0.28); (b) Critical State (h=4.2 m, l/h=0.36).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.21 State of Soil for Case 8–1 (s=0.4 m, l=1.5 m): (a) Failure State (h=8.0 m, l/h=0.19); (b) Critical State (h=5.0 m, l/h=0.3).
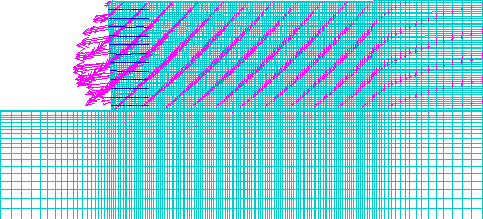
LEGEND: Maximum Vector
Figure 4.22 Displacement Vectors for Case 8–1 (s=0.4 m, l=1.5 m): (a) Failure State (h=8.0 m, l/h=0.19); (b) Critical State (h=5.0 m, l/h=0.30).
LEGEND: Maximum Displacement
Figure 4.23 Distorted Grid for Case 8–1 (s=0.4 m, l=1.5 m): (a) Failure State (h=8.0 m, l/h=0.19); (b) Critical State (h=5.0 m, l/h=0.30).
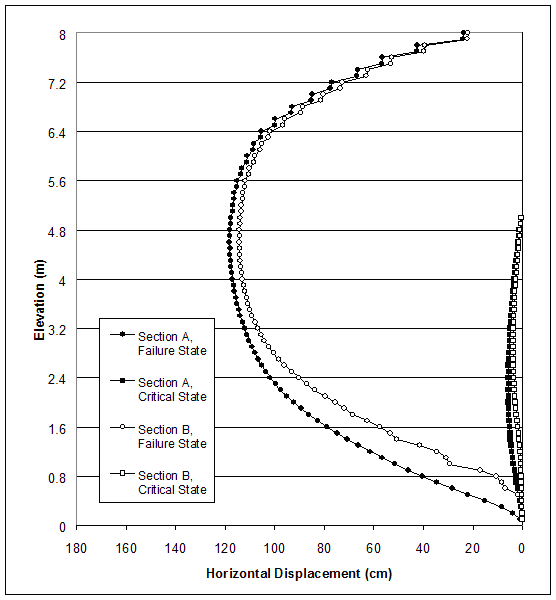
Figure 4.24 Horizontal Displacements for Case 8–1 (s=0.4 m, l=1.5 m) at Failure (h=8.0 m, l/h=0.19) and Critical State (h=5.0 m, l/h=0.30).
(a)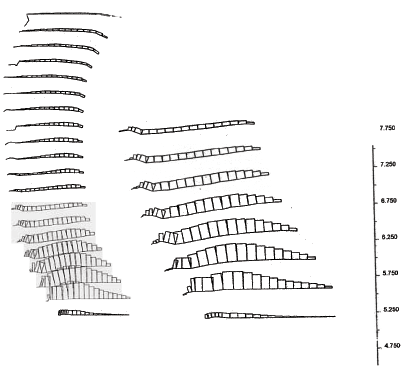
(b)
Figure 4.25 Axial Force Distribution in Reinforcement for Case 8–1 (s=0.4 m, l=1.5 m): (a) Failure State (h=8.0 m, l/h=0.19); (b) Critical State (h=5.0 m, l/h=0.30).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.26 State of Soil for Case 2 (s=0.4 m, l=1.5 m): (a) Failure State (h=6.0 m, l/h=0.25); (b) Critical State (h=4.4 m, l/h=0.34).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.27 State of Soil for Case 3 (s=0.2 m, l=1.5 m): (a) Failure State (h=4.2 m, l/h=0.36); (b) Critical State (h=4.0 m, l/h=0.38).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.28 State of Soil for Case 7 (s=0.6/0.2 m, l=1.5 m): (a) Failure State (h=6.0 m, l/h=0.25); (b) Critical State (h=5.0 m, l/h=0.30).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.29 State of Soil for Case 8–2 (s=0.4 m, l=1.5 m): (a) Failure State (h=5.4 m, l/h=0.28); (b) Critical State (h=3.2 m, l/h=0.47).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.30 State of Soil for Case 8–3 (s=0.2 m, l=1.5 m): (a) Failure State (h=5.0 m, l/h=0.30); (b) Critical State (h=2.2 m, l/h=0.68).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.31 State of Soil for Case 12 (s=0.6 m, l=1.5 m): (a) Failure State (h=6.0 m, l/h=0.25); (b) Critical State (h=4.6 m, l/h=0.33).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.32 State of Soil for Case 2 (s=0.6 m, l=1.5 m): (a) Failure State (h=4.6 m, l/h=0.33); (b) Critical State (h=2.6 m, l/h=0.58).
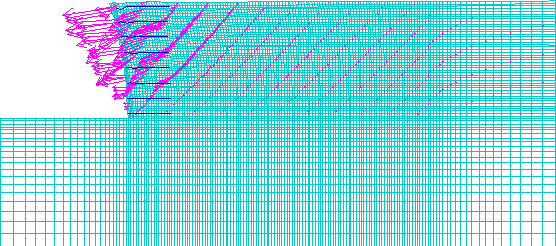
LEGEND: Maximum Vector
Figure 4.33 Displacement Vectors for Case 2 (s=0.6 m, l=1.5 m): (a) Failure State (h=4.6 m, l/h=0.33); (b) Critical State (h=2.6 m, l/h=0.58).
LEGEND: Maximum Displacement
Figure 4.34 Distorted Grid for Case 2 (s=0.6 m, l=1.5 m): (a) Failure State (h=4.6 m, l/h=0.33); (b) Critical State (h=2.6 m, l/h=0.58).
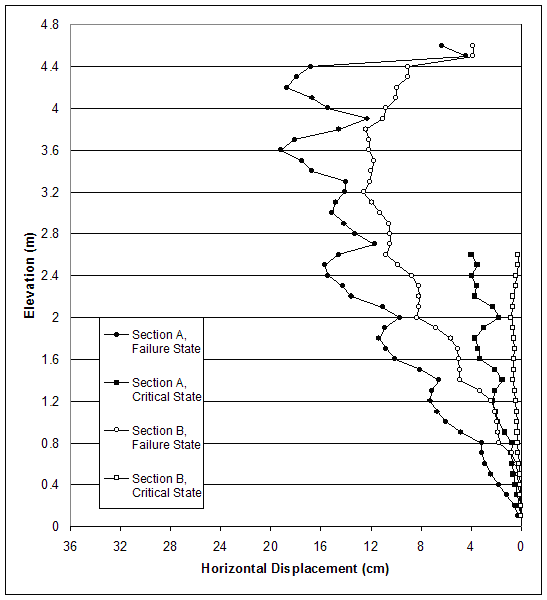
Figure 4.35 Horizontal Displacements for Case 2 (s=0.6 m, l=1.5 m) at Failure State (h=4.6 m, l/h=0.33) and Critical State (h=2.6 m, l/h=0.58).
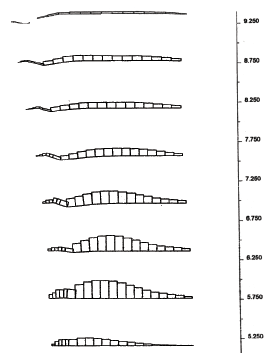
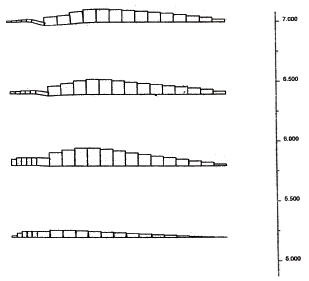
Figure 4.36 Axial Force Distribution in Reinforcement for Case 2 (s=0.6 m, l=1.5 m): (a) Failure State (h=4.6 m, l/h=0.33); (b) Critical State (h=2.6 m, l/h=0.58).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.37 State of Soil for Case 4 (s=0.6 m, l=1.5 m): (a) Failure State (h=5.4 m, l/h=0.28); (b) Critical State (h=3.8 m, l/h=0.39).
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.38 Case 1 (s=0.4 m, l=1.5 m, h=5.0 m): (a) State of Soil; (b) Axial Force Distribution in Reinforcement.
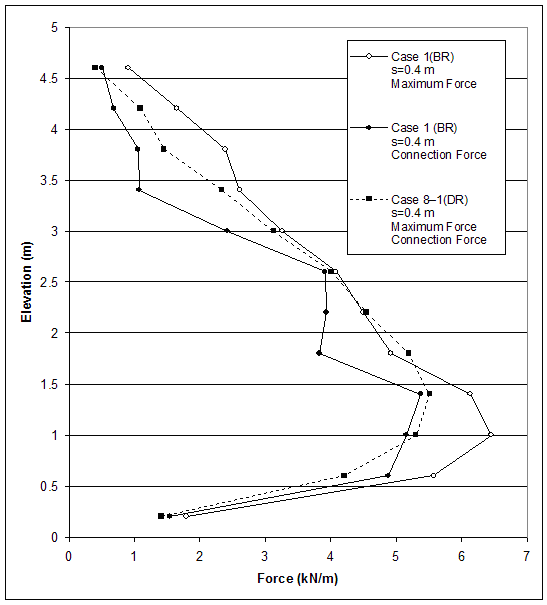
Figure 4.39 Connection Force and Maximum Force in Reinforcement for Case 1 (s=0.4 m, h=5.0 m, BR) and Case 8–1 (s=0.4 m, h=5.0 m, DR): Effects of Reinforcement Stiffness.
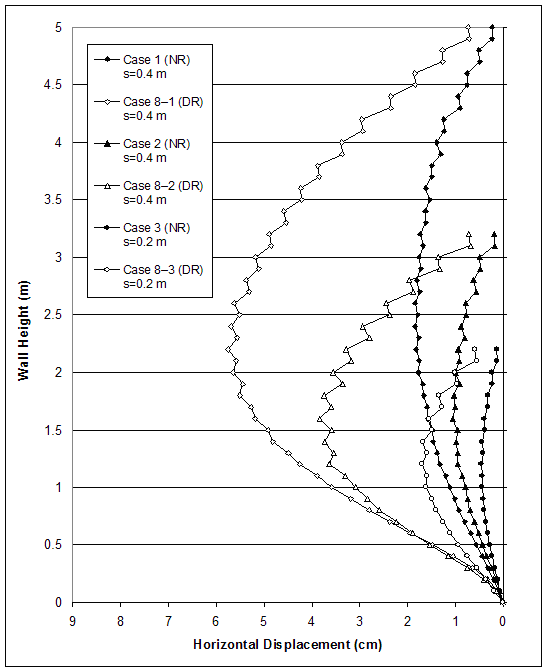
Figure 4.40 Horizontal Displacements along Section A: Comparison with Respect to Reinforcement Stiffness. (Note: NR in graph not previously defined.)
Figure 4.41 State of Soil for Cases 2 and 8–2 (s=0.4 m, h=3.2 m, l=1.5 m): (a) Case 2 (BR); (b) Case 8–2 (DR).
Figure 4.42 Axial Force Distributions in Reinforcement for Cases 2 and 8–2 (s=0.4 m, h=3.2 m, l=1.5 m): (a) Case 2 (BR); (b) Case 8–2 (DR).
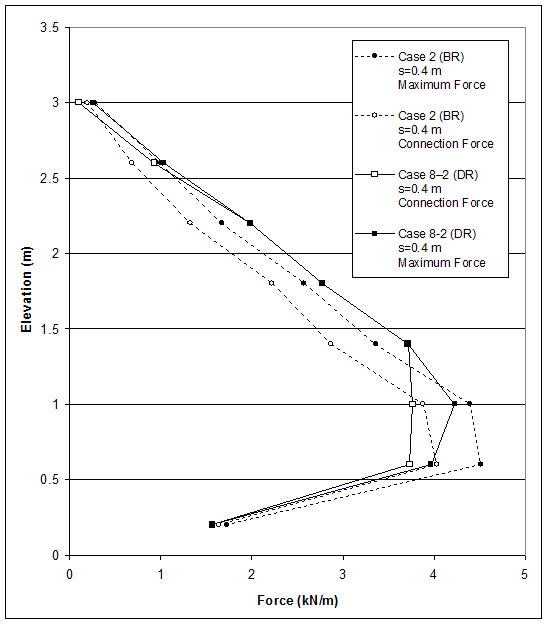
Figure 4.43 Connection Force and Maximum Force in Reinforcement for Case 2 (s=0.4 m, h=3.2 m, BR) and Case 8–2 (s=0.4 m, h=3.2 m, DR): Effects of Reinforcement Stiffness.
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.44 State of Soil for Cases 3 and 8–3 (s=0.2 m, h=2.2 m, l=1.5 m): (a) Case 3 (BR); (b) Case 8–3 (DR).
Figure 4.45 Axial Force Distributions in Reinforcement for Cases 3 and 8–3 (s=0.2 m, h=2.2 m, l=1.5 m): (a) Case 3 (BR); (b) Case 8–3 (DR).
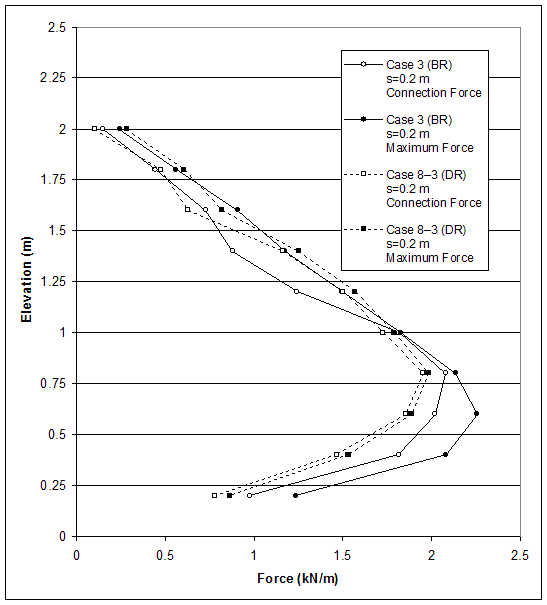
Figure 4.46 Connection Force and Maximum Force in Reinforcement for Case 3 (s=0.2 m, h=2.2 m, BR) and Case 8–3 (s=0.2 m, h=2.2 m, DR): Effects of Reinforcement Stiffness.
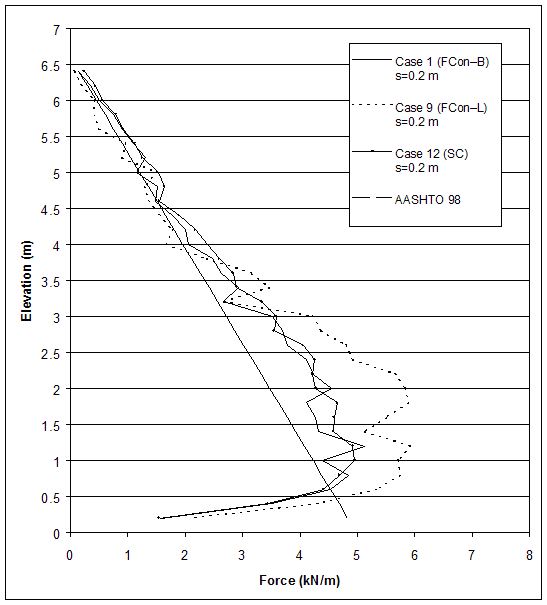
Figure 4.47 Effects of Connection Strength on Connection Force for Cases with Small Reinforcement Spacing (s=0.2 m). (Should "Connection Force" be added over AASHTO in the graph above?)
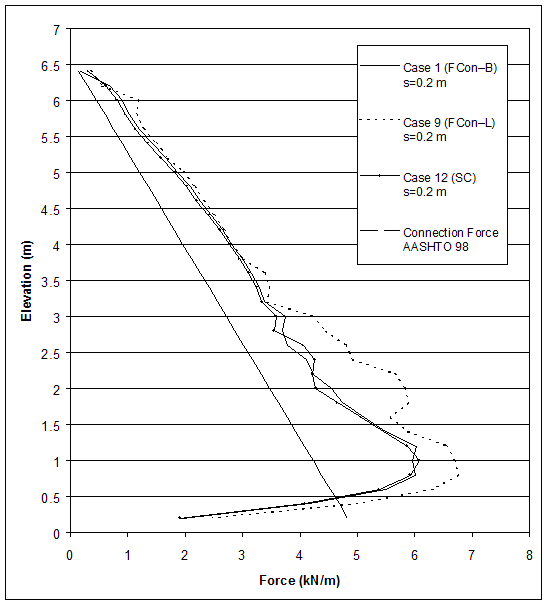
Figure 4.48 Effects of Connection Strength on Maximum Force in Reinforcement for Cases with Small Reinforcement Spacing (s=0.2 m).
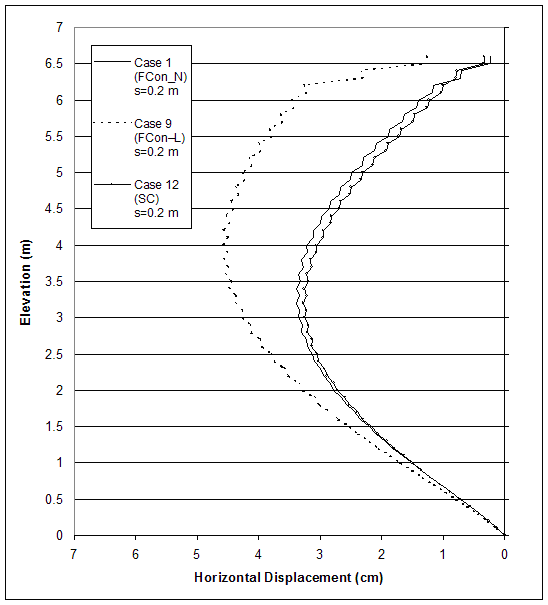
Figure 4.49 Effects of Connection Strength on Horizontal Displacements along Section A for Cases with Small Reinforcement Spacing (s=0.2 m).
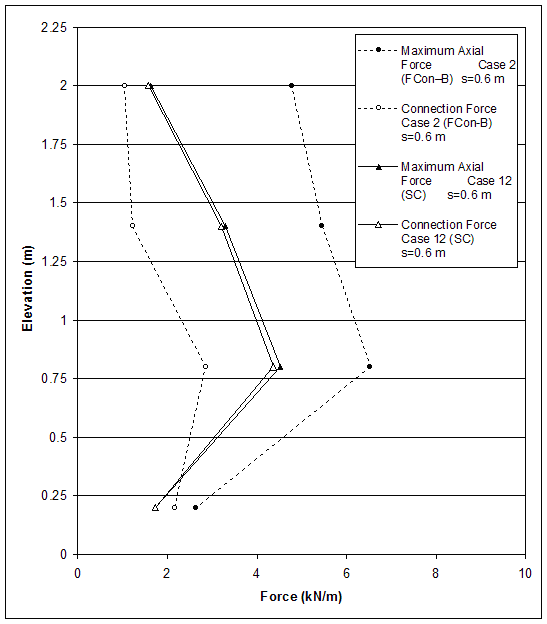
Figure 4.50 Effects of Connection Strength on Connection Force and Maximum Force in Reinforcement for Cases with Large Reinforcement Spacing (s=0.6 m).
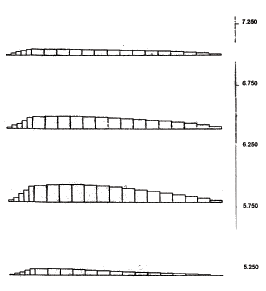
Figure 4.51 Axial Force Distribution in Reinforcement for Case 12 (l=1.5 m): (a) s=0.2 m, h=6.6 m; (b) s=0.6 m, h=2.6 m.
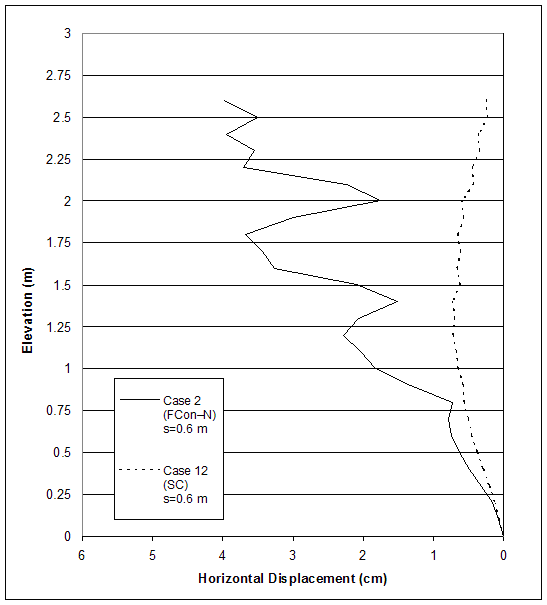
Figure 4.52 Effects of Connection Strength on Horizontal Displacements along Section A for Cases with Large Reinforcement Spacing (s=0.6 m).
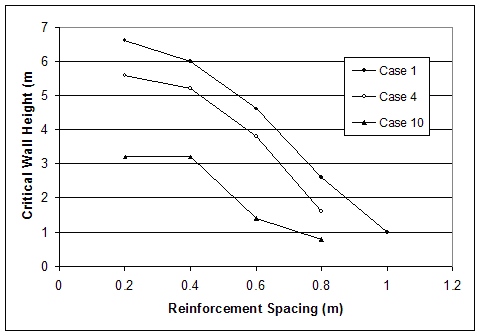
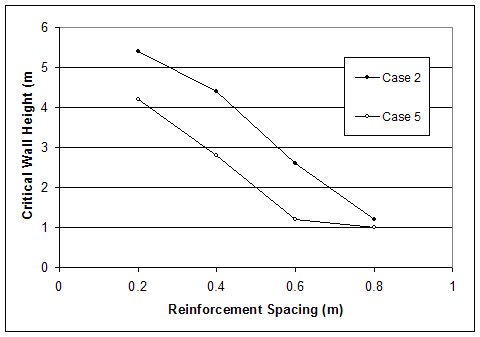
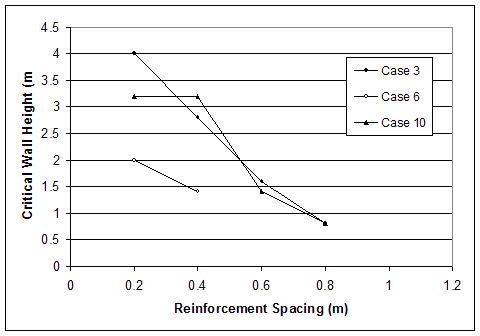
Figure 4.53 Effects of Foundation Strength on Critical Wall Height.
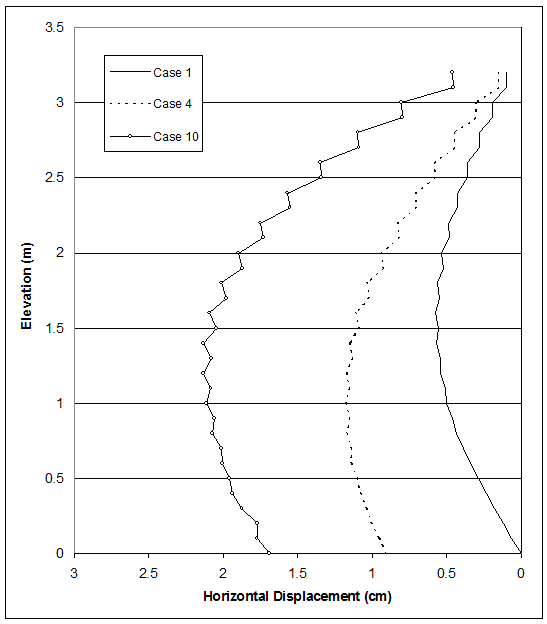
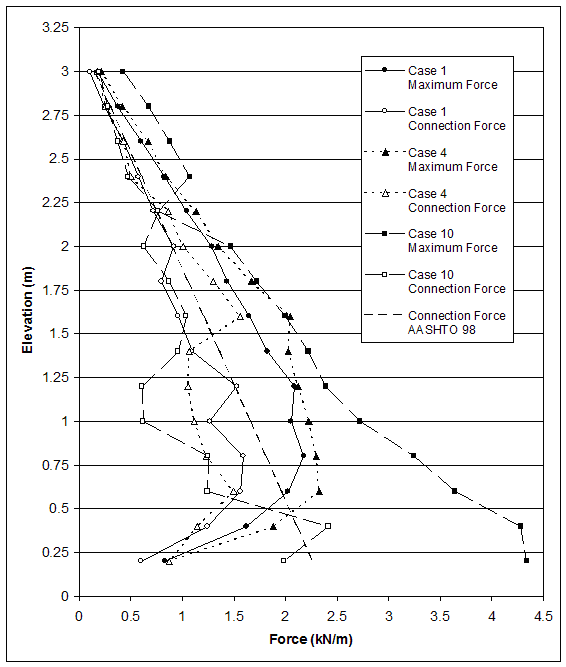
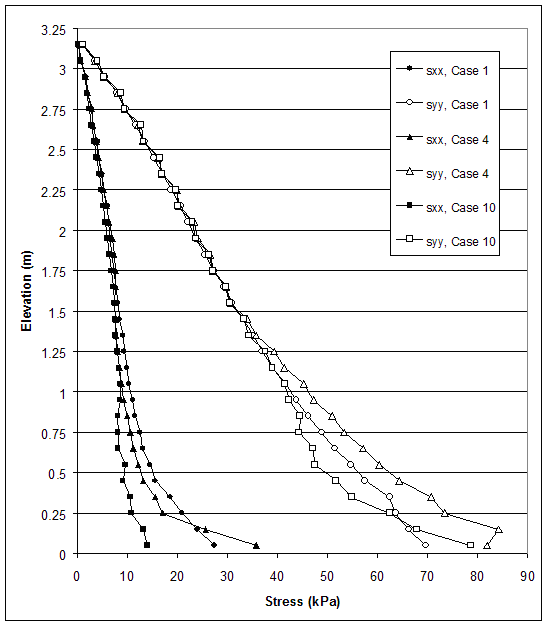
Figure 4.54 Effects of Foundation Strength for Cases 1, 4, and 10 (s=0.2 m, l=1.5 m h=3.2 m) on: (a) Horizontal Displacements along Section A; (b) Connection Force and Maximum Axial Force in Reinforcement; (c) Stresses along Section A.
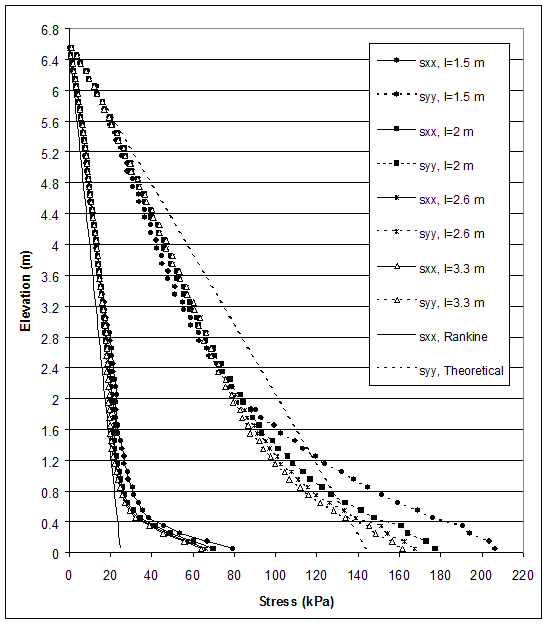
Figure 4.55 Stress Distributions along Section A for Critical and Stable States of Case 1 (s=0.2 m, h=6.6 m, l/h=0.23–0.5).
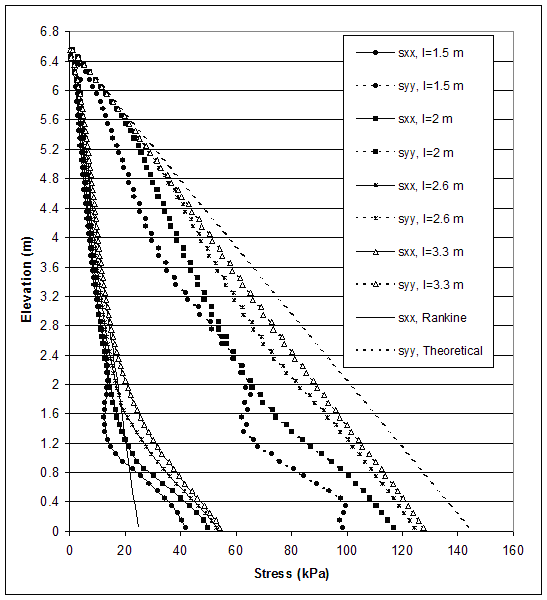
Figure 4.56 Stress Distributions along Section C for Critical and Stable States of Case 1 (s=0.2 m, h=6.6 m, l/h=0.23–0.5).
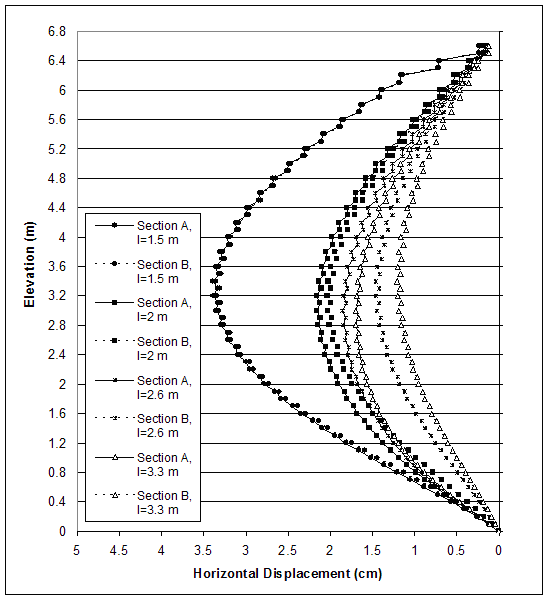
Figure 4.57 Horizontal Displacements along Sections A and B for Critical and Stable States of Case 1 (s=0.2 m, h=6.6 m, l/h=0.23–0.5).
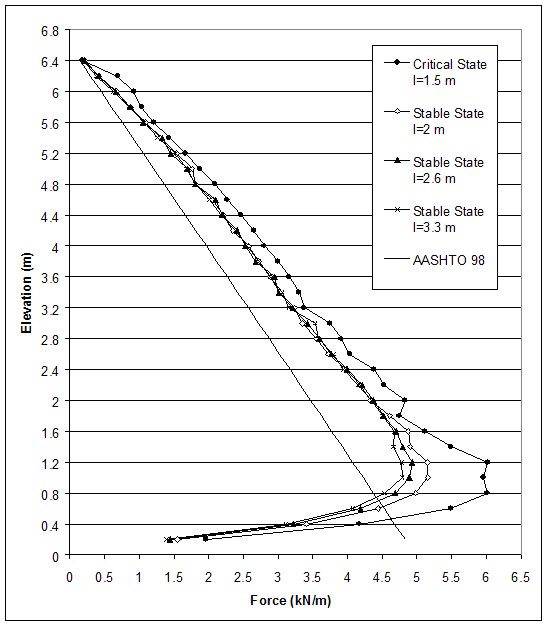
Figure 4.58 Maximum Axial Force in Reinforcement for Critical and Stable States of Case 1 (s=0.2 m, h=6.6 m, l/h=0.23–0.5).
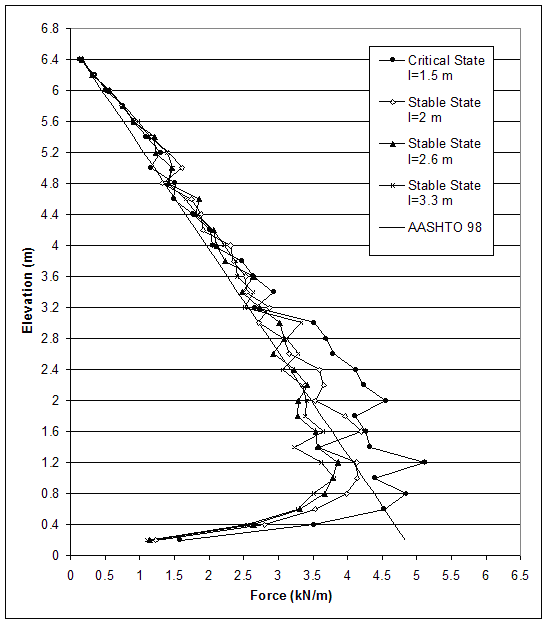
Figure 4.59 Connection Force for Critical and Stable States of Case 1 (s=0.2 m, h=6.6 m, l/h=0.23–0.5).
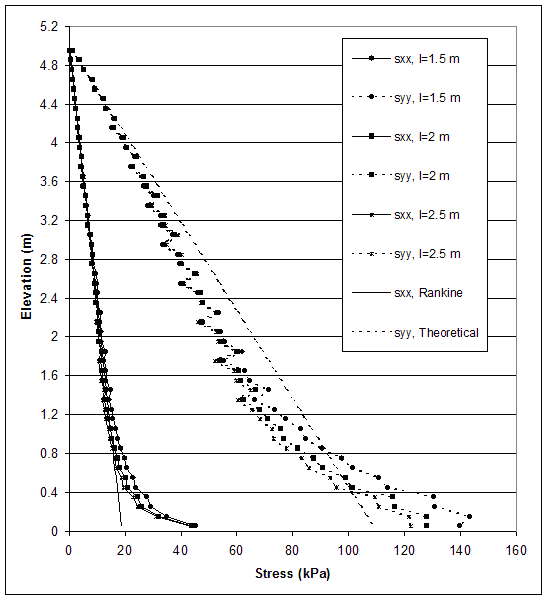
Figure 4.60 Stress Distributions along Section A for Critical and Stable States of Case 8–1 (s=0.4 m, h=5.0 m, l/h=0.3–0.5).
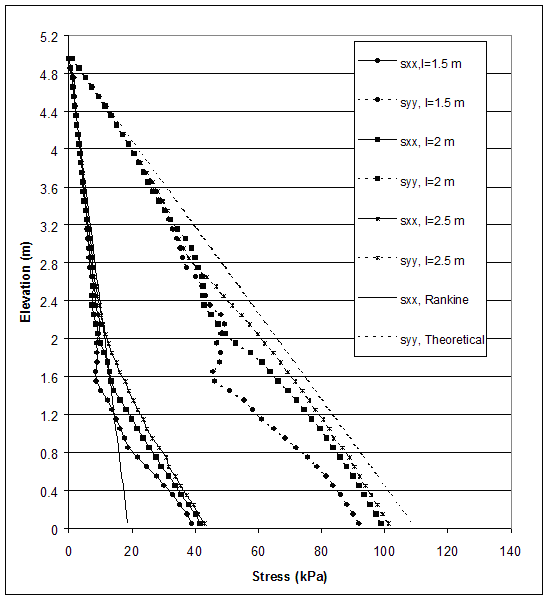
Figure 4.61 Stress Distributions along Section C for Critical and Stable States of Case 8–1 (s=0.4 m, h=5.0 m, l/h=0.3–0.5).
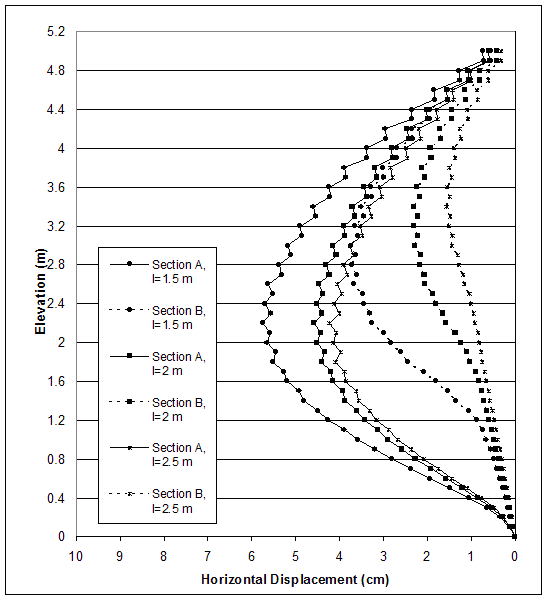
Figure 4.62 Horizontal Displacements along Sections A and B for Critical and Stable States of Case 8–1 (s=0.4 m, h=5.0 m, l/h=0.3–0.5).
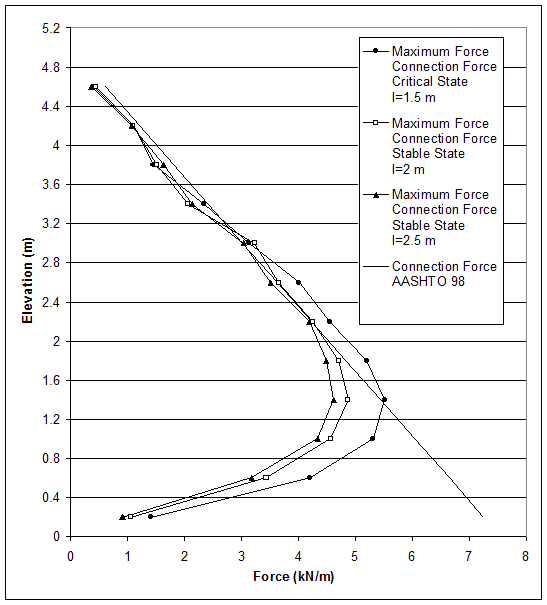
Figure 4.63 Connection Force and Maximum Axial Force in Reinforcement for Critical and Stable States of Case 8–1 (s=0.4 m, h=5.0 m, l/h=0.3–0.5).
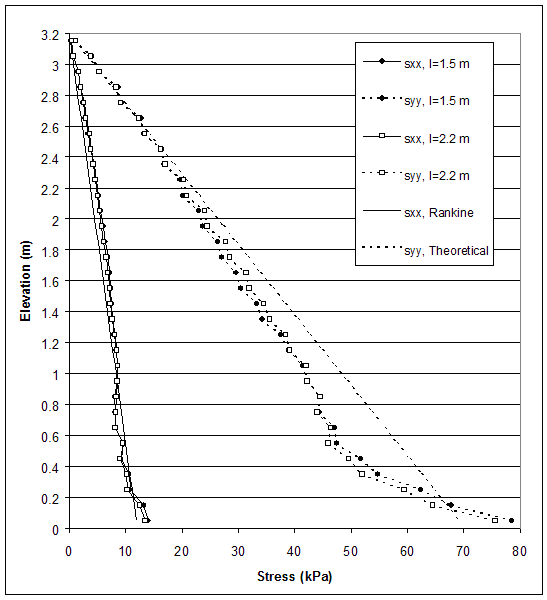
Figure 4.64 Stress Distributions along Section A for Critical and Stable States of Case 10 (s=0.2 m, h=3.2 m, l/h=0.47–0.7).
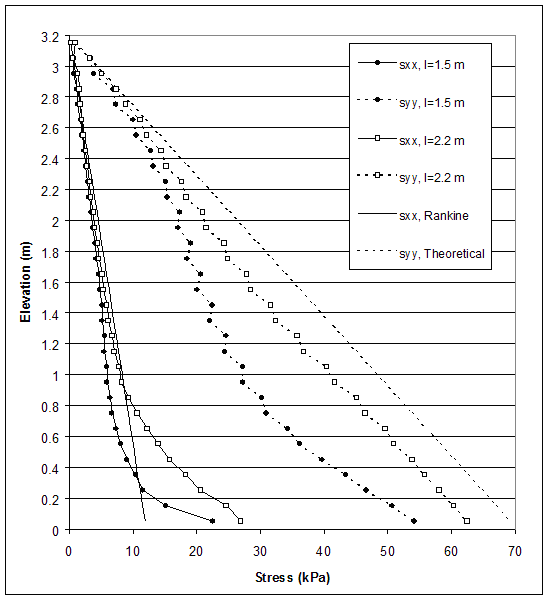
Figure 4.65 Stress Distributions along Section C for Critical and Stable States of Case 10 (s=0.2 m, h=3.2 m, l/h=0.47–0.7).
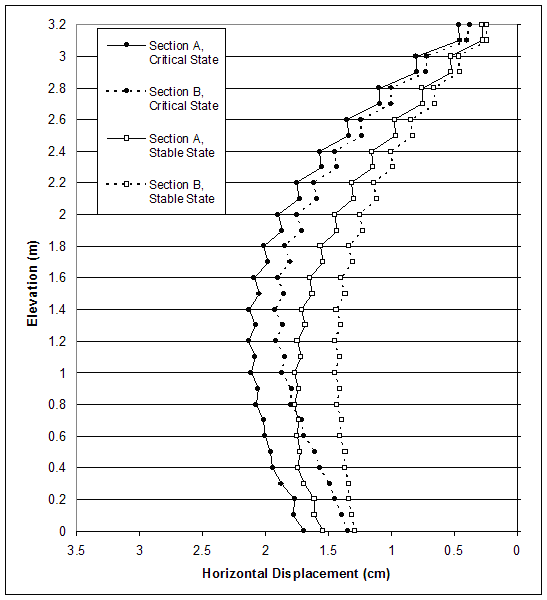
Figure 4.66 Horizontal Displacements along Sections A and B for Critical and Stable States of Case 10 (s=0.2 m, h=3.2 m, l/h=0.47–0.7).
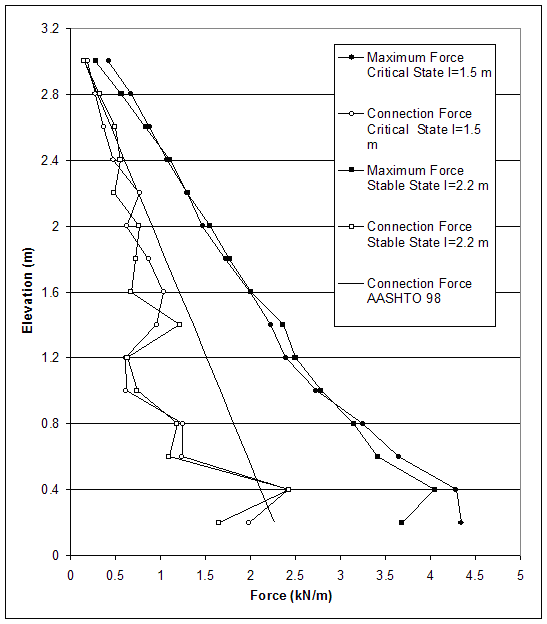
Figure 4.67 Connection Force and Maximum Axial Force in Reinforcement for Critical and Stable States of Case 10 (s=0.2 m, h=3.2 m, l/h=0.47–0.7).
Figure 4.68 Effects of Secondary Reinforcement: Axial Force Distribution in Reinforcement for Case 7 (s=0.6/0.2 m), (a) h=2.6 m; (b) h=5.0 m.
| Elastic |
At Yield in Shear or Volume |
Elastic, Yield in Past |
Figure 4.69 Effects of Secondary Reinforcement: State of Soil for Case 7 (h=2.6 m, s=0.6/0.2 m).
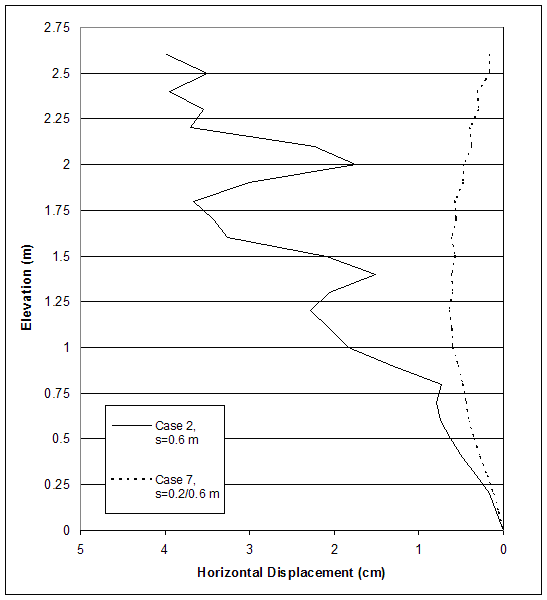
Figure 4.70 Effects of Secondary Reinforcement: Horizontal Displacements along Section A for Cases 2 and 7 (h=2.6 m).
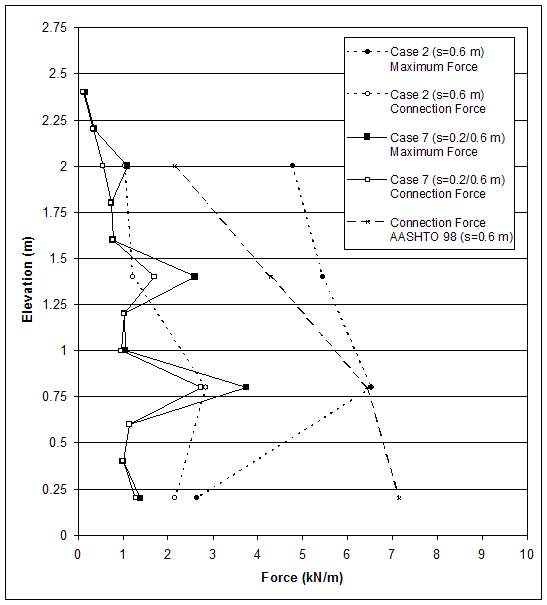
Figure 4.71 Effects of Secondary Reinforcement: Connection Force and Maximum Axial Force in Reinforcement for Cases 2 and 7 (h=2.6 m).
| Case | Spacing (m) | First Slip Surface Fully Developed | Wall Height at Which Plastic Zones Occur for the First Time in: | Mode of Failure | |||
|---|---|---|---|---|---|---|---|
| at Wall Height (m) | Type | Foundation Soil | Reinforced Soil | Backfill Soil | |||
| 1 | 0.2 | 6.6 | External | - | 6.0 | 3.8 | External mode |
| 0.4 | 5.8 | External | - | 4.0 | 3.2 | Mixed mode: external mode is prevailing over compound mode | |
| 0.6 | 4.4 | Compound | - | 1.4 | 2.6 | Mixed mode: compound mode is prevailing over connection mode | |
| 0.8 | 1.8 | Internal | - | 1.0 | 2.2 | Connection mode | |
| 1.0 | 1.0 | Internal | - | 1.0 | 1.4 | Connection mode | |
| 2 | 0.2 | 3.4 | Compound | - | 3.0 | 2.4 | Mixed mode: external mode is prevailing over compound mode |
| 0.4 | 2.8 | Compound | - | 1.4 | 2.0 | Mixed mode: compound mode is prevailing over external mode | |
| 0.6 | 1.4 | Internal | - | 1.0 | 1.4 | Mixed mode: connection mode is prevailing over compound mode | |
| 0.8 | 1.0 | Internal | - | 0.8 | - | Connection mode | |
| 6 | 0.4 | 1.2 | Internal | 0.4 | 0.4 | 1.2 | Mixed mode: connection mode is prevailing over deep-seated mode |
| 7 | 0.6/0.2 | 2.6 | Compound | - | 1.2 | 2.2 | Compound mode |
| 8-1 | 0.4 | 1.8 | Internal | - | 1.6 | 3.0 | Compound mode |
| 8-2 | 0.4 | 1.6 | Internal | - | 1.4 | 2.0 | Compound mode |
| 8-3 | 0.2 | 1.2 | Compound | - | 1.2 | 1.2 | Compound mode |
| 9 | 0.2 | 6.4 | External | - | 6.0 | 3.2 | External mode |
| 10 | 0.2 | 3 | External | 0.4 | 0.4 | 2.2 | Deep-seated mode |
| 0.4 | 3 | External | 0.4 | 0.4 | 1.8 | Deep-seated mode | |
| 0.6 | 1.4 | Internal | 0.4 | 0.4 | 1.8 | Mixed mode: connection mode is prevailing over deep-seated mode | |
| 0.8 | 0.8 | Internal | 0.4 | 0.4 | - | Connection mode | |
| 11 | 0.2 | 5.4 | External | - | 5.4 | 3.6 | External mode |
| 12 | 0.2 | 6.6 | External | - | 6.0 | 3.8 | External mode |
| 0.6 | 2.6 | Compound | - | 1.2 | 1.8 | Compound mode | |
| Case | Reinforcement Spacing (m) | ||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| 1 | 6.6 | 6.0 | 4.6 | 2.6 | 1.0 |
| 2 | 5.4 | 4.4 | 2.6 | 1.2 | - |
| 3 | 4.0 | 2.8 | 1.6 | 0.8 | - |
| 4 | 5.6 | 5.2 | 3.8 | 1.6 | - |
| 5 | 4.2 | 2.8 | 1.2 | 1.0 | - |
| 6 | 2.0 | 1.4 | - | - | - |
| 7 | - | - | 5.0 | - | - |
| 8- 1 | - | 5.0 | - | - | - |
| 8- 2 | - | 3.2 | - | - | - |
| 8- 3 | 2.2 | - | - | - | - |
| 9 | 6.6 | - | - | - | - |
| 10 | 3.2 | 3.2 | 1.4 | 0.8 | - |
| 11 | 6.0 | - | - | - | - |
| 12 | 6.6 | - | 4.6 | - | - |
| LEGEND: | Prevailing Mode of Failure: | |
|---|---|---|
| External Mode (Direct Sliding/Toppling) | ||
| Deep-Seated Mode | ||
| Compound Mode | ||
| Connection Mode | ||
| Case | Spacings (m) | Maximum Axial Force | |||||
|---|---|---|---|---|---|---|---|
| Failure State | Critical State | ||||||
| Value (kN/m) | Elevation (m) | Wall Height (m) | Value (kN/m) | Elevation (m) | Wall Height (m) | ||
| 1 | 0.2 | 20.5 | 0.4 | 8.6 | 6.0 | 1.2 | 6.6 |
| 0.4 | 27.7 | 0.6 | 8.2 | 9.6 | 1.0 | 6.0 | |
| 0.6 | 15.8 | 0.8 | 6.2 | 8.1 | 0.8 | 4.6 | |
| 0.8 | 10.6 | 1.0 | 4.0 | 4.6 | 1.0 | 2.6 | |
| 1.0 | 7.9 | 1.2 | 2.0 | 0.5 | 0.2 | 1.0 | |
| 2 | 0.2 | 22.5 | 0.6 | 6.6 | 8.1 | 0.8 | 5.4 |
| 0.4 | 27.2 | 0.6 | 6.0 | 9.5 | 1.0 | 4.4 | |
| 0.6 | 25.4 | 0.8 | 4.6 | 6.5 | 0.8 | 2.6 | |
| 0.8 | 7.8 | 1.0 | 1.8 | 1.4 | 0.2 | 1.2 | |
| 3 | 0.2 | 10.8 | 0.4 | 4.2 | 9.3 | 0.4 | 4.0 |
| 0.4 | 17.2 | 0.2 | 3.8 | 8.7 | 0.6 | 2.8 | |
| 0.6 | 8.2 | 0.8 | 2.0 | 4.6 | 0.8 | 1.6 | |
| 0.8 | 2.6 | 0.2 | 1.0 | 0.7 | 0.2 | 0.8 | |
| 4 | 0.2 | 8.8 | 0.6 | 7.0 | 4.8 | 0.6 | 5.6 |
| 0.4 | 10.9 | 0.6 | 6.0 | 7.6 | 1.0 | 5.2 | |
| 0.6 | 15.8 | 1.4 | 5.4 | 7.2 | 0.8 | 3.8 | |
| 0.8 | 6.0 | 1.0 | 1.8 | 2.5 | 1.0 | 1.6 | |
| 5 | 0.2 | 21.3 | 0.2 | 5.4 | 7.8 | 0.2 | 4.2 |
| 0.4 | 11.1 | 0.2 | 3.8 | 5.6 | 0.2 | 2.8 | |
| 0.6 | 8.7 | 0.8 | 2.4 | 2.0 | 0.2 | 1.2 | |
| 0.8 | 4.2 | 0.2 | 1.2 | 3.3 | 0.2 | 1.0 | |
| 6 | 0.2 | 7.8 | 0.2 | 2.4 | 4.8 | 0.2 | 2.0 |
| 0.4 | 15.1 | 0.2 | 2.6 | 4.8 | 0.2 | 1.4 | |
| 7 | 0.6/0.2 | 40.2 | 1.2 | 6.0 | 17.8 | 1.2 | 5.0 |
| 8- 1 | 0.4 | 40.6 | 1.0 | 8.0 | 5.5 | 1.4 | 5.0 |
| 8- 2 | 0.4 | 24.9 | 0.6 | 5.4 | 4.2 | 1.0 | 3.2 |
| 8- 3 | 0.2 | 18.2 | 0.6 | 5.0 | 2.0 | 0.8 | 2.2 |
| 9 | 0.2 | 16.1 | 0.4 | 8.2 | 6.8 | 0.8 | 6.6 |
| 10 | 0.2 | 11.4 | 0.2 | 4.4 | 4.3 | 0.2 | 3.2 |
| 0.4 | 15.0 | 0.2 | 4.4 | 6.1 | 0.2 | 3.2 | |
| 0.6 | 8.2 | 0.2 | 2.8 | 3.3 | 0.8 | 1.4 | |
| 0.8 | 4.4 | 0.2 | 1.0 | 1.1 | 0.2 | 0.8 | |
| 11 | 0.2 | 15.3 | 0.4 | 7.2 | 6.1 | 0.8 | 6.0 |
| 12 | 0.2 | 23.1 | 0.4 | 8.8 | 6.1 | 1.0 | 6.6 |
| 0.6 | 47.0 | 0.8 | 6.0 | 16.1 | 0.8 | 4.6 | |
| Case | Spacings (m) | Maximum Connection Force | |||||
|---|---|---|---|---|---|---|---|
| Failure State | Critical State | ||||||
| Value (kN/m) | Elevation (m) | Wall Height (m) | Value (kN/m) | Elevation (m) | Wall Height (m) | ||
| 1 | 0.2 | 17.9 | 0.4 | 8.6 | 5.1 | 1.2 | 6.6 |
| 0.4 | 23.5 | 0.6 | 8.2 | 7.4 | 1.0 | 6.0 | |
| 0.6 | 13.1 | 0.8 | 6.2 | 6.8 | 0.8 | 4.6 | |
| 0.8 | 6.7 | 1.0 | 4.0 | 2.8 | 1.0 | 2.6 | |
| 1.0 | 1.4 | 0.2 | 2.0 | 0.4 | 0.2 | 1.0 | |
| 2 | 0.2 | 20.7 | 0.4 | 6.6 | 6.0 | 0.6 | 5.4 |
| 0.4 | 22.4 | 0.6 | 6.0 | 7.4 | 0.6 | 4.4 | |
| 0.6 | 12.4 | 0.8 | 4.6 | 2.9 | 0.8 | 2.6 | |
| 0.8 | 0.4 | 0.2 | 1.8 | 1.2 | 0.2 | 1.2 | |
| 3 | 0.2 | 9.3 | 0.4 | 4.2 | 7.1 | 0.4 | 4.0 |
| 0.4 | 13.5 | 0.6 | 3.8 | 5.0 | 0.6 | 2.8 | |
| 0.6 | 2.7 | 0.8 | 2.0 | 1.9 | 0.2 | 1.6 | |
| 0.8 | 0.9 | 0.2 | 1.0 | 0.6 | 0.2 | 0.8 | |
| 4 | 0.2 | 5.9 | 0.6 | 7.0 | 3.0 | 0.6 | 5.6 |
| 0.4 | 6.6 | 1.0 | 6.0 | 4.6 | 0.6 | 5.2 | |
| 0.6 | 6.9 | 2.0 | 5.4 | 3.0 | 0.2 | 3.8 | |
| 0.8 | 1.2 | 0.2 | 1.8 | 1.2 | 0.2 | 1.6 | |
| 5 | 0.2 | 6.4 | 0.6 | 5.4 | 4.4 | 0.2 | 4.2 |
| 0.4 | 7.6 | 0.2 | 3.8 | 4.1 | 0.2 | 2.8 | |
| 0.6 | 3.8 | 0.2 | 2.4 | 1.3 | 0.2 | 1.2 | |
| 0.8 | 1.8 | 0.2 | 1.2 | 1.5 | 0.2 | 1.0 | |
| 6 | 0.2 | 2.9 | 0.4 | 2.4 | 1.5 | 0.4 | 2.0 |
| 0.4 | 4.6 | 0.6 | 2.6 | 1.9 | 0.2 | 1.4 | |
| 7 | 0.6/0.2 | 2.9 | 0.2 | 6.0 | 10.6 | 0.8 | 5.0 |
| 8- 1 | 0.4 | 30.9 | 0.6 | 8.0 | 5.5 | 1.4 | 5.0 |
| 8- 2 | 0.4 | 23.4 | 0.6 | 5.4 | 3.8 | 1.0 | 3.2 |
| 8- 3 | 0.2 | 15.7 | 0.2 | 5.0 | 2.0 | 0.8 | 2.2 |
| 9 | 0.2 | 14.0 | 0.4 | 8.2 | 5.9 | 1.2 | 6.6 |
| 10 | 0.2 | 4.2 | 0.4 | 4.4 | 2.4 | 0.4 | 3.2 |
| 0.4 | 5.2 | 0.6 | 4.4 | 2.2 | 0.6 | 3.2 | |
| 0.6 | 3.9 | 0.2 | 2.8 | 1.9 | 0.2 | 1.4 | |
| 0.8 | 1.4 | 0.2 | 1.0 | 0.8 | 0.2 | 0.8 | |
| 11 | 0.2 | 13.9 | 0.4 | 7.2 | 4.5 | 0.8 | 6.0 |
| 12 | 0.2 | 22.0 | 0.4 | 8.8 | 5.0 | 1.0 | 6.6 |
| 0.6 | 34.3 | 0.8 | 6.0 | 12.5 | 0.8 | 4.6 | |
| Parameter | Case 1 (s=0.4 m) |
Case 8- 1 (s=0.4 m) |
|
|---|---|---|---|
| Reinforcement type (table 3.5) | Baseline | Ductile | |
| Mode of failure (table 4.1) | External mode | Compound mode | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
6.0 | 5.0 | |
| Plastic zones distribution | Figure 4.5 | Figure 4.31 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - |
| Reinforced soil | 4.0 | 1.6 | |
| Backfill soil | 3.2 | 3.0 | |
| Slip surface developed for the first time | At wall height (m) | 5.8 | 1.8 |
| Type (figure 4.3) | External | Internal | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 58 | 53 |
| Type (figure 4.3) | External | Compound | |
| Wall height h=5.0 m | Maximum force in reinforcement | 6.46 kN at elevation 1.0 m |
5.51 kN at elevation 1.4 m |
| Maximum connection force | 5.38 kN at elevation 1.4 m |
5.51 kN at elevation 1.4 m |
|
| Maximum displacement (cm) | 2.9 | 7.3 | |
| Number of steps | 278508 (Grid 159′321) |
485049 (Grid 159′221) |
|
| Parameter | Case 2 (s=0.4 m) |
Case 8- 2 (s=0.4 m) |
|
|---|---|---|---|
| Reinforcement type (table 3.5) | Baseline | Ductile | |
| Mode of failure (table 4.1) | Compound mode | Compound mode | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
4.4 | 3.2 | |
| Plastic zones distribution | Figure 4.58 | Figure 4.75 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - |
| Reinforced soil | 1.4 | 1.4 | |
| Backfill soil | 2.0 | 2.0 | |
| Slip surface developed for the first time | At wall height (m) | 2.8 | 1.6 |
| Type (figure 4.3) | Compound | Internal | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 50 | 45 |
| Type (figure 4.3) | External | Compound | |
| Wall height h=3.2 m | Maximum force in reinforcement | 4.51 kN at elevation 0.6 m |
4.23 kN at elevation 1.0 m |
| Maximum connection force | 4.03 kN at elevation 0.6 m |
3.76 kN at elevation 1.0 m |
|
| Maximum displacement (cm) | 1.7 | 5.2 | |
| Number of steps | 126614 (grid 159′321) |
173555 (grid 159′181) |
|
| Parameter | Case 3 (s=0.2 m) |
Case 8- 3 (s=0.2 m) |
|
|---|---|---|---|
| Reinforcement type (table 3.5) | Baseline | Ductile | |
| Mode of failure (table 4.1) | Compound mode | Compound mode | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
4.0 | 2.2 | |
| Plastic zones distribution | Figure 4.60 | Figure 4.76 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - |
| Reinforced soil | 1.2 | 1.2 | |
| Backfill soil | 1.2 | 1.2 | |
| Slip surface developed for the first time | At wall height (m) | 2.4 | 1.2 |
| Type (figure 4.3) | Compound | Compound | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 45 | 41 |
| Type (figure 4.3) | Compound | Compound | |
| Wall height h=2.2 m | Maximum force in reinforcement | 2.26 kN at elevation 0.6 m |
1.98 kN at elevation 0.8 m |
| Maximum connection force | 2.08 kN at elevation 0.8 m |
1.95 kN at elevation 0.8 m |
|
| Maximum displacement (cm) | 0.8 | 2.4 | |
| Number of steps | 51792 (grid 159′321) |
90776 (grid 159′181) |
|
| Parameter | Case 1 | Case 9 | Case 12 | |
|---|---|---|---|---|
| Connection type (table 3.6) | FCon- B | FCon- L | SC | |
| Mode of failure (table 4.1) | External | External | External | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
6.6 | 6.6 | 6.6 | |
| Plastic zones distribution | Figure 4.5 | Figure 4.77 | Figure 4.82 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - | - |
| Reinforced soil | 6.0 | 6.0 | 6.0 | |
| Backfill soil | 3.8 | 3.2 | 3.8 | |
| Slip surface developed for the first time | At wall height (m) | 6.6 | 6.4 | 6.6 |
| Type (figure 4.3) | External | External | External | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 54 | 52 | 56 |
| Type (figure 4.3) | External | External | External | |
| Wall height h=6.6 m | Maximum force in reinforcement | 6.02 kN at elevation 1.2 m |
6.77 kN at elevation 0.8 m |
6.08 kN at elevation 1.0 m |
| Maximum connection force | 5.12 kN at elevation 1.2 m |
5.93 kN at elevation 1.2 m |
4.96 kN at elevation 1.2 m |
|
| Maximum displacement (cm) | 4.4 | 5.6 | 4.2 | |
| Number of steps | 419538 (grid 159′321) |
375455 (grid 159′201) |
573000 (grid 159′321) |
|
| Parameter | Case 2 (s=0.6 m) |
Case 12 (s=0.6 m) |
|
|---|---|---|---|
| Connection type (table 3.6) | FCon- B | SC | |
| Mode of failure (table 4.1) | Connection | Compound | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
2.6 | 4.6 | |
| Plastic zones distribution | Figure 4.44 | Figure 4.83 | |
| Wall height at which plastic zones Occur for first time in (table 4.1) | Foundation soil | - | - |
| Reinforced soil | 1.0 | 1.2 | |
| Backfill soil | 1.4 | 1.8 | |
| Slip surface developed for the first time | At wall height (m) | 1.4 | 2.6 |
| Type (figure 4.3) | Internal | Compound | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 65 | 50 |
| Type (figure 4.3) | Internal | Compound | |
| Wall height h=2.6 m | Maximum force in reinforcement | 6.53 kN at elevation 0.8 m |
4.85 kN at elevation 0.8 m |
| Maximum connection force | 2.85 kN at elevation 0.8 m |
4.32 kN at elevation 0.8 m |
|
| Maximum displacement (cm) | 7.1 | 1.2 | |
| Number of steps | 248497 (grid 159′321) |
89516 (grid 159′221) |
|
| Parameter | Case 1 | Case 4 | Case 10 | |
|---|---|---|---|---|
| Foundation soil type (table 3.3) | Very stiff soil | Baseline stiffness high strength |
Baseline stiffnes slow strength |
|
| Strength of reinforced soil | High | High | High | |
| Strength of backfill soil | High | High | Low | |
| Mode of failure (table 4.1) | External | External | Deep-seated | |
| Critical wall height (m), (table 4.5) | 6.6 | 5.6 | 3.2 | |
| Plastic zones distribution | Figure 4.5 | Figure 4.64 | Figure 4.18 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | 1.8 | 0.4 |
| Reinforced soil | 6.0 | 5.6 | 0.4 | |
| Backfill soil | 3.8 | 3.4 | 2.2 | |
| Slip surface developed for the first time | At wall height (m) | 6.6 | 5.4 | 3.0 |
| Type (figure 4.3) | External | External | External | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 54 | 60 | 62 |
| Type (figure 4.3) | External | External | External | |
| Wall height h=3.2 m | Maximum force in reinforcement | 2.18 kN at elevation 0.8 m |
2.33 kN at elevation 0.6 m |
4.34 kN at elevation 0.2 m |
| Maximum connection force | 1.59 kN at elevation 0.8 m |
1.50 kN at elevation 0.6 m |
2.41 kN at elevation 0.4 m |
|
| Maximum displacement (cm) | 1.1 | 3.0 | 3.7 | |
| Parameter | Case 2 (s=0.6 m) |
Case 7 (s=0.6/0.2 m) |
|
|---|---|---|---|
| Mode of failure (table 4.1) | Connection | Compound | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
2.6 | 5.0 | |
| Plastic zones distribution | Figure 4.44 | Figure 4.74 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - |
| Reinforced soil | 1.0 | 1.2 | |
| Backfill soil | 1.4 | 2.2 | |
| Slip surface developed for the first time | At wall height (m) | 1.4 | 2.6 |
| Type (figure 4.3) | Internal | Compound | |
| Slip surface at critical State (table 4.2) | Slope (deg) | 65 | 46 |
| Type (figure 4.3) | Internal | Compound | |
| Wall height h=2.6 m | Maximum force in reinforcement | 6.53 kN at elevation 0.8 m |
3.75 kN at elevation 1.2 m |
| Maximum connection force | 2.85 kN at elevation 0.8 m |
2.55 kN at elevation 0.8 m |
|
| Maximum displacement (cm) | 7.1 | 1.0 | |
| Number of steps | 248497 (grid 159′321) |
79737 (grid 159′181) |
|
| Parameter | Case 1 (s=0.2 m) |
Case 11 (s=0.2 m) |
|
|---|---|---|---|
| Soil dilation (deg) | 15 | 0 | |
| Mode of failure (table 4.1) | External mode | External mode | |
| Critical wall height (m) (table 4.5, figure 4.1- a) |
6.6 | 6.0 | |
| Plastic zones distribution | Figure 4.5 | Figure 4.81 | |
| Wall height at which plastic zones occur for first time in (table 4.1): | Foundation soil | - | - |
| Reinforced soil | 4.0 | 5.4 | |
| Backfill soil | 3.2 | 3.6 | |
| Slip surface developed for the First Time | At wall height (m) | 6.6 | 5.4 |
| Type (figure 4.3) | External | External | |
| Slip surface at critical state (table 4.2) | Slope (deg) | 54 | 57 |
| Type (figure 4.3) | External | External | |
| Wall height h=6.0 m | Maximum force in reinforcement | 4.903 kN at elevation 1.2 m |
6.06 kN at elevation 0.8 m |
| Maximum connection force | 3.89 kN at elevation 1.2 m |
4.52 kN at elevation 0.8 m |
|
| Maximum displacement (cm) | 3.24 | 5.2 | |
| Number of steps (grid 159′321) | 303203 | 455957 | |
