U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number:
FHWA-RD-03-089
|
Previous | Table of Contents | Next
The process of obtaining and processing the modal vibration test data from the bridge substructures involved two steps. The first was to acquire the data in the field with various source and receiver locations using the DP420 signal analyzer as discussed in chapter 4. Example results of this field data from the DP420 appear in the following section. The second step was to combine all data from the various and multiple source and receiver combinations and perform a modal analysis of each bridge substructure for each test condition. The modal analysis procedures that provided frequency, damping, and mode shape data for the substructures are discussed in the third section of the chapter, followed in the fourth section by comparisons of dynamic bridge responses for the undamaged, excavated, and sheared pile cases for bents 2 and 12. The purpose of the comparisons is to evaluate the potential of the flexibility TF data (inverse of stiffness) to indicate sound, scoured, and broken pile foundations directly while in the field. The concluding section examines the flexibility TF results to determine if there was a direct field indication of shallow versus deep foundations for the Old Reliance versus Woodville bridges.
The initial field test geometry and nodes used on bents 2 and 12 of structure 4 of the Trinity River Relief Bridge are shown in figures 40 and 41, respectively. In the initial tests, vibration measurements were not performed at all node locations above ground because symmetry was assumed in the responses of the bents. In the final tests, vibration measurements were performed at all selected node locations for each bridge substructure. Because only three data acquisition channels were connected to the seismic accelerometer receivers for each dynamic loading along with the chirped sine-excitation-force input from the Vibroseis load cell, the repeatability of dynamic loading and the resultant responses were very important. The excitation and response data were found to be very repeatable, and in the final analyses, at least 14 TF measurements were used to extract the modal shapes for each test series performed on each bridge substructure. The following discussions provide examples of the data gathered and processed in the field using the DP420 signal analyzer. The examples include the time, spectral, and TF data gathered from one test on bent 2 (piles plus footing).
In the initial tests of bent 2, accelerometers were placed at nodes 24, 25, 6, 26, 7, and 8. (Node 8 was on top of the deck over the beam; all other receiver locations were on the pile sides or bottom of the beam, as shown in figure 40.) The geometry for initial tests of bent 12, shown in figure 41, is similar to bent 2. The following paragraphs discusses example time-domain data results for bent 2.
Figure 40. Diagram. Node locations on bent 2.
Figure 41. Diagram. Node locations on bent 12.
For initial tests of bent 2, the Vibroseis was centered over nodes 6, 7, and 8 on top of the deck over the beam. The Vibroseis was excited by a chirp sine pulse from 3 Hz up to about 80 Hz for 5 to 6 cycles for averaging. Excitation loads ranged from 44,500 N (10,000 lbf) to more than 445,000 N (100,000 lbf) peak-to-peak. The Vibroseis induced nonlinear responses in the piles for loads greater than 178,000 N (40,000 lbf) peak-to-peak, and the piles were visibly moving up and down at these higher loading forces. Because it was desirable to keep the responses of the bridge linear, modal analyses were performed largely of test series where the Vibroseis chirped force was kept below about 178,000 N (40,000 lbf) peak-to-peak.
Example bent 2 time-domain data records are shown in figure 42 for the forcing function of the Vibroseis at node 8, and the corresponding acceleration responses are shown in figures 43, 44, and 45 for a vertical accelerometer at node 27V (north pile), a horizontal accelerometer at node 27H, and a vertical accelerometer at node 24V (south pile), respectively. Figure 42 shows an example plot of the Vibroseis excitation load force in poundforce versus time in seconds for about 6 s of data from a single chirp pulse. The excitation force ranged from peak-to-peak values of about 26,700 N (6,000 lbf) at 3 Hz near time 0 s to a maximum of about 124,600 N (28,000 lbf) at 0.5 s. A second peak loading force occurred at about 2.5 s with a value of about 80,100 N (18,000 lbf) peak-to-peak. The increase in the sinusoidal chirped frequency of excitation from 3 Hz at the start of the chirp pulse at about 0 s to near 80 Hz is readily apparent with increasing time in figure 42.
Figure 42. Graph. Vibroseis at node 8 of bent 2.
Figures 43, 44, and 45 show the calibrated acceleration responses of the seismic accelerometers in units of inches/s2 versus time (1 unit of gravitational acceleration = 1 G = 386 inches/s2 or 9.8 m/s2). Review of the accelerometer responses in figures 43, 44, and 45 shows the largest accelerations were measured by the vertical accelerometer of node 27, which is expected because it is most directly below the excitation force at node 8. In addition, figures 43, 44, and 45 show an increase in responses at the approximate times that the excitation force increased. The peak acceleration for the three accelerometers of about 0.4 G, or 4.06 m/s2 (160 inches/s2) peak-topeak was measured at node 27V, and it occurred at about 0.5 s and 2.5 s (figure 43). These peak acceleration times agree with the peak excitation force results of figure 42. These peak forces and accelerations are attributed to resonances in the Vibroseis that magnified the excitation force.
Figure 43. Graph. Vertical accelerometer at node 27 of bent 2.
Figure 44. Graph. Horizontal accelerometer at node 27 of bent 2.
Figure 45. Graph. Vertical accelerometer at node 24 of bent 2.
The average linear frequency spectra calculated by the DP420 for the time-domain data test series of figures 42 through 45 are presented in figure 46 for bent 2. The vertical scales of the plots in figure 46 are the spectral amplitude in force or acceleration units, and the horizontal scale is the frequency in Hz from 0 to 55 Hz. Review of the force frequency spectrum (G11 in figure 46) shows peak excitation forces at about 14 Hz and 47 Hz that correspond to the timedomain peak excitation forces discussed previously.
Figure 46. Graphs. Average spectra of figures 42 through 45 for bent 2.
TFs, also known as frequency response functions, relate input force (F) and output response in terms of acceleration (A), velocity (V), or displacement (D) for linearly elastic systems as a function of frequency, as shown in figures 47, 48, and 49:
Figure 47. Equation. Accelerance TF.
| where | 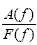 | is the accelerance TF. |
Figure 48. Equation. Mobility TF.
| where | 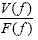 | is the mobility TF. |
Figure 49. Equation. Flexibility TF.
| where | 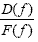 | is the flexibility TF. |
The inverses of the mobility and flexibility TFs are mechanical impedance and stiffness, respectively.
The DP420 was used to field process the time-domain data and save and store the accelerance, mobility (integrated once from accelerance), and flexibility (integrated twice from accelerance) TFs from each test series in the research. To illustrate this, the accelerance TFs for the excitation force at node 8V and the acceleration responses at nodes 27V, 27H, and 24V are shown in figure 50 for bent 2 and the data of figures 42, 43, 44, 45, and 46. Review of this figure shows apparent resonances between 10 Hz to 20 Hz in the A/F, or m/s2-N (inch/s2/lbf or inch/s2-lbf) accelerance plots.
Flexibility lexibility TF plots of the data from figures 42, 43, 44, 45, and 46 are shown in figure 51. The top three plots are the flexibility TF, and the bottom three plots are data coherence. A coherence greater than 0.9 is good, with most of the data exceeding this throughout the plotted frequency range of 5 Hz to 55 Hz. Coherence is related to signal-to-noise ratio, and a value of 1.0 indicates the response resulting from the input with nil contamination caused by noise. Review of the flexibility TF plots shows that the effect of frequency has been removed and the resonant peaks at about 15 Hz are more clearly apparent than in the accelerance plots (compare figures 50 and 51).
Because the flexibility (inch/lbf) TF plots showed the resonances most clearly, and they are the simplest to understand (the inverse of flexibility is stiffness (lbf/inch)), flexibility plots were chosen to compare modal test results of bent 2 (figure 51) and bent 12 (figure 52). The data for bent 12 were from nodes located on bent 12 in the same configuration as nodes on bent 2. Comparison of these two figures shows that bent 2 was more flexible than bent 12, that is, less stiff. The peak flexibility in the vertical direction for bent 2 (piles plus footing) was about 3.42 x 10-9 m/N (600 nanoinches/lbf (600 x 10-9 inch/lbf)); the peak flexibility in the vertical direction for bent 12 (piles only) was about 1.71 nm/N (300 nanoinches/lbf).
Figure 50. Graphs. Accelerance TF for figures 42 through 45 for bent 2.
Figure 51. Graphs. Flexibility TFs with coherences for figures 42 through 50 for bent 2.
Figure 52. Graphs. Bent 12 flexibility TFs with coherences for test configuration identical to bent 2.
The next step in processing the field modal vibration test data was to combine the accelerance TF results of all of the test series (from a given linear force excitation level) to obtain mode shapes, resonant frequencies, and damping information for the tested bents. This was done to provide input and a basis of comparison to experimental results discussed later in this chapter in the sections on the Trinity River bents 2 and 12 and on the Woodville and Old Reliance bridge bents. The processed modal data were also used with theoretical modeling results and structural parameter estimation studies discussed in chapter 6.
The first step in the modal processing was to curve fit the accelerance data for bent 2, discussed in the following paragraphs. The derived mode shapes, resonant frequency, and damping results from curve-fitting of each bent’s data are illustrated after that. A detailed discussion of modal vibration testing and analysis is found in Ewins.(29)
The DP420 dynamic testing data were processed by the commercial PCMODAL software Because accelerance TFs in the PCMODAL software are derived from the power spectrum of the excitation, the power spectrum of the acceleration response, and the cross-power spectrum between the excitation and response, the recorded field data were recalled from the DP420 dynamic signal analyzer and resaved with the PCMODALspecified data format.
After this data conversion to a PCMODAL format was accomplished, curve-fits of the PCMODAL-calculated accelerance results were conducted within fixed frequency bandwidths for each accelerometer and Vibroseis location used in a given test series. The following research curve-fitting criteria were established:
As a result, the curve-fitting was begun by setting the bandwidth at the valley-to-valley (negative peak-to-negative peak) positions in the magnitude plots (or the peak-to-peak positions in the imaginary plots). Next, the bandwidth was adjusted to obtain the bestlooking curve fits from a visual perspective on the computer screen in all of the real, imaginary, magnitude, and Nyquist plots for all measurement combinations. If appropriate, based on all of the measurement location results, occasional efforts were made to fit two modes even if there was only one visualized peak within the bandwidth.
The modal constants, frequencies, and damping ratios were calculated during the curvefitting and saved in the residual data files by the PCMODAL software. Examples of curve-fits are shown in figures 53 through 55 for the bent 2 accelerance TFs of figure 50. Review of these figures shows the resulting resonant frequency values in hertz and the associated damping percentages that were derived from the curve-fitting of the experimental accelerance data using PCMODAL.
Figure 53. Graph. Curve-fit for accelerance TF, bent 2, node 27V/node 8V.
Figure 54. Graph. Curve-fit for accelerance TF, bent 2, node 27H/node 8V.
Figure 55. Graph. Curve-fit for accelerance TF, bent 2, node 24V/node 8V.
After all of the accelerance TFs from a given test series were curve-fitted, PCMODAL was used to calculate mode shapes for each identified vibration mode frequency. Based on the measurement location, direction, and data quality, only one residual data file at each measurement location and direction was selected to extract the mode shapes. In general, the residual data files with the peak-to-peak forces below 176 kilonewtons (kN) (40,000 lbf) were selected. This is because higher dynamic loads would induce nonlinear behavior, especially for the soil around the concrete piles.
The selected residual data files were combined to obtain the relative magnitudes and phases of vibrations at each measurement location and direction to get the mode shape, frequency, and damping associated with the curve-fitted accelerance data. The mode shapes can be displayed in both static and dynamic fashions on the computer screen with PCMODAL. To illustrate a static mode shape display, the first mode shape from initial tests of bent 2 (piles plus footing) is shown in figure 56. Review of this figure shows the deflected mode shape for the first mode, a fundamental first mode frequency of 15.13 Hz, and damping of 0.165 (16.5 percent).
The primary curve fitting with PCMODAL and subsequent vibration mode shape, frequency, damping, magnitude, and phase were performed on the results from the more comprehensive final visit to bents 2 and 12, as discussed in the next section.
Figure 56. Diagram. First mode shape, frequency, and damping for bent 2.
As discussed in chapter 4, bents 2 and 12 were tested for three cases in the final site visit:
The second and third cases were intended to simulate scour (excavated piles) and earthquake damage (broken piles). Two topics are covered in the following paragraphs. First, the possibility of determining damaged substructure conditions through fieldobtainable flexibility TF plots is examined. Second, a more sophisticated approach involving modal curve-fitting and modal analyses is considered. The field data for the modal curve-fitting and modal analyses are from the simplest geometry of bent 12 (piles only).
The node points and geometry of bents 2 and 12 are shown in figures 57 and 58, respectively. The node points are the same for both bents, but bent 2 has the additional strip footing around the piles at ground level. Loads were applied to the bridge deck over the pile beams of the bents at nodes 2, 4 (center point), and 6 for the first two cases and at nodes 2 and 4 for the third case. (No load was applied to node 6 because of safety concerns; a load over the broken south piles might have led to the collapse of the bridge.)
Figure 57. Diagram. Node points and geometry of bent 2.
Figure 58. Diagram. Node points and geometry of bent 12.
If flexibility plots are to indicate damage directly in the field, it would have been expected to see a shift downward in frequency of the vibration modes and an associated increase in flexibility (inches/lbf, or m/N), which means a decrease in stiffness (lbf/inch, or N/m). The frequency of the vibration modes decreases because natural frequencies decrease as stiffness decreases. It should also be noted that the closer the loading point is to the member, the greater its response is to excitation. Presumably, the flexibility TF results will be more sensitive to a locally damaged member as well. Furthermore, the simplest mode to detect and interpret in the field is the fundamental vertical mode of vibration for bridges.
To examine this, flexibility plots are shown in figures 59, 60, and 61 for the case of thirdpoint loading of the bridge deck between each of the four piles. In figure 59, the loading is applied to the bridge deck at node 2, and the response is read from the vertical accelerometer on the underside of the pile cap at node 2. In figure 60, the loading is applied to node 4, and the response is read from the underside of the pile cap at node 4. Three flexibility plots are presented in figures 59 and 60. The plots denote the following pile cases: i—initial undamaged, sound piles; e—excavated piles; and n—the broken south pile.
In figure 61, the loading is applied to node 6 and the responses are read from the underside of the pile cap at nodes 6, 10, and 11. In figure 61, only the case of the undamaged pile is considered. The three flexibility plots are for the responses at the three different nodes: 6, 10, and 11.
Review of figures 59 and 60 indicates there is the expected reduction in the first and second mode frequencies (about 0.8 Hz) and an increase in flexibility between the initial and excavated pile cases. There is almost no change in frequency and a smaller increase in flexibility between the excavated and broken pile cases. Comparing the results from node 2 (figure 59), which is furthest from the excavated and damaged piles, with results from node 4 (figure 60) shows that the greater flexibility increase resulting from excavating piles and breaking a pile occurred closer to the damage, as expected.
Figure 59. Graph. Bent 12 flexibility TFs at node 2 for intact (i), excavated (e), and broken (n) piles.
Figure 60. Graph. Bent 12 flexibility TFs at node 4 for intact (i), excavated (e), and broken (n) piles.
Figure 61. Graph. Bent 12 flexibility TFs at nodes 6, 10, and 11 for the intact pile
Because the south-center and south piles are the members that were directly excavated and damaged, comparison of the flexibility results for the four piles should provide the best indication of whether field modal tests can directly indicate damaged substructure. These plots are shown in figures 62 through 65 for the cases of loading at the closest node to each pile and the vertical accelerometer response at either node 8, 9, 10, or 11, which are respectively the top receiver locations on each pile. (See figure 58 for bent 12 test geometry.) In the figure captions, the loading node, or node where the Vibroseis truck applies the force, is the denominator of the TF and the response node, which is the receiver location or node where the vertical accelerometer is read, is the numerator of the TF. Review of these figures shows that the south and north piles are the most flexible. Further review shows the first and second mode frequencies shift to a slightly lower frequency for the excavated versus initial sound pile cases, with no real shift in frequency among the excavated and broken pile cases. Of further interest is that the flexibility increases significantly between the initial, excavated, and broken cases for the south, south-center, and north-center piles, but for not the north pile, which is the farthest from the damage. The effect of the broken pile on increasing flexibility was likely somewhat muted; although the concrete was broken for the south pile, the four rebars were still intact.
Figure 62. Graph. Bent 12 flexibility TFs for node 8/node 2 for intact (i), excavated (e), and broken (n) piles.
Figure 63. Graph. Bent 12 flexibility TFs for node 9/node 4 for intact (i), excavated (e), and broken (n) piles.
Figure 64. Graph. Bent 12 flexibility TFs for node 10/node 4 for intact (i), excavated (e), and broken (n) piles.
Figure 65. Graph. Bent 12 flexibility TFs for node 11/node 6 for intact (i) and excavated (e) piles.
For bent 2, the flexibility results for the top loading and pile cap beam responses are shown in figures 66, 67, and 68. Each figure involves the loading and response at a single node: figure 66 for node 2, figure 67 for node 4, and figure 68 for node 6. The top loading to top vertical accelerometer results are shown in figures 69 through 72. In the captions to figures 69 through 72, the loading node, or node where the Vibroseis truck applies the force, is the denominator of the TF; the response node, which is the receiver location or node where the vertical accelerometer is read, is the numerator of the TF. Bent 2 flexibility plots showed similar behavior and trends as those discussed for bent 12. The frequency decrease after excavation was about 0.7 Hz. The effect of breaking the south pile resulted in a more pronounced increase in flexibility for bent 2 than for bent 12. The increase in flexibility was about 25 percent for the excavated case and 60 percent for the broken pile case as compared to the initial sound case.
The flexibility results show promise for being able to directly identify substructure damage if a baseline of the sound response of a bridge has been determined above all critical members. The damage will be indicated by a small decrease in frequency and an increase in flexibility (corresponding decrease in stiffness). This result is not surprising because it is predicted theoretically, and in a sense, a flexibility modal TF test is a dynamic load test. However, it is expected that more complicated substructures where loading may or may not be close to the damaged member would not show as much of an effect in the flexibility results. The drawbacks of this flexibility TF approach are the need to put sensors on critical members and to test before damage is caused. These actions are necessary to establish a basis for judging and identifying, in future tests, the extent of damage.
Figure 66. Graph. Bent 2 flexibility TFs at node 2 for intact (i), excavated (e), and broken (n) piles.
Figure 67. Graph. Bent 2 flexibility TFs at node 4 for intact (i), excavated (e), and broken (n) piles.
Figure 68. Graph. Bent 2 flexibility TFs at node 6 for intact (i) and excavated (e) piles.
Figure 69. Graph. Bent 2 flexibility TFs for node 8/node 2 for intact (i), excavated (e), and broken (n) piles.
Figure 70. Graph. Bent 2 flexibility TFs for node 9/node 2 for intact (i), excavated (e), and broken (n) piles.
Figure 71. Graph. Bent 2 flexibility TFs for node 10/node 6 for intact (i) and excavated (e) piles.
Figure 72. Graph. Bent 2 flexibility TFs for node 11/node 6 for intact (i) and excavated (e) piles.
Because bent 12 had the simplest test geometry with piles only, it was selected for detailed modal analysis with the PCMODAL software. Three vibration modes were identified as a result of the curve-fitting analyses: Mode 1 Vertical; Mode 2 Vertical; and Mode 2 Horizontal. Tests were performed for loading at nodes 2, 4, and 6, but only results of the center, symmetrical loading at node 4 and the loading at node 2 (farthest from the damaged south piles) are presented here. Results are presented only from node 4 and node 2 to evaluate differences between the sound, excavated, and broken south piles and the sound north piles. The following paragraphs discuss the results for each of these vibration modes
Modal Analysis Results for Mode 1 VerticalFor the first vertical mode analysis, results of the individual curve-fits of the modal vibration data for center loading at node 4 are shown in figure 73. Data are given for nodes 2, 4, 6, and 8 through 15. For each node, three sets of values are given for, first, frequency (Hz) and second, damping (percent). The top values at each node are the readings when all piles are sound (the sound pile case). The middle values are the readings when the south and south-central piles are excavated (the excavated pile case). The bottom values are the readings when the south pile is broken (the broken or broken south pile case). For center loading at node 4, the averages of the frequencies at nodes 2, 4, 6, and 8 through 15 for the first vertical mode analysis are 14.78 Hz for the sound pile case, 13.90 Hz for the excavated pile case, and 13.90 Hz for the broken pile case; thus, comparing the sound to the excavated first mode vertical frequencies shows a decrease of about 0.9 Hz. No significant change in frequency was noted between the excavated and the broken pile cases. Probably this is because the four vertical rebars in the south pile were not broken; only the concrete was broken.
For the first vertical mode analysis, results of the individual curve-fits of the modal vibration data for center loading at node 4 are shown in figure 73. Data are given for nodes 2, 4, 6, and 8 through 15. For each node, three sets of values are given for, first, frequency (Hz) and second, damping (percent). The top values at each node are the readings when all piles are sound (the sound pile case). The middle values are the readings when the south and south-central piles are excavated (the excavated pile case). The bottom values are the readings when the south pile is broken (the broken or broken south pile case). For center loading at node 4, the averages of the frequencies at nodes 2, 4, 6, and 8 through 15 for the first vertical mode analysis are 14.78 Hz for the sound pile case, 13.90 Hz for the excavated pile case, and 13.90 Hz for the broken pile case; thus, comparing the sound to the excavated first mode vertical frequencies shows a decrease of about 0.9 Hz. No significant change in frequency was noted between the excavated and the broken pile cases. Probably this is because the four vertical rebars in the south pile were not broken; only the concrete was broken.
The corresponding absolute magnitudes of the mode shape (normalized to node 4) and the phases (plus or minus in degrees relative to node 4) are shown in figure 74. The mode shape magnitudes are normalized to node 4, which is assigned a value of 1.0; the phase is also relative to node 4, which is at 0 degrees (in-phase). Review of figure 74 shows fairly symmetrical responses for the sound pile case but an asymmetrical response for the excavated and broken pile cases. Responses at nodes 11 and 15 for the fully excavated and then broken south pile cases show similar increased magnitudes and out-of-phase responses versus the sound pile case.
For the sound pile case, figures 75 and 76 allow comparisons between the effects of center loading at node 4 and loading at node 2. Figure 75 gives frequency (in hertz) and damping (in percent) for nodes 4 and 2 loading. Figure 76 gives magnitude (normalized to node 4) and phase (in degrees relative to node 4) for node 4 loading and node 2 loading. For both figures, the top values at each node are the results of center loading at node 4; the bottom values are the results of loading at node 2. The average frequencies and damping for the two loading points are similar—approximately 14.8 Hz for frequency and approximately 9 percent for damping. The largest difference between the two loading points is in the phase. Reflecting the asymmetric location of node 2, the phase resulting from node 2 loading shifts approximately 150 degrees from left to right (the north pile to the south pile).
Figure 73. Diagram. Bent 12, Mode 1 Vertical, node 4 (center) loading, frequency and damping.
Figure 74. Diagram. Bent 12, Mode 1 Vertical, node 4 (center) loading, magnitude and phase.
Figure 75. Diagram. Bent 12, Mode 1 Vertical, loading at nodes 2 and 4, frequency and damping.
Figure 76. Diagram. Bent 12, Mode 1 Vertical, loading at nodes 2 and 4, magnitude and phase.
Modal Analysis Results for Mode 2 VerticalFor the second vertical mode, figures 77 through 80 present data corresponding to figures 73 through 76 of the first vertical mode. The average frequencies for the second vertical mode with node 4, or center, loading are 21.88 Hz for the sound pile case, 21.20 Hz for the excavated pile case, and 20.77 Hz for the broken pile case; thus, for the second vertical mode, the excavated pile case decreases about 0.7 Hz from the sound pile case. The decrease in frequency resulting from breaking the pile is about 0.4 Hz. This smaller decrease in frequency for the excavated-to-broken pile case as compared to the sound-to-excavated pile case likely results because the four vertical rebars in the south pile were not broken; only the concrete was broken.
The corresponding relative absolute magnitude of the mode shape (normalized to node 4) and the phase (plus or minus in degrees relative to node 4) are shown in figure 78. The mode shape magnitudes are normalized to node 4, which is assigned a value of 1.0, and the phase is also relative to node 4, which is at 0 degrees (in-phase). Figure 78 shows asymmetrical responses for the sound, excavated, and broken pile cases.
For the sound pile case, figures 79 and 80 allow comparisons between the effects of center loading at node 4 and loading at node 2. Figure 79 gives frequency (in hertz) and damping (in percent) for nodes 4 and 2 loading. Figure 80 gives magnitude (normalized to node 4) and phase (in degrees relative to node 4) for nodes 4 and 2 loading. In both figures, the top values at each node are the results of center loading at node 4, and the bottom values are the results of loading at node 2. The largest phase difference is found from one edge pile to the other in node 2 loading, caused by the asymmetric nature of node 2 loading.
Figure 77. Diagram. Bent 12, Mode 2 Vertical, node 4 (center) loading, frequency and damping.
Figure 78. Diagram. Bent 12, Mode 2 Vertical, node 4 (center) loading, magnitude and phase.
Figure 79. Diagram. Bent 12, Mode 2 Vertical, loading at nodes 2 and 4, frequency and damping.
Figure 80. Diagram. Bent 12, Mode 2 Vertical, loading at nodes 2 and 4, magnitude and phase.
Modal Analysis Results for Mode 2 HorizontalFigures 81 through 84 present data for the second horizontal mode, corresponding to figures 73 through 76 of the first vertical mode. Second horizontal mode data are calculated from horizontal accelerometers. The average frequencies for the second horizontal mode with node 4, or center, loading are 21.84 Hz for the sound pile case, 20.66 Hz for the excavated pile case, and 20.63 Hz for the broken pile case; thus, for the second horizontal mode, the excavated pile case decreases about 1.2 Hz from the sound pile case. The decrease in frequency resulting from breaking the pile is about 0.03 Hz. This smaller decrease in frequency from the excavated-to-broken pile case as compared to the sound-to-excavated pile case likely results because the four vertical rebars in the south pile were not broken; only the concrete was broken.
The corresponding relative absolute magnitude of the mode shape (normalized to node 4) and the phase (plus or minus in degrees relative to node 4) are presented in figure 82. The mode shape magnitudes are normalized to node 4, which is assigned a value of 1.0, and the phase is also relative to node 4, which is at 0 degrees (in-phase). Figure 78 shows asymmetrical responses for the sound, excavated, and broken pile cases.
For the sound pile case, figures 83 and 84 allow comparisons between the effects of center loading at node 4 and loading at node 2. Figure 83 gives frequency (in hertz) and damping (in percent) for nodes 4 and 2 loading. Figure 84 gives magnitude (normalized to node 4) and phase (in degrees relative to node 4) for nodes 4 and 2 loading. For both figures, the top values at each node are the results of center loading at node 4, and the bottom values are the results of loading at node 2. The largest phase difference is found from one edge pile to the other in node 2 loading, resulting from the asymmetric nature of node 2 loading.
Summary of Modal Curve-Fitting Analysis Results
The clearest indication of damage was provided by the decrease in frequency of the first and second vibration modes among the cases of sound, excavated, and broken piles. Changes in magnitude and phase from symmetrical to asymmetrical also indicated damage in some cases. The other analysis result of damping did not prove to be a damage indicator. Considering the additional effort required to perform the PCMODAL curvefits, and the fact that the modal frequency peaks are apparent in the field flexibility TFs, the extra effort required to perform the curve-fits did not result in that much additional information from a substructure damage perspective.
Figure 81. Diagram. Bent 12, Mode 2 Horizontal, node 4 (center) loading, frequency and damping.
Figure 82. Diagram. Bent 12, Mode 2 Horizontal, node 4 (center) loading, magnitude and phase.
Figure 83. Diagram. Bent 12, Mode 2 Horizontal, loading at nodes 2 and 4, frequency and damping.
Figure 84. Diagram. Bent 12, Mode 2 Horizontal, loading at nodes 2 and 4, magnitude and phase.
These two bridges were selected for this research because they were of similar design in similar soil conditions, except that the Woodville Road Bridge had a footing foundation, while the Old Reliance Road Bridge had a similar size pile cap footing on top of steel BP (bearing pile) piles. The modal analysis nodes and accelerometer and force excitation locations are shown in figures 34 and 39 in chapter 4 for the Woodville and Old Reliance Bridges, respectively.
A hypothesis is that different resonant frequencies and modal TF responses will be measured for bridges with shallow versus deep foundation systems even when the bridges are otherwise virtually identical. To examine this hypothesis, figures 85 and 86 present flexibility TF results for the Woodville and Old Reliance bridges. For each bridge, the Vibroseis force was applied directly over the top vertical accelerometer on each of the two bridge columns. For figure 85, the Vibroseis force was applied at node 17, and the response reading was taken at the vertical accelerometer at node 9. In figure 86, the Vibroseis force was applied at node 18, and the response reading was taken at the vertical accelerometer at node 10. The figures show that the flexibility TFs are similar for loading at nodes 17 and 18 for each bridge itself, but very different between the two bridges.
Thus, an initial conclusion might be that modal testing can differentiate between shallow versus deep foundations for otherwise similar bridges. However, the first vertical mode resonant peak, 9 Hz, for Old Reliance with the steel piles is not greater than the first vertical mode resonant peak, 10 Hz, for Woodville. Therefore, at least in the case of the Old Reliance and Woodville bridges, contrary to expectations, steel piles plus pile cap do not result in greater stiffness than footing alone. Moreover, the flexibility, and inversely the stiffness magnitudes, is similar for the two bridges. Finally, the first three resonant peaks for Old Reliance are all at lower frequencies than for Woodville. In view of these facts, modal testing might have limited capability of uniquely and clearly determining shallow versus deep foundations, unless otherwise identical bridge structures are situated in similar soils. Furthermore, at least one of the foundations tested probably should have a known shallow or deep foundation system to serve as the basis against which unknown foundation systems can be judged. Finally, modal testing to determine unknown depths of foundations for scour safety evaluation is unlikely to be successful.
Figure 85. Graph. Woodville and Old Reliance Bridges, flexibility TFs, node 9/node 17. 96
Figure 86. Graph. Woodville and Old Reliance Bridges, flexibility TFs, node 9/node 18 97