Enhanced Abutment Scour Studies for Compound Channels
CHAPTER 2. LITERATURE REVIEW
In this chapter, the literature on compound-channel hydraulics and both clear-water and live-bed bridge abutment scour is reviewed. The connection between these two topics is an important contribution of this research, so a brief summary of previous research done on each topic is given.
COMPOUND-CHANNEL HYDRAULICS
A compound channel consists of a main channel, which carries base flow and frequently occurring runoff up to bank-full flow conditions, and a floodplain on one or both sides that carries overbank flow during times of flooding. Both channel roughness and the depth of the flow, and hence flow-channel geometry, can be drastically different in the main channel and the floodplains. In general, floodplain flows are relatively shallow, with slow-moving flow adjacent to faster-moving flow in the main channel, which results in a complex interaction that includes momentum transfer between the main-channel and floodplain flows. This phenomenon is more pronounced in the immediate interface region between the main channel and the floodplain, where there exists a strong transverse gradient of the longitudinal velocity. Because of the velocity gradient and anisotropy of the turbulence, there are vortexes rotating about both the vertical and horizontal axes along the main channel/floodplain interface.(25-27) These vortexes are responsible for the transfer of water mass, momentum, and species concentration from the main-channel flow into the floodplain flow. The result is that for a given stage, the total flow in the compound channel is less than what would be calculated as the sum of the flows in the main channel and the floodplain assuming no interaction.(25)
Several attempts have been made at quantifying the momentum transfer at the main channel/floodplain interface using the concepts of imaginary interfaces that are included or excluded as the wetted perimeter and defined at varying locations with or without the consideration of an apparent shear stress acting on the interface (see references 17 and 28 through 31). The resulting distribution of the discharge between the main channel and the floodplain caused by the interaction at the interface must be correctly predicted in water-surface profile computations and in calculations of approach floodplain velocities for the prediction of abutment scour.
The current version of WSPRO (as well as the Hydrologic Engineering Center River Analysis System (HECRAS) divides the compound channel into subsections using a vertical interface between the main channel and the floodplain, but neglects any contribution of the interface to the wetted perimeter of the subsections. In effect, the interaction between the main channel and the floodplain is neglected because this procedure is equivalent to assuming no shear stress at the interface. Wright and Carstens(28) proposed that the interface be included in the wetted perimeter of the main channel, and that a shear force equal to the mean boundary shear stress in the main channel be applied to the floodplain interface. Yen and Overton,(29) on the other hand, suggested the idea of choosing an interface on which shear stress was, in fact, nearly zero. This led to several methods of choosing an interface, including a diagonal interface from the top of the main-channel bank to the channel centerline at the free surface, and a horizontal interface from bank to bank of the main channel. Wormleaton and Hadjipanos(32) compared the accuracy of the vertical, diagonal, and horizontal interfaces in predicting the separate main-channel and floodplain discharges measured in an experimental 1.21-meter (m) flume, having a fixed ratio of floodplain width to main-channel half-width of 3.2.(30) The wetted perimeter of the interface was either fully included or fully excluded in the calculation of the hydraulic radius of the main channel. The results showed that even though a particular choice of interface might provide a satisfactory estimate of total channel discharge, nearly all of the choices tended to overpredict the separate main-channel discharge and underpredict the floodplain discharge. It was further shown that these errors were magnified in the calculation of the kinetic energy flux correction coefficients used in water-surface profile computations.
In a modification of the earlier method, Wormleaton and Merrett(17) applied a correction factor called the 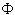 index to the main-channel and floodplain discharges calculated by a particular choice of interface (vertical, diagonal, or horizontal), which was either included or excluded from the wetted perimeter. The index to the main-channel and floodplain discharges calculated by a particular choice of interface (vertical, diagonal, or horizontal), which was either included or excluded from the wetted perimeter. The 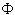 index was defined as the ratio of the boundary shear force to the streamwise component of fluid weight(33) as a measure of apparent shear force. If the index was defined as the ratio of the boundary shear force to the streamwise component of fluid weight(33) as a measure of apparent shear force. If the 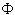 index is less than unity on the main-channel interface, for example, then the apparent shear force resulting from the main channel/floodplain interaction resists the fluid motion in the main channel. This modified method was applied to the experimental results from the very large compound channel at Hydraulics Research, Wallingford Ltd. (Wallingford, Oxfordshire, U.K.). The channel is 56 m long by 10 m wide, with a total flow capacity of 1.1 cubic meters per second (m3/s). In the experiments, the ratio of the floodplain width to the main-channel half-width varied from 1 to 5.5, and the ratio of the relative floodplain depth to the main-channel depth varied from 0.05 to 0.50. The calculated main-channel and floodplain discharges, when multiplied by the square root of the index is less than unity on the main-channel interface, for example, then the apparent shear force resulting from the main channel/floodplain interaction resists the fluid motion in the main channel. This modified method was applied to the experimental results from the very large compound channel at Hydraulics Research, Wallingford Ltd. (Wallingford, Oxfordshire, U.K.). The channel is 56 m long by 10 m wide, with a total flow capacity of 1.1 cubic meters per second (m3/s). In the experiments, the ratio of the floodplain width to the main-channel half-width varied from 1 to 5.5, and the ratio of the relative floodplain depth to the main-channel depth varied from 0.05 to 0.50. The calculated main-channel and floodplain discharges, when multiplied by the square root of the 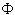 index for each subsection, showed considerable improvement when compared to the measured discharges, regardless of the choice of interface. The difficulty of the method is in the prediction of the F index. A regression equation was proposed for this purpose, with the index for each subsection, showed considerable improvement when compared to the measured discharges, regardless of the choice of interface. The difficulty of the method is in the prediction of the F index. A regression equation was proposed for this purpose, with the 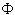 index given as a function of the velocity difference between the main channel and the floodplain, the floodplain depth, and the floodplain width. The regression equation is limited to the range of experimental variables observed in the laboratory. index given as a function of the velocity difference between the main channel and the floodplain, the floodplain depth, and the floodplain width. The regression equation is limited to the range of experimental variables observed in the laboratory.
Ackers(34) has also proposed a discharge calculation method for compound channels using the Wallingford data. He suggested a discharge adjustment factor that depends on coherence, which was defined as the ratio of the full-channel conveyance (with the channel treated as a single unit with perimeter weighting of boundary friction factors) to the total conveyance calculated by summing the subsection conveyances. Four different zones were defined as a function of the relative depth (the ratio of the floodplain to the total depth), with a different empirical equation for the discharge adjustment for each zone.
Myers and Lyness(18) have proposed a two-step method for predicting the distribution of flow between the main channel and the floodplains for a compound channel in overbank flow. First, they propose a power relationship between the ratio of the total discharge to the bank-full discharge and the ratio of the total depth to the bank-full depth. They show that from both laboratory and field data that such a relationship is independent of bed slope and scale, and is dependent only on geometry for similar roughnesses in the main channel and the floodplain. Second, they divide the total discharge obtained from the first step into the main-channel and floodplain components, assuming that the ratio of main channel-to-floodplain discharge is an inverse power function of the ratio of the total depth to the floodplain depth. In this case, the relationship was not shown to be universal for different geometry, scale, and roughness. This approach is, in reality, a conveyance weighting method that does not account explicitly for the interaction between the main channel and the floodplain.
The variation of Manning's n with depth further complicates the problem of water-surface profile computations and velocity predictions in compound channels.(16,35) In addition, the existence of multiple critical depths can lead to difficulties in both computing and interpreting water-surface profiles. Blalock and Sturm(36) and Chaudhry and Bhallamudi(37) have suggested the use of a compound-channel Froude number in computational procedures for determining multiple critical depths in compound channels. Blalock and Sturm(36) used the energy equation, while Chaudhry and Bhallamudi(37) employed the momentum equation to define a compound-channel Froude number. Blalock and Sturm(38) showed from their experimental results that the energy and momentum approaches resulted in the same values for critical depth. Yuen and Knight(39) have confirmed from their experimental results that the compound-channel Froude number suggested by Blalock and Sturm(36) gives values for critical depth that are reasonably close to the measured values. Sturm and Sadiq(40) have demonstrated the usefulness of their compound-channel Froude number for computing and interpreting water-surface profiles in compound channels having two values for critical depth: one in overbank flow and one in main-channel flow alone.
Numerical analysis of flow characteristics in compound open channels, particularly for the case of an obstruction, such as a bridge abutment on the floodplain, have received rather limited attention in comparison to experimental studies. Most numerical models have been developed for the parabolic flow situation, which has a predominantly longitudinal flow direction with no reverse flow (e.g., uniform or gradually varied flow). There are, however, a few studies applied to an elliptical flow situation (with flow separation and recirculation allowed), but these are applicable only to a simple rectangular channel. The effect of compound-channel hydraulics on flow characteristics in the region close to obstructions is in need of further investigation.
One- and two-dimensional numerical models have been used to compute complex flow fields, such as those in compound open-channel flow. Some of the two-dimensional models(41-42) are applicable to the boundary-layer type of flow, in which the flow can be described by a set of differential equations that are parabolic in the longitudinal (flow) direction.(43) The flow situation in a compound open channel can become even more complex if structures, such as bridge piers or abutments, are placed in the floodplain. In this situation, at least for the regions near the structure, the parabolic flow assumption becomes invalid. This is because there is no longer any predominant flow direction in the region close to the structure. The flow will separate downstream from the structure and a recirculating region with a reverse flow and an adverse pressure gradient will be formed that violates the parabolic flow assumption. In addition, the water-surface elevation no longer varies only in the streamwise coordinate. Because of the presence of the obstruction, there exists a rapid variation in water depth near a bridge abutment, both in the longitudinal and transverse directions. The water-surface elevation upstream from the abutment increases and forms a backwater profile. These flow characteristics are associated with an elliptical flow field that has additional complexity because of the intercoupling of the velocity and pressure (water depth) fields.
Three-dimensional models have been developed and applied primarily to the case of uniform flow in a compound channel.(44-46) These models allow the simulation of turbulence-driven secondary motion in the transverse plane of a compound open channel, as well as the Reynolds' turbulent shear stresses. Experimental measurements by Tominaga and Nezu(27) using a fiber-optic laser Doppler anemometer showed a pair of longitudinal vortexes at the main channel/floodplain interface, with an inclined secondary current directed from the intersection of the main channel and the floodplain bed toward the free surface. The numerical model of Naot, et al.,(46) was able to reproduce this behavior. The numerical results of Krishnappen and Lau(44) using an algebraic stress model demonstrated good agreement with measured divisions of flow between the main channel and the floodplain using data from Knight and Demetriou(31) and Wormleaton, et al.(30) Pezzinga's nonlinear k-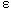 turbulence model(47) was used to compare the effects of various main channel/floodplain subdivisions (vertical, horizontal, diagonal, and bisector) on computed subsection discharges. The diagonal interface and the interface formed by the bisector of the corner angle between the main channel and the floodplain gave the best results for both the discharge distribution and the kinetic energy correction coefficients. turbulence model(47) was used to compare the effects of various main channel/floodplain subdivisions (vertical, horizontal, diagonal, and bisector) on computed subsection discharges. The diagonal interface and the interface formed by the bisector of the corner angle between the main channel and the floodplain gave the best results for both the discharge distribution and the kinetic energy correction coefficients.
In this research, the velocity field is sought in the bridge approach section and near the face of a bridge abutment that terminates on the floodplain where the width-to-depth ratio of the flow is large and the vertical mixing is strong. Under these conditions, the velocity field can be computed adequately from the depth-averaged equations of motion, including the regions of adverse pressure gradient and flow separation, especially if a k-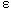 turbulence closure model is used.(42, 48-53) Biglari(54) and Biglari and Sturm(55) applied a depth-averaged k- turbulence closure model is used.(42, 48-53) Biglari(54) and Biglari and Sturm(55) applied a depth-averaged k-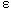 turbulence model in elliptical form to the problem of flow around a bridge abutment on a floodplain. turbulence model in elliptical form to the problem of flow around a bridge abutment on a floodplain.
ABUTMENT SCOUR
Early experimental research on scour around abutments was, in some cases, motivated by a desire to predict local scour around spur dikes; however, the results of these studies have been applied to the problem of abutment scour. Ahmed(56) proposed a scour-depth relationship for spur dikes that used the "flow intensity," or flow rate per unit width in the contracted section, as the independent variable in agreement with previous regime formulas. Laursen and Toch(57) argued that in live-bed scour around bridge piers and abutments, the approach flow velocity has no effect on equilibrium scour depth because increases in velocity not only increase the sediment transport into the scour hole from upstream, but also increase the strength of the vortex responsible for transporting sediment out of the scour hole. This argument applies in cases where there is appreciable sediment in bed-load transport. If the sediments in transport are fine and mostly carried as suspended loads, the assumptions of live-bed scour behavior may not be appropriate.
Garde, et al.,(58) studied experimentally the scour around spur dikes in a rectangular channel and related the nondimensional ratio of scour depth to approach depth, ds/y1, to the approach Froude number, F1, and to the geometric contraction ratio, m, which is defined as the ratio of the width of the contracted opening to the approach channel width. In addition, the coefficient of proportionality and the exponent in the Froude number were found to depend on sediment size. Some sediment transport occurred in the approach flow for these experiments.
Liu, et al.,(59) considered the scour around bridge constrictions caused by abutment models in 1.2-m- (4-foot (ft)-) wide and 2.4-m- (8-ft-) wide flumes. Their experimental results for live-bed scour indicated that the ratio of the abutment length to the normal depth, La/y0, and the uniform-flow Froude number were the most important influences on the dimensionless scour depth. The normal depth was determined with sediment in equilibrium transport before the abutment was placed in the flume. They proposed an equation for equilibrium live-bed scour depth ds:
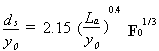 | (1) |
where La = abutment length (vertical wall), y0 = normal depth of flow, and F0 = Froude number of uniform flow. The experimental values of La/y0 varied from approximately 1 to 10, and the Froude numbers varied from 0.3 to 1.2. In a separate series of experiments, clear-water scour was studied by pre-forming the scour hole and determining the flow conditions necessary to just initiate sediment motion in the bottom of the scour hole. In this case, the dimensionless clear-water scour depth was found to be directly proportional to F0/m, where F0 = uniform-flow Froude number and m = geometric contraction ratio defined by the ratio of the constricted channel width to the approach channel width. The coefficient of proportionality was approximately 12.5.
Gill(60) argued from his experimental results on the scour of sand beds around spur dikes that the distinction between clear-water and live-bed scour is unimportant for the design determination of maximum scour depth. He proposed that the maximum scour depth be based on the geometric contraction ratio, m, and on the ratio of the sediment size to the flow depth based on both clear-water and live-bed scour experiments having a duration of 6 hours. His proposed equation is:
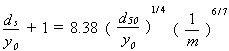 | (2) |
where y0 = initial uniform-flow depth, d50 = median sediment grain size, and m = geometric contraction ratio given by the ratio of the contracted width to the full channel width.
Laursen(61) developed scour-depth relationships for bridge abutments that were based on treating the abutment as a limiting case of scour through a long flow constriction. Live-bed scour was considered to be a function only of the ratio of the abutment length to the approach flow depth, La/y1, and the ratio of the discharge per unit width in the overbank flow region to the discharge per unit width in the scour region. The scour region was assumed to have a constant width of 2.75 times the scour depth. In a subsequent analysis of relief-bridge scour,(13) which was considered to be a case of clear-water scour, the same approach was taken in relating the abutment scour to that which would take place in a long constriction. The contracted width was assumed to be equal to a scour-hole width of 2.75 times the scour-hole depth. This assumption resulted in an implicit relationship for scour depth:
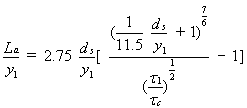 | (3) |
where La = abutment length, y1 = approach flow depth, ds = maximum scour depth, 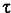 1 = bed shear stress in the approach flow, and 1 = bed shear stress in the approach flow, and 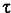 c = critical shear stress for initiation of sediment motion. c = critical shear stress for initiation of sediment motion.
In a comprehensive experimental study of the effect of flow depth on clear-water scour around abutments, Tey(62) held constant the ratio of approach shear stress to critical shear stress, 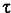 1/ 1/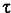 c, at a value of 0.90, while varying the flow depth and the abutment length and shape. The results showed an increasing scour depth with increasing flow depth, but at a decreasing rate as the depth became larger. The length of the abutment obstructing the approach flow and the abutment shape were also found to influence the scour depth. Longer abutments and blunter abutment shapes caused deeper scour holes. c, at a value of 0.90, while varying the flow depth and the abutment length and shape. The results showed an increasing scour depth with increasing flow depth, but at a decreasing rate as the depth became larger. The length of the abutment obstructing the approach flow and the abutment shape were also found to influence the scour depth. Longer abutments and blunter abutment shapes caused deeper scour holes.
Froehlich(12) completed a regression analysis of 164 laboratory experiments from 11 separate sources on clear-water scour around abutments or spur dikes. His proposed regression equation is:
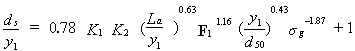 | (4) |
where ds = scour depth; y1 = approach flow depth, K1 = geometric shape factor for abutment and embankment, K2 = embankment skewness factor, La = abutment length, F1 = approach Froude number, d50 = median sediment grain size, and 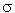 g = geometric standard deviation of the sediment size distribution. Froehlich further proposed that a factor of safety (FS) of 1 should be added to the value of ds/y1 obtained from the regression analysis, and it has been included on the right-hand side of equation 4. Currently, HEC-18 recommends the live-bed scour equation obtained by Froehlich's regression analysis of other investigators' results for this case because equation 4 seems to greatly overestimate abutment scour. The live-bed scour equation is: g = geometric standard deviation of the sediment size distribution. Froehlich further proposed that a factor of safety (FS) of 1 should be added to the value of ds/y1 obtained from the regression analysis, and it has been included on the right-hand side of equation 4. Currently, HEC-18 recommends the live-bed scour equation obtained by Froehlich's regression analysis of other investigators' results for this case because equation 4 seems to greatly overestimate abutment scour. The live-bed scour equation is:
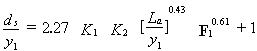 | (5) |
with FS = 1 included on the right-hand side. In both equations 4 and 5, Froehlich calculated the approach Froude number based on an average velocity and depth in the obstructed area of the approach-flow cross section. While this worked well for the experimental results that he used, which were for rectangular channels, it is not clear what the representative approach velocity and depth should be in natural channels subject to overbank flow.
Melville(14) summarized a large number of experimental results on clear-water abutment scour
from rectangular channels and proposed a design method for maximum scour depth that depends on empirical correction factors for flow intensity, abutment shape, alignment, and length. He classified abutments as short (La/y1 < 1) or long (La/y1 > 25), and suggested that the maximum clear-water scour depth was 2La for the former case and 10y1 for the latter case. For intermediate abutment lengths, the equilibrium clear-water scour depth was given as:
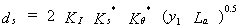 | (6) |
where KI = flow-intensity factor (V1/Vc), V1 = approach velocity, Vc = critical velocity for initiation of sediment motion, Ks* = abutment shape factor, K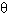 * = abutment alignment factor, y1 = approach flow depth, and La = abutment length. * = abutment alignment factor, y1 = approach flow depth, and La = abutment length.
Subsequently, Melville(24) suggested that the same methodology could be applied to both bridge piers and abutments, albeit with slightly different equations. He further showed that sediment size effects appear only in the flow-intensity factor for clear-water scour as long as La/d50 > 25. Abutment shape effects were reported to be important only for shorter abutments (i.e., Ks* = 1.0 for vertical-wall abutments; 0.75 for wingwall abutments; and from 0.45 to 0.60 for spill-through abutments), depending on the sideslope, but only if La/y1 = 10. For long abutments (La/y1 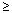 25), Ks* 25), Ks* 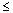 1.0 with a linear relationship between Ks* and La/y1 for the intermediate range of La/y1 = 10 to 25. It must be emphasized that all of Melville's integrated abutment/pier results(24) are considered to be for abutments that are significantly shorter than the floodplain width itself so that flow contraction effects are not important. 1.0 with a linear relationship between Ks* and La/y1 for the intermediate range of La/y1 = 10 to 25. It must be emphasized that all of Melville's integrated abutment/pier results(24) are considered to be for abutments that are significantly shorter than the floodplain width itself so that flow contraction effects are not important.
Live-bed abutment scour results were also summarized by Melville(24) for short abutments using Dongol's data.(63) Under clear-water conditions (V1 < Vc), the scour depth increased to a maximum at V1/Vc = 1. For live-bed conditions (V1 > Vc), the scour depth decreased slightly as V1 increased, but then increased again to a value equal to the maximum clear-water scour. Piers showed the same behavior under live-bed conditions.
Melville and Ettema(64) and Melville(15) reported research results on abutment scour in a compound channel, but for the case of an abutment terminating in the main channel rather than on the floodplain. It was proposed that the scour depth in this instance could be calculated as the scour in an equivalent rectangular channel of the same width and with a depth equal to the main-channel depth by multiplying equation 6 by a geometric factor given as:
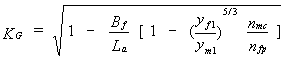 | (7) |
where La = abutment length extending into main channel, Bf = width of floodplain, yf1 = depth of flow in floodplain, ym1 = depth of flow in main channel, nmc = Manning's n in main channel, and nfp = Manning's n in floodplain.
Sturm and Janjua(19-20) conducted a series of experiments in a compound channel consisting of a main channel and a floodplain with the abutment terminating in the floodplain, and showed that the approach flow distribution and its readjustment by the abutment in the contracted section are important factors that should be included in equations for predicting scour depth in natural channels. On the basis of a dimensional analysis and the application of Laursen's(13) analysis of relief bridge scour in a long contraction to compound channels, they proposed a relationship given as:
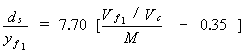 | (8) |
where ds = equilibrium scour depth, yf1 = approach floodplain flow depth, Vf1 = approach floodplain flow velocity, Vc = critical velocity, and M = discharge contraction ratio defined as the fraction of the total discharge in the bridge approach section over a width determined by extending the bridge opening upstream to the approach section. Melville(15) postulated that these experimental results gave smaller scour depths than his equation for intermediate-length abutments because the experiments had not reached equilibrium; however, subsequent experimental results given by Sturm and Sadiq(23) for a different compound-channel geometry, but at much longer scour durations, were similar to those of Sturm and Janjua.(20)
Young, et al.,(65) developed a regression equation for clear-water as well as live-bed abutment scour using the calculated contraction scour as a nondimensionalizing parameter for the abutment scour depth. More recently, Young, et al.,(66) suggested an abutment scour equation:
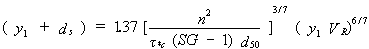 | (9) |
where y1 = approach depth in meters, ds = scour depth in meters, n = Manning's resistance factor, 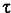 *c = critical value of Shields' parameter, SG = specific gravity of sediment, d50 = median particle size in meters, and VR = resultant velocity adjacent to the tip of the abutment in meters per second. The resultant velocity is calculated from Vx/cos *c = critical value of Shields' parameter, SG = specific gravity of sediment, d50 = median particle size in meters, and VR = resultant velocity adjacent to the tip of the abutment in meters per second. The resultant velocity is calculated from Vx/cos 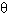 , where Vx = mean contraction velocity from continuity and , where Vx = mean contraction velocity from continuity and 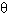 = 69.85 (a/A)0.2425 (with a coefficient of determination of r2 = 0.54), where a = blocked flow area by the abutment and A = total unobstructed flow area including the main channel to the median flow bisector. Equation 9 is not dimensionally homogeneous and is meant for the International System of Units (SI), known as the metric system. It was tested on an experiment by Lim(67) with a very short abutment (La/y1 = 1) and showed good agreement for this case. = 69.85 (a/A)0.2425 (with a coefficient of determination of r2 = 0.54), where a = blocked flow area by the abutment and A = total unobstructed flow area including the main channel to the median flow bisector. Equation 9 is not dimensionally homogeneous and is meant for the International System of Units (SI), known as the metric system. It was tested on an experiment by Lim(67) with a very short abutment (La/y1 = 1) and showed good agreement for this case.
Chang(68) has applied Laursen's long contraction theory to both clear-water and live-bed scour. He suggested a velocity adjustment factor, kv, to account for the nonuniform velocity distribution in the contracted section, and a spiral-flow adjustment factor, kf, at the abutment toe that depends on the approach Froude number. The value of kv was based on potential flow theory, and kf was determined from a collection of abutment scour experiments in rectangular laboratory flumes.(69) The resulting scour equation was:
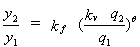 | (10) |
where y2 = flow depth in contracted section after scour, y1 = approach flow depth, q1 = flow rate per unit width in approach section, q2 = flow rate per unit width in contracted section, and 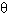 = 0.857 for clear-water scour. The value of kv = 0.8 (q1/q2)1.5 + 1 and kf = 0.1 + 4.5F1 for clear-water scour, while kf = 0.35 + 3.2F1 for live-bed scour. The approach Froude number F1 = V1/(gy1)0.5. Equation 10 does not include the effect of sediment size on clear-water abutment scour. It has since been modified(70) to the form: = 0.857 for clear-water scour. The value of kv = 0.8 (q1/q2)1.5 + 1 and kf = 0.1 + 4.5F1 for clear-water scour, while kf = 0.35 + 3.2F1 for live-bed scour. The approach Froude number F1 = V1/(gy1)0.5. Equation 10 does not include the effect of sediment size on clear-water abutment scour. It has since been modified(70) to the form:
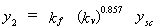 | (11) |
where y2 = total depth of flow at the abutment including scour depth, ysc = total depth of flow including the contraction scour depth only, and kf and kv are unchanged from the previous formulation. The value of ysc is calculated from q2/Vc, where q2 = unit discharge at the contraction and Vc = critical velocity obtained from the expressions given by Neill.(71) The evaluation of q2 is unclear for the case of the contracted section having a compound section with a variable q2 across the cross section.
Lim(67) has derived an equation for predicting clear-water abutment scour:
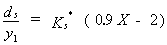 | (12) |
where ds = scour depth, y1 = approach flow depth, Ks* = abutment shape factor, and X is expressed as:
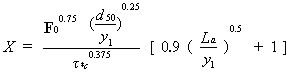 | (13) |
where F0 = approach value of the densimetric grain Froude number, 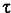 *c = critical value of Shields' parameter, d50 = median grain size, and La = abutment length. Equations 12 and 13 are derived on the basis of satisfying continuity before and after scour, evaluating the velocity before and after scour in the contracted section from a power law with an exponent of 1/3, and using an expression for the shear velocity in the contracted expression proposed by Rajaratnam and Nwachuku.(72) The latter expression is limited to values of La/y1 *c = critical value of Shields' parameter, d50 = median grain size, and La = abutment length. Equations 12 and 13 are derived on the basis of satisfying continuity before and after scour, evaluating the velocity before and after scour in the contracted section from a power law with an exponent of 1/3, and using an expression for the shear velocity in the contracted expression proposed by Rajaratnam and Nwachuku.(72) The latter expression is limited to values of La/y1 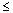 1. Lim tested equations 12 and 13 on his own abutment scour data as well as on data from Dongol,(63) Rajaratnam,(73) and Liu, et al.,(59) that were, for the most part, limited to very short abutments with La/y1 1. Lim tested equations 12 and 13 on his own abutment scour data as well as on data from Dongol,(63) Rajaratnam,(73) and Liu, et al.,(59) that were, for the most part, limited to very short abutments with La/y1 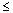 1. 1.
Lim(74) has also proposed an abutment scour-prediction equation for live-bed scour. He assumed that the sediment transport in a strip of the approach section, with a width equal to the abutment length plus the scour-hole width, is carried completely through the scour-hole width in the contracted section. The scour-hole width is estimated as ds/tan 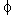 , where , where 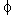 = angle of repose of the bed material. Then, by using a sediment transport relationship similar to that of Meyer-Peter and Muller (Julien(75)), and by making the same assumptions as for his clear-water scour equation, the resulting equation given by Lim for live-bed scour is: = angle of repose of the bed material. Then, by using a sediment transport relationship similar to that of Meyer-Peter and Muller (Julien(75)), and by making the same assumptions as for his clear-water scour equation, the resulting equation given by Lim for live-bed scour is:
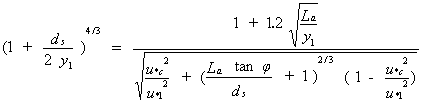 | (14) |
where u*1 = approach value of shear velocity and u*c = critical value of shear velocity. When u*c/u*1 > 1, the term [1 - (u*c/u*1)2] is taken as equal to zero and equation 14 reduces to the clear-water scour case according to Lim. This equation still suffers from the dependence on abutment length and the limitation on the expression for shear stress for very short abutments as pointed out for the clear-water scour case by Richardson.(76)
An equation in Highways in the River Environment(77) was developed from the U.S. Army Corps of Engineers' field data for scour at the end of spur dikes on the Mississippi River. It is recommended in HEC-18 for predicting scour around long abutments with La/y1 > 25. The equation is:
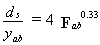 | (15) |
where yab = depth of flow at the abutment and Fab = Froude number based on the velocity and depth adjacent to the abutment.
TIME DEVELOPMENT OF SCOUR
Within the context of this report, the time to equilibrium of the scour process is important in establishing the necessary duration of the experiments. In addition, as discussed in a previous report by the author,(78) one consequence of developing scour equations from laboratory data for the equilibrium condition is that in the field case for small watersheds, the duration of the design discharge may be considerably shorter than the time to reach equilibrium. The result is an overestimate of field scour for a given design event.
Time development of scour was first studied in Laursen's pioneering research on scour by jets.(79) Laursen argued that clear-water scour is an asymptotic process in which scour depth increases linearly with the logarithm of time. Theoretically, equilibrium would never be reached under these circumstances except at infinity. Thus, as a practical matter, some limiting depth of scour is determined in laboratory experiments during long durations when the rate of change in the scour depth is very small. Most of the research on the time development of scour has been done for situations other than abutment scour (e.g., jet scour, pier scour, or hydraulic structure scour). Carstens(80) has proposed a general method for determining the time development of scour by combining: (1) the sediment continuity equation, (2) a sediment pickup function, and (3) an assumed scour-hole shape that is geometrically similar at all times. He showed that the simultaneous solution of these three equations agreed with Laursen's experimental results for the time development of scour from a horizontal jet, although the experimental data were used to develop the sediment pickup function.
Raudkivi and Ettema(81) showed from their experimental results on the development of pier scour that dimensionless scour depth (ds/b) was linearly proportional to the logarithm of td50/b3, where ds = scour depth, b = cylindrical pier diameter, d50 = median sediment grain diameter, and t = time. Yanmaz and Altinbilek(82) applied Carstens' method to the problem of time development of scour around bridge piers. The resulting differential equation was solved numerically to obtain a curve of ds/b as a function of dimensionless time:
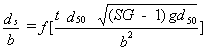 | (16) |
where SG = specific gravity of the sediment. The function was linear with the logarithm of dimensionless time up to a large value of time after which it leveled off in agreement with their experimental results. Kothyari, et al.,(83) proposed a different approach in which the temporal variation of scour around a bridge pier was calculated in successive time steps governed by: (1) the time required for removal of one sediment grain by the primary vortex and (2) the resulting gradual decrease of shear stress in the scour hole as it grew larger.
Chiew and Melville(84) suggested from their experimental results on scour development around bridge piers an empirical relationship for a dimensionless equilibrium time, t* = V1te/b, as a function of V1/Vc, where V1 = approach velocity, Vc = critical velocity, b = pier diameter, and te = equilibrium time. The equilibrium time was defined as the time at which the rate of increase of scour depth was less than 5 percent of the pier diameter in 24 hours. The experimental results were then presented as the ratio of scour depth at a given time to equilibrium scour depth (dst/ds) as a function of the ratio of elapsed time to equilibrium time (t/te) for various constant values of V1/Vc.
A relationship for time development of scour is proposed in this report based on the experimental results for compound channels. It is used to better describe the effect of event duration on the scour depth, and it is incorporated into the proposed scour-prediction procedure. However, it must be used carefully, because scour can be cumulative over many events.
Back to Top
Previous | Table of Contents | Next
|
