U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-046 Date: October 2004 |
Previous | Table of Contents | Next
The concept of risk for acceptance plans, in general, and PWL, in particular, since that is our selected quality measure, is very similar to the concepts of accuracy and precision that are discussed in chapter 5 and the concepts of hypothesis testing and verification that are discussed in chapter 7.
In hypothesis testing, there are two types of errors. A type I error occurs when a true null hypothesis is incorrectly rejected. A type II error occurs when an incorrect hypothesis is erroneously accepted. The probability of making a type I error is known as the α risk, while the probability of making a type II error is known as the β risk. When testing a null hypothesis, the α risk is also known as the level of significance.
The terms α and β have been applied in the highway construction industry for many years. However, these terms are related to a situation where the decision is either to accept or reject the hypothesis. In a highway construction scenario, the null hypothesis that is being tested is that the contractor's product meets the specification requirements. In such a scenario, the α and β risks apply as they do in any other hypothesis testing situation. Oftentimes, however, the decision is not simply to accept or reject the material, but to accept it at an incentive payment (positive price adjustment, or bonus) or at a disincentive payment (negative price adjustment, or penalty).
The Transportation Research Board (TRB) has published the following definitions for α and β risks:(4)
Seller's Risk (a) (also called a type I error): The probability that an acceptance plan will erroneously reject acceptable quality level (AQL) material or construction with respect to a single acceptance quality characteristic. It is the risk that the contractor or producer takes in having AQL material or construction rejected.
Buyer's Risk (b) (also called a type II error): The probability that an acceptance plan will erroneously fully accept (100 percent or greater) rejectable quality level (RQL) material or construction with respect to a single acceptance quality characteristic. It is the risk that the highway agency takes in having RQL material or construction fully accepted. (The probability of having RQL material or construction accepted (at any pay) may be considerably greater than the buyer's risk.)
When α and β risks are applied to materials or construction, they are really only appropriate for the case of acceptance or rejection decisions. When materials may not only be accepted or rejected, but may also be accepted at an adjusted payment, then the concept of α and β risks does not strictly apply. In such cases, which are perhaps more common than acceptance or rejection decisions, then much more involved analyses than just calculating α and β risks are necessary.
In an attempt to address the deficiencies in the use of α and β for price-adjustment acceptance plans, a new term (α100) has been proposed. This is defined as the probability that AQL material will receive less than 100-percent payment. Just as with any term that tries to define a single point in a payment continuum, α100 provides only a little additional information regarding the realm of possible payments for a given quality of material.
The only single term that truly attempts to consider the totality of possible payments for a given quality of material is EP. However, even this term is not sufficient since it considers only the average payment that a contractor can expect to receive for a very large number of production lots of a given quality level. EP fails to consider the amount of variability in the individual payment values that comprise the calculation of EP. To fully evaluate the risks in a price-adjustment acceptance plan, it is necessary to determine OC curves and EP curves, and also to investigate the amount of variability in the individual payment values about the EP curve.
TRB defines OC and EP curves as:(4)
OC Curve: A graphic representation of an acceptance plan that shows the relationship between the actual quality of a lot and either: (1) the probability of its acceptance (for accept/reject acceptance plans) or (2) the probability of its acceptance at various payment levels (for acceptance plans that include pay-adjustment provisions).
EP Curve: A graphic representation of an acceptance plan that shows the relationship between the actual quality of a lot and its EP (i.e., mathematical pay expectation, or the average pay the contractor can expect to receive over the long run for submitted lots of a given quality). (Both OC and EP curves should be used to evaluate how well an acceptance plan is theoretically expected to work.)
The definition of OC curves indicates that multiple curves might be plotted for the probability of receiving various levels of payment for a given actual quality level. The obvious difficulty with this is that if, as is recommended, an equation is used to calculate the payment factor, then there are an infinite number of OC curves that could be developed. Certain values are obvious candidates (e.g., the probability of receiving full payment or, if there is a remove-and-replace provision for very poor quality, the probability of requiring removal and replacement). It is difficult to view a plot with numerous OC curves (one for each of many selected payment levels) and to interpret it with a great deal of significance.
The EP curve, in essence, converts the family of OC curves into a single curve that represents the average payment that would be received in the long run for a given level of quality. This is the single curve that provides the most meaningful and useful information for a contractor or highway agency. However, even an EP curve is not sufficient since it does not consider the amount of variability in the individual payment values. This is why most of the analyses presented in this report consider not only bias or accuracy, but also standard deviation, to indicate the variability in addition to the average alone.
Risks are traditionally determined separately for each individual quality characteristic. This process can be quite complicated, particularly if there are unusual provisions incorporated into the specification. Although not identified specifically as risk analysis at the time, much of the information presented in chapter 5 is directly related to the concept of risk. In this section, the material from chapter 5 that is related to the PWL quality measure is revisited and discussed in light of its application to risk analysis.
The computer simulation routines that were used to determine figures 9 through 12 were developed to calculate the information necessary to plot OC and EP curves when using either PWL or PD as the quality measure. The routines were actually developed for PD since the calculations are slightly less involved. While the programs can print the results for either PD or PWL, the calculations are performed for PD and are then converted to PWL if necessary.
To illustrate the process of evaluating risks, the following payment equation, which is from the AASHTO Quality Assurance Guide Specification and which has been used many times in other chapters, is used:(3)
![]() (29)
(29)
While this equation is not necessarily recommended, it has been used by a number of agencies. This equation is simple because it is a single straight line. It would be preferable to use either more than one straight line over different regions or to use some form of curved payment equation. This would allow for a shallower slope (i.e., lower payment reduction) for quality levels near the AQL and for a steeper slope that allows the price reductions to increase by a greater amount as the quality departs more from the AQL. For the purposes of illustration, equation 29 will work well. We also need to select values for AQL and RQL in terms of PWL. For this example, we will use 90 PWL as the AQL value and 60 PWL as the RQL value.
Also, suppose that the acceptance plan calls for removal and replacement of the material if the calculated PWL estimate is less than 60 (i.e., less than the RQL value). Therefore, the α risk (i.e., the risk that the AQL material will be rejected) is the probability that an AQL population will have an estimated PWL value of less than 60. This can be determined by simulating a large number of lots from an AQL population and determining the percentage of them that have PWL estimated values of less than 60.
The results of such a computer simulation of 1000 lots for a sample size = 4 are plotted in figure 74. The horizontal line on the plot in figure 74 indicates the α risk. It is the probability that AQL material will be rejected and is shown on the plot as the difference between 100-percent probability of acceptance and the probability of acceptance at AQL = 90 PWL. The α risk is about 0.025 (or 2.5 percent). This seems like a low risk, but remember that this is the risk of rejection. The curve in figure 74 is the probability of receiving at least some payment. While rejection is unlikely, there may be a significant chance of receiving less than full payment.
Figure 74. OC curve for an acceptance plan that calls for rejection if the estimated PWL is less than 60, sample size = 4.
In fact, the probability of receiving at least 100-percent payment can be determined in the same way as the probability of acceptance, except that the probability in question is the probability of having an estimated PWL ≥ 90. This value of 90 is calculated as the PWL value that yields 100-percent payment from equation 29.
The probability of receiving at least 100-percent payment is shown in figure 75, along with the probability of acceptance at any price. While the probability of receiving at least some payment is quite high for AQL material, the probability of receiving 100-percent or greater payment is only about 0.60 (or 60 percent). Therefore, for this example, the value of α100 would be about 1.00 - 0.60 = 0.40 (or 40 percent). That is the risk that the AQL material would receive less than full payment.
From this example, it appears that α is quite low at about 2.5 percent and that α100 is quite high at about 40 percent. However, neither of these numbers tells the full story. For one thing, they apply only to one specific level of quality-AQL = 90 PWL. Secondly, they address only two specific points on the payment continuum-receiving greater than zero payment and greater than or equal to 100-percent payment.
Figure 75. OC curves for the probabilities of receiving at least some payment and at least 100-percent payment, sample size = 4.
Neither of these pieces of information is sufficient to fully evaluate the risk associated with this payment plan. Many other curves, such as the probability of receiving at least 90-percent payment or of receiving at least 104-percent payment, could be added to the plot. In reality, there is a continuous payment region that runs from the curve for the probability of receiving at least some payment to the curve for the probability of receiving some high payment. The maximum payment of 105 percent can only be averaged if the population has 100 PWL; it cannot be plotted except as a point at the upper right-hand corner. However, the curve representing, say, 104.5-percent payment can be calculated and is plotted in figure 76, along with the curves for greater than zero payment and greater than or equal to 100-percent payment.
Figure 76 shows that the probability of receiving at least 104.5-percent payment for AQL material is approximate 47 percent. To at least some extent, this should help to balance the fact that there is about a 40-percent probability of receiving less than 100-percent payment. To evaluate the overall long-term performance of the acceptance plan and the potential payment risks for the contractor, it is necessary to determine the EP curve for the plan.
Figure 76. OC curves for the probabilities of receiving various payments, sample size = 4.
Figure 77 shows the EP curve for the payment schedule in equation 29, with the added provision that estimated PWL values of less than 60 receive no payment (i.e., they require removal and replacement at the contractor's expense). Figure 77 shows that the EP in the long run for AQL material is less than 100 percent. It is generally accepted that the EP for AQL material should be 100 percent. Therefore, the difference between the EP at the AQL in figure 77 and 100 percent can be thought of as a long-term payment risk for the contractor.
Since it has been shown that the sample PWL is an unbiased estimator of the true PWL of the population, the EP curve should exactly follow the shape of the payment equation. Indeed, that is what happened with the simulations that were done using this same payment equation in chapter 5. Why, then, does the EP at the AQL not equal the value of 100 that is given by the equation? When the EP does not equal the value stated by the payment equation, it usually means that some payment barrier has interfered with the ability of the EP to average out to the value in the payment equation.
Figure 77. EP curve for the payment relationship Pay = 55 + 0.5PWL, with an RQL provision, sample size = 4.
For the plot in figure 77, the reason that the EP did not equal 100 at the AQL can be attributed to the provision requiring zero payment for estimated PWL values of less than 60. If the payment equation were allowed to apply throughout its total range, then the EP would have been able to reach 100 at the AQL. The reason that this did not happen can be shown by looking at the distribution of the estimated PWL values and their corresponding payment factors (shown in the histograms in figure 78). The histograms show that because of the variability of the small sample size, there were a number of times when the estimated PWL value for a lot was less than 60 even though the population PWL was 90. Similarly, there were many times when the estimated PWL was as high as 100.
When the estimated PWL was less than 60, a payment factor of zero was used to represent the remove-and-replace provision. This resulted in a number of zero payments for lots that are shown at the far left side of the payment histogram. Had these PWL values not been assigned as zero, the EP value could have been 100 at the AQL. To show this, the EP curve was calculated again without the remove-and-replace provision. This EP curve is shown in figure 79. The EP at the AQL is 100 percent and the EP curve exactly follows the payment equation.
Figure 78a Distribution of estimated PWL values for an AQL population.
Figure 78b. Distribution of payment factors for an AQL population.
Figure 79. EP curve for the payment relationship Pay = 55 + 0.5PWL, sample size = 4.
The most common reason that the EP curve deviates from the payment equation is when there is no provision to allow for incentive, or bonus, payments. This, once again, creates a boundary at 100-percent payment. With no incentive payments, with a population at an AQL of 90 PWL, there will be times when the estimated PWL will be less than 90 and times when it will be greater than 90 (see the histogram in figure 78). When the estimated PWL is less than 90, a price reduction will be applied. When the estimated PWL is greater than 90, the payment will still be 100 percent if there is no incentive payment. There will be no payments greater than 100 percent to balance the payments less than 100 percent to allow the average payment (i.e., the EP) to be 100 percent.
As is shown in chapter 5, one way to reduce the variability of the individual estimated PWL values is to increase the size of the sample that is taken. This reduces the variability about the EP value and, thus, reduces the risks by increasing the likelihood that the estimated PWL values will be close to the true value.
The effect of sample size is not evaluated again in this chapter. However, the reduction in variability is shown very clearly in figures 9 through 12.
Figure 79 clearly shows that even the maximum 5-percent bonus provided by equation 29 was sufficient to offset the times when the PWL for an AQL population is underestimated. This may not seem reasonable in light of the fact that equation 29 allows for only a 5-percent bonus, while allowing penalties that can theoretically reach as much as 45 percent. The reason that this can happen is related to the distribution of the estimated PWL values, particularly for the small sample sizes that are typically used in highway materials and construction.
The reason for this discrepancy is shown in figure 75 in the OC curve for the probability of receiving at least 100-percent payment. The OC curve shows that there is about a 40-percent chance of receiving less than 100-percent payment, while there is about a 60-percent chance of receiving 100-percent or greater payment. The fact that the sample PWL is an unbiased estimator of the population PWL does not mean that there is an equal chance of a high or low estimate. The fact that the average of the sampling distribution for individual PWL estimates has a mean equal to the true population PWL is what makes the estimator unbiased. In other words, the distribution of the estimates does not need to be symmetrical for the estimator to be unbiased.
It is the skewed distribution of sample PWL estimates that allows for a smaller bonus to offset larger penalties. The skewness of the distribution of the estimated PWL values and, hence, the estimated payment values can be shown with histograms.
Figure 80 shows histograms of the distribution of sample PWL estimates for a population with actual PWL = 90 and sample size = 4 for one-sided and two-sided specification limits. The histograms show that the distribution is skewed to the right for both one- and two-sided specifications, and that about 60 percent of the values lie above the actual PWL of 90.
Figure 81 shows similar histograms for a population with an actual PWL of 50. The two-sided specification exhibits the same skewness to the right, but with 60 percent below the actual PWL of 50. However, for the one-sided specification limit, the distribution appears to be symmetrical, with about 50 percent on either side of the actual PWL of 50.
The reason that the two distributions are different lies in the fact that it is the standard deviation that causes the estimated PWL distribution to be skewed. The only way for a one-sided specification to have 50 PWL is if the population mean is centered on the specification limit. Any population that is centered on the one specification limit will have 50 PWL, regardless of the value of its standard deviation.
To illustrate why it is the standard deviation that causes the skewness in PWL estimates, it is necessary to look at the sampling distributions for sample means and sample standard deviations. It is well known that for any sample size, the distribution of the sample means from a normal distribution will be normally distributed with the mean equal to the population mean. This indicates that the sample mean should lead to a symmetrical distribution of sample PWL values.
However, it is also known that the sample variance follows a chi-square distribution. The chi-square distribution is skewed to the right, but the amount of skewness decreases as the sample size increases. Since the sample standard deviation is the square root of the sample variance, the distribution of the sample standard deviations will also be skewed. This is shown in figure 82, which shows the distribution of 1000 sample standard deviation values for sample sizes = 3, 5, and 10. Note that the spread of the values becomes less and the shape of the distribution approaches symmetry as the sample size increases.
Appendix H presents a more detailed discussion regarding the distributions of sample PWL estimates and how these distributions vary depending on the population PWL value.
Figure 80. Distributions of sample PWL estimates for a population with 90 PWL.
Figure 81a. Distributions of sample PWL estimates for a population with 50 PWL and one-sided speculations.
Figure 81b. Distributions of sample PWL estimates for a population with 50 PWL and two-sided speculations.
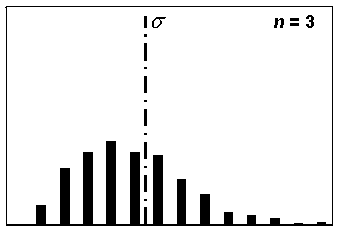
Figure 82a. Distribution of sample standard deviations for a sample size, n = 3, based on 1000 simulated samples.
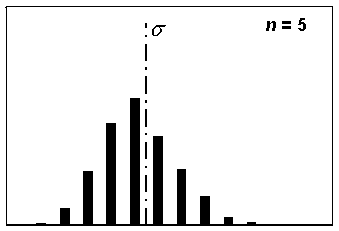
Figure 82b. Distribution of sample standard deviations for a sample size, n = 5, based on 1000 simulated samples.
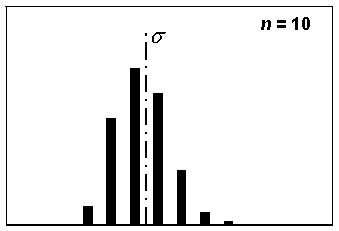
Figure 82c. Distribution of sample standard deviations for a sample size, n = 10, based on 1000 simulated samples.
The procedures presented above for OC and EP curves are primarily for the case of acceptance based on a single property. When, as will often be the case, there are multiple acceptance properties, it will be necessary for the agency to develop sophisticated computer simulation methods to complete a full analysis of the risks. These analyses will be quite involved and will be dependent on the quality characteristics chosen for acceptance and whether or not a performance model for predicting service life has been adopted by the agency. Another factor that will impact the analysis is whether a composite quality measure has been developed, or whether the individual quality measures will in some way, perhaps by adding, multiplying, or averaging, be combined into a composite payment factor. The topics of performance models and composite quality measures are addressed in chapter 11.
To illustrate the difficulty of trying to evaluate risks when there is more than one acceptance property, an example will be shown based on the use of two acceptance characteristics. The problem is simpler if it can be assumed that the characteristics are independent and, therefore, have a correlation coefficient of 0. If this might not be the case, then it must be determined whether or not it is necessary to develop separate EP contours or surfaces for each different possible set of correlation coefficients.
The same simulation routines that were presented in chapter 8 for evaluating two correlated quality characteristics can be used to develop a form of a two-variable EP curve. In chapter 8, it was shown that the EPs for two correlated variables did not change as the weighting factors or the value of their correlation coefficients varied. However, although the EPs did not vary, the standard deviations of the individual combined payment factors did vary with both the correlation coefficient and the weightings used when combining the individual payment factors.
Changes in the weighting factors are not likely to be a problem since they are usually part of the acceptance plan and, therefore, remain constant. The agency would have to decide whether or not it wished to evaluate the variability of the combined payment factors, or whether it was sufficient that the EP values matched the payment equations (i.e., that they were unbiased). If it is decided to only consider the EP, then a method needs to be developed to present the EP values in a way that can be used to assess the payment risks involved. One way to do this is by using contours or surfaces to represent the EP values as the actual PWL values for both acceptance characteristics vary. If only EP is considered, then the two variable EP contours or surfaces should not change with changes in the correlation coefficients.
To illustrate how this approach might be used to develop EP curves or surfaces, 1000 samples of size = 5 were simulated for correlation coefficients of +0.5 and -0.5, using several different methods for combining the individual payment factors into a combined payment factor. The simulations were conducted with actual PWL values ranging from 95 to 10 for both populations. The results of some of these simulation analyses are presented here for illustration.
Table 52 shows the results of simulations where the combined payments were determined as the average of the two individual payments. The individual payment factors were calculated using equation 29. The results show that there is no difference in the EP values when the correlation coefficient is +0.75, 0.00, or -0.75. The correct values for any cell in the table are determined by inserting the actual PWL values for variables 1 and 2 into equation 29. The EP values in the table are very close to what they should be to match the payment equation.
To illustrate how the EP values for two variables could be shown graphically, figure 83 shows EP contours for the EP values shown in table 53. These EP values were determined by multiplying the two individual payments, which were each obtained from equation 29. The values were based on a correlation coefficient of +0.50. Figure 84 shows another way in which the EP values could be represented as a surface in a three-dimensional plot. Still another two-dimensional approach for presenting the EP values for two variables is shown in figure 85. In this figure, the values in table 53 are plotted with one variable on the horizontal axis and the EP values on the vertical axis. The second variable is then plotted with a separate curve for each of a number of different PWL values.
While the three-dimensional approach is theoretically a good way to visualize how the EP values vary with the population PWL values, the two-dimensional methods are probably a more practical way to present the information. None of these visualization approaches would work if the number of acceptance variables were three or greater.
From the example above, it may appear that the evaluation of the risks can be complicated. The complexity becomes much greater when provisions in addition to a simple payment equation are added to the acceptance plan. In the past, a popular provision has been to state that even if the estimated PWL indicates a payment reduction, no price reduction will be applied if all of the individual test results are within the specification limits. This would not only have the effect of raising the EP values, it would also make it much more complicated to simulate the specification to establish the EP values.
Another provision that might require analyses to fully understand the potential risks is a remove-and-replace, or leave in at zero payment, provision. These are the most extreme penalties that can be imposed; thus, it is incumbent upon the specifying agency to fully evaluate the risks for the contractor before implementing such a provision. It is relatively easy to evaluate the risk that removal and replacement will be required when there is a single acceptance quality characteristic. It merely requires the same approach that was used to determine the OC curves in figures 74 through 76. This is illustrated with a simple example.
Table 52. EP values using Pay = 55 + 0.5PWL for two individual payment factors and then averaging them, sample size = 5.
| PWL Variable 1 | PWL Variable 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 10 | 30 | 50 | 60 | 70 | 80 | 90 | 95 | |
| Correlation Coefficient = +0.75 | ||||||||
| 10 | 60.0 | 64.8 | 69.9 | 72.5 | 75.1 | 77.8 | 80.0 | 81.2 |
| 30 | 64.8 | 70.0 | 75.0 | 77.3 | 80.0 | 82.6 | 85.1 | 86.3 |
| 50 | 70.0 | 74.9 | 80.0 | 82.5 | 84.7 | 87.5 | 90.2 | 91.3 |
| 60 | 72.5 | 77.7 | 82.2 | 85.0 | 87.7 | 89.9 | 92.5 | 93.5 |
| 70 | 75.3 | 80.0 | 84.8 | 87.4 | 90.5 | 92.8 | 95.2 | 96.2 |
| 80 | 77.4 | 82.6 | 87.4 | 90.5 | 92.3 | 95.0 | 97.4 | 98.7 |
| 90 | 80.1 | 85.1 | 90.0 | 92.6 | 95.2 | 97.5 | 100.1 | 101.2 |
| 95 | 81.2 | 86.3 | 91.5 | 94.0 | 96.2 | 98.9 | 101.2 | 102.5 |
| Correlation Coefficient = 0.00 | ||||||||
| 10 | 59.9 | 64.8 | 70.2 | 72.5 | 74.9 | 77.4 | 79.7 | 81.2 |
| 30 | 65.0 | 70.0 | 75.3 | 77.3 | 80.1 | 82.3 | 85.2 | 85.9 |
| 50 | 69.9 | 75.0 | 79.8 | 82.6 | 85.1 | 87.3 | 89.9 | 91.4 |
| 60 | 72.8 | 77.3 | 82.6 | 85.2 | 87.8 | 89.9 | 92.6 | 93.7 |
| 70 | 74.9 | 80.2 | 85.5 | 87.4 | 90.1 | 92.3 | 95.1 | 96.4 |
| 80 | 77.6 | 82.7 | 87.4 | 89.8 | 92.6 | 95.1 | 97.4 | 98.8 |
| 90 | 80.0 | 84.8 | 89.6 | 92.6 | 94.9 | 97.7 | 99.7 | 101.2 |
| 95 | 81.3 | 86.0 | 91.3 | 93.6 | 96.4 | 98.9 | 101.1 | 102.5 |
| Correlation Coefficient = -0.75 | ||||||||
| 10 | 59.9 | 65.0 | 70.2 | 72.6 | 74.9 | 77.5 | 80.0 | 81.1 |
| 30 | 64.9 | 69.7 | 75.0 | 77.6 | 79.9 | 82.4 | 85.0 | 86.0 |
| 50 | 69.8 | 75.0 | 79.9 | 82.6 | 85.1 | 87.6 | 90.3 | 91.1 |
| 60 | 72.5 | 77.4 | 82.5 | 84.9 | 87.6 | 89.8 | 92.5 | 94.0 |
| 70 | 74.9 | 80.2 | 84.9 | 87.6 | 90.0 | 92.4 | 94.7 | 96.2 |
| 80 | 77.5 | 82.6 | 87.5 | 90.2 | 92.8 | 95.0 | 97.6 | 98.8 |
| 90 | 79.9 | 84.9 | 90.2 | 92.5 | 94.8 | 97.4 | 100.1 | 101.2 |
| 95 | 81.2 | 86.2 | 91.3 | 94.0 | 96.4 | 98.9 | 101.0 | 102.6 |
Table 53. EP values using Pay = 55 + 0.5PWL for two individual payment factors and then multiplying them, sample size = 5, correlation coefficient = +0.5.
| PWL Variable 1 | PWL Variable 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 10 | 30 | 50 | 60 | 70 | 80 | 90 | 95 | |
| 10 | 35.9 | 42.1 | 48.2 | 50.6 | 54.2 | 56.8 | 60.2 | 61.3 |
| 30 | 42.1 | 49.1 | 56.5 | 59.8 | 62.8 | 66.4 | 69.8 | 71.4 |
| 50 | 48.9 | 56.7 | 64.7 | 68.6 | 72.7 | 76.6 | 80.6 | 81.6 |
| 60 | 51.2 | 59.5 | 68.4 | 72.9 | 77.3 | 80.7 | 85.2 | 87.0 |
| 70 | 54.4 | 63.2 | 72.4 | 77.3 | 81.5 | 85.8 | 90.0 | 92.3 |
| 80 | 57.5 | 66.8 | 75.7 | 80.9 | 86.0 | 90.9 | 95.2 | 97.5 |
| 90 | 59.9 | 70.1 | 80.5 | 84.9 | 90.6 | 95.1 | 99.7 | 102.0 |
| 95 | 61.4 | 72.2 | 82.2 | 86.7 | 92.7 | 97.6 | 102.9 | 105.0 |
Figure 83. EP contours for the values in table 53.
Figure 84. EP surface for the values in table 53.
Figure 85. EP curves for the values in table 53.
Suppose that an acceptance plan calls for a sample size = 5 and requires that the material be removed and replaced if the estimated PWL value is less than 60. The OC curve for the probability that removal and replacement will be required is determined by the probability that a population with any given PWL value will yield a sample PWL of less than 60. The OC curve (the probability of acceptance) associated with the remove-and-replace decision is shown in figure 86. This OC curve represents the probability that the material will NOT require removal and replacement. The probability that removal and replacement would be required would be 1.00 minus the value indicated on the vertical axis.
Since small sample sizes, usually n = 3-5, are often involved in the acceptance decision, there is a large amount of variability in the estimated PWL value for any given population. Table 54 shows the probability that populations of various quality levels would have an estimated PWL of less than 60 for a single quality characteristic and would thus require removal and replacement.
Figure 86. OC curve for an acceptance plan that calls for rejection if the estimated PWL is less than 60, sample size = 5.
Suppose that the agency had selected 90 PWL as the AQL for the acceptance plan. Table 54 shows that when the sample size = 3 for an AQL population (i.e., 90 PWL), each single quality characteristic has more than a 5-percent chance of yielding a sample result that indicates that removal and replacement are required. For sample size = 5, this probability drops to about 1 percent.
To further complicate the situation, many acceptance plans call for up to four or more acceptance characteristics. If the same remove-and-replace provision is applied if any of the acceptance characteristics has an estimated PWL of less than 60, then the risks are considerably greater. Assume that our example acceptance plan has four acceptance characteristics and requires removal and replacement if any of them have estimated PWL values of less than 60. If we assume that the four characteristics are independent, table 54 shows the probability that at least one of the four characteristics will trigger the remove-and-replace provision.
For a sample size = 3, there is about a 20-percent chance that an AQL population will require removal and replacement. Even for a sample size = 5, there is more than a 4-percent chance of the need for removal and replacement.
Table 54. Probability that populations with various quality levels would require removal and replacement for the example in figure 86.
| Population PWL | With One Quality Characteristic | With Four Independent Quality Characteristics | ||||
|---|---|---|---|---|---|---|
| n 3 | n = 4 | n = 5 | n = 3 | n = 4 | n = 5 | |
| 100 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 95 | 0.014 | 0.003 | 0.001 | 0.055 | 0.012 | 0.004 |
| 90 | 0.054 | 0.027 | 0.011 | 0.199 | 0.104 | 0.043 |
| 85 | 0.121 | 0.068 | 0.044 | 0.403 | 0.245 | 0.165 |
| 80 | 0.199 | 0.146 | 0.106 | 0.588 | 0.468 | 0.361 |
| 75 | 0.285 | 0.240 | 0.197 | 0.739 | 0.666 | 0.584 |
| 70 | 0.366 | 0.339 | 0.302 | 0.838 | 0.809 | 0.763 |
| 65 | 0.471 | 0.449 | 0.423 | 0.922 | 0.908 | 0.889 |
| 60 | 0.563 | 0.555 | 0.549 | 0.964 | 0.961 | 0.959 |
| 55 | 0.631 | 0.651 | 0.670 | 0.981 | 0.985 | 0.988 |
| 50 | 0.710 | 0.735 | 0.758 | 0.993 | 0.995 | 0.997 |
| 45 | 0.790 | 0.822 | 0.854 | 0.998 | 0.999 | 1.000 |
| 40 | 0.841 | 0.887 | 0.906 | 0.999 | 1.000 | 1.000 |
| 35 | 0.894 | 0.927 | 0.944 | 1.000 | 1.000 | 1.000 |
| 30 | 0.938 | 0.961 | 0.971 | 1.000 | 1.000 | 1.000 |
| 25 | 0.958 | 0.979 | 0.988 | 1.000 | 1.000 | 1.000 |
| 20 | 0.981 | 0.993 | 1.000 | 1.000 | 1.000 | 1.000 |
| 15 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 5 | 1.000 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 |
| 0 | 1.000 | 1.000 | 1.000 | 0.055 | 1.000 | 1.000 |
OC and EP curves describe the operation of an acceptance plan such that the risks can be evaluated throughout the entire quality regime. If the risks are considered to be acceptable, no modifications to the initial acceptance plan are necessary. However, if the risks are considered to be unacceptable in terms of being too high for either or both parties, a reassessment of the acceptance plan is necessary.
There is no easy answer to the question "Are the risks acceptable?" The decision regarding what does or does not constitute an acceptable level of risk will, to a great extent, be a subjective one. There is, however, one factor that is not subjective. There is generally universal agreement that the EP should be 100 percent for quality that is at exactly the AQL. Although it should not be confused with the statistical risk (α), the agency may wish to consider the average payment risk to the contractor if the EP is less than 100 percent at the AQL, or to the agency if the EP is greater than 100 percent at the AQL. The EP at the RQL is another point that is often specifically considered.
It must be remembered that the EP alone is not a complete measure, particularly the likelihood that any individual lot will receive a correct payment factor. The variability of the individual payment factors about the EP curve must also be considered. Ultimately, the decision regarding what constitutes acceptable or unacceptable risks rests with the individual agency.