Performance-Related Specifications for Pcc Pavements. Volume II: Appendix B-Field Demonstrations

 

Introduction

As a first step in investigating the practicality and implementability of the revised prototype PRS, the research team conducted the first shadow field trial in Ottumwa, Iowa in October 1996.  The field trial was labeled a shadow operation because it did not interfere with the contractor’s construction procedures or SHA’s acceptance procedures.  Therefore, contractor pay was not affected in any way by the pay factors computed using the prototype approach.

This chapter discusses all aspects of the original field trial, including the chosen lot and sublot definitions, sampling and testing plan, PRS pay adjustment calculations, problems encountered, and a summary of the lessons learned.

Objectives of the Field Trial   

The overall objective of the original field trial was to verify the draft specification’s effectiveness, identify potential problem areas, and determine its reasonableness. Specific objectives of the field trial included:

• Evaluating the definitions and procedures for determining PRS lots and sublots.

• Applying and evaluating the PRS acceptance sampling and testing plans in terms of their practicality, timeliness, and reliability.  An evaluation of the field management of the sampling and testing and reporting procedures was conducted, and problem areas were identified.

• Applying and evaluating the calculation procedure used to determine contractor pay for each lot.  The trial was limited in the sense that the contractor pay was not affected by the results.

• Obtaining feedback from the contractor and the SHA on the reasonableness and potential improvements of the PRS.

Explanation of Level 1 and Level 2 PRS Procedures   

Two different implementation levels of the draft specification were investigated at the original field trial.  As a means of addressing many implementation obstacles, the research team has proposed the development of these different levels of the draft specification—titled simply Level 1 and Level 2.  The two PRS levels mainly differ in the AQC sampling and testing methods and the payment adjustment procedures.  Both the Level 1 and Level 2 draft specifications were applied and investigated as part of the field trial. A more detailed explanation of both levels is included in the following paragraphs.

Introduction to a Level 1 PRS

The Level 1 PRS is based on the prototype specification previously developed for the FHWA.^(1,2)  It includes five AQC’s: concrete strength, slab thickness, entrained air content, initial smoothness, and percent consolidation around dowels.   The agency may choose to include any or all of these AQC’s in the specification.  The proposed Level 1 PRS may be implemented using the SHA’s current field sampling and laboratory testing procedures.  Therefore, the Level 1 PRS should be readily implementable in any SHA with minimal change to the agency’s current acceptance procedures.

In the Level 1 PRS, pavement performance may be defined by any or all of the following distress indicators: transverse slab cracking (fatigue), transverse joint faulting, transverse joint spalling, and pavement smoothness over time.   Performance models for each of the distress indicators are based on the quality level of one or more of the included AQC’s.  Calculated life-cycle costs (LCC’s) (for both the as-designed and as-constructed pavements) are based on a chosen rehabilitation policy and defined unit costs.  All of this simulation is conducted using the revised PaveSpec (Microsoft^Ò Windows^ä-based) software.

The pay factor computation method used in the Level 1 PRS is based on calculating independent pay factors for each AQC.  Each of these pay factors is determined from a series of developed pay factor vs. AQC mean curves and corresponding pay factor equations.  These curves, each specific to a different as-constructed AQC standard deviation, are created by correlating simulated lot pay factors over a range of AQC means.  Each calculated pay factor is, therefore, a function of the measured as-constructed mean and standard deviation, target mean and standard deviation, and the chosen sample size.

Final payment for the lot is based on an agency-selected composite pay factor (CPF) equation, expressed as a simple mathematical manipulation of the individual AQC pay factors.  It is suggested that the SHA apply a cap (maximum value) to this overall CPF for budgetary purposes.

Introduction to a Level 2 PRS

The proposed Level 2 PRS is an expansion and refinement of the proposed Level 1 PRS.  Theoretically, the Level 2 PRS represents the dynamic transition from the proposed Level 1 specification to an ideal PRS that would include all AQC’s that affect pavement performance.  The current Level 2 PRS is, therefore, defined by the research being conducted under this project.  It is understood that the definition of this Level 2 PRS will change when future research work provides improved or additional distress indicator prediction models and AQC sampling or testing methods.

A Level 2 specification may also be based on the measurement of the same five AQC’s used in the Level 1 approach.  A major difference between the proposed Level 1 and Level 2 PRS is that all AQC’s included in the proposed Level 2 PRS are ideally measured on the in-place pavement.  Pavement performance is determined using the same distress indicator prediction models defined for the Level 1 approach.  All performance simulation and cost calculations are performed using the PaveSpec software.

The pay factor computation method used in the Level 2 PRS calculates lot-based pay factors by comparing simulated as-designed (target) and as-constructed LCC’s directly.  Interactions of AQC’s are included in the simulations (e.g., an increase in flexural strength may counteract a decrease in slab thickness).  The pay factor calculation is based on the premise of liquidated damages.  Measured AQC sample means and standard deviations are incorporated into the pavement performance simulation, and the LCC is then used as the one overall representative quality characteristic.  Final payment for the lot is based on the one overall pay factor simulated using PaveSpec.

Project Information

The field trial project location was carefully selected for the original shadow PRS.  The research team searched for not only an appropriate project, but an appropriate SHA/contractor team as well.  The researchers defined a desirable SHA/contractor team as one that possessed the following:

• Considerable interest in PRS.

• Experience with quality control/quality assurance (QC/QA) specifications.

• Willingness to facilitate the field trial.

After careful consideration, the research team chose the following project for the field trial:

State:    Iowa

County:    Wapello

Highway:    Iowa State Route 23

Location:    1.61 km southeast of Eddyville and extending southeast on Iowa State Route 23 to near Chillicothe

Project Length:    9.31 km of mainline paving

Description:    New construction of two lanes (in one direction)—expansion from a two-lane (one lane in each direction) to a four-lane (two lanes in each direction) divided highway

Contractor:    Fred Carlson Co.

  Specification Development

One important aspect of the PRS approach is that the developed specifications are project-specific.  Therefore, the representative Level 1 and Level 2 specifications were developed prior to going to the field by tailoring the PRS methodology to the field trial project conditions (design, climatic, and traffic).   The development of the respective specifications involved a number of steps, each of which is described below.  (Note: Due to the timing of this project, this PRS demonstration was completed using the original prototype specification and PaveSpec 1.0 software.^(1-3))

Definition of Pavement Performance

For the original field trial, pavement performance was defined in terms of all four available distress indicators (transverse slab cracking, transverse joint faulting, transverse joint spalling, and pavement smoothness over time [expressed in terms of present serviceability rating (PSR)]).

Selection of AQC's to be Included in the Specification

For this specific project, the following four AQC’s (and sampling/testing methods, where appropriate) were selected for inclusion in both specification levels:

• Concrete Strength.

• Slab Thickness.

• Entrained Air Content.

• Initial Smoothness.

Under the current research project, the PRS was expanded to include percent consolidation around dowels as a fifth AQC; however, the methods for incorporating percent consolidation around dowels into the PRS procedure were not available at the time of the construction of this project.

Identifying Constant Inputs

Constant variables are defined as those variables required by the distress indictor models that do not differ between the as-designed and as-constructed pavements.  These variables define many of the pavement’s design characteristics and can be grouped into categories such as traffic, climatic, design (materials, slab support, and load transfer), and cost information.  Values for the constant variables (representing this project) were either obtained from the Iowa Department of Transportation (Iowa DOT) or assumed using engineering judgment. The specific constants used for this field trial are presented in table 1.  (Note: The constant inputs presented in table 1 are those required by the old distress prediction models used in the prototype PaveSpec software.^(1-3)  These variables differ slightly from those constant values required by the new distress indicator models included in the revised PaveSpec 2.0 software [as shown in figure 1 of volume I].)

Table 1.  Constant inputs defining the original field trial project (Ottumwa, Iowa).

Definition of the Required As-Designed AQC Target Values

One very important responsibility that falls on the agency is identifying the as-designed target means and standard deviations of the chosen AQC’s.  It is important because the contractor pay will be based on how well the contractor matches these chosen values.  The as-designed means and standard deviations define the quality levels for which the agency is willing to pay 100 percent of the bid price (on average).  Since expected pay (EP) curves were not available to identify the agency-desired AQC quality levels (interpreting EP curves is the method recommended in volume I), engineering judgment was used to determine the as-designed AQC target means and standard deviations based on the current Iowa DOT specifications.   Explanations of the interpretive methods used are included in the following sections.

Concrete Strength

Section 2301.31 of the Iowa construction specification discussed concrete strength.  Iowa addresses strength by requiring that the placed concrete achieve a designated minimum flexural strength by a designated minimum age.   No price adjustments are applied based on strength. Therefore, the achievement of the required minimum strength is only used to determine when the contractor can have access to the pavement with his/her vehicles.  The table in section 2301.31 of the Iowa DOT design manual contains the required minimum flexural strengths and corresponding minimum ages for different combinations of concrete class and cement type.  The data from that table are presented in table 2.

Table 2.  Iowa DOT concrete strength specification guidelines (from the Iowa DOT rigid design manual—Section 2301.31).

Notes: 1.  The original Iowa table was expressed in English units.  The strength values shown in this table have been converted to metric.

2.  10 days for concrete 203 mm or more in thickness.

3.  2.76 MPa strength required if placed after September 15.

4.  5 days for concrete 229 mm or more in thickness.

The Ottumwa project used a Class C concrete with a Type I cement.  Based on these characteristics, and the fact that the design thickness was 279 mm (see note 4 of table 2), a minimum third-point loading flexural strength (modulus of rupture) of 3.45 MPa was required in 5 days.  Since there was not a clear expected 28-day modulus of rupture or compressive strength associated with this mix, the expected modulus of rupture was assumed to be equal to a commonly used design value of 4.48 MPa.   (Note: This is the mean strength used to design the pavement using the American Association of State and Highway Transportation Officials [AASHTO] guide.)  A coefficient of variation of 0.1 was assumed, giving an expected standard deviation of 0.45 MPa.  This includes point-to-point materials and testing variation.  It represents the standard deviation between individual specimens; in other words, no averaging of test results is completed prior to the calculation of the standard deviation. These values were used to define the as-designed target strength for the Level 1 PRS.

Under the Level 2 PRS, concrete strength was chosen to be investigated using a 3-day core compressive strength.  This compressive strength was then converted to a 28-day compressive strength using maturity concepts.  Therefore, it was important to determine the 28-day compressive strength equivalent to a 28-day modulus of rupture of 4.48 MPa. Equation 1 was used for this conversion.

M_{R(28 days)}  =  0.83035 * [f’_{C(28 days)}]^0.5                 (1)

where

M_{R(28 days)}  =  28-day third-point portland cement concrete (PCC) modulus of rupture, MPa.  This equation is converted from the equation M_{R(28 days)}  =  10 * [f’_{C(28 days)}]^0.5 expressed in English units (psi).

f’_{C(28 days)}  =  28-day compressive strength, MPa.

Equation 1 may be rewritten so that compressive strength is a function of modulus of rupture.  This equation results in the following:

f’_{C(28 days)}  =  [M_{R(28 days)} / 0.83035]²                 (2)

Therefore, the expected 28-day compressive strength mean may be calculated as the following (using equation 2):

f’_{C(28 days)}  =  [(4.48 MPa) / 0.83035]²

                    =   29.13 MPa

A coefficient of variation of 0.10 was also assumed for compressive strength, thus making the expected 28-day compressive strength standard deviation approximately 2.91 MPa.  These values were used to define the as-designed target strength for the Level 2 PRS.

Slab Thickness

Section 2301.35 of the Iowa specification discusses the pay adjustments made based on slab thickness.  Pay adjustments are made based on a calculated quality index (QI) of the cores. This QI is calculated using equation 3.

QI  =  (X – T)/S                 (3)

where

QI  =  Quality index for the lot pavement thickness.

X  =  Mean core thickness for the lot, mm.

T  =  Current agency design thickness determined from the pavement design procedure, mm. (Provided by the agency as 279 mm.)

S  =  Core thickness standard deviation for the lot, mm.

Therefore, the QI will be negative if the current agency design thickness is larger than the mean core thickness of the lot.

For any assumed target standard deviation, an appropriate corresponding PRS target mean may be computed by rewriting equation 3 so that the measured core thickness (X) is a function of QI, S, and T.  The computed measured core thickness is then assumed to be the representative PRS target mean thickness (X_TARGET).   This relationship is shown in equation 4.

X_TARGET  =  (QI * S) + T                 (4)

where

X_TARGET  =  PRS target mean thickness, mm.

QI  =  Quality index for the lot pavement thickness.

S  =  Assumed core thickness standard deviation for the lot, mm.

T  =  Current agency design thickness determined from the pavement design procedure, mm. (Provided by the agency as 279 mm.)

The specific payment schedule is included in Section 2301.35 of the Iowa design specification and summarized in table 3.  Note that the percent payment identifies the pay adjustment as a percentage of the contract unit bid price.

Table 3.  Iowa DOT payment schedule for slab thickness (from the Iowa DOT rigid design manual—Section 2301.35).

Percent Payment	QI Range
103	1.25 or more
101	0.86 to 1.24
100	0.41 to 0.85
98	0.20 to 0.40
95	0.00 to 0.19
90	-0.25 to -0.01
80	-0.40 to -0.26
70	-0.41 or less

 

Note: If a QI of -0.41 or less is obtained, additional cores shall be taken to determine the extent and severity of the deficiencies.   Depending on the results of this study, the engineer will require one of the following procedures:

(a) The deficient lot shall be removed and replaced with pavement at the contractor’s expense, meeting the contract requirements.  Payment for the replaced pavement will be as provided above.

(b) The pavement represented by cores deficient from design thickness by more than 2.54 cm shall be replaced.  These areas will be defined by limits one-half the distance to the next core that is not deficient from design thickness by more than 2.54 cm.  The remainder of the deficient lot may be left in place and paid for at 70 percent of the contract price.

If all lots for each contract item have a quality index of 1.25 or more, the percentage of payment will be 105 percent for the project.

Given this specification, we can see that 100-percent pay will be paid for QI’s computed in the range of 0.41 to 0.85.  The midpoint of 0.63 is, therefore, used to estimate the target thickness mean.  Based on engineering judgment, a PRS target thickness standard deviation (representing good thickness quality control) was assumed to be 6 mm for this project.  This standard deviation represents point-to-point variation as measured from cores, and includes both construction process and measurement variation.  A corresponding target thickness is then computed based on a QI of 0.63, a standard deviation of 6 mm, and a current agency design thickness of 279 mm.  This target thickness mean is calculated as the following, using equation 4:

X_TARGET  =  (QI * S) + T

= (0.63 * 6 mm) + 279 mm

= 283 mm

Therefore, a target thickness mean and standard deviation of 283 and 6 mm, respectively, were chosen for the field trial.  (Note: Although the methods outlined in volume I recommend setting the PRS target thickness mean equal to the current agency design thickness [279 mm for this project], here it was believed that the agency was actually asking for better quality.  Therefore, the PRS target thickness mean was adjusted appropriately.)

Entrained Air Content

Section 2301.04 of the Iowa specification discusses entrained air content.  Under the Iowa specification, entrained air content is measured with a pressure air meter on "fresh or unvibrated" concrete.  The specification provides the following guidelines for the desired entrained air content range (measured as a percentage):

• Minimum = 6.0 percent.

• Maximum = 8.0 percent.

• Target = 7.0 percent.

Based on this acceptable range of 6.0 to 8.0 percent, the Iowa specification was translated into a representative target mean and standard deviation.  The target mean was chosen to be 7.0 percent (the midpoint of this acceptable range), and the target standard deviation was assumed to be equal to 0.5 percent, based on engineering judgment.

Initial Smoothness

The Iowa DOT’s Supplemental Specifications for Pavement Smoothness, SS-5130 (dated July 12, 1994), contains guidelines for initial smoothness.  The Ottumwa project is a primary road, mainline, not curbed, with a posted speed of greater than 45 mi/h (72.4 km/h).  Therefore, the smoothness requirements in mm/km are contained in Schedule A as determined by the table titled Schedule for Identification of Pavements and Bridge Approach Sections in Iowa’s supplemental specification.  Table 4 presents the pertinent pay adjustments (contained in Schedule A) of the smoothness specification.

Table 4.  Pertinent Iowa DOT payment schedule for initial smoothness.

Notes: 1. For single lift pavements, if all segments in a project qualify for 100-percent payment with no grinding, the qualifying incentive payment as indicated in note 3 will be increased by $50 per segment.

2. For each segment of pavement that has an initial index within the limits listed, with no grinding, the contractor will receive a pay adjustment as shown in the tabulation for the appropriate category. The original table was expressed in English units; the smoothness values shown in this table have been converted to metric.

3. If all segments in a section of pavement in this category qualify for 100-percent payment with no grinding, the qualifying incentive payment will be increased by $100 per segment.

4. For segments with an initial index of 111 to 158 mm/km, the contractor may grind the surface to a final index of 110 mm/km or better or accept a price reduction for each segment of pavement in non-compliance equal to the amount shown for the appropriate category.

5. For segments with an initial index of 159 mm/km and greater, the contractor shall grind the surface to a final index of 110 mm/km or better. In lieu of grinding the surface to a final index of 110 mm/km or better, the contractor may elect to replace part or all of the segment.

Based on the payment schedule presented in table 4, the range for 100-percent pay is a measured initial smoothness of 48 to 110 mm/km.   Therefore, a value of 79 mm/km (the midpoint of this range) was chosen as the target initial smoothness mean, while the target initial smoothness standard deviation was assumed to be 16 mm/km (based on engineering judgment).  The standard deviation of initial smoothness includes both variations between profiles and testing variability.

Summary of Chosen Target Values

The estimated target means and standard deviations for the four chosen AQC’s are summarized for the Level 1 and Level 2 PRS in tables 5 and 6, respectively.

Table 5.  Estimated Level 1 AQC target means and standard deviations for the Iowa field trial project.

¹ Computed from individual tests (no averaging is performed); thus, it includes both materials/process and testing measurement variation.

Table 6.  Estimated Level 2 AQC target means and standard deviations for the Iowa field trial project.

¹ Computed from individual tests (no averaging is performed); thus, it includes both materials/process and testing measurement variation.

Definition of Lots and Sublots

One of the final steps in preparing for the development of preconstruction output is the identification of the number of lots and sublots per lot to be analyzed.  The following definitions were used as a guide for the selection of lot and sublot lengths at the original field trial:

Lot—A discrete quantity of constructed pavement to which an acceptance procedure (and corresponding pay adjustment) is applied.  All pavement placed within a lot shall consist of the same mix design and material sources; shall be subjected to the same support conditions (base type, base thickness, subbase type, subbase thickness, subgrade treatment); and shall consist of the same design characteristics (joint spacing, drainage, shoulder type, dowel bar diameter, traffic, and AQC design values).  The target lot length shall be equal to one day’s production or less.  The minimum lot length shall not be less than 0.16 km. Any section of lesser length shall be added to the preceding lot.

Sublot—A portion of a lot. Each lot is divided into sublots of approximately equal surface area.  Sublot lengths are selected so that one or more samples may be taken from each sublot for each considered AQC.  The minimum sublot length shall not be less than 0.16 km (to accommodate the measurement of initial smoothness).  Any section of lesser length shall be added to the preceding sublot.  Each as-constructed sublot should initially be assumed to be equal to the chosen target sublot length.

Three consecutive days of mainline paving (one lot per day for October 1 through October 3, 1996) were selected to be investigated for this project.   Prior to arriving at the site, it was estimated that the contractor would be paving approximately 0.76 km per day.  Based on the available research team personnel and sampling and testing equipment, it was decided to obtain three or four sublots per lot with a target sublot length of 0.20 km.

During the acceptance procedures, the following guidelines were used to determine the actual sublot lengths in the field:

• Minimum sublot length was 0.16 km—requirements for sampling initial smoothness.
  
  
• Maximum sublot length was 0.48 km.
  
  
• The final sublot length in a lot was determined using the following guidelines:
  
  
  1. If the final sublot length was less than 0.16 km, then that material was added to the previous sublot.  If additional samples were taken from locations within this final sublot length (locations determined prior to construction), they were included with the samples representing the previous sublot.
     
     
  2. If the final sublot length was greater than 0.16 km, but less than the chosen target sublot length of 0.20 km, then the actual final sublot length was used.

Development of PRS Preconstruction Output

The final step in the specification development process involves the development of preconstruction output.  For the Level 1 specification, this involves constructing individual pay factor charts (and corresponding pay factor equations) for the four AQC’s. Individual AQC pay factors (representing the as-constructed quality) may be computed using these equations by knowing the as-constructed AQC lot means and standard deviations.  (Note: Each pay factor chart is specific to the chosen constant values, target means, and target standard deviations.)

For the Level 2 specification, this involves estimating the target as-designed life-cycle cost (LCC_DES).  A Level 2 overall lot pay factor may then be calculated as a function of LCC_DES, the determined as-constructed life-cycle cost (LCC_CON), and the chosen contract bid price.  More information on developing preconstruction output is provided in chapter 7 of volume I, in the section titled Step-By-Step Guide to Generating PRS Preconstruction Output.  The specific procedure used to develop the preconstruction output representing the original field trial project is explained in detail in the following sections.

Level 1—Development of Individual AQC Pay Factor Curves

The following step-by-step procedure was used to develop Level 1 pay factor charts and corresponding pay factor equations for the original field trial.  (Note: Each of these steps is accomplished using the PaveSpec PRS demonstration software.)

1. Define lots and sublots.  As previously discussed, the lot size was defined as one day of mainline paving and estimated to be 762 linear meters.  It was decided to divide each lot into three or four sublots based on the amount of paving the contractor completed.  Since pay factors are dependent on the number of sublots, it was decided to develop AQC pay factor charts and equations for both cases.

2. Define the number of samples per sublot.  A sampling frequency of two samples per sublot was used for each AQC at the field trial.  In a Level 1 PRS, we assume that all of the material in a lot are represented by the same statistical population.  Because of this assumption, the total sample size N may be represented by the number of sublots n times the number of samples per sublot.   Therefore, the total sample size N was 6 and 8 for the cases of three and four sublots, respectively.

3. Define the Level 1 AQC target means and standard deviations.  The Level 1 target as-designed AQC means and standard deviations for this project were defined in table 5.

4. Choose a range of as-constructed means for each AQC.  Reasonable ranges of AQC means were selected that defined the values to be used in the PaveSpec simulations.  These chosen ranges of simulation means for each AQC (based on the chosen AQC target values) are presented in table 7.

Table 7.  As-constructed AQC mean ranges for simulation.

5. Choose specific as-constructed AQC standard deviation levels for the simulation of pay factor curves.  The pay factor curves not only depend on the as-constructed AQC mean, but the as-constructed AQC standard deviation as well.  Therefore, three different standard deviation levels were chosen (for each AQC) representing very good, good, and poor AQC quality control.  Table 8 contains the different levels of AQC standard deviation used in the simulation of individual AQC pay factor curves.

Table 8.  As-constructed AQC standard deviation levels for simulation.

6. Simulate the target as-designed LCC’s. In order to calculate pay factors for different hypothetical levels of as-constructed AQC quality, the target as-designed LCC’s had to be simulated.  The PaveSpec specification simulation software was used to estimate target as-designed LCC means from 500 simulation lots for 3 and 4 sublots (both with 2 AQC samples per sublot).  Each of the 500 lots was simulated by randomly selecting AQC samples from the target value distributions summarized in table 5.  The simulations were conducted using a 60-year analysis life (twice the design life) and included 5 percent of the calculated user costs.  The resulting simulated Level 1 mean as-designed present worth (PW) LCC values (for the cases of three and four sublots per lot) were the following:

LCC_DES (3 sublots) = $ 488,412/ km

LCC_DES (4 sublots) = $ 492,034/ km

To better demonstrate the PRS methodology, the distresses over time associated with a typical sublot at this project (reflecting the chosen constant inputs and AQC target means only) are presented in table 9.  (Note: Only the first 50 years of the 60-year analysis life are displayed in table 9.)  These data show that the first asphalt overlay is predicted to be applied at the end of year 35, thereby resulting in the setting of the PSR value to an assumed value of 4.50, and the zeroing of the other distresses.  Associated LCC’s are computed based on a maintenance and rehabilitation (M & R) plan defined by the following detailed procedures:

• The first year of overlay application is triggered when PSR £ 3.0.  (Note: Other distresses are still displayed for the year in which an overlay is applied, because they are addressed as part of the pre-overlay repair.)

• Any cracked slab or spalled joint is replaced in the year in which it is determined to be failed (e.g., if it is determined that five slabs are cracked in year one, all five slabs are assumed to be replaced in year one).

• After the application of the first global rehabilitation (asphalt overlay), the following apply:

1. Transverse cracking, transverse joint spalling, and transverse joint faulting are no longer predicted (i.e., they are set equal to zero for the remaining years).

2. PSR is set equal to an assumed value of 4.50.

3. Additional asphalt overlays are applied using an assumed overlay life of 20 years.

4. The PSR is assumed to decrease linearly from 4.50 to 3.00 over the assumed 20-year life.

Table 9.  Typical distresses over time representative of the as-designed pavement at the Iowa field trial project.

These M & R procedures are used to determine sublot LCC’s that are then summarized into overall lot LCC’s used to compute pay factors.

7. Simulate as-constructed LCC’s and calculate an independent AQC pay factor for each hypothetical as-constructed mean/standard deviation pair.  The hypothetical as-constructed mean/as-constructed standard deviation pair values (coming from combinations of means and standard deviations defined in steps 5 and 6) were used to define individual sessions in the PaveSpec software.  Each AQC was investigated independently for each session (for example, if strength was being investigated, all of the other AQC as-constructed means and standard deviations were set equal to the target values).  Each pair was used in PaveSpec to simulate a corresponding LCC_CON.   A pay factor was calculated for each pair using equation 5.

PF_LOT  =  100 * (BID + [LCC_DES – LCC_CON]) / BID                 (5)

where

PF_LOT  =  Overall pay factor for the as-constructed lot, percent.

BID  =  Representative contractor's unit bid price for the lot, $/km.

            =  $176,295/km for this project.

LCC_DES  =  Target as-designed life-cycle unit cost for the lot (simulated in step 6 using target AQC’s), PW$/km.

LCC_CON  =  As-constructed life-cycle unit cost for the lot (computed using AQC test results from the as-constructed lot), PW$/km.

The simulated pay factors (from PaveSpec) representing lot sample sizes of N=6 (three sublots) and N=8 (four sublots) are summarized by AQC in tables 10 through 13.

Table 10.  28-day modulus of rupture—simulated Level 1 pay factors for three and four sublots and two samples per sublot (lot sample size N=6 and N=8, respectively).

Table 11.  Slab thickness—simulated Level 1 pay factors for three and four sublots and two samples per sublot (lot sample size N=6 and N=8, respectively).

Table 12.  Entrained air content—simulated Level 1 pay factors for three and four sublots and two samples per sublot (lot sample size N=6 and N=8, respectively).

Table 13.  Initial smoothness—simulated Level 1 pay factors for three and four sublots and two samples per sublot (lot sample size N=6 and N=8, respectively).

— not applicable

8. Plot charts of pay factor versus AQC mean.  The simulated pay factors determined in step 7 can be graphed easily as a function of the AQC mean.  Each AQC pay factor chart contains three different curves corresponding to the three different standard deviation levels chosen in step 5.  Best-fit regression equations were fit through each pay factor curve representing one chosen as-constructed AQC standard deviation.  Figure 1 contains AQC pay factor charts for the case when three sublots are used (or N=6).  Figure 2 contains AQC pay factor charts for the case when four sublots are used (or N=8).  Table 14 summarizes the best-fit pay factor regression equations at different as-constructed AQC standard deviations for the cases of three and four sublots.

Figure 1. Level 1 individual AQC pay factor charts for the case of three sublots (lot sample size N=6).

 

Figure 2. Level 1 individual AQC pay factor charts for the case of four sublots (lot sample size N=8).

 

Table 14.  Level 1 AQC best-fit regression equations for three and four sublots (lot sample size N=6 and N=8, respectively).

Level 2—Development of the LCC_DES

The LCC_DES was simulated using the same procedure discussed in step 6 of the Level 1 explanation.  The PaveSpec specification simulation software was used to estimate target as-designed life-cycle cost means from 500 simulation lots for the cases of 3 and 4 sublots (both with 2 AQC samples per sublot).  The simulations were conducted using a 60-year analysis life (twice the design life) and included 5 percent of the calculated user costs.  These resulting simulated Level 2 LCC_DES values were the following:

LCC_DES (3 sublots)  =  $ 488,412 /km

LCC_DES (4 sublots)  =  $ 492,034 /km

Sampling and Testing Plan

Field sampling and testing was conducted for the acceptance of concrete strength, slab thickness, air content, and initial smoothness.  Details of the sampling and testing methods used for each AQC are discussed in the following sections.  A summary of all of the Level 1 and Level 2 acceptance sampling and testing (including sampling method; number, location, and timing of sampling; and a testing summary) is contained in tables 15 and 16, respectively.

Table 15.  Summary of the Level 1 sampling and testing conducted at the PRS field trial.

AQC	Sampling Method	Sampling Summary			Testing Summary
		Number of Samples Per Sublot	Location of Samples	Timing of Sampling
Concrete Strength	Beams	(2)—152-mm x 152-mm x 762-mm beams	One beam each was taken at two randomly selected longitudinal locations	Material taken from in front of paver during construction	2 beams (1 each from 2 longitudinal locations) were tested for flexural strength (using third-point loading) at 28 days.
Slab Thickness	Cores	(2)—102-mm diameter cores	One core each was cut at two randomly selected locations	Cores were cut at 4 days (96 hours equivalent maturity)	Thickness for each of the 2 cores was determined by averaging 3 independent core length measurements (per core) taken with a ruler.
Entrained Air Content	Pressure Meter	(2)—pressure meter tests	One test was taken at two randomly selected longitudinal locations	Material taken from in front of paver during construction	Entrained air content was determined directly using a pressure meter.
Initial Smoothness	California Profilograph	(2)—passes with the profilograph	One pass down the center of each of two lanes	Next day after construction (as soon as contractor and State allow)	Each of the 2 profiles traces was reduced using a 5.1-mm blanking band. The smoothness results were then converted to units of mm/km.

Table 16.  Summary of the Level 2 sampling and testing conducted at the PRS field trial.

AQC	Sampling Method	Sampling Summary			Testing Summary
		Number of Samples Per Sublot	Location of Samples	Timing of Sampling
Concrete Strength	Cores	(2)—102-mm diameter cores	One core was cut at each of two randomly selected locations	Cores were cut at 4 days (96 hours equivalent maturity)	The cores were tested for compressive strength at 4 days. The 4-day compressive strengths were translated to 28-day flexural (third-point loading) strengths using maturity concepts.
	Thermocouple Tree	(1)—thermocouple tree	One randomly selected location	Placed in the pavement base in front of the paver (prior to paving)	Temperature at mid-depth in the pavement was monitored over time for maturity.
Slab Thickness	Cores	(2)—102-mm diameter cores (same samples used for Level 1)	Thickness was measured on the two cores taken for concrete strength	Cores were cut at 4 days (96 hours equivalent maturity)	The thickness for each core was determined by averaging 3 independent core length measurements (per core) taken with a ruler.
Entrained Air Content	Pressure Meter	(2)—pressure meter tests (same samples used for Level 1)	One test was taken at two randomly selected longitudinal locations	Material taken from in front of paver during construction	Entrained air content was determined directly using a pressure meter.
Initial Smoothness	California Profilograph	(2)—passes with the profilograph (same samples used for Level 1)	One pass down the center of each of two lanes	Next day after construction (as soon as contractor and State allow)	Each of the 2 profile traces was reduced using a 5.1-mm blanking band. The smoothness results were then converted to units of mm/km.

Concrete Strength

Data were collected during the field trial so that both the Level 1 and Level 2 PRS prototypes could be evaluated.  The Level 1 strength pay factor was calculated using the 28-day strength data from beams cast in the field and cured under standard laboratory conditions for a 28-day period.  The Level 2 PRS was investigated to evaluate the possibility of providing the contractor with a quicker indication of the strength results so that he may make adjustments sooner.   Therefore, the Level 2 pay factor was based on a 28-day flexural strength predicted from early age (4-day) cores.  (Note: 3-day cores were desired; however, due to the relatively cold field curing conditions, the 3-day sampling was postponed.)

In order to predict the 28-day flexural strength at a significantly earlier age at the Iowa field trial, strength development and interstrength relationship curves for the specific concrete mixture ingredients needed were developed in the laboratory prior to the beginning of construction.  After obtaining adequate amounts of the coarse and fine aggregates, cement, flyash, and admixtures to be used for the field trial concrete, concrete beam and cylinder specimens were cast in the laboratory.  The maturity of the laboratory samples was measured over the curing period, and the samples were tested for compressive strength, splitting tensile strength, and flexural strength (third-point loading) at ages of 1, 3, 5, 7, 14, 21, and 28 days.   The maturity of the concrete at these test intervals was recorded based on the calculated Arrhenius method of maturity in accordance with ASTM C 1074, Standard Practice for Estimating Concrete Strength by the Maturity Method.⁽⁵⁾  The datum temperature was calculated using the procedure outlined in the annex of the test method, with mortar samples cured in three different temperature water baths and tested at incremental ages based on the final setting time of the mortars.

A curve representing the strength development for these tests was plotted over the maturity period and is presented in figure 3.  An interstrength relationship curve was then developed by plotting flexural versus compressive strength over equivalent maturity intervals.  A best-fit equation was then determined from the plotted data points. This developed interstrength relationship is shown in figure 4.

Figure 3.  Laboratory-developed compressive strength versus maturity curve for the Iowa field trial concrete mix.

 

Figure 4.  Laboratory-developed flexural versus compressive interstrength relationship for the Iowa field trial mix.

Once the strength and maturity standards were developed in the laboratory, they were used in the field to predict the 28-day flexural strength required for input into the PaveSpec computer program.  Each sublot in the field was instrumented with maturity measuring devices allowing the equivalent laboratory maturity to be established for the samples tested at 4 days of age.  Each measured compressive strength was plotted against its equivalent maturity (at the time of testing).

Invariably, the data points did not fall directly on the developed maturity curve.  Representative values were then estimated using the vertical shift method.  This method essentially involves shifting the developed curve vertically until it passes through the plotted data point.  The specific procedure used to determine equivalent 28-day compressive strengths consists of the following:

1. Compute the difference between sample compressive strength and the compressive strength determined from the lab maturity curve (both values are computed at a maturity equal to the sample testing maturity).

2. Determine the estimated 28-day laboratory compressive strength (using the lab maturity curve) at an equivalent 28-day maturity.

3. Estimate the sample’s 28-day compressive strength (28-day equivalent maturity) by adding the computed difference (computed in step 1) to the estimated 28-day laboratory compressive strength (computed in step 2).

More information on using this procedure to estimate 28-day strengths using maturity concepts is contained in chapter 5 of volume I in the section titled Available AQC Sampling and Testing Procedures.

Slab Thickness

Slab thickness was measured on all cores taken for the Level 2 investigation of concrete strength (i.e., no additional cores were cut from the pavement for the determination of slab thickness).  These samples were used for acceptance in both specification levels. Level 1 acceptance was based on the computed mean and standard deviation of all of the cores’ thickness measured within the entire lot. Level 2 acceptance was based on the average core thickness measured within each sublot.   Details of the specific Level 1 and Level 2 sampling and testing procedures are shown in tables 15 and 16, respectively.

Entrained Air Content

Entrained air content was measured in the field using pressure meter tests on fresh concrete.  Two samples were taken from each sublot (one each for two different random locations) and used for acceptance under both specification levels.  Details of the Level 1 and Level 2 sampling and testing procedures are shown in tables 15 and 16, respectively.

Initial Smoothness

Initial smoothness was measured at the Iowa field trial using a California profilograph.  Two passes were made with the profilograph (by the SHA) for each sublot.  The passes consisted of one pass down the center of each of the two lanes.  The collected profilograms were then reduced (5.1-mm blanking band) by the SHA using a computerized method to obtain initial profile indices.  These computed profile indices were used for the acceptance of initial smoothness in both specification levels. Additional details of the specific Level 1 and Level 2 sampling and testing procedures are shown in tables 15 and 16, respectively.

Project Layout

The sampling and thermocouple tree locations were randomly selected for each sublot using the guidelines set forth in volume I, in the section titled Selection of Random Sampling Locations (chapter 5).  A summary of the project layout and selected sampling and thermocouple tree locations is contained in table 17.   Detailed project layout diagrams of lots 1, 2, and 3 are presented in figures 5, 6, and 7, respectively.

Table 17.  Summary of lot and sublot layout and sampling locations.

Construction Date	Lot	Sublot	Starting Station	Ending Station	Sublot Length, m	Lot Length, m	Longitudinal Sample Locations		Thermocouple Tree Station
							Longitudinal Sample ID	Longitudinal Sample Station
10/1/96	1	1.1	106+80	116+20	287	707	1.1.A	108+02	113+40
							1.1.B	113+30
		1.2	116+20	121+50	162		1.2.A	117+20	121+45
							1.2.B	120+65
		1.3	121+50	129+98	258		1.3.A	122+85	125+60
							1.3.B	124+80
10/2/96	2	2.1	129+98	135+50	168	975	2.1.A	132+04	131+81
							2.1.B	133+40
		2.2	135+50	141+95	197		2.2.A	135+75	140+35
							2.2.B	140+30
		2.3	141+95	148+40	197		2.3.A	142+90	146+85
							2.3.B	147+25
		2.4	148+40	161+95	413		2.4.A	149+85	154+40
							2.4.B	154+40
							2.4.C (air only)	155+45
							2.4.D (air only)	159+15
10/3/96	3	3.1	161+95	168+50	200	926	3.1.A	163+50	167+93
							3.1.B	167+90
		3.2	168+50	175+00	198		3.2.A	170+30	174+80
							3.2.B	174+75
		3.3	175+00	181+50	198		3.3.A	178+35	180+70
							3.3.B	180+70
		3.4	181+50	192+34	330		3.4.A	182+50	184+10
							3.4.B	184+10

Figure 5.  Lot 1 project layout at the Iowa field trial.

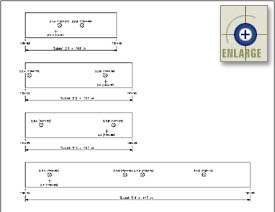
Figure 6.  Lot 2 project layout at the Iowa field trial.

Figure 7.  Lot 3 project layout at the Iowa field trial.

Sampling and Testing Results

Summaries of the Level 1 and Level 2 samples collected for each lot (using the sampling and testing procedures outlined in tables 15 and 16) are presented in tables 18 and 19, respectively.

Table 18.  Summary of Level 1 field sampling and testing results for each lot.

LOT 1
Construction Date	Sublot	Sample Number	Measured 28-day Flexural Strength (from beams), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/1/96	1.1	1	4.83	303	7.2	68
		2	4.65	298	7.3	44
	1.2	1	4.79	305	6.3	71
		2	4.55	316	6.6	8
	1.3	1	5.10	313	8.4	14
		2	4.79	307	7.3	14
Average	—	—	4.78	307	7.2	36
Std Dev	—	—	0.20	7	0.8	30
LOT 2
Construction Date	Sublot	Sample Number	Measured 28-day Flexural Strength (from beams), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/2/96	2.1	1	4.79	307	7.6	47
		2	5.03	304	6.7	8
	2.2	1	4.65	318	7.3	71
		2	5.00	318	7.0	13
	2.3	1	4.79	309	8.2	84
		2	4.83	306	6.7	96
	2.4	1	4.90	302	7.2	122
		2	4.59	302	7.2	47
Average	—	—	4.82	308	7.2	62
Std Dev	—	—	0.16	7	0.5	41
LOT 3
Construction Date	Sublot	Sample Number	Measured 28-day Flexural Strength (from beams), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/3/96	3.1	1	4.34	310	7.8	169
		2	5.07	316	8.2	79
	3.2	1	4.90	307	7.2	140
		2	4.38	312	8.3	57
	3.3	1	4.48	315	7.2	153
		2	4.52	310	8.1	13
	3.4	1	4.93	315	7.8	155
		2	4.69	296	7.6	55
Average	—	—	4.66	310	7.8	103
Std Dev	—	—	0.29	7	0.4	61

Table 19.  Summary of Level 2 field sampling and testing results for each lot.

LOT 1
Construction Date	Sublot	Sample Number	Estimated 28-day Flex. Str. (from 4-day cores), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/1/96	1.1	1	4.88	303	7.2	68
		2	4.60	298	7.3	44
	1.2	1	4.67	305	6.3	71
		2	4.69	316	6.6	8
	1.3	1	4.64	313	8.4	14
		2	4.70	307	7.3	14
Average	—	—	4.70	307	7.2	36
Std Dev	—	—	0.10	7	0.8	30
LOT 2
Construction Date	Sublot	Sample Number	Estimated 28-day Flex. Str. (from 4-day cores), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/2/96	2.1	1	4.83	307	7.6	47
		2	5.06	304	6.7	8
	2.2	1	4.89	318	7.3	71
		2	4.96	318	7.0	13
	2.3	1	4.92	309	8.2	84
		2	4.84	306	6.7	96
	2.4	1	5.02	302	7.2	122
		2	4.95	302	7.2	47
Average	—	—	4.93	308	7.2	62
Std Dev	—	—	0.08	7	0.5	41
LOT 3
Construction Date	Sublot	Sample Number	Estimated 28-day Flex. Str. (from 4-day cores), MPa	Slab Thickness, mm	Plastic Entrained Air Content, %	Initial Smoothness, mm/km
10/3/96	3.1	1	4.86	310	7.8	169
		2	4.89	316	8.2	79
	3.2	1	4.95	307	7.2	140
		2	4.82	312	8.3	57
	3.3	1	4.90	315	7.2	153
		2	4.92	310	8.1	13
	3.4	1	4.76	315	7.8	155
		2	4.89	296	7.6	55
Average	—	—	4.88	310	7.8	103
Std Dev	—	—	0.06	7	0.4	61

Calculation of Shadow Pay Factors

Level 1 Pay Factors

The Level 1 shadow pay factors were calculated using the measured AQC lot means and standard deviations presented in table 18.  The measured standard deviations are then used to select the appropriate equations from table 14.  (Note: The appropriate equations are those developed for standard deviation values nearest to the measured value.)  Level 1 AQC pay factors are then determined by interpolating between pay factors computed using the selected appropriate equations.  A detailed explanation of the calculation of the lot 1 pay factors is contained below.  The same procedures were used to calculate pay factors for lots 2 and 3.

Pay Factor Calculations for Lot 1

The measured as-constructed AQC means and standard deviations representing lot 1 are the following:

• 28-day Flexural Strength:    Mean = 4.78 MPa, Std Dev = 0.20 MPa.
• Slab Thickness:    Mean = 307 mm, Std Dev = 7 mm.
• Entrained Air Content:    Mean = 7.2%, Std Dev = 0.8%.
• Initial Smoothness:    Mean = 36 mm/km, Std Dev = 30 mm/km.

Lot 1 contains only three sublots; therefore, the equations (presented in table 14) representing the case of three sublots are used to calculate individual AQC pay factors.

Lot 1 As-Constructed 28-day Beam Flexural Strength (Mean = 4.78 MPa, Std Dev = 0.20 MPa):

At a mean of 4.78 MPa, and a standard deviation of 0.00 MPa:

PF_{S-(4.78, 0.00)}  =   –27.3878(4.78)² + 295.6802(4.78) – 665.9437 = 121.64%                 (6)

At a mean of 4.78 MPa, and a standard deviation of 0.45 MPa:

PF_{S-(4.78, 0.45)}  =  –17.8866(4.78)² + 214.0493(4.78) – 500.0361 = 114.44%                 (7)

The pay factor for the case with strength mean and standard deviation equal to 4.78 and 0.20 MPa is interpolated (using an assumed linear relationship) by the following equation:

PF_{S-(4.78, 0.20)}  =  PF_{S-(4.78, 0.45)} + (PF_{S-(4.78, 0.00)} – PF_{S-(4.78, 0.45)}) * [(0.45 MPa – 0.20 MPa) / (0.45 MPa – 0.00 MPa)]                 (8)

                        =   114.44% + (121.64% – 114.44%) * [(0.25 MPa)/(0.45 MPa)]

                        =   118.44%

Lot 1 As-Constructed Thickness (Mean = 307 mm, Std Dev = 7 mm):

At a mean of 307 mm, and a standard deviation of 6 mm:

PF_{T-(307, 6)}  =  1.6254(307) – 360.3357 = 138.66%                 (9)

At a mean of 307 mm, and a standard deviation of 13 mm:

PF_{T-(307, 13)}  =  1.6887(307) – 381.1839 = 137.25%                 (10)

The pay factor for the case with thickness mean and standard deviation equal to 307 and 7 mm is interpolated (using an assumed linear relationship) by the following equation:

PF_{T-(307, 7)}  =  PF_{T-(307, 13)} + (PF_{T-(307, 7)} – PF_{T-(307, 13)}) * [(13 mm – 7 mm) / (13 mm – 6 mm)]                 (11)

                        = 137.27% + (138.66% – 137.27%) * [(6 mm)/(7 mm)]

                        = 138.46%

Lot 1 As-Constructed Entrained Air Content (Mean = 7.2%, Std Dev = 0.8%):

The computed as-constructed entrained air content mean was found to be greater than the target mean strength value of 7.0 percent.  When this case occurs, the pay factors are assumed to be held constant at the pay factor values computed using the target mean.  Therefore, individual entrained air content pay factors were computed with an assumed mean equal to 7.0 percent.

At a mean of 7.0 percent and a standard deviation of 0.5 percent:

PF_{A-(7.0, 0.5)}  =  1.825(7.0) + 87.225 = 100.00%                 (12)

At a mean of 7.0 percent and a standard deviation of 1.5 percent:

PF_{A-(7.0, 1.5)}  =  1.675(7.0) + 87.425 = 99.15%                 (13)

The pay factor for the case with entrained air content mean and standard deviation equal to 7.0 and 0.8 percent, respectively, was interpolated (using an assumed linear relationship) by the following equation:

PF_{A-(7.0, 0.8)}  =  PF_{A-(7.0, 1.5)} + (PF_{A-(7.0, 0.5)} – PF_{S-(7.0, 1.5)}) * [(1.5% – 0.8%) / (1.5% – 0.5%)]                 (14)

                        =   99.15% + (100.00% – 99.15%) * [(0.7%)/(1.0%)]

                        =   99.75%

This computed value is, therefore, used to represent the case where entrained air content mean and standard deviation are equal to 7.2 and 0.8 percent, respectively.

Lot 1 As-Constructed Initial Smoothness (Mean = 36 mm/km, Std Dev = 30 mm/km):

At a mean of 36 mm/km, and a standard deviation of 16 mm/km:

PF_{SM-(36, 16)}  =  –7.6401E-07(36)³ – 2.941E-04(36)² – 3.7398E-04(36) + 102.23                 (15)

                        =   101.80%

At a mean of 36 mm/km, and a standard deviation of 47 mm/km:

PF_{SM-(36, 47)}  =  –7.6401E-07(36)³ – 2.941E-04(36)² – 3.7398E-04(36) + 100.48                 (16)

                        =   100.05%

The pay factor for the case with initial smoothness mean and standard deviation equal to 36 and 30 mm/km is interpolated (using an assumed linear relationship) by the following equation:

PF_{SM-(36, 30)}  =  PF_{SM-(36, 47)} + (PF_{SM-(36, 16)} – PF_{SM-(36, 47)}) * [(47 mm/km – 30 mm/km) / (47 mm/km – 16 mm/km)]                 (17)

                            =   100.05% + (101.80% – 100.05%) * [(17 mm/km) / (31 mm/km)]

                            =   101.01%

Calculation of the Lot 1 Composite Pay Factor Equation

Finally, the overall lot CPF is computed as a function of the individually determined AQC pay factors.  The product method was chosen to define the CPF equation at the Iowa field trial.  The product CPF method involves multiplying the individual AQC pay factors (expressed as decimals, e.g., 103 percent = 1.03). The resulting lot CPF equation is expressed as the following:

CPF_LOT   =  PF_S * PF_T * PF_A * PF_SM                 (18)

where

PF_S  =  Independently determined pay factor (expressed as a decimal) for concrete strength.

PF_T  =  Independently determined pay factor (expressed as a decimal) for slab thickness.

PF_A  =  Independently determined pay factor (expressed as a decimal) for entrained air content.

PF_SM  =  Independently determined pay factor (expressed as a decimal) for initial smoothness.

More information on selecting CPF equations is contained in chapter 6 of volume I, in the section titled Defining a Level 1 Composite Pay Factor Equation.

For the Iowa shadow field trial, the lot 1 CPF was computed as follows, using equation 18:

CPF_LOT   =  PF_S * PF_T * PF_A * PF_SM

                =   (1.1844) * (1.3846) * (0.9975) * (1.0001) = 1.6360

which translates to 163.6%.

A practical overall lot pay factor cap of 110 percent was then applied for demonstration purposes.  This chosen maximum value would be subjectively determined (for budgetary purposes) by each SHA.  More information on choosing limits for computed CPF’s is contained in chapter 6 of volume I, in the section titled Selecting Pay Factor Limits.

To better illustrate the basis of the PRS method, table 20 shows a comparison of typical as-constructed distresses for lot 1 (based on the computed lot 1 AQC Level 1 means discussed in this section) to the typical distresses estimated for the as-designed pavement (presented previously in table 9).  (Note: Only the first 50 years of the 60-year analysis life are displayed in table 20.)  The distress data show that the as-designed pavement would typically require an asphalt overlay at year 35, while the quality measured for the as-constructed lot 1 would postpone the first year of overlay until year 45.

Table 20.  Comparison of typical as-designed distresses over time to typical distresses representing the as-constructed lot 1 (level 1 samples) at the Iowa field trial project.

All of the calculated Level 1 pay factors for lots 1, 2, and 3 are summarized in table 21.

Table 21.  Summary of Level 1 AQC values and calculated pay factors.

The Level 2 pay factors were determined directly through simulation using the measured as-constructed means and standard deviations (presented in table 19).  Pay factors were simulated (from 500 simulated lots and including 5-percent user costs) using both sets of flexural strength data (i.e., directly from 28-day beam breaks and estimated from 4-day core compressive strengths using maturity concepts).  All of the calculated Level 2 pay factors for lots 1, 2, and 3 are summarized in table 22.

Table 22.  Summary of Level 2 AQC values and calculated pay factors.

Summary of Lessons Learned

A number of valuable lessons were learned from the original field trial experience.  A few of these are summarized briefly below.

• Fix the sublot length to one constant value—It quickly became apparent that varying sublot lengths in the field causes much confusion.  As a result of the original field trial experience, it is recommended that one target sublot length be chosen and used to lay out all sublots prior to the paving of each lot.  This can be done on a day-by-day (lot-by-lot) basis.

• Choose a practical target sublot length—It also became obvious that the sublot length chosen for the first day of paving (0.16 km) was impractical for the type and amount of sampling and testing being conducted.  There simply was not enough time to complete all of the testing and get to the next randomly selected location.   Therefore, it is important to consider the type and amount of sampling and testing required, the personnel available, and the location of the testing facilities relative to the job site when choosing an appropriate target sublot length.

• Choose a minimum length between longitudinal sampling locations—As previously stated, it was often very difficult to conduct sampling at the randomly selected locations due to the selection of sampling locations that were too close to each other.  In response to this problem, it is recommended that the SHA decide on a practical minimum length between sampling locations when samples are required to be taken from the fresh concrete during the construction process.

• Limit pay factors to chosen practical maximum values—The original field trial demonstrated the need for SHA’s to select practical maximum pay factors.  At the field trial, the contractor generally provided an extra 25 mm of pavement thickness on each of the three investigated lots.  This extra thickness resulted in relatively large pay factors.  Since it would be impossible for almost any SHA to make pay adjustments of this magnitude, it is realized that the pay factors will need to be capped at some agency-chosen practical value.  The pay factor maximums could be applied to the individual AQC pay factors, the overall lot pay factor, or both.  For demonstration purposes at the original field trial, the final overall pay factor was capped at 110 percent for both specification levels.

Summary

This chapter summarizes the results of the first shadow field trial conducted to demonstrate the prototype PRS.^(1-3)  The Level 1 method proved to be a valid, practical PRS method that should be easily implementable by most SHA’s.  All aspects of the field trial were discussed, including definitions of lots and sublots, the developed sampling and testing plan, and shadow PRS pay adjustment calculations.  Valuable experience was obtained from the Iowa field trial, and all of the lessons learned were used to revise the prototype PRS developed under the previous FHWA research.^(1-3)