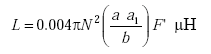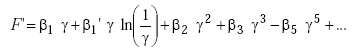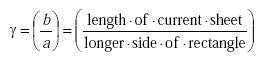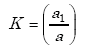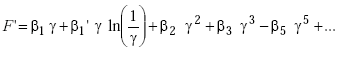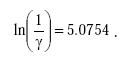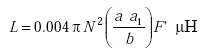U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
Publication Number: FHWA-HRT-06-139
Date: October 2006
|
|
Traffic Detector Handbook:Third Edition—Volume II
APPENDIX B.CURRENT SHEET FORMULA FOR CALCULATION OF LOOP INDUCTANCE
A formula for calculating the inductance produced by a rectangular current sheet is given by(1)
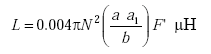 |
(B-1) |
where
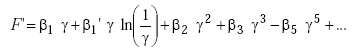 |
(B-2) |
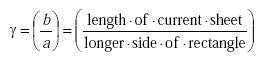 |
(B-3) |
| N = number of turns and |
| α1 = length of shorter side of loop. |
Inductive loops are modeled as very short solenoids. |
The term, “length of current sheet,” is defined as the axial length of a coil or solenoid. For an inductive loop, the length of the current sheet is equivalent to the height of the wires in the slot, as described in the sample calculation that follows. Since the length of the current sheet is very small compared to the longer side of the rectangle, γ is also very small. The factor F’ adjusts for the fact that inductive loops perform as very short solenoids (i.e., the loop area is much greater than the turn spacing).
The values of β are obtained from Table B-1. The factor K that appears in the table is given by
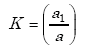 |
(B-4) |
Table B-1. Values of β coefficients for short rectangular solenoids.(2)
| K | β1 | β1’ | β2 | β3 | β5 | β7 |
|---|
| 1.00 |
0.4622 | 0.6366 | 0.2122 | −0.0046 | 0.0046 | −0.0382 |
| 0.95 |
0.4574 | 0.6534 | 0.2234 | −0.0046 | 0.0053 | |
| 0.90 |
0.4512 | 0.6720 | 0.2358 | −0.0046 | 0.0064 | −0.0525 |
| 0.85 |
0.4448 | 0.6928 | 0.2496 | −0.0042 | 0.0080 | |
| 0.80 |
0.4364 | 0.7162 | 0.2653 | −0.0031 | 0.0103 | −0.0831 |
| 0.75 |
0.4260 | 0.7427 | 0.2829 | −0.0010 | 0.0141 | |
| 0.70 |
0.4132 | 0.7730 | 0.3032 | 0.0026 | 0.0198 | −0.1564 |
| 0.65 |
0.3971 | 0.8080 | 0.3265 | 0.0085 | 0.0291 | |
| 0.60 |
0.3767 | 0.8488 | 0.3537 | 0.0179 | 0.0432 | −0.3372 |
| 0.55 |
0.3500 | 0.8970 | 0.3858 | 0.0331 | 0.0711 | |
| 0.50 |
0.3151 | 0.9549 | 0.4244 | 0.0578 | 0.1183 | −0.7855 |
| 0.40 |
0.1836 | 1.1141 | 0.5305 | 0.1697 | 0.3898 | −2.403 |
| 0.30 |
0.0314 | 1.3359 | 0.7074 | 0.5433 | 2.0517 | −7.85 |
| 0.20 |
−0.6409 | 1.9099 | 1.0610 | 2.3230 | 14.507 | 15.51 |
| 0.10 |
−3.2309 | 3.5014 | 2.1220 | 22.5480 | 497.36 | 14280.00 |
SAMPLE INDUCTANCE CALCULATION
An example from reference 1 is used to demonstrate the calculation of the self inductance for a short, three-turn, 6- by 6-foot (1.8- by 1.8-m) loop, using the current sheet model described above.
| The following parameters are used: |
| a1 | = 6 ft = 182.88 cm |
| a | = 6 ft = 182.88 cm |
| N | = 3 turns |
| P | = turn spacing = 150 mils = 0.381 cm |
| b | = N P = (3)(0.381) = 1.143 cm |
| γ = (b/a) | = 1.143/182.88 = 0.00625 cm |
| K | = (a1 / a) = 1. |
From Table B-1,
| | β1 | = 0.4622 |
| | β1’ | = 0.6366 |
| | β2 | = 0.2122 |
| | β3 | = -0.0046 |
| | β5 | = 0.0046 |
| | β7 | = -0.0382. |
Solving Equation B-2 for F’ yields
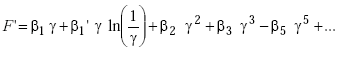 | (B-5) |
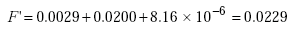 | (B-6) |
where
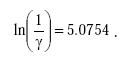 | (B-7) |
Using Equation B-1, the inductance of the loop is found as
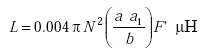 | (B-8) |
or
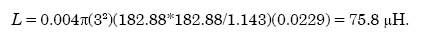 | (B-9) |
REFERENCES
- Grover, F.W. Inductance Calculations. Dover Publications, Inc. 1962.
- Y. Niwa, “A Study of Coils Wound on Rectangular Frames with Special Reference to the Calculation of Inductance,” Research of the Electrotechnical Laboratory, No. 141, Tokyo, Japan, 1924.
Previous | Table of Contents | Next