U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-095
Date: November 2004 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Manual for LS-DYNA Soil Material Model 147PDF Version (1.96 MB)
PDF files can be viewed with the Acrobat® Reader® CHAPTER 1. THEORY MANUALINTRODUCTIONThis document is the final report for the development of the Federal Highway Administration's (FHWA's) soil model implemented into LS-DYNA. This report is in three sections: (1) a description of the justification and detailed theory of the model, (2) a user's manual that was submitted for inclusion in the LS-DYNA user's manual, and (3) examples that show the expected results of the model. The original research plan was submitted to Martin Hargrave of FHWA and the FHWA organized Centers of Excellence in Finite Element Crash Analysis in September 1999. The material model was developed and changes requested by the centers of excellence were implemented in 2000. During this time, the user-defined material models in LS-DYNA were used. The model was verified and preliminary validation took place in 2001. The model was implemented as a standard material model in version 970 of LS-DYNA in February 2002. The soil model in the production version was checked against analyses done with the user-defined version in spring 2002. A user ran identical analyses and other analyses to validate the model in summer 2002. A significant difference between the soil material model discussed in this report and the wood material model discussed in another report is that the wood material model was based on extensive experimental data. In the case of the soil model, there was no material property data available for the applications needed (road-base materials). This lack of data caused the material model to be developed based on the one set of data available and the general behavior of cohesionless soils. In addition, some behaviors could not be validated and default properties for the soils used in road-base testing could not be uniquely defined. The goal of this research was to develop a soil material model in LS-DYNA that will represent the soils used for National Cooperative Highway Research Program (NCHRP) 350 roadside safety hardware testing. In this section of the report, the theory for the soil material model is presented. Investigative work done prior to development of the model is discussed first. The investigative work was for the purpose of determining the critical behaviors of the material that must be included in a model and establishing whether an existing model could be enhanced to meet these requirements or whether a new material model had to be developed. The critical behaviors and how they can be modeled, followed by details of a review of currently used soil material models, are also discussed. Also in this section, model development areas, including details of the algorithms and implementation, are described. PRELIMINARY WORKThe investigative work included determining the critical behaviors of NCHRP 350 soil. Material models already in LS-DYNA were investigated to see if one of them, if enhanced, would be suitable, and what enhancements would be necessary for the modeling of soils in roadside safety applications. Determination of Critical Behaviors Behaviors that were critical to soil modeling in roadside safety applications were determined through discussions with roadside safety testers and analysts, by performing literature reviews, and by studying road-base laboratory test results. Most soil data that have been used for past soil model development in LS-DYNA are from laboratory tests that have relatively high confinement.(5) For roadside safety applications, the soil will have low or no confinement. Therefore, the laboratory data used to evaluate and develop the model must be at low or no confinement. Maximum pressures will be less than 30 megapascals (MPa).(6) Most of the basic triaxial shear test data (from the laboratory) used to determine critical behaviors and develop algorithms have been from the U.S. Army Corps of Engineers (USACE) geological database. The specific soil used is a crushed limestone road base that conforms to NCHRP 350 soil, grade B (see table 1). However, the larger aggregate was removed so that uniform stresses/strains could be achieved in standard specimen sizes for triaxial shear tests. Additional data from the roadside safety testing subcontractor were used to verify and validate the new soil model developed for LS-DYNA. Elastic behavior of soil is isotropic. This requirement is based on the fact that road-base soils are well graded and not stratified. The standard soil is considered to be cohesionless (i.e., it has no tensile strength). This behavior is common to soils that contain little clay. Elastic behavior mainly affects unloading and the isotropic compression (volumetric) behavior because road-base material tends to have very low shear strength at low confinement (< 0.5 MPa). Very little shear stress is needed to initiate nonrecoverable energy dissipation (plasticity and damage). Soil behavior is greatly affected by void ratio, compaction, and excess pore-water pressure. Experimental data for a standard road base show that undrained conditions (high moisture content) can greatly affect the amount of deformation. Compaction tends to increase the initial yield strength and the ultimate strength. The void ratio is directly related to compaction. Reduction in the void ratio increases the strength and the bulk modulus of the soil. Figure 1 shows two commonly used models for yield surfaces. The three axes shown are the three principal stress axes. The generator axis for each surface is the pressure axis. The surface on the left is the Mohr-Coulomb model (a typical soil yield surface) and, for comparison, the surface on the right is the standard Von Mises model (a typical metal yield surface). The yield (onset of plasticity) and ultimate (peak) strength of soil are pressure-dependent. This means that the plasticity surface is dependent on both the pressure and the shear stresses. This behavior differs from metals where the plasticity surface is only a function of the shear stresses. Experimental evidence for cohesionless soil shows that, at low pressures, the yield surface is triangular in the deviatoric plane as shown in figure 2.(3) For the Waterways Experiment Station (WES) road-base soil, the ratio of minimum stress (triaxial extension) to maximum stress (triaxial compression) in the deviatoric plane is 0.70. Table 1. Gradation data for USACE road-base soil tests.
Figure 1 (a) Pressure-dependent (Mohr-Coulomb) and (b) pressure-independent (Von Mises) yield surfaces. Figure 2. Yield surface in deviatoric plane for cohesionless soils. Figure 3 shows the peak principal stress difference versus the average normal stress for the crushed limestone road-base material. The peak principal stress difference is also the maximum shear strength at the given pressure. This plot presents the shear strength as a function of pressure for the road-base material. Notice that for the pressure range indicated in the figure, the shear strength of this soil varies linearly with pressure. Figure 3. Principal stress difference (peak shear strength) versus pressure (average normal stress) for road-base material. At high confinement, the road-base soil can have significant peak shear strength (> 120 MPa). At low confining pressures, the standard soil dilates (expands) near peak shear stresses. At high confining pressures (> 100 MPa), the standard soil will stop expanding. This change in volumetric behavior is one of the reasons for employing a cap model. For roadside safety analysis applications, there are no pressures greater than 30 MPa; thus, it is believed that a cap model is not needed. A fully associative plasticity model predicts dilation of the material after the yield strength is reached. The standard soil at low confining pressures typically exhibits strain softening. That is, at pressures below 30 MPa, the soil strain hardens from the yield stress to the ultimate stress, then the strain softens. Strain softening can be a major source of energy dissipation; thus, it is believed that it must be included in the material model. The strength of the soil increases at high strain rates. No experimental strain rate data were found for road-base materials, but data for cohesionless (sandy) soils show significant strain-rate effects. However, we are not convinced that strain-rate behavior is a critical behavior, because applicable rates are relatively low for roadside safety applications. The moisture content of the soil can affect the elastic moduli, the shear strength, and the softening behavior of the soil. Figure 4 shows the force-deflection curves measured in two steel posts in NCHRP 350 soil bogie tests.(8) The tests were identical except for the moisture content (5 percent versus 26 percent). The peak force for the relatively dry soil was much higher, and the stiffness was much greater. Figure 5 shows the energy absorbed during the two tests. The amount of energy absorbed at a given deflection was much larger for the low-moisture-content NCHRP 350 soil. The effects of moisture are complicated and are different for different soil types. For instance, granular soils with low relative densities show little effect on bulk modulus, while clayey soils show significant effects. Fortunately, the NCHRP 350 soil is granular and the test facilities typically run their tests at a low moisture content (3 percent to 7 percent). However, we believe that the ability to simulate actual field conditions is important, so techniques to simulate moisture effects were implemented. The degree of saturation and the void ratio are critical parameters in the determination of moisture effects. Moisture effects on shear strength can be introduced by including an excess pore-water pressure algorithm. Compaction is the decrease in the void ratio and the increase in the relative density. Compaction in granular soils tends to increase the shear strength slightly and lessen the amount of volumetric strain that causes the onset of excess pore-water pressure effects. Figure 4. Force deflection for two steel posts in soil test with different moisture contents (5 percent and 26 percent). Figure 5. Energy versus deflection for two steel posts in soil bogie test with different moisture contents. Evaluation of the Utility of Models Already in LS-DYNA Several material models available in LS-DYNA were reviewed as possible soil model candidates, from the simplest (material model 5) to the most complex (material model 25). Most of the candidate models in LS-DYNA are extensions of material model 5 (soil and foam). Two of the exceptions to this are model 16 (pseudo-tensor model) and model 25 (geological cap model). Model 5 and its extensions, model 14 (soil and foam with failure), and model 79 (hysteretic soil) are basically an analytical pressure-dependent yield surface. They all must have confinement to be stable (see the LS-DYNA user's manual for model 5). For the roadside application, the top surface of the soil is not confined and is at zero pressure during a significant portion of the analysis. However, both model 5 and model 79 were evaluated with single-element runs. Both of these models were indeed found to be unstable in unconfined states. Material model 14 and model 78 (soil and concrete) are for analyses in high-pressure regions. Model 14 was evaluated previously and it was found that it does not simulate low-/zero-pressure behavior well. Material model 25 (geological cap model) was also evaluated. This model is complex, but does handle low-confinement behavior well. This model was first evaluated with single-element runs. It performed well, it was stable (see figure 6), and it predicted peak stress level accurately. However, model 25 cannot simulate strain softening. Despite this shortcoming, it is the only existing model that could simulate much of the basic behavior needed for roadside safety applications. However, model 25 is very inefficient for this application since it uses a cap surface. Because of the relatively low confinement that soil has in roadside safety applications, a cap surface is not needed Because of the cap/shear surface intersection (non-smooth) in model 25, there are many corners in the yield surface. These corners cause the algorithm to be very complex and inefficient. In addition, model 25 would need extensive enhancements, including:
Based on these observations, it was concluded that none of the existing models are adequate, and it was decided to develop a new soil material model. The theoretical basis for this new model is presented in the next section. Figure 6. Model 25 single-element run, triaxial compression at 3.4 MPa compared to WES data. MODEL DEVELOPMENTThe objectives of the material model development effort in order of priority were: accuracy, robustness, efficiency (speed), and ease of use. The choices made in the model are balanced between these objectives. The following subsections describe the characteristics of the algorithms necessary to model soil for roadside safety applications. Elastic Constitutive Behavior We assumed that the elastic properties of the soil are isotropic. Bulk and shear moduli were used as input parameters. Standard soil tests (i.e., triaxial shear tests and uniaxial strain tests) produce these parameters directly. To simulate the effects of voids, the bulk modulus was made to be a function of volumetric strain. As the volumetric strain increases, the modulus increases to simulate the collapse of voids and the stiffening of the material. The effects of moisture content/excess pore pressure were also simulated with changes to the elastic moduli. As the remaining voids of the soil become filled with moisture, the material becomes more incompressible. To simulate the effects of excess pore-water pressure, a function that involves the nonporous bulk modulus (inverse of soil compressibility), the porosity, and the degree of saturation was used:
where: Ki = nonporous bulk modulus ncu = current porosity = w = volumetric strain corresponding to the volume of air voids =n(1- – S)
D1 = material constant controlling the stiffness before the air voids are collapsed n = porosity of the soil = e = void ratio = S = degree of saturation = 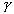 sp, m c, P w = soil density, specific gravity, moisture content, and water density. sp, m c, P w = soil density, specific gravity, moisture content, and water density.
Figure 7 shows the effect of the D1 parameter on the pressure-volumetric strain relationship (bulk modulus). The elastic moduli are used to determine the elastic stresses and the elastic trial stresses. The bulk modulus is always a monotonically increasing value (i.e., j is the time-step index),
Note that the standard practice of treating compressive stresses and strains as positive quantities is followed. Figure 7: Yield Surface Behavior The initial yield surface is where the soil initially starts to dissipate nonrecoverable strain energy. A well-documented yield surface used for soils is the Mohr-Coulomb surface. However, the standard Mohr-Coulomb surface has two significant deficiencies for our use: The first deficiency is that the surface comes to a point (singularity) at the intersection with the pressure axis (zero shear strength). This region of the yield surface is critical in roadside safety applications because of the low confinement. This type of singularity can cause both numerical and efficiency problems in the plasticity algorithm. To ensure an accurate, robust, and efficient algorithm, the yield surface needs to be convex and smooth. Second, the Mohr-Coulomb surface is hexagonal or circular in the deviatoric plane (see figure 8). Based on the experimental evidence, the yield surface should be able to become triangular in shape at low confinement pressures. (9) To correct these deficiencies, a modified Mohr-Coulomb surface was adopted. The yield surface was modified based on the work of Abbo and Sloan.(9) The standard Mohr-Coulomb yield surface, , is represented as:
where: P = pressure
K (
c = amount of cohesion The modified yield surface is a hyperbola fitted to the Mohr-Coulomb surface. At the crossing of the pressure axis (zero shear strength), the modified surface is a smooth surface. At this point, it is perpendicular to the pressure axis. The equation for the modified Mohr-Coulomb surface is:
Here, is a parameter for determining how close the modified surface is fitted to the standard Mohr-Coulomb yield surface. If is zero, then the standard Mohr-Coulomb surface is recovered. The input parameter should be set close to zero, based on numerical considerations. Figure 9 shows the modified Mohr-Coulomb surface in shear stress versus pressure space. It is almost identical to the original surface, except at low shear stresses.
Figure 8. Standard Mohr-Coulomb yield surface in principal stress space.
Figure 9. Comparison of Mohr yield surfaces in shear stress — Pressure space (standard — (A)/green, modified —(B)/red. To remedy the second deficiency, the shape in the deviatoric plane, the standard Mohr-Coulomb K (
Here, cos
Figure 10. Yield surface with e = 0.55. Excess Pore-Water Pressure Behavior For some soils, excess pore-water pressure can make a significant difference on the shear strength of the soil, especially for near-saturated conditions. Because of the loading typical for roadside safety applications (i.e., many soils have low permeability), water in the voids will not have time to flow; therefore, the water will cause an excess pressure increase as the impact load collapses the air voids in the soil. To simulate this behavior, a standard (practical) soil mechanics technique(11) is used for reducing the total pressure, , by the excess pore-water pressure, , to get an "effective pressure":
Figure 11. Effects on pressure because of pore-water pressure. Figure 11 shows how pore-water pressure affects the algorithm for the plasticity surface. The excess pore-water pressure reduces the total pressure, which will lower the shear strength, The water in the voids of the soil causes the excess pore-water pressure. As the air void volume is reduced to zero during loading, the pore-water pressure increases. The water in the remaining voids causes the effective load on the soil particles to be reduced. To calculate the pore-water pressure, , an expression similar to the equation used for the moisture effects on the bulk modulus was used:
where: K sk = bulk modulus for soil without air voids (skeletal bulk modulus) n cur = current porosity = Max[0, (w - Ev) ] w = volumetric strain corresponding to the volume of air voids = n(1-S)
D2 = material constant controlling the pore-water pressure before the air voids are collapsed n = porosity of the soil = e = void ratio = S = degree of saturation =
Pore-water pressure is not allowed to become negative ( u Figure 12 is a plot of the pore pressure versus volumetric strain for different parameter values. With the D2 parameter set relatively high compared to Ksk, there is no pore pressure until the volumetric strain is greater than the strains associated with the air voids. However, as D2 is lowered, the pore pressure starts to increase before the air voids are totally collapsed. The Ksk parameter affects the slope of the post-void collapse pressure-volumetric behavior Parameter D2 can be found from Skempton pore-water pressure parameter B, where B is defined as:(11)
where: Ksk=bulk modulus of the soil without air voids This method does not include the dissipation of excess pore-water pressure as a function of time. The rate of dissipation can be a function of the loading rate and soil parameters, such as permeability. However, at this time, the lack of experimental data on road-base material on typical roadside tests would make this type of dissipative model useless. However, if experimental data and the required parameters for roadside tests become available, then a dissipative model could be easily inserted.
Figure 12. Effects of parameters on pore-water pressure. Strain Hardening Behavior Figure 13 shows the principal stress difference versus principal strain difference results of a triaxial compression test at a lateral stress of 6.9 MPa for a standard soil. The unloading portion of the curve shows that there was very little elastic (recoverable) strain in this test. The nonlinear part of the loading portion of the curve is pre-peak (plastic) hardening. The amount of hardening increases as the lateral confinement increases (i.e., there is less hardening at lower confining pressures). To simulate this nonlinear hardening behavior, the friction angle was increased as a function of the effective plastic strain:
where:
N = fraction of the peak strength internal friction angle where nonlinear behavior begins (0 < N H (the input parameter) determines the stiffness of the nonlinear hardening Figure 14 shows the effect on the yield surface of an increase in
Figure 13. Principal stress difference versus principal strain difference for triaxial compression test at
Figure 14. Hardening of yield surface. Strain Softening Behavior Figure 15 is a plot of the principal stress difference versus axial strain result for the same experiment as shown in figure 13. The principal stress difference softens (i.e., decreases) after it has reached its peak. The area under the curve in figure 15 after the peak stress is reached is the strain energy dissipated by the material because of strain softening. The strain energy dissipated in this post-peak region is almost as great as the strain energy dissipated in the pre-peak region. To simulate this behavior, a continuum damage algorithm was implemented. The strain softening (damage) algorithm is based on the work of J.W. Ju and J.C. Simo. They proposed a strain-energy-based damage criteria.(12-13) The major advantage of their method is that the strain softening is uncoupled from the plasticity algorithm. The plasticity algorithm uses undamaged stresses. This means that the plasticity algorithm can be implemented and verified independently of the damage algorithm.
Figure 15. Principal stress difference versus axial strain for triaxial compression test at For the damage criterion,
where: P = pressure and When
where d = isotropic damage parameter and the damage parameter is found at step j+1 as:
Here, r j+1 is a damage threshold surface, which is updated in this manner:
Typically, the damage, d, varies from 0 to a maximum of 1. However, some soils can have residual strength that is pressure-dependent. The residual strength is represented by , an internal friction angle. The maximum damage allowed is related to the internal friction angle of residual strength by:
If Q res > 0, then d max, the maximum damage, will not reach 1, and the soil will have residual strength. The damage parameter is used to reduce the effective internal stress If damage parameter d is allowed to become 1, then the internal stress is zero, which for a finite element code such as LS-DYNA (explicit) causes the internal forces (element stiffness) to become zero. By not allowing the damage parameter d to become 1, this keeps a residual stiffness in the element. Therefore, by setting When material models include strain softening, special techniques must be used to prevent mesh sensitivity. Mesh sensitivity is the tendency of the finite element model/analysis to produce significantly different results as the element size is reduced. Mesh sensitivity occurs because softening in the model concentrates in one element. As the element size is reduced, the failure becomes localized in smaller volumes; this causes less energy to be dissipated by the softening, leading to instabilities or at least mesh-sensitive behavior. To eliminate or reduce the effects of strain-softening mesh sensitivity, the softening parameter,
Figure 16. Definition of the void formation paramater.
where: Then,
where: If G f is made very small relative to K Strain-Rate Behavior There are some experimental data that suggest that soil strength is strain-rate-dependent. (11) Based on the earlier evaluation of a steel post in soil experiments,(14) strength enhancements caused by high strain rates may not be needed for roadside safety applications. However, since the development and implementation of strain-rate-dependent effects are relatively easy and will not affect the overall efficiency if they are not used, strain-rate effects were implemented into the soil model. The two-parameter Devaut-Lions viscoplastic update algorithm developed by Y. Murray was used. (15) This algorithm interpolates between the elastic trial stress and the inviscid stress. The inviscid stresses are on the plasticity surface Figure 17 shows the behavior of
Figure 17. Zeta versus strain rate for different parameters. INCORPORATION INTO LS-DYNAThe above discussion describes the equations and the form of the soil model. In this section, the implementation of the model into LS-DYNA is discussed. The intermediate equations were determined using the symbolic algebra program Mathematica ®. First, the elastic moduli and undamaged stresses are found (see figure 18). The bulk modulus function needs the current total volumetric strain. The undamaged stresses are recovered from the damaged stresses based on the current value of the damage variable d. Next, the elastic trial stresses are determined (see figure 19Error! Reference source not found.) and it is determined whether the state of stress is within the current yield surface. If it is, the routine bypasses the plasticity algorithm.
Figure 18. Elastic moduli and undamaged stresses.
Figure 19. Elastic trial stresses The total strains are split into elastic and plastic strains:
The stress increment at step j+1 is then:
To compute the stress increments, it is first necessary to determine the plastic strain increments. The latter are determined by assuming an associated flow rule (see figure 20). Note that the gradient of the yield function is taken at the stress state of the previous time step; this is consistent with the explicit algorithm used in LS-DYNA. The explicit form of the gradients is presented in appendix A. The increment in the hardening parameter
Figure 20. Determination of plastic strains.
Figure 21.Update of stresses and history variables.
Figure 22. Viscoplasticity update. Next, the effect of the strain rates on the strength of the material is determined. The effective strain rate must be found and used to determine the viscoplasticity scale factor. If the effective strain rate is less than 0.00001, the step is assumed to be static and the algorithm is skipped. The viscoplasticity scale factor interpolates between the elastic trial stress and the inviscid stress (see figure 22). The strain softening algorithm transforms the effective (undamaged) stresses to the damaged stresses (see figure 23). The damage is assumed to be isotropic. The damage scale factor is determined based on total volumetric strain energy. It is desirable for strain to soften based on tensile volumetric (dilation) strain energy. In this routine, compressive strain values are considered to be positive and, therefore, the increment of volumetric strain energy is subtracted. When the element starts to dilate, the volumetric strain energy starts to increase. The initial damage threshold (a user input parameter) is input with a value close to zero. Finally, the history variable to be plotted is updated, erosion (failure) is determined, and the routine is exited. Once the model was verified and preliminarily validated, the material model source code was implemented into the production version of LS-DYNA in February 2002. We next checked that the soil model was correctly implemented into LS-DYNA. An independent evaluator then began the investigation of the validity of the soil model.
Figure 23. Damage update |