U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-HRT-04-095
Date: November 2004 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Manual for LS-DYNA Soil Material Model 147PDF Version (1.96 MB)
PDF files can be viewed with the Acrobat® Reader® CHAPTER 2. USER'S MANUALThe user's manual was written as the model was being implemented, verified, and validated. The user's manual consists of a user input guide (much like material model sections in the LS-DYNA user's manual); a brief theory manual (LSTC theory manual), which is a condensed version of the first section of this report; and a discussion of the use of the model. Both manuals will be added to an updated LS-DYNA manual. The user's manual addresses the basics of the model, input parameters, and basic equations. Table 2 contains a brief description of the user input variables for the soil model, along with the corresponding symbols used in the LSTC theory manual. The bold text is the LSTC theory manual symbol, which is typically followed by a brief description and then the user input value symbol. The parameters that need to be specified are dependent on the soil and the specific application. Table 2. Input parameters for soil model.
USER INPUT GUIDEFHWA Soil Material Model Input *MAT_FHWA_SOIL_OPTION
This is material type 147. This is an isotropic material with damage and is available for solid elements in LS-DYNA. The model has a modified Mohr-Coulomb surface to determine the pressure-dependent peak shear strength. It was developed for applications involving road-base soils. *MAT_FHWA_SOIL_NEBRASKA It is an option to use the default properties determined for soils used at the University of Nebraska at Lincoln. The default units used for this material are millimeter (mm), millisecond (ms), and kilogram (kg). If different units are desired, the conversion factors must be input. Card Format
*MAT_NCHRP_SOIL_blank Define the following cards: Card Format
THEORY MANUALMAT_FHWA_SOIL A brief discussion of the FHWA soil model is given. The elastic properties of the soil are isotropic. The implementation of the modified Mohr-Coulomb plasticity surface is based on the work of Abbo and Sloan. (9) The model is extended to include excess pore-water effects, strain softening, kinematic hardening, strain-rate effects, and element deletion. The modified yield surface is a hyperbola fitted to the Mohr-Coulomb surface. At the crossing of the pressure axis (zero shear strength), the modified surface is a smooth surface and it is perpendicular to the pressure axis. The yield surface is given as
where: P=pressure
K (
c = amount of cohesion, J3 = third invariant of the stress deviator ahyp = parameter for determining how close to the standard Mohr-Coulomb yield surface the modified surface is fitted If ahyp is input as zero, the standard Mohr-Coulomb surface is recovered. The input parameter ahyp should be set close to zero, based on numerical considerations, but always less than . It is best not to set the cohesion, c, cot To generalize the shape in the deviatoric plane, the standard Mohr-Coulomb K (
where: J3 = third invariant of the stress deviator e = material parameter describing the ratio of triaxial extension strength to triaxial compression strength If e is set to 1, then a circular cone surface is formed. If e is set to 0.55, then a triangular surface is formed. K ( To simulate nonlinear strain hardening behavior, the friction angle is increased as a function of the effective plastic strain:
where:
An = fraction of the peak strength internal friction angle where nonlinear behavior begins, 0 < An The input parameter E1 determines the rate of the nonlinear hardening. If there is no strain hardening, then To simulate the effects of moisture and air voids, including excess pore-water pressure, both the elastic and plastic behaviors can be modified. The bulk modulus is:
where: Ki = nonporous bulk modulus n cur = current porosity = w = volumetric strain corresponding to the volumne of the air voids = n (1-S)
D 1 = material constant controlling the stiffness before the air voids are collapsed n = porosity of the soil = e = void ratio = S = degree of saturation = 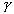 sp, m c, P w = soil density, specific gravity, moisture content, and water density. sp, m c, P w = soil density, specific gravity, moisture content, and water density.
Figure 24 shows the effect of the D 1 parameter on the pressure-volumetric strain relationship (bulk modulus). The bulk modulus will always be a monotonically increasing value, that is:
Note that the model is following the standard practice of assuming that compressive stresses and strains are positive. If the input parameter is zero, then the standard linear elastic bulk modulus behavior is used.
Figure 24. Pressure versus volumetric strain showing the effects of the D subscript 1 parameter. If D1 is not set to zero, the bulk modulus input should be the fully collapsed bulk modulus. To simulate the loss of shear strength caused by excess pore-water effects, the model uses a standard soil mechanics technique(11) of reducing the total pressure, P, by the excess pore-water pressure, u, to get an "effective pressure," P' :
Figure 25. Effects on pressure caused by pore-water pressure. Figure 25 shows how pore-water pressure affects the algorithm for the plasticity surface. The excess pore-water pressure reduces the total pressure, which lowers the shear strength,
where: Ksk = bulk modulus for soil without air voids (skeletal bulk modulus) ncur = current porosity = Max[0, (w-ev)] w = volumetric strain corresponding to the volume of air voids =n(1- S)
D2= material constant controlling the pore-water pressure before the air voids are collapsed D2 n = porosity of the soil = e = void ratio = S = degree of saturation =
The increment pore-water pressure is zero if the incremental mean strain is negative (tensile). Figure 26 is a plot of the pore pressure versus volumetric strain for different parameter values. With the D2 parameter set relatively high compared to Ksk, there is no pore pressure until the volumetric strain is greater than the strains associated with the air voids. However, as D2 is lowered, the pore pressure starts to increase before the air voids are totally collapsed. The Ksk parameter affects the slope of the post-void collapse pressure-volumetric strain behavior The parameter D2 is found from Skempton pore-water pressure parameter B, where B is defined as:(7)
Figure 26. Effects of D subscript 2 and K subscript SK parameters on pore-water pressure. To simulate strain softening behavior, the FHWA soil model uses a continuum damage algorithm. The strain-based damage algorithm is based on the work of J.W. Ju and J.C. Simo. They proposed a strain-based damage criterionthat is uncoupled from the plasticity algorithm.(12,13) For the damage criterion ,
where: d = isotropic damage parameter (diso) The damage parameter is found at step j + 1 as:
where
The mesh-sensitivity parameter, Typically, the damage, d, varies from 0 to a maximum of 1. However, some soils can have a residual strength that is pressure-dependent. The residual strength is represented by The maximum damage allowed is related to the internal friction angle of residual strength by:
If When material models include strain softening, special techniques must be used to prevent mesh sensitivity. Mesh sensitivity is the tendency of the finite element model/analysis to produce significantly different results as the element size is reduced. Mesh sensitivity occurs because the softening in the model is concentrated in one element. As the element size is reduced, the failure becomes localized in smaller volumes, which causes less energy to be dissipated by the softening. This can lead to instabilities or, at least, mesh-sensitive behavior. To eliminate or reduce the effects of strain softening mesh sensitivity, the softening parameter,
with
If Gf is made very small relative to Strain-rate-enhanced strength is simulated by a two-parameter Devaut-Lions viscoplastic update algorithm developed by Y. Murray.(15) This algorithm interpolates between the elastic trial stress (beyond the plasticity surface) and the inviscid stress. The inviscid stresses ( As The model allows element deletion if needed. As the strain softening (damage) increases, the effective stiffness of the element can become very small, causing severe element distortion and "hourglassing." The element can be "deleted" to remedy this behavior. There are two input parameters that affect the point of element deletion. Damlev is the damage threshold where element deletion will be considered. Epsmax is the maximum principal strain where the element will be deleted. Both d MAT_FHWA_SOIL_NEBRASKA This option gives the soil parameters that were used to validate the material model with experiments performed at the University of Nebraska at Lincoln. The units of these default inputs are milliseconds, kilograms, and millimeters. There are no required input parameters except for material ID (MID). If different units are desired, the appropriate unit conversion factors can be input. DISCUSSION OF SOIL MODEL USEMaterial models for geomaterials (soils, concrete, rock, etc.) tend to be complex. The determination of the input parameters for the models is complicated. In addition, modeling different loading conditions and accurate simulation of boundary conditions add to the complexity involved in using these material models. There are two methods that are typically used to determine the material input variables for soils. The most accurate method is to perform laboratory tests that include both triaxial compression and uniaxial strain tests. These tests can be used to determine the elastic moduli, yield surface parameters, and softening parameters. Typically, these tests use drained soil conditions. Laboratory tests with undrained soil conditions can be used to determine the pore-water effects. A second method is to use full-scale testing of the specific application (e.g., a bogie impacting a steel post) to fit the parameters in a trial-and-error method. This method requires more time by the analyst. Since the soil model is nonlinear, there may not be a set of unique input parameters that can be determined. Compaction of the soil is typically used to remove some of the air voids that exist in disturbed soils. However, the density, pore-water effects, stiffness, and strength are also changed upon compacting the soil. To simulate compaction in highway safety applications where the soil is exposed, we recommend that the values for the soil density, pore-water effects, stiffness, and strength be modified. Applying pressure to the ground surface to account for the effects of compaction is a less accurate method that will incorrectly simulate how the soil is deformed at the surface. In full-scale testing or applications, the soil typically extends to infinity. Analyses typically do not extend to infinity, so some type of boundary condition must be applied to the exterior surfaces of a soil analysis model (except for soil surfaces exposed to atmospheric pressure). Standard boundaries reflect dynamic disturbances (stress waves), which does not happen in the real applications. Such reflections can cause serious contamination of the analysis results. Exterior boundaries for analyses involving soil need a nonreflecting boundary. A partial nonreflecting boundary exists in LS-DYNA. This boundary is an impedance-matching boundary, which is only good for high-frequency (highly transient) behavior. At this time, there is no nonreflecting boundary that matches both low- (quasi-static) and high- (highly transient) frequency behaviors. Also, only linear behavior is assumed. Thus, to use the current nonreflecting boundary, the material near the boundaries must only behave linearly. Also, the nonreflecting boundary should only experience high-frequency behavior. |