|
Previous | Table of Contents | Next
Appendix D-Proposed Revisions To The AASHTO LRFD Bridge Design Specifications
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 3.5.1-1 |
Item No. 1
Revise the unit weight of concrete in Table 3.5.1-1 as follows:
Plain Concrete Lightweight 0.110 KCF
Sand-Lightweight 0.120 KCF
Normal Weight fc' ≤ 5.0 KSI 0.145 KCF
5.0 < fc' ≤ 15.0 KSI 0.140 + 0.001 fc' KCF
Item No. 2
Revise C3.5.1 as follows:
Table 1 provides traditional unit weights. The unit weight of granular materials depends upon the degree of compaction and water content. The unit weight of concrete is primarily affected by that the unit weight of the aggregate, which varies by geographical location, and increases with concrete compressive strength. The unit weight of reinforced concrete is generally taken as 0.005 KCF greater than the unit weight of plain concrete. The values provided for wood include the weight of mandatory preservatives. The weight of transit rails, etc., is to be used only for preliminary design.
Item No. 3
Add the following to 3.3 Notation
3.3.1 General
fc' = specified compressive strength of concrete for use in design (KSI) (3.5.1) |
Other Affected Articles |
5.4.2.4 |
Background |
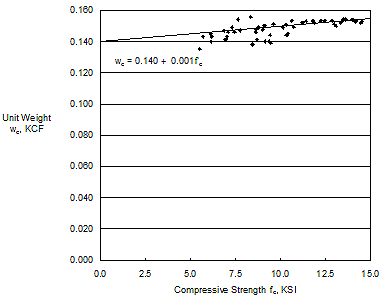
Variation of unit weight with concrete compressive strength.
Analysis of data from the FHWA Showcase projects and other sources indicates a trend that the unit weight of concrete increases as concrete strength increases.(1,2,3) Unit weights range from about 0.140 to 0.155 KCF (2.24 to 2.48 Mg/m3) with an average increase of about 0.001 KCF for every 1.0 KSI increase in compressive strength (2.3 kg/m3 for every 1 MPa). The proposed change recognizes this increase and differentiates between the unit weight of plain and reinforced concrete. |
Anticipated Effect on Bridges |
More precise calculation of dead load.
|
References |
- High Performance Concrete, Compact Disc, Federal Highway Administration, Version 3.0, February 2003.
- Burg, R. G. and Ost, B. W., "Engineering Properties of Commercially Available High-Strength Concretes," PCA Research and Development Bulletin RD104T, Portland Cement Association, Skokie, IL, 1992.
- Burg, R. G. and Fiorato, A. E., "High-Strength Concrete in Massive Foundation Elements," PCA Research and Development Bulletin RD117, Portland Cement Association, Skokie, IL, 1999.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.1 |
In 5.1 Scope, revise first paragraph as follows:
The provisions in this section apply to the design of bridge and retaining wall components constructed of normal density or lightweight concrete and reinforced with steel bars, welded wire fabric reinforcement, and/or prestressing strands, bars, or wires. The provisions are based on concrete strengths varying from 2.4 KSI to 10.0 KSI, except as noted.
|
Other Affected Articles |
5.4.2.1 |
Background |
- Both welded wire fabric reinforcement and prestressing wire are used in concrete members. Article 5.11 already addresses the development, anchorage, and splices of welded wire fabric.
- Revisions are being proposed that will increase the maximum compressive strength for which some provisions are applicable.
|
Anticipated Effect on Bridges |
Recognize the use of these materials in bridge members.
|
References |
None
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.3 |
Revise 5.3 Notation for fc' as follows:
fc' = specified compressive strength of concrete for use in design (KSI) (5.4.2.1).
|
Other Affected Articles |
None |
Background |
For the design purposes of section 5, the concrete age is not important. The designer should specify the age based on the anticipated strength development of the concrete and the intended application. |
Anticipated Effect on Bridges |
Allow more economical construction by avoiding strength developments that are not required for the intended application. |
References |
None
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or (X) Addition ( ) SI ( ) US (X) both versions C5.4.1 |
In C5.4.1, revise second paragraph as follows:
Occasionally, it may be appropriate to use materials other than those included in the AASHTO LRFD Bridge Construction Specifications; for example, when concretes are modified to obtain very high strengths through the introduction of special materials, such as:
- Silica fume,
- Cements other than Portland or blended hydraulic cements,
- Proprietary high early strength cements,
- Ground granulated blast-furnace slag and
- Other types of reinforcing materials.
In these cases the specified properties of such materials should be measured using the testing procedures defined in the contract documents.
|
Other Affected Articles |
AASHTO LRFD Bridge Construction Specifications 8.3.7 |
Background |
- Ground granulated blast-furnace slag has been added to the list since it is used in HPC in bridge construction and is currently not covered in the Bridge Construction Specifications.(1)
- The last paragraph has been revised to identify where the tests are defined.
|
Anticipated Effect on Bridges |
Allow the use of ground granulated blast-furnace slag.
|
References |
- High Performance Concrete, Compact Disc, Federal Highway Administration, Version 3.0, February 2003.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or (X) Addition ( ) SI ( ) US (X) both versions 5.4.2.1 |
Item No. 1.
In 5.4.2.1 Compressive Strength, revise second paragraph as follows:
Design concrete strengths above 10.0 KSI shall be used only when allowed by specific articles or when physical tests are made to establish the relationships between the concrete strength and other properties. Specified concrete with strengths below 2.4 KSI should not be used in structural applications.
Item No. 2
In 5.4.2.1 Compressive Strength, revise the sixth paragraph as follows:
The sum of Portland cement and other cementitious materials shall be specified not to exceed 800 PCY except for Class P(HPC) where the sum of portland cement and other cementitious materials shall be specified not to exceed 1000 PCY.
|
Other Affected Articles |
Item No. 1
All those that reference strengths greater than 10.0 KSI
Item No. 2
Table C5.4.2.1-1 |
Background |
Item No. 1
Ready-mixed concretes with actual compressive strengths in excess of 10 KSI (70 MPa) have been available for many years. These strengths can now be achieved in precast, prestressed concrete. In three FHWA-sponsored HPC projects, strengths in excess of 10 KSI (70 MPa) were specified and successfully achieved.(1) Age of 28 days has been eliminated since concrete age is not important for use in design.
Various revisions to other articles are being proposed. Where research has shown that existing articles or revised articles are applicable to concrete members with strengths in excess of 10 KSI (70 MPa), the use of higher strengths should be allowed without the need for more physical tests.
Item No. 2
Many high-strength concretes require a cementitious materials content in excess of 800 PCY to achieve the specified strength.(1) |
Anticipated Effect on Bridges |
Allow longer span lengths, wider girder spacings, or shallower sections through the use of higher strength concrete.
|
References |
- High Performance Concrete, Compact Disc, Federal Highway Administration, Version 3.0, February 2003.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
( ) Revision or (X) Addition ( ) SI ( ) US (X) both versions LRFD 5.4.2.1-1 |
Item No. 1
In Table C5.4.2.1-1, add the following two new classes of high performance concrete:
| Class of Concrete |
Minimum Cement Content |
Maximum W/CM Ratio |
Air Content Range |
Coarse Aggregate |
Compressive Strength |
| PCY |
LBS Per LBS |
% |
Nominal Size, Square Size |
KSI |
P(HPC) |
(1) |
0.40 |
As specified in the contract |
0.75-IN. to
No. 4 |
> 6.0 as specified in the contract |
A(HPC) |
(1) |
0.45 |
As specified in the contract |
(1) |
4.0 |
- Minimum cementitious materials content and coarse aggregate size to be selected to meet other performance criteria specified in the contract.
Item No. 2
In C5.4.2.1 add two new descriptions to the fourth paragraph as follows:
Class P(HPC) concrete is intended for use in prestressed concrete when strengths in excess of 6.0 KSI are specified and should always be used for specified concrete strengths greater than 10.0 KSI.
Class A(HPC) concrete is used in cast-in-place substructures and superstructures when low permeability or other performance characteristics are specified.
|
Other Affected Articles |
AASHTO LRFD Bridge Construction Specifications Table 8.2.2-1 and 8.4.3 |
Background |
With high performance concrete, it is desirable that the specifications be performance based. The introduction of two new classes of concrete is a move in this direction. Class P(HPC) is intended for use in prestressed concrete members with a specified concrete compressive strength greater than 6.0 KSI (41 MPa). Class A(HPC) is intended for use in cast-in-place construction where performance criteria in addition to concrete compressive strengths are specified. Other criteria might include shrinkage, chloride permeability, freeze-thaw resistance, deicer scaling resistance, abrasion resistance, or heat of hydration.(1,2)
The proposed change to the heading of the third column will affect all classes of concrete listed in the existing table and makes the table more consistent with the state-of-the-art of concrete technology.
Square Size of Openings has been changed to Nominal Size because the listed quantities are aggregate sizes.
The requirement to measure concrete strength at 28 days has been deleted because later ages are more relevant for high-strength concrete. The designer should specify the age based on the anticipated strength development of the concrete and the intended application.
For both classes of concrete, a minimum cement content is not included since this should be selected by the producer based on the specified performance criteria. A maximum water/cementitious materials has been retained to be consistent with the existing water/cement ratios for Class P and Class A concretes. For Class P(HPC) concrete, a maximum size of coarse aggregate is specified since it is difficult to achieve the higher concrete compressive strengths with aggregates larger than 3/4 in (19 mm). For Class A(HPC) concrete, the maximum aggregate size should be selected by the producer based on the specified performance criteria. |
Anticipated Effect on Bridges |
Encourage the use of high performance concrete with higher strength, lower permeability, or other properties. |
References |
- Goodspeed, C. H., Vanikar, S., and Cook, R., "High Performance Concrete Defined for Highway Structures," Concrete International, Vol. 18, No. 2, February 1996, pp. 62-67.
- High Performance Concrete, Compact Disc, Federal Highway Administration, Version 3.0, February 2003.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.4.2.3 |
Item No. 1
Revise 5.4.2.3 as follows:
5.4.2.3 Shrinkage and Creep
5.4.2.3.1 General
Values of shrinkage and creep, specified herein and in Articles 5.9.5.3 and 5.9.5.4, shall be used to determine the effects of shrinkage and creep on the loss of prestressing force in bridges other than segmentally constructed ones. These values in conjunction with the moment of inertia, as specified in Article 5.7.3.6.2, may be used to determine the effects of shrinkage and creep on deflections. The provisions of Article 5.4.2.3 shall be applicable for specified concrete strengths up to 15.0 KSI.
When mix-specific data are not available, estimates of shrinkage and creep may be made using the provisions of Articles 5.4.2.3.2 and 5.4.2.3.3 or other acceptable prediction methods.
For segmentally constructed bridges, a more precise estimate shall be made, including the effect of:
- Specific materials,
- Structural dimensions,
- Site conditions,
- Construction methods, and
- Concrete age at various stages of erection.
5.4.2.3.2 Creep
The creep coefficient may be taken as:
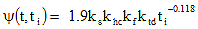 (5.4.2.3.2-1) (5.4.2.3.2-1)
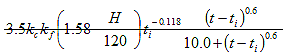
for which:
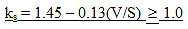 (5.4.2.3.2-2) (5.4.2.3.2-2)
khc = 1.56 - 0.008H (5.4.2.3.2-3)
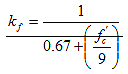
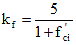 (5.4.2.3.2-4) (5.4.2.3.2-4)
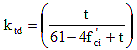 (5.4.2.3.2-5) (5.4.2.3.2-5)
where:
H = relative humidity (%). In the absence of better information, H may be taken from Figure 5.4.2.3.3-1.
ks = factor for the effect of the volume-to-surface ratio of the component
kf = factor for the effect of concrete strength
khc = humidity factor for creep
ktd = time development factor
t = maturity of concrete (Day), defined as age of concrete between time of loading for creep calculations, or end of curing for shrinkage calculations, and time being considered for analysis of creep or shrinkage effects.
ti = age of concrete when load is initially applied (Day)
V/S = volume-to-surface ratio
f'ci = specified compressive strength of concrete at time of prestressing for pretensioned members and at time of initial loading for non-prestressed members. If concrete age at time of initial loading is unknown at design time,
f'ci , may be taken as 0.80 fc' (KSI)
In determining the maturity of concrete at initial loading, ti, one day of accelerated curing by steam or radiant heat may be taken as equal to seven days of normal curing.
The surface area used in determining the volume to area ratio should include only the area that is exposed to atmospheric drying. For poorly ventilated enclosed cells, only 50 percent of the interior perimeter should be used in calculating the surface area. For pretensioned stemmed members (I‑beams, T-beams, and box beams), with an average web thickness of 6 to 8 IN, the value of ks may be taken as 1.00.
5.4.2.3.3 Shrinkage
For concretes devoid of shrinkage-prone aggregates, the strain due to shrinkage, 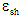 , at time, t, may be taken as: , at time, t, may be taken as:
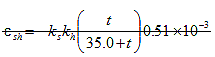
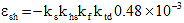 (5.4.2.3.3-1) (5.4.2.3.3-1)
for which:
khs = (2.00 - 0.014 H) (5.4.2.3.3-2)
where:
t = drying time(Day)
= size factor
khs = humidity factor for shrinkage
If the moist-cured concrete is exposed to drying before five days of curing have elapsed, the shrinkage as determined in Equation 1 should be increased by 20 percent.
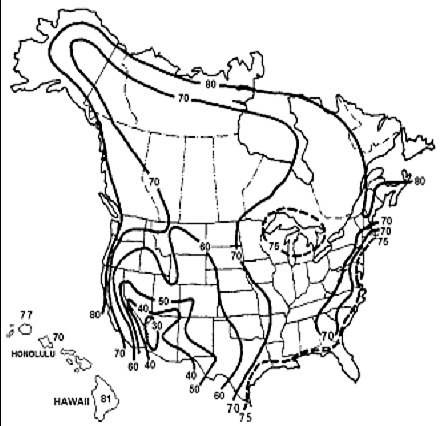
Figure 5.4.2.3.3-1 - Annual Average Ambient Relative Humidity in Percent
Item No. 2
Revise C5.4.2.3 as follows:
C5.4.2.3.1
Creep and shrinkage of concrete are variable properties that depend on a number of factors, some of which may not be known at the time of design.
Without specific physical tests or prior experience with the materials, the use of the empirical methods referenced in these Specifications cannot be expected to yield results with errors less than ± 50 percent.
C5.4.2.3.2
The methods of determining creep and shrinkage, as specified herein and in Article 5.4.2.3.3, are based on Huo et al. (2001), Al-Omaishi (2001), Tadros (2002), and Collins and Mitchell (1991). These methods are based on the recommendation of ACI Committee 209 as modified by additional recently published data.
Other applicable references include Rusch et al. (1983), Bazant and Wittman (1982), and Ghali and Favre (1986).
The creep coefficient is applied to the compressive strain caused by permanent loads in order to obtain the strain due to creep.
Creep is influenced by the same factors as shrinkage, and also by:
- Magnitude and duration of the stress,
- Maturity of the concrete at the time of loading, and
- Temperature of concrete.
Creep shortening of concrete under permanent loads is generally in the range of 1.5 0.5 to 4.0 times the initial elastic shortening, depending primarily on concrete maturity at the time of loading.
Figure 1 is based on the equation below (PCI 1977):
The factors for the effects of volume-to-surface ratio are an approximation of the following formulas:
For creep:
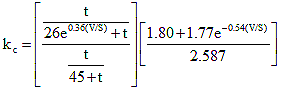 (C5.4.2.3.2-1) (C5.4.2.3.2-1)
For shrinkage:
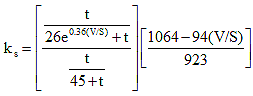 (C5.4.2.3.2-2) (C5.4.2.3.2-2)
The maximum V/S ratio considered in the development of Equations C1 and C2 was 6.0 IN. Ultimate creep and shrinkage are less sensitive to surface exposure than intermediate values at an early age of concrete. For accurately estimating intermediate deformations of such specialized structures as segmentally constructed balanced cantilever box girders, it may be necessary to resort to experimental data or use the more detailed Equations C5.4.2.3.2-1 and C5.4.2.3.2-2.
C5.4.2.3.3
Shrinkage of concrete can vary over a wide range from nearly nil if continually immersed in water to in excess of 0.0008 for thin sections made with high shrinkage aggregates and sections that are not properly cured.
Shrinkage is affected by:
- Aggregates characteristics and proportions,
- Average humidity at the bridge site,
- W/C ratio,
- Type of cure,
- Volume to surface area ratio of member, and
- Duration of drying period.
Large concrete members may undergo substantially less shrinkage than that measured by laboratory testing of smaller specimens of the same concrete. The constraining effects of reinforcement and composite actions with other elements of the bridge tend to reduce the dimensional changes in some components.
Item No. 3
Add the following to Section 5 References:
Huo, X. S., Al-Omaishi, N., and Tadros, M. K., "Creep, Shrinkage, and Modulus of Elasticity of High Performance Concrete," ACI Materials Journal, Vol. 98, No. 6, November-December 2001, pp. 440-449.
Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph.D. Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
Tadros, M. K., Al-Omaishi, N., Seguirant, S. P, and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
|
Other Affected Articles |
5.9.5 |
Background |
Recent research has indicated that high-strength concrete undergoes less ultimate creep and shrinkage than conventional concrete.(1-3) Creep and shrinkage develop relatively more rapidly in higher strength concrete than conventional concrete. The revised formulas take these effects into account, yet produce comparable results to preceding formulas for a concrete strength at release, f'ci, of 4.0 KSI or a concrete strength at service of 5.0 KSI. Due to the high variability of creep and shrinkage and due to the limitation imposed on applicability of the methods presented herein, some of the correction factors (e.g. the relative humidity factor) were unified between creep and shrinkage, and some were simplified (e.g. the volume/surface ratio factor). All factors were reformulated such that they are equal to unity when average conditions exist, e.g. concrete strength at release = 4 KSI, H = 70 percent and V/S ratio = 3.5. The proposed formulas yield approximately the same results as the current formulas when f'ci = 0.8f'c = 4 KSI. The proposed revisions are the results of NCHRP Project 18-07.(3) |
Anticipated Effect on Bridges |
More realistic results of prestress losses and deflections, especially when high-strength concrete is used.
|
References |
- Huo, X. S., Al-Omaishi, N., and Tadros, M. K., "Creep, Shrinkage, and Modulus of Elasticity of High Performance Concrete," ACI Materials Journal, Vol. 98, No. 6, November-December 2001, pp. 440-449.
- Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph. D. Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
- Tadros, M. K., Al-Omaishi, N., Seguirant, S. P, and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.4.2.4 |
Item No. 1
Revise 5.4.2.4 as follows:
5.4.2.4 Modulus of Elasticity
In the absence of measured data, the modulus of elasticity, Ec, for concretes with unit weights between 0.090 and 0.155 KCF and specified compressive strengths up to 15.0 KSI may be taken as:
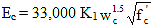 (5.4.2.4-1) (5.4.2.4-1)
where:
K1 = factor for type of aggregate to be taken as 1.0 unless determined by physical tests
wc = unit weight of concrete (KCF)
When the measured unit weight of concrete is unknown, wc for normal weight concrete may be taken as 0.140 + 0.001 fc' but not less than 0.145 KCF.
fc' = specified compressive strength of concrete (KSI)
Item No. 2
Add the following at the end of C5.4.2.4:
Test data show that the modulus of elasticity of concrete is influenced by the stiffness of the aggregate. The factor K1 is included to allow the calculated modulus to be adjusted for different types of aggregate and local materials. Unless a value has been determined by physical tests, K1 should be taken as 1.0. Use of a measured K1 factor permits a more accurate prediction of modulus of elasticity and other values that utilize it. The value of K1 can be determined by measuring Ec, wc, and f'c for a range of concrete strengths using the same aggregates and then calculating the optimum value of K1 to fit the measured values.
Test data shows that the unit weight of normal weight concrete increases by about 0.001 KCF for each 1.0 KSI increase in compressive strength.
Item No. 3
In 5.3 Notation, add the following:
K1 = correction factor for type of aggregate to be taken as 1.0 unless determined by physical tests (5.4.2.4).
|
Other Affected Articles |
3.5.1
All articles that include Ec (Changes are not needed.) |
Background |
Using a significant amount of test data, NCHRP Project 18-07 identified that the accuracy of the existing equation for predicting modulus of elasticity can be improved by the proposed modifications.(1) A more accurate prediction of modulus of elasticity is needed in calculating prestress losses and camber of high-strength concrete girders as the values are larger than for conventional strength concrete girders. |
Anticipated Effect on Bridges |
More accurate prediction of prestress losses and camber.
|
References |
- Tadros, M. K., Al-Omaishi, N., Seguirant, S. P, and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.4.2.6 |
Item No. 1
Revise 5.4.2.6 as follows:
5.4.2.6 Modulus of Rupture
Unless determined by physical tests, modulus of rupture, fr, in KSI, for specified concrete strengths up to 15.0 KSI may be taken as:
When physical tests are used to determine modulus of rupture, the tests shall be performed in accordance with AASHTO T 97 "Standard Method of Test for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading)" and shall be performed on concrete using the same proportions and materials as specified for the structure.
Item No. 2
Add the following to the beginning of C5.4.2.6:
Data show that most modulus of rupture values are between 0.24 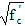 and 0.37 and 0.37 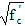 . It is appropriate to use the lower bound value when considering service load cracking. The purpose of the minimum reinforcement in article 5.7.3.3.2 is to assure that the nominal moment capacity of the member is at least 20 percent greater than the cracking moment. Since the actual MOR could be as much as 50 percent greater than 0.24 . It is appropriate to use the lower bound value when considering service load cracking. The purpose of the minimum reinforcement in article 5.7.3.3.2 is to assure that the nominal moment capacity of the member is at least 20 percent greater than the cracking moment. Since the actual MOR could be as much as 50 percent greater than 0.24 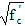 the 20 percent margin of safety could be lost. Using an upper bound is more appropriate in this situation. the 20 percent margin of safety could be lost. Using an upper bound is more appropriate in this situation.
The properties of higher strength concretes are particularly sensitive to the constitutive materials. If test results are to be used in design, it is imperative that tests be made using concrete with not only the same mix proportions, but also the same materials as the concrete used in the structure.
|
Other Affected Articles |
5.7.3.3.2 (No change required)
5.7.3.4 (No change required)
5.7.3.6.2 (No change required) |
Background |
Item No. 1
The value of 0.24 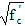 has been traditionally used for modulus of rupture (MOR) for concrete. Data show that this value greatly underestimates the MOR at higher compressive strengths. ACI 363 indicates that a value for MOR of 0.37 has been traditionally used for modulus of rupture (MOR) for concrete. Data show that this value greatly underestimates the MOR at higher compressive strengths. ACI 363 indicates that a value for MOR of 0.37 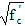 could be used for concrete compressive strengths from 3 to 12 KSI.(1) However, examination of other data shows that most MOR values fall between these two limits.(2-10) Thus, the AASHTO value of 0.24 could be used for concrete compressive strengths from 3 to 12 KSI.(1) However, examination of other data shows that most MOR values fall between these two limits.(2-10) Thus, the AASHTO value of 0.24 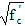 appears to be an appropriate lower bound while the ACI 363 value of 0.37 appears to be an appropriate lower bound while the ACI 363 value of 0.37 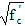 appears to be an appropriate upperbound. Since the cracking moment is directly proportional to the MOR, use of these values yields lower and upper limits of the cracking moment. It is appropriate to use the lower bound value of the MOR when considering service load stresses, serviceability (whether a member is cracked and possible crack widths), or deflections, where lower values of a cracking moment yield more critical quantities. However, the upper bound value is more appropriate for determining minimum amounts of reinforcement. The purpose of the minimum reinforcement in 5.7.3.3.2 is to assure that the nominal moment capacity of member is at least 20 percent greater than the cracking moment. If the cracking moment is too close to the nominal moment capacity, the beam could fail in a brittle manner. Since the data show that the actual MOR could be as much as 50 percent greater than the lower bound MOR, the actual cracking moment could be as much as 50 percent greater than that calculated using the lower bound MOR. This effectively removes the 20 percent margin of safety. Using the upper bound value of MOR alleviates this problem. appears to be an appropriate upperbound. Since the cracking moment is directly proportional to the MOR, use of these values yields lower and upper limits of the cracking moment. It is appropriate to use the lower bound value of the MOR when considering service load stresses, serviceability (whether a member is cracked and possible crack widths), or deflections, where lower values of a cracking moment yield more critical quantities. However, the upper bound value is more appropriate for determining minimum amounts of reinforcement. The purpose of the minimum reinforcement in 5.7.3.3.2 is to assure that the nominal moment capacity of member is at least 20 percent greater than the cracking moment. If the cracking moment is too close to the nominal moment capacity, the beam could fail in a brittle manner. Since the data show that the actual MOR could be as much as 50 percent greater than the lower bound MOR, the actual cracking moment could be as much as 50 percent greater than that calculated using the lower bound MOR. This effectively removes the 20 percent margin of safety. Using the upper bound value of MOR alleviates this problem.
The existing provisions of the code allow the use of measured values for the modulus of rupture in design calculations. The properties of higher strength concretes are particularly sensitive to the constitutive materials. In many specifications, structural concrete is specified by a class or type with given proportions. The actual constitutive materials are often specified in broad terms rather then being specified as specific materials. Thus, a given type or class of concrete could be made with any one of a number of different aggregates, cements or admixtures. However, a concrete made with crushed limestone will have different properties from a concrete with the same proportions but using a gravel aggregate especially at higher compressive strengths. If test results are to be used in design, it is imperative that tests be made using concrete with not only the same proportions, but the same materials as used in the actual structure. |
Anticipated Effect on Bridges |
This change provides a more reasonable estimate of the cracking moment, Mcr. The cracking moment is used to assess minimum reinforcement requirements for beams (5.7.3.3.2), to determine if crack control reinforcement is needed in slabs (5.7.3.4), and to determine the effective moment of inertia for deflection calculations (5.7.3.6.2).
|
References |
- ACI Committee 363, "State-of-the-Art Report on High-Strength Concrete (ACI 363R-92)," American Concrete Institute, Farmington Hills, MI, 1992, 55 pp.
- Price, W. H., "Factors Influencing Concrete Strength," Journal of the American Concrete Institute, Vol. 47, February 1951, pp. 417-432.
- Walker, S. and Bloem, D. L., "Effect of Aggregate Size on Properties of Concrete," Journal of the American Concrete Institute, Vol. 57, No. 3, September 1960, pp. 283-98.
- Zia, P., Leming, M. L., Ahmad, S., Schemmel, J. J., Elliot, R. P., and Naaman, A. E., Mechanical Behavior of High Performance Concrete, Vol. 1 - Summary Report, SHRP Report C-361, Strategic Highway Research Program, National Research Council, Washington, D. C., 1993.
- Zia, P., Leming, M. L., Ahmad, S., Schemmel, J. J., and Elliot, R. P., Mechanical Behavior of High Performance Concrete, Vol. 2, - Production of High Performance Concrete SHRP Report C‑362, Strategic Highway Research Program, National Research Council, Washington, D. C., 1993.
- Zia, P., Ahmad, S., Leming, M. L., Schemmel, J. J., and Elliot, R. P., Mechanical Behavior of High Performance Concrete, Vol. 3 - Very Early Strength Concrete, SHRP Report C-363, Strategic Highway Research Program, National Research Council, Washington, D. C., 1993.
- Zia, P., Ahmad, S., Leming, M. L., Schemmel, J. J., and Elliot, R. P., Mechanical Behavior of High Performance Concrete, Vol. 4 - High Early Strength Concrete, SHRP Report C-364, Strategic Highway Research Program, National Research Council, Washington, D. C., 1993.
- Zia, P., Ahmad, S., Leming, M. L., Schemmel, J. J., and Elliot, R. P., Mechanical Behavior of High Performance Concrete, Vol. 5 - Very High Strength Concrete, SHRP Report C-365, Strategic Highway Research Program, National Research Council, Washington, D. C., 1993.
- Khan, A. A., Cook, W. D., and Mitchell, D., "Tensile Strength of Low, Medium, and High-Strength Concretes at Early Ages," ACI Materials Journal, Vol. 93, No. 5, September-October 1996, pp. 487-493.
- High Performance Concrete, Compact Disc, Federal Highway Administration, Version 3.0, February 2003.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.4.6.2 |
Revise 5.4.6.2 Size of Ducts, as follows:
The inside diameter of ducts shall be at least 0.25-IN larger than the nominal diameter of single bar or strand tendons. For multiple bar or strand tendons, the inside cross-sectional area of the duct shall be at least 2.0 times the net area of the prestressing steel with one exception where tendons are to be placed by the pull-through method, the duct area shall be at least 2.5 times the net area of the prestressing steel.
The size of ducts shall not exceed 0.4 times the least gross concrete thickness at the duct. For precast, pretensioned concrete beams, this requirement may be waived if the clear cover to the duct is not less than 1.5 IN.
|
Other Affected Articles |
None |
Background |
The limit on maximum duct diameter of 0.4 times web thickness is unnecessarily restrictive in spliced I-girders, where high-strength concrete is increasingly used in practice. Many bridges have already been constructed with 7-in (175-mm) thick webs using 15 0.6-in (15.2-mm) strand tendons.(1-4) The Esker Overhead Bridge had 6-in (152-mm) thick web I-girders and 12 0.6-in (15.2-mm) strand tendons. Most of these bridges do not meet the 0.4 limit provision. The bridges have been performing satisfactorily. In all cases, the minimum web width has been set as the sum of twice the minimum concrete cover plus two stirrup bar diameters plus one duct diameter. The previous requirement of duct diameter not exceeding 0.4 web width is based on segmental box girder construction where the entire bridge cross section consists of two or three webs and where the spans are relatively large. Precast, prestressed I-girders are plant produced and the cross section of the bridge generally consists of at least four I-girders. Application of the 0.4 rule to spliced I‑girders unnecessarily increases the web width and therefore the weight of the girder. This considerably impairs the cost-effectiveness of spliced I-girder systems as they become increasingly popular. |
Anticipated Effect on Bridges |
The proposed revision brings consistency between the LRFD Specifications and practice. It encourages more utilization of high-strength spliced girder bridges without designers having to supercede the requirements of this section.
|
References |
- "State-of-the-Art Report of Spliced Girder Bridges," PCI, 1994, 134 pp.
- Janssen, H. H. and Spaans, L., "Record Span Spliced Bulb-Tee Girders Used in Highland View Bridge," PCI Journal, Vol. 39, No. 1, January/February 1994, pp. 12-19.
- Fitzgerald, J. B. and Stelmark, T. W., "Spliced Bulb-Tee Girders Bring Strength and Grace to Pueblo's Main Street Viaduct," PCI Journal, Vol. 41, No. 6, November/December 1996, pp. 40-54.
- PCI Bridge Design Manual, Chapter 11, (to be published).
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.5.4.1 5.9.4.1.1 |
Item No. 1
Revise the first paragraph of 5.5.4.1 as follows:
5.5.4 Strength Limit State
5.5.4.1 General
The strength limit state issues to be considered shall be those of strength and stability. For pretensioned concrete members, the strength limit state shall be considered the primary design method for member capacity in compression under all load combinations including prestress transfer, lifting, erection, deck placement, dead loads, and live loads.
Item No. 2
Revise 5.9.4.1.1 as follows:
5.9.4.1.1 Compression Stresses
The compressive stress limit for pretensioned and post-tensioned concrete components, including segmentally constructed bridges, shall be 0.6fci(KSI). This limit may be waived if the strength design provisions of Articles 5.7.2, 5.7.3.1.1, and 5.7.3.2.1 are satisfied.
Item No. 3
Revise the first paragraph of 5.9.4.2.1 as follows:
5.9.4.2.1 Compression Stresses
Compression shall be investigated using the Service Limit State Load Combination 1 specified in Table 3.4.1-1. The limits in Table 1 shall apply. Compressive stress limits specified in Table 1 may be waived for flexural member if the strength limit state provisions according to Article 5.7.3.2 are satisfied at prestress transfer, at time of cast-in-place deck placement, and time of application of full dead load plus live loads. Further, the deflection and camber at various loading stages must be checked, using conventional analysis methods, for various design and construction limitations.
|
Other Affected Articles |
5.5.3.1 |
Background |
Working stress design should be replaced consistently with the strength design method for design of prestressed concrete members.(1) Precast pretensioned members, in particular, are produced in a plant-controlled environment. Signs of inadequate concrete compressive strength are observed immediately. Linear stress analysis and compressive stress limits do not realistically represent member failure due to prestress release. Immediate and long-term camber should be calculated using conventional methods, and setting an allowable compression limit does not directly or indirectly guarantee acceptable camber. "Overloading" of prestressed members due to prestress release is not as probable as in externally loaded compression members. Prestress is an internal force. Concrete deformation causes relief of prestress. The possibility of strand buckling in a prestressed member does not exist, while that of reinforcing bars in a conventionally reinforced compression member does exist. Finally, prestress is not released to the concrete member unless the concrete compressive strength is experimentally verified to be adequate.
This proposed change is particularly beneficial for high-strength concrete as it provides the opportunity to use lower concrete strengths at release of the prestressing strands while maintaining the same concrete design strength. This allows release of the strands at an earlier concrete age, reduces manufacturing time, and makes high-strength concrete more practical. |
Anticipated Effect on Bridges |
Consistent design for conventionally reinforced and prestressed concrete flexural members. Improved account for the influence of concrete strength on design.
|
References |
- Noppakunwijai, P., Al-Omaishi, N., Tadros, M. K., and Krause, G., "Prestressed Concrete Compression Limits at Service Load," PCI Journal, Vol. 47, No. 5, September-October 2002.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.7.1 |
Revise 5.7.1 as follows:
The following assumptions may be used in the design of reinforced, prestressed, and partially prestressed concrete components for all compressive strength levels:
- The modular ratio is calculated as follows:
- Es/Ec for reinforcing bars
- Ep/Ec for prestressing tendons
|
Other Affected Articles |
None |
Background |
A modular ratio of 6 corresponds to a concrete compressive strength of about 7000 psi. Consequently, limiting the ratio to 6 does not allow the properties of higher strength concrete to be properly considered. A rational approach is to use the predicted values for all strengths of concrete. |
Anticipated Effect on Bridges |
More rational design procedure.
|
References |
None
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.8.2.8 |
Item No. 1
Revise 5.8.2.8 as follows:
5.8.2.8 Design and Detailing Requirements
Transverse reinforcement shall be anchored at both ends in accordance with the provisions of Article 5.11.2.6. For composite flexural members, extension of beam shear reinforcement into the deck slab may be considered when determining if the development and anchorage provisions of Article 5.11.2.6 are satisfied.
The design yield strength of nonprestressed transverse reinforcement shall not exceed 60.0 KSI except in prestressed concrete beams where the design yield strength shall not exceed 75.0 KSI. For design yield strengths of nonprestressed transverse reinforcement in excess of 60.0 KSI, the yield strength shall be the stress corresponding to a strain of 0.0035. The design yield strength of prestressed transverse reinforcement shall be taken as the effective stress, after allowance for all prestress losses, plus 60.0 KSI, but not greater than fpy.
Components of inclined flexural compression and/or flexural tension in variable depth members shall be considered when calculating shear resistance.
Item No 2
Revise C5.8.2.8 as follows:
C5.8.2.8
To be effective, the transverse reinforcement should be anchored at each end in a manner that minimizes slip. With welded wire reinforcement in prestressed concrete members, the specially fabricated reinforcement should be detailed to have welded joints only in the flanges where the shear stress is low. This eliminates the potential for fatigue fracture at the welded joints.
Some of the provisions of Article 5.8.3 are based on the assumption that the strain in the transverse reinforcement has to attain a value of 0.002 to develop its yield strength. For prestressed tendons, it is the additional strain required to increase the stress above the effective stress caused by the prestress that is of concern. Research by Griezic (1994), Ma (2000), and Bruce has indicated that the performance of higher strength steels as shear reinforcement has been satisfactory. Use of relatively small diameter deformed WWR at relatively small spacing, compared to individually field tied reinforcing bars results in improved quality control and improved member performance in service.
The components in the direction of the applied shear of inclined flexural compression and inclined flexural tension can be accounted for in the same manner as the component of the longitudinal prestressing force, Vp.
Item No. 3
Add the following references to Section 5 References:
Griezic, A., Cook, W. D., and Mitchell, D., "Tests to Determine Performance of Deformed Welded Wire Fabric Stirrups," ACI Structural Journal, Vol. 91, No. 2, March-April 1994, pp. 211-220.
Ma, Z., Tadros, M. K., and Baishya, M., "Shear Behavior of Pretensioned High-Strength Concrete Bridge I-Girders," ACI Structural Journal, Vol. 97, No. 1, January-February 2000, pp. 185-192.
Bruce, R. N., Russell, H. G., and Roller, J. J., "Fatigue and Shear Behavior of HPC Bulb-Tee Girders," Louisiana Transportation Research Center, Baton Rouge, LA. To be published.
|
Other Affected Articles |
5.8.3 (Changes not needed) |
Background |
High strength steels are especially effective in high-strength prestressed concrete members with narrow web widths. The effectiveness of using higher yield strengths has been demonstrated in several research projects.(1-7) Measured shear strengths of beams have exceeded calculated design strengths even when measured yield strengths of reinforcement greater than 60 ksi were used in the calculations.
Research and practice in a number of states has shown that the use of welded wire reinforcement (WWR) improves quality and efficiency of product fabrication, improves structural performance and reduces reinforcement congestion in members.(1, 4-9) Fatigue of reinforcement should not be a concern in this application as prestressed concrete members are designed to be uncracked due to unfactored service loads, and as the specially fabricated WWR used as shear reinforcement is detailed to have welded joints only in the flanges where shear stress is low anyway. If conventionally reinforced members are designed with WWR shear reinforcement, then the fatigue requirements given in article 5.5.3 should be invoked. |
Anticipated Effect on Bridges |
More economical construction.
|
References |
- Griezic, A., Cook, W. D., and Mitchell, D., "Tests to Determine Performance of Deformed Welded Wire Fabric Stirrups," ACI Structural Journal, Vol. 91, No. 2, March-April 1994, pp. 211-220.
- Shahawy, M. A. and Batchelor, B. deV., "Shear Behavior of Full-Scale Prestressed Concrete Girders: Comparison Between AASHTO Specifications and LRFD Code," PCI Journal, Vol. 41, No. 3, May-June 1996, pp. 48-62.
- "Reader Comments on Shear Behavior of Full-Scale Prestressed Concrete Girders: Comparison Between AASHTO Specifications and LRFD Code," PCI Journal, Vol. 42, No. 3, May-June 1997, pp. 72-93.
- Ma, Z. and Tadros, M. K., "Simplified Method For Shear Design Based on AASHTO Load and Resistance Factor Design Specifications," Paper No. 99-0266, Transportation Research Record 1688, Transportation Research Board, Washington, D.C., November 1999, pp. 10-20.
- Ma, Z., Tadros, M. K., and Baishya, M., "Shear Behavior of Pretensioned High-Strength Concrete Bridge I-Girders," ACI Structural Journal, Vol. 97, No. 1, January-February 2000, pp. 185-192.
- Tadros, M. K. and Yehia, S., "Shear of Design of High Strength Concrete NU I-Girders," Final Report for Nebraska Department of Roads.
- Bruce, R. N., Russell, H. G., and Roller, J. J., "Fatigue and Shear Behavior of HPC Bulb-Tee Girders," Louisiana Transportation Research Center, Baton Rouge, LA. To be published.
- Furlong, R. W., Fenves, G. I., and Kasl, E. P., "Welded Structural Wire Reinforcement for Columns," ACI Structural Journal, Vol. 88, No. 5, September-October 1991, pp. 585-591.
- Guimaraes, G. N., Kreger, M. E., and Jirsa, J. O., "Evaluation of Joint-Shear Provisions for Interior Beam-Column-Slab Connections Using High-Strength Materials," ACI Structural Journal, Vol. 89, No. 1, January-February 1992, pp. 89-98.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.9.5.1,2,3 |
Item No. 1
Revise 5.9.5.1, 5.9.5.2, and 5.9.5.3 as follows:
5.9.5 Loss of Prestress
5.9.5.1 Total Loss of Prestress
Values of prestress losses specified herein shall be applicable for specified concrete strengths up to 15.0 KSI.
In lieu of more detailed analysis, prestress losses in members prestressed in a single stage, relative to the stress immediately before transfer, may be taken as:
- In pretensioned members
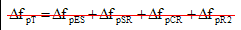
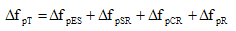 (5.9.5.1-1) (5.9.5.1-1)
- In posttensioned members
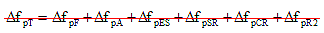
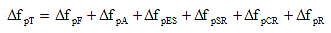 (5.9.5.1-2) (5.9.5.1-2)
where:
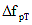 = total loss (KSI) = total loss (KSI)
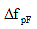 = loss due to friction (KSI) = loss due to friction (KSI)
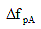 = loss due to anchorage set (KSI) = loss due to anchorage set (KSI)
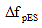 = sum of all losses or gains due to elastic shortening or extension at the time of application of prestress and external loads (KSI) = sum of all losses or gains due to elastic shortening or extension at the time of application of prestress and external loads (KSI)
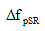 = loss due to shrinkage (KSI) = loss due to shrinkage (KSI)
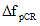 = Loss due to creep of concrete (KSI) = Loss due to creep of concrete (KSI)
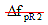
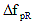 = loss due to relaxation of steel after transfer (KSI) = loss due to relaxation of steel after transfer (KSI)
For fully tensioned low-relaxation strands, 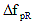 may be assumed constant at 2.5 KSI. For other types of prestressing steels, the manufacturer's recommendations shall be used. The Commentary to Article 5.9.5.4.2 also gives an alternative relaxation loss prediction method. may be assumed constant at 2.5 KSI. For other types of prestressing steels, the manufacturer's recommendations shall be used. The Commentary to Article 5.9.5.4.2 also gives an alternative relaxation loss prediction method.
For posttensioned members, consideration should be given to a loss of tendon force, as indicated by pressure readings, within the stressing equipment.
5.9.5.2 Instantaneous Losses
5.9.5.2.1 Anchorage Set
The magnitude of anchorage set shall be the greater of that required to control the stress in the prestressing steel at transfer or that recommended by the manufacturer of the anchorage. The magnitude of the set assumed for the design and used to calculate set loss shall be shown in the contract documents and verified during construction.
5.9.5.2.2 Friction
5.9.5.2.2a Pretensioned Construction
For draped prestressing tendons, losses that may occur at the hold-down devices should be considered.
5.9.5.2.2b Posttensioned Construction
Losses due to friction between the internal prestressing tendons and the duct wall may be taken as:
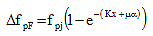 (5.9.5.2.2b-1) (5.9.5.2.2b-1)
Losses due to friction between the external tendon across a single deviator pipe may be taken as:
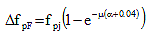 (5.9.5.2.2b-2) (5.9.5.2.2b-2)
where:
fpj = stress in the prestressing steel at jacking (KSI)
x = length of a prestressing tendon from the jacking end to any point under consideration (FT)
K = wobble friction coefficient (per FT of tendon)
µ = coefficient of friction
α = sum of the absolute values of angular change of prestressing steel path from jacking end, or from the nearest jacking end if tensioning is done equally at both ends, to the point under investigation (RAD)
e = base of Napierian logarithms
Values of K and µ should be based on experimental data for the materials specified and shown in the contract documents. In the absence of such data, a value within the ranges of K and µ as specified in Table 1 may be used.
For tendons confined to a vertical plane, α shall be taken as the sum of the absolute values of angular changes over length x.
For tendons curved in three dimensions, the total tridimensional angular change α shall be obtained by vectorially adding the total vertical angular change, αv, and the total horizontal angular change, αh.
Table 5.9.5.2.2b-1 - Friction Coefficients for Posttensioning Tendons
| Type of Steel |
Type of Duct |
K> |
μ |
Wire or strand |
Rigid and semirigid galvanized metal
sheathing |
0.0002 |
0.15-0.25 |
Polyethylene |
0.0002 |
0.23 |
Rigid steel pipe
deviators for external tendons |
0.0002 |
0.25 |
High-strength bars |
Galvanized metal
sheathing |
0.0002 |
0.30 |
5.9.5.2.3 Elastic Shortening
5.9.5.2.3a Pretensioned Members
The elastic shortening prestress loss in pretensioned members due to transfer of the prestressing force to the concrete member, and the elastic elongation gain of prestress due to the accompanying application of member self weight, as well as the elastic gain due to any subsequent dead or live load shall be taken as:
 (5.9.5.2.3a-1) (5.9.5.2.3a-1)
where:
fcgp = concrete stress at the center of gravity of prestressing tendons due to the action applied (initial prestressing force at transfer, self-weight of member, superimposed dead, or live load) at the section being considered in analysis (KSI). In most applications, it is adequate to calculate prestress losses at the section of maximum positive moment and use it for design of other sections of the member.
Ep = modulus of elasticity of prestressing steel (KSI)
Ect = modulus of elasticity of concrete at time of load application (KSI)
The total loss or gain due to elastic shortening is the sum of the effects of prestress and applied loads. When transformed section properties are used in stress analysis, losses or gains due to elastic shortening are automatically accounted for and a separate calculation of 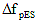 shall not be undertaken. shall not be undertaken.
5.9.5.2.3b Posttensioned Members
The loss due to elastic shortening in posttensioned members, other than slab systems, may be taken as:
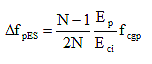 (5.9.5.2.3b-1) (5.9.5.2.3b-1)
where:
N = number of identical prestressing tendons
fcgp = sum of concrete stresses at the center of gravity of prestressing tendons due to the prestressing force after jacking and the self-weight of the member at the sections of maximum moment (KSI)
fcgp values may be calculated using a steel stress reduced below the initial value by a margin dependent on elastic shortening, relaxation, and friction effects.
For posttensioned structures with bonded tendons, fcgp may be taken at the center section of the span or, for continuous construction, at the section of maximum moment.
For posttensioned structures with unbonded tendons, the fcgp value may be calculated as the stress at the center of gravity of the prestressing steel averaged along the length of the member.
For slab systems, the value of 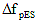 may be taken as 25 percent of that obtained from Equation 1. may be taken as 25 percent of that obtained from Equation 1.
5.9.5.3 Approximate Lump Sum Estimate of Time-Dependent Losses
Replace the existing article with the following:
For standard precast, pretensioned members subject to normal loading and environmental conditions and pretensioned with low relaxation strands, the long-term prestress loss, 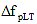 , due to creep of concrete, shrinkage of concrete, and relaxation of steel may be estimated using the following formula: , due to creep of concrete, shrinkage of concrete, and relaxation of steel may be estimated using the following formula:
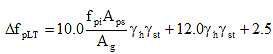 (5.9.5.3-1) (5.9.5.3-1)
for which:
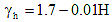
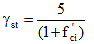
where:
fpi = prestressing steel stress just before transfer to the concrete member (KSI)
Aps = area of prestressing steel (IN2)
Ag = gross area of concrete member (IN2)
γh = correction factor for relative humidity of the ambient air
γst = correction factor for specified concrete strength at time of prestress transfer to the concrete member
For members of unusual dimensions, level of prestressing, construction schedule, or concrete constituent materials and for post-tensioned members, the Refined Method of Section 5.9.5.4 or computer time-step methods should be used.
Equation 1 does not include any elastic shortening loss at time of prestress transfer or elastic elongation gain due to application of deck weight, superimposed dead loads, or live loads. These elastic losses and gains are automatically accounted for if transformed section properties are used in stress analysis.
Item No. 2
Revise C5.9.5.1, C5.9.5.2, and C5.9.5.3 as follows:
C5.9.5.1
For segmental construction, lightweight concrete construction, multi-stage prestressing, and bridges where more exact evaluation of prestress losses is desired, calculations for loss of prestress should be made in accordance with a time-step method supported by proven research data. See references cited in Article C5.4.2.3
Data from control tests on the materials to be used, the methods of curing, ambient service conditions, and pertinent structural details for the construction should be considered.
Accurate estimate of total prestress loss requires recognition that the time-dependent losses resulting from creep, shrinkage, and relaxation are also interdependent. If needed, rigorous calculation of prestress losses should be made in accordance with a method supported by research data. See references cited in Article C5.4.2.3. However, undue refinement is seldom warranted or even possible at the design stage because many of the component factors are either unknown or beyond the control of the Designer.
Losses due to anchorage set, friction, and elastic shortening are instantaneous, whereas losses due to creep, shrinkage, and relaxation are time-dependent.
For multistage construction and/or prestressing, the prestress losses should be computed in consideration of the elapsed time between each stage. Such computation can be handled with the time-steps method.
This article has been revised on the basis of new analytical investigations. The presence of a substantial amount of nonprestressed reinforcement, such as in partially prestressed concrete, influences stress redistribution along the section due to creep of concrete with time, and generally leads to smaller loss of prestressing steel pre-tension and larger loss of concrete pre-compression.
The loss across stressing hardware and anchorage devices has been measured from 2 to 6 percent (Roberts 1993) of the force indicated by the ram pressure times the calibrated ram area. The loss varies depending on the ram and the anchor. An initial design value of 3 percent is recommended.
C5.9.5.2.1
Anchorage set loss is caused by the movement of the tendon prior to seating of the wedges or the anchorage gripping device. The magnitude of the minimum set depends on the prestressing system used. This loss occurs prior to transfer and causes most of the difference between jacking stress and stress at transfer. A common value for anchor set is 0.375 IN, although values as low as 0.0625 IN are more appropriate for some anchorage devices, such as those for bar tendons.
For wedge-type strand anchors, the set may vary between 0.125 IN and 0.375 IN, depending on the type of equipment used. For short tendons, a small anchorage seating value is desirable, and equipment with power wedge seating should be used. For long tendons, the effect of anchorage set on tendon forces is insignificant, and power seating is not necessary. The 0.25-IN anchorage set value, often assumed in elongation computations, is adequate but only approximate.
Due to friction, the loss due to anchorage set may affect only part of the prestressed member.
Losses due to elastic shortening may also be calculated in accordance with Article 5.9.5.2.3, C5.9.5.2.3a, or other published guidelines (PCI 1975; Zia et al. 1979). Losses due to elastic shortening for external tendons may be calculated in the same manner as for internal tendons.
C5.9.5.2.2b
Where large discrepancies occur between measured and calculated tendon elongations, in-place friction tests are required.
The 0.04 radians in Equation 2 represents an inadvertent angle change. This angle change may vary depending on job-specific tolerances on deviator pipe placement and need not be applied in cases where the deviation angle is strictly controlled or precisely known, as in the case of continuous ducts passing through separate longitudinal bell-shaped holes at deviators. The inadvertent angle change need not be considered for calculation of losses due to wedge seating movement.
For slender members, the value of x may be taken as the projection of the tendon on the longitudinal axis of the member. A friction coefficient of 0.25 is appropriate for 12 strand tendons. A lower coefficient may be used for larger tendon and duct sizes.
αv and αh may be taken as the sum of absolute values of angular changes over length, x, of the projected tendon profile in the vertical and horizontal planes, respectively.
The scalar sum of αv and αh may be used as a first approximation of α.
When the developed elevation and plan of the tendons are parabolic or circular, the α can be computed from:
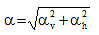 (C5.9.5.2.2b-1) (C5.9.5.2.2b-1)
When the developed elevation and the plan of the tendon are generalized curves, the tendon may be split into small intervals, and the above formula can be applied to each interval so that:
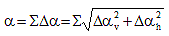 (C5.9.5.5.2.2b-2) (C5.9.5.5.2.2b-2)
As an approximation, the tendon may be replaced by a series of chords connecting nodal points. The angular changes, 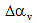 and and 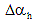 , of each chord may be obtained from its slope in the developed elevation and in plan. , of each chord may be obtained from its slope in the developed elevation and in plan.
Field tests conducted on the external tendons of a segmental viaduct in San Antonio, Texas, indicate that the loss of prestress at deviators is higher than the usual friction coefficient (μ = 0.25) would estimate.
This additional loss appears to be due, in part, to the tolerances allowed in the placement of the deviator pipes. Small misalignments of the pipes can result in significantly increased angle changes of the tendons at the deviation points. The addition of an inadvertent angle change of 0.04 radians to the theoretical angle change accounts for this effect based on typical deviator length of 3.0 FT and placement tolerance of ±3/8 IN. The 0.04 value is to be added to the theoretical value at each deviator. The value may vary with tolerances on pipe placement.
The measurements also indicated that the friction across the deviators was higher during the stressing operations than during the seating operations.
See Podolny (1986) for a general development of friction loss theory for bridges with inclined webs and for horizontally curved bridges.
C5.9.5.2.3a
In calculating fcgp, using conventional gross cross section properties, it is necessary to perform an iteration. For example, for the combined effects of initial prestress and member weight, the yet-to-be-determined initial prestress after transfer must be used. The prestress may be assumed to be 90 percent of the initial prestress before transfer and the analysis recycled until acceptable accuracy is achieved. To avoid iteration, equations similar to Equation C1 may be used.
When transformed section properties are used in stress analysis, losses, or gains due to elastic shortening are automatically accounted for and 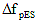 should not be calculated separately. should not be calculated separately.
The loss due to elastic shortening in pretensioned members may be determined by the following alternative equation:
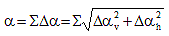 (C5.9.5.2.3a-1) (C5.9.5.2.3a-1)
where:
Aps = area of prestressing steel (IN2)
Ag = gross area of section (IN2)
Eci = modulus of elasticity of concrete at transfer (KSI)
Ep = modulus of elasticity of prestressing tendons (KSI)
em = average eccentricity at midspan (IN)
fpbt = stress in prestressing steel immediately prior to transfer as specified in Table 5.9.3-1 (KSI)
Ig = moment of inertia of the gross concrete section (IN4)
Mg = midspan moment due to member self-weight (K-IN)
Elastic elongation gain due to other applied loads may be estimated from Equation C1 with the prestress term set equal to zero, the moment due to the load being considered replacing Mg and the modulus of elasticity of concrete at time of load application replacing Eci.
Alternatively, transformed section properties may be used in stress analysis. In which case, there is no need for separate calculation of elastic losses or gains as they are automatically accounted for.
C5.9.5.2.3b
The loss due to elastic shortening in posttensioned members, other than slab systems, may be determined by the following alternative equation:
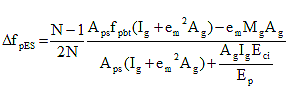 (C5.9.5.2.3b-1) (C5.9.5.2.3b-1)
where:
Aps = area of prestressing steel (IN2)
Ag = gross area of section (IN2)
Eci = modulus of elasticity of concrete at transfer (KSI)
Ep = modulus of elasticity of prestressing tendons (KSI)
em = average eccentricity at midspan (IN)
fpbt = stress in prestressing steel immediately prior to transfer as specified in Table 5.9.3-1 (KSI)
Ig = moment of inertia of the gross concrete section (IN4)
Mg = midspan moment due to member self-weight (K-IN)
N = number of identical prestressing tendons
fpj = stress in the prestressing steel at jacking (KSI)
For posttensioned structures with bonded tendons, 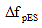 may be calculated at the center section of the span or, for continuous construction, at the section of maximum moment. may be calculated at the center section of the span or, for continuous construction, at the section of maximum moment.
For posttensioned structures with unbonded tendons, 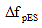 can be calculated using the eccentricity of the prestressing steel averaged along the length of the member. can be calculated using the eccentricity of the prestressing steel averaged along the length of the member.
For slab systems, the value of 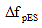 may be taken as 25 percent of that obtained from Equation C1. may be taken as 25 percent of that obtained from Equation C1.
For posttensioned construction, 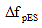 losses can be further reduced below those implied by Equation 1 with proper tensioning procedures such as stage stressing and retensioning. losses can be further reduced below those implied by Equation 1 with proper tensioning procedures such as stage stressing and retensioning.
If tendons with two different numbers of strand per tendon are used, "N" may be calculated as:
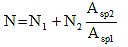 (C5.9.5.2.3b-2) (C5.9.5.2.3b-2)
where:
N1 = number of tendons in the larger group
N2 = number of tendons in the smaller group
Asp1 = cross-sectional area of a tendon in the larger group (IN2)
Asp2 = cross-sectional area of a tendon in the smaller group (IN2)
C5.9.5.3
Replace the existing commentary with the following:
The losses or gains due to elastic deformations at the time of prestress or load application should be added to the time-dependent losses to determine total losses. However, these elastic losses (or gains) must be taken equal to zero if transformed section properties are used in stress analysis.
The approximate estimates of time-dependent prestress losses given in Equation 1 were derived as approximations of the terms in the refined method for a wide range of standard precast prestressed concrete I-beams, box beams, inverted tee beams, and voided slabs. The members were assumed to be fully utilized, i.e. level of prestressing is such that concrete tensile stress at full service loads is near the maximum limit. It is further assumed in development of the approximate method that live load moments produce about one-third of the total load moments, which is reasonable for I-beam and inverted tee composite construction and conservative for non-composite boxes and voided slabs. They were calibrated with full-scale test results and with the results of the refined method, and found to give conservative results (Al-Omaishi 2001 and Tadros et al. 2002). The approximate method should not be used for members of uncommon shapes (i.e. having V/S ratios much different from 3.5 IN, level of prestressing, or construction schedule.
Item No. 3
Add the following to Section 5 References:
Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph. D. Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
Tadros, M. K., Al-Omaishi, N., Seguirant, S. P., and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
|
Other Affected Articles |
Service load analysis, deflection |
Background |
The proposed revisions are the results of an extensive theoretical and experimental research on NCHRP Project 18-07.(1,2) Seven full-scale bridge girders were instrumented in four states, Nebraska, New Hampshire, Texas, and Washington. The research included material properties of a number of high-strength concrete mixes including those used in the bridge projects. The results of experiments from previous research were also examined. It was found that concrete creep and shrinkage were dependent on concrete strength in addition to the parameters previously recognized. Also, apparent neglect, or implicit inclusion, of elastic elongation gain of steel stress due to external load application causes confusion among designers who wish to use computer software for design and wish to invoke the higher transformed section properties to optimize their design. In the proposed prestress loss estimates, no elastic shortening loss or elastic gain need be considered if transformed section properties are used. Only long-term loss due to creep, shrinkage and relaxation are estimated and introduced to the cross section as a "negative" prestress force to be applied in addition to the initial prestress just before release and the external gravity loads, to calculate concrete stress at service. It was found that the great majority of the loss takes place before application of the deck weight in composite construction. This is reflected in the coefficients established in the approximate loss method with the estimated loss assumed to be fully applied to the precast section properties. |
Anticipated Effect on Bridges |
More accurate prediction of prestress losses and camber. Extension of design provisions to concrete strengths greater than 10,000 psi.
|
References |
- Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph. D. Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
- Tadros, M. K., Al-Omaishi, N., Seguirant, S. P., and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.9.5.4 |
Item No. 1
Replace 5.9.5.4 with the following:
5.9.5.4 Refined Estimates of Time-Dependent Losses
5.9.5.4.1 General
More accurate values of creep-, shrinkage-, and relaxation-related losses than those specified in Article 5.9.5.3 may be determined in accordance with the provisions of this article for non-segmental prestressed members.
For concrete of containing lightweight aggregates, very hard aggregates, or unusual chemical admixtures, the estimated material properties used in this Article and based on Article 5.4.2.3 may be inaccurate and actual test results should be used for their estimation.
For segmental construction and for all considerations other than preliminary design, prestress losses shall be determined by the time-step method and the provisions of Article 5.9.5, including consideration of the time-dependent construction method and schedule shown in the contract documents.
The provisions given below are for precast pretensioned girders with cast-in-place composite deck or topping. For precast pretensioned girders without composite topping and for precast or cast-in-place post-tensioned nonsegmental girders, they are applicable in a modified form as shown in Articles 5.9.5.4.4 and 5.9.5.4.5, respectively.
5.9.5.4.2 Long-Term Losses Between Transfer and Time of Deck Placement
5.9.5.4.2a Due to Shrinkage of Girder Concrete
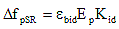 (5.9.5.4.2-1) (5.9.5.4.2-1)
for which:
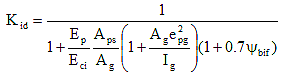 (5.9.5.4.2-2) (5.9.5.4.2-2)
where:
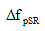 = prestress loss due to shrinkage of girder concrete between transfer and deck placement = prestress loss due to shrinkage of girder concrete between transfer and deck placement
εbid = concrete shrinkage strain of girder between transfer and deck placement
Kid = transformed section coefficient that accounts for time-dependent interaction between concrete and bonded steel in the section being considered for time period between transfer and deck placement
epg = eccentricity of strands with respect to centroid of girder
ψbif = girder creep coefficient at final time for concrete loaded at transfer
5.9.5.4.2b Due to Creep of Girder Concrete
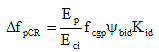 (5.9.5.4.2-3) (5.9.5.4.2-3)
where:
= prestress loss due to creep of girder concrete between transfer and deck placement
fcgp = concrete stress at center of gravity of prestressing steel at transfer (KSI)
εbid = girder creep coefficient at time of deck placement due to loading introduced at transfer
5.9.5.4.2c Due to Relaxation of Prestressing Strands
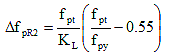 (5.9.5.4.2-4) (5.9.5.4.2-4)
where:
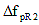 = prestress loss due to relaxation of prestressing strands between transfer and deck placement = prestress loss due to relaxation of prestressing strands between transfer and deck placement
fpt = stress in prestressing strands immediately after transfer, taken not less than 0.55fpy in Equation 4
KL = 30 for low relaxation strands and 7 for other prestressing steel, unless more accurate manufacturer's data are available
The relaxation loss, 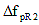 , may be assumed equal to 1.2 KSI for low-relaxation strands , may be assumed equal to 1.2 KSI for low-relaxation strands
5.9.5.4.3 Long-Term Losses between Time of Deck Placement and Final Time
5.9.5.4.3a Due to Shrinkage of Girder Concrete
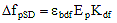 (5.9.5.4.3-1) (5.9.5.4.3-1)
for which:
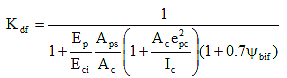 (5.9.5.4.3-2) (5.9.5.4.3-2)
where:
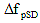 = prestress loss due to shrinkage of girder concrete between time of deck placement and final time = prestress loss due to shrinkage of girder concrete between time of deck placement and final time
εbdf = shrinkage strain of girder between time of deck placement and final time
Kdf = transformed section coefficient that accounts for time-dependent interaction between concrete and bonded steel in the section being considered for time period between deck placement and final time
epc = eccentricity of strands with respect to centroid of composite section
Ac = area of composite section calculated using the gross concrete section properties of the girder and the deck and the deck-to-girder modular ratio
Ic = moment of inertia of composite section calculated using the gross concrete section properties of the girder and the deck and the deck-to-girder modular ratio at service
5.9.5.4.3b Due to Creep of Girder Concrete:
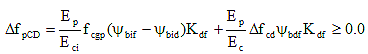 (5.9.5.4.3-3) (5.9.5.4.3-3)
where:
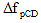 = prestress loss due to creep of girder concrete between time of deck placement and final time = prestress loss due to creep of girder concrete between time of deck placement and final time
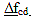 = change in concrete stress at centroid of prestressing strands due to long-term losses between transfer and deck placement, combined with deck weight and superimposed loads = change in concrete stress at centroid of prestressing strands due to long-term losses between transfer and deck placement, combined with deck weight and superimposed loads
ψbdf = girder creep coefficient at final time for loading age at deck placement
5.9.5.4.3c Due to Relaxation of Prestressing Strands
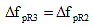 (5.9.5.4.3-4) (5.9.5.4.3-4)
where:
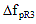 = prestress loss due to relaxation of prestressing strands in composite section between time of deck placemen and final time = prestress loss due to relaxation of prestressing strands in composite section between time of deck placemen and final time
For low-relaxation strands, 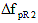 may be assumed equal to 1.2 KSI may be assumed equal to 1.2 KSI
5.9.5.4.3d Due to Shrinkage of Deck Concrete
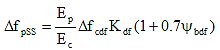 (5.9.5.4.3-5) (5.9.5.4.3-5)
for which:
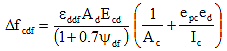 (5.9.5.4.3-6) (5.9.5.4.3-6)
where:
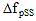 = prestress loss due to shrinkage of deck composite section = prestress loss due to shrinkage of deck composite section
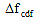 = change in concrete stress at centroid of prestressing strands due to shrinkage of deck concrete = change in concrete stress at centroid of prestressing strands due to shrinkage of deck concrete
εddf = shrinkage strain of deck concrete between placement and final time
Ad = area of deck concrete
Ecd = modulus of elasticity of deck concrete
ed = eccentricity of deck with respect to the transformed composite section, taken negative in common construction
ψdf = creep coefficient of deck concrete at final time due to loading introduced shortly after deck placement (i.e. overlays, barriers, etc.)
5.9.5.4.4 Precast Pretensioned Girders Without Composite Topping
The equations in Article 5.9.5.4.2 are applicable to girders with non-composite deck or topping, or with no topping. The values for time of "deck placement" in those equations may be taken as values at time of non-composite deck placement or values at time of installation of precast members without topping.
The equations in Article 5.9.5.4.3 are applicable to girders with non-composite deck or topping, or with no topping. Time of "deck placement" in those equations may be taken as time of non-composite deck placement or values at time of installation of precast members without topping. Area of "deck" for these applications shall be taken as zero.
5.9.5.4.5 Posttensioned Nonsegmental Girders
Long-term prestress losses for post-tensioned members after tendons have been grouted may be calculated using the provisions of Articles 5.9.5.4.2 through 5.9.5.4.5.
Item No. 2
Revise C5.9.5.4 as follows:
C5.9.5.4.1
Estimates of losses due to each time-dependent source, such as creep, shrinkage, or relaxation, can lead to a better estimate of total losses compared with the values given using Article 5.9.5.3. Table 5.9.5.3-1. The individual losses are based on recent research by Tadros et al (2002), which aimed at extending applicability of the provisions of these Specifications to high-strength concrete. The new approach additionally accounts for interaction between the precast and the cast-in-place concrete components of a composite member and for variability of creep and shrinkage properties of concrete by linking the loss formulas to the creep and shrinkage prediction formulae of Article 5.4.2.3.
C5.9.5.4.2
Equations 5.9.5.4.2-4 and 5.9.5.4.3-4 5.9.5.4.4b-1 to 5.9.5.4.4c-2 are given for relaxation losses are appropriate for normal temperature ranges only. Relaxation losses increase with increasing temperatures.
C5.9.5.4.2
Relative humidity, H, may be obtained from local weather statistics or from Figure 5.4.2.3.3-1.
C5.9.5.4.2c
A more accurate equation for prediction of relaxation loss between transfer and deck placement is given in Tadros et al. (2002):
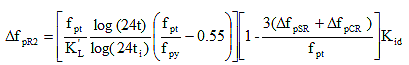
where the KL is a factor accounting for type of steel, equal to 45 for low relaxation steel and 10 for stress relieved steel, t is time in days between strand tensioning and deck placement. The term in the first square brackets is the intrinsic relaxation without accounting for strand shortening due to creep and shrinkage of concrete. The second term in square brackets accounts for relaxation reduction due to creep and shrinkage of concrete. The factor Kid accounts for the restraint of the concrete member caused by bonded reinforcement. It is the same factor used for the creep and shrinkage components of the prestress loss. The equation given in Article 5.9.5.4.2c is an approximation of the above formula with the following typical values assumed: ti=0.75 day, t=120 days, 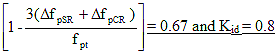
C5.9.5.4.3b
The "≥ to 0.0" in Equation 3 is needed because a negative value could result in some cases of partial prestressing, but 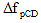 should not be taken less than 0.0. should not be taken less than 0.0.
C5.9.5.4.4b
Generally, the initial relaxation loss is now determined by the Fabricator. Where the Engineer is required to make an independent estimate of the initial relaxation loss, or chooses to do so as provided in Article 5.9.5.1, the provisions of this article may be used as a guide. If project-specific information is not available, the value of fpj may be taken as 0.80 fpu for the purpose of this calculation.
Item No. 3
Add the following to 5.3 Notation or revise the existing notation:
Ac = area of composite section calculated using the gross concrete section properties of the girder and the deck and the deck-to-girder modular ratio (IN2) (5.9.5.4.3a)
Ad = area of deck concrete (IN2) (5.9.5.4.3d)
Ecd = modulus of elasticity of deck concrete (KSI) (5.9.5.4.3d)
ed = eccentricity of deck with respect to the transformed composite section, taken as negative in common construction (IN) (5.9.5.4.3d)
epc = eccentricity of strands with respect to centroid of composite section (IN) (5.9.5.4.3a)
epg = eccentricity of strands with respect to centroid of girder (IN) (5.9.5.4.2a)
Ic = moment of inertia of composite section calculated using the gross concrete section properties of the girder and the deck and the deck-to-girder modular ratio at service (IN4) (5.9.5.4.3a)
Kdf = transformed section coefficient that accounts for time-dependent interaction between concrete and bonded steel in the section being considered for time period between deck placement and final time (5.9.5.4.3a) (5.9.5.4.3b)
Kid = transformed section coefficient that accounts for time-dependent interaction between concrete and bonded steel in the section being considered for time period between transfer and deck placement (5.9.5.4.2a) (5.9.5.4.2b)
KL = factor accounting for type of steel taken as 30 for low relaxation strands and 7 for other prestressing steel, unless more accurate manufacturer's data are available (5.9.5.4.2c)
K'L = factor accounting for type of steel (C5.9.5.4.2c)
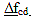 = change in concrete stress at centroid of prestressing strands due to long-term losses between transfer and deck placement, combined with deck weight and superimposed loads (KSI) (5.9.5.4.3b) = change in concrete stress at centroid of prestressing strands due to long-term losses between transfer and deck placement, combined with deck weight and superimposed loads (KSI) (5.9.5.4.3b)
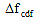 = change in concrete stress at centroid of prestressing strands due to shrinkage of deck concrete (KSI) (5.9.5.4.3d) = change in concrete stress at centroid of prestressing strands due to shrinkage of deck concrete (KSI) (5.9.5.4.3d)
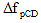 = prestress loss due to creep of girder concrete between time of deck placement and final time (KSI) (5.9.5.4.3b) = prestress loss due to creep of girder concrete between time of deck placement and final time (KSI) (5.9.5.4.3b)
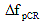 = prestress loss due to creep of girder concrete between transfer and deck placement (KSI) (5.9.5.4.2b) = prestress loss due to creep of girder concrete between transfer and deck placement (KSI) (5.9.5.4.2b)
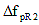 = prestress loss due to relaxation of prestressing strands between transfer and deck placement (KSI) (5.9.5.4.2c) = prestress loss due to relaxation of prestressing strands between transfer and deck placement (KSI) (5.9.5.4.2c)
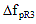 = prestress loss due to relaxation of prestressing strands in composite section between time of deck placemen and final time (KSI) (5.9.5.4.3c) = prestress loss due to relaxation of prestressing strands in composite section between time of deck placemen and final time (KSI) (5.9.5.4.3c)
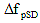 = prestress loss due to shrinkage of girder concrete between time of deck placement and final time (KSI) (5.9.5.4.3a) = prestress loss due to shrinkage of girder concrete between time of deck placement and final time (KSI) (5.9.5.4.3a)
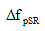 = prestress loss due to shrinkage of girder concrete between transfer and deck placement (KSI) (5.9.5.4.2a) = prestress loss due to shrinkage of girder concrete between transfer and deck placement (KSI) (5.9.5.4.2a)
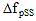 = prestress loss due to shrinkage of deck composite section (KSI) (5.9.5.4.3d) = prestress loss due to shrinkage of deck composite section (KSI) (5.9.5.4.3d)
εbdf = shrinkage strain of girder between time of deck placement and final time (IN/IN) (5.9.5.4.3a)
εbid = concrete shrinkage strain of girder between transfer and deck placement (IN/IN) (5.9.5.4.2a)
εddf = shrinkage strain of deck concrete between placement and final time (IN/IN) (5.9.5.4.3d)
ψbdf = girder creep coefficient at final time due to loading at deck placement (5.9.5.4.3b)
ψbid = girder creep coefficient at time of deck placement due to loading introduced at transfer (5.9.5.4.2b) (5.9.5.4.3b)
ψbif = girder creep coefficient at final time for concrete due to loading introduced at transfer (5.9.5.4.2a) (5.9.5.4.3b)
ψdf = creep coefficient of deck concrete at final time due to loading introduced shortly after deck placement (i.e. overlays, barriers, etc.) (5.9.5.4.3d)
Item No. 4
Add the following to Section 5 References:
Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph.D., Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
Tadros, M. K., Al-Omaishi, N., Seguirant, S. P., and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
|
Other Affected Articles |
Service load analysis, deflection |
Background |
The proposed revisions are the results of an extensive theoretical and experimental research on NCHRP Project 18-07.(1,2) Seven full-scale bridge girders were instrumented in four states, Nebraska, New Hampshire, Texas, and Washington. The research included material properties of a number of high-strength concrete mixes including those used in the bridge projects. The results of experiments from previous research were also examined. It was found that concrete creep and shrinkage were dependent on concrete strength in addition to the parameters previously recognized. Also, apparent neglect or implicit inclusion of elastic elongation gain of steel stress due to external load application causes confusion among designers who wish to use computer software for design and wish to invoke the higher transformed section properties to optimize their design. In the proposed prestress loss estimates, no elastic shortening loss or elastic gain need be considered if transformed section properties are used. Only long-term loss due to creep, shrinkage and relaxation are estimated and introduced to the cross section as a "negative" prestress force to be applied in addition to the initial prestress just before release and the external gravity loads, to calculate concrete stress at service. It was found that the great majority of the loss takes place before application of the deck weight in composite construction. This is reflected in the coefficients established in the approximate loss method with the estimated loss assumed to be fully applied to the precast section properties. |
Anticipated Effect on Bridges |
More accurate prediction of prestress losses and camber. Extension of design provisions to concrete strengths greater than 10,000 psi.
|
References |
- Al-Omaishi, N., "Prestress Losses in High Strength Pretensioned Concrete Bridge Girders," Ph.D. Dissertation, University of Nebraska-Lincoln, December 2001, 265 pp.
- Tadros, M. K., Al-Omaishi, N., Seguirant, S. P., and Gallt, J. G., "Prestress Losses in High Strength Concrete Bridge Girders," NCHRP 18-07 Final Report, August 2002.
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.12.2 |
Item No. 1
Revise 5.12.2 Alkali-Silica Reactive Aggregates as follows:
5.12.2 Alkali-Silica Reactive Aggregates
Alkali-silica reactive aggregates shall not be used in concrete unless they can be shown to have a history of satisfactory performance in field applications and will be used with same materials at approximately the same mix proportions, or have been tested with standard procedures in AASHTO M6 or M80 and determined to have expansions below the acceptable limits.
Item No. 2
Revise C5.12.2 as follows:
C5.12.2
Alkali-silica reactive aggregates exist throughout the world. In the United States , most are found in the West and Midwest. In most states, public agencies have identified locations where reactive aggregates occur. When in doubt, the Designer should investigate this possibility.
Mitigation procedures for alkali-silica reactivity using either a performance specification or a prescriptive type specification are given in AASHTO M 6 and M 80. |
Other Affected Articles |
AASHTO M 6 and M 80 |
Background |
Alkali-silica reactive aggregates can be used satisfactorily provided that the necessary precautions are taken. For example, use of pozzolans or slag and lithium salts have been shown to mitigate the deleterious expansions. Proposed revisions to AASHTO M 6 and M 80 have been developed to more specifically address alkali-silica reactivity. |
Anticipated Effect on Bridges |
More durable structures.
|
References |
None
(Submitted by: ) |
| 20XX AGENDA ITEM (proposed to T-10) |
(X) Revision or ( ) Addition ( ) SI ( ) US (X) both versions LRFD 5.13.4.4.1 |
Revise 5.13.4.4.1 as follows:
5.13.4.4.1 Pile Dimensions
Prestressed concrete piles may be octagonal, square, or circular and shall conform to the minimum dimensions specified in Article 5.13.4.3.1.
Prestressed concrete piles may be solid or hollow. For hollow piles, precautionary measures, such as venting shall be taken to prevent breakage due to internal water pressure during driving, ice pressure in trestle piles, or gas pressure due to decomposition of material used to form the void.
|
Other Affected Articles |
None |
Background |
The requirement for a minimum wall thickness appears to be unjustified if the minimum concrete cover to steel as specified in 5.12.3 are used. Further, the minimum effective prestress of 0.7 KSI in 5.13.4.4.3 assures a relatively high level of concrete compression. Removal of the limit would allow for efficient use of high-strength concrete cylindrical piles. It also allows for utilization of high-strength fiber reinforced concrete piles without the constraint associated with conventionally reinforced piles. |
Anticipated Effect on Bridges |
Removal of unnecessary wall thickness limitation would result in reduced pile weight and increased pile capacity with higher strength concrete.
|
References |
None
(Submitted by: ) |
Previous | Table of Contents | Next
FHWA-HRT-05-057
|
