U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

Report
This report is an archived publication and may contain dated technical, contact, and link information
Publication Number: FHWA-RD-02-078
Date: November 2003

Bottomless Culvert Scour Study: Phase I Laboratory Report

6. RECOMMENDED PROCEDURES FOR ESTIMATING MAXIMUM SCOUR FOR BOTTOMLESS CULVERTS

PROCEDURE USING GKY METHOD FOR REPRESENTATIVE VELOCITY AND SMB EQUATION FOR CRITICAL VELOCITY

The GKY method for representative velocity and the SMB equation for critical velocity with the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth as the independent regression variable gave the best R2 value, regressing the KADJ (see equation 3) to compute the maximum scour for the laboratory data. The SMB method for computing critical velocity, however, is independent of the flow depth and produces much lower critical velocities than the other methods for fine particle sizes. This will, in turn, result in overly conservative scour estimates for field situations.

The procedure is:

Step 1: Compute representative velocity using:

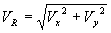Equation 62. V subscript R equals the square root of the sum of V subscript X, which is the velocity in the flow direction in feet per second, squared, plus V subscript Y, which is the velocity orthogonal to the flow direction, in feet per second, squared.     (62)

with

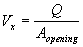Equation 63. V subscript X equals Q divided by A subscript opening.     (63)

and

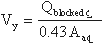Equation 64. V subscript Y equals Q subscript blocked CL, which is the approach flow blocked by the embankment on one side of the channel centerline, CFS, divided by 0.43 times A subscript ACL, which is the total approach flow area on one side of the channel centerline, in feet squared.     (64)

where:

Vx= velocity in the flow direction, ft/s
Vy= velocity orthogonal to the flow direction, ft/s
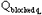Uppercase Q lowercase the word blocked with centerline= approach flow blocked by the embankment on one side of the channel centerline, ft3/s
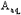Uppercase A lowercase a with centerline= total approach flow area on one side of the channel centerline, ft2
Ablocked = approach flow area that is blocked by the embankments on one side of the channel, ft2

Step 2: Determine critical velocity by applying the SMB equations. The Shields Manning equations can be combined to yield:

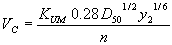Equation 65. V subscript C equals K subscript UM, which is 1.49 for U.S. customary units and 1.0 for SI units, times 0.28 times D subscript 50 to the one-half power times Y subscript 2 to the one-sixth power, all divided by N, which is Manning's roughness.     (65)

where:

KUM= 1.0 for SI units or 1.49 for U.S. customary units
n= Manning's roughness

Blodgett's equations for average estimates of Manning's n for sand- and gravel-bed channels are:

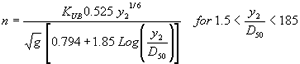Equation 66. N equals the product of K subscript UB, which is 1.0 for U.S. customary units and 1 divided by 1.49 for SI units, times 0.525 times Y subscript 2 to the one-sixth power, all divided by the product of the square root of G, which is the acceleration of gravity, times the sum of 0.794 plus 1.85 log of Y subscript 2 divided by D subscript 50. This is for 1.5 is less than Y subscript 2 divided by D subscript 50 is less than 185.     (66)
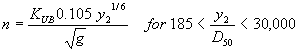Equation 67. N equals the product of K subscript UB times 0.105 times Y subscript 2 to the one-sixth power, all divided by the square root of G. This is for 185 is less than Y subscript 2 divided by D subscript 50 is less than 30,000.     (67)

where:

g= acceleration of gravity
= 9.81 m/s2 for SI units or 32.2 ft/s2 for U.S. customary units
KUB= 1/1.49 for SI units or 1.0 for U.S. customary units

Step 3: Calculate y2 using:

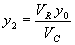Equation 68. Y subscript 2 equals the product of V subscript R times Y subscript 0, divided by V subscript C.     (68)

Step 4: Use following regression equation to compute KADJ:

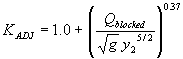Equation 69. K subscript ADJ equals 1.0 plus the following quotient raised to the 0.37 power: Q subscript blocked, which is the portion of the approach flow to one side of the channel centerline, cubic feet per second, divided by product of the square root of G times Y subscript 2 raised to the five-seconds power.     (69)

with:

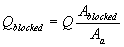Equation 70. Q subscript blocked, which is the approach flow blocked by the embankment on one side of the channel centerline, cubic feet per second, equals Q times the quotient of A subscript blocked, which is the approach flow area that is blocked by the embankments on one side of the channel, in feet squared, divided by A subscript A, which is the total approach flow area on one side of the channel in feet squared.     (70)

where:

Qblocked= approach flow blocked by the embankment on one side of the channel centerline, ft3/s
Aa= total approach flow area on one side of the channel, ft2
Ablocked= approach flow area that is blocked by the embankments on one side of the channel, ft2

Step 5: Compute maximum scour according to:

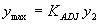Equation 71. Y subscript max equals K subscript ADJ times Y subscript 2.     (71)

PROCEDURE USING MARYLAND DOT (CHANG) METHOD FOR REPRESENTATIVE VELOCITY AND CRITICAL VELOCITY

The recommended procedure is based on using the Maryland DOT (Chang) method for computing both representative velocity and critical velocity. For computing the KADJ factor, the method using the blocked discharge normalized by the acceleration of gravity (g) and the computed equilibrium depth as the independent regression variable was chosen because it is considered to be more applicable to field situations.

The procedure is:

Step 1: Compute representative velocity using the Maryland DOT (Chang) method:

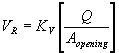Equation 72. V subscript R equals K subscript V, which is the velocity coefficient to account for flow concentration where side flow converges with main channel flow based on potential flow assumptions, times the quotient of Q, which is the total discharge through the culvert in cubic feet per second, divided by A subscript opening, which is the average flow area within the culvert in square feet.     (72)

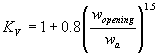Equation 73. K subscript V equals 1 plus 0.8 times the following quotient raised to the 1.5 power: W subscript opening, which is the average flow width in the culvert in feet, divided by W subscript A, which is the width of flow in the approach section in feet.     (73)

where:

KV= velocity coefficient to account for flow concentration where side flow converges with main channel flow based on potential flow assumptions
Q= total discharge through the culvert, ft3/s
Aopening= average flow area within the culvert, ft2
Wopening= average flow width in the culvert, ft
wa= width of flow in the approach section, ft

These equations are dimensionally homogeneous and are independent of the system of units as long as they are consistent.

Step 2: Determine critical velocity using the Maryland DOT (Chang) method:

  • For D50 > 0.03 m (0.1 ft):
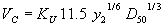Equation 74. V subscript C equals the product of K subscript U, which is 1.0 for U.S. customary units and 0.55217 for SI units, times 11.5 times Y subscript 2 to the one-sixth power times D subscript 50 to the one-third power.     (74)

where:

y2= equilibrium flow depth, m or ft
D50= sediment size, m or ft
KU= 0.55217 for SI units or 1.0 for U.S. customary units
  • For 0.03 m (0.1 ft) > D50 > 0.0003 m (0.001 ft):
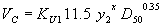Equation 75. V subscript C equals the product of K subscript U1, which is 1.0 for U.S. customary units and 0.3048 to the 0.65 minus X power for SI units, times 11.5 times Y subscript 2 to the X power times D subscript 50 to the 0.35 power.     (75)

The exponent x is calculated using equation 13:

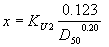Equation 76. X equals K subscript U2, which is 1.0 for U.S. customary units and 0.788 for SI units, times the quotient of 0.123 divided by D subscript 50 to the 0.20 power.     (76)

where:

y2= equilibrium flow depth, m or ft
D50= sediment size, m or ft
KU1= for SI units or
1.0 for U.S. customary units
x= exponent from equation 13
KU2= 0.788 for SI units or
1.0 for U.S. customary units
  • For 0.0003 m (0.001 ft) > D50:
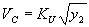Equation 77. V subscript C equals K subscript U times the square root of Y subscript 2.     (77)

where:

y2= equilibrium flow depth, m or ft
D50= sediment size, m or ft
KU= 0.55217 for SI units or 1.0 for U.S. customary units

Step 3: Calculate y2 using:

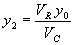Equation 78. Y subscript 2 equals the product of V subscript R times Y subscript 0 divided by V subscript C.     (78)

Step 4: Use the following regression equation to compute KADJ:

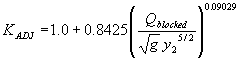Equation 79. K subscript ADJ equals 1.0 plus 0.8425 times the following quotient raised to the 0.09029 power: Q subscript blocked, which is approach flow blocked by the embankment on one side of the channel, cubic feet per second, divided by product of the square root of G times Y subscript 2 raised to the five-seconds power.     (79)

with

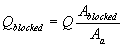Equation 80. Q subscript blocked equals Q times the quotient of A subscript blocked, which is the approach flow area that is blocked by the embankments on one side of the channel in feet squared, divided by A subscript A, which is the total approach flow area on one side of the channel in feet squared.     (80)

where:

Qblocked= approach flow blocked by the embankment on one side of the channel, ft3/s
Aa= total approach flow area on one side of the channel, ft2
Ablocked= approach flow area that is blocked by the embankments on one side of the channel, ft2
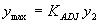Equation 81. Y subscript max equals K subscript ADJ times Y subscript 2.     (81)

Step 5: Compute maximum scour according to:

Previous | Table of Contents | Next

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse
U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101