U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-009 Date: March 2017 |
Publication Number: FHWA-HRT-16-009 Date: March 2017 |
This chapter discusses various approaches in FWD data analysis and interpretation for flexible pavements, including a review of common backcalculation programs in terms of their underlying assumptions, required inputs and resulting outputs, overall advantages and disadvantages, and user friendliness. Flexible pavement modeling issues, such as the effects of temperature and moisture, stiff layer, layer thicknesses; and nonlinear, viscoelastic, and dynamic material behavior, are also discussed. In addition, this chapter includes recommendations on the use of FWD data for mechanistic-empirical pavement design, along with suggestions for future research needs.
There are various approaches for FWD data analysis and interpretation. These can be broken down according to (1) the methods of analysis for calculating pavement response (forward analysis) and (2) the methods for interpretation of pavement response (backcalculation). Each of these is described in the following sections.
Methods of calculating pavement response (forward calculation) include (1) closed-form solutions based on Boussinesq’s original halfspace solution, (2) layered elastic solutions based on Burmister’s original two- and three-layer solutions, and (3) finite element solutions.(63–65) Some of the common computer programs for flexible pavement analysis are presented in table 2, along with their basis and characteristics.
Table 2. Flexible pavement analysis programs.(66)
| Software Name |
Method Used in Response Model |
Type1 | Nonlinearity | Rheology | Anisotropy | Interface | Climate Effects |
Dynamic Loading |
Axle Spectrum |
Tyre Characteristics |
Stochastic | Crack Propagation |
Thermal Effects |
Cumulated Damage |
Fatigue | Permanent Def. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APAS-WIN | Multilayer | 3 | — | — | — | — | Y | — | Y | Y | — | — | Y | — | Y | — |
| AXYDIN | Axi-symmetric FEM | 1 | — | — | — | — | — | Y | — | — | — | — | — | — | — | — |
| BISAR/SPDM | Multilayer | 3 | — | — | — | Y | Y | — | Y | — | — | — | — | — | Y | Y |
| CIRCLY | Multilayer | 3 | — | — | Y | Y | — | — | Y | Y | — | — | — | Y | Y | — |
| CAPA-3D | 3D-FEM | 3 | Y | Y | Y | Y | — | Y | — | Y | — | Y | Y | Y | Y | Y |
| CESAR | 3D-FEM | 3 | Y | Y | Y | Y | Y | Y | — | Y | Y | Y | — | Y | Y | Y |
| ECOROUTE2 | Multilayer | 1 | — | — | — | Y | — | — | — | Y | — | — | — | Y | — | — |
| ELSYM 5 | Multilayer | 1 | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| KENLAYER | Multilayer | 2 | Y | Y | — | Y | — | Y | — | Y | — | — | — | Y | Y | Y |
| MICHPAVE | Axi-symmetric FEM | 1 | Y | — | — | — | — | — | — | — | — | — | — | — | Y | — |
| MMOPP | Multilayer | 2 | Y | — | — | — | Y | Y | Y | Y | Y | Y | — | Y | Y | Y |
| NOAH | Multilayer | 3 | — | — | Y | Y | Y | Y | Y | — | — | — | Y | Y | ||
| ROADENT/ WESLEA3 | Multilayer | 2 | — | — | — | Y | Y | — | Y | Y | — | — | — | — | — | — |
| SYSTUS | 3D-FEM | 2 | Y | Y | Y | Y | — | Y | — | Y | — | Y | — | — | — | — |
| VAGDIM 95 | Multilayer | 3 | — | — | — | — | Y | — | — | — | — | — | Y | Y | Y | Y |
| VEROAD | Multilayer | 1 | — | Y | — | — | — | — | Y | Y | Y | — | — | — | — | — |
| VESYS | Multilayer | 3 | — | — | — | — | Y | — | Y | Y | Y | — | — | Y | Y | Y |
Def. = Deformation.
Y = Yes.
— Indicates properties not considered in the program.
1Type: 1 = Response only, 2 = Response + Partial Performance, and 3 = Full Design Procedure. See section 2.4 of reference 66.
2Model was not used in the project because of lack of availability.
3Only the response model WESLEA was evaluated in the project.
The most useful solution in the first category is MET, which is based on Odemark’s assumptions.(33) In this method, the deflections of a multilayered pavement system with moduli Ei and layer thicknesses hi can be obtained using a single layer of thickness H and modulus E provided that H satisfies the equation in figure 68.
Figure 68. Equation. Odemark transformation.
This method is reported to produce results that are as good as or better than those from layered elastic and finite element solutions, when compared with measured data.(33,34) The method can also be adapted to handle nonlinear subgrade materials. Another clear advantage of this method is its simplicity, which leads to significant savings in computation time, a feature that is particularly useful in backcalculation because many iterations are usually required.
The layered elastic solutions are by far the most commonly used among all methods. They are generally restricted to linear elastostatic analysis and have been shown to produce good results if material behavior remains in the linear range. Numerous pavement-specific computer programs (such as CHEVRON, ELSYM5, and BISAR) have been developed using the n-layer solution provided by Schiffman.(35) The basic assumptions in this category of solutions are the following:
Surface load is uniformly distributed over a circular area.
All layers are homogeneous, isotropic, and linearly elastic.
Upper layers extend horizontally to infinity.
Bottom layer is a semi-infinite halfspace.
Some of the available computer programs do allow for nonlinear response (e.g., NELAPAV, PADAL) or viscoelastic response (e.g., VESYS, KENPAVE).
A number of computer programs based on FEA have also been used for pavement analysis, including three-dimensional (3-D) general purpose (structural mechanics) programs such as SAP®, ABAQUS®, and ANSYS®, and pavement-specific programs for two-dimensional axisymmetric (e.g., ILLIPAVE, MICHPAVE) and 3-D solutions (CAPA-3D). The main advantage of using FEA is the ability to handle material variability and nonlinearity in both vertical and horizontal directions, and to include any number of sophisticated constitutive models. However, most of these programs involve a large number of elements and input parameters, and therefore are much more time-consuming to set up and to run. Hence, their use has been limited mainly to the pavement research community, although there has been a growing interest in their use among pavement engineers in recent years.
Computer programs for dynamic analysis of pavement systems use either dynamic damped-elastic finite-layer or finite element models for their forward solutions. The finite layer solutions are based on Kausel’s formulation, which subdivides the medium into discrete layers that have a linear displacement function in the vertical direction and satisfy the wave equation in the horizontal direction.(67) Examples of programs containing such solutions include UTDYNAF, UTFWD, GREEN, and SAPSI. (See references 68 through 71.) The computer program SCALPOT models the asphalt concrete layer as a viscoelastic material using a two-parameter power law model, while the SAPSI program allows the layer material properties to be complex and frequency-dependent.(72) Al-Khoury et al. developed an efficient forward solution for the dynamic analysis of flexible pavements using the spectral element technique for the simulation of wave propagation in layered systems.(73) The method can model each layer as one element without the need for subdivision into several sublayers.
Existing backcalculation routines can be categorized in three major groups, depending on the techniques used to reach the solution. These three techniques can be applied to any of the forward analysis methods previously discussed. The first group is based on iteration techniques, which repeatedly use a forward analysis method in an iterative process. The layer moduli are repeatedly adjusted until a suitable match between the calculated and measured deflection basins is obtained. The second group is based on searching a database of deflection basins. A forward calculating scheme is used to generate a database, which is then searched to find a best match for the observed deflection basin. The third group is based on the use of regression equations fitted to a database of deflection basins generated by a forward calculation scheme. Each of these schemes is described in the following sections.
Closed-Form Method
The original ELMOD3 program uses the Odemark-Boussinesq method of equivalent layer thickness concept and the radius of curvature method.(32) Initially, the subgrade material properties, stiffness and nonlinearity, are calculated using the deflections from the outer sensors. The radius of curvature from the central sensors can be used to assess the stiffness of the upper pavement layer. The stiffness of remaining layers is then calculated based on the overall pavement response to the applied load. This ensures that the proposed pavement structure results in the correct central deflection under the measured load.
The surface modulus concept is very useful for estimating the subgrade modulus and for diagnosing stress-sensitive subgrade material and the presence of stiffer layers. It uses Boussinesq’s original closed-form equations (see figure 69 and figure 70.) relating the vertical deflection on the surface of a homogeneous, isotropic, linearly elastic halfspace δZ and the elastic (Young’s) modulus E as follows:
Figure 69. Equation. Deflection for uniformly distributed load.
Figure 70. Equation. Deflection for point load.
Where:
P = Surface load (force).
r = Radial distance from center of load.
a = Radius of loaded area.
μ = Poisson’s ratio.
These equations can be used directly to backcalculate the surface modulus Eo given a measured surface deflection due to a known load. For a multilayered pavement system, the calculated surface modulus at the center underestimates the modulus of the surface layer, and it overestimates the modulus of the subgrade. However, as illustrated in figure 71, the surface modulus approaches a constant value at large radii; this value corresponds to the subgrade modulus, illustrating a basic principle of backcalculation, which is that the outer deflections can be used to determine the moduli of the deeper layers. If the surface modulus increases with increasing radial distance, then it is an indication of a stress-sensitive (nonlinear) subgrade or the presence of a stiff layer.(33) The effect of Poisson’s ratio is relatively small for most typical values.
By permission of D.P. Orr, Director, Cornell Local Roads Program
1 mm = 0.039 inches.
1 MPa = 145 lbf/inch2.
Figure 71. Graph. Surface modulus for a three-layer pavement and a halfspace.(35)
Iterative Deflection Basin Fit Methods
In this approach, layer moduli are repeatedly changed until the calculated deflection basin matches the measured one (see figure 72) within a specified tolerance. The flowchart in figure 38 (see chapter 3) illustrates this process.
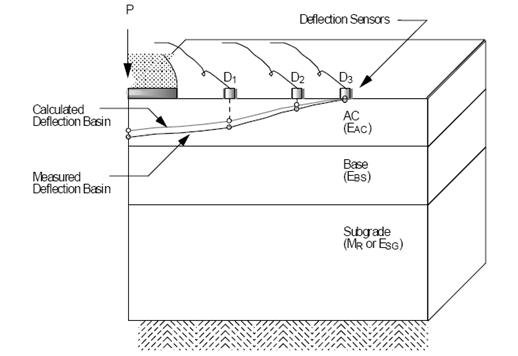
©Washington State Department of Transportation
Figure 72. Diagram. Matching measured and calculated deflection basins.(40)
The main steps of the iteration process are as follows:(37)
Step 1: Measure surface deflections at known radial distances from the center of the loaded area.
Step 2: Enter layer thicknesses, load application characteristics, and Poisson’s ratios for each layer.
Step 3: Start the forward calculation process using initially assumed layer modulus values (seed moduli), which are required as input. Seed moduli are sometimes generated by the program using measured deflections and regression equations; otherwise, the user must specify them. At this stage, some programs use a database approach to obtain seed moduli.
Step 4: Use data specified in step 2 and the latest set of layer moduli to calculate surface deflections at the same radial offsets at which the deflections were measured.
Step 5: Perform an error check to assess whether the measured and calculated surface deflections are within specified tolerance limits. At this stage, different techniques are used to adjust the set of layer moduli so the new set of moduli reduces the error quantified by the objective function. The method by which the moduli are adjusted is the main differentiating factor between most iterative-based programs. Repeat steps 4 and 5 until the value of the objective function is sufficiently small or the adjustments to the layer moduli are very small.
The search algorithm is usually achieved by minimizing an objective function of any set of independent variables (i.e., layer moduli, thicknesses, etc.), which is commonly defined as the weighted sum of squares of the differences between calculated and measured surface deflections, shown in figure 73:
Figure 73. Equation. Objective function to be minimized in the search algorithm for minimizing differences between measured and computed deflections.
Where:
wjm = Measured deflection at sensor j.
wjc = Calculated deflection at sensor j.
aj = Weighing factor for sensor j.
The equation in figure 73 can be solved using nonlinear optimization methods, which locate the least value of the objective function. Many minimization techniques are available in the literature, including the following:(42)
Factored secant update method.
Modified Levenberg-Marquardt algorithm.
Modified Powell hybrid algorithm.
One of the problems of this approach is that the multidimensional surface represented by the objective function may have many local minima. As a result, the program may converge to different solutions for different sets of seed moduli. Another problem is that the convergence can be very slow, requiring numerous calls to a mechanistic analysis program.
An example of an iterative program is EVERCALC©, which uses the Levenberg-Marquardt minimization algorithm.(43) The program seeks to minimize an objective function formed as the sum of squared relative differences between the calculated and measured surface deflections. EVERCALC© is a robust, efficient, and accurate program, and uses the CHEVRON computer program for forward calculations.
The series of programs with names ending in “DEF” use an assumed linear variation in logarithmic space between layer moduli and surface deflections to revise the layer moduli after each iteration. These programs employ a gradient search technique, and the “correct” set of moduli is searched in an iterative manner. The CHEVDEF program is one such example in which the CHEVRON program is used for forward calculations. A set of seed moduli are required to be entered by the user in this program to start the iteration process.(44,74) The linearization of the model in logarithmic space simplifies the search for a new set of moduli. However, the results obtained by these programs are highly dependent on the initial seed moduli.
In addition to the original radius of curvature method, the newer ELMOD5 program has options where the deflection basins (calculated using the Odemark-Boussinesq MET, WESLAYER, or finite element method) are matched iteratively with the convergence criteria based on the degree of fit between the measured and calculated deflection basins.
The search method can also take the form of solving the linear set of equations shown in figure 74.
Figure 74. Equation. Deflection basins matched iteratively with the convergence criteria.
Where:
[F]k= kth iteration of the m x n matrix of partial derivatives ∂ fj/ ∂ Ei, where j = 1 to m and m is the number of deflections measured, and i = 1 to n where n is the number of layers in the pavement.
{d}k = kth iteration difference vector, Eik+1– Eik, between the new and old moduli.
{r}k = kth iteration residual vector, wjc – wjm, between the most recently calculated and the measured surface deflections.
An example of an iterative program using the above search method is MICHBACK©, which uses the modified Newton-Raphson (also called secant) method. The method of least-squares is used to solve the overdetermined system of equations (m equations in n unknowns, m > n) in the figure 74 equation. If desired, weighting factors can be used for each sensor measurement to emphasize some deflection measurements over others. MICHBACK© also uses the CHEVRONX computer program for forward calculations.
Database Approach
In this method, a forward calculation program is used to generate a database of deflection basins for different combinations of layer moduli, specified layer thicknesses, material properties, pavement types, and loading conditions. The measured deflection basin is compared with the deflection basins in the database using a search algorithm, and a set of moduli are interpolated from the layer moduli that produces the closest calculated deflection basins in the database.
The MODULUS backcalculation program, which uses databases generated by the WESLEA program, is one such example.(36,37)The number of basins required to obtain a suitable database depends on the number of layers and the expected moduli ranges provided by the user. Wide ranges require generation of a greater number of basins than narrow ones. The generated deflection basins are then searched using the Hookes-Jeeves algorithm, and a three-point Lagrangian method is used to interpolate the values of the moduli between the various deflection basins. The program seeks to obtain a set of moduli that minimize an objective function defined as the relative sum of squared differences between the measured and calculated surface deflections. The program always converges, although the chances of converging to a local minimum cannot be ruled out.(38) The program performs a convexity test to determine the likelihood of having converged to a local minimum, and the user is warned if this test is not satisfied.
Backcalculation based on a database search is especially suitable when a large number of pavements with a similar configuration need to be tested in succession. For these situations the database, once generated, can be used repeatedly to backcalculate values of the modulus of the various pavement layer for all similar pavements, and the time required to generate the database can be minimized. This technique can be used with a database generated from any linear or nonlinear program.(38)
Statistical Analysis
This method is similar to the database approach, the only difference being how the database is used. The database is created by using any forward calculation routine, and then statistical analysis is performed to generate regression equations. These equations use the deflections as independent variables and attempt to predict the values of the layer moduli. Pavements of different configurations can be grouped separately to yield different equations for more accurate predictions. Different prediction equations are required for each pavement layer, and pavements with a different number of layers must be treated separately.
This technique is best suited for agencies that deal with limited and known types and configurations of pavement. Database generation to include all the expected combinations of pavement layers in the initial stages can offset this disadvantage to a large extent. Once the regression equations are obtained, this technique is simple and extremely quick. The results, on the other hand, vary in accuracy depending on how well the database used to generate the statistical equations represents the pavement being analyzed.
Dynamic Backcalculation Methods
Most dynamic backcalculation methods use dynamic, damped-elastic finite-layer or finite element models for their forward solutions, as previously discussed. Dynamic backcalculation methods are based on either frequency or time domain solutions. For the former procedure, the applied load and measured deflection time histories are transformed into the frequency domain by using FFT. Backcalculation of layer parameters is done by matching the calculated steady-state (complex) deflection basin with the frequency component of the measured sensor deflections at one or more frequencies. In time domain backcalculation, the measured deflection time histories are directly compared with the predicted results from the forward program. One of the advantages of this method is that matching can be achieved for any time interval desired. Uzan compared the two methods and concluded that time domain backcalculation was preferred over frequency domain backcalculation.(75)
Numerous computer programs for performing automated backcalculation have been written. Some of the known static backcalculation computer programs and their characteristics are presented in table 3. Different versions of these programs exist, with improved and/or updated editions being released periodically. Most of the automated backcalculation programs rely on static analysis and a linear elastic layer program. Notable exceptions include ELMOD®, which can use either Odemark’s method or the finite element method in addition to the layered elastic solution, and MODCOMP©, which can handle nonlinear material properties.
Table 3. Commonly available backcalculation computer programs for flexible pavements.
| Program Name |
Developer | Forward Calculation Method |
Forward Calculation Subroutine |
Backcalculation Method |
Nonlinear Analysis |
Layer Interface Analysis |
Maximum Number of Layers |
Seed Moduli |
Range of Acceptable Modulus |
Ability to Fix Modulus |
Convergence Scheme |
Error Weighting Function |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BISDEF© | USACE-WES | Multilayer Elastic Theory | BISAR | Iterative | No | Variable | Number of deflections; best for 3 unknowns | Required | Required | Yes | Sum of squares of absolute error | Yes |
| BOUSDEF | Zhou et al. (Oregon State) | MET | MET | Iterative | Yes | Fixed (rough) | At least 4 | Required | Required | N/A | Sum of percent errors | N/A |
| CHEVDEF | USACE-WES | Multilayer Elastic Theory | CHEVRON | Iterative | No | Fixed (rough) | Number of deflections; best for 3 unknowns | Required | Required | Yes | Sum of squares of absolute error | Yes |
| COMDEF | USACE-WES | Multilayer Elastic Theory | BISAR | Database | No | Fixed (rough) | 3 | No | No | N/A | Various | No |
| DBCONPAS | Tia et al. (University of Florida) | Finite Element | FEACONS III | Database | Yes? | Yes? | N/A | No | No | N/A | NA | N/A |
| ELMOD®/ ELCON | Ullidtz (Dynatest®) | MET | MET | Iterative | Yes (subgrade only) | Fixed (rough) | 4 (exclusive of rigid layer) | No | No | Yes | Relative error of 5 sensors | No |
| ELSDEF | Texas A&M, USACE-WES | Multilayer Elastic Theory | ELSYM5 | Iterative | No | Fixed (rough) | Number of deflections; best for 3 unknowns | Required | Required | Yes | Sum of squares of absolute error | Yes |
| EMOD | PCS/Law | Multilayer Elastic Theory | CHEVRON | Iterative | Yes (subgrade only) | Fixed (rough) | 3 | Required | Required | Yes | Sum of Relative squared error | No |
| EVERCALC© | Mahoney et al. | Multilayer Elastic Theory | CHEVRON | Iterative | Yes | Fixed (rough) | 3 (exclusive of rigid layer) | Required | Required | Yes | Sum of absolute error | No |
| FPEDD1 | Uddin | Multilayer Elastic Theory | BASINF? | Iterative | Yes | Fixed (rough) | N/A | Program Generated | NA | N/A | NA | No |
| ISSEM4 | Ullidtz, Stubstad | Multilayer Elastic Theory | ELSYM5 | Iterative | Yes (finite cylinder concept) | Fixed (rough) | 4 | Required | Required | Yes | Relative deflection error | No |
| MICHBACK© | Harichandran et al. | Multilayer Elastic Theory | CHEVRONX | Newton method | No | Fixed (rough) | Number of deflections; best for 3 unknowns | Required | Required | Yes | Sum of relative squared error | NA |
| MODCOMP5 | Irwin, Szebenyi | Multilayer Elastic Theory | CHEVRON | Iterative | Yes | Fixed (rough) | 2 to 15 layers; maximum of 5 unknown layers | Required | Required | Yes | Relative deflection error at sensors | No |
| MODULUS | Texas Transportation Institute | Multilayer Elastic Theory | WESLEA | Database | Yes? | Fixed? | 4 unknowns plus stiff layer | Required | Required | Yes | Sum of relative squared error | Yes |
| PADAL | Brown et al. | Multilayer Elastic Theory | n/a | Iterative | Yes (subgrade only) | Fixed ? | n/a | Required | N/A | N/A | Sum of relative squared error | N/A |
| RPEDD1 | Uddin | Multilayer Elastic Theory | BASINR ? | Iterative | Yes | Fixed ? | n/a | Program Generated | N/A | N/A | n/a | No |
| WESDEF | USACE-WES | Multilayer Elastic Theory | WESLEA | Iterative | No | Variable | 5 | Required | Required | Yes | Sum of squares of absolute error | Yes |
N/A = Not applicable.
Accuracy and Reliability
Many of the programs written for production purposes are intended to get to an accurate solution reliably. While most static backcalculation programs usually converge to a solution reasonably quickly and reliably, one cannot assert the uniqueness of the set of layer moduli derived from any search method. For this reason, many programs use various controls to guide the iterative search toward an “acceptable” set of layer moduli. These include (1) making some assumptions about the type of pavement system being analyzed (e.g., assuming that layer moduli decrease with depth, that the subgrade modulus is constant with depth, that a rigid layer exists a certain depth, and so on), and (2) limiting the acceptable range of moduli for each individual layer type.
Required Inputs
Required inputs typically include peak sensor deflections and their location, peak load values, the number of layers in the pavement system and their thicknesses, and assumed values for Poisson’s ratios. Most programs also require seed moduli as input, although some have methods that generate these from the measured deflections or from regression equations.
Resulting Outputs
Typical outputs include the measured and calculated deflections, the differences and percent differences, the final set of layer moduli, and the error sums. Most of the existing backcalculation programs allow for 3 to 5 layers; a notable exception is the MODCOMP5 program, which allows up to 15 layers (with a maximum of 5 unknown layers).
User Friendliness
Because many of the backcalculation programs are written for production purposes, they are user friendly, require minimum involvement from the user, and provide various features intended to be useful for project-level analysis. Conversely, those programs written for use in research tend to lack the features needed for production. They also usually allow and require significant involvement from the user. These include dynamic backcalculation programs that rely on dynamic analysis to calculate the deflection time histories, and those that use available, general-use finite element method programs.
Advantages and Disadvantages
Attempting to do a one-on-one comparison of different backcalculation programs for the purpose of identifying the best one is a difficult task. All of these programs have different pros and cons, and each may be particularly useful in a specific situation. Before making such comparisons, one should first define the purpose in doing backcalculation and the evaluation criteria that one will use. In general, the advantage of using simpler methods is that they are very fast and easy to use. Their disadvantage is that they are limited in their interpretation of the FWD data. For example, most static backcalculation programs are limited to three layers. This may not be sufficient to characterize realistic pavement profiles, which may comprise five or more layers and cannot be used to allow for variation of subgrade modulus with depth, for example. On the other hand, more advanced methods of backcalculation, which will theoretically allow for the backcalculation of a larger number of parameters, are computationally expensive and time consuming. Also, they are not guaranteed to converge when using real field-measured data.
A number of computer programs have been developed for dynamic backcalculation of flexible pavement layer parameters. Each program employs a particular forward model and a specific backcalculation scheme. All of these programs require the time histories of the load and deflection sensors. Theoretically, because these time histories contain more information than just the peak values of load and deflection, dynamic backcalculation programs can backcalculate a larger number of parameters when using synthetically generated deflection time histories. However, there are serious challenges when using measured field data. For example, the frequency-domain solutions can lead to large errors if the measured FWD records are truncated before the motions fully decay in time.
Time-domain backcalculation solutions present another set of challenges. For example, the time synchronization between the load and sensor records and the digitization of the response can be problematic. Noise in the data and the ill-posed nature of the inversion problem can be amplified when matching traces of time histories, requiring special filtering and regularization techniques that are not easy to implement. In addition, unlike frequency-domain analysis where the properties are backcalculated at each frequency independently, time-domain backcalculation precludes making a choice about the behavior of material properties with frequency; that is, it either assumes a constant HMA modulus (similar to static backcalculation) or a prescribed function of the HMA layer modulus with frequency (e.g., linear relation in the log-log space). While this assumption may be acceptable for unbound materials, it may significantly affect the predicted response of the HMA layer because of its viscoelastic nature. Finally, none of these programs are considered ready for production mode because they usually require a lot of involvement from the user, are computationally very expensive, and have not been fully evaluated for use with field-measured data. Some of the dynamic backcalculation computer programs and their characteristics are presented in table 4. A brief overview of the programs developed to date is also provided.
Table 4. Dynamic backcalculation programs for flexible pavements.
| Program | Domain | Inverse Method | Forward Program | Reference |
|---|---|---|---|---|
| BKGREEN | Frequency | Nonlinear least-square optimization | GREEN | 70 |
| No name | Frequency/ Time | Newton’s method | UTFWIBM | 76 |
| PAVE-SID | Frequency | System Identification (SID) | SCALPOT | 72 |
| FEDPAN | Time | Linear least squares | SAP IV | 77 |
| No name1 | Frequency | Levenberg-Marquardt | SAPSI | 78 |
| No name1 | Frequency | Secant Update Levenberg-Marquardt Powell Hybrid |
LAMDA | 79 |
| No name1 | Time | Gauss-Newton method | FEM | 80 |
| DYNABACK | Frequency/ Time | Newton’s method with least-square or SVD method | SAPSI | 81, 82, 46 |
| EVERCALCII | Time | Nonlinear least square optimization with Tikhonov regularization and continuation method | FEM | 83 |
1Program was developed for internal study and was never assigned a label.
Uzan presented two dynamic linear backcalculation procedures, one in the time domain and the other in the frequency domain.(76) Both approaches use the program UTFWIBM as the forward model and Newton’s method as the backcalculation solution.
PAVE-SID is a computer program that uses the SCALPOT program to generate frequency response curves; a system identification technique is applied for matching computed frequency data to extract pavement properties.(72) SCALPOT computes the dynamic response of a horizontally layered viscoelastic halfspace to a time dependent surface pressure distribution.
BKGREEN models the pavement as a layered elastic system in terms of dynamic Green flexibility influence functions using Kausel’s formulation of discrete Green functions for dynamic loads in linear viscoelastic layered media.(70,67) Backcalculation is done at multiple frequencies, and the set of layer moduli is determined using a nonlinear least squares technique. The calculation can experience some computational difficulties at certain frequencies because of the numerical complications associated with implementing infinite integration in computer codes.
Al-Khoury et al. developed an axisymmetric layered solution as a forward model using the spectral element technique, and used the modified Levenberg-Marquardt and Powell hybrid methods for solving the resulting system of nonlinear equations.(73,79,84)
Losa used SAPSI as the forward program and a nonlinear least squares optimization technique (Levenberg-Marquardt method) for multifrequency backcalculation.(78,71)
FEDPAN is a finite element program that can perform both static and dynamic backcalculation for three-layer pavement systems using the CHEVDEF backcalculation algorithm.(77,44) This program can simulate the effects of pavement inertia and damping in the dynamic analysis, and material nonlinearity in the static analysis.
Meier and Rix developed an ANN solution that has been trained to backcalculate pavement layer moduli for three-layer flexible pavement systems using synthetic dynamic deflection basins.(47) The dynamic pavement response was calculated using an elastodynamic Green function solution based on Kausel’s formulation.(67)
Work by Chatti developed the DYNABACK computer program, which allows for different dynamic backcalculation algorithms for both frequency-based and time-based solutions.(81,82,46) The DYNABACK program uses the SAPSI program as its forward solution and an expanded version of the modified Newton-Raphson algorithm in the MICHBACK© program as its backcalculation solution.(71,85) The solution uses the least squares minimization technique to solve the real-valued gradient matrix equation. The DYNABACK program includes two basic solutions with several options for backcalculating different layer parameters: (1) frequency-domain backcalculation at one or multiple frequencies and (2) time-domain backcalculation using peak responses or time history traces. Theoretically, single frequency backcalculation can be used to backcalculate up to 8 parameters while multiple frequency backcalculation can be used to backcalculate up to 15 parameters. The same is true for time domain backcalculation using peak responses and traces, respectively. However, when using measured deflection time histories, the number of backcalculated parameters must be reduced to fewer than eight.
Finally, Turkiyyah has been developing an improved EVERCALCII program that uses the complete FWD sensor time histories to recover pavement layer moduli distribution and thicknesses using thin “computational layers” that discretize the profile.(83) In this solution, physical layer thicknesses may be obtained, after backcalculation of thin computational layer moduli, by grouping thin layers of similar moduli values. Two regularization techniques are employed: one involves the absolute values of the moduli to prevent physically unrealistic solutions with large layer moduli, while the second controls the gradient of the moduli in the vertical direction to prevent convergence to profiles with neighboring layers that alternate between high and low moduli. In addition, a continuation scheme is used to control the weights on the regularization terms to overcome the ill-posed nature of the optimization problem. Because this solution relies on backcalculating the moduli of a relatively large number of elements that make up these thin computational layers, the computational effort for solving the inverse problem is very significant. Efforts are underway to speed up the forward (finite element method) solution.
The primary issues related to FWD data analysis and interpretation are (1) errors in measurement (relevant to static and dynamic backcalculation) and (2) signal noise and truncation (relevant for dynamic analysis only). These topics are discussed in the following sections.
According to Irwin, there are three main sources of errors in FWD data: (1) seating errors, (2)random errors, and (3) systematic errors.(35) Irwin, Yang, and Stubstad showed that even very small deflection errors (on the order of 2 μm or less) can lead to very large errors in the backcalculated moduli.(86)
Seating Errors
Seating errors are caused by the rough texture of pavements and are of more critical importance in testing HMA pavements. These errors can be eliminated by applying one or two drops at each new test point. This causes the deflection sensors to become seated.
Random Errors
Random errors are associated with the analog-to-digital conversion of the deflections and are on the order of ±2 μm.(86) Random errors cannot be completely eliminated, but they can be reduced by taking multiple readings and averaging the results. This reduction is proportional to the square root of the number of observations used in computing the mean. For example, if four replicate FWD drops (with the same height) at the same point were averaged, the random error would be reduced by half. Care must be taken to ensure that no liquefaction or compaction has taken place because of the additional drops.(35)
Systematic Errors
Systematic errors are associated with the particular FWD equipment and its specific sensors. Systematic errors are on the order of ±2 percent. FWD specifications therefore call for an accuracy of ±2 percent or ±2 μm, whichever is larger. This specification combines the systematic error and the random error. Systematic errors can be reduced to 0.3 percent or less for each individual sensor, including the load cell, through calibration.(35)
The sensitivity of dynamic backcalculation solutions to signal noise is high. Basically, noisy data alters the error function surface enough to lead optimization astray. This can cause the search algorithm to diverge, or to converge to a different modulus when regularization techniques are used. The remedy to noise is to preprocess the raw data by filtering out the high frequency content of the signal (anything above 100 Hz) in deflection and load pulse data.
Another issue that is relevant to dynamic analysis is the existence of a nonphysical time lag between the load and deflection pulses that may be caused by synchronization problems in the data acquisition system. In addition, most FWD load and deflection pulses are cut off before the complete decay of the time histories. This generates a discontinuity in the slope of the function leading to significant errors in the frequency content of the signals. This truncation problem can lead to large errors in the backcalculated layer parameters when using a frequency-based solution.(81)
Several specific modeling issues are in play when considering backcalculation solutions, as described in the following subsections.
As described in chapter 2, the FWD test consists of dropping a large weight from a specified height, which creates a 20- to 60-ms impulse load, simulating a moving wheel load. This creates waves in the pavement system and underlying subgrade soil. These elastic waves propagate with distance and are partly reflected at the interface between any given two successive layers, with the remaining wave energy penetrating and propagating to the next layer, and the process is repeated. These waves bounce up and down a few hundred times in a given test. The deflection time histories lag the load pulse, with the time lag increasing as the distance between the load plate and the sensor increases. So, clearly, the FWD test is dynamic.
The difference between static response and dynamic response can be defined in terms of the internal forces involved. In static analysis, only elastic forces are considered. On the other hand, viscous and inertial forces are considered in addition to the elastic forces in dynamic analysis. The question therefore is whether the effects of viscous and inertial forces are significant enough that one cannot afford to ignore them when characterizing the in situ conditions of a pavement system under an FWD test. Most pavement engineers argue that backcalculation is an exercise that determines pavement parameters, and not properties, that are to be used within a given mechanistic framework. Therefore, it is acceptable to use static analysis and to backcalculate parameters that are compatible with the current mechanistic-empirical design framework that is grounded in static and not dynamic analysis. However, advocates for dynamic analysis maintain that such an approach takes advantage of more information provided by the test, which allows for backcalculating more parameters such as layer thicknesses or the modulus versus frequency curve of the HMA layer. Also, in certain cases, such as the existence of a stiff layer or water table at shallow depth, the effect of dynamics on pavement response may be more important.
When pavement structures are thin enough or the applied loads and corresponding stresses are high enough, the subgrade material likely exhibits stress-softening, nonlinear behavior (i.e., its response increases at a higher rate than the load or stress increases). This translates to the subgrade modulus changing with depth and radial distance from the load. If the forward model uses a layered solution that assumes linear material behavior, it can only use one modulus value for an entire layer. Consequently, the backcalculated modulus that is required to match the measured deflections is an averaged value. Typically, the backcalculated subgrade modulus is higher than the laboratory-based value by a factor of about 1.3 to 3.(87)
On the other hand, granular (cohesionless) materials used in bases and subbases are stress-dependent in a different (positive) way (i.e., their modulus increases with increasing confinement). Similar to the subgrade modulus, this leads to a base/subbase modulus that varies with depth and radial distance from the load, and any linear backcalculation exercise can only lead to an averaged modulus value, assuming linear behavior in the forward model leads to an underestimation of the base/subbase modulus. The combination of the above phenomena often leads to a base modulus that is lower than the subgrade modulus despite the fact that the base material is superior to that of the subgrade. One way of addressing this problem is to introduce an artificial layer. However, a more direct way of addressing the problem is to treat the subgrade as a nonlinear elastic material with stress-dependent modulus as shown in figure 75.(88)
Figure 75. Equation. Stress-dependent elastic modulus.(88)
Where:
E = Modulus value.Ullidtz argues that the effect of the positive nonlinearity in granular base/subbase layers on backcalculation results is less important.(88)
Ideally, only the finite element method can model the variation of moduli with depth and radial distance. However, there are models based on layered elastic theory that can handle nonlinear behavior approximately (e.g., NELAPAVE and KENPAVE). Ullidtz combines MET described previously with a stress-dependent subgrade modulus, as described in figure 75, to handle material nonlinearity, and reports that this approach is superior to the finite element method.(88)
A stiff layer condition can exist if there is shallow bedrock, a stiff clay layer, or a groundwater table. The effect of a stiff layer at a shallow depth can be very significant. Assuming the subgrade layer to be a semi-infinite halfspace, while in reality the subgrade layer is only a few meters thick, causes the backcalculated moduli for the upper pavement layers to be incorrect. Generally, when the stiff layer is deeper than about 12 m (39 ft), its presence has little or no influence on the backcalculated moduli. The depth to the stiff layer can be evaluated by using a relationship between the deflection, δz, and 1/r, where r is the radius at which it occurs (see figure 76). Several regression equations for different HMA layer thicknesses can be used as a function of ro and deflection basin parameters.(40)
An alternative, and arguably better, way to determine the depth to the stiff layer is to use the free vibration response from FWD deflection sensor measurements and one-dimensional wave propagation theory.(89) Chatti, Ji, and Harichandran modified Roesset’s equations to account for different conditions, as shown in the equations in figure 77 and figure 78.(46)
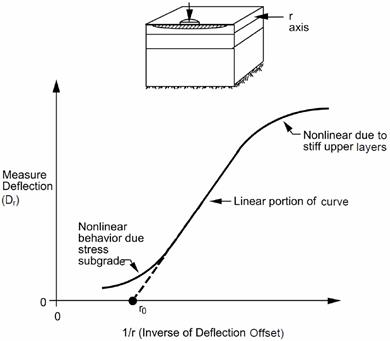
©Washington State Department of Transportation
Figure 76. Graph. Plot of the inverse of deflection offset versus measured deflection.(40)
Figure 77. Equation. Saturated subgrade with bedrock.(46)
Figure 78. Equation. Nonsaturated subgrade with bedrock or groundwater table.(46)
Where:
Db = Depth of bedrock.
Vs = Shear-wave velocity of subgrade = [(Esg/(2(1–u2)))/ ρ]0.5.
Esg = Modulus of the subgrade.
ρ = Unit weight of the subgrade.
u = Poisson’s ratio of subgrade.
Td = Natural period of free vibration (see figure 79).
As defined here, the shear wave velocity of the subgrade, Vs, is a function of the subgrade modulus, the subgrade unit weight, and the subgrade Poisson’s ratio. This value can be determined using an iterative procedure developed by Lee, Kim, and Ranjithan.(90)
©K. Chatti
1 mil = 0.0254 mm.
Figure 79. Graph. Natural period, Td, from sensor deflection time histories.(46)
Temperature and moisture conditions in the pavement vary over time. This variation occurs daily as well as seasonally. A pavement is strongest during the freezing season (in a freezing climate) because of the frozen state of the underlying materials. On the other hand, even in a freezing environment, the pavement can be at its weakest state during a thaw period, even if that period is short and temporary (e.g., on a sunny day in late winter, during the warmest hours around midday). In areas where there is little or no freezing, seasonal variations can be very important in terms of moisture changes, which affect the modulus of the subgrade and to a lesser extent that of the base layer. For the HMA layers, hourly temperature variations during a given day need to be taken into account because temperature gradients exist in the pavement, which can lead to modulus variation with depth. Also, seasonal variations can have a major effect on the modulus of an HMA layer. These effects must be considered when performing backcalculation. It is crucial to test the pavement at different times of the year to gain information about the seasonal variation. Testing should also be conducted at different times during the day to account for daily temperature variations.
Several other issues may need to be addressed in backcalculation analysis, including the following:
Major cracks in the pavement, or testing near a pavement edge or joint, can cause the deflection data to depart drastically from the assumed conditions.
Layer thicknesses are often not known, and subsurface layers can be overlooked.
Layer thicknesses are not uniform, and materials in the layers are not homogeneous.
Some pavement layers are too thin to be backcalculated in the pavement model.
The required input material properties for HMA pavements in the new MEPDG that are relevant to the use of FWD data and backcalculation results are (1) the time-temperature dependent dynamic modulus E* for the HMA layer(s), (2) the resilient moduli for the unbound base/subbase and subgrade materials, and (3) the elastic modulus of the bedrock, if present.(7) The MEPDG also provides an option for considering nonlinear material parameters for the unbound layers for level 1 analysis. However, the performance models used in the software have not been calibrated for nonlinear conditions; therefore, this option is not considered further in this report.
For new HMA design, level 1 analysis requires conducting E* laboratory testing (ASTM D3496) at loading frequencies and temperatures of interest for the given mixture.(91) Level 2 analysis does not require E* laboratory testing; instead, the user can enter asphalt mix properties (gradation parameters) and laboratory binder test data (from G* testing or other conventional binder tests). The MEPDG software calculates the corresponding asphalt viscosity values; it then uses the modified Witczak equation to predict E* and develops the master curve for the HMA mixture.(7) This same procedure is used for level 3 analysis to estimate the HMA dynamic modulus except no laboratory test data are required for the binder.
For rehabilitation design, determination of the HMA layer dynamic modulus follows the same general concepts described above, except the software allows use of a modified procedure to account for damage incurred in the HMA layer during the life of the existing pavement.(7) The procedure therefore determines a “field damaged” dynamic modulus master curve as follows:
For level 1 analysis, the MEPDG calls for the following procedure:(7)
Step 1: Conduct FWD tests in the outer wheelpath over the project to be rehabilitated; calculate the mean backcalculated HMA modulus, Edam, for the project, combining layers with similar materials and including cracked as well as uncracked areas; record the HMA layer temperature at the time of testing and determine the layer thickness along the project using coring or ground-penetrating radar (GPR) testing.
Step 2: Determine mix volumetric parameters (air void content, asphalt content, and gradation) and asphalt viscosity parameters (regression intercept (A) and regression slope of viscosity temperature susceptibility (VTS)) from cores and follow the same procedure for determining binder viscosity-temperature properties as for new or reconstruction design.
Step 3: Develop an undamaged dynamic modulus master curve using the modified Witczak equation and the data from step 2 at the same temperature recorded in the field and at an equivalent frequency corresponding to the FWD pulse duration.
Step 4: Estimate the fatigue damage in the HMA layer (dac) using the Edam obtained from step 1 and the undamaged dynamic modulus, E*, obtained from step 3.
Step 5: Calculate α'= (1 – dac) α; where α is a function of mix gradation parameters.
Step 6: Determine the field-damaged dynamic modulus master curve using α' instead of α in the modified Witczak equation.
For level 2 and level 3 analyses, no FWD testing is required. The level 2 procedure is similar to the level 1 procedure, in that field cores are used to obtain the undamaged modulus; however, estimates for fatigue damage of the existing asphalt layer is determined through a detailed pavement condition survey and the calibrated MEPDG distress models. For the level 3 procedure, no coring or testing is required; instead, typical estimates of HMA mix parameters (typical volumetric and binder properties) are entered, and the program calculates the undamaged master curve.
For unbound materials (and bedrock), only level 1 analysis calls for FWD testing in rehabilitation and reconstruction designs. The resilient modulus, Mr, for each unbound layer (including the subgrade) can be either determined in the laboratory using cyclic triaxial tests or backcalculated using standard backcalculation procedures. As discussed previously, while the MEPDG does allow for the generalized nonlinear, stress-dependent model in the design procedure, this approach is not recommended at this time because the performance models in the software have not been calibrated for nonlinear conditions; therefore, the option of backcalculating the k1, k2, and k3 parameters in the nonlinear model is not discussed.(7) Consequently, the discussion only includes the backcalculation and use of “effective” moduli that would account for any stress sensitivity, cracks, or any other anomalies in any layer within the existing pavement. For level 2 analysis, correlations with strength test data are used. For level3, the MEPDG lists typical modulus values based on soil classification, but warns that they are very approximate and strongly recommends some form of testing, especially using FWD testing and backcalculation (as in level 1).(7)
The MEPDG notes that the reason for caution is related to using the wrong assumptions: either a fairly strong subgrade material may be erroneously assumed to be semi-infinite while it may actually be less than 1 m (3 ft) thick (e.g., as part of an embankment), or conversely, a weak subgrade soil may be assumed to be semi-infinite while it may, in reality, be overlying a stronger soil or bedrock.(7)
Similar to unbound materials, only level 1 analysis calls for FWD testing in rehabilitation and reconstruction designs. The modulus, E or Mr, for any chemically stabilized layer (including lean concrete and cement stabilized base, as well as lime/cement/flyash stabilized soils) can be either determined in the laboratory or backcalculated using standard backcalculation procedures. Layer thicknesses can be obtained by coring or using NDT techniques such as GPR. The MEPDG recommends performing limited testing on cored lime stabilized soil specimens to verify/confirm the backcalculated values and notes that backcalculation of modulus values for layers less than 150 mm (6 inches) thick located below other paving layers may be problematic, thus requiring laboratory testing.(7)
For level 2 analysis, correlations with strength test data are used. For level 3, the MEPDG calls for estimating the moduli based on experience or historical records and lists typical modulus values.(7) The MEPDG also notes that semirigid cementitiously stabilized materials are more prone to deterioration owing to repeated traffic loads when used in HMA pavements and suggests some typical (minimum) values for such deteriorated materials.(7)
It should be clear from the previous discussion that the analysis in the MEPDG software always uses an E* master curve and therefore does not accept a constant modulus value for the HMA layer(s). This is necessary because the analysis calculates different HMA moduli for the different sublayers comprising the HMA layer(s) as a function of depth, speed, and axle type, as explained in appendix CC of the MEPDG.(7) For rehabilitation of existing pavements, the current MEPDG procedure (level 1) calls for (static) backcalculation of layer moduli, which leads to constant backcalculated moduli for all layers, including the HMA layer. To maintain compatibility of backcalculated layer moduli with the forward analysis in the software, the MEPDG procedure calls for adjusting the HMA dynamic modulus using the damage factor dac (ratio of backcalculated HMA modulus to predicted E* value using the Witczak equation).(7) This effectively shifts the undamaged master curve down while essentially maintaining the variation with frequency as predicted by the Witczak equation. The procedure also calls for adjusting the master curve using the aged viscosity value in the predictive E* equation, which would shift the master curve upward; however, this upward shift will be negligible compared with the downward shift using the backcalculated modulus for the damaged HMA layer, Ei (as explained in previous subsection on HMA Materials).
Ideally, one should be able to determine a curve of HMA layer modulus as a function of frequency using a (dynamic) frequency-based backcalculation algorithm. This would give a more direct estimation of the HMA layer modulus with frequency from actual field conditions as opposed to relying on a laboratory-derived curve such as the Witczak equation. However, care should be taken in interpreting and using such data with the existing MEPDG performance predictions because they have been calibrated using laboratory-derived moduli. Also, recent analyses show that while dynamic backcalculation methods can backcalculate layer moduli and thicknesses accurately from synthetically generated FWD data for pavement systems with threeor more layers, they present some serious challenges when using field data.(46) The frequency-domain method can lead to large errors if the measured FWD records are truncated before the motions fully decay in time. Dynamic, time-domain backcalculation algorithms present another challenge in that they cannot directly determine the HMA modulus as a function of frequency. They either assume a constant HMA modulus (similar to static backcalculation) or a prescribed function of the HMA layer modulus with frequency (e.g., a linear relation in the log-log space).