U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-009 Date: March 2017 |
Publication Number: FHWA-HRT-16-009 Date: March 2017 |
This diagram shows a typical pavement deflection basin. On the original flat surface of the pavement is a loading block labeled “Load P.” Beneath the original flat surface is a deflected surface that represents the shape of the original surface if subjected to the Load P. The deflected surface has its greatest deflection directly under the Load P, and the deflections decrease as the distance from the Load P increases. The physical area between the original surface and the deflected surface is referred to as the “Deflection Basin.”
This diagram shows the load transfer concept. Two drawings are shown, arranged top to bottom. The top drawing, entitled “0 percent load transfer,” shows two Portland cement concrete slabs with the left slab curling down at the joint, creating a bump in the road. The left slab is labeled “delta function subscript L equals 0.66 millimeters (Loaded),” meaning the applied load creates a deflection of 0.66 mm in the slab edge. The right side is labeled “delta function subscript U equals 0 millimeters (Unloaded),” meaning no deflection takes place in the right slab as a result of the loading on the left slab. The bottom drawing, entitled “100 percent load transfer,” shows the left and right slabs sharing the load (as a result of a dowel bar inserted across the joint), which is still applied to the left slab. The two slabs are deflected slightly, but equally, with the left slab labeled “delta function subscript L equals 0.33 millimeters (Loaded),” and the right side labeled “delta function subscript U equals 0.33 millimeters (Unloaded).” (1 mm = 0.039 inches)
This diagram is a schematic drawing of the Benkelman Beam device. A support beam with a handle that is 55.5 inches long is shown. A pivot at one end of the support beam attaches it to a measurement probe that is more than 96 inches long. (1 inch = 25.4 mm)
This graph shows typical output of a vibrating steady-state force generator. The x-axis is time with no units or measurements. The y-axis is load, with no units or data labels given. A sinusoidal curve is used to show the load as a function of time. The term “static load” is indicated in the drawing, representing the midpoint of the sinusoidal loading curve. The term “dynamic force (peak-to-peak)” is also shown, representing the difference in load between the maximum and minimum values on the sinusoidal curve.
This diagram is a schematic illustration of the Dynaflect device. The top part of the figure shows the Dynaflect with load wheels in the test position. It shows a covered trailer with small “loading wheels” that descend into position under the trailer along with five geophones that have cords running to the housing and tow bar. The bottom part of the figure shows the configuration of Dynaflect load wheels and geophones. It shows that the loading wheels are 20 inches apart, with the geophones set in a line that is equidistant from each wheel (the first geophone is directly between the two wheels, 10 inches from each wheel; the remaining geophones are spaced every 12 inches forward toward the tow bar. (1 inch = 25.4 mm)
This diagram is a falling weight deflectometer testing schematic. The deflection sensors are spaced at 12-inch intervals, beginning at 12 inches on one side of the load plate and extending directly under the load plate to the other side of the load cell to the farthest point, which is 72 inches from the center of the load plate. A buffering system is located on top of the load plate. A weight is suspended above the buffering system at an unspecified drop height. (1 inch = 25.4 mm)
This photo shows a Dynatest® heavy-weight falling weight deflectometer (FWD). This FWD, which is similar to the schematic in figure 6, is trailer-mounted and has an operations control computer located in the tow vehicle (i.e., a van to which the trailer is attached).
This photo shows a KUAB 2m-FWD. This falling weight deflectometer (FWD) is similar to the schematic in figure 6 and is also trailer-mounted like the Dynatest FWD shown in figure 7. However, the KUAB FWD has a metal housing completely enclosing the loading system, a dual buffering system, and a segmented load plate.
This diagram is a schematic drawing of a rolling dynamic deflectometer (RDD). The RDD is truck-mounted and has the loading system and rolling deflection sensors located midway between the front and rear tires. The deflectometer applies large cyclic loads to the pavement and measures the induced cyclic deflections as it moves along the roadway. Also shown on the truck is a diesel engine driven hydraulic pump that powers the loading system, which is transmitted to the pavement via loading rollers. The rolling deflection sensors are located at multiple distances in front of the loading rollers.
This diagram is a schematic of the rolling dynamic deflectometer’s loading and deflection measurement system. On the pavement are rolling deflection sensors and two loading rollers. On the sides of the loading rollers are load cells. The loading frame has air springs on each side that support static force. Centered on the loading frame is a stilt structure, which contains a hydraulic actuator. An arrow labeled “reaction mass” is located above the hydraulic actuator, indicating dynamic force.
This photo shows a dual-wheel, single-axle semi-trailer equipped with a rolling weight deflectometer collecting deflection data on a four-lane highway. A 7.8-m (25.5-ft) aluminum beam beneath the trailer contains four spot laser sensors mounted 2.6 m (8.5 ft) apart.
BB equals the sum of 1.33269 plus the product of 0.93748 times FWD.
BB equals the product of 1.61 times FWD.
BB equals the product of 22.5 times D.
BB equals the product of 22.3 times D, minus 2.73.
BB equals the sum of 2.57 plus the product of 1.27 times RR.
FWD equals the sum of -3.40 plus the product of 1.21 times RR.
This diagram is a schematic that shows typical flexible and rigid pavement deflection responses under loading. It shows that the flexible pavement has a more centered load response throughout the pavement, base course, and subgrade—a response with a deep deflection basin. For the rigid pavement, it shows that the load response is distributed more outwardly from the load—a response with a shallower deflection basin.
This graph shows nonlinear pavement deflection response. The x-axis is load from 0 to 50 kN. The y-axis is deflection from 0 to 0.40 mm. At a load of 40 kN, the projected deflection is delta function of subscript 40-kN equals 0.25 mm, and the measured deflection is delta function of subscript 40-kN equals 0.35 mm. (25.4 mm = 1 inch) (1 kN = 224.8 lbf)
This graph shows hot mix asphalt elastic modulus as a function of mid-depth pavement temperature. The x-axis is temperature from 0 to 60 degrees Celsius. The y-axis is AC modulus from 0 to 16,000 MPa. Many data points and a regression curve are included in the graph, which shows that the stiffness of the asphalt layer decreases as the temperature increases (from about 12,000 MPa at 15 degrees Celsius to 3,000 MPa at 48 degrees Celsius). (°C = °F — 32)/1.8)
This graph shows variation in backcalculated k-value due to variation in temperature gradient. The x-axis is station from 0 to 25. The y-axis is k-value from 0 to 90 kPa per mm. For Section 133019 on April 24, 1996, testing was done at 7:30 a.m. (Ta equals 37 degrees, Ts equals 34 degrees), 11:10 a.m. (Ta equals 61 degrees, Ts equals 73 degrees), 2:10 p.m. (Ta equals 72 degrees, Ts equals 97 degrees), and 5 p.m. (Ta equals 75 degrees, Ts equals 90 degrees). The figure shows that the temperature differences cause the slab to be unsupported and, as a result, greater deflections may occur. The 7:30 a.m. tests had the highest k-values, followed by the 11:30 a.m. tests, and the 5 p.m. tests. The 2:10 p.m. tests had the lowest k-values. (°C = (°F — 32)/1.8) (1 MPa = 145 lbf/inch2)
This graph shows daily variation in the calculated load transfer efficiencies (leave side of joint). The x-axis is station from 130 to 170 m. The y-axis is load transfer efficiency from 0 to 100 percent. Tests performed were at 10:44 a.m. (Ta equals 75 degrees, Ts equals 63 degrees), 1:12 p.m. (Ta equals 77 degrees, Ts equals 75 degrees), and 3:14 p.m. (Ta equals 82 degrees, Ts equals 81 degrees). This figure shows that the afternoon tests produce a higher LTE percentage, indicating that FWD testing should be conducted in the morning or during cold periods of the year.
(°C = (°F — 32)/1.8) (1 m = 3.28 ft)
This graph shows variation in the calculated load transfer efficiencies (LTE) for two slabs tested at different temperature gradients and weighted average slab temperatures. The x-axis is equivalent linear gradient from -0.80 to 1.00 degrees Celsius per cm. The y-axis is LTE from 0 to 100 percent. Measured are a doweled (restrained) and an undoweled (unrestrained) slab. Data points show that the undoweled slab’s LTE is more affected by equivalent linear gradient and average slab temperature present at the time of testing. (°C = (°F — 32)/1.8) (1 cm = 0.39 inches)
This graph shows the relationship between load transfer efficiencies (LTE) and equivalent linear temperature gradients for two joints with low LTEs. The x-axis is equivalent linear gradient from -0.80 to 1.00 degrees Celsius per cm. The y-axis is LTE from 0 to 100 percent. Measured are a doweled (restrained) and an undoweled (unrestrained) slab. Data points show that the undoweled slab’s LTE is again more affected by equivalent linear gradient and average slab temperature present at the time of testing. As for the doweled slab, even when the LTE is low, it remains unaffected. (°Celsius = (°Fahrenheit — 32)/1.8) (1 cm = 0.39 inches)
This graph shows seasonal effects on pavement deflection. The x-axis is time from December to November. The y-axis is deflection, with no units or data labels given. The curve shows that during a period of deep frost (winter), the deflection is low. During a period of strength loss (spring), the deflections increase considerably. Next, during a period of rapid strength recovery (early summer), deflections dip back down. Finally, during a period of slow strength recovery (late summer through fall), deflections gradually decrease and then level out.
These four graphs show monthly variation in elastic modulus (in MPa) for individual pavement layers and subgrade. Each graph has an x-axis of time from May 1994 to May 1997. Spikes in the moduli occur during the winter months. (1 MPa = 145 lbf per square inch)
This graph shows seasonal variation in backcalculated subgrade modulus. The x-axis is date of testing. The y-axis is E subscript subgrade from 0 to 350 MPa and k-value from 0 to 350 expressed in units of 0.25 kPa per mm. Shown is a noticeable decrease in the support conditions observed during the springtime March 1996 tests, where the E subscript subgrade dips from about 200 to 115 MPa and the k-value dips from about 260 to 135 units of 0.25 kPa per mm. (1 MPa = 145 lbf/inch2)
This graph shows seasonal variation in load transfer efficiency (LTE) and portland cement concrete surface temperature. The x-axis is date of testing from 1995 to 1997. The y-axis is LTE from 0 to 100 percent. Measured are the approach LTE, the leave LTE and the surface temperature. For the most part, the LTE data points follow the surface temperature data points, increasing when the temperatures increase and decreasing when the temperatures decrease. (°C = (°F — 32)/1.8)
This diagram shows a simply supported beam with a concentrated load at midspan. A load is applied to the center of the beam, which is supported only at its two ends, and the beam deflects by an amount delta (see equation in figure 30). The illustration is used to show the fundamental engineering mechanics of loads and deflections on a concrete slab.
Uppercase delta (the midspan deflection of the beam) equals the quotient of the product of P times the cube of L divided by the product of 48 times E times I, end product.
I equals the quotient of the product of b times h cubed, end product, divided by 12.
This diagram shows a schematic of the stress zone under the falling weight deflectometer load. The following three layers are shown: the hot-mix asphalt surface, the granular base, and the subgrade. A load is shown on the surface. Deflection sensors are shown at load center and three others at equal distances out from the load center. Stress points for nonlinear layers are shown in the granular base and top of the subgrade.
M subscript R equals the quotient of the product of 0.24 times P, end product, divided by the product of d subscript r times r, end product.
d subscript 0 equals the product of 1.5 times p times a times the sum of the following: 1 divided by the product of M subscript R times the square root of the quantity 1 plus the square of the product of, the quotient of, D divided by a, end quotient, times the cube root of the quotient of E subscript p divided by M subscript R, end quotient, end cube root, end product, end quantity, end quotient, plus the difference of 1 minus the quotient of 1 divided by the square root of the quantity 1 plus the square of the quotient of D divided by a, end quotient, end quantity, end difference, divided by E subscript p.
H equals, the product of, the summation of all values from n to i, end summation, times C times h subscript i times the quotient of E subscript i divided by E, end quotient, to the one-third, end product. To the right is noted: C equals 0.8 to 0.9.
Delta function subscript z equals, the quotient of, the product of 2 times P, end product, divided by the product of pi times E times q, end product, end quotient, times the quantity sum of 1 minus the square of mu, end quantity.
Delta function subscript z equals, the quotient of P, divided by the product of pi times E times r, end product, end quotient, times the quantity sum of 1 minus the square of mu, end quantity.
This chart shows a typical iterative backcalculation flow chart. It shows that layer moduli are repeatedly changed until the calculated deflection basin matches the measured deflection basin within a specified tolerance. “Occasional” movement is shown with dashed lines, and the “Usual Path” is shown with solid lines. At the top left of the figure is a box labeled “Measure Deflection,” which occasionally feeds to a box labeled “Seed Moduli,” but usually feeds to a box labeled “Error Check.” If “Error Check” is “OK,” it feeds to a box labeled “Results”; if “Not OK,” it feeds to a box labeled “Search for Moduli.” It then occasionally feeds to a box labeled “Controls on Range of Moduli,” but usually feeds to a “Deflection Calculation” box, which then feeds back to the “Error Check” box. If the backcalculation process went to the “Controls on Range of Moduli” box, it would then proceed to the “Seed Moduli” box, which usually proceeds to “Deflection Calculation” and occasionally proceeds back to the “Measure Deflection” box. The “Layer Thickness Load” box stands alone and points back to “Deflection Calculation,” which is in the center.
f equals the summation of all the values in the range from m to j equals 1, end summation, times a subscript j times the square of the difference w subscript jm minus w subscript jc.
min (x is an element of R superscript n) of E(x) equals the norm of f times (x), end norm, 2 over 2 times the summation of all the values in the range from nr to i equals 1, times the summation of all the values in the range from nt to j equals 1, times the square of the norm f subscript rec times parenthesis i, j end parenthesis, minus f subscript com parenthesis i, j, x end parenthesis, end norm.
This diagram shows an artificial neural network architecture. “Input Signal” is labeled at the top pointing down to four circles. The interconnected units pass information in the form of signal patterns down to seven additional circles. The signal patterns are then passed down to three more circles. The information output from these circles is labeled “Output Signal.”
N subscript j equals the summation of all the values in the range from n to i minus 1, end summation, times w subscript ji times x subscript i.
a subscript j equals f times N subscript j equals the quotient of 1 divided by the sum of 1 plus e raised to the -N subscript j power, end sum, end quotient.
This diagram shows an artificial neural network for backcalculating pavement moduli. The diagram is similar in structure to figure 26. The input signals are labeled d subscript 0, d subscript 1, d subscript 2, d subscript 3, d subscript 4, d subscript 5, d subscript 6, h subscript ac, and h subscript b. The output signals are labeled E subscript ac, E subscript b, and E subscript s.
AREA equals the quotient of 1 divided by product of 2 times W subscript 0, end quotient, times open bracket the product of W subscript 0 times r subscript 1, end product, plus open parenthesis the summation of all the values in the range from n minus 1 to i equals 1, end summation, times W subscript i times the difference r subscript i plus 1 , minus r subscript I, end difference, end parenthesis, plus W subscript n times open parenthesis, the difference r subscript n minus r subscript n minus 1, end parenthesis, end bracket.
This diagram shows two different sensor configurations commonly used in falling weight deflectometer testing and for AREA computations. The top part of the diagram shows the standard sensor configuration, which includes the load plate (D subscript 0) and three sensors spaced at increasing distances from the load plate at 12-inch, 24-inch, and 36-inch intervals (D subscript 12, D subscript 24, and D subscript 36). The bottom part of the figure shows the Strategic Highway Research Program sensor configuration, which includes the load plate (D subscript 0) and six sensors spaced at increasing distances from the load plate at 8-, 12-, 18-, 24-, 36-, and 60-inch intervals (D subscript 8, D subscript 12, D subscript 18, D subscript 24, D subscript 36, and D subscript 60). (1 inch = 25.4 mm)
AREA equals the sum 6 plus 12 times the quotient of d subscript 12 divided by d subscript 0, end quotient, plus 12 times the quotient d subscript 24 divided by d subscript 0, end quotient, plus 6 times the quotient d subscript 36 divided by d subscript 0, end quotient.
AREA equals the sum of 4 plus 6 times the quotient of d subscript 8 divided by d subscript 0, end quotient, plus 5 times the quotient d subscript 12 divided by d subscript 8, end quotient, plus 6 times the quotient d subscript 18 divided by d subscript 0, end quotient, plus 9 times the quotient d subscript 24 divided by d subscript 0, end quotient, plus 18 times the quotient d subscript 36 divided by d subscript 0, end quotient, plus 12 times the quotient d subscript 60 divided by d subscript 0, end quotient.
This graph shows the variation in AREA with lowercase script l. The x-axis is the radius of relative stress lowercase script l for 10 to 80 inches. The y-axis is the area from 15 to 35 inches. The AREA curves are based on four sensors with 12-inch spacing. One AREA curve represents a dense liquid with a distributed load (a equals 5.9055 inches); another AREA curve represents dense liquid with a point load. Both of these curves begin at 15 inches for lowercase script l equals 10 inches, rise quickly to 30 inches at lowercase script l equals 27 inches, and then level off to 34 inches at lowercase script l equals 80 inches. Two other AREA curves, elastic solid with distributed load (a equals 5.9055 inches) and elastic solid with point load, begin at 22 inches for lowercase script l equals 10 inches, rise quickly to 31 inches at lowercase script l equals 30 inches, and then level off to 35 inches at lowercase script l equals 80 inches. (1 inch = 2.54 cm).
Lowercase script l equals quotient of, the product of E times the cube of h, end product, divided by the product of 12 times the difference 1 minus the square of mu, end difference, times k, end quotient, raised to the one-fourth power.
Lowercase script l equals quotient of, the product of E times the cube of h, end product, divided by the product of 6 times the quantity sum of 1 minus the square of mu, end quantity, times C, end quotient, raised to the one-third power; where C equals quotient of E subscript S divided by sum of 1 minus mu squared subscript S.
k equals quotient of the product of P times d superscript asterisk subscript r, end product, divided by the product of d subscript r times the square of lowercase script l. C equals quotient of the product of 2 times P times d superscript asterisk subscript r, end product, divided by the product of d subscript r times lowercase script l.
D equals the quotient of the product of E times the cube of h, end product, divided by the product of 12 times the quantity 1 minus the square of mu, end quantity, end product, end quotient.
E subscript PCC equals the quotient of the product of 12 times lowercase script l raised to the fourth power times the quantity 1 minus the square of mu, end quantity times k, end product, divided by the cube of h, end quotient.
F times parenthesis E, k end parenthesis equals the product of the summation of all the values in the range from i equals 0 to n, end summation, times alpha subscript i, times the square of the difference, product of w times r subscript i, end product, minus W subscript i, end difference, end product.
The quotient of the product of the summation of all the values in the range from n to i equals 0, times alpha subscript i times f subscript i, times lowercase script l, times f apostrophe subscript i, times lowercase script l, end product, divided by the product of the summation of all the values in the range from n to i equals 0, times alpha subscript i times the square of the product of f subscript i times lowercase script l, end product, end quotient, equals the quotient of the product of the summation of all the values in the range from n to i equals 0, times alpha subscript i times W subscript i, times f apostrophe subscript i, times lowercase script l, end product, divided by the product of the summation of all the values in the range from n to i equals 0, times alpha subscript i times W subscript i times f subscript i times lowercase script l, end product, end quotient.
E subscript PCC equals the quotient of the product of 6 times the square of the difference 1 minus mu subscript PCC, end difference, times the cube of lowercase script l subscript e, times E subscript S, end product, divided by the product of the cube of h subscript PCC times the difference 1 minus the square of mu subscript S, end difference, end product, end quotient.
This graph shows the computation of the k-value. The x-axis is sensor offset from 0 to 220 inches. The y-axis is deflection from 0 to 4 mils. The following formula is shown: Volumetric k (PCI) equals Force (lbs.) divided by sum of range from n equals 1 to 7 times Area subscript n times square inches times distance to centroid times 2 times pi. The AREA parameter is obtained by first computing the individual Area Segments A1 through A7 comprising the deflection basin. The individual AREA segments are defined by coordinates of sensor offset and deflection as follows: A1 (15, 2.8), A2 (25, 2.7), A3 (35, 2.6), A4 (48, 2.5), A5 (60, 2.3), A6 (75, 1.9), and A7 is the remaining space from 1.9 to 0 deflection from 75 to 180 inches. (This point is determined as the extension of a straight line through the outermost two deflection readings.) (1 inch = 25.4 mm)
Outer AREA equals the product of 6 times the sum of the quantity 1 plus the product of 2 times the quotient of d subscript 24 divided by d subscript 12, end quotient, end product, plus the product of 2 times the quotient of d subscript 36 divided by d subscript 12, end quotient, end product, plus the product of 2 times the quotient of d subscript 48 divided by d subscript 12, end quotient, end product, plus the product of 2 times the quotient of d subscript 60 divided by d subscript 12, end quotient, end product, plus the quotient of d subscript 72 divided by d subscript 12, end quotient, end product.
E subscript e equals the quotient of the product of 12 times lowercase script l raised to the fourth power times the quantity 1 minus the square of mu, end quantity, times k, end product, divided by the cube of h, end quotient.
F times parenthesis E, k end parenthesis, equals the product of the summation of all the values in the range from n to i equals 0, end summation, times alpha subscript i, times the square of the quantity lowercase w subscript i minus uppercase W subscript i, end quantity, end product.
LTE equals the product of beta times quotient of d subscript u divided by d subscript lowercase script l, end quotient, times 100, end product. Beta equals quotient of d subscript 0center divided by d subscript 12center, end quotient.
This diagram shows examples of poor load transfer and good load transfer. Two drawings are shown, top and bottom. The top drawing, entitled “poor load transfer,” shows two slabs, with the left slab deflected 1.02 mm (0.40 inches) under a load, and the right slab not deflected at all. The load transfer is calculated as 0 percent (0 mm per 1.02 mm times 100 percent). The bottom drawing, entitled “good load transfer,” shows the two slabs sharing the load via a dowel that has been inserted across the joint. The load applied to the left slab results in the two slabs undergoing the same deflection of 0.51 mm (0.020 inches). The load transfer is calculated as 100 percent (0.51 mm per 0.51 mm times 100 percent). (1 mm = 0.039 inches)
This diagram shows slab curling due to temperature differentials in the slab. The top drawing shows that in the daytime, the slab curls downward, creating a void under the slab. The bottom drawing shows that in the nighttime, the slab corners curl upward, creating voids under the corners of the slab.
This graph shows an example void detection plot using falling weight deflectometer (FWD) deflection data. The x-axis is corner deflection from 0 to 50 mils. The y-axis is FWD load from 0 to 20 kips. The approach slab deflection plot has the following data points: (3, 0), (12, 5), (18, 8), and (21, 13). The leave slab deflection plot has the following data points: (12, 0), (29, 7), (37, 8), and (41, 12).
ISM equals the quotient of P divided by d subscript 0.
ISM subscript ratio equals the quotient of ISM subscript slab_center divided by ISM subscript slab_joint, end quotient, or ISM subscript ratio equals the quotient of ISM subscript slab_center divided by ISM subscript slab_corner, end quotient.
H equals the product of the summation of all the values in the range from n to i, times C times h subscript i, times the quotient of E subscript i divided by E, end quotient, raised to the one-third power. Note that C equals 0.8 to 0.9.
Delta function subscript z equals the product of the quotient of the product of 2 times P, end product, divided by the product of pi times E times a, end quotient, times the quantity 1 minus the square of mu, end quantity, end product.
Delta function subscript z equals the product of the quotient of P divided by the product of pi times E times r, end quotient, times the quantity 1 minus mu squared, end quantity, end product.
This graph shows surface modulus for a three-layer pavement and a halfspace. The x-axis is radius from 0 to 2,000 mm. The y-axis is surface modulus from 0 to 500 MPa. The three-layer pavement curve begins at 450 MPa at radius of 0 mm, decreases to 180 MPa at radius of 200 mm, and then levels off to about 70 MPa at radius of 700 mm. The halfspace curve begins at 55 MPa at radius of 0 mm and remains around this level out to a radius of 1,800 mm. (1 mm = 0.039 inches, 1 MPa = 145 lbf per square inch)
This diagram shows matching measured and calculated deflection basins. A three-dimensional drawing of a three-layer pavement structure is shown. The bottom layer is the subgrade (M subscript R or E subscript SG), the middle layer is the base (E subscript BS), and the surface layer is AC (E subscript AC). Three deflection sensors are shown on the surface. A calculated deflection basin line is shown in the AC layer gradually reaching the surface by sensor 3. A measured deflection basin line is shown just below that also gradually reaches the surface by sensor 3.
f equals the product of the summation of all the values in the range from m to j equals 1, times a subscript j, times the square of the quantity w subscript jm minus w subscript jc, end quantity, end product.
Open bracket F end bracket superscript k, set d end set superscript k, equals set r end set superscript k.
E equals the product of C times the quotient of the quantity lowercase sigma subscript 1 divided by p, end quantity, raised to the n power, end product.
This graph shows a plot of inverse of deflection offset versus measured deflection. The x-axis is 1/r (inverse of deflection offset), with no units or data labels given. The y-axis is measured deflection, with no units or data labels given. The figure depicts an s-shaped curve for the deflection as a function of 1/r. The curve starts at the origin, increases slowly at first and then increases sharply before leveling off.
D subscript b equals the quotient of the product of V subscript S times T subscript d, end product, divided by 1.35, end quotient.
D subscript b equals the quotient of the product of V subscript S times T subscript d, end product, divided by pi minus the product of 2.24 times u, end quotient.
This graph illustrates the natural period, T subscript d, from sensor deflection time histories. The deflections from seven sensors are graphed. The x-axis is time from 0 to 140 ms. The y-axis is deflection -10 to 30 mils. The sensors show that the natural period occurs between 40 and 80 ms.
This figure illustrates the E-to-k conversion process incorporated in the Mechanistic-Empirical Pavement Design Guide. On the left side of the figure is a pavement structure with six layers. The bottom layer is bedrock, followed by natural subgrade, compacted subgrade, subbase course (unbound, stabilized), base course (unbound, asphalt, cement), and concrete slab (jointed plain concrete pavements (JPCP), continuous reinforced concrete pavement (CRCP)). On the right side of the figure is a three-layer structure that shows the concrete slab (JPCP, CRCP) and base course (unbound, asphalt, cement) resting on a spring-like foundation. The spring-like foundation represents the bottom four layers in the six-layer pavement structure. It possesses an effective k-value, which is a composite stiffness obtained through backcalculation.
Lowercase script l equals the fourth root of the quotient of the product of E subscript PCC times the cube of h, end product, divided by the product of 12 times the quantity 1 minus the square of mu, end quantity, times k, end product, end quotient. Â
AREA subscript 36 equals the product of 6 times the sum of 1 plus the product of 2 times the quotient of d subscript 12 divided by d subscript 0, end quotient, end product, plus the product of 2 times the quotient of d subscript 24 divided by d subscript 0, end quotient, end product, plus the quotient of d subscript 36 divided by d subscript 0, end quotient, end sum.
AREA subscript 60 equals the sum of 4 plus the product of 6 times the quotient of d subscript 8 divided by d subscript 0, end quotient, end product, plus the product of 5 times the quotient of d subscript 12 divided by d subscript 0, end quotient, end product, plus the product of 6 times the quotient of d subscript 18 divided by d subscript 0, end quotient, end product, plus the product of 9 times the quotient of d subscript 24 divided by d subscript 0, end quotient, end product, plus the product of 18 times the quotient of d subscript 36 divided by d subscript 0, end quotient, end product, plus the product of 12 times the quotient of d subscript 60 divided by d subscript 0, end quotient, end product, end sum.
AREA subscript 72 equals the product of 6 times the sum of 1 plus the product of 2 times the quotient of d subscript 12 divided by d subscript 0, end quotient, end product, plus the product of 2 times the quotient of d subscript 24 divided by d subscript 0, end quotient, end product, plus the product of 2 times the quotient of d subscript 36 divided by d subscript 0, end quotient, end product, plus the product of 2 times the quotient of d subscript 48 divided by d subscript 0, end quotient, end product, plus the product of 2 times the quotient of d subscript 60 divided by d subscript 0, end quotient, end product, plus the quotient of d subscript 72 divided by d subscript 0, end sum, end product.
Lowercase script l equals bracket, the quotient of the product of the log of the quotient of k subscript 1 minus AREA, divided by k subscript 2, end quotient, end log, divided by negative k subscript 3, end quotient, raised to the 1 divided by k subscript 4 power.
d superscript asterisk subscript r equals a time e raised to the power negative b times e superscript negative c times lowercase script l.
k equals the quotient of the product of P times d superscript asterisk subscript r, end product, divided by the product of d subscript r times the square of lowercase script l, end product, end quotient.
E subscript PCC equals the quotient of the product of 12 times lowercase script l raised to the fourth power times the quantity 1 minus the square of mu, end quantity, times k, end product, divided by the cube of h, end quotient.
F parenthesis E, k end parenthesis equals the product of the summation of all the values in the range from n to i equals 0, end summation, times alpha subscript i times the quantity of the square of the difference of lowercase w subscript i minus capital W subscript i, end quantity, end product.
w subscript i times r equals the product of the quotient of p divided by k, end quotient, times f subscript i times lowercase script l, end product. f parenthesis r end parenthesis equals 1 minus the product of C subscript 1 times a subscript lowercase script l times ber times s, end product, minus C subscript 2 times a subscript lowercase script l times bei times s, end product (for 0 is less than r is less than a). f parenthesis r end parenthesis equals the sum of the product of C subscript 3 times a subscript lowercase script l times ker times s, end product, plus C subscript 4 times a subscript lowercase script l times kei times s, end product, end sum (for r greater than a).
C subscript 1 equals negative a subscript lambda ker apostrophe a subscript lambda; C subscript 2 equals a subscript lambda kei apostrophe a subscript lambda; C subscript 3 equals negative a subscript lambda ber apostrophe a subscript lambda; and C subscript 4 equals negative a subscript lambda bei apostrophe a subscript lambda.
F parenthesis E, k end parenthesis, is equivalent to F parenthesis lowercase script l, k end parenthesis, equals the product of the summation of all the values in the range from n to i equals 0, end summation, times alpha subscript i times the square of the quantity quotient of p divided by k, end quotient, times f subscript i times lowercase script l minus W subscript i, end quantity, end product.
Partial derivative F divided by partial derivative k equals 0, and partial derivative F divided by partial derivative lowercase script l equals 0.
k equals the product of p times the quotient of the product of the summation of all the values in the range from n to i equals 0, end summation, times a subscript i times the square of the quantity f subscript i times lowercase script l end quantity, end product, divided by the product of the summation of all the values in the range from n to i equals 0, end summation, times a subscript i times capital W subscript i, times f subscript i times parenthesis lowercase script l end parenthesis, end product, end quotient, end product. Â
The quotient of the product of the summation of all values in the range from n to i equals 0, end summation, times a subscript i times f subscript i, times lowercase script l times f apostrophe subscript i, times lowercase script l, end product, divided by the product of the sum of all the values in the range from n to i equals 0, end summation, times a subscript i times the square of the quantity f subscript i times lowercase script l, end product, equals the quotient of the product of the summation of all the values in the range from n to i equals 0, end summation, times a subscript i times W subscript i, times f apostrophe subscript i times lowercase script l end product, divided by the product of the summation of all the values in the range from n to i equals 0, end summation, times a subscript i times W subscript i, times f subscript i times lowercase script l end product, end quotient. Â Â
D subscript e equals the sum of D subscript 1 plus D subscript 2.
D subscript e equals the quotient of the product of E subscript e times the cube of h subscript e, end product, divided by product of 12 times the quantity 1 minus the square of mu subscript e, end quantity, end product, end quotient.
mu subscript e equals mu subscript 1 equals mu subscript 2.
E subscript e times the cube of h subscript e equals E subscript e times the cube of h subscript 1 equals E subscript 1 times the cube of h subscript 1 plus E subscript 2 times the cube of h subscript 2.
Beta equals the quotient of E subscript 2 divided by E subscript 1.
E subscript 1 equals the product of the quotient of cube of h subscript 1 divided by the sum of the cube of h subscript 1 plus beta times the cube of h subscript 2, end sum, end quotient, times E subscript e, end product.
E subscript 2 equals the product of the quotient of the cube of h subscript 1 times beta, divided by the sum of the cube of h subscript 1 plus beta times the cube of h subscript 2, end sum, end quotient, times E subscript e, end product.
The quotient of E subscript e times the cube of h subscript e divided by 12 equals the sum of the quotient of E subscript 1 times the cube of h subscript 1 divided by 12, end quotient, plus the product of E subscript 1 times h subscript 1, times the square of the quantity x minus the quotient of h subscript 1 divided by 2, end quotient, end quantity, end product, plus the quotient of E subscript 2 times the cube of h subscript 2 divided by 12, end quotient, plus the product of E subscript 2 times h subscript 2 times the square of the quantity h subscript 1 minus x plus the quotient of h subscript 2 divided by 2, end quotient, end product, end quantity; where x equals the quotient of the sum of the quotient of the square of h subscript 1 divided by 2, plus the product of h subscript 2 times beta times the sum of h subscript 1 plus quotient of h subscript 2 divided by 2, end quotient, end product, end sum, all divided by h subscript 1 plus product of beta times h subscript 2, end product, end quotient.
E subscript 1 equals the quotient of the cube of h subscript 1 divided by the sum of the cube of h subscript 1, plus the product of beta times the cube of h subscript 2, end product, plus the product of 12 times h subscript 1 times the square of the quantity x minus the quotient of h subscript 1 divided by 2, end quotient, end quantity, end product, plus the product of 12 times beta times h subscript 2 times the square of the quantity h subscript 1 minus x plus the quotient of h subscript 2 divided by 2, end quotient, end quantity, end product, end sum, times E subscript e.
epsilon subscript i equals the product of the quotient of the difference lowercase w subscript i minus capital W subscript i, end difference, divided by capital W subscript i, end quotient, times 100 percent, end product.
epsilon subscript b equals the quotient of the product of the summation of all the values in the range from n to i equals 1, end summation, times epsilon subscript i, end product, divided by n, end quotient.
AF subscript lowercase script l subscript est equals 1 minus 0.89434e raised to the power negative 0.61662 times the quantity L divided by lowercase script l subscript est, end quantity, raised to the 1.04831 power.
AF subscript d subscript 0 equals 1 minus 1.15085e raised to the power negative 0.71878 times the quantity L divided by lowercase script l subscript est, end quantity, raised to the 0.80151 power.
L equals the square root of the product of L subscript act times W subscript act.
L equals the square root of 2 times L subscript act.
k equals the quotient of k subscript est divided by the product of the square of quantity AF subscript lowercase script l subscript est end quantity, times AF subscript d subscript 0 end product, end quotient.
FS equals the sum of the product of 43.5 times the quantity E divided by 10 to the power six, end quantity, end product, plus 488.5.
This diagram shows the layout of joint load transfer efficiency (LTE) testing on hot mix asphalt overlaid portland cement concrete pavements. Shown are two slabs with a joint or crack in the center. A falling weight deflectometer loading plate is shown on the left slab. The center of the loading plate is located approximately 9 inches from the slab edge. One deflection sensor, labeled D subscript L, is located on the left slab 3 inches from the joint or crack. A second deflection sensor, labeled D subscript UL, is located on the right slab 3 inches from the joint or crack. A formula for computing LTE is given as follows: LTE equals the quantity D subscript UL divided by D subscript L end quantity times 100 percent. (1 inch = 2.54 cm)
OuterAREA equals the product of 6 times the sum of 1 plus the product of 2 times the quotient of d subscript 24 divided by d subscript 12, end quotient, plus the product of 2 times the quotient of d subscript 36 divided by d subscript 12, end quotient, plus the product of 2 times the quotient of d subscript 48 divided by d subscript 12, end quotient, plus the product of 2 times the quotient of d subscript 60 divided by d subscript 12, end quotient, plus the quotient of d subscript 72 divided by d subscript 12, end quotient, end sum, end product.
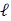 ) and the outer-AREA for the seven-sensor configuration.
) and the outer-AREA for the seven-sensor configuration. Lowercase script l equals the quantity of natural logarithm of the quotient of the difference 60 and OuterAREA, end difference, divided by 301.8, end quotient, divided by negative 0.6223, end quantity, raised to the 2.501 power.
k equals the quotient of the product of P times d subscript r superscript *, end product, divided by the product of d subscript r times the square of l, end product, end quotient.
d subscript r superscript asterisk equals the product of a times e raised to the power negative b times e raised to the power negative c times lowercase script l, end product.
Lowercase script l equals the fourth root of the quotient of the product of E subscript e times the cube of h subscript e, end product, divided by the product of 12 times the quantity 1 minus the square of mu, end quantity times k, end product, end quotient.
E subscript e equals the quotient of the product of 12 times lowercase script l raised to the fourth power times the quantity 1 minus the square of mu, end quantity, times k, end product, divided by the cube of h subscript e, end quotient.
The quotient of the product of E subscript e times the cube of h subscript e, end product, divided by 12 end quotient, equals the sum of the quotient of the product of E subscript 1 times the cube of h subscript 1, end product, divided by 12, end quotient, plus the product of E subscript 1 times h subscript 1 times the square of the quantity x minus quotient of h subscript 1 divided by 2, end quotient, end quantity, end product, plus the quotient of the product of E subscript 2 times the cube of h subscript 2, end product, divided by 12, end quotient, plus the product of E subscript 2 times h subscript 2 times the square of the quantity h subscript 1 minus x plus the quotient of h subscript 2 divided by 2, end quotient, end quantity, end product, end sum. Where x equals the quotient of the sum of the quotient of the square of h subscript 1 divided by 2, end quotient, plus the product of beta times h subscript 2 times the quantity h subscript 1 plus the quotient of h subscript 2 divided by 2, end quotient, end quantity, end product, end sum, divided by the sum of h subscript 1 plus the product of beta times h subscript 2, end product, end sum, end quotient.
E subscript AC equals E subscript 1 equals the quotient of the product of E subscript e times the cube of the sum of h subscript 1 plus h subscript 2, end sum, end product, divided by the sum of the cube of h subscript 1 plus the product of beta times the cube of h subscript 2, end product, plus the product of 12 times h subscript 1 times the square of the quantity x minus the quotient of h subscript 1 divided by 2, end quotient, end quantity, end product, plus the product of 12 times h subscript 2 times the square of the quantity h subscript 1 minus x plus the quotient of h subscript 2 divided by 2, end quotient, end quantity, end product, end sum, end quotient. E subscript PCC equals E subscript 2 equals product of beta times E subscript 1.
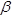 .
. This graph shows the sensitivity of the backcalculated moduli values to the assumed value of the modular ratio, beta. The x-axis is the modular ratio from 0 to 25. The y-axis is the relative elastic modulus from 0 to 2. Plots for asphalt concrete (AC) modulus and portland cement concrete (PCC) modulus are given, based on an AC thickness of 4 inches and a PCC thickness of 10 inches. The PCC modulus begins at (5, 0.85) and slowly curves up to (20, 1.5). The AC modulus begins at (5, 1.7), decreases rapidly to (10, 0.93), and then less rapidly to (20, 0.55). (1 inch = 2.54 cm)
F parenthesis E, k end parenthesis equals the product of the summation of all of the values in the range from n to i equals 0 times alpha subscript i times the square of the quantity lowercase w subscript i minus uppercase W subscript i, end quantity, end product.
The log of E subscript AC equals 6.451235 minus the product of 0.000164671 times t subscript p superscript 1.92544 end product.