U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

Report
This report is an archived publication and may contain dated technical, contact, and link information
Publication Number: FHWA-RD-07-052
Date: September 2007

Long Term Pavement Performance Project Laboratory Materials Testing and Handling Guide

Protocol P07 (Continuation)
Test Method for Determining The Creep Compliance, Resilient Modulus and Strengthof Asphalt Materials Using The Indirect Tensile Test Device (AC07)

Appendix B
Data Analysis Algorithms

B1. INTRODUCTION

This appendix contains the algorithms used to determine the resilient modulus, creep compliance and indirect tensile strength for specimens tested using the P07 testing protocol. The algorithms presented herein are based upon the data format, data sampling rates and file structures used for LTPP P07 testing purposes. If formats, sampling rates or file structures used are different than outlined herein, the algorithms should be modified appropriately.

These algorithms are based upon the methods developed by Dr. Reynaldo Roque et al. and documented in the report referenced in Section 4.4 of this protocol. Dr. Roque and his colleagues developed two programs: MRFHWA to reduce and analyze resilient modulus data, and ITLTFHWA to reduce and analyze creep compliance and indirect tensile strength data. The user's guide for the software is available as a separate document. The data analysis methods used in MRFHWA and ITLTFHWA are documented in this appendix.

This appendix is divided into four sections as follows:

B1. Introduction
B2. Resilient Modulus Data Analysis Algorithm
B3. Creep Compliance Data Analysis Algorithm
B4. Indirect Tensile Strength Analysis Algorithm

B2. RESILIENT MODULUS DATA ANALYSIS ALGORITHM

An outline of the resilient modulus data analysis algorithm that is used in the "MRFHWA" software, and described in the report by Roque et al. is presented in section B2.2. The algorithm is described graphically in section B2.3.

B2.1 Subscript Convention

For the purpose of clarity, a subscript convention has been developed. The subscript 'i' represents the specimen number (i = 1, 2, or 3), the subscript 'j' represents the cycle number (j = 1, 2, or 3), and the subscript 'k' represents the specimen face (k = 1 or 2). Thus a variable may have up to three subscripts of the following form: Xi,j,k.

B2.2 Analysis

A separate analysis must be performed for each of the three temperatures.

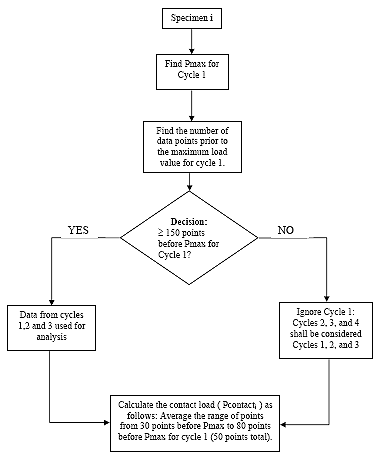
B2.2.1 Select Cycles

For each of the three specimens, determine which three cycles of the five recorded in the data file shall be used for analysis. Find the maximum load (Pmax) of the first recorded cycle in the data file. If the maximum occurs at or after 150 points from the start of the file, then the first three cycles recorded in the data file shall be used for subsequent analysis. If the maximum occurs less than 150 points from the start of the file, then the second, third and fourth cycles recorded in the test shall be used. From now on, regardless of which cycles have been selected for analysis, they shall be referred to as cycles 1, 2 and 3, respectively.

B2.2.2 Calculate Contact Load (Pcontacti)

For each of the three specimens calculate the contact load. Only one contact load shall be calculated for each specimen as follows:

(1) Determine the point at which the maximum load (Pmax) occurs for cycle 1.

(2) Select the range of cells from 80 points before Pmax to 30 points before Pmax (50 points total)

(3) Average the load values in the selected range as follows:

Eq. B1: 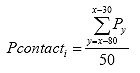P contact sub i equals the ratio of the sum from y equals x minus 80 to x minus 30 of P sub y over 50

where: Pcontacti = the contact load for specimen i, lbs.

Py = the load at point y, lbs.

x = the point at which Pmaxi,1 occurs

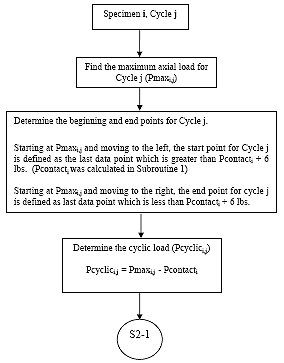
B2.2.3 Determine Cycle Start and End Points

For each cycle j on each specimen i, determine the start and end points as follows. Determine Pmax for cycle j

(1) Starting at Pmax, and moving to the left, the start of cycle j is defined as the last data point for which the load is greater than Pcontacti + 6 lbs (2.7 kg). This value shall be referred to as spi,j.

(2) Starting at Pmax and moving to the right, the end point for cycle j is defined as the last data point for which the load is less than Pcontacti + 6 lbs (2.7 kg). This value shall be referred to as epi,j.

B2.2.4 Determine the Cyclic Load

For each cycle j on each specimen i, determine the cyclic load (Pcyclici,j) as follows:

Eq. B2: Pcyclici, j = Pmaxi, j Pcontacti

where: Pcyclici,j = the cyclic load for cycle j of specimen i, lbs.

Pmaxi,j = the maximum load for cycle j of specimen i, lbs. Pcontacti = the contact load of specimen i, lbs

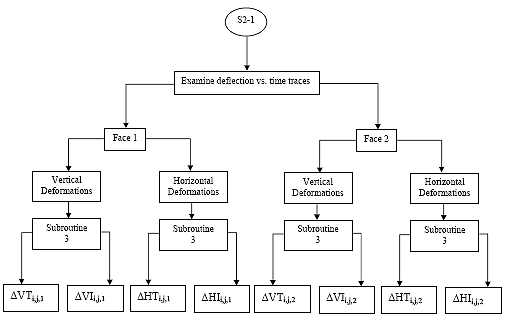
B2.2.5 Calculate the maximum deformations:

On each of the two sawn faces of the sample, deformations are measured in the horizontal and vertical axes. Thus for each sample there will be a total of four deformation vs. time traces. From each of these traces, pick off the maximum deformation for each of the three cycles, within the cycle start and end points defined in section B2.2.3. These deformations will be referred to in the following format:

{H,V}maxi,j,k, inches

where {H,V} refers to the axis in which the deformation was measured (horizontal or vertical) and subscripts i, j and k refer to the specimen, cycle and face, as defined in section B2.1.

B2.2.6 Determine minimum deformations:

For {H,V}maxi,j,k calculated in section 4.2.5 there will be two corresponding minimum deformations: Total and Instantaneous, as shown in Figure 3 of the main body of this procedure. To calculate these minimum deformations two regression lines must be developed. These minimum deformations shall be referred to in the following format:

{H,V}min{I,T}i,j,k, inches

where {H,V} refers to the axis in which the deformation was measured (horizontal or vertical), {I,T} refers to the type of deformation (instantaneous or total) and subscripts i, j and k refer to the specimen, cycle and face, as defined in section B2.1.

To calculate {H,V}min{I,T}i,j,k, two regression lines must be developed from the deformation vs. time trace.

B2.2.6.1 Regression Line 1

(1) Starting at {H,V}maxi,j,k and moving to the right, select the 5th through 17th data points (13 data points total).

(2) Perform a least squares linear regression on deformation vs. time for the selected data points. The resulting equation shall be as follows:

Eq. B3 Deformation equals m sub 1 times Time plus b sub 1

Where: m1 = the slope of regression line 1, and
b1 = the Y-intercept of regression line 1

B2.2.6.2 Regression Line 2

(1) Starting at the start point of cycle j+1 and moving to the left, select first 300 data points (300 data points total).

(2) Perform a least squares linear regression on deformation versus time for the selected data points. The resulting equation shall be as follows:

Eq. B4 Deformation equals m sub 2 times time plus b sub 2

Where: m2 = the slope of regression line 2, and
2 = the Y-intercept of regression line 2

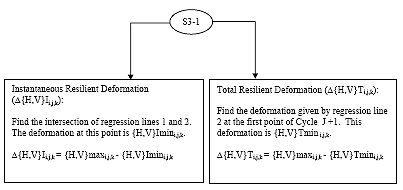
B2.2.6.3 Calculate {H,V}minI i,j,k

{H,V}minIi,j,k is the deformation at the intersection of regression lines 1 and 2.

Eq. B5 {H, V}minI sub i, j, k equals b sub 1 plus m sub 2 times the ratio of b sub 2 minus b sub 1 over m sub 1 minus m sub 2

B2.2.6.4 Calculate {H,V}minTi,j,k {H,V}minTi,j,k is the deformation calculated from regression line 1 and the first point of cycle j+1

Eq.B6 {H, V}min T sub i, j, k equals b sub 2 plus m sub 2 times sp sub i, j+1

B2.2.7 Calculate the total and instantaneous recoverable deformations

The total and instantaneous recoverable deformations shall be referred to as D{H,V}Ti,j,k and D{H,V}Ii,j,k respectively.

Eq. B7 delta {H, V}{I, T}sub i, j, k equals {H, V}max sub i, j, k minus {H, V}min{I, T} sub i, j, k

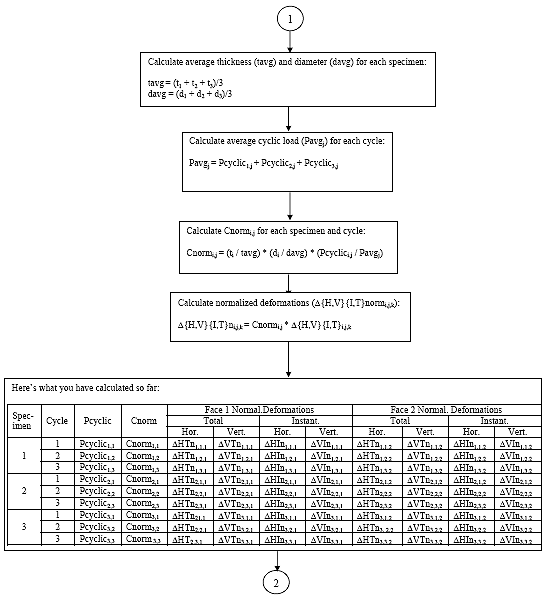
B2.2.8 Calculate average thickness and diameter

Eq. B8 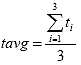tavg equals the ratio of the sum from i equals 1 to 3 of t sub i over 3

Eq. B9 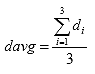davg equals the ratio of the sum from i equals 1 to 3 of d sub i over 3

Where: tavg = the average thickness for all the specimens, inches

ti = the thickness of specimen i, in

davg = the average thickness for all the specimens, inches

di = the diameter of specimen i, in

vB2.2.9 Calculate the average cyclic load

Eq. B10 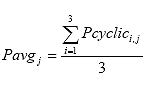Pavg sub j equals the ratio of the sum from i equals 1 to 3 of Pcyclic sub i, j over 3

Where: Pavgj = the average cyclic load for cycle j, lbs.

Pcyclici,j = the cyclic load for cycle j of specimen i, lbs.

B2.2.10 Calculate the deformation normalization factors

Eq. B11 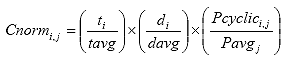Cnorm sub i, j equals the ratio of t sub i over tavg times the ratio of d sub i over davg times the ratio of Pcyclic sub i, j over Pavg sub j

Where: Cnormi,j = the deformation correction factor for cycle j of specimen i,

ti = the thickness of specimen i, in.

tavg = the average thickness of the specimens, in.

di = the diameter of specimen i, in.

davg = the average diameter of the specimens, in.

Pcyclici,j = the cyclic load for cycle j of specimen i, lb.

Pavgj = the average cyclic load for cycle j lb.

B2.2.11 Calculate the normalized deformations

Eq. B12 delta {H, V}{I, T}n sub i, j, k equals Cnorm sub i, j, k times delta {H, V}{I, T}sub i, j, k

Where: D{H,V}{I,T}ni,j,k = the normalized deformation for face k and cycle j of specimen i, in.

Cnormi,j = the deformation correction factor for cycle j of specimen i,

D{H,V}{I,T}i,j,k = the deformation for face k and cycle j of specimen i, in.

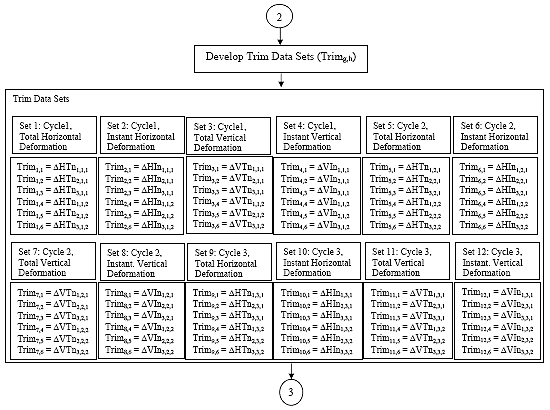
B2.2.12 Average deformation data sets

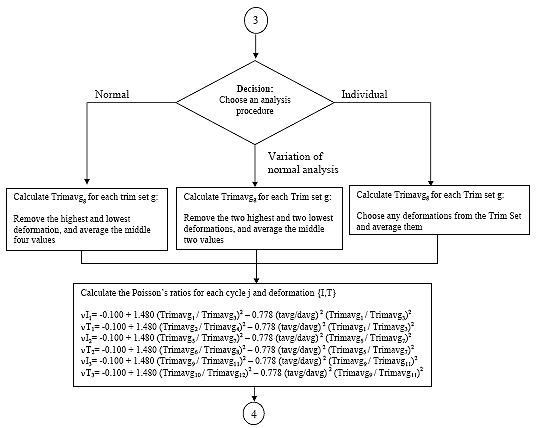
There are 12 deformation data sets. A deformation data set consists of all the recoverable deformations calculated for a given axis {H,V}, measurement point {I,T} and cycle j. Average the deformation data sets by one of the following methods:

B2.2.12.1 Method 1: Normal Analysis

For each deformation data set, remove the highest and lowest deformation and average the remaining four. This average shall be referred to as D{H,V}{I,T}navgj

B2.2.12.2 Method 2: Variation of Normal Analysis

For each deformation data set, remove the tow highest and the two lowest deformations and average the remaining two. This average shall be referred to as D{H,V}{I,T}navgj

B2.2.12.3 Method 3: Individual Analysis

For each deformation data set, remove any deformations and average the remaining deformations. This average shall be referred to as D{H,V}{I,T}navgj

B2.2.13 Calculate Poisson's ratios

Eq. B13 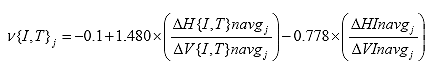nu {I, T}sub j equals -0.1 plus 1.480 times the ratio of delta H {I, T}navg sub j over delta V {I, T}navg sub j minus 0.778 times the ratio of delta HInavg sub j over delta VInavg sub j

B2.2.14 Calculate the cycle averaged deformations

Eq. B14 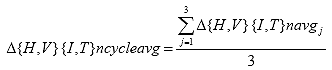delta {H, V}{I, T}ncycleavg equals the ratio of the sum from j equals 1 to 3 of delta {H, V}{I, T}navg sub j over 3

B2.2.15 Calculate the resilient modulus correction factors

Eq. B15 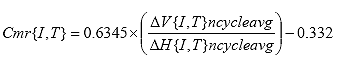Cmr{I, T} equals 0.6345 times the ratio of delta V{I, T}ncycleavg over delta H{I, T}ncycleavg minus 0.332

B2.2.16 Calculate resilient modulus

Eq. B16 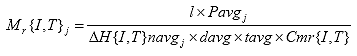M sub r {I, T} sub j equals l times Pavg sub j over the result of delta H {I, T}navg sub j times davg times tavg times Cmr {I, T}

B2.2.18 Repeat sections B2.2.1 through B2.2.17 for each temperature.

B2.3 Resilient Modulus Data Analysis Algorithm Flowchart

B2.3.1 Main Procedure

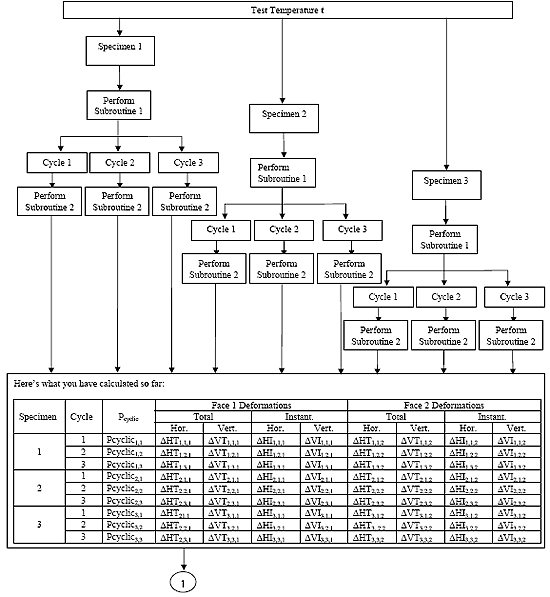
Flow chart illustrating that for each temperature t, 3 specimens are tested. For each specimen, the first step is to perform subroutine 1 and under subroutine 1, there are 3 cycles and under each cycle, subroutine 2 is performed. At the end of this process, you will have for each cycle, Pcyclic, delta HT, delta VT, delta HI, delta VI for both faces.

Flow chart continuing from the previous flow chart. At this point, the average thickness and diamter is calculated for each speciemn. The average cyclic load is calculated for each cycle. Next, calculate Cnorm sub i, j for each specimen and cycle. Then calculate the normalized defomrations. At this point, you will have for each specimen and cycle Cnorm, and the normalized total and instantaneous deformations in both the horizontal and vertical directions for both faces of the sample.

Flow chart continuing from prevous flow chart. At this point, the cycle averaged trim deformation is calculated for each orientation {H, V} and deformation {I, T}. Then the resilient modulus correction factors are calculated. Next the instantaneous and total resilient modulus is calculated for each cycle. For each cycle, report the instantaneous Poisson's ratio, total Poisson's ratio, instantaneous resilient modulus, and total resilient modulus.

N/A

N/A

B2.3.2 Subroutine 1

Flow chart identifying the steps in Subroutine 1. For each specimen, find Pmax for cycle 1. Then find the number of data points prior to the maximum load value for cycle 1. Then determine if 150 or more points before Pmax for cycle 1. If so, data from cycles 1, 2, and 3 are used for analysis. If not, the ignore cycle 1 and cycles 2, 3, and 4 shall be considered as cycles 1, 2, and 3. Then calculate the contact load by averaging the range of points from 30 points before Pmax to 80 points before Pmax for cycle 1.

B2.3.3 Subroutine 2

Flow chart detailing the steps of Subroutine 2. For each specimen i and cycle j, find the maximum axial load for cycle j. Then determine the beginning and ending points for cycle j. Starting at Pmax sub i, j and moving to the left, the start point for cycle j is defined as tghe last data point which is greater than Pcontact sub i plus 6 lbs. Starting at Pmax sub i, j and moving to the right, the end point for cycle j is defined as the last data point which is less than Pcontact sub i plus 6 lbs. Next determine the cyclic load.

B2.3.4 Subroutine 3

For each orientation, specimen i, cycle j, and face k, determine the maximum deformation. From the deformation versus time trace, within the cycle start and end points determined in subroutine 2, find the maximum deformation. There will be 12 traces per test (3 specimens by 2 faces per specimen by 2 orientations per face). Two regression lines will need to be developed for each trace. First, determine the regression range. For regression line 1, starting at {H, V}max sub i, j, k select the 5th through 17th points to the right. For regression line 2, starting at the cycle j end point, select the 299 data points to the left and the first data point of cycle j + 1. Then perform a linear least squares regression of the selected data points.

Flow chart continuing from previous flow chart. After performing regression, find the instantaneous resilient deformation by finding the intersection of regression lines 1 and 2. Find the total resilient deformation by finding the deformation given by regression line 2 at the first point of cycle j+1.

B3. CREEP COMPLIANCE DATA ANALYSIS ALGORITHM

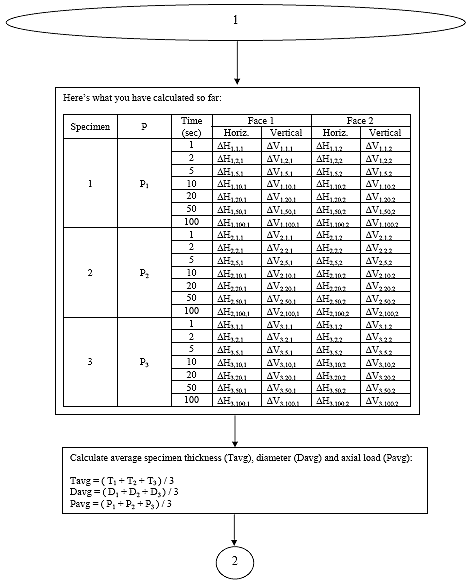
An outline of the creep compliance data analysis algorithm that is used in the "ITLTFHWA" software, and described in the report by Roque et al. is presented in section B3.2. The algorithm is described graphically in section B3.3.

B3.1 Subscript Convention

For the purpose of clarity, a subscript convention has been developed. The subscript 'i' represents the specimen number (i = 1, 2, or 3), the subscript 'j' represents the creep time (j = 1, 2, 5, 10, 20, 50, or 100), and the subscript 'k' represents the specimen face (k = 1 or 2). Thus a variable may have up to three subscripts of the following form: Xi,j,k.

B3.2 Analysis

A separate analysis must be performed for each of the three temperatures at which creep compliance data is collected.

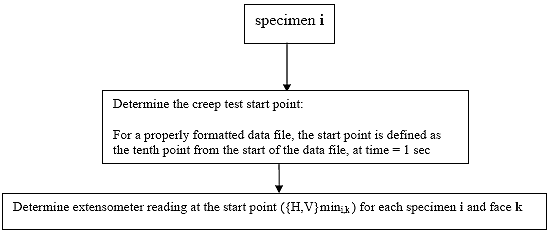
B3.2.1 Determine the creep test start point

The 10th data point in the file is always assumed to be the starting point of the test. It is essential that when the test is performed that exactly 10 data points are collected prior to the initial application of the creep load otherwise this analysis algorithm will produce erroneous results. Since the data sampling rate should be constant at 10 Hz, the creep load should be applied exactly 1 second after the data acquisition is initiated.

B3.2.2 Determine initial extensometer readings

Determine the extensometer reading ({H,V}mini,k) at the starting point of the creep test for each specimen i and face k. The starting point was defined in Section B3.2.1.

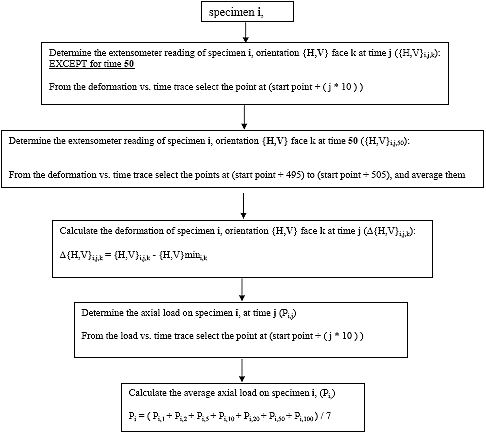
B3.2.3 Determine the extensometer reading for each creep time j

The Table B2 indicates the data point that corresponds to a certain creep time j for each face k of each specimen i.

Table B 2. Extensometer reading data points
Extensometer reading at time j Data Point
{H,V}i,1,k 20th point in data file
{H,V}i,2,k 30th point in data file
{H,V}i,5,k 60th point in data file
{H,V}i,10,k 110th point in data file
{H,V}i,20,k 210th point in data file
{H,V}i,50,k Average 505th point through 515th point (11 points total)
{H,V}i,100,k 1010th point in data file

For a 100-second creep test, the deformations at 50 seconds are used to calculate the Poisson's ratio for the experiment. To prevent a spike in the data from influencing the Poisson ratio value, the average of the 505th point through the 515th point (11 points total) is taken as the deformation at 50 seconds.

B3.2.4 Calculate deformations for each creep time j, face k, and orientation {H,V} of each specimen i.

Eq. B20 delta {H, V} sub i, j, k equals {H, V} sub i, j, k minus {H, V} min sub i, k

Where: D{H,V}i,j,k = the deformation for creep time j of face k of each specimen i, in.

{H,V}i,j,k = the extensometer reading for creep time i of face k of each specimen i, in.

{H,V}mini,k = the extensometer reading at the start of the creep test for each face k of each specimen i, in.

B3.2.5 Determine the axial load (Pi,j) for each creep time j of each specimen i.

Table B 3. Axial load data points
Axial load at time j Data Point
Pi,1 20th point in data file
Pi,2 30th point in data file
Pi,5 60th point in data file
Pi,10 110th point in data file
Pi,20 210th point in data file
Pi,50 510th point in data file
Pi,100 1010th point in data file

B3.2.6 Determine the average axial load (Pi) on specimen i

Eq. B21 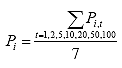P sub i equals the ratio of the sum over t equals 1, 2, 5, 10, 20, 50, 100 of P sub i, t over 7

where: Pi = the average axial load for specimen i, lbs.

Pi,t = the axial load for specimen i at time = t, lbs.

B3.2.7 Calculate the average specimen thickness (tavg), the average specimen diameter (davg), and the average axial load (Pavg).

Eq. B22 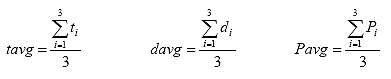tavg equals the ratio of the sum from i equals 1 to 3 of t sub i over 3; davg equals the ratio of the sum from i equals 1 to 3 of d sub i over 3; Pavg equals the ratio of the sum from i equals 1 to 3 of P sub i over 3

Where: tavg = the average specimen thickness, in.

davg = the average specimen diameter, in.

Pavg = the average axial load, lbs.

ti = the thickness of specimen i, in.

di = the diameter of specimen i, in.

Pi = the axial load for specimen i, lbs.

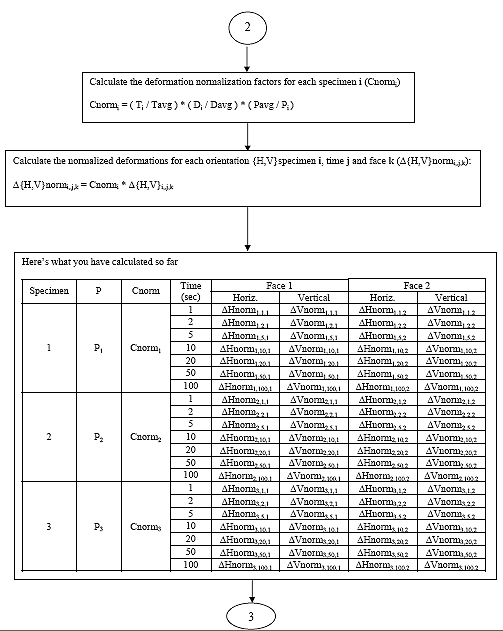
B3.2.8 Calculate the deformation normalization factor (Cnormi) for each specimen i.

Eq. B23 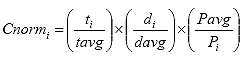Cnorm sub i equals the ratio of t sub i over tavg times the ratio of d sub i over davg times the ratio of Pavg over P sub i

Where: Cnormi = the deformation normalization factor for specimen i.

tavg = the average specimen thickness, inches.

davg = the average specimen diameter, inches.

Pavg = the average axial load, lbs.

ti = the thickness of specimen i, inches.

di = the diameter of specimen i, inches.

Pi = the axial load for specimen i, lbs.

B3.2.9 Calculate the normalized deformations (D{H,V}normi,j,k) for time j and face k of each specimen i.

Eq. B24 Pavg equals the ratio of the sum from i equals 1 to 3 of P sub i over 3

Where: D{H,V}normi,j,k = the normalized deformations for time j and face k of specimen i, inches.

D{H,V}i,j,k = the deformation for creep time j of face k of each specimen i, inches.

Cnormi = the deformation normalization factor for specimen i.

B3.2.10 Average deformation data sets

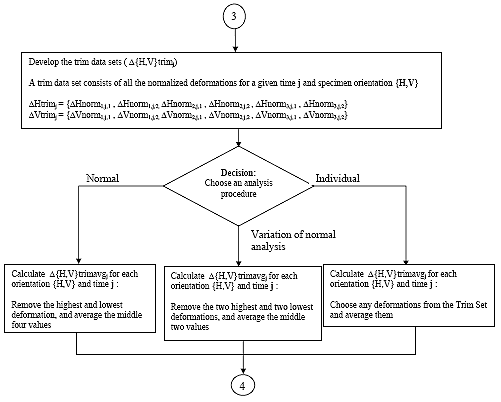
There are 14 "trim" data sets. A deformation data set consists of all the recoverable deformations calculated for a given orientation {H,V}, and time j. Average the deformation data sets by one of the following methods:

B3.2.10.1 Method 1: Normal Analysis

For each trim data set, remove the highest and lowest deformation and average the remaining four. This average shall be referred to as D{H,V}trimavgj for time j.

B3.2.10.2 Method 2: Variation of Normal Analysis

For each trim data set, remove the two highest and the two lowest deformations and average the remaining two. This average shall be referred to as D{H,V}trimavgj for time j.

B3.2.10.3 Method 3: Individual Analysis

For each trim data set, remove any deformations and average the remaining deformations. This average shall be referred to as D{H,V}trimavgj for time j.

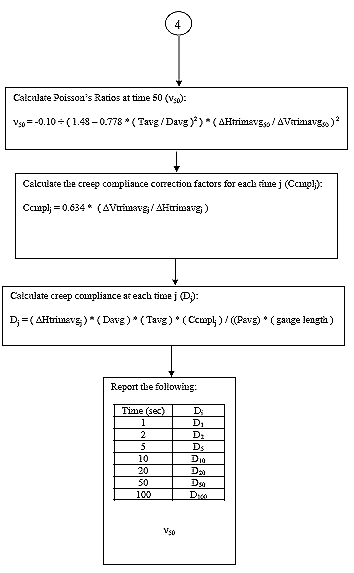
B3.2.11 Calculate the Poisson's Ratio at time = 50.

Eq. B25 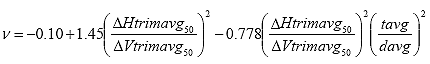nu equals -0.10 plus 1.45 times the square of the ratio of delta Htrimavg sub 50 over delta Vtrimavg sub 50 minus 0.778 times the square of the ratio of delta Htrimavg sub 50 over delta Vtrimavg sub 50 times the square of the ratio of tavg over davg

Where: ? = the Poisson's Ratio

DHtrimavg50 = the average horizontal trimmed deformation at time = 50, in.

DVtrimavg50 = the average vertical trimmed deformation at time = 50, in.

tavg = the average specimen thickness, in.

davg = the average specimen diameter, in.

B3.2.12 Calculate the creep compliance correction factor (Ccmply) for each time j.

Eq. B26 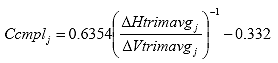Ccmpl sub j equals 0.6354 times the ratio to the power of -1 of delta Htrimavg sub j over delta Vtrimavg sub j minus 0.332

Where: Ccmplj = the creep compliance correction factor at time j.

DHtrimavgj = the average horizontal trimmed deformation at time j, in.

DVtrimavgj = the average vertical trimmed deformation at time j, in.

B3.2.13 Calculate the creep compliance for each time j.

Eq. B27 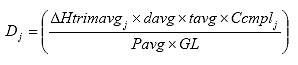D sub j equals the ratio of delta H trimavg sub j times davg times tavg times Ccmpl sub j over Pavg times GL

Where: Dj = the creep compliance at time j, 1/psi

DHtrimavgj = the average horizontal trimmed deformation at time j, in.

davg = the average specimen diameter, in.

tavg = the average specimen thickness, in.

Ccmplj = the creep compliance correction factor at time j.

Pavg = the average axial load, lbs.

GL = the extensometer gauge length (1 inch [25 mm] for a nominal 4-inch [102-mm] specimen diameter, 1.5 inches [38 mm] for a nominal 6-inch [152-mm] specimen diameter).

B3.3 Creep Compliance Data Analysis Flow Charts

B3.3.1 Main Procedure

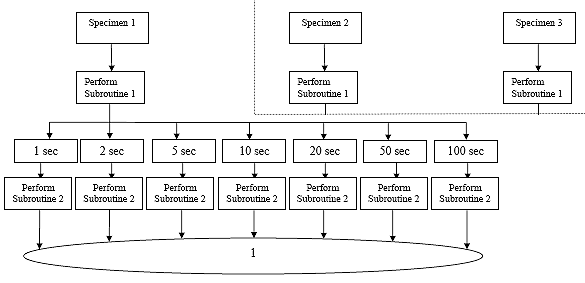
Flow chart describing the data analysis for creep compliance. For each of three specimens, the first step is to perform subroutine 1. Then for each of 7 time intervals (1 sec, 2 sec, 5 sec, 10 sec, 20 sec, 50 sec, and 100 sec) perform subroutine 2.

Flow chart continuation from the previous flow chart. After having performed subroutine 2, you have for each of three specimens, a load. And for each specimen at each of the 7 time intervals (1 sec, 2 sec, 5 sec, 10 sec, 20 sec, 50 sec, and 100 sec) you have a deformation in both the horizontal and vertical direction for each of the two faces of the specimen. From there, you calculate the average specimen thickness, diameter, and axial load.

Flow chart continuing from the flow chart on the previous page. At this point, calculate the deformation normalization factors for each specimen i. Then calculate the normalized deformations for each orientation (horizontal and vertical), specimen i, time j, and face k. You now have for each of the three specimens, a load level, Cnorm, and for each of the 7 time intervals, the normalized horizontal deformation and normalized vertical deformation for each face.

Flow chart continuing from the flow chart on the previous page. At this point, calculate the deformation normalization factors for each specimen i. Then calculate the normalized deformations for each orientation (horizontal and vertical), specimen i, time j, and face k. You now have for each of the three specimens, a load level, Cnorm, and for each of the 7 time intervals, the normalized horizontal deformation and normalized vertical deformation for each face.

Flow chart continuation from the previous flow chart. The next step is to calculate the Poisson's ratios at time 50. Then calcualte the creep compliance correction factors for each time j. Then calculate the creep compliance at each time j. For each of the seven time intervals report the creep compliance factor along with the Poisson's ratio at time 50.

B3.3.2 Subroutine 1

Flow chart describing subroutine 1. For each specimen i, determine the creep test start point. For a properly formatted data file, the start point is defined as the tenth point from the start of the data file at time of 1 sec. Then determine the extensometer reading at the start point for each specimen i and face k.

B3.3.3 Subroutine 2

Flow chart describing subroutine 2. For each specimen i, determine the extensometer reading of specimen i, orientation (horizontal, vertical), face k at time j except for time 50. From the deformation vs. time trace slect the point at start point plus j times 10. Then determine the extensometer reading of specimen i, orientation {H, K}, face k at time 50. From the deformation vs. time trace select the points at start point plus 495 to start point plus 505 and average them. Then calculate the deformation of specimen i, orientation {H, V}, face k at time j. Then determine the axial load on specimen i at time j. From the load vs. time trace select the point at start point plus j times 10. Then calculate the average axial load on specimen i.

B4. INDIRECT TENSILE STRENGTH DATA ANALYSIS ALGORITHIM

An outline of the indirect tensile strength algorithm that is used in the "ITLTFHWA" software, and described in the report by Roque et al. is presented in section B4.2. The algorithm is described graphically in section B4.3.

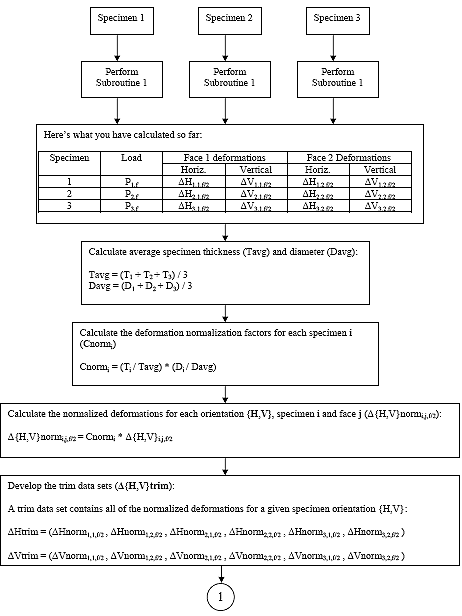
B4.1 Subscript Convention

For the purpose of clarity, a subscript convention has been developed. The subscript 'i' represents the specimen number (i = 1, 2 or 3), the subscript 'j' represents the specimen face (j =1 or 2) and the subscript 't' represents the time at which a value was measured. Thus a variable may have up to three subscripts of the following form: Xi,j,t.

B4.2 Analysis

B.4.2.1 Invert Load Values

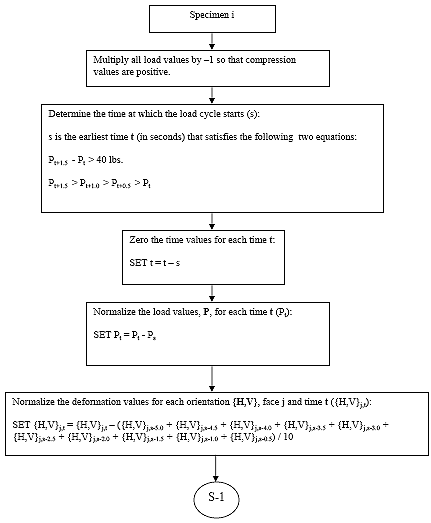
For each of the three specimens, multiply all load values by -1, so that compression values are positive.

B.4.2.2 Determine Cycle Start Time (tsi):

For specimen i, determine the time at which the load cycle starts. The load cycle start time is defined as the first time t that satisfies the following two requirements:

1) The load must continuously increase over the three data points subsequent to tsi, as shown below:

Eq. B28 P sub i, 1.5 plus ts sub i must be greater than P sub i, 1.0 plus ts sub i must be greater than P sub i, 0.5 plus ts sub i must be greater than P sub i, ts sub i

2) The load must increase by at least 40 lbs (18 kg) over the three data points subsequent to tsi, as shown below:

Eq. B29 P sub (t plus 1.5) minus P sub t must be greater than 40 lbs

B4.2.3 Zero the Time Values

For each specimen i, subtract tsi from each time value, so that the load cycle starts at t = 0.

B4.2.4 Zero the Load Values

For each specimen i, subtract the initial load value, Pi,0 from each load value, so that the load at the time the cycle starts is 0.

B4.2.5 Calculate the Deformation Zero Value ({H,V}si,j)

For each specimen i, face j, and orientation {H,V}, the deformation zero value is equal to the average of the 10 deformation values prior to the load cycle start, as shown below:

Eq. B30 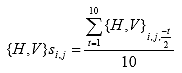{H, V}s sub i, j equals the ratio of the sum from t equals 1 to 10 of {H, V} sub i, j, (-t over 2) over 10

B4.2.6 Zero the Deformation Values

For each specimen i, face j, and orientation {H,V}, subtract {H,V}si,j from the respective deformation value.

B4.2.7 Determine the Failure Load (Pi,tfi)

B4.2.7.1 Determine tfi,j

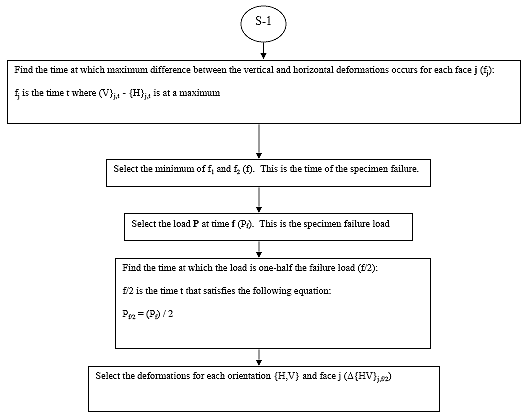
For each specimen i, and face j, determine the time where Vi,j,t - Hi,j,t is at a maximum (tfi,j).

B4.2.7.2 Determine Time of Specimen Failure (tfi)

For each specimen i, the time of specimen failure (tfi) is the minimum of tfi,1 and tfi,2.

B4.2.7.3 Determine the Failure Load (Pi,tfi)

For each specimen i, the failure load is the load P corresponding to time tfi.

B4.2.9 Determine the Deformations at Half the Failure Load (?{H,V}i,j)

B4.2.9.1 Determine the Time of Half Failure Load (thi)

For each specimen i, thi is the time that satisfies the following equation:

Eq. B31 P sub i, th sub j equals the ratio of P sub i, tf sub j over 2

B4.2.9.2 Determine Deformations at Time thi

For each specimen i, face j and orientation {H,V}, select the deformations at time thi. This value shall be referred to as ?{H,V}i,j.

B4.2.10 Calculate the Average Specimen Thickness and Diameter

Calculate the average specimen thickness (Tavg) and diameter (Davg) as shown below:

Eq. B32 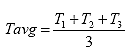Tavg equals the ratio of the sum of T sub 1, T sub 2, and T sub 3 over 3

Eq. B33 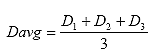delta {H,V}norm sub i, j equals Cnorm sub i times delta {H, V}norm sub i, j

B4.2.11 Calculate the Deformation Normalization Factors (Cnormi)

For each specimen i, calculate the deformation normalization factors as shown below:

Eq. B34 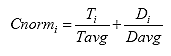Cnorm sub i equals the ratio of T sub i over Tavg plus the ratio of D sub i over Davg

B4.2.12 Calculate the Normalized Deformations (?{H,V}normi,j)

Eq. B35 delta {H,V}norm sub i, j equals Cnorm sub i times delta {H, V}norm sub i, j

B4.2.13 Average deformation data sets

There are 2 "trim" data sets. A deformation data set consists of all the normalized deformations calculated for a given orientation {H,V}. Average the deformation data sets by one of the following methods:

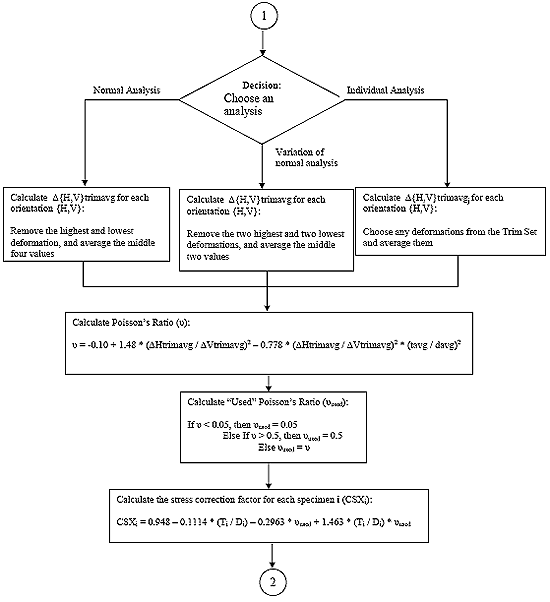
B4.2.13.1 Method 1: Normal Analysis

For each trim data set, remove the highest and lowest deformation and average the remaining four. This average shall be referred to as D{H,V}trimavg.

B4.2.13.2 Method 2: Variation of Normal Analysis

For each trim data set, remove the two highest and the two lowest deformations and average the remaining two. This average shall be referred to as D{H,V}trimavg.

B4.2.13.3 Method 3: Individual Analysis

For each trim data set, remove any deformations and average the remaining deformations. This average shall be referred to as D{H,V}trimavg.

B4.2.14 Calculate Poisson's Ratio (?)

Eq. B36 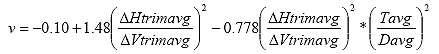nu equals -0.10 plus 1.48 times the square of the ratio of delta Htrimavg over delta Vtrimavg minus 0.778 times the square of the ratio of delta Htrimavg over delta Vtrimavg times the square of the ratio of Tavg over Davg

B4.2.15 Calculate "Used" Poisson's Ratio (?used)

B4.2.15.1 Case 1: ? > 0.5

If the ? calculated in step B4.2.14 is greater than 0.5, then ? used = 0.5.

B4.2.15.2 Case 2: ? < 0.05

If the ? calculated in step B4.2.14 is less than 0.05, then ? used = 0.05.

B4.2.15.3 Case 3: 0.05 < ? < 0.5

If the ? calculated in step B4.2.14 is between 0.05 and 0.5, then ? used = ?.

B4.2.16 Calculate the Stress Correction Factors

For each specimen i, calculate the stress correction factors as follows:

Eq. B37 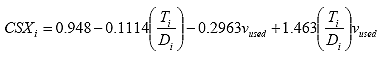CSX sub i equals 0.948 minus 0.1114 times the ratio of T sub i over D sub i minus 0.2963 times nu sub used plus 1.463 times the ratio of T sub i over D sub i times nu sub used

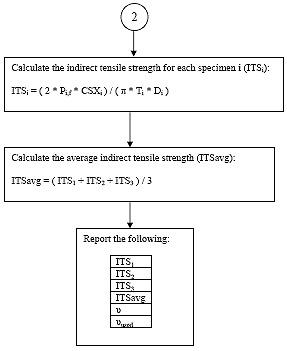
B4.2.17 Calculate the Indirect Tensile Strength

For each specimen i, calculate the indirect tensile strength as follows:

Eq. B38 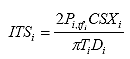ITS sub i equals 2 times P sub i, tf sub j times CSX sub i divided by the result of pi times T sub i times D sub i

B4.2.18 Calculate the Average Indirect Tensile Strength

Eq. B39 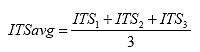ITSavg equals the ratio of the sum of ITS sub 1, ITS sub 2, ITS sub 3 over 3

B4.3 Indirect Tensile Strength Analysis Flowcharts

B4.3.1 Main Procedure

Flow chart describing the analysis procedure for indirect tensile strength analysis. For each of three specimens, perform subroutine 1. After subroutine 1, you will have for each of the three specimens, P sub f, and the horizontal and vertical deformations at f/2 for each face. Then calculate the average specimen thickness and average diameter. Then calculate the deformation normalization factors for each specimen i. Next, calculate the normalized deformations for each orientation {H, V}, specimen i, and face j. The ndevelop the trim data sets where a trim data set contains all of the normalized deformations for a given specimen orientation.

Flow chart continuation from flow chart on the previous page. The next step is to choose an analysis - normal analysis, variation of normal analysis, or individual analysis. For normal analysis, calculate the average deformation for each orientation by removing the highest and lowest deformation and averaging the middle four values. For the variation of normal analysis, calculate the average deformation by removing the two highest and two lowest deformations and averaging the middle two values. For the individual analysis, calculate the average deformation by choosing any deformations from the trim set and averaging them. The next step regardless of the averaging procedure is to calculate the Poisson's ratio. The calculate the "Used" Poisson's ratio. If nu is less than 0.05 then nu sub used is 0.05. Else, if nu is greater than 0.5 then nu sub used is 0.5. Else, nu sub used is nu. Then, calculate the stress correction factor for each specimen i.

Flow chart continuation from the previous page. The next step is to calculate the indirect tensile strength for each specimen i. Then calculate the average indirect tensile strength. Report the indirect tensile strength for each of the three specimens, the average indirect tensile strength, nu, and nu sub used.

B.4.3.2 Subroutine 1

Flow chart describing the procedure from subroutine 1. For each specimen i, multiply all load values by -1 so that compression values are positive. Then determine the time at which the load cycle starts. s is the earliest time t, in seconds, that satisfies the follow two criteria: P sub t plus 1.5 minus P sub t is greater than 40 lbs and P sub t plus 1.5 is greater than P sub t plus 1.0 is greater than P sub t plus0 0.5 is greater than P sub t. The next step is to zero the time values for each time t by setting t equal to t minus s. Then normalized the load values, P, for each time t. The next step is to normalize the deformation values for each orientation {H, V}, face j, and time t.

Continuation of the Flow chart describing the procedure from subroutine 1. For each specimen i, multiply all load values by -1 so that compression values are positive. Then determine the time at which the load cycle starts. s is the earliest time t, in seconds, that satisfies the follow two criteria: P sub t plus 1.5 minus P sub t is greater than 40 lbs and P sub t plus 1.5 is greater than P sub t plus 1.0 is greater than P sub t plus0 0.5 is greater than P sub t. The next step is to zero the time values for each time t by setting t equal to t minus s. Then normalized the load values, P, for each time t. The next step is to normalize the deformation values for each orientation {H, V}, face j, and time t.

LTPP LABORATORY MATERIAL HANDLING AND TESTING
LABORATORY MATERIAL TEST DATA
CREEP COMPLIANCE, RESILIENT MODULUS AND INDIRECT TENSILE STRENGTH
LAB DATA SHEET T07 - SAMPLE SUMMARY INFORMATION

ASPHALT CONCRETE LAYER (ASPHALTIC CONCRETE PROPERTIES)

LTPP TEST DESIGNATION AC07/LTPP PROTOCOL P07

LABORATORY PERFORMING TEST:___________________________________________________________

LABORATORY IDENTIFICATION CODE: ___ ___ ___ ___

1. STATE CODE: ___ ___ 2. SHRP ID: ___ ___ ___ ___
3. LAYER NO: ___ 4. FIELD SET: ___
DATA ITEM SPECIMEN 1 SPECIMEN 2 SPECIMEN 3
5. TEST NO ___ ___ ___
6. SAMPLE AREA (SA-) ___ ___ ___ ___ ___ ___
7. LOCATION NO __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __
8. LTPP SAMPLE NO __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __ __
9. AVG. THICKNESS (mm) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
10. AVG. DIAMETER (mm) ___ ___ ___ . ___ ___ ___ ___ . ___ ___ ___ ___ . ___
11. BULK SPECIFIC GRAVITY ___ . ___ ___ ___ ___ . ___ ___ ___ ___ . ___ ___ ___
12. COMMENT 1 ___ ___ ___ ___ ___ ___
13. COMMENT 2 ___ ___ ___ ___ ___ ___
14. COMMENT 3 ___ ___ ___ ___ ___ ___
15. Other Comments      
1. STATE CODE: ___ ___ 2. SHRP ID: ___ ___ ___ ___
3. LAYER NO: ___ 4. FIELD SET: ___
DATA ITEM SPECIMEN 1 SPECIMEN 2 SPECIMEN 3
RESILIENT MODULUS TEST
16. DATA FILENAME, TEST 1 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
17. TEST 1 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
18. DATA FILENAME, TEST 2 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
19. TEST 2 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
20. DATA FILENAME, TEST 3 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
21. TEST 3 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
22. ANALYSIS FILENAME _ _ _ _ _ _ _ _ . MRO
CREEP COMPLIANCE TEST
23. DATA FILENAME, TEST 1 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
24. TEST 1 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
25. DATA FILENAME, TEST 2 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
26. TEST 2 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
27. DATA FILENAME, TEST 3 _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
28. TEST 3 TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
29. ANALYSIS FILENAME _ _ _ _ _ _ _ _ . OUT
INDIRECT TENSILE STRENGTH TEST
30. DATA FILENAME _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT _ _ _ _ _ _ _ _ . DAT
31. TEST TEMP. (°C) ___ ___ . ___ ___ ___ . ___ ___ ___ . ___
32. ".OUT" FILENAME _ _ _ _ _ _ _ _ . OUT
33. ".STR" FILENAME _ _ _ _ _ _ _ _ . STR
34. ".FAM" FILENAME _ _ _ _ _ _ _ _ . FAM
GENERAL REMARKS:___________________________________________________________________________
SUBMITTED BY, DATECHECKED AND APPROVED, DATE
____________________________________________________________
LABORATORY CHIEF
Affiliation______________________		Affiliation______________________

 

<< PreviousContentsNext >>

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse
U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101